2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 江西省数字国土重点实验室, 江西 南昌 330013
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, Nanchang 330013, China
一般地,在测绘数据处理中,通常假设观测值只包含偶然误差,不含有系统误差和粗差。但是由于仪器、观测条件、气候等因素的影响,观测值中不可避免地会包含系统误差,而且有时所选用的函数模型[1-3]会包含着模型误差。当系统误差部分是偶然误差的1/3或更小时,则可将系统误差的影响忽略不计[4],反之,则需要考虑系统误差,若处理过程中不削弱或消除系统误差的影响,则会得到不可靠的参数结果,甚至是错误的结果[5]。如何解决此类问题已是测绘数据处理研究的问题之一,统计学界在20世纪80年代提出的半参数回归分析模型为解决该问题提供了发展方向。针对半参数模型,从理论到应用方面,已有了较多的研究成果,早在1978年,文献[6]将最小二乘配置理论应用到地球重力场研究中,且在后来文献[7]发现最小二乘配置是半参数模型的一种特殊形式;在GPS数据处理方面,文献[1]将半参数模型引入到GPS中基线解算存在系统误差的问题中,并取得了较好的效果。随后文献[8-13]将半参数模型引入到测绘的数据处理当中,并对半参数平差模型的估计方法做了进一步扩展,极大地推动了半参数模型在测绘领域中的应用发展。
在不考虑系数矩阵误差时,上述半参数模型即是基于最小二乘进行求解的,但是在很多情况下,系数矩阵也同样含有偶然误差,因此,文献[14]提出能兼顾观测向量误差和系数矩阵误差的总体最小二乘法(total least squares,TLS)。自总体最小二乘的提出,无论是其估计理论[15-18],还是其应用方面[19-22]关于TLS的研究成果十分丰富。针对系数矩阵存在随机元素和非随机元素以及呈现结构化特征的情况,文献[23]把errors-in-variables(EIV)模型转化为Partial EIV模型,推导出基于Partial EIV模型的总体最小二乘方法。文献[24]中指出Partial EIV模型较EIV模型的几个优势有:①Partial EIV模型是EIV模型更加一般的表达形式,包括了一般情况下加权总体最小二乘算法需要特殊处理的各种情况;②Partial EIV模型提取了系数矩阵中的不同的随机元素,因此其误差改正估计量个数减少,相应地提高了计算效率;③模型算法的简单形式便于后续中估值的精度评定工作。因此,文献[25-29]针对Partial EIV模型进行进一步的研究与运用。但是,目前已有文献中总体最小二乘方法并没有考虑观测数据存在系统误差的问题。显然,当系统误差存在时会使得解算的参数结果及其精度受到较大影响;因此,研究总体最小二乘解决系统误差的方法同样是非常必要的。本文在Partial EIV模型的基础上,给观测值增加非参数部分(系统误差),从而构建Partial EIV半参数模型,结合补偿最小二乘准则,对该准则进行相应的变化得到补偿总体最小二乘准则,推导基于Partial EIV半参数模型的系统误差处理方法,以削弱系统误差对参数估计值的影响。
1 Partial EIV半参数模型的求解 1.1 Partial EIV半参数模型EIV模型表达式为[30]:
函数模型
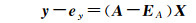 (1)
(1)
随机模型
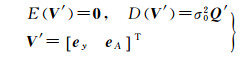 (2)
(2)
式中,y∈Rn×1表示观测向量;ey表示观测向量y的随机误差;A∈Rn×m表示系数矩阵;EA代表系数矩阵A所包含的随机误差;X∈Rm×1表示待估的未知参数;eA=vec(EA)是将EA按列向量化后得到的nm×1向量;σ02表示先验单位权方差;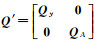
考虑到观测向量和系数矩阵中同时含有系统误差的情况,分别给系数矩阵和观测向量中加入SA和Sy,得到式(3)所示的函数模型
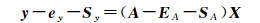 (3)
(3)
但是,在实际问题中,系数矩阵A中存在随机元素和非随机元素以及呈现结构化特征的情况,故文献[23]对A中的元素作适当的提取变换,从而将EIV模型改写为Partial EIV模型如下
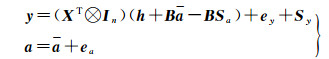 (4)
(4)
将式(4)改写为如下形式
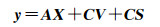 (5)
(5)
式中,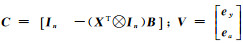
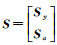
随机模型
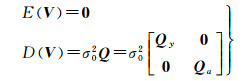 (6)
(6)
式中,a是系数矩阵A中不同元素组成的t×1列向量;a为其真值;ea表示为误差向量,相应的Sa为矩阵SA中的不同元素组成的t×1列向量;h和B分别是由vec(A)构造的nm×1列向量和nm×t的固定矩阵;In表示n×n的单位矩阵。
1.2 Partial EIV半参数模型的求解补偿最小二乘方法[5]是用来估计非参数回归模型的,相应的Partial EIV半参数模型的准则函数表达式为
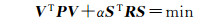 (7)
(7)
式中,VTPV表示观测值与估计值之间残差拟合部分;STRS表示对向量S的某种度量;R为一个适当给定的正定矩阵;α为平衡VTPV和STRS的因子,称为平滑因子。
按求条件极值的拉格朗日乘数法,设拉格朗日乘子K为n×1的列向量,构造函数
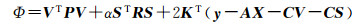 (8)
(8)
分别对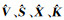
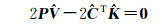 (9)
(9)
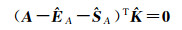 (10)
(10)
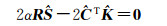 (11)
(11)
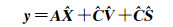 (12)
(12)
由式(9)得
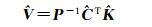 (13)
(13)
将式(13)代入式(12)得
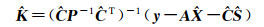 (14)
(14)
将式(14)代入式(10)得
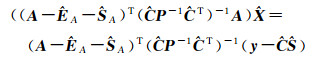 (15)
(15)
则由式(15)可得
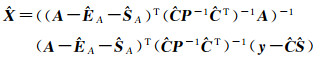 (16)
(16)
令Â=A-ÊA-ŜA,M=ĈP-1ĈT,则式(16)可化为
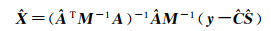 (17)
(17)
在式(15)两边同时加上(A-ÊA-ŜA)T(ĈP-1ĈT)-1(-ÊA-ŜA)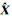
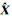
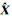
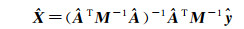 (18)
(18)
将式(14)代入式(11)得
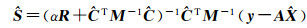 (19)
(19)
在上述公式求解中,需要同时考虑到正则化矩阵R的选取及平滑因子α的确定。
1.3 正则化矩阵R的选取 1.3.1 时间序列法时间序列法[31]是将观测值看成一个时间序列,因为信号是随时间连续变化的,因此认为相邻时刻的信号变化不是很大,且当信号是非随机量时,根据这些特点来构造正则化矩阵
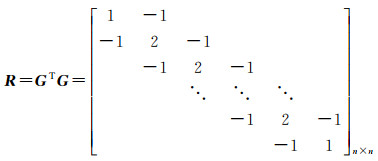 (20)
(20)
式中,
距离法[31]可以选取某种合适的函数,如某种距离函数来度量矩阵R
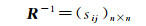 (21)
(21)
式中sij表示ti与tj之间某种距离。如取sij=|tj-ti|,若t表示平面坐标(x, y),则取欧氏距离
本文主要通过L曲线法[32]来确定平滑因子,L曲线法的基本原理:对于不同的平滑因子α可以得到以α当作自变量构造的信号范数和噪声范数
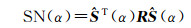 (22)
(22)
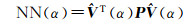 (23)
(23)
通过得到不同点(SN(α), NN(α)),然后将这些点进行拟合,就能够得到一条光滑的曲线,这条曲线形似字母L,通过这个“L”来定平滑因子α的方法就称之为L曲线法。平滑因子的确定可以通过两种方法[33]:(1)曲线上的点离原点距离最小时对应的值,即(SN(α))2+(NN(α))2=min;(2)曲线上曲率最大的点对应的值。其中最大曲率法的相应推导公式如下。
将式(4)化为
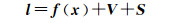 (24)
(24)
式中,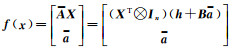
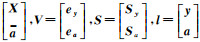
将f(x)在近似值x0处展开至一次项
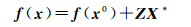 (25)
(25)
式中,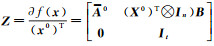
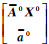
将式(25)代入式(24),并令L=l-f(x0),得到L=ZX*+V+S。
按求条件极值的拉格朗日乘数法,设拉格朗日乘子k为(n+t)×1的列向量,构造函数
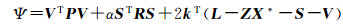 (26)
(26)
分别对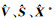
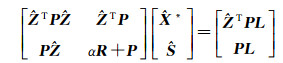 (27)
(27)
将式(27)变为(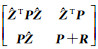
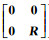
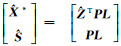
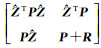
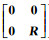
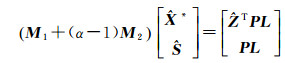 (28)
(28)
式(28)中M1为对称正定的矩阵,故存在矩阵W使得式(29)—式(30)成立
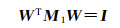 (29)
(29)
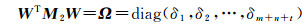 (30)
(30)
由式(29)、式(30)可得
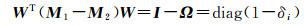 (31)
(31)
其中0≤δi≤1,i=1, 2, …, m+n+t。
令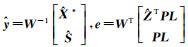
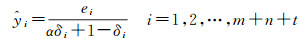 (32)
(32)
因此根据上式可得
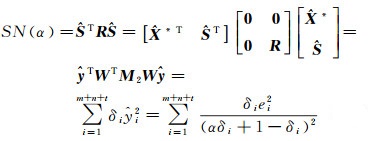 (33)
(33)
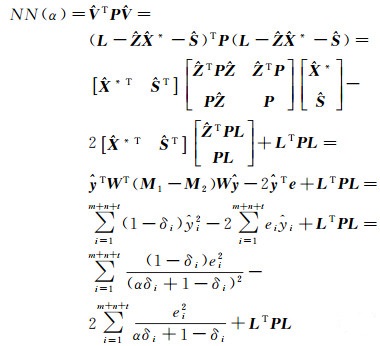 (34)
(34)
式(33)、式(34)分别对α求导得
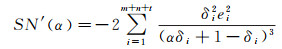 (35)
(35)
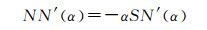 (36)
(36)
由式(36)可得到NN″(α)=-SN′(α)-αSN″(α),故L曲线的曲率为
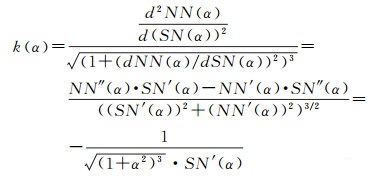 (37)
(37)
本文具体的迭代算法流程如下:
(1) 给定平滑因子α一定的区间,并且按照一定的步长取值;
(2) 初值: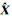
(3) 更新Ci(α)=[In-(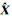
(4) 更新矩阵Âi+1(α)=A-ÊA-ŜA,通过式(18)计算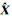
(5) 重复步骤(3)和(4),直到满足||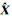
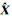
(6) 通过L曲线法确定平滑因子α,则该平滑因子所对应的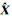
在算例中采用以下4种方案进行解算:
方案1:不含系统误差时运用文献[25]的算法解算;
方案2:含系统误差时运用文献[25]的算法解算;
方案3:含系统误差时运用本文的算法解算,其中平滑因子采用L曲线法的最短距离确定;
方案4:含系统误差时运用本文的算法解算,其中平滑因子采用L曲线法的最大曲率确定。
2.1 算例1假设有线性模型y=AX,X=[2 3]T,A=(aij)100×2,其中ai1=i/20,ai2=(i/20)2,系统误差为S=[s1s2…s100]T,si=2sin(ti),ti=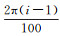
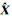
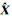
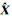
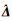
| 参数估计 | 真值 | 方案1 | 方案2 | 方案3 | 方案4 |
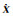 | 2 | 2.047 1 | 3.192 9 | 1.672 3 | — |
| 3 | 2.985 4 | 2.637 2 | 3.002 0 | — | |
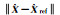 | 0 | 0.049 3 | 1.246 8 | 0.327 7 | — |
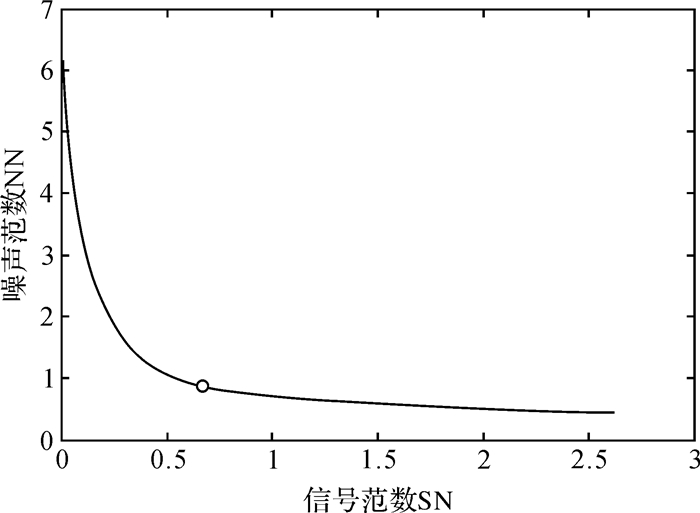
|
| 图 1 算例1中确定平滑因子的L曲线 Fig. 1 The L-curve used to determine the smoothing factor in the first example |
| 二范数值 | 方案1 | 方案2 | 方案3 | 方案4 |
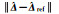 | 1.109 2 | 1.358 7 | 1.094 7 | — |
| ||ê-êref|| | 2.333 4 | 3.425 1 | 2.226 5 | — |
2.2 算例2
平面坐标转换模型为[34]
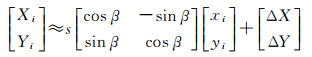 (38)
(38)
式中,s为尺度因子;β为旋转角度参数;ΔX、ΔY为平移参数;(Xi, Yi)、(xi, yi)分别为目标坐标系和原始坐标系对应的坐标。
将式(38)展开,并令a=scos β, b=ssin β,则可以转化为如下形式
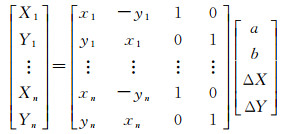 (39)
(39)
根据文献[13]的模拟方法,首先给定原坐标系下的真值,起始值、步长和终止值分别为-2、0.5、2;参数真值分别为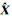
分别给原坐标系和目标坐标系模拟加入的系统误差如下
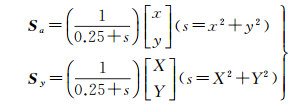 (40)
(40)
取正则化矩阵R
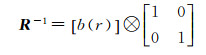 (41)
(41)
取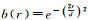
在算例中,若没有特别说明,则默认为正则化矩阵通过式(41)确定;在方案3中使用以上两种确定正则化矩阵方法分别进行计算,方案3中采用式(41)的称为方案3(1),采用式(20)的称为方案3(2),分别通过方案1、方案2、方案3、方案4求解参数,各方案求得的参数估值如表 3所示,其中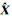
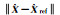
| 参数估计 | 真值 | 方案1 | 方案2 | 方案3(1) | 方案3(2) | 方案4 |
| â | 0.500 | 0.506 993 38 | 0.394 372 32 | 0.621 856 10 | 0.408 262 62 | 0.400 852 37 |
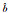 | -0.866 | -0.860 444 39 | -0.671 471 26 | -1.082 948 15 | -0.684 901 31 | -0.684 422 94 |
 | 10 | 9.989 993 63 | 10.039 307 95 | 9.940 822 28 | 10.038 546 95 | 10.047 196 45 |
| ΔŶ | -10 | -9.999 394 49 | -10.046 750 53 | -9.919 840 41 | -10.046 602 91 | -10.038 140 91 |
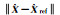 | 0 | 0.013 436 86 | 0.229 650 28 | 0.215 327 09 | 0.211 847 55 | 0.215 619 89 |
|
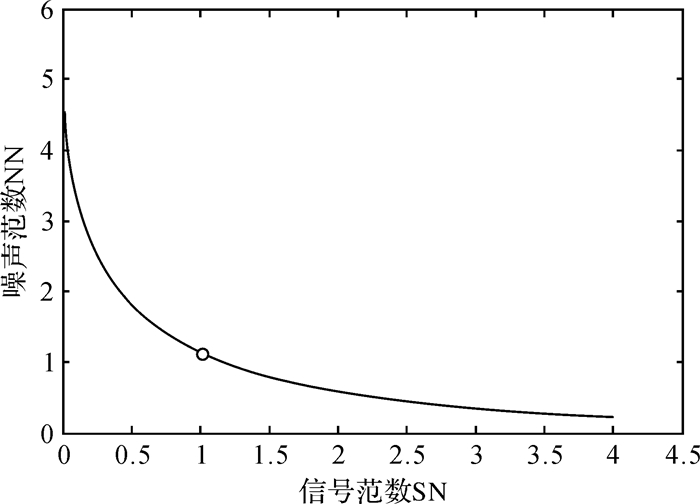
| 图 2 算例2中确定平滑因子的L曲线 Fig. 2 The L-curve used to determine the smoothing factor in the second example |
同时在该算例中考虑加入与式(40)不同系统误差的情况,分别按照如下模拟的系统误差加入到原始坐标系和目标坐标系中
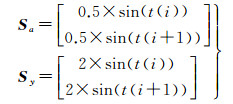 (42)
(42)
式中,t(i)=2×π×(i-1)/81,i=1, 2, …, 81。
正则化矩阵仍采用式(41)确定,分别采用方案1、方案2、方案3、方案4求解参数,各方案求得的参数估值如表 4所示,表中各符号表达式含义同上。
| 参数估计 | 真值 | 方案1 | 方案2 | 方案3 | 方案4 |
| â | 0.500 | 0.506 993 38 | 0.908 932 95 | 1.622 456 14 | 1.040 813 97 |
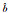 | -0.866 | -0.860 444 39 | -1.497 101 17 | -2.801 645 32 | -1.749 496 63 |
 | 10 | 9.989 993 63 | 9.967 980 57 | 10.006 657 63 | 9.975 649 70 |
| ΔŶ | -10 | -9.999 394 49 | -9.991 017 15 | -9.930 831 97 | -9.973 264 22 |
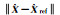 | 0 | 0.013 436 86 | 0.752 720 88 | 2.238 606 88 | 1.036 488 74 |
2.3 算例3
进行一直线拟合的模拟算例,设直线模型为y=ax+b, 其中a=2,b=1.5,自变量x坐标真值通过matlab中randperm函数生成0到20的10个数据,并相应的计算其对应的因变量y的值,模拟的真值及其相应的权列于表 5中。给真值加入单位权中误差为0.1且服从正态分布的随机误差,并且同时按照算例2中式(40)方式给其加入系统误差,从而得到模拟值。
| 点号 | x | px | y | py | 点号 | x | px | y | py |
| 1 | 3 | 50 | 7.5 | 10 | 6 | 7 | 30 | 15.5 | 50 |
| 2 | 20 | 70 | 41.5 | 50 | 7 | 1 | 69 | 3.5 | 50 |
| 3 | 10 | 20 | 21.5 | 30 | 8 | 16 | 70 | 33.5 | 70 |
| 4 | 15 | 40 | 31.5 | 10 | 9 | 9 | 45 | 19.5 | 80 |
| 5 | 8 | 55 | 17.5 | 40 | 10 | 14 | 88 | 29.5 | 65 |
同算例2,若没有特别说明,则默认为正则化矩阵通过式(41)确定;方案3中采用式(41)确定正则化矩阵的称为方案3(1),采用式(20)确定正则化矩阵的称为方案3(2),通过方案1、方案2、方案3、方案4求解参数,求得的参数估值见表 6,其中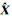
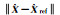
| 参数估计 | 真值 | 方案1 | 方案2 | 方案3(1) | 方案3(2) | 方案4 |
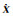 | 2 | 1.999 500 64 | 1.994 673 89 | 1.995 588 10 | 1.996 880 50 | 1.995 672 91 |
| 1.5 | 1.504 083 32 | 1.567 981 19 | 1.552 099 62 | 1.535 905 66 | 1.550 714 67 | |
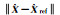 | 0 | 0.004 113 74 | 0.068 189 51 | 0.052 286 09 | 0.036 040 91 | 0.050 898 93 |
|
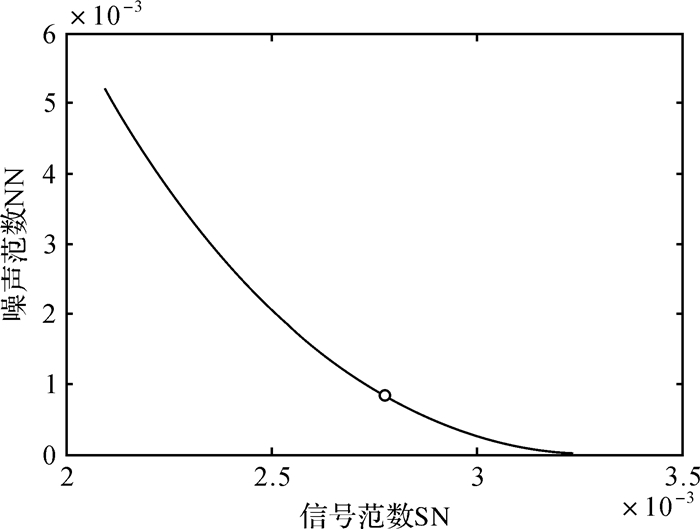
| 图 3 算例3中确定平滑因子的L曲线 Fig. 3 The L-Curve used to determine the smoothing factor in the third example |
同样在该算例中考虑加入与式(40)不同系统误差的情况,分别按照如下模拟的系统误差加入到x和y中。
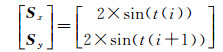 (43)
(43)
式中,t(i)=2×π×(i-1)/10,i=1, 2, …, 10。
正则化矩阵仍然采用式(41)确定,分别采用方案1、方案2、方案3、方案4求解参数,各方案求得的参数估值见表 7,表中各符号表达式含义同上。
| 参数估计 | 真值 | 方案1 | 方案2 | 方案3 | 方案4 |
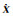 | 2 | 1.999 500 64 | 1.969 036 73 | 1.949 991 74 | 1.948 302 75 |
| 1.5 | 1.504 083 32 | 1.885 443 10 | 1.967 408 09 | 1.968 457 72 | |
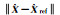 | 0 | 0.004 113 74 | 0.386 684 77 | 0.470 075 68 | 0.471 301 65 |
2.4 算例分析
从以上算例的表 1、表 3及表 6中的结果可以看出,由于系统误差的存在,导致Partial EIV模型计算得到的结果受到影响,与真值的偏差比较大,因此选择合理有效的方法对系统误差进行处理就显得很有必要。
从表 1中各方案参数估值与真值之间的二范数可知,方案1的二范数最小,其效果最优,这是因为其观测值中不含有系统误差,所以结果较好;但是给观测值加入系统误差后,参数估计的结果受影响较大,故方案2的结果相比于方案3(本文方法)而言较差,偏离真值较大,然而方案3能够在一定程度上抵御系统误差对参数结果的影响,能够得到相对可靠的参数解。此时方案4(基于本文的最大曲率法来确定平滑因子)在算例1中并不适用,因为该算例只考虑到观测向量含有系统误差的情况,而基于最大曲率确定平滑因子的推导是顾及观测向量和系数矩阵同时含有系统误差的情况。同时从表 2也可看出,系统误差对于观测向量残差及系数矩阵残差均有一定的影响,但是本文方法能够部分的削弱系统误差的影响。
从表 3和表 6的结果看来,通过两种方法确定平滑因子α的各方案得到的结果差别不大,效果相当;针对选取不同的正则化矩阵情况,算例2及3中分别进行了相应的试验,从表 3及表 6中方案3二者结果看来,使用方案3(2)(正则化矩阵选用时间序列法)解算时,得到结果更好,说明该方法能够更好地抵消系统误差的影响,因此建议坐标转换及直线拟合的参数解算中正则化矩阵可选取时间序列法。
考虑在算例2与3中加入不同系统误差的情况,若按照观测值为时间序列,且假设相邻时刻的系统误差变化相差不是很大时加入,如式(42)与(43),从表 4及表 7中方案3与方案4的结果看来,通过本文方法并不能够削弱系统误差的影响,这说明此时加入的系统误差并不合理,因此针对不同的观测数据,其模拟加入的系统误差也不一样。
3 结论若观测值中含有系统误差,则会对Partial EIV模型的总体最小二乘参数估计值产生影响,因此提出相应的解决方法就显得很有必要。本文给出了Partial EIV半参数模型,根据补偿最小二乘准则给出了相应的补偿总体最小二乘准则条件下的公式推导过程,并给出了相应的迭代算法,以尝试通过该方法削弱系统误差对未知参数估值的影响,通过对文中算例中的各方案比较分析得出,本文给出的算法在一定程度上能够削弱系统误差对参数估值的影响,这说明基于Partial EIV半参数模型的系统误差处理方法是有效可行的。
文中平滑因子的确定采用了L曲线法中的最短距离法和最大曲率法,从算例结果看二者效果相当,然而最大曲率法的公式推导相对来说比较复杂,且在本文中若只顾及观测向量含有系统误差时,最大曲率法并不适用,因此建议在基于Partial EIV半参数模型求解系统误差处理时,通过最短距离法来确定其中的平滑因子。对于正则化矩阵的选取问题,建议在坐标转换及直线拟合的参数解算中可考虑选取时间序列法,但是较多的是根据系统误差的特性进行选取,因为此时的协方差矩阵是可求的,这可以用来描述观测数据点之间的相关程度的大小。与此同时分别在算例2与3中加入与算例1相同特性的系统误差,然而通过文中结果表明,此时并不能够削弱系统误差的影响,反而结果更差,这说明加入的系统误差并不合理,因此对于不同的观测数据,其系统误差的特性也不尽相同。
因此,本文建议在解算过程中仍需顾及系统误差的特性及正则化矩阵和平滑因子的选取。
| [1] | JIA M. Mitigation of Systematic Errors of GPS Positioning Using Vector Semiparametric Models[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the US Institute of Navigation. Salt Lake City: 2000: 1938-1947. |
| [2] |
杨元喜, 张双成.
导航解算中的系统误差及其协方差矩阵拟合[J]. 测绘学报, 2004, 33(3): 189–194.
YANG Yuanxi, ZHANG Shuangcheng. Fittings of Systematic Errors and Covariance Matrices in Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 189–194. DOI:10.3321/j.issn:1001-1595.2004.03.001 |
| [3] |
康双双. 半参数模型在航空重力测线网平差中的应用研究[D]. 武汉: 中国地质大学, 2012. KANG Shuangshuang. The Application of Semiparametric Model in Airline Network Adjustment of Airborne Gravimetry[D]. Wuhan: China University of Geosciences, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10491-1012446573.htm |
| [4] |
武汉大学测绘学院测量平差学科组.
误差理论与测量平差基础[M]. 2版. 武汉: 武汉大学出版社, 2009.
Surveying Adjustment Group of School of Geodesy and Geomatics. Error Theory and Foundation of Surveying Adjustment[M]. 2ed ed. Wuhan: Wuhan University Press, 2009. |
| [5] |
孙海燕, 吴云.
半参数回归与模型精化[J]. 武汉大学学报(信息科学版), 2002, 27(2): 172–174, 207.
SUN Haiyan, WU Yun. Semiparametric Regression and Model Refining[J]. Geomatics and Information Science of Wuhan University, 2002, 27(2): 172–174, 207. |
| [6] | MORITZ H. Least-squares Collocation[J]. Reviews of Geophysics, 1978, 16(3): 421–430. DOI:10.1029/RG016i003p00421 |
| [7] |
王振杰, 欧吉坤.
半参数模型与拟合推估模型的比较[J]. 测绘通报, 2004(9): 4–6.
WANG Zhenjie, OU Jikun. Comparisons between Collocation Model and Semi-parametric Model[J]. Bulletin of Surveying and Mapping, 2004(9): 4–6. DOI:10.3969/j.issn.0494-0911.2004.09.002 |
| [8] |
潘雄, 孙海燕.
半参数模型约束条件下估计量的统计诊断[J]. 湖北民族学院学报(自然科学版), 2003, 21(3): 1–3.
PAN Xiong, SUN Haiyan. Statistical Diagnosis of the Smoothing Parameter for Semi-parameter Model on Constrained Condition[J]. Journal of Hubei Institute for Nationalities (Natural Science Edition), 2003, 21(3): 1–3. |
| [9] |
潘雄. 半参数模型的估计理论及其应用[D]. 武汉: 武汉大学, 2005. PAN Xiong. The Estimation Theory and Application Research in Semi-parametric Model[D]. Wuhan: Wuhan University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031323.htm |
| [10] |
丁士俊, 陶本藻.
自然样条半参数模型与系统误差估计[J]. 武汉大学学报(信息科学版), 2004, 29(11): 964–967.
DING Shijun, TAO Benzao. Semiparametric Regression Model with Natural Spline and Systematic Error Estimation[J]. Geomatics and Information Science of Wuhan University, 2004, 29(11): 964–967. |
| [11] |
丁士俊, 陶本藻.
半参数模型核光滑估计与模拟分析[J]. 大地测量与地球动力学, 2004, 24(4): 24–28.
DING Shijun, TAO Benzao. Kernel Smoothing Estimate of Semiparametric Model and Simulation Analysis[J]. Journal of Geodesy and Geodynamics, 2004, 24(4): 24–28. |
| [12] |
潘雄, 孙海燕.
半参数测量平差模型参数的二阶段估计[J]. 测绘科学, 2004, 29(3): 19–21.
PAN Xiong, SUN Haiyan. Two Stage Estimation of Parameter for Semiparametric Survey Adjustment Models[J]. Science of Surveying and Mapping, 2004, 29(3): 19–21. |
| [13] |
王振杰. 大地测量中不适定问题的正则化解法研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2003. WANG Zhenjie. Research on the Regularization Solutions of Ill-Posed Problems in Geodesy[D]. Wuhan: Institute of Geodesy and Geophysics Chinese Academy of Sciences, 2003. http://cdmd.cnki.com.cn/Article/CDMD-80057-2004041260.htm |
| [14] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883–893. DOI:10.1137/0717073 |
| [15] | SCHAFFRIN B. A Note on Constrained Total Least-squares Estimation[J]. Linear Algebra and Its Applications, 2006, 417(1): 245–258. DOI:10.1016/j.laa.2006.03.044 |
| [16] | SCHAFFRIN B, WIESER A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [17] |
王乐洋.
基于总体最小二乘的大地测量反演理论及应用研究[J]. 测绘学报, 2012, 41(4): 629.
WANG Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 629. |
| [18] | AMIRI-SIMKOOEI A, JAZAERI S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Journal of Geodetic Science, 2012, 2(2): 113–124. |
| [19] |
王乐洋, 许才军, 鲁铁定.
边长变化反演应变参数的总体最小二乘方法[J]. 武汉大学学报(信息科学版), 2010, 35(2): 181–184.
WANG Leyang, XU Caijun, LU Tieding. Inversion of Strain Parameter Using Distance Changes Based on Total Least Squares[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 181–184. |
| [20] |
王乐洋, 于冬冬.
病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575–581.
WANG Leyang, YU Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575–581. DOI:10.13485/j.cnki.11-2089.2014.0091 |
| [21] |
王乐洋, 吴飞, 吴良才.
GPS高程转换的总体最小二乘拟合推估模型[J]. 武汉大学学报(信息科学版), 2016, 41(9): 1259–1264.
WANG Leyang, WU Fei, WU Liangcai. Total Least Squares Fitting Estimation Model for GPS Height Transformation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1259–1264. |
| [22] | NEITZEL F. Generalization of Total Least-squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751–762. DOI:10.1007/s00190-010-0408-0 |
| [23] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661–675. DOI:10.1007/s00190-012-0552-9 |
| [24] |
刘经南, 曾文宪, 徐培亮.
整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5): 505–512.
LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505–512. |
| [25] |
王乐洋, 余航, 陈晓勇.
Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22–29.
WANG Leyang, YU Hang, CHEN Xiaoyong. An Algorithm for Partial EIV Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22–29. DOI:10.11947/j.AGCS.2016.20140560 |
| [26] |
赵俊, 归庆明.
部分变量误差模型的整体抗差最小二乘估计[J]. 测绘学报, 2016, 45(5): 552–559.
ZHAO Jun, GUI Qingming. Total Robustified Least Squares Estimation in Partial Errors-in-variables Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 552–559. DOI:10.11947/j.AGCS.2016.20150374 |
| [27] | SHI Yun, XU Peiliang, LIU Jingnan, et al. Alternative Formulae for Parameter Estimation in Partial Errors-in-variables Models[J]. Journal of Geodesy, 2015, 89(1): 13–16. DOI:10.1007/s00190-014-0756-2 |
| [28] |
赵俊, 归庆明, 陈晨. TLS方法解算时间序列模型及其在卫星钟差预报中的应用[C]//第六届中国卫星导航学术年会论文集. 西安: 中国卫星导航系统管理办公室学术交流中心, 2015. ZHAO Jun, GUI Qingming, CHEN Chen. Times Series Model Solved by TLS Method and Applications in Prediction of Satellite Clock Error[C]//Proceedings of the 6th China Satellite Navigation Conference. Xi'an: China Satellite Navigation Office-Academic Exchange Center, 2015. |
| [29] | ZENG Wenxian, LIU Jingnan, YAO Yibin. On Partial Errors-in-variables Models with Inequality Constraints of Parameters and Variables[J]. Journal of Geodesy, 2015, 89(2): 111–119. DOI:10.1007/s00190-014-0775-z |
| [30] |
曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013. ZENG Wenxian. Effect of the Random Design Matrix on Adjustment of an EIV Model and its Reliability Theory[D]. Wuhan: Wuhan University, 2013. https://mall.cnki.net/lunwen-1013210882.nh.html |
| [31] |
丁士俊. 测量数据的建模与半参数估计[D]. 武汉: 武汉大学, 2005. DING Shijun. Survey Data Modeling and Semiparametric Estmating[D]. Wuhan: Wuhan University, 2005. https://www.cnki.com.cn/lunwen-2006031321.html |
| [32] |
王振杰, 欧吉坤, 曲国庆, 等.
用L-曲线法确定半参数模型中的平滑因子[J]. 武汉大学学报(信息科学版), 2004, 29(7): 651–653.
WANG Zhenjie, OU Jikun, QU Guoqing, et al. Determining the Smoothing Parameter in Semi-parametric Model Using L-Curve Method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(7): 651–653. |
| [33] | HANSEN P C, O'LEARY D P. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487–1503. DOI:10.1137/0914086 |
| [34] | JAZAERI S, AMIRI-SIMKOOEI A R, SHARIFI M A. Iterative Algorithm for Weighted Total Least Squares Adjustment[J]. Survey Review, 2014, 46(334): 19–27. DOI:10.1179/1752270613Y.0000000052 |


