2. 地球空间信息技术协同创新中心, 湖北 武汉 430079;
3. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079;
4. 东华理工大学测绘工程学院, 江西 南昌 330013
2. Collaborative Innovation Centre for Geospatial Technology, Wuhan 430079, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
4. Faculty of Geomatics, East China University of Technology, Nanchang 330013, China
相位整周模糊度的快速、准确解算是GNSS实时高精度定位的关键问题,也是GNSS研究领域中的热点问题。在众多整周模糊度解算方法中,基于整数最小二乘法(integer least squares,ILS)的搜索方法由于具有最高的成功率而被广泛采用[1-5]。ILS搜索是指在给定空间内寻找出满足模糊度残差二次型最小的一组整数解,为快速获得该组整数解,目前最为流行的是基于震荡式收缩策略的SEVB(Schnorr-Euchner and Viterbo-Biglieri)算法[6-9]。其中,震荡式搜索策略是指从Bootstrap估计点开始向两侧呈“Z字型”枚举[10];收缩策略是指每获得一组二次型更小的解,则进行搜索空间的更新[11-12]。通过上述两个策略,SEVB算法可以迅速减小搜索空间,从而减少搜索节点数,实现模糊度快速估计,因此该算法也被LAMBDA方法(V3.0)所采用。
采用SEVB算法处理时,首先将初始搜索空间设置为无穷大,以确保获得的第一组整数候选解为Bootstrap估计解,然后基于该组整数解进行搜索空间的收缩和震荡式枚举过程。但是当模糊度解算精度较差时,Bootstrap成功率偏低,此时获得的Bootstrap估计解偏离ILS估计解较多,求得的搜索空间相对偏大,需进行多次枚举才能实现搜索半径的更新,导致搜索过程缓慢,耗时明显增大。针对这一问题,本文通过限制初始搜索空间大小和简化搜索算法实现过程两个方面对SEVB算法进行改进,以期提高搜索效率。
1 模糊度解算的整数最小二乘模型假定â和Qââ分别为模糊度的浮点解和方差协方差阵,其整数最小二乘估计的估计准则为[5]
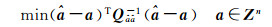 (1)
(1)
式中,a为模糊度最优整数解。式(1)也被称为整数最小二乘估计的目标函数。
为加快整数最小二乘模糊度解算速度,通常需先进行整数变换[13-20]。本文采用LAMBDA方法构建整数变换矩阵Z,对模糊度解向量和方差阵变换过程如下
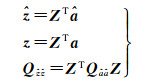 (2)
(2)
式中,ẑ、z和Qẑẑ分别为整数变换后的模糊度浮点解、模糊度整数解及方差协方差阵。
整数变换后,式(1)更新为
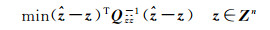 (3)
(3)
对Qââ和Qẑẑ矩阵分别进行Cholesky分解(LTDL),有
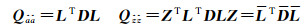 (4)
(4)
式中,L、L为单位下三角矩阵;D、D为对角矩阵。
假设式(3)对应的搜索空间大小为χ2,并考虑式(4),则有
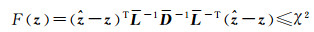 (5)
(5)
定义序贯条件估值z=z-L-T(z-ẑ),代入式(5)得到
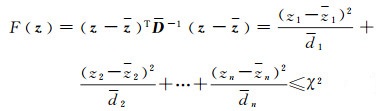 (6)
(6)
式中,di为矩阵D的主对角线元素,另有
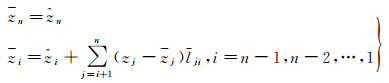 (7)
(7)
式中,zi为zi的条件估值。
由式(6)和式(7)即可推导出模糊度搜索过程,从i=n处开始,有
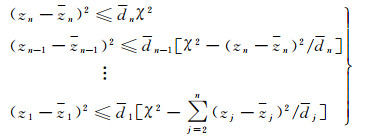 (8)
(8)
由式(8)可知,SEVB算法采用深度优先的方法逐层搜索,每一层内的搜索区间大小取决于搜索空间χ2以及该层对应的条件方差di。在第一次搜索时,χ2被设置为无穷大,从第n层到第1层进行序贯取整得到第1个模糊度候选组(称为Bootstrap估计解),将该组解的目标函数值F(z)作为新的搜索空间大小χ′2,之后在更新后的χ′2内继续搜索,若第1层仍有解则又得到一个候选组,若无解则返回第2层的下一个整数点。依此类推,每当有新候选组的目标函数值小于当前空间大小χ′2时,则更新χ′2值,实现搜索空间的不断收缩[6]。
为了使搜索空间更快的收缩,需从模糊度的条件估值zi处开始呈“Z字形”震荡式搜索
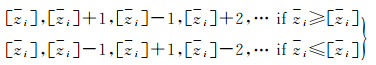 (9)
(9)
式中,i为当前的层数;[·]为取整符号。
由于搜索空间的大小可以不断收缩,通常SEVB算法具有很高的搜索效率。但当模糊度解算的精度较差时,Bootstrap估计解与ILS估计解偏差较大,造成第1次的搜索空间很大,需要多次重复不必要的节点枚举才能将搜索空间缩小到较小的范围内,大大增加了搜索耗时。因此,本文从简化算法实现和限制初始搜索空间大小两个方面对现有的SEVB算法进行改进。
3 改进的SEVB搜索算法针对现有SEVB算法存在的上述不足,本文在其基础上进行了优化,增加了两点改进策略,改进后的算法称为MSEVB(Modified SEVB)。
3.1 改进策略1初始搜索空间不再设为无穷大,而是首先计算出一个空间较小的初值,该初值既要尽可能的小,又要保证搜索空间内有整数解。初值计算方式分为两种情形[21-22]:
(1) 如果ncands≤n+1(n为模糊度维数,ncands为待输出的候选组个数),构造出n+1个二次型值。第1个二次型值通过对模糊度浮点解序贯取整计算得到,然后仍按照序贯取整的方法,依次对n维模糊度中的一个分量取次接近整数,得到其余n个二次型值。对这n+1个二次型值从小到大排序,取第ncands个二次型值作为初始空间大小χ02。
(2) 如果ncands>n+1,使用椭球体积公式
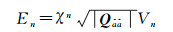 (10)
(10)
式中,En为搜索椭球体积,并有近似关系int En=ncands;|·|为取行列式值;Vn为体积函数,其计算公式为
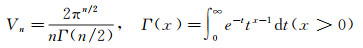 (11)
(11)
则可得到初始空间大小
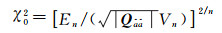 (12)
(12)
现有SEVB算法采用下式计算序贯条件估值[6]
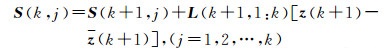 (13)
(13)
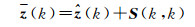 (14)
(14)
由式(13)可知,每次计算条件估值时均需对S(k, j), (j=1, 2, …, k)重新计算,而当搜索遇到死节点时(尤其是在搜索空间较大时,包含更多的死节点数),第1:k-1层的计算信息实际上是不必要的,即产生了计算冗余。改进策略2通过将S(k, j), (j=1, 2, …, k)转换为计算S(k, k),可以减少不必要的计算量,从而减少整体搜索耗时。改进后的计算公式为
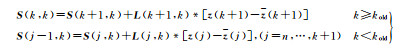 (15)
(15)
式中,kold为上一次节点枚举时所在的层数。
综上所述,MSEVB算法的计算步骤为:
(1) 参数输入及初始化。需输入的参数包括模糊度浮点解ẑ及方差协方差阵Qẑẑ;初始化主要指对初始搜索空间大小χ02以及第1次Bootstrap估计时的初值进行设置,其中搜索过程从第n层处开始。
(2) 判断当前局部空间大小newDist与χ02的关系。若满足newDist < χ02则向下一层搜索,采用式(15)计算下一层的序贯条件估值,更新newDist并再次判断其与χ02关系,若仍满足newDist < χ02则继续向下一层搜索,依此类推;若不满足newDist < χ02则返回到上一层的下一个整数点,更新newDist并重复步骤(2)。
(3) 若能一直向下搜索直到第1层,则成功找到一个模糊度候选组,使用该候选组的目标函数值对χ02进行更新。之后在新的χ02内继续搜索第1层的下一个整数点,若仍满足newDist < χ02,则又找到一个候选组,再次对χ02进行更新,尝试下一个整数点;当第1层没有整数点时则返回到第2层的下一个整数点,更新newDist并回到步骤(2)。
(4) 当重新返回到第n层时则整个搜索过程结束,最后一次得到的候选组即为最优整数解。
MSEVB算法的实现流程如图 1所示。其中k为当前搜索节点所在的层数;maxDist为初始搜索空间大小,每找到一个新的候选组即对其进行更新;ẑ(k)为模糊度浮点解;z(k)为浮点解的序贯条件估值;z(k)为对序贯条件估值邻近取整;z为搜索得到的模糊度候选组;sgn为符号函数。
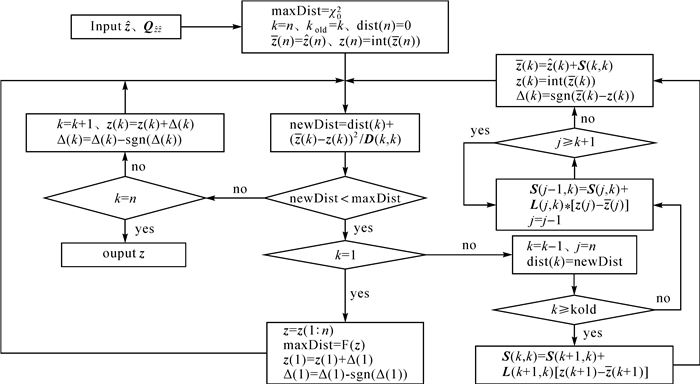
|
| 图 1 MSEVB算法流程 Fig. 1 The flow chart of MSEVB algorithm |
4 试验验证 4.1 仿真分析
为在普遍意义下验证上述MSEVB算法的有效性和评估其具体性能,参照文献[6]采用的方法模拟出大量的样本数据进行计算分析,模拟数据包括模糊度浮点解â和方差协方差阵Qââ。
搜索耗时的大小随着模糊度解算精度的降低或模糊度维数的增加而增大,而模糊度解算精度可用整数序贯取整成功率Ps_ib来衡量,当解算精度较高时Ps_ib值较大,反之亦然。Ps_ib定义如下[23-24]
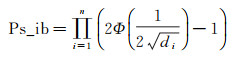 (16)
(16)
式中,di为Qẑẑ经过LTDL分解后的矩阵D的主对角线元素,又称为条件方差。
因此设计了两组试验分别从不同的角度进行验证:第1组试验选取特定的模糊度维数,分析搜索耗时与Ps_ib的关系;第2组试验选取特定的Ps_ib,分析搜索耗时与模糊度维数的关系。为提高搜索效率,在执行搜索过程之前都进行了相同的降相关处理。
试验环境为:基于联想电脑(Intel Core i7-3520 CPU,2.90 GHz,4 GB内存,Win7系统)和MATLAB 2012b软件进行。
4.1.1 试验1试验1分别采用20、30、40、50维共4组数据,检验SEVB算法和MSEVB算法的搜索耗时随Ps_ib变化的关系。其中Ps_ib的大小可通过对方差协方差阵乘以一个比例因子来控制[25]
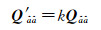 (17)
(17)
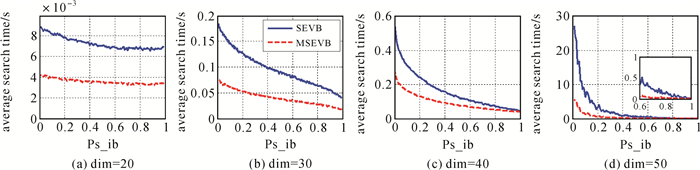
式中,当k>1时Q′ââ 精度降低,Ps_ib减小;当k < 1时Q′ââ 精度提高,Ps_ib增大,调整k的大小使Ps_ib从1至0取100组不同的值,取值间隔为0.01。为减小偶然误差的影响,在每个Ps_ib下随机生成1000组样本并分别采用两种算法进行搜索,计算两种算法1000次搜索的平均耗时大小,结果如图 2所示(其中的小图为对局部区域的突出放大)。
|
| 图 2 不同精度下SEVB及MSEVB算法平均搜索耗时变化趋势图 Fig. 2 The trend chart of SEVB and MSEVB average search time under different Ps_ib |
由图 2可见,MSEVB和SEVB两种算法解算耗时随着Ps_ib的降低,搜索耗时逐渐增大,且在较高维时呈近似于指数增加的趋势;而MSEVB解算效率高于SEVB算法,尤其是在低成功率下具有更加显著的计算优势。该结果表明,通过限制初始空间大小(策略1)和优化节点计算过程(策略2)可以有效地减少冗余计算步骤,降低模糊度搜索过程中的计算复杂度,进而减少计算耗时。
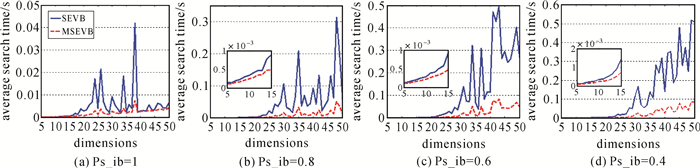
4.1.2 试验2试验2采用5~50维的模糊度数据,并控制Ps_ib取1、0.8、0.6、0.4等4种情况,以进一步比较不同维数下两种搜索算法的计算耗时。每个维数下均随机生成1000组样本并进行搜索,分别计算两种搜索算法的平均耗时大小,结果如图 3所示(其中5~20维时两种算法图像基本重合,增加小图对该区域进行突出放大)。
|
| 图 3 The trend chart of SEVB and MSEVB average search time under different Ps_ib Fig. 3 The trend chart of SEVB and MSEVB average search time under different dimensions |
图 3为4种不同的Ps_ib情形下,SEVB和MSEVB算法在不同维数下的平均搜索耗时变化趋势图。如图所示,随着模糊度维数增加,两种搜索算法的耗时整体上呈增大趋势,其中SEVB算法耗时增长十分迅速且波动较大,而MSEVB算法增长相对缓慢且更为平稳,整体上具有良好的计算稳定性。
综合图 2和图 3的结果可知,当模糊度解算维数较高(20维以上)且对应的Ps_ib较低时,采用常规的SEVB算法通常需要较多的解算耗时,此时MSEVB可以有效地减少模糊度的搜索耗时,提高模糊度解算效率。
4.2 实测验证为进一步检验MSEVB算法在实际情形下的效果,采用一组动态车载GNSS观测数据(基准站位于武汉市某科技园楼顶,流动站为武汉市梁子湖大道上的跑车),按照表 1进行基线解算获得模糊度的浮点解â 和方差协方差阵Qââ 。为衡量模糊度的解算精度,通常采用模糊度精度因子(ambiguity dilution of precision, ADOP)作为评价指标[26],其定义如下[27]
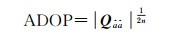 (18)
(18)
| 接收机型号 | NovAtel 638 |
| 系统和频率 | BDS(B1,B2) GPS(L1,L2,L3) |
| 起始时间 | 2016-11-12T01:30:23 |
| 历元数 | 4550 |
| 采样间隔 | 1 s |
| 截止高度角 | 10° |
| 基线长 | 22.1~24.3 km |
| 伪距/相位权比 | 1:100 |
| GPS/BDS权比 | 1:0.8 |
| 处理模式 | 单历元 |
式中,n为模糊度的维数。
模糊度维数和ADOP值如图 4所示,可以看到模糊度维数基本在35维以上,ADOP值在0.1左右。
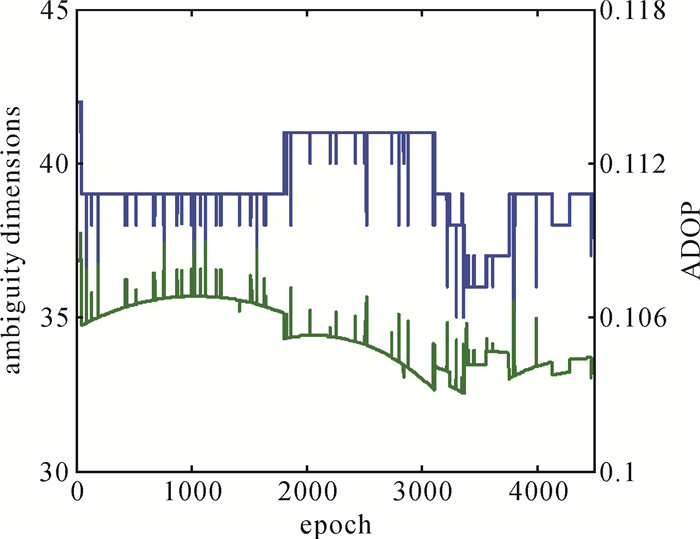
|
| 图 4 不同历元下的模糊度维数和ADOP值 Fig. 4 Ambiguity dimensions and ADOP under different epochs |
由于该组实测数据的模糊度维数和解算精度较高,其序贯取整成功率Ps_ib趋近于1。为充分体现MSEVB算法相对于SEVB算法的性能提升,仍参考文献[25]的处理方法,对Qââ矩阵乘以一个比例因子,控制Ps_ib的大小并令其取0.8、0.6、0.4共3种情况,分别采用SEVB和MSEVB算法逐历元进行解算。两种算法在所有历元下的搜索耗时如图 5所示,其中原始数据的结果用Ps_ib=1表示。
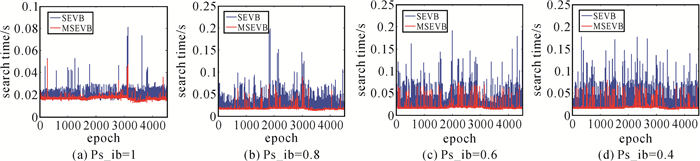
|
| 图 5 不同精度下SEVB及MSEVB算法平均搜索耗时随历元变化趋势图 Fig. 5 The trend chart of SEVB and MSEVB average search time under different Ps_ib and epochs |
由图 5可以看出,在以上4种情形下,MSEVB算法的耗时均明显小于SEVB算法,即使当解算精度较高时(Ps_ib=1)MSEVB的整体耗时也低于SEVB。此外,从图中可以看到,随着解算精度降低,SEVB算法的耗时波动范围越来越大,而MSEVB算法的整体耗时波动较小,总能维持在较小的范围内,具有更好的稳定性。
图 6反映了Ps_ib=0.4情形下SEVB和MSEVB耗时的概率分布情况。可以看到,SEVB靠中心右侧的部分较多,而MSEVB靠中心右侧的部分较少,主要集中分布在左侧,且其中心相比于SEVB更小,从另一个角度展现出MSEVB算法具有更高稳定性以及更少的搜索耗时。
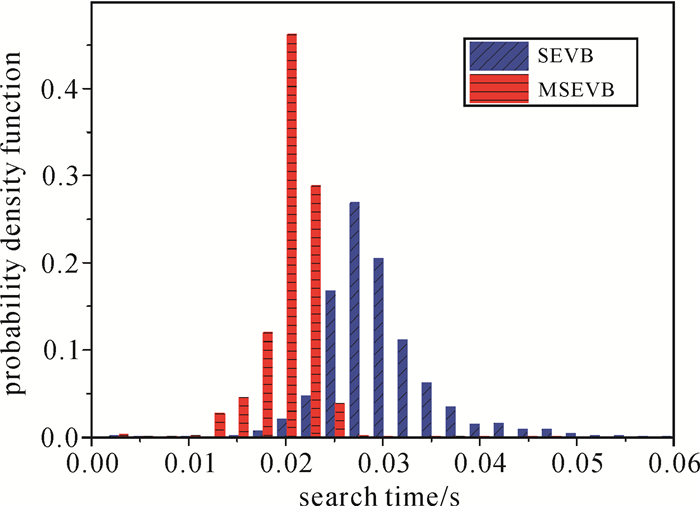
|
| 图 6 SEVB及MSEVB算法的耗时概率分布图 Fig. 6 Probability distribution of SEVB and MSEVB search time |
表 2统计了不同Ps_ib下两种算法在全部历元内的平均及最大搜索耗时,最后一列“promote”反映了MSEVB算法相比于SEVB算法的提升效率。可以看到在不同解算精度下MSEVB平均耗时均小于SEVB,且随精度降低MSEVB耗时增长较为缓慢,而SEVB算法耗时增长较为明显,因此Ps_ib越小则MSEVB算法的性能提升越明显,Ps_ib=0.4时平均搜索效率可提升33.18%。
| Ps_ib | SEVB/s | MSEVB/s | promote /(%) | ||
| mean | max | mean | max | ||
| 1 | 0.023 2 | 0.085 9 | 0.018 5 | 0.051 9 | 25.41 |
| 0.8 | 0.025 1 | 0.196 2 | 0.019 8 | 0.079 9 | 26.77 |
| 0.6 | 0.028 2 | 0.192 8 | 0.021 5 | 0.068 0 | 31.16 |
| 0.4 | 0.029 7 | 0.177 3 | 0.022 3 | 0.074 7 | 33.18 |
5 结论
现有的SEVB算法在浮点模糊度精度较差时,由于初始空间设定为无穷大,所得到的模糊度初始估计候选组(Bootstrap估计解)偏离真值较大,导致模糊度搜索空间难以有效地收缩,且空间内包含较多的死节点造成冗余计算较多(见式(13)),致使搜索耗时较大,影响了整周模糊度的整体解算效率。
针对这一问题,本文在SEVB算法基础上,从限制初始空间大小和优化分层节点计算过程两个方面开展了算法改进,提出了一种改进的SEVB搜索算法(MSEVB算法)。分别基于仿真数据和动态车载实测数据从不同角度对MSEVB算法进行了效果验证与分析,得到以下结论:
(1) 对于确定的模糊度维数来说,随着模糊度精度的降低,相应的成功率Ps_ib减小,SEVB算法的搜索耗时显著增加,而改进的MSEVB算法耗时增长较小,因而具有更高的搜索效率,且Ps_ib越小,MSEVB算法的性能提升效果越明显。
(2) 在相同的模糊度解算精度下,随着模糊度维数的增加,MSEVB算法相比于SEVB算法的耗时增长更加平缓且波动更小,维数越高,改进算法的解算优势越明显。
综上所述,本文的MSEVB算法是基于现有的SEVB算法发展而来的,是对SEVB算法的完善,不仅在低精度、高维模糊度的搜索方面具有更为明显的效率优势,而且可以整体上保证模糊度解算效率相对更加可靠稳定。
| [1] | ABIDIN H Z. On the Construction of the Ambiguity Searching Space for on-the-fly Ambiguity Resolution[J]. Navigation, 1993, 40(3): 321–338. DOI:10.1002/navi.1993.40.issue-3 |
| [2] | FREI E, BEUTLER G. Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach FARA: Theory and First Results[J]. Manuscripta Geodaetica, 1990, 15(4): 325–356. |
| [3] | EULER H J, LANDAU H. Fast GPS Ambiguity Resolution on-the-fly for Real-time Application[C]//Proceedings of the 6th International Geodetic Symposium on Satellite Positioning. Columbus, Ohio: [s. n. ], 1992: 650-659. |
| [4] | CHEN Dingsheng. Development of a Fast Ambiguity Search Filtering (FASF) Method for GPS Carrier Phase Ambiguity Resolution[D]. Calgary, Alberta: University of Calgary, 1994. |
| [5] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65–82. DOI:10.1007/BF00863419 |
| [6] | CHANG X W, YANG X, ZHOU T. MLAMBDA: A Modified LAMBDA Method for Integer Least-squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552–565. DOI:10.1007/s00190-005-0004-x |
| [7] | LI Bofeng, VERHAGEN S, TEUNISSEN P J G. GNSS Integer Ambiguity Estimation and Evaluation: LAMBDA and Ps-LAMBDA[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin Heidelberg: Springer, 2013: 291-301. |
| [8] | XU Peiliang, SHI Chuang, LIU Jingnan. Integer Estimation Methods for GPS Ambiguity Resolution: An Applications Oriented Review and Improvement[J]. Survey Review, 2012, 44(324): 59–71. DOI:10.1179/1752270611Y.0000000004 |
| [9] |
于兴旺. 多频GNSS精密定位理论与方法研究[D]. 武汉: 武汉大学, 2011. YU Xingwang. Multi-frequency GNSS Precise Positioning Theory and Method Research[D]. Wuhan: Wuhan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10486-1011403758.htm |
| [10] | SCHNORR C P, EUCHNER M. Lattice Basis Reduction: Improved Practical Algorithms and Solving Subset Sum Problems[J]. Mathematical Programming, 1994, 66(1-3): 181–199. DOI:10.1007/BF01581144 |
| [11] | VITERBO E, BIGLIERI E. A Universal Decoding Algorithm for Lattice Codes[C]//Proceedings of Colloques Sur le Traitement du Signal et des Images. Juan-les-Pins: GRETSI, Groupe d'Etudes du Traitement du Signal et des Images, 1993: 611-614. |
| [12] | VITERBO E, BOUTROS J. A Universal Lattice Code Decoder for Fading Channels[J]. IEEE Transactions on Information Theory, 1999, 45(5): 1639–1642. DOI:10.1109/18.771234 |
| [13] | LIU L T, HSU H T, ZHU Y Z, et al. A New Approach to GPS Ambiguity Decorrelation[J]. Journal of Geodesy, 1999, 73(9): 478–490. DOI:10.1007/PL00004003 |
| [14] | XU Peiliang. Random Simulation and GPS Decorrelation[J]. Journal of Geodesy, 2001, 75(7-8): 408–423. DOI:10.1007/s001900100192 |
| [15] | XU Peiliang. Parallel Cholesky-based Reduction for the Weighted Integer Least Squares Problem[J]. Journal of Geodesy, 2012, 86(1): 35–52. DOI:10.1007/s00190-011-0490-y |
| [16] | ZHOU Yangmei. A New Practical Approach to GNSS High-Dimensional Ambiguity Decorrelation[J]. GPS Solutions, 2011, 15(4): 325–331. DOI:10.1007/s10291-010-0192-6 |
| [17] |
周扬眉, 刘经南, 刘基余.
回代解算的LAMBDA方法及其搜索空间[J]. 测绘学报, 2005, 34(4): 300–304.
ZHOU Yangmei, LIU Jingnan, LIU Jiyu. Return-calculating LAMBDA Approach and Its Search Space[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(4): 300–304. |
| [18] |
刘宁, 熊永良, 冯威, 等.
单频GPS动态定位中整周模糊度的一种快速解算方法[J]. 测绘学报, 2013, 42(2): 211–217.
LIU Ning, XIONG Yongliang, FENG Wei, et al. An Algorithm for Rapid Integer Ambiguity Resolution in Single Frequency GPS Kinematical Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 211–217. |
| [19] |
刘经南, 于兴旺, 张小红.
基于格论的GNSS模糊度解算[J]. 测绘学报, 2012, 41(5): 636–645.
LIU Jingnan, YU Xingwang, ZHANG Xiaohong. GNSS Ambiguity Resolution Using the Lattice Theory[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 636–645. |
| [20] |
刘万科, 卢立果, 单弘煜.
一种快速解算高维模糊度的LLL分块处理算法[J]. 测绘学报, 2016, 45(2): 147–156.
LIU Wanke, LU Liguo, SHAN Hongyu. A New Block Processing Algorithm of LLL for Fast High-dimension Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 147–156. DOI:10.11947/j.AGCS.2016.20150370 |
| [21] | TEUNISSEN P J G, De JONGE P J, TIBERIUS C C J M. The Volume of the GPS Ambiguity Search Space and Its Relevance for Integer Ambiguity Resolution[C]//Proceedings of the 9th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1996). Kansas: [s. n. ], 1996: 889-898. |
| [22] | JONGE De P, TIBERIUS C C J M. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects[M]. Delft: Delft Geodetic Computing Centre, 1996: 1-47. |
| [23] | TEUNISSEN P J G. Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606–612. DOI:10.1007/s001900050199 |
| [24] | TEUNISSEN P J G. An Optimality Property of the Integer Least-squares Estimator[J]. Journal of Geodesy, 1999, 73(11): 587–593. DOI:10.1007/s001900050269 |
| [25] | VERHAGEN S, LI Baofeng, TEUNISSEN P J G. Ps-LAMBDA: Ambiguity Success Rate Evaluation Software for Interferometric Applications[J]. Computers & Geosciences, 2013, 54(3): 361–376. |
| [26] | ODIJK D, TEUNISSEN P J G. ADOP in Closed form for a Hierarchy of Multi-frequency Single-baseline GNSS Models[J]. Journal of Geodesy, 2008, 82(8): 473–492. DOI:10.1007/s00190-007-0197-2 |
| [27] | TEUNISSEN P J G, ODIJK D. Ambiguity Dilution of Precision: Definition, Properties and Application[C]//Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997). Kansas City: [s. n. ], 1997: 891-899. |



