在地理学领域,时间距离常作为衡量可达性或经济联系强度的一个重要指标,用于区域的交通可达性、城市空间分布格局、社会经济过程等的分析研究中[1-5]。因此时间距离的有效可视化表达对于地理空间的数据分析和规律探索具有重要意义。
时间地图(time-space map)是时间距离可视化的一种有效手段,它的研究最早可以追溯到20世纪60年代[6-7]。时间地图是将地理空间中的两个地理实体之间的时间距离替代传统地图中的空间距离[8-10]。根据点空间分布结构的不同可分为网络型[11-13]和中心型两种方法体系。中心型时间地图描述的是各个点到特定中心点的时间距离,它一般有两种类型:一种是采用了不规则等时线法(irregular isochrones),类似于等高线,即在地图上使用不规则的曲线将距离中心点相等时间的点连接起来[14-15];另一种则是同心圆式等时线法(concentric isochrones)[16-18],该方法是将原图作变形处理,使得中心点与周围点之间的距离表示时间距离,这样从中心点起算的等时线是同心圆式的。
作为一种典型的线性Cartogram[8],同心圆式等时线法更为专注地表达时间距离,更符合人类的心象认知,能够让人从全新的视角快速且有效地认知和解读中心点与周围点之间的时间距离关系。由于该方法需要对原地理空间扭曲变形,且自动生成过程复杂,目前对该方法的自动生成研究并不多。文献[16]利用薄板样条函数变形技术实时生成同心圆式的等时线图。文献[17]利用三角剖分技术来构建中心型时间地图,其基本思想是以控制点集为顶点对原地图进行三角剖分,然后对每个三角形内的点进行仿射变换。文献[18]基于移动最小二乘法对地图进行仿射变换,其核心思想是基于控制点位置的变化,利用移动最小二乘算法获得描述整幅图像的变形函数,该变形函数能够将原地图上的任一点一一映射到时间地图中。虽然上述研究对中心型时间地图的构建进行了初探,但仍存在以下3个问题:
(1) 以往研究更多地关注时间地图的变形转换过程,忽略了时间地图与原地图的尺度一致性问题,因此难以直接对时间地图和原地图进行对比分析。
(2) 以往研究都较好地完成原地图(以边界为例)整体变形转换,但在局部区域会出现“线交叉”这样错误的拓扑关系表达,影响整体可视化效果和易读性,会给用户带来读图认知上的困惑。
(3) 以往研究较少顾及对时间地图空间变形的可视化表达。空间变形的表达能够揭示地理空间和时间空间两个空间模型分布特征的相似性,探索时间地图的空间变形规律和趋势。
为解决上述问题,本文提出了一种带有约束条件的移动最小二乘变形算法,并以真实的铁路时间数据为例构建以北京市为中心的时间地图,验证该方法的可行性和有效性。
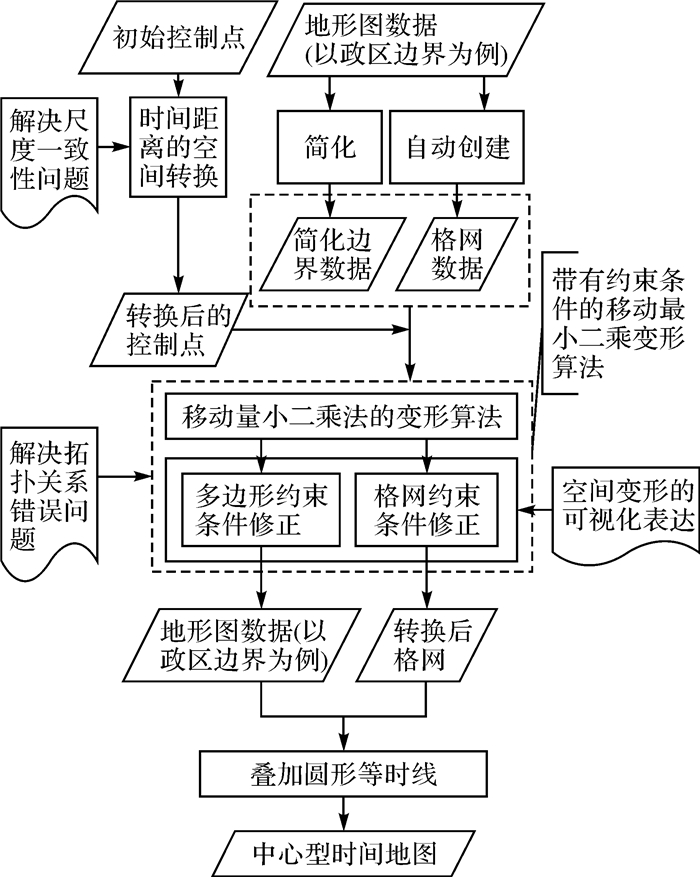
1 整体思路首先在时间距离的空间转换中,设计了距离恒定性等原则,保证时间地图与原地图保持尺度一致性,便于两者进行比较分析;然后提出了一种带有约束条件的移动最小二乘算法对原地图进行变形转换,保证了拓扑关系的正确性,并对时间地图所产生的空间变形进行可视化。图 1是基于移动最小二乘法的中心型时间地图的构建方法的整体思路。
|
| 图 1 基于移动最小二乘法的中心型时间地图构建方法整体思路 Fig. 1 The general idea of construction method of a central time-space map based on moving least squares method |
该方法需要两种不同类型的数据,第一类数据是控制点数据,该数据包含控制点集的空间坐标和该点到中心点的时间,然后通过时间距离的空间转换,获得所有控制点转换后的空间坐标,在这个过程中通过设定距离恒定性等原则来解决尺度一致性问题。第二类数据是需要转换的地形图数据(以政区边界为例),由于国家或者地区的边界通常非常复杂,一方面为了降低地形图数据的转换难度,另一方面本研究空间尺度为国家(nation)尺度,对精度的要求并不很高,因此可以对政区边界进行简化处理。另外通过该地形图的空间范围可以生成相应的正方形格网数据,格网数据的转换变形可作为对时间地图空间变形的可视化。
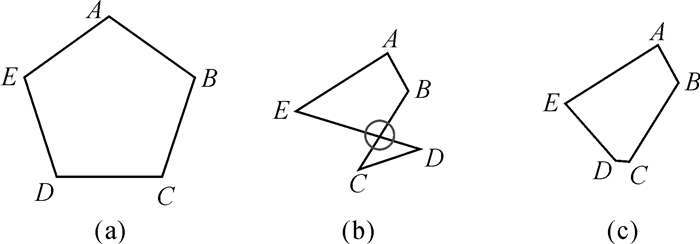
根据控制点集的空间位置变化,利用移动最小二乘算法获得描述整幅地图的变形函数,对地形图数据进行空间转换。在这个过程中会产生一定的拓扑错误。一般来说有两个方面原因:一是地理空间向时间空间的转换中,任何一种空间转换方法都不可避免地会使原地理空间产生一定程度的扭曲和变形;二是由于空间距离和时间距离难以保持正相关性(即A、B两点与中心点O的空间距离SOA>SOB,时间距离也保持同样的关系TOA>TOB),造成转换后会出现“线交叉”这样的“错误”表达。从空间认知的角度出发,空间拓扑关系是人们最易认知的空间关系[19],如若出现错误,会让人产生读图的困惑。因此需要尽可能地保留正确的空间拓扑关系,也即是不产生明显的拓扑错误。如图 2所示,当原图 2(a)中多边形经过变换后,但是变换后的图 2(b)的拓扑关系发生了错误,因此还需要增加约束条件对错误的拓扑关系进行修正(图 2(c))。
|
| 图 2 基于约束条件的多边形拓扑错误修正 Fig. 2 Correction of polygon topology error based on constraints |
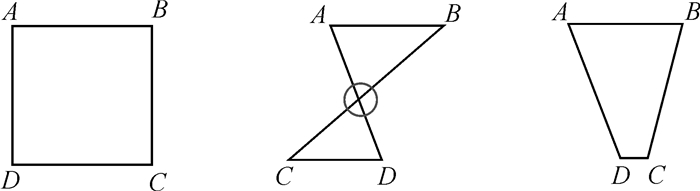
正方形格网的变形可以度量时间地图的空间变形,但在转换中同样会出现错误的拓扑关系,如图 3所示。与多边形相比,格网有更为明确的方位关系,因此两者的约束条件也不同。另外,转换后格网拓扑错误的出现与其疏密程度也有很大的关系。
|
| 图 3 基于约束条件的格网拓扑关系修正 Fig. 3 Correction of gird topology error based on constraints |
最后,为加强可视化效果,在转换后的地图上叠加同心圆式等时线,完成中心型时间地图的构建。
2 时间距离的空间转换时间距离的空间转换是将时间距离数据转换成可以在地图上表达的空间距离数据,并求得转换后各点的新坐标。文献[3]基于超制图学思想将时间距离转换成空间距离,但由于选择的标准化参数不合适,使得最后转换得到的距离数据“整体偏小”,地图上呈现出所有点向中心点收缩的趋势。这显然不符合一般规律(周围点向中心点收缩或者向外扩张),容易让人产生错误的认知。结合已有研究,本文在时间距离向空间距离转换的过程中主要基于以下3个原则:
(1) 方向不变性[20],以保证正确的方位关系。
(2) 使用欧氏距离计算空间距离。
(3) 距离恒定性,也即是中心点到各个点的空间距离总和在转换前后始终保持恒定。这样,原地图与转换后的时间地图保持尺度一致性,便于比较和分析。
定义:设二维平面上点集P={p1, p2, …, pn},pi(xi, yi)∈P,中心点O的空间坐标(xo, yo)。中心点O到点pi空间距离为si,时间为ti。中心点O到点集P中所有点的空间距离总和为S,时间总和为T,则
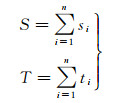
设中心点O到点pi的时间距离转换后的空间距离为s′i,
 (1)
(1)
接下来,根据方向不变性求出点pi在时空转换后的新空间坐标
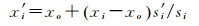 (2)
(2)
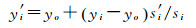 (3)
(3)
这样,利用上述公式便可获得点集P中所有点时空转换后的空间坐标,也就获得了所有点的空间位置变化。
这里引入一个时空变化参数r,其中ri=s′i/si,ri值表示该点在转换后沿中心点方向向内收缩或向外扩张程度。0 < ri < 1,也即是s′i < si,则转换后该点向中心点方向收缩,值越小,表示收缩程度越大;ri=1,也即是s′i=si,则转换后该点保持原有坐标不变;ri>1,也即是s′i>si,则转换后该点沿与中心点方向向外扩张,值越大,表示扩张程度越大。
3 带有约束条件的移动最小二乘变形算法 3.1 移动最小二乘法的基本原理移动最小二乘法是基于控制点的图像变形方法最常用的方法之一,最早由Schaefer等引入到图像变形方法中,此后诸多学者也都对该方法进行了改进和持续研究[21-23]。其基本思想是:根据控制点集位置前后的变化,利用移动最小二乘原理求得一个变形函数f,使得对于原始图上任一点v,f(v)是点v变形后图像上的位置,f一般需要具备平滑性、插值性和确定性3个性质。
定义:二维地图上控制点集为P={p1, p2, …, pn},pi∈P,变换后的控制点集为Q={q1, q2, …, qn},qi∈Q。对于地图上任一点v,根据移动最小二乘法的理论模型,存在变形函数f使下式取得最小值
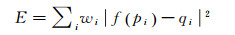 (4)
(4)
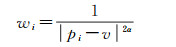 (5)
(5)
式中,pi和qi为控制点集中点的坐标,用行向量表示。wi是权值函数,α为调节变形效果的参数,一般取1或2,α越大意味着权重值与距离的关系越密切。由于wi的取值随着v的位置不同而变化,每个点都有着与其他点不一样的权值函数,随之也有着与其他点不同的变形函数,所以称之为移动最小二乘法。
一般的, 变形函数f分解为线性转换矩阵M和平移变换项Y,对于二维图形,可以用2×2的矩阵和的1×2行向量来表示M和Y。变形函数f可以用下式表示
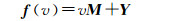 (6)
(6)
将公式(6)代入式(4),求最小值,即对f的变量求导数且等于0
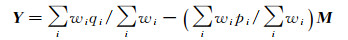 (7)
(7)
这样可得变形函数的一般形式
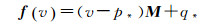 (8)
(8)
式中,p*和q*为加权质心
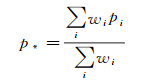 (9)
(9)
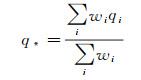 (10)
(10)
在此基础上,公式(4)可以改写为
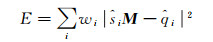 (11)
(11)
这里,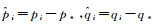
移动最小二乘法对线性变换矩阵M并没有作限制。实际应用中,对于不同的变形要求,可以对M作不同的限制,从而形成不同的变形效果。常见的变换形式有仿射变换,相似变换以及刚性变换,本文对M设置为一般的仿射变换,包含了缩放、错切、旋转等变换成分。
对公式(11)求导使其等于零,可得出
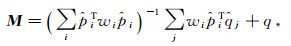 (12)
(12)
则可得出仿射变换变形函数f,
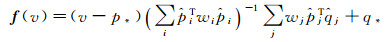 (13)
(13)
f(v)的结果是一个1×2的矩阵,即是地图中任一点v所对应的转换后的新坐标。
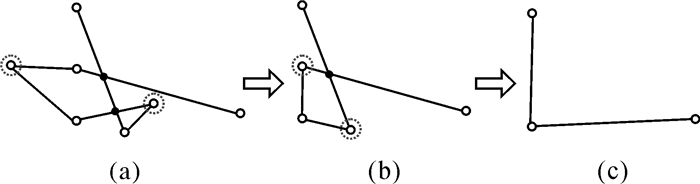
3.2 多边形和格网约束条件 3.2.1 多边形约束条件多边形在转换时出现的主要拓扑错误是多边形的边界产生了自相交错误。关于多条线段相交检测最常用的算法是基于扫描线的Bentley-Ottmann算法[24]。但该算法应用到多边形边界自相交检测时,仅检测非邻近边相交的交点,对于邻近边端点相交则不予考虑。如图 4(a)所示,仅黑色点被检测,而白色端点是不予检测的。当检测出多边形边界自相交后,对相交的邻近区域的边界线进行调整,通过去除边界上急剧变化的点(图中虚线框所标示的点),使得边界线趋于平滑直至不出现自相交情况,如图 4(a)到4(b),直至4(c)。
|
| 图 4 多边形边界拓扑错误的检测和修改 Fig. 4 Detection and modification of polygon boundary topological errors |
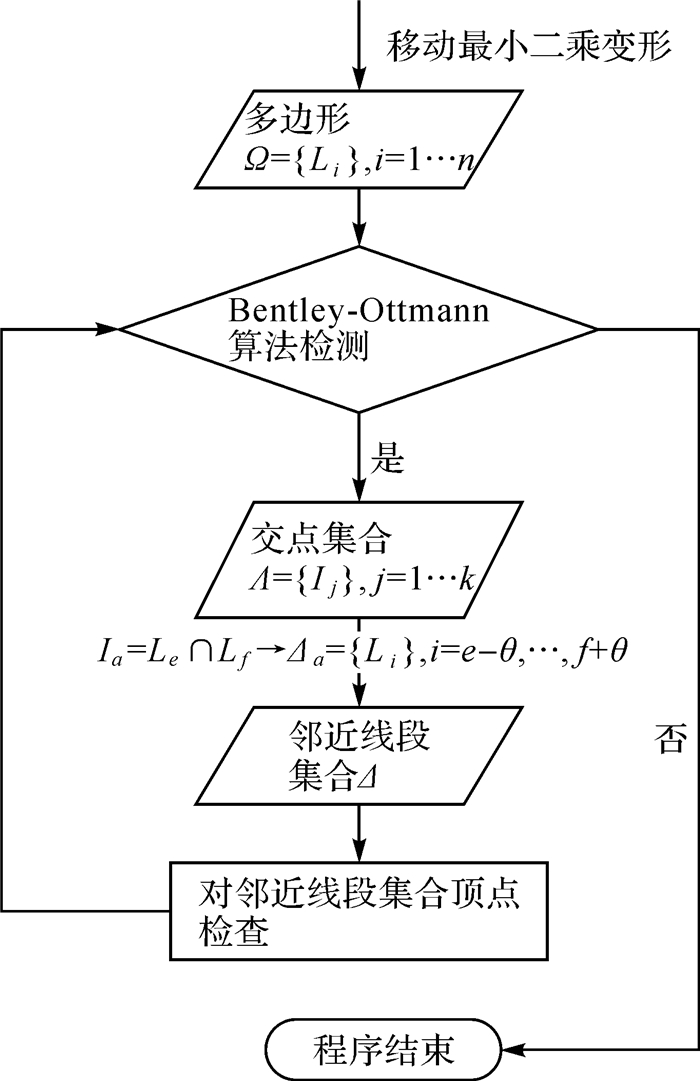
假定多边形由n个线段L组成,Ω={Li},i=1, …, n。经过Bentley-Ottmann算法检测出k个交点集合Λ={Ij},j=1, …, k,其中第a个交点Ia,a∈{1, …, k}。由线段Le, Lf(e, f∈{1, …, n})相交而成,那么交点Ia对应的邻近线段集合Δa={Li}, i=e-Θ, e-Θ+1,…, f+Θ-1,f+Θ,Θ为一个固定阈值。依次对k个交点所对应的邻近线段集合Δ的顶点夹角逐次进行检查,如果夹角小于一个给定阈值σ(σ取值过小,迭代次数过多,难以消除交叉点;取值过大,会使得边界变形太大,根据试验数据特点,本文取值为80°。),就去除该顶点,直至该区域线段集合不再产生自相交问题。整个算法如图 5所示。
|
| 图 5 多边形约束条件算法流程图 Fig. 5 The flow chart of polygon constraints algorithm |
3.2.2 格网约束条件
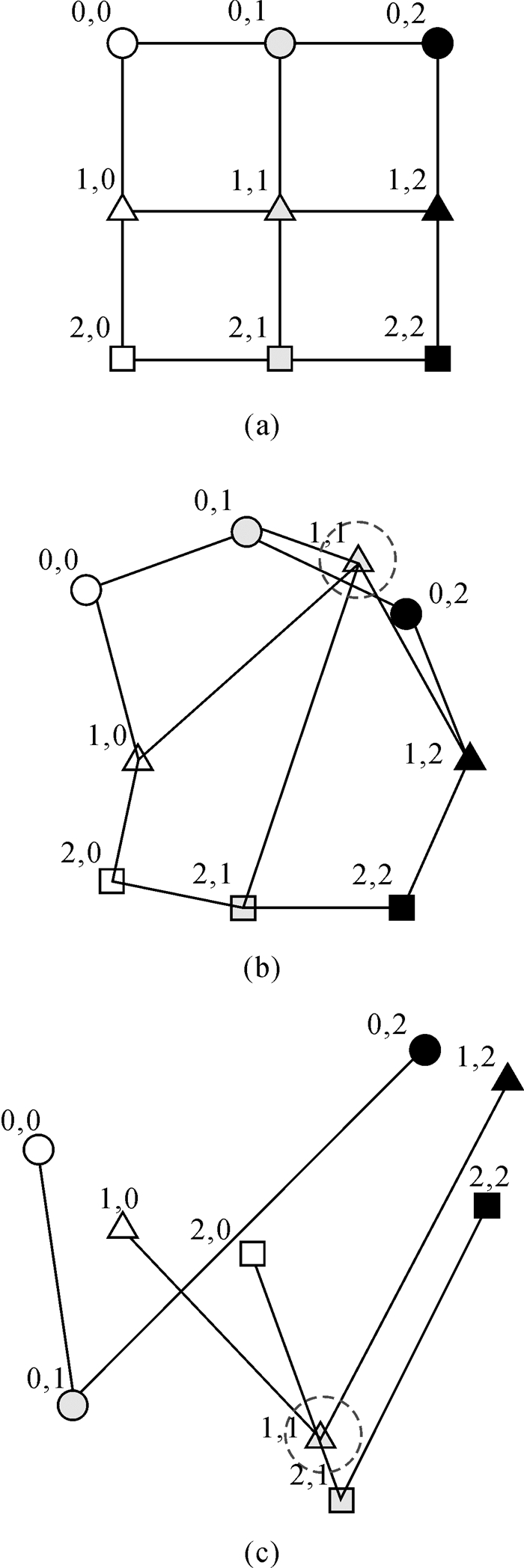
格网的方位关系明确,因此最简单的约束方法是四方向(东、西、南、北)约束,即某一格网点P变换后的位置,无论在X和Y方向上,也都必须介于它在原始格网的相邻两点转换后的位置之间。如果违背了该约束条件,则要调整该点P坐标直至符合四方向约束原则。但是四方向约束并不能完全保证格网的相对位置关系正确,如下图所示,图 6(a)是原始的3×3格网,共9个点,图上标示出每个点的行号和列号。图 6(b),6(c)均是变换后的9个点,虚线圆圈表示的点都符合四方向约束原则,但格网线出现了线交叉。因此有必要将四方向约束原则扩展至八方向约束(东、西、南、北、东南、东北、西南、西北),从而避免线交叉。
|
| 图 6 四方向约束条件下的线交叉现象 Fig. 6 Line crossing in four-direction constraints |
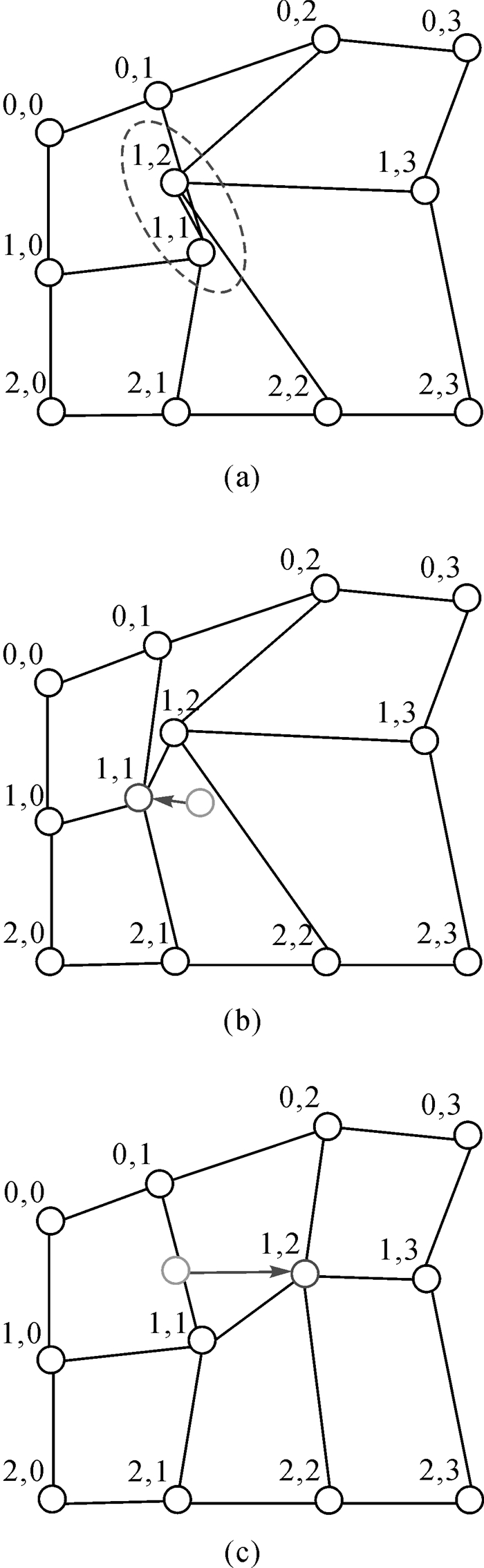
当检测出格网点拓扑冲突时,紧接着需要解决的问题是如何进行有效的调整。如图 7(a)所示,出现拓扑错误的原因是点(1,1)应该在点(1,2)的左边,因此有两种调整策略,一种如图 7(b)所示,保持点(1,2)位置不变,将点(1,1)强行移动到点(1,2)的左边;另一种如图 7(c)所示,保持点(1,1)位置不变,将点(1,2)强行移动到点(1,1)的右边。
|
| 图 7 两种不同移动冲突点的方案 Fig. 7 Two strategies for moving conflict points |
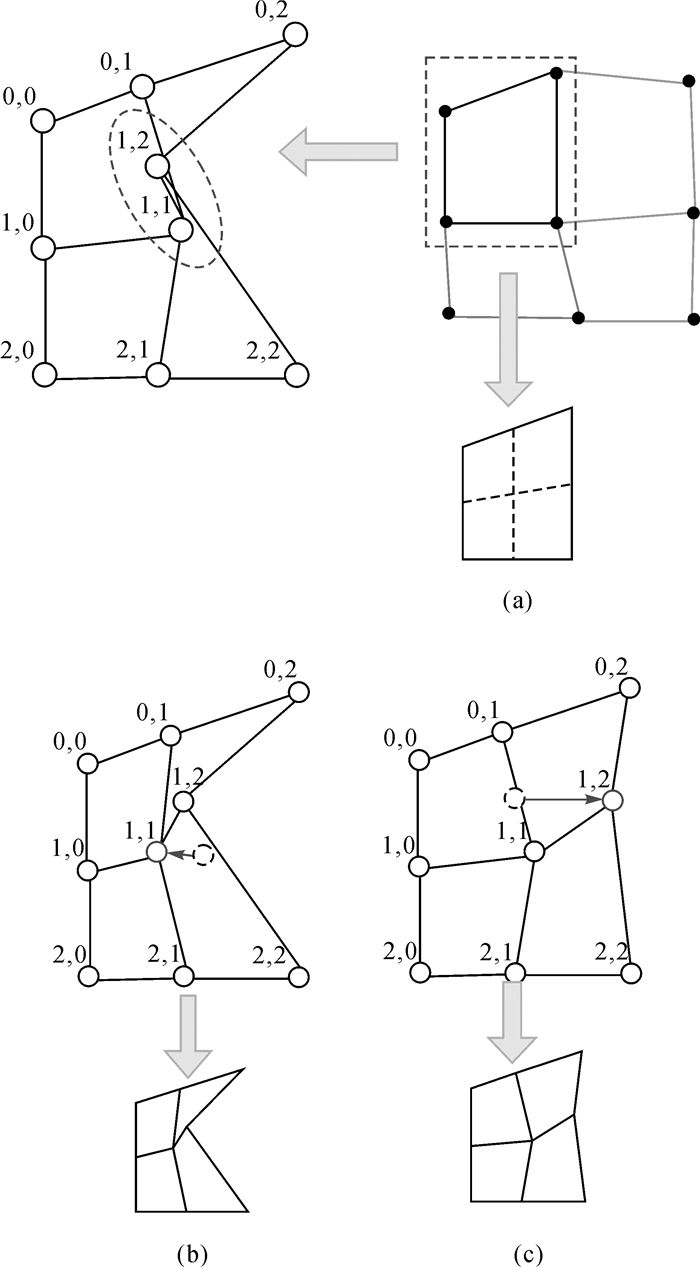
如何对两种方案进行取舍呢?本文取舍的基本依据是在保持拓扑关系相对正确的前提下,能够使调整后的格网保持原来格网的整体变形趋势的方案最优。将格网按照稀疏程度分成若干级别,如2×2格网为第1级别,4×4格网为第2级别,依此类推。假定当第k级格网产生了错误的拓扑关系时,将不同方案调整后的格网和第k-1级格网插值所产生的第k级格网进行比较,从而确定何种方案最优。图 8(a)上是第k-1级格网,其中虚框是第k级格网产生错误拓扑关系的区域。图 8(a)下是由第k-1级格网根据插值预估出来的第k级格网。而图 8(b)下和图 8(c)下则是根据不同方案调整后的简化图,不难发现图 8(c)和图 8(a)在整体形态上更为接近。因此认为图 8(c)调整方案更优。
|
| 图 8 两种方案的比较 Fig. 8 The comparison of two solutions |
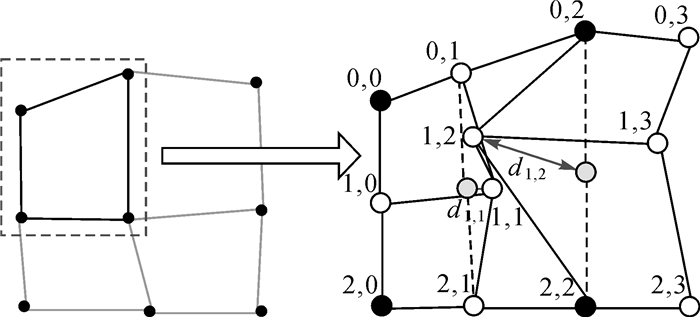
从计算机自动实现的角度而言,比较两个冲突点与上一级格网参考点(该点可能是上一级格网点,也可能是插值点)之间的距离,距离越近,表示该冲突点更好地保持了原格网的整体形态,因此保留距离近的点,移动距离远的点。如图 9所示,黑色格网点表示上一级格网点,灰色点是插值点。图中点(1,2)和点(1,1)为冲突点,显然d1, 2>d1, 1,因此移动点(1,2)。
|
| 图 9 最优方案的计算机自动实现 Fig. 9 The algorithm of determining the optimal solution |
4 实例——以北京市为中心的中国铁路时间地图的构建 4.1 时间数据来源和时间距离的空间转换
近些年中国铁路的快速发展大大加强了区域间的联系,缩短了中心城市与其他城市间的时空距离[25]。为了探索北京市与全国城市间的时间距离关系,本文根据12306网站提供的铁路时刻表,统计了2016年北京市到全国307个市县的最短铁路旅行时间,这里有两点数据说明:
(1) 307个市县中包含具有铁路信息的地级城市,并对如新疆的稀疏区域增加了部分县作为控制点。另外,香港、澳门和台北市的时间数据分别以广州,珠海和福州的时间数据为基础并考虑两者间的空间距离。
(2) 考虑到本研究涉及的空间尺度为国家尺度,对所有市县统一“以点代面”,时间统计不考虑换乘时间,也不考虑同一城市不同车站间的距离(如郑州东站和郑州站均视为“郑州”)。
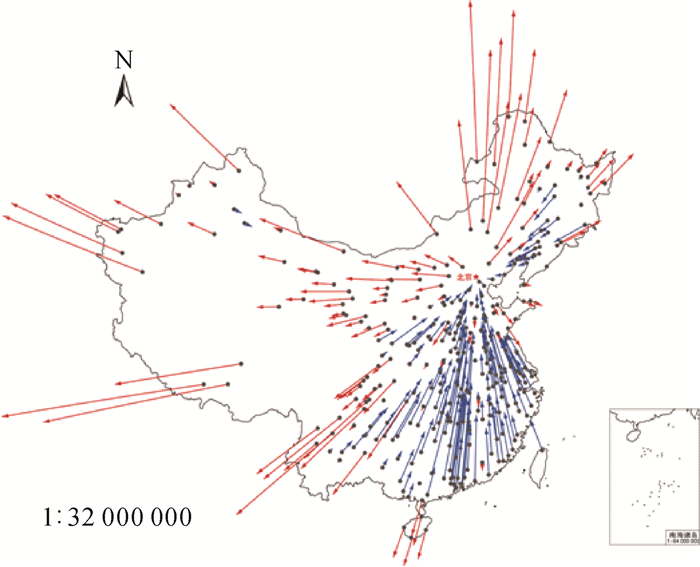
在获得北京市到307个市县的铁路时间后,根据公式(2)、(3),计算获得所有市县变换后的空间坐标和时空转换参数,篇幅所限,下表 1仅列出部分城市的数据。图 10是根据铁路时间获得的307个市县控制点的位置变化。
| 城市名称 | 原始坐标 | 变换后坐标 | 时空变化参数r | |||
| 经度 | 纬度 | 经度 | 纬度 | |||
| 北京 | 116.381 | 39.924 | 116.381 | 39.924 | ||
| 郑州 | 113.650 | 34.757 | 115.031 | 37.369 | 0.494 | |
| 石家庄 | 114.490 | 38.045 | 115.427 | 38.976 | 0.504 | |
| 南京 | 118.773 | 32.048 | 117.658 | 35.719 | 0.534 | |
| 武汉 | 114.292 | 30.568 | 115.257 | 34.891 | 0.538 | |
| 长沙 | 112.981 | 28.201 | 114.492 | 33.410 | 0.556 | |
| 济南 | 117.006 | 36.667 | 116.729 | 38.111 | 0.557 | |
| 广州 | 113.261 | 23.119 | 114.612 | 30.395 | 0.567 | |
| 西安 | 108.949 | 34.262 | 112.151 | 36.701 | 0.569 | |
| 上海 | 121.469 | 31.238 | 119.302 | 34.937 | 0.574 | |
| 天津 | 117.203 | 39.131 | 116.858 | 39.464 | 0.580 | |
| 杭州 | 120.159 | 30.266 | 118.581 | 34.299 | 0.582 | |
| 合肥 | 117.276 | 31.863 | 116.910 | 35.157 | 0.591 | |
| 香港 | 114.154 | 22.281 | 114.987 | 28.875 | 0.626 | |
| 贵阳 | 106.711 | 26.577 | 110.212 | 31.409 | 0.638 | |
|
| 图 10 根据铁路时间获得307个市县点的位置变化,红色箭头表示向外扩张,蓝色表示向内收缩 Fig. 10 Position changes of 307 cities according to the railway time, red vectors devote expansion, while blue indicates shrink |
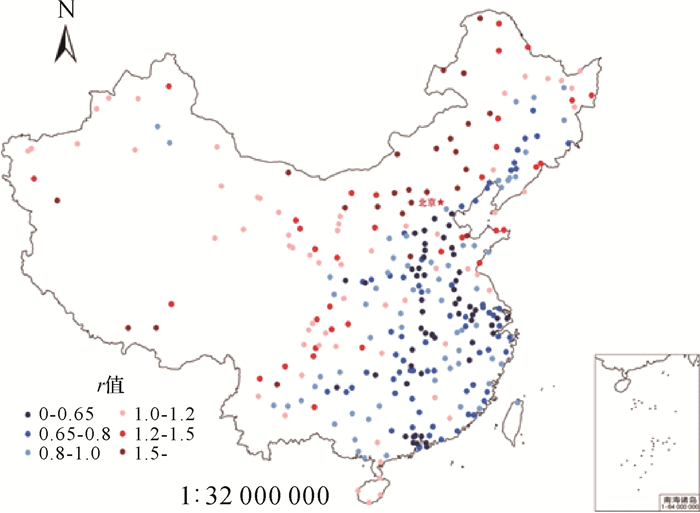
根据时空变化参数r对307个市县点的收缩或扩张程度进行可视化,如图 11示。红色表示该点向外扩张,蓝色表示向内收缩,颜色的深浅表示收缩或扩张程度,颜色越深,程度越大。从图上可以看到,向内收缩的城市主要分布在中国的中部和东南部以及东北部分地区。向外扩张的城市主要分布于中国的北部和西部地区。并且,北京—上海方向和北京—广州方向沿线城市的收缩程度较大,很明显这是因为高铁沿线城市通行时间短,时间收敛较大[1]。
|
| 图 11 中国307个市县点的时间距离收缩或扩张程度图 Fig. 11 The map of China's cities time-space conversion degree |
4.2 大陆边界数据和格网数据的变形转换
由于中国不同区域的铁路交通发展状况很不均衡,空间距离和时间距离难以完全保持正相关性,比如,从北京到广州的空间距离大于北京到厦门的,但是铁路时间距离上却是相反的关系。因此,需要使用约束条件修正边界和格网转换时出现的拓扑错误。
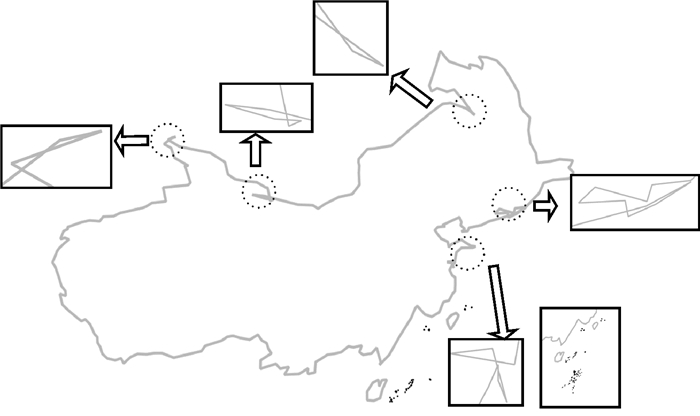
4.2.1 大陆边界数据的变形转换首先需要对1:400万的数据进行综合和简化。根据4.1节中获得的307个市县控制点位置的变化对边界进行移动最小二乘变形转换,结果如图 12所示,台湾岛和海南岛没有产生拓扑错误,但是大陆的边界上有5处拓扑错误。
|
| 图 12 转换后边界出现的拓扑错误 Fig. 12 Topological errors in transformed boundary 本图仅为试验数据,不作为版图展示。 |
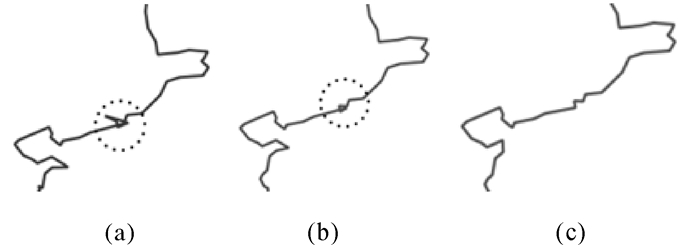
根据多边形约束条件,对大陆边界数据进行处理,图 13(a)到图 13(c)依次是三次迭代的结果,修正了出现的拓扑错误,并对大陆的边界进行了光滑处理。
|
| 图 13 依据约束条件修正边界拓扑错误 Fig. 13 Correct boundary errors based on constrains 本图仅为试验数据,不作为版图展示。 |
4.2.2 格网数据的变形转换
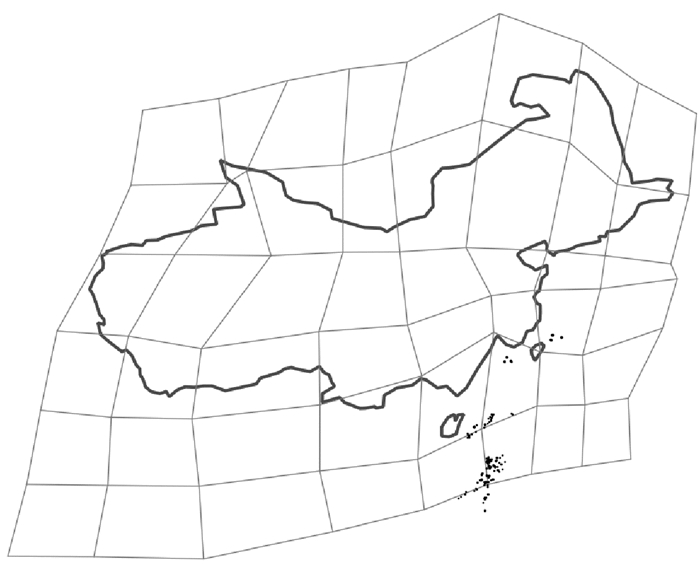
当格网较稀疏时一般不会产生拓扑错误,如图 14是间隔为8度的格网。
|
| 图 14 间隔为8度的格网的变形转换结果 Fig. 14 The result of the transformation of the grids at 8 degree intervals 本图仅为试验数据,不作为版图展示。 |
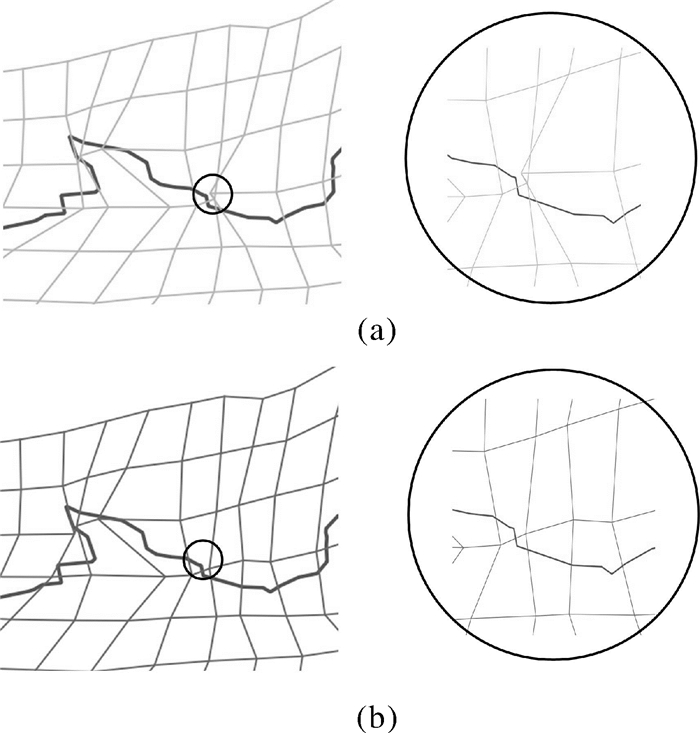
但是当格网进一步加密的时候,则产生了拓扑错误。图 15(a)是间隔为4度的出现拓扑错误的格网,图 15(b)是通过约束条件调整后的格网。
|
| 图 15 间隔为4度的格网变形转换产生的拓扑错误修正 Fig. 15 The correction of topology errors resulting from grids deformation conversion at 4 degree intervals 本图仅为试验数据,不作为版图展示。 |
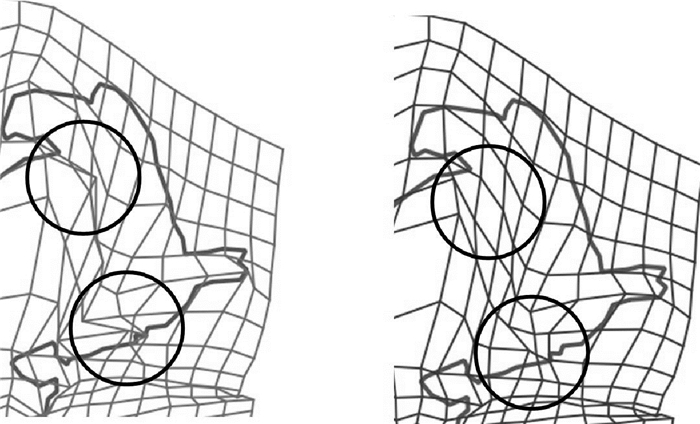
格网再进一步加密,产生的拓扑错误更多。图 16是2度间隔的格网应用约束条件的前后对比图,不难发现格网的拓扑错误得到了有效的修正,且保持了总体的变形特征和趋势。
|
| 图 16 间隔为2度的格网变形转换产生的拓扑错误修正 Fig. 16 The correction of topology errors resulting from grids deformation conversion at 2 degree intervals 本图仅为试验数据,不作为版图展示。 |
4.3 以北京市为中心的时间地图
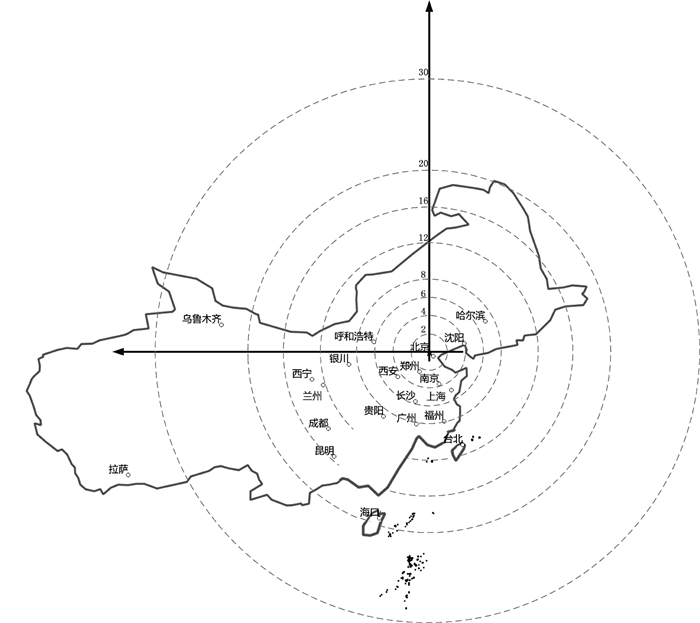
地图数据经过变形转换后,地图上中心点与任意一点的距离表示的是两点之间的时间距离。为了加强可视化效果,让人更容易感知时间距离的大小,以北京为中心,绘制同心圆式等时线,如图 17所示(图幅所限,仅标注部分城市)。从图上可以快速了解北京市与各个城市之间的时间距离关系,比如可快速获知北京市3小时可达城市。
|
| 图 17 以北京为中心的同心圆式等时线图 Fig. 17 The Beijing-centered concentric circular isochronal map 本图仅为试验数据,不作为版图展示。 |
4.4 时间地图空间变形的可视化
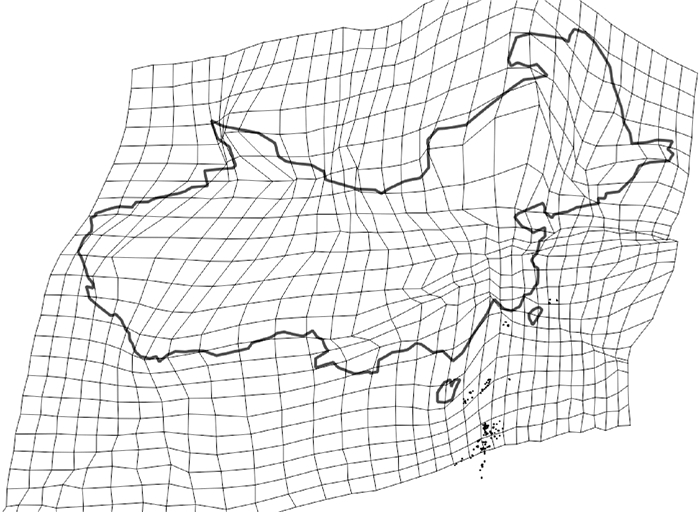
时间地图的空间变形反映的是地理空间和时间空间相互关联程度。从最后变形后的时间地图可以看出,整体上西部和东北部区域向外扩张、东南部向内收缩。并且在东南区域和部分东北区域,变形较为剧烈,且呈现向中心点收缩趋势,而大部分西部区域变形较为均匀,这与该区域具有铁路时间信息的市县点数量较少有关系,如图 18所示。
|
| 图 18 间隔为2度的格网变形表现时间地图的变形 Fig. 18 The deformations of grids at 2 degree intervals the deformations of time-space map 本图仅为试验数据,不作为版图展示。 |
5 总结与展望
本文以真实的铁路时间数据为例,基于带有约束条件的移动最小二乘方法有效地完成了地理空间到时间空间的尺度一致性转换,规避了拓扑错误,并以一种新颖而有效的可视化方法——中心型时间地图表达时间距离。由于该方法从人的心象认知出发,专注于时间距离的表达,能够让人快速认知中心点与周围点之间的时间距离关系。除此以外,通过对地理空间和时间空间模型分布相异性的对比分析,直观地揭示出时间地图的空间变形规律和趋势,并可为进一步的基于时间距离的交通可达性、空间结构变化等研究提供基础。
在该方法的研究基础上,今后的研究重点是进一步挖掘时间距离数据背后隐含的地理规律和趋势,与其他相近数据(如费用)进行对比与分析,深入挖掘不同数据间的关联关系;对比分析不同时间的时间地图以探索时间距离变化过程中的规律和特征。为应对进一步的研究,还需要进一步扩展相关的统计数据,比如在时间数据统计时还需将车次数量作为权重考虑。
| [1] |
蒋海兵, 徐建刚, 祁毅.
京沪高铁对区域中心城市陆路可达性影响[J]. 地理学报, 2010, 65(10): 1287–1298.
JIANG Haibin, XU Jiangang, QI Yi. The Influence of Beijing-Shanghai High-Speed Railways on Land Accessibility of Regional Center Cities[J]. Acta Geographica Sinica, 2010, 65(10): 1287–1298. DOI:10.11821/xb201010013 |
| [2] |
靳海攀, 郑林, 张敬伟.
基于时间距离的鄱阳湖生态经济区经济联系变化网络分析研究[J]. 经济地理, 2013, 33(6): 148–154.
JIN Haipan, ZHENG Lin, ZHANG Jingwei. Network Analysis of Economic Contacts Variability in Poyang Lake Ecological Economic Zone based on Travel Time Cost[J]. Economic Geography, 2013, 33(6): 148–154. |
| [3] |
余金艳, 刘卫东, 王亮.
基于时间距离的C2C电子商务虚拟商圈分析——以位于北京的淘宝网化妆品零售为例[J]. 地理学报, 2013, 68(10): 1380–1388.
YU Jinyan, LIU Weidong, WANG Liang. Analysis of Virtual Trading Area of C2C E-commerce based on Temporal Distance:A Case Study of 50 Cosmetics Retail Stores on TAOBAO in Beijing[J]. Acta Geographica Sinica, 2013, 68(10): 1380–1388. DOI:10.11821/dlxb201310007 |
| [4] |
陆军, 宋吉涛, 梁宇生, 等.
基于二维时空地图的中国高铁经济区格局模拟[J]. 地理学报, 2013, 68(2): 147–158.
LU Jun, SONG Jitao, LIANG Yusheng, et al. The Simulation of Spatial Distribution Patterns of China's HSR-economic Zones based on the 2D Time-space Map[J]. Acta Geographica Sinica, 2013, 68(2): 147–158. DOI:10.11821/xb201302001 |
| [5] |
王永超, 吴晓舜, 刘洋, 等.
基于可达性的沈阳经济区中心地空间结构演变[J]. 地域研究与开发, 2013, 32(1): 56–60.
WANG Yongchao, WU Xiaoshun, LIU Yang, et al. The Evolution of the Structure of Central Places in Shenyang Economic Zone Based on Accessibility[J]. Areal Research and Development, 2013, 32(1): 56–60. |
| [6] | BUNGE W. Theoretical Geography[D]. Washington: University of Washington, 1960. |
| [7] | TOBLER W R. Map Transformations of Geographic Space[D]. Washington: University of Washington, 1961. |
| [8] |
王丽娜, 江南, 李响, 等.
Cartogram表示方法研究综述[J]. 计算机辅助设计与图形学学报, 2017, 29(3): 393–405.
WANG Lina, JIANG Nan, LI Xiang, et al. A Survey of Cartogram[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(3): 393–405. |
| [9] | BUCHIN K, VAN GOETHEM A, HOFFMANN M, et al. Travel-Time Maps: Linear Cartograms with Fixed Vertex Locations[C]//Proceedings of the 8th International Conference on Geographic Information Science. Vienna, Austria: Springer International Publishing, 2014: 18-33. |
| [10] | KAISER C, WALSH F, FARMER C J Q, et al. User-centric time-distance representation of road networks[C]//Proceedings of the 6th International Conference on Geographic Information Science. Berlin Heidelberg: Springer, 2010: 85-99. |
| [11] | AXHAUSEN K W, DOLCI C, FR? HLICH P, et al. Constructing Time-Scaled Maps:Switzerland from 1950 to 2000[J]. Transport Reviews, 2008, 28(3): 391–413. DOI:10.1080/01441640701747451 |
| [12] | SHIMIZU E, INOUE R. A New Algorithm for Distance Cartogram Construction[J]. International Journal of Geographical Information Science, 2009, 23(11): 1453–1470. DOI:10.1080/13658810802186882 |
| [13] | AHMED N, MILLER H J. Time-Space Transformations of Geographic Space for Exploring, Analyzing and Visualizing Transportation Systems[J]. Journal of Transport Geography, 2007, 15(1): 2–17. DOI:10.1016/j.jtrangeo.2005.11.004 |
| [14] |
何亚坤, 艾廷华, 禹文豪.
等时线模型支持下的路网可达性分析[J]. 测绘学报, 2014, 43(11): 1190–1196.
HE Yakun, AI Tinghua, YU Wenhao. Accessibility Analysis of Road Network Supported by Isochrone Model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1190–1196. DOI:10.13485/j.cnki.11-2089.2014.0183 |
| [15] |
李文翎, 李尚智, 黎雅雯, 等.
基于GIS的广州城市时间地图研究[J]. 热带地理, 2008, 8(3): 218–222, 227.
LI Wenling, LI Shangzhi, LI Yawen, et al. A Study on Urban Temporal Map of Guangzhou Based on GIS Based on GIS[J]. Tropical Geography, 2008, 8(3): 218–222, 227. |
| [16] | HONG S, KIM Y S, YOON J C, et al. Traffigram: Distortion for Clarification via Isochronal Cartography[C]//Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. Toronto, Ontario, Canada: ACM Press, 2014: 907-916. |
| [17] | BIES S, VAN KREVELD M. Time-Space Maps from Triangulations[C]//Proceedings of the 20th International Conference on Graph Drawing. Redmond, WA: Springer, 2012: 511-516. |
| [18] | ULLAH R, KRAAK M J. An Alternative Method to Constructing Time Cartograms for the Visual Representation of Scheduled Movement Data[J]. Journal of Maps, 2015, 11(4): 674–687. DOI:10.1080/17445647.2014.935502 |
| [19] |
刘瑜, 龚咏喜, 张晶, 等.
地理空间中的空间关系表达和推理[J]. 地理与地理信息科学, 2007, 23(5): 1–7.
LIU Yu, GONG Yongxi, ZHANG Jing, et al. Representation and Reasoning of Spatial Relations in Geographical Space[J]. Geography and Geo-information Science, 2007, 23(5): 1–7. |
| [20] |
沈陈华, 王旭姣, 司亚莉, 等.
基于旅行者运动轨迹的时间地图变换[J]. 地理研究, 2015, 34(6): 1160–1172.
SHEN Chenhua, WANG Xujiao, SI Yali, et al. Time-space Map Transformation Based on Travelers' Motion Trajectory[J]. Geographical Research, 2015, 34(6): 1160–1172. |
| [21] | SCHAEFER S, MCPHAIL T, WARREN J. Image deformation using moving least squares[J]. ACM Transactions on Graphics (TOG), 2006, 25(3): 533–540. DOI:10.1145/1141911 |
| [22] |
刘婷. 移动最小二乘图像变形方法研究[D]. 大连: 大连理工大学, 2008. LIU Ting. Study on Image Deformation Based on Moving Least Squares[D]. Dalian: Dalian University of Technology, 2008. |
| [23] |
杜晓荣, 平淑文, 张永.
基于移动最小二乘法的图形图像局部变形技术[J]. 系统仿真学报, 2015, 27(4): 816–823.
DU Xiaorong, PING Shuwen, ZHANG Yong. Graphics and Image Local Deformation Based on Moving Least Squares Method[J]. Journal of System Simulation, 2015, 27(4): 816–823. |
| [24] | BENTLEY J L, OTTMANN T A. Algorithms for Reporting and Counting Geometric Intersections[J]. IEEE Transactions on Computers, 1979, 28(9): 643–647. |
| [25] |
王士君, 冯章献, 刘大平, 等.
中心地理论创新与发展的基本视角和框架[J]. 地理科学进展, 2012, 31(10): 1256–1263.
WANG Shijun, FENG Zhangxian, LIU Daping, et al. Basic Perspective and Preliminary Framework for the Theoretical Innovation and Development of Central Place Theory in New Times[J]. Progress in Geography, 2012, 31(10): 1256–1263. DOI:10.11820/dlkxjz.2012.10.002 |



