2. 信息工程大学地理空间信息学院, 河南 郑州 450001;
3. 西安测绘研究所, 陕西 西安 710000;
4. 中国电子科技集团公司第三十九研究所, 陕西 西安 710065
2. School of Geographic Spatial Information, Information Engineering University, Zhengzhou 450001, China;
3. Xi'an Institute of Surveying and Mapping, Xi'an 710000, China;
4. No. 39 Research Institute, China Electronics Technology Group Corporation, Xi'an 710065, China
随着甚长基线干涉测量(VLBI)技术在天体物理、天体测量、大地测量和深空探测等领域应用的深入[1-9],有时需要在有限场地内建造一面以上的射电望远镜(射电天线),彼此之间的可能遮掩问题是不容忽视的。关于具体的测站位置选取,还需考虑地形(山体、台地)、周围建筑等静态地物的遮掩,以及无线电环境、气候、水文、地质等复杂因素[10-16]。
本文从一具体的工程实践需求出发,探讨有限场地条件下两射电天线间的互掩问题。具体为,中国科学院上海天文台佘山25 m射电天线自1987年开始运行[17],设计寿命15 a,至今已超期服役十数载,结构、面板、电子接收设备等均已过于陈旧。尤其是在S波段主动发射干扰日益严重的情况下,亟须依照天体测量与空间大地测量新一代VLBI技术标准(VLBI2010)研建新的测量系统[18-21]。考虑到观测资料时间序列的系统延续性[22],新旧测量系统并行工作一段时间是非常必要的,为此计划在佘山25 m射电天线现有园区新建13 m天线测量系统。本文依据具体的场地条件分析两天线间的互掩问题,为新建系统的位置选取、塔基高度设计等提供理论支持。分析方法也可供类似工程实践参考。
1 分析素材与基本考虑 1.1 佘山25 m天线参考点的地面高度计算机技术成功应用于机械控制领域之后,新建射电天线普遍采用地平式(方位俯仰座架),以方便实现对天体周日视运动和有限远目标轨道运动的精确跟踪[1]。所谓方位俯仰座架,即用于跟踪观测目标、采集电磁信号的天线,其指向可以在方位、俯仰两维方向旋转,分别由相互独立、并由计算机协调控制的电机系统予以驱动。一般设计为两等效旋转轴相交、且彼此正交,如此以保持在天线不同指向时,信号传输的电路径长度基本恒定,有效规避后续信号处理的复杂化。在具体的结构设计上分为轮轨式和转台式。前者适用于大型天线,结构稳固,转速较慢。后者适用于小型天线,结构紧凑,转速较快。一般地,将两旋转轴的交点称为射电天线的参考点,或者本地不动点、旋转中心等。
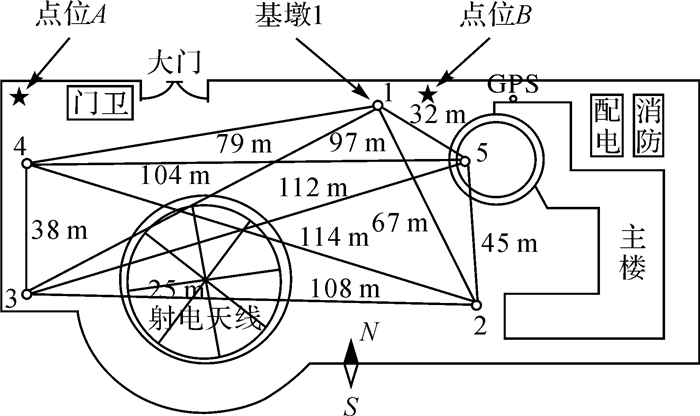
根据2008年佘山25 m射电天线归心测量[23, 24],局域网布设如图 1所示,基墩1顶面的地面高度约1.0 m。此顶面至25 m天线旋转中心的垂直距离约15.5 m。如此推算得25 m天线参考点的地面高度约16.5 m。此推算值与根据施工图纸估算的地面高度十分接近。
|
| 图 1 佘山25 m天线园区与局域网 Fig. 1 The yard of the 25 m antenna at Sheshan and the local control network |
1.2 佘山25 m天线外接球面的半径
假设天线结构和主反射面均为纯正的几何体,不存在各种(重力、热、风载)形变和加工、安装等误差。不难理解,方位俯仰座架下,天线口面边缘上所有点到天线参考点的距离都相等,且不随天线的不同指向而变化。设此距离为d,于是在天线不同指向时,口面边缘描绘出的空间轨迹位于以天线参考点为心、以d为半径的球面上,称此球面为天线的外接球面。
为尽量减小风、雨雪、冰雹和温度变化等环境因素对天线的影响,有时对天线建造外围保护罩。一般采用(多面体)球状结构,且考虑到形变、机械加工和施工误差等因素,其半径略大于上述外接球面半径。已存在许多此类工程实践,因而上述天线外接球面的概念是成立的。
对于佘山25 m天线,此外接球面半径可以从2008年的归心测量[23]数据中予以估算,也可以根据设计图纸进行估计,具体约为14.0 m。
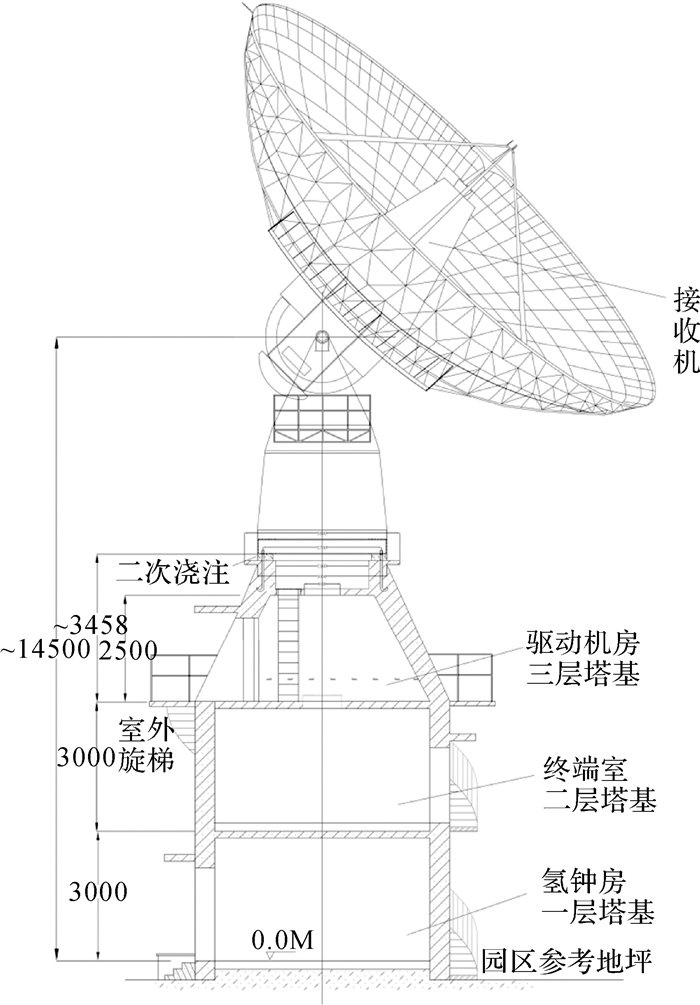
1.3 拟建13 m天线参考点的设计高度和外接球面半径依照图 2,拟建13 m天线参考点的设计地面高度约14.5 m。由仿真和设计图纸,其外接球面的半径约8.3 m。
|
| 图 2 13 m天线塔基设计 Fig. 2 Design of supporting tower of the 13 m antenna |
1.4 两天线水平距离
图 1所示的佘山25 m天线园区示意中,点位A、B至25 m天线参考点的水平距离分别约为50.0 m、80.0 m。
1.5 基本考虑对于天线乙某一给定的指向,若天线甲对天线乙构成了遮掩,即表明天线甲在以天线乙(参考点)为中心的球面上的投影面积S不为零,亦即天线甲对天线乙所张的立体角Ω不为零。若此球面的半径为R,则Ω=S/R2。显然,此Ω的具体取值有关于天线甲的具体结构和具体指向,但是限定在天线甲外接球面对乙所构成的立体角范围之内。
常规天测与测地VLBI观测S/X波段配置时,单颗河外射电源的跟踪积分时间约为2~5 min,每期(session)24 h(小时)约观测500颗源,且为从实测资料解算天顶方向对流层附加延迟改正,所测源须尽量全天均匀分布,大小方位角和高低仰角等须频繁交替观测。在VLBI2010技术标准下(如此处的13 m天线),单源积分时间短于1 m,天线将更加频繁地大范围切换指向。可见,分析两VLBI天线系统的动态互掩问题,两天线特定指向下的互掩并非关键,重点在于确定一天线外接球面对于另一天线的立体角大小。
2 球冠与球冠缺的面积及对球心的立体角 2.1 球冠如图 3所示,不难证明球心半张角为ϕ、球半径为R的球冠的面积S为
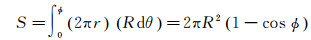 (1)
(1)

|
| 图 3 球冠面积与对球心的立体角 Fig. 3 The area of a spherical crown and its solid angle to the sphere center |
式中,r、θ为积分变量,且r=Rsin θ,以及θ自球冠顶点O起算,最大值为球冠对球心的半张角ϕ。S对球心所张的立体角Ω(球面上的面积与球半径平方之比)为
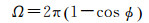 (2)
(2)
单位为平方弧度(sr)。
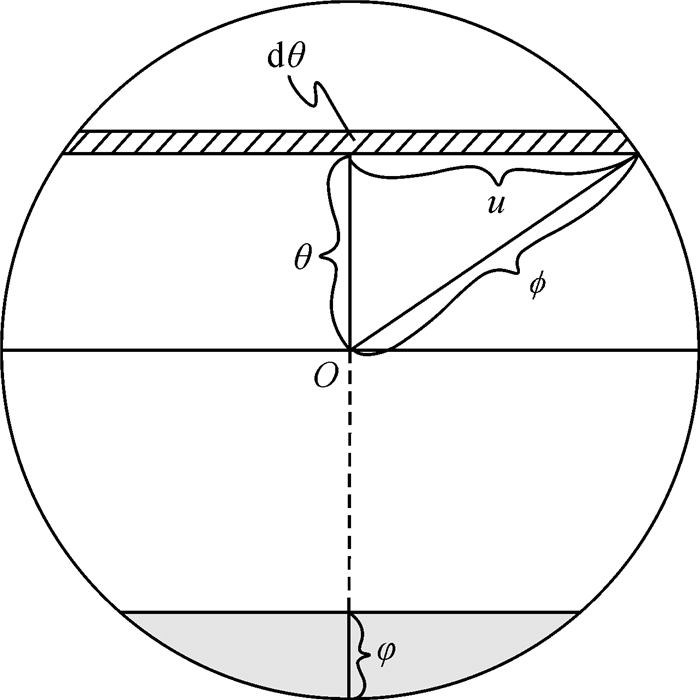
2.2 球冠缺将图 3所示球冠以顶点O为中心进行俯视投影,如图 4所示,ϕ的定义不变。θ、u均为球面上的弧长。θ自顶点O起算、向上为正。注意θ在图 3中的域值范围为[0, ϕ],而在图 4中则为[-ϕ, ϕ]。θ为积分变元,只要正确应用上、下限,则此差异不影响积分结果。
|
| 图 4 球冠和球冠缺面积的数值积分计算 Fig. 4 Numerical integral of the area of spherical crown and crown part |
如图 4所示,θ为沿过球冠顶点的大圆弧,u为小圆弧且与θ正交,二者与大圆弧长ϕ构成了球面直角三角形,由边的余弦公式[25]
 (3)
(3)
由小圆弧与大圆弧的关系,式(3)表示为
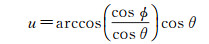 (4)
(4)
(可类比理解为,地理纬度ϕ处,经度变化λ时的大圆弧长为λcos ϕ。)因而球冠的面积为
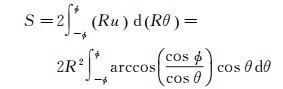 (5)
(5)
式(5)的显式积分结果不易推导,可采用数值积分方法予以近似计算,进而得球冠对球心的立体角为
 (6)
(6)
式中,R为球的半径。
球冠缺情况下,即球冠被某平面截除了如图 4灰色区域所示部分之后所剩余的部分。简单起见,假设此截平面与变元u所在平面平行,并假设自下边缘向球冠顶点方向缺失了φ(球心角、大圆弧),此时的球冠缺面积可由式(5)通过改变积分下限获得,即
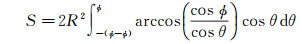 (7)
(7)
球冠缺对球心的立体角仍如式(6)。
由式(5)、式(7)经数值积分所得球冠、球冠缺的面积仅为近似值。为提高球冠缺情况下数值积分近似计算的精度,若球冠缺大于半个球冠,可首先应用式(1)精确计算半个球冠的面积,再近似计算剩余面积(图 4中虚线所示区域),此时球冠缺的面积为
 (8)
(8)
若球冠缺小于半个球冠,则直接应用式(7)。
为检验数值积分近似计算的精度,假设ϕ=20°,由式(2)得球冠对球心的立体角精确值约为1 243.929 0平方度(sd)。取dθ的步长分别为2.5、1.0、0.1、0.01、0.001和0.000 1°,φ=0时(为整个球冠、未被截取)由式(7)得到的对应立体角数值积分计算值分别约为1 224.030 8、1 238.887 7、1 243.769 4、1 243.923 9、1 243.928 8和1 243.929 0 sd。比较可见,数值积分的步长越小则所得计算结果与真值之差便越小,但是计算时间肯定将越长。当积分步长不大于0.01°时,数值积分结果的最大相对误差远小于0.001%,可见此处设计的球冠(缺)数值积分方法是可行的,作为射电天线互掩问题的近似估计,其计算精度已经足够。
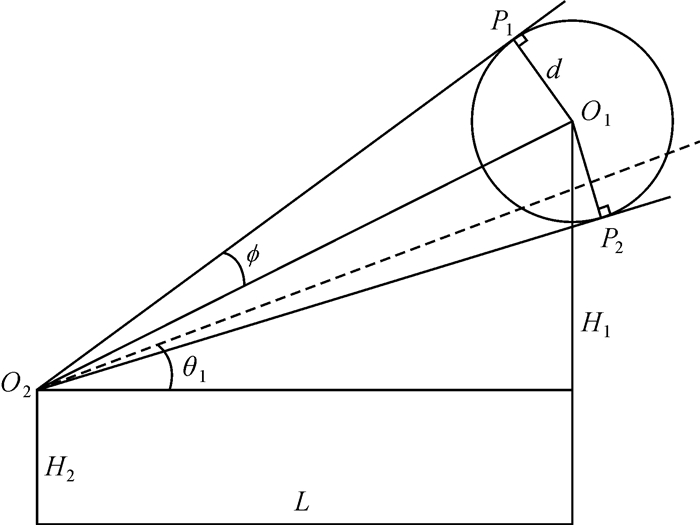
3 互掩分析与计算 3.1 遮掩分析如图 5所示,设天线1、2的参考点分别为O1、O2,高度分别为H1、H2,水平距离为L,天线1的外接球面半径为d。由图 5所示几何关系易得
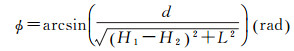 (9)
(9)
|
| 图 5 遮掩分析 Fig. 5 Analysis of shielding effect |
此即天线1外接球面对天线2遮掩所成球冠的半张角。
设图 5中θ1为天线2的截止观测仰角。若天线1对天线2的遮掩球冠位于θ1以上,为完整球冠情况,可直接由式(2)计算天线1对天线2的遮掩立体角。若遮掩球冠位于θ1以下,则显然不构成有效遮掩, 或遮掩为0。若介于上述两种情况之间时,如图 6所示,为侧视图,各量定义同图 4、图 5。其中,灰色区域代表天线1外接球面对天线2的遮掩球冠。天线1对天线2构成了遮掩,但并非完整球冠,而是以O2处仰角为θ1的等高圈截除后的剩余部分,即图 6中灰色、非阴影部分。有效遮掩为球冠缺的面积和立体角计算情况,深灰色区域所示为积分变元(ϕ、θ、u、φ等的定义同图 4)。球冠缺小于半个球冠时可应用式(7),球冠缺大于半个球冠时可应用式(8)。

|
| 图 6 互掩计算 Fig. 6 Calculation of the shielding effect |
3.2 遮掩计算
由于地表附近的水汽分布极其不均匀,大气对射电波的湿延迟修正误差较大,因而在常规天测与测地VLBI观测试验中一般限定观测的截止俯仰角不小于5°(文献[2])。
如前文所述,13 m天线的参考点高度约14.5 m、外接球面半径约8.3 m。25 m天线的参考点高约16.5 m、外接球面半径约14.0 m。可见25 m天线参考点位于13 m天线参考点地平以上。13 m天线分别位于图 1所示点位A、B时,25 m天线对13 m天线的遮掩均为球冠缺情况,具体计算结果如表 1所示。从中可见,由于13 m天线位于图 1所示点位A时的距离相对较近,限定5°截止仰角时25 m天线所形成的遮掩较大,约324.3 sd。考虑到5°以上天区面积约18 829 sd,此遮掩不足1.8%,尚非特别严重。若13 m天线位于图 1所示的点位B,对应数据小于0.5%,遮掩情况有所改善。
| 点位 | L /m | H1 /m | H2 /m | r /m | ϕ /(°) | -(ϕ-φ) /(°) | Ω /(sd) |
| 观测截止仰角0° | |||||||
| A | 50 | 16.5 | 14.5 | 14.0 | 16.2 | -2.3 | 486.5 |
| B | 80 | 10.1 | -1.4 | 187.8 | |||
| 观测截止仰角5° | |||||||
| A | 50 | 16.5 | 14.5 | 14.0 | 16.2 | 2.7 | 324.3 |
| B | 80 | 10.1 | 3.6 | 88.7 | |||
13 m天线对25 m天线的遮掩计算结果如表 2所示。5°以上的遮掩仅约为可观测天区的0.1%,基本可忽略。
| 点位 | L /m | H1 /m | H2 /m | r /m | ϕ /(°) | -(ϕ-φ) /(°) | Ω /(s-deg) |
| 观测截止仰角0° | |||||||
| A | 50 | 14.5 | 16.5 | 8.3 | 9.5 | 2.3 | 99.6 |
| B | 80 | 6.0 | 1.4 | 38.7 | |||
| 观测截止仰角5° | |||||||
| A | 50 | 14.5 | 16.5 | 8.3 | 9.5 | 7.3 | 18.9 |
| B | 80 | 6.0 | 6.4 | 0.0 | |||
若其他条件保持不变,仅将13 m天线参考点的设计高度从目前的14.5 m降低为13.5 m,25 m天线造成的遮掩情况如表 3所示。与表 1中对应数据的比较可见,限定截止仰角为5°,点位A时13 m天线参考点的降低所造成的被25 m天线遮掩的天区面积增加较为显著,降低1 m对应于增加遮掩约36 sd。点位B处对应的增加仅约14 sd。类似计算表明,若13 m天线参考点增高至15.5 m,25 m天线遮掩约分别减少36、13 sd。总之,13 m天线位于图 1中的点位A时,两天线相对较近,存在一定的相互遮掩问题,但尚可接受。相比而言,位于点位B时的情况略好、即互掩略小。
| 点位 | L /m | H1 /m | H2 /m | r /m | ϕ /(°) | -(ϕ-φ) /(°) | Ω /(sd) |
| 截止仰角0° | |||||||
| A | 50 | 16.5 | 13.5 | 14.0 | 16.2 | -3.4 | 516.3 |
| B | 80 | 10.1 | -2.1 | 200.4 | |||
| 截止仰角5° | |||||||
| A | 50 | 16.5 | 13.5 | 14.0 | 16.2 | 1.6 | 360.3 |
| B | 80 | 10.1 | 2.9 | 102.3 | |||
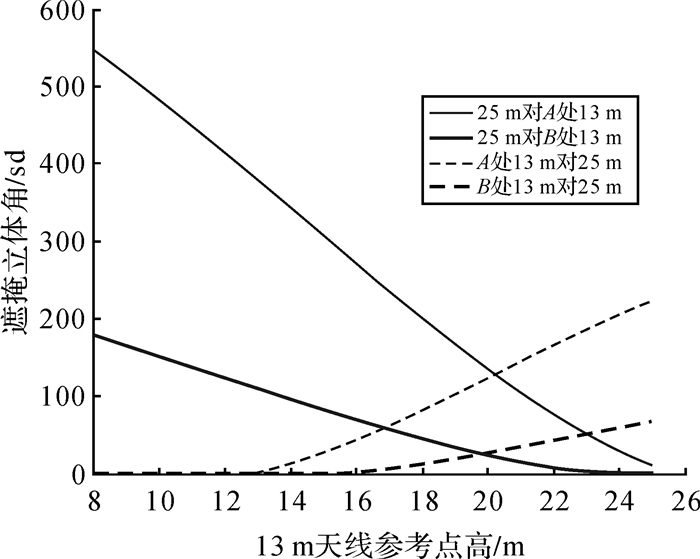
再次,仅改变13 m天线参考点的高度、即改变其塔基设计高度,两天线的互掩情况如图 7所示,其中“25 m对A处13 m”表示13 m天线位于图 1中点位A时,5°以上截止仰角25 m天线所形成的遮掩,其他类推。可见,随着13 m天线参考点高度的增加,25 m天线所构成的遮掩基本为线性减小,13 m对25 m天线的遮掩则线性增加。若取13 m天线参考点约高20 m时,两天线的互掩基本相当。但是考虑到塔基越高,所受到的风载、温载形变和不均匀沉降的影响将越大,因而采用目前14.5 m高度的13 m天线参考点设计是基本合理和可接受的。
|
| 图 7 两天线互掩随13 m天线参考点高度的变化 Fig. 7 Mutual shielding effect of the two antennas versus the height of reference point of the 13 m antenna |
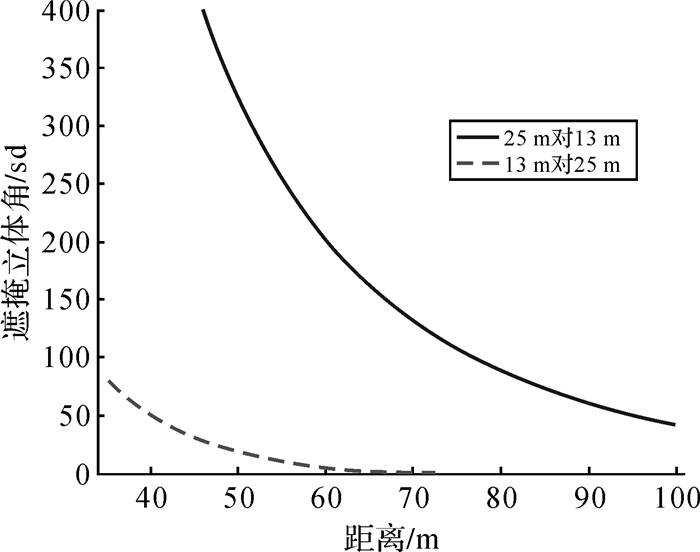
若保持两天线参考点高度及外接球面半径不变,仅改变彼此之间的水平距离,5°观测截止仰角下的互掩情况如图 8所示。如所预期,距离给定时,25 m天线对13 m天线的遮掩要相对严重。在水平距离40~100 m范围之内,25 m天线对13 m天线的遮掩基本为线性变化。具体考证表明,5°观测截止仰角下,水平距离大于72.4 m时,13 m天线不对25 m天线构成遮掩,水平距离大于183.5 m时,25 m天线不对13 m天线构成遮掩。
|
| 图 8 两天线互掩随彼此之间水平距离的变化 Fig. 8 Mutual shielding effect of the two antennas versus the horizontal distance |
4 结论与讨论
基于实际工程建设需要,本文分析了有限场地内两射电天线的互掩问题,给出了具体的分析方法和计算结果。结论为,依照目前工程建设和设计参数,13 m天线位于图 1所示点位A时,5°截止仰角25 m天线所造成的天区遮掩约占可观测天区的1.8%,并非特别严重。点位B时略好,不足0.5%。但是点位B更靠近园区内主楼(如图 1所示,高约8 m),属于不利因素。13 m天线塔基设计高度也是影响遮掩情况的显著因素,兼顾风载、温载和不均匀沉降等因素的影响,采用目前14.5 m的设计是可以接受的。本文分析方法和分析结果对于工程实施中的站点位置选取、天线塔基高度设计等具有参考意义。分析方法也可供类似工程实践参考。
| [1] | THOMPSON A R, MORAN J M, SWENSON Jr G W. Interferometry and Synthesis in Radio Astronomy[M]. 2nd ed. New York: John Wiley & Sons, Inc., 2001. |
| [2] | ROLAND J, BRITZEN S, KUDRYAVTSEVA N A, et al. Modeling Nuclei of Radio Galaxies from VLBI Radio Observations: Application to the BL Lac Object S51803+784[J]. Astronomy & Astrophysics, 2008, 483(1): 125–135. |
| [3] | SOVERS O J, FANSELOW J L, JACOBS C S. Astrometry and Geodesy with Radio Interferometry: Experiments, Models, Results[J]. Reviews of Modern Physics, 1998, 70(4): 1393–1454. DOI:10.1103/RevModPhys.70.1393 |
| [4] | CARTER W E, ROBERTSON D S, PYLE T E, et al. The Application of Geodetic Radio Interferometric Surveying to the Monitoring of Sea-level[J]. Geophysical Journal International, 1986, 87(1): 3–13. DOI:10.1111/gji.1986.87.issue-1 |
| [5] | HEKI K, TAKAHASHI Y, KONDO T, et al. The Relative Movement of the North American and Pacific Plates in 1984-1985, Detected by the PACIFIC VLBI Network[J]. Tectonophysics, 1987, 144(1-3): 151–158. DOI:10.1016/0040-1951(87)90014-X |
| [6] | LI Jinling, GUO Li, QIAN Zhihan, et al. The Application of the Instantaneous States Reduction to the Orbital Monitoring of Pivotal Arcs of the Chang'E-1 Satellite[J]. Science in China Series G: Physics, Mechanics and Astronomy, 2009, 52(12): 1833–1841. DOI:10.1007/s11433-009-0279-7 |
| [7] | LI Jinling, GUO Li, QIAN Zhihan, et al. Determination of the Controlled Landing Trajectory of Chang'E-1 Satellite and the Coordinate Analysis of the Landing Point on the Moon[J]. Chinese Science Bulletin, 2010, 55(13): 1240–1245. DOI:10.1007/s11434-010-0093-7 |
| [8] |
李金岭, 张津维, 刘鹂, 等.
应用于深空探测的VLBI技术[J]. 航天器工程, 2012, 21(2): 62–67.
LI Jinling, ZHANG Jinwei, LIU Li, et al. VLBI Technique Applied in Deep Space Exploration[J]. Spacecraft Engineering, 2012, 21(2): 62–67. |
| [9] |
李金岭, 刘鹂, 马茂莉, 等.
中国VLBI网火星快车卫星跟踪资料的定位归算[J]. 宇航学报, 2010, 31(7): 1718–1723.
LI Jinling, LIU Li, MA Maoli, et al. Positioning Reduction of the Mars Express Tracking Data by the Chinese VLBI Network[J]. Journal of Astronautics, 2010, 31(7): 1718–1723. |
| [10] |
李维华, 胡汉明, 陈国强, 等.
毫米波射电天文观测站选址报告[J]. 云南天文台台刊, 1987(2): 90–98.
LI Weihua, HU Hanming, CHEN Guoqiang, et al. Report of Site Selection for a Millimeter Wave Radio Astronomical Station[J]. Publications of Yunnan Observatory, 1987(2): 90–98. |
| [11] |
侯金良.
天文选址的主要参数及测量方法[J]. 天文学进展, 1994, 12(2): 126–132.
HOU Jinliang. Site Testing Parameters and Their Measurements[J]. Progress in Astronomy, 1994, 12(2): 126–132. |
| [12] |
吴晓庆, 马成胜, 翁宁泉, 等.
一种用于天文台选址的气象参数和大气湍流测量系统[J]. 量子电子学报, 2001, 18(2): 184–187.
WU Xiaoqing, MA Chengsheng, WENG Ningquan, et al. A Meteorological Parameter and Atmospheric Turbulence Measurement System for Locating Astronomical Observatory[J]. Chinese Journal of Quantum Electronics, 2001, 18(2): 184–187. |
| [13] |
楼柯, 刘忠, 吴铭蟾, 等.
云南红外太阳塔选址及其结果[J]. 云南天文台台刊, 2002(4): 60–67.
LOU Ke, LIU Zhong, WU Mingchan, et al. Site Test for Infrared Solar Tower in Yunnan[J]. Publications of Yunnan Observatory, 2002(4): 60–67. |
| [14] |
彭骏, 马振锋.
青藏高原东坡加密观测站址选取分析[J]. 高原气象, 2004, 23(Sl): 150–155.
PENG Jun, MA Zhenfeng. Analysis on Selecting Intensive Meteorological Observing Station Locations on the East Side of Qinghai-Xizang Plateau[J]. Plateau Meteorology, 2004, 23(Sl): 150–155. |
| [15] |
徐八林, 刘黎平, 杨明, 等.
高山雷达站选址对估测降水的影响分析[J]. 气象科技, 2006, 34(3): 340–343.
XU Balin, LIU Liping, YANG Ming, et al. Impact Analysis of Radar Location on Precipitation Estimation over Alpine Areas[J]. Meteorological Science and Technology, 2006, 34(3): 340–343. |
| [16] |
刘文建, 阳力.
CORS参考站选址的探讨[J]. 地理空间信息, 2008, 6(6): 53–55.
LIU Wenjian, YANG Li. Research on CORS Reference Station Location[J]. Geospatial Information, 2008, 6(6): 53–55. |
| [17] |
钱志瀚.
甚长基线干涉仪测量余山地区的地壳垂直运动[J]. 中国科学院上海天文台年刊, 1996(17): 52–56.
QIAN Zhihan. Determination of the Crustal Vertical Motion at Sheshan Area, Shanghai by VLBI[J]. Annals of Shanghai Observatory Academia Sinica, 1996(17): 52–56. |
| [18] | PETRACHENKO B, NIELL A, BEHREND D, et al. Design Aspects of the VLBI2010 System[R]. Washington, DC: NASA, 2009: 13-67. |
| [19] | PETRACHENKO W T, NIELL A E, COREY B E, et al. VLBI2010: Next Generation VLBI System for Geodesy and Astrometry[M]//KENYON S, PACINO M C, MARTI U. Geodesy for Planet Earth. Berlin, Heidelberg: Springer, 2012: 999-1005. |
| [20] | SUN Jing, B?HM J, NILSSON T, et al. New VLBI2010 Scheduling Strategies and Implications on the Terrestrial Reference Frames[J]. Journal of Geodesy, 2014, 88(5): 449–461. DOI:10.1007/s00190-014-0697-9 |
| [21] |
夏金超, 李金岭, 韩延本.
关于新一代甚长基线干涉系统VLBI2010计划[J]. 地球物理学进展, 2010, 25(5): 1623–1627.
XIA Jinchao, LI Jinling, HAN Yanben. On the Next Generation of the VLBI System-VLBI2010[J]. Progress in Geophysics, 2010, 25(5): 1623–1627. |
| [22] | B?CKMANN S, ARTZ T, NOTHNAGEL A. VLBI Terrestrial Reference Frame Contributions to ITRF2008[J]. Journal of Geodesy, 2010, 84(3): 201–219. DOI:10.1007/s00190-009-0357-7 |
| [23] |
李金岭, 乔书波, 刘鹂, 等.
2008年佘山25 m射电天线归心测量[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1387–1391.
LI Jinling, QIAO Shubo, LIU Li, et al. Site Survey at Sheshan 25 m Radio Telescope in 2008[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1387–1391. |
| [24] |
李金岭, 乔书波, 刘鹂.
坐标变换方法用于佘山25 m射电天线归心测量的资料解析[J]. 测绘科学, 2010, 35(2): 69–71.
LI Jinling, QIAO Shubo, LIU Li. The Application of Coordinate Transformation into Data Analysis of Site Survey at Sheshan 25 m Radio Telescope[J]. Science of Surveying and Mapping, 2010, 35(2): 69–71. |
| [25] |
苗永宽.
球面天文[M]. 北京: 科学出版社, 1983.
MIAO Yongkuan. Spherical Astronomy[M]. Beijing: Science Publishing of China, 1983. |


