2. 北京中测智绘有限责任公司, 北京 100830
2. Smart Mapping Technology Lnc., Beijing 100830, China
随着倾斜摄影、无人机摄影、车载相机摄影、普通手持相机摄影等新的数据获取方法的引入,航空摄影测量的数据源日趋多源化,同时,地理空间信息也逐步进入了大数据时代[1],传统的航空摄影测量技术手段已经难以处理多源化、大规模的影像数据,学者们针对这些新的数据也做了大量的研究[2-5],但区域网平差的效率问题始终没有得到很好的解决。有的学者对法方程矩阵的带宽进行了优化[6-9],还有学者则直接提出了一种块状稀疏矩阵压缩格式,并采用预条件共轭梯度法(preconditioned conjugate gradient,PCG)以及不精确牛顿解法来求解法方程,大幅减少了平差所需的内存,提高了平差效率,同时保证平差精度与传统方法相当[10-11],但也同时指出,如果影像数持续增加(超过2万张影像),该矩阵压缩方法仍然需要耗费大量内存,将可能导致内存无法开辟而使得平差无法进行。本文是文献[10]的后续研究,为了解决影像数据持续增加带来的问题,本文将不存储法方程,而是引入图形处理器(graphics processing unit, GPU)并行计算,实时的计算法方程,法方程的求解方法仍然采用PCG及不精确牛顿解法,该方法在提高平差效率的同时,还使得法方程求解过程易于并行化实现,为GPU并行计算的引入提供了必要条件。
近年来,随着GPU通用计算的发展,GPU的应用已经不仅仅局限于图形显示领域,很多CPU的计算任务也可以由GPU并行计算来完成,而且GPU提供了数十倍乃至于上百倍于CPU的计算性能,使得GPU在非图形显示的高性能计算领域得到了广泛的应用。GPU的高性能计算能力主要得益于其远多于CPU的计算核心数,但是其数据逻辑运算单元较少,因此GPU更加擅长于大量简单的运算工作,而CPU则擅长于处理复杂的计算任务(如大量的逻辑判断,复杂的数据依赖等情况)。
本文研究的区域网平差问题中,法方程的构建以及求解过程就需要高性能计算能力的支撑,特别是随着大数据时代的到来,区域网平差需要求解的法方程数据量更大,计算能力需求也大幅增加。尽管有很多有效的矩阵分解、求逆等大型矩阵的计算工具,但是矩阵的存储问题、区域网平差流程的并行化问题仍然没有得到解决。使用GPU并行计算是解决大数据量问题的重要手段。在此之前,也有很多学者在GPU并行区域网平差方面做了很多研究工作[12-28]。在算法方面,有些方法应用了共轭梯度法(CG),但是没有使用预条件矩阵,也没有使用不精确牛顿解来降低求解法方程时的迭代次数[12-14]。有些方法仍然存储了法方程,处理大数据时,仍需要大量的内存[13-17]。在技术流程方面,传统区域网平差流程需要进行全面的修改,以便于引进GPU并行计算,而且在GPU内存使用、任务分配及GPU代码设计等方面都需要进行具体的优化,才能达到最优的并行效率,但是上述方法中,文献[17]和文献[29]最大化地利用了GPU高性能计算的特点,没有存储法方程系数矩阵,而是实时地计算法方程,但是二者在具体的GPU内存使用和任务分配等方面的描述较少,且其处理精度也不高。本文所做的工作就是结合预条件共轭梯度法及不精确牛顿解法,引入GPU并行计算,通过对传统的区域网平差流程进行全面改进,使其能够进行并行化设计,为GPU并行计算的引入提供必要条件。并行任务分配必须满足负载均衡的原则,才能使得并行效率得到最大化;同时GPU内存的协调调度对GPU并行计算也是至关重要的,有大量试验表明,如果内存处理不得当,其运算效率会受到严重影响,甚至会低于普通GPU并行算法。因此,为了使得平差效率最大化,本文重点阐述了GPU并行计算的任务分配及内存调度方法。
综上所述,本文引入GPU并行计算,使用预条件共轭梯度法及其不精确牛顿解法求解区域网平差流程中,建立适用于GPU并行计算的全新的区域网平差技术流程,同时对GPU并行计算中的内存使用,任务分配等具体环节进行优化,以最大化GPU并行计算的效率。
1 理论与方法 1.1 基于预条件共轭梯度法的区域网平差区域网平差的数学模型在文献[10]中已有详细的描述,本文仅给出简单的介绍。传统的法方程表达形式如式(1) 所示
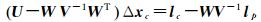 (1)
(1)
式中, U对应于法方程中外方位元素未知数部分;V对应于法方程中地面点未知数部分;W表示二者的协方差矩阵;Δxc表示外方位元素未知数向量;lc表示法方程常数项中外方位元素部分;lp表示法方程常数项中地面点未知数部分。
此时,通过解算式(1) 可以得到外方位元素未知数改正数,地面点未知数则通过利用新的外方位元素进行前方交会得到。为了避免对法方程直接求逆,本文引入了预条件共轭梯度法对法方程式(1) 进行求解。同时为了进一步降低迭代次数,还引入了不精确牛顿解法、预条件共轭梯度法和不精确牛顿解法在文献[10]中有详细的介绍,本文不再赘述。
1.2 GPU并行区域网平差技术流程引入GPU并行计算、预条件共轭梯度法及不精确牛顿解法后,全新的区域网平差技术流程如图 1所示。与文献[10]中的流程类似,不同点是本文的流程中有两个步骤是在GPU中运行的(图 1中,被填充的步骤),其计算结果被拷贝回CPU内存,然后继续下一步流程。

|
| 图 1 GPU并行区域网平差技术流程 Fig. 1 The whole workflow of the GPU parallel bundle adjustment |
如图 1所示,新的区域网平差流程可以分为两个迭代循环,一个是区域网平差迭代,一个是预条件共轭梯度法迭代,后者包含于前者,每一次区域网平差迭代,都包含一个预条件共轭梯度法迭代循环,该迭代循环是用来求解法方程的。只有当区域网平差迭代收敛后,整个区域网平差流程结束。
1.3 GPU并行区域网平差优化GPU并行计算的效率容易受到GPU并行任务分配以及GPU内存的使用方案的影响。各线程的计算任务应当满足均衡性才能最大地发挥并行计算的高效性。另外,GPU全局内存容量大,一般可达到2~4 GB,且所有的线程均可以访问,但是其存取效率与存取的顺序有着密切的联系,如果存取的顺序正好满足全局内存读取的一致性,则存取效率高,否则其存取效率变得十分低下。共享内存的存取效率高,不受存取顺序的影响,但是同一个块(block)内的线程才能访问该块的共享内存,不同的块之间的线程无法访问对方的共享内存。而且共享内存的存储容量非常小(本文所使用GPU的共享内存仅有48 KB)。因此合理地使用各种内存,会直接影响到GPU并行计算的效率。综上所述,GPU并行计算任务的优化,主要包括GPU并行任务分配优化以及内存的使用优化。本文中的区域网平差技术流程有两个步骤使用了GPU并行计算,下文将对这两个步骤的并行任务分配和内存使用策略进行详细讨论。
1.3.1 GPU并行区域网平差任务分配针对图 1中使用GPU并行计算的两个步骤:① 计算常数项以及预条件矩阵;② 计算矩阵向量积。其任务分配情况各有不同。
1.3.1.1 常数项向量以及预条件矩阵的并行计算任务分配常数项以及预条件矩阵的计算方法在文献[10]中有明确的描述,利用每一个像点及其对应的物方点坐标,外方位元素可以计算得到常数项向量的一个分量,将所有像点计算得到的常数项向量的分量累加起来,即可得到完整的常数项向量。预条件矩阵是一个块状对角矩阵,由对角线上的块状子矩阵组成,每一个像点在计算常数项向量时,同时也可以计算得到其对应的预条件矩阵分量,将所有像点计算得到的预条件矩阵的分量累加起来,即可得到完整的预条件矩阵。因此常数项向量以及预条件矩阵的计算可以放在同一个并行任务中进行。其任务分配方法有两种,以物方点为单位进行任务分配和以像方点为单位进行任务分配。在平差原始数据中,每一个连接点是由一个物方点,以及该物方点在若干影像上成像得到的像点坐标组成,一个物方点对应至少2个像方点,不同的物方点对应的像点数存在较大差别,最少2个,最大可达到数百个(与测区影像的重叠度有关)。如图 2所示,从向下的箭头代表以物方点为单位分配的任务,向上的箭头代表以像方点为单位分配的任务,可见以物方点为单位分配的任务计算量各不相同,任务量根据该物方点所包含的像点数有关,显然该任务分配方法不满足并行任务负载均衡的原则。而以像点为单位分配的任务计算量均为一个像点的计算量,各任务之间负载十分均衡,有利于并行计算效率达到最大化。因此本文对该步骤采用以像点为单位分配计算任务,即每个像点的计算任务交给一个GPU线程去计算,然后累加每个线程的结果,即可得到完整的常数项向量和预条件矩阵。

|
| 图 2 以物方点为单位以及以像方点为单位的任务分配方式 Fig. 2 The ground-point based task assignment |
1.3.1.2 法方程系数矩阵与残差向量(预条件共轭梯度法)的矩阵向量积的并行计算任务分配
法方程系数矩阵一般是指改化后的法方程系数矩阵,即法方程里面仅含有外方位元素未知数相关的部分,地面点未知数部分已经被消去了。改化的法方程系数矩阵中每一组外方位元素在对角线上存在一个矩阵,每两组外方位元素(对应于具有重叠度的两张影像)在非对角线上存在一个协方差矩阵,这个协方差矩阵的构成必须是依赖于两个像点,如果仍然以像点为单位进行任务分配,在计算非对角线上的协方差矩阵时,不同像点对应的线程需要进行通信,此时便不满足各线程之间独立性要求。但如果以物方点为单位进行任务分配,则各线程之间负载不均衡。针对上述问题,本文采用一种基于协方差的任务分配方法,如图 3所示,同一个物方点所对应的每两个像点构成一个计算任务,假设一个物方点对应3个像点,则该物方点需要分配9个线程(如图 3中,3个编号分别为5、6、7的像点, 组成9个绿色方格,每个绿色方格代表一个线程),每个线程处理其中每两个像点的计算任务。这样,各线程之间的任务既满足负载均衡的要求也满足独立运算的要求了。

|
| 图 3 基于协方差的任务分配方式 Fig. 3 Parallel task assignment based on covariance task; a rectangle represents a thread |
1.3.2 GPU并行区域网平差内存使用优化
区域网平差的输入数据主要包括,连接点数据(包括控制点数据)和外方位元素数据。相对于连接点数据,外方位元素数据较小,而且在一次区域网平差迭代中,外方位元素的值不会发生改变,因此可以将其存储在只读的纹理内存中。连接点数据则存储在全局内存中。连接点数据包括物方点坐标数据及其对应的若干个像点坐标数据。如前所述,GPU中的全局内存容量最大,但是其存取速度受到存取顺序的影响,为了使每一个线程按顺序读取每一个像点,可以将像点数据和物方点数据分开存储,所有的像点数据按照线程读取顺序来存储,物方点数据则按照像点顺序存储。
按照前一节的任务分配,每一个线程都会生成一个临时向量,如果将这些临时向量直接累加至全局内存中,则会导致大量线程同时访问全局内存中同一个地址,因此会严重影响累加的速度。但如果将每一个临时向量都存储在全局内存中,则需要大量的全局内存空间。为了解决这一矛盾,可考虑充分使用GPU的块内共享内存。假设GPU核函数被分配了64个块,每个块256个线程,则总线程数为64×256=16 384。本文的内存使用策略是将每一个块中的所有线程(256个线程)的临时向量存储在该块的共享内存中。在全局内存中开辟64个结果向量的内存空间,每一个块对应一个全局内存位置,用于累加该块中所有线程的运算结果。当每个块的所有线程都运行结束时,使用该块中的一个线程(一般为0号线程)将共享内存中的临时向量,累加至全局内存中对应于该块的内存位置,所有块都运行结束并累加结束后,将每个块计算得到的结果(存储至全局内存中的64个向量)累加起来,即可得到最终完整的结果向量。这样需要的全局内存仅为64个结果向量的大小,需要的共享内存仅为256个临时向量的大小。以计算常数项向量为例,假设测区影像数为1024,且未知数仅包含外方位元素,则常数项向量所需内存空间为1024×6×4 bytes=24 kB,而每个线程计算得到的临时向量的大小为6×4 Bytes,使用上述共享内存方法所需的全局内存空间仅为64×24 KB=1.5 MB,共享内存空间仅为256×6×4 Bytes=6 KB。而且各线程直接访问共享内存的效率比访问全局内存的效率要高得多,因此采用上述共享内存加全局内存的数据存储方法既有利于节省内存空间,同时也提高了内存访问效率。
2 试验结果与分析 2.1 数据及试验环境本文直接使用文献[10]中试验数据来进行对比试验,共10组数据,分别是真实的无人机数据,手机拍摄的影像数据以及网络上下载的图片数据。测区的影像数最小为40,最大的测区影像数达到13 682,具体的数据信息见文献[10]。本文中所有试验使用的主机配置为Inter(R) Core(TM) i7-6700HQ CPU 2.60 GHz, 8.00 GB RAM,显卡配置为NVIDIA GeForce GTX970M,显存3 GB,软件环境为Windows 10操作系统,GPU程序开发使用Microsoft Visual Studio 2013以及CUDA 8.0平台。
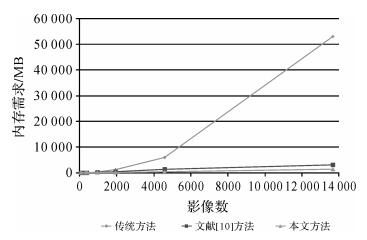
2.2 内存使用对比分别采用传统的方法,文献[10]的方法以及本文方法对10组试验数据进行处理,统计程序运行过程中的实际内存使用情况,其结果如表 1所示,不同方法的内存消耗如图 4所示。
|
| 图 4 不同方法的内存消耗对比 Fig. 4 Comparison of memory requirement of different methods |
从表 1和图 4可以看出,当影像数较少时,本文方法所需内存较大,这主要是由于使用GPU计算时,CUDA配置占用了一部分CPU内存,当影像数增加至1000左右时,本文方法对内存的需求明显低于传统办法的内存需求,文献[10]的方法虽然在一定程度上减少了内存需求,但是由于该方法还是存储了压缩后的法方程系数矩阵,而本文方法则完全不存储法方程系数矩阵,因此本文方法则需要更少的内存。传统的方法对内存的需求随着影像数的增加呈现近似指数式增长,当影像数逐渐增大至10 000张以上时,传统的办法需要至少53 GB内存,文献[10]的方法经过对法方程系数矩阵压缩后仅需要约3 GB内存,而本文方法不存储法方程系数矩阵,仅需要约1.5 GB内存用于存储平差必需的原始数据(连接点,内外方位元素数据等)。可以推断,若影像数继续增加,文献[10]的方法所需内存还会继续增加,并最终导致普通计算机无法开辟如此大内存而使得平差失败,本文的GPU并行算法所需的存储空间仅与平差原始数据的大小相关,若可以将这些原始数据存放在磁盘或者其他外部存储设备中,理论上本文方法可以处理的影像数可以达到系统的磁盘或者外部存储设备的容量上限,但实际情况中仍需要考虑这些磁盘或者外部存储设备的读取效率。
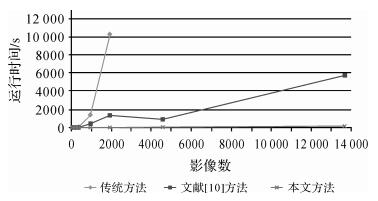
2.3 平差效率对比3种方法对10组数据处理所消耗的时间对比如表 2所示,不同算法的计算耗时如图 5所示。
| s | |||||
| 测区 | 影像数 | 地面点 | 传统方法 | 文献[10]的方法 | 本文方法 |
| 1 | 40 | 8272 | 1.0 | 0.968 | 1.0 |
| 2 | 52 | 64 063 | 42.3 | 39.6 | 3.6 |
| 3 | 84 | 127 939 | 21.5 | 22.0 | 2.5 |
| 4 | 88 | 64 298 | 55.4 | 50.1 | 4.8 |
| 5 | 228 | 249 829 | 103.3 | 64.7 | 5.1 |
| 6 | 394 | 100 368 | 501.9 | 38.7 | 8.9 |
| 7 | 961 | 187 103 | 1 422.1 | 444.6 | 22.3 |
| 8 | 1936 | 649 673 | 10 301.8 | 1 368.4 | 40.5 |
| 9 | 4585 | 1 324 582 | N/A | 935.5 | 82.7 |
| 10 | 13 682 | 4 456 117 | N/A | 5 766.7 | 170.6 |
|
| 图 5 不同算法的计算耗时对比 Fig. 5 The computation time for different methods |
从表 2和图 5可以看出,传统方法平差的计算耗时也随着影像数的增加呈现指数式增加,文献[10]的方法效率比传统方法有所提升,而本文算法的计算效率最高,且随着影像数的增加,仅仅呈现出线性的增长趋势。文献[10]的方法的计算速度比传统方法提升了3~10倍,而本文方法则大幅提升了10~25倍。且随着数据量的增大,本文方法效率的提升幅度越大。值得指出的是,当影像数达到4585及以上时,传统的算法由于受到内存大小的限制,无法进行平差,文献[10]的方法和本文方法仍然可以正常进行平差处理。同时也可以推断,当影像数继续增加时,即便是在配备大内存的图形工作站上,文献[10]的方法也必将受到内存的限制而无法进行,若可以将原始数据存放在磁盘或者其他外部存储设备中,理论上本文方法可以处理的影像数没有上限。
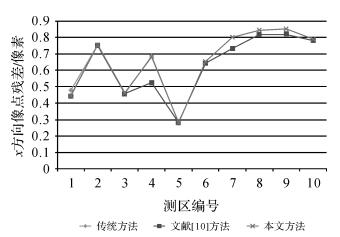
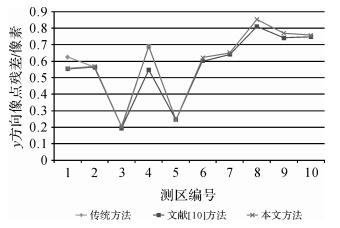
2.4 平差精度对比本文算法在内存使用和计算效率方面均优于传统的算法和文献[10]中的方法,为了进一步验证本文方法在平差精度方面的表现,本节将比较3种方法的平差精度。还是对上述10组数据分别采用3种方法进行处理,并将其精度指标进行对比分析(本文由于没有使用控制点和检查点,因此精度指标用相对精度来衡量,即用像点残差来表示)。具体精度统计信息如表 3所示,3种方法平差后在x、y方向的残差如图 6和图 7所示。
| 像素 | |||||||||
| 数据 | 影像数 | 传统方法 | 文献[10]方法 | 本文方法 | |||||
| x | y | x | y | x | y | ||||
| 1 | 40 | 0.48 | 0.62 | 0.44 | 0.55 | 0.44 | 0.55 | ||
| 2 | 52 | 0.75 | 0.56 | 0.75 | 0.56 | 0.76 | 0.57 | ||
| 3 | 84 | 0.46 | 0.20 | 0.46 | 0.19 | 0.46 | 0.20 | ||
| 4 | 88 | 0.69 | 0.69 | 0.53 | 0.55 | 0.68 | 0.69 | ||
| 5 | 314 | 0.28 | 0.25 | 0.28 | 0.25 | 0.28 | 0.24 | ||
| 6 | 394 | 0.64 | 0.60 | 0.64 | 0.60 | 0.65 | 0.62 | ||
| 7 | 961 | 0.73 | 0.64 | 0.73 | 0.64 | 0.80 | 0.65 | ||
| 8 | 1936 | 0.82 | 0.81 | 0.82 | 0.81 | 0.84 | 0.85 | ||
| 9 | 4585 | N/A | N/A | 0.82 | 0.74 | 0.85 | 0.77 | ||
| 10 | 13 682 | N/A | N/A | 0.78 | 0.75 | 0.79 | 0.76 | ||
|
| 图 6 3种方法平差后在x方向的残差对比 Fig. 6 The comparison of reprojection error of the conventional method and proposed method in x direction |
|
| 图 7 3种方法平差后在y方向的残差对比 Fig. 7 The comparison of reprojection error of the conventional method and proposed method in y direction |
如表 3和图 6、图 7所示,文献[10]的方法在平差精度上与传统算法相当,本文方法的精度略低于另外两种方法,可能是由于GPU并行计算仅支持单精度浮点计算,但是这种精度差异在实际应用中可忽略不计。
2.5 与同类方法对比文献[17]也是用GPU并行计算以及预条件共轭梯度法进行区域网平差,其使用的数据大部分也来自于本文从网上下载的数据(http://grail.cs.washington.edu/projects/bal/), 从该网址中找到了与本文中相同的3组试验数据,并将其试验精度结果与本文的精度结果进行对比,如表 4所示。
该方法与本文的方法均使用了GPU并行计算,且均不存储法方程系数矩阵,因此在内存消耗方面是一致的,都只需要将连接点以及外方位元素数据载入内存即可;速度方面,文献[17]的方法的效率略高,但是差距不大,可以说计算效率是属于同级别的,引起这种实际效率差别的原因是多方面的,可能是使用的软硬件环境有所区别(文献[17]使用的是两个Telsa C1060系列的GPU,而本文使用的是单个NVIDIA GeForce GTX970M GPU;文献[17]中试验的软件运行环境是Linux操作系统,而本文是在Windows 10操作系统下展开),也有可能是由于文献[17]的区域网平差流程与本文有所差异。另外,值得注意的是,本文的方法的精度要比文献[17]的方法好,本文的精度可达到子像素级,而文献[17]的方法精度均大于一个像素,这其中的原因可能是由于文献[17]在平差迭代过程中设置了较低的退出门槛(阈值),迭代次数较少,这同时也可能是文献[17]的速度比本文要快的原因之一。
综上所示,本文算法不仅节省了内存使用量,提高了计算速度,同时还保证了平差的最终精度与传统算法相当。
3 结论本文是文献[10]的后续研究,针对文献[10]中遇到的内存瓶颈问题,本文在文献[10]的研究基础上,引入了计算速度更加高效的GPU并行计算,在平差的过程中不存储法方程系数矩阵,而且在需要的时候,利用GPU实时的计算法方程系数矩阵中的相关位置的值,并在此基础之上,建立了全新的GPU并行区域网平差方法流程,使之在保证计算精度的同时,可以节省内存使用量,并提高计算速度。本文共使用了10组真实数据,包括无人机影像、倾斜影像、手机影像,以及网络下载的影像分别进行对比试验。通过对试验数据的对比分析,可以得出以下结论:① 当影像数较少时,本文算法由于使用GPU计算时CUDA配置占用了部分CPU内存,因此导致总占用内存较大,而当影像数增大至1000以上时,本文算法比文献[10]的方法进一步节省了2~3倍的内存空间,且随着影像数的继续增加,本文算法将更具优势;② 本文算法的计算速度比文献[10]的方法也提高了10~20倍;③ 本文算法比传统算法以及文献[10]的方法的精度略有降低,但该精度差异在实际应用中处于可接受范围。
本算法虽然节省了内存空间,提高了计算速度,但是由于本算法使用预条件共轭梯度法以及不精确牛顿解法迭代求解法方程,同时又使用了仅有单浮点精度的GPU并行计算,因此本算法的稳定性仍需要大量真实数据进行测试验证。另外本文方法虽然不存储法方程系数矩阵,但是内存中仍然存储了平差原始数据(连接点数据,内外方位元素数据等),而随着影像数增加,这些平差原始数据所需的内存也会随之增加,最后也必将导致内存不足,若可以将这些平差原始数据存储在磁盘或者外部存储设备中,理论上本算法能够处理的影像数没有上限。
| [1] | 李德仁. 展望大数据时代的地球空间信息学[J]. 测绘学报, 2016, 45(4): 379–384. LI Deren. Towards Geo-spatial Information Science in Big Data Era[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 379–384. DOI:10.11947/j.AGCS.2016.20160057 |
| [2] | MARQUARDT D W. An Algorithm for Least-squares Estimation of Nonlinear Parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431–441. DOI:10.1137/0111030 |
| [3] | 陈驰, 杨必胜, 彭向阳. 低空UAV激光点云和序列影像的自动配准方法[J]. 测绘学报, 2015, 44(5): 518–525. CHEN Chi, YANG Bisheng, PENG Xiangyang. Automatic Registration of Low Altitude UAV Sequent Images and Laser Point Clouds[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 518–525. DOI:10.11947/j.AGCS.2015.20130558 |
| [4] | 闫利, 费亮, 叶志云, 等. 大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–338. YAN Li, FEI Liang, YE Zhiyun, et al. Automatic Tie-points Extraction for Triangulation of Large-scale Oblique Multi-view Images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 310–338. DOI:10.11947/j.AGCS.2016.20140673 |
| [5] | 季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94–107. JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 94–107. |
| [6] | 王祥, 张永军, 黄山, 等. 旋转多基线摄影光束法平差法方程矩阵带宽优化[J]. 测绘学报, 2016, 45(2): 170–177. WANG Xiang, ZHANG Yongjun, HUANG Shan, et al. Bandwidth Optimization of Normal Equation Matrix in Bundle Block Adjustment in Multi-baseline Rotational Photography[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 170–177. DOI:10.11947/j.AGCS.2016.20150282 |
| [7] | 林诒勋. 稀疏矩阵计算中的带宽最小化问题[J]. 运筹学学报, 1983, 2(1): 20–27. LIN Yixun. Band Width Minimization Problem in Sparse Matrix Computations[J]. Chinese Journal of Operations Research, 1983, 2(1): 20–27. |
| [8] | GIBBS N E, POOLE JR W G, STOCKMEYER P K. An Algorithm for Reducing the Bandwidth and Profile of a Sparse Matrix[J]. SIAM Journal on Numerical Analysis, 1976, 13(2): 236–250. DOI:10.1137/0713023 |
| [9] | 郑志镇, 李尚健, 李志刚. 稀疏矩阵带宽减小的一种算法[J]. 华中理工大学学报, 1998, 26(12): 43–45. ZHENG Zhizhen, LI Shangjian, LI Zhigang. A New Algorithm for Reducing Bandwidth of Sparse Matrix[J]. Journal of Huazhong University of Science & Technology, 1998, 26(12): 43–45. |
| [10] | 郑茂腾, 张永军, 朱俊峰, 等. 一种快速有效的大数据区域网平差方法[J]. 测绘学报, 2017, 46(2): 188–197. ZHENG Maoteng, ZHANG Yongjun, ZHU Junfeng, et al. A Fast and Effective Block Adjustment Method with Big Data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 188–197. DOI:10.11947/j.AGCS.2017.20160293 |
| [11] | ZHENG Maoteng, ZHANG Yongjun, ZHOU Shunping, et al. Bundle Block Adjustment of Large-scale Remote Sensing Data with Block-based Sparse Matrix Compression Combined with Preconditioned Conjugate Gradient[J]. Computers & Geosciences, 2016(92): 70–78. |
| [12] | LIU Xin, GAO Wei, HU Zhanyi. Hybrid Parallel Bundle Adjustment for 3D Scene Reconstruction with Massive Points[J]. Journal of Computer Science and Technology, 2012, 27(6): 1269–1280. DOI:10.1007/s11390-012-1303-3 |
| [13] | 佟国峰, 蒋昭炎, 叶柠, 等. 大场景三维重建中多核并行捆集调整算法[J]. 控制与决策, 2013, 28(29): 1403–1408. TONG Guofeng, JIANG Zhaoyan, YE Ning. Multi-core Bundle Adjustment Algorithm Using Parallel Processing in Large-scale 3D Scene Reconstruction[J]. Control and Decision, 2013, 28(29): 1403–1408. |
| [14] | AGARWAL S, SNAVELY N, SEITZ S M, et. al. Bundle Adjustment in the Large[C]//DANⅡLIDIS K, MARAGOS P, PARAGIOS N. Computer Vision-ECCV 2010. Berlin Heidelberg:Springer, 2010:29-42. |
| [15] | AGARWAL S, FURUKAWA Y, SNAVELY N, et al. Building Rome in a Day[J]. Communications of the ACM, 2011, 54(10): 105–112. DOI:10.1145/2001269 |
| [16] | LI Ruipeng, SAAD Y. GPU-accelerated Preconditioned Iterative Linear Solvers[J]. The Journal of Supercomputing, 2013, 63(2): 443–466. DOI:10.1007/s11227-012-0825-3 |
| [17] | WU Changchang. Multicore Bundle Adjustment[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Colorado Springs, CO:IEEE, 2011:3057-3064. |
| [18] | CHOUDHARY S, GUPTA S, NARAYANAN P J. Practical Time Bundle Adjustment for 3D Reconstruction on the GPU[C]//Proceedings of the 11th European Conference on Trends and Topics in Computer Vision-Volume Part Ⅱ. Heraklion, Crete, Greece:Springer, 2010:423-435. |
| [19] | SÁNCHEZ J R, ÁLVAREZ H, BORRO D. Towards Real Time 3D Tracking and Reconstruction on a GPU Using Monte Carlo Simulations[C]//Proceedings of the 9th IEEE International Symposium on Mixed and Augmented Reality. Seoul, South Korea:IEEE, 2010:185-192. |
| [20] | BENNER P, EZZATTI P, KRESSNER D, et al. A Mixed-Precision Algorithm for the Solution of Lyapunov Equations on Hybrid CPU-GPU Platforms[J]. Parallel Computing Archive, 2011, 37(8): 439–450. DOI:10.1016/j.parco.2010.12.002 |
| [21] | BHASKARAN-NAIR K, MA Wenjing, KRISHNAMOORTHY S, et al. Noniterative Multireference Coupled Cluster Methods on Heterogeneous CPU-GPU Systems[J]. Journal of Chemical Theory and Computation, 2013, 9(4): 1949–1957. DOI:10.1021/ct301130u |
| [22] | CHAI Jun, SU Huayou, WEN Mei, et al. Resource-efficient Utilization of CPU/GPU-based Heterogeneous Supercomputers for Bayesian Phylogenetic Inference[J]. The Journal of Supercomputing, 2013, 66(1): 364–380. DOI:10.1007/s11227-013-0911-1 |
| [23] | TAN Y S, LEE B S, HE Bingsheng, et al. A Map-reduce Based Framework for Heterogeneous Processing Element Cluster Environments[C]//Proceedings of the 12th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGrid). Ottawa, ON, Canada:IEEE, 2012:57-64. |
| [24] | WEN Mei, SU Huayou, WEI Wenjie, et al. Using 1000+ GPUs and 10000+ CPUs for Sedimentary Basin Simulations[C]//Proceedings of 2012 IEEE International Conference on Cluster Computing (CLUSTER). Beijing, China:IEEE, 2012:27-35. |
| [25] | NEWCOMBE R A, LOVEGROVE S J, DAVISON A J. DTAM:Dense Tracking and Mapping in Real-time[C]//Proceedings of 2011 IEEE International Conference on Computer Vision. Barcelona, Spain:IEEE, 2011:2320-2327. |
| [26] | ACOSTA A, CORUJO R, BLANCO V, et al. Dynamic Load Balancing on Heterogeneous Multicore/MultiGPU Systems[C]//Proceedings of 2010 International Conference on High Performance Computing and Simulation (HPCS). Caen, France:IEEE, 2010:467-476. |
| [27] | AGULLEIRO J I, VÁZQUEZ F, GARZÓN E M, et al. Hybrid Computing:CPU+ GPU Co-processing and Its Application to Tomographic Reconstruction[J]. Ultramicroscopy, 2012(115): 109–114. |
| [28] | AGULLO E, AUGONNET C, DONGARRA J, et al. QR Factorization on a Multicore Node Enhanced with Multiple GPU Accelerators[C]//Proceedings of 2011 IEEE International Parallel & Distributed Processing Symposium. Anchorage, AK:IEEE, 2011:932-943. |
| [29] | HNSCH R, DRUDE I, HELLWICH O. Modern Methods of Bundle Adjustment on the GPU[C]//ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume Ⅲ-3, 2016 XXⅢ ISPRS Congress. Prague, Czech Republic:Copernicus Publications, 2016. |



