2. 信息工程大学五院, 河南 郑州 450001
2. The Fifth College of the Information Engineering University, Zhengzhou 450001, China
在航空/航天光学遥感中,如果观测对象为水下目标,则来自目标的电磁波要穿过水和空气两种介质才能到达相机焦平面成像,此时可运用双介质立体摄影测量方法获取水下目标点的三维大地坐标[1-5]。
成像光线在单介质(水或空气)中可视为一条直线,在双介质(水和空气)中可视为一条折线。在双介质立体摄影测量中,如果能直接建立水下目标点与对应像点间的折线关系模型,则利用立体影像上的同名像点,按照物像折线关系模型就可以直接交会得到水下目标点的三维大地坐标[6-11]。但在实际应用中,通常仅有遥感图像的单介质空中物像直线关系或其近似模型,此时对于水下目标点,只能先利用立体影像上的相应同名像点,按照空中物像直线关系或其近似模型,联立求解出虚拟的水中点位(不妨也称为“摄影测量交会点”)的三维大地坐标,然后再按照光线在空气和水中的折线传播规律,对摄影测量交会点的三维大地坐标进行折光改正,进而得到水下目标点的三维大地坐标[12-19]。本文主要研究后一种情况的折射改正问题。
现有的研究成果[12-19]几乎都提到了“在双介质成像情况下水下目标的空中同名直线光线不相交情况的存在”。但是在推导折射改正公式时,却都忽略了空中同名直线光线不相交情况对物方坐标折射改正的影响,因而得到的折射改正公式具有很大的近似性或不合理性,由此得到的水下目标点的三维大地坐标也必然存在不合理误差。
针对上述问题,首先根据水下目标点的双介质立体成像几何特点,分析空中同名直线光线不相交情况对物方大地坐标折射改正的不利影响,然后用水下目标的空中同名直线光线公垂线段的中点作为摄影测量交会点的理论位置,在此基础上建立摄影测量交会点与水下真实物点的相互位置关系,推导出水下目标点的水深和大地坐标计算公式(即折射改正公式)。为了验证所提算法的正确性和有效性,开发了相应的双介质立体摄影测量软件,并利用WorldView-2卫星遥感影像及相关数据进行了算法的合理性试验、理论误差测算和精度改善情况试验,取得了预期的结果。
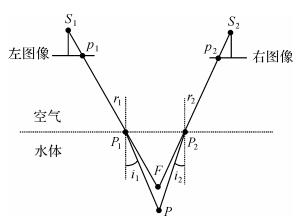
1 空中同名光线延长线不相交对折射改正的影响如图 1所示, P为水下目标点, P在立体像对左、右图像上的像点分别为p1、p2;在双介质成像情况下,左图像上像点p1的成像光线为折线S1P1P(其中像点p1在直线S1P1上,S1为获取左图像时的相机镜头中心位置,P1为成像光线与空气和水分界面的交点);右图像上同名像点p2的成像光线为折线S2P2P(其中像点p2在直线S2P2上,S2为获取右图像时的相机镜头中心位置,P2为成像光线与空气和水分界面的交点)。如果仅有遥感图像的单介质空中物像直线关系模型,则可先按照单介质立体摄影测量原理,利用同名像点p1、p2的像坐标,按照直线S1P1和S2P2的数学模型,联立求解出摄影测量交会点F的大地坐标(图 1中F为直线S1P1和S2P2延长线的交点);然后再按照光在空气和水中的折线传播规律,对F的大地坐标进行折光改正,进而将F修正为目标点P。
|
| 图 1 双介质立体摄影测量原理平面示意图 Fig. 1 Sketch of two-media stereophotogrammetry |
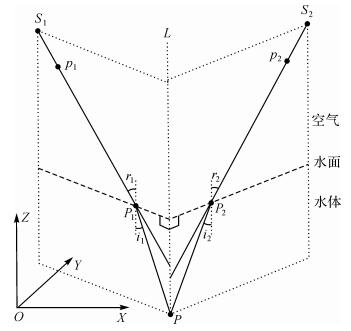
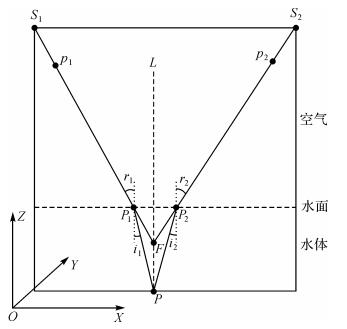
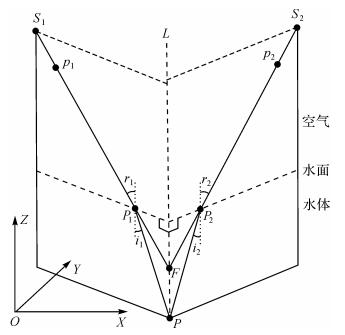
实际上,在双介质成像情况下,三维空间中的直线S1P1和S2P2的延长线并不一定相交。如图 2所示,直线S1P1的延长线在折线S1P1P确定的垂直于水面的平面内,直线S2P2的延长线在折线S2P2P确定的垂直于水面的平面内。如果这两个平面不重合且直线S1P1和S2P2关于L不对称(L为两个平面的交线, L经过目标点P且垂直于水面),则两条空间异面直线S1P1和S2P2的延长线就不会相交。只有这两个平面重合(即水下目标点P位于两个摄站连线的正下方,参见图 3)或者成像光线关于L对称(参见图 4)时,直线S1P1和S2P2的延长线才会相交,且交点一定位于L上。
|
| 图 2 空中同名光线延长线不相交情况 Fig. 2 The case of non-intersection of two aerial corresponding rays |
|
| 图 3 空中同名光线延长线相交情形之一(空中同名光线所在平面重合) Fig. 3 A case of intersection of two aerial corresponding rays (the two rays are in the same plane) |
|
| 图 4 空中同名光线延长线相交情形之二(空中同名光线关于L对称) Fig. 4 A case of intersection of two aerial corresponding rays (the two rays are symmetric with respect to L) |
在双介质摄影测量中,直线S1P1和S2P2的延长线不相交情况是大量存在的,而相交情况只是特例。在直线S1P1和S2P2延长线不相交情况下,按照单介质立体摄影测量原理求解出的摄影测量交会点F的理论位置,是决定物方折射改正的最主要依据。虽然文献[12-19]都注意到了空中同名直线光线不相交情况的存在,但都没有回答这种情况下摄影测量交会点F理论位置究竟在哪里?所以不可能从根本上解决不相交情况对折射改正的影响。例如,文献[12—13]只是近似地按照直线S1P1和S2P2延长线相交时的几何关系进行物方坐标折射改正(即按照图 3和图 4所示的几何关系进行物方坐标折射改正),文献[14—19]仅按图 5所示的单像几何关系进行物方坐标折射改正,其不合理性是显而易见的,这样做的结果必然导致明显的折射改正误差。为克服现有算法不足,本文从确定摄影测量交会点F的理论位置着手研究更严密的物方坐标折射改正算法。

|
| 图 5 单幅影像的物像几何关系 Fig. 5 Geometry of two-media photogrammetry using a single image |
2 基于严密物像几何关系的折光改正算法
不失一般性,假设L与水面的交点为M,直线S1P1的延长线与L的交点为F1,直线S2P2的延长线与L的交点为F2,按照直线S1P1和S2P2的数学模型联立求解出的点位为F,各点的相对关系如图 6所示。理论上, F的最优解应为两条空间异面直线S1P1和S2P2的公垂线段的中点。当S1P1和S2P2不相交时, F不在L上(注意P、F2、F1和M都在L上)。特殊情况下,当S1P1和S2P2的延长线相交时,F、F2和F1重合为一点且该点一定在L上。

|
| 图 6 双介质立体摄影测量主要点位之间的关系 Fig. 6 Geometry of two-media stereophotogrammetry (including main photogrammetric points) |
假设P1、F1、P2、F2的大地坐标分别为(XP1, YP1, ZP1)、(XF1, YF1, ZF1)、(XP2, YP2, ZP2)和XF2, YF2, ZF2,空间异面直线S1P1和S2P2的公垂线段在S1P1延长线上的垂足为M,在S2P2延长线上的垂足为N,则由解析几何可推导出M的大地坐标XM, YM, ZM为
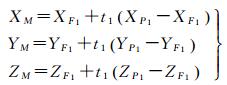 (1)
(1)
N的大地坐标XN, YN, ZN为
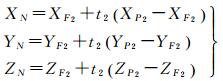 (2)
(2)
当F取最优解时(即F取线段MN的中点), F的大地坐标XF, YF, ZF为
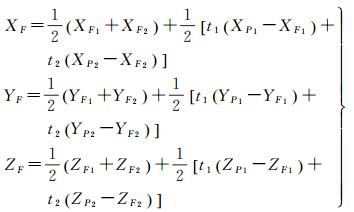 (3)
(3)
式中
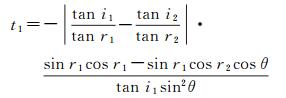 (4)
(4)
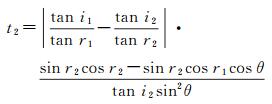 (5)
(5)
式中,i1为左像点p1对应的水下目标点P的辐射光线照射到水面点P1的入射角;r1为左像点p1对应的水下目标点P的辐射光线穿过水面点P1的折射角;i2为右像点p2对应的水下目标点P的辐射光线照射到水面点P2的入射角;r2为右像点p2对应的水下目标点P的辐射光线穿过水面点P2的折射角;θ为空中同名直线光线S1P1和S2P2的夹角(即交会角)。
利用直线光线S1P1和直线光线S2P2的单位方向向量,可推导出θ的表达式如下
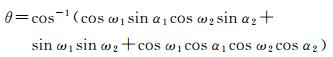 (6)
(6)
式中,α1为左像点p1对应的空中直线光线S1P1的前视角;ω1为左像点p1对应的空中直线光线S1P1的侧视角;α2为右像点p2对应的空中直线光线S2P2的后视角;α2为右像点p2对应的空中直线光线S2P2的侧视角。
从式(3) 可以看出:F是由线段F1F2中点加上一个偏移量ΔX, ΔY, ΔZ得到的,该偏移量ΔX, ΔY, ΔZ表达式如下
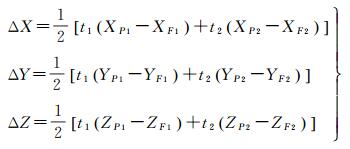 (7)
(7)
所以F到线段F1F2中点的距离δ为
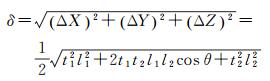 (8)
(8)
式中,l1、l2分别为线段F1P1和F2P2的长度。
假设F1、F2、P的水深(即图 6中线段F1M、F2M、PM的长度)分别为h1、h2、hP,则由三角形几何关系可得
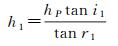 (9)
(9)
 (10)
(10)
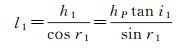 (11)
(11)
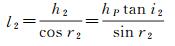 (12)
(12)
在双介质光学遥感中,同名像点p1、p2对应的r1、r2一般是已知的。由折射定律可知
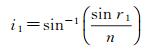 (13)
(13)
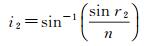 (14)
(14)
式中, n是水相对空气的折射率(在水温为20℃时,n=1.332 99)。
利用WorldView-2卫星遥感影像及其观测参数实际验算的结果表明:F到线段F1F2中点的距离δ并不大(参见表 2),相较于双介质摄影测量能力而言,可以近似地将摄影测量交会点F和线段F1F2中点视为同一点。由此可得:线段F1F2中点的大地坐标近似等于F的大地坐标,而F的水深hF可用F1F2中点的水深来代替,即
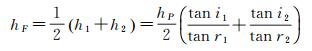 (15)
(15)
整理可得P的水深hP如下
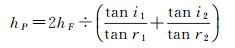 (16)
(16)
假如已知任意一个水陆交界点的大地坐标X0, Y0, Z0,由于水面可视为水平面,所以有
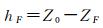 (17)
(17)
将式(17) 代入式(16) 可得
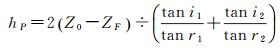 (18)
(18)
考虑到P与线段F1F2中点的平面坐标相同,可得P的大地坐标为
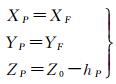 (19)
(19)
式(18) 和式(19) 就是在求出摄影测量交会点F的大地坐标XF, YF, ZF和任意一个水陆交界点的高程Z0后,求取P的水深hP和大地坐标XP, YP, ZP的计算公式。除了合理地将摄影测量交会点F和线段F1F2中点视为同一点,其余公式都是在严密的成像几何关系基础上推导出来的,所以相对现有算法更严密。另外,当S1P1和S2P2的延长线相交时,F、F1和F2 3点重合,可视为S1P1和S2P2延长线不相交情况的特例,因此上述公式对S1P1和S2P2延长线相交情况也是适用的。
3 试验与分析下面通过两个双介质立体摄影测量试验来验证本文算法的合理性以及对高程测量精度的影响。一是利用WorldView-2立体影像的观测参数计算摄影测量交会点F到线段F1F2中点的距离δ(各符号含义参见图 6),并根据计算结果来验证本文算法的合理性以及由此引起的理论误差大小;二是利用WorldView-2立体影像及其观测参数进行浅海海底地形测量试验,并将本文算法的结果与最有代表性的Murase算法[13]的结果进行比较,来验证本文算法对高程测量精度的改善能力。
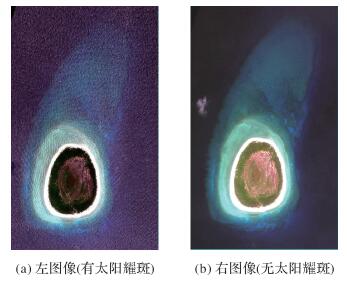
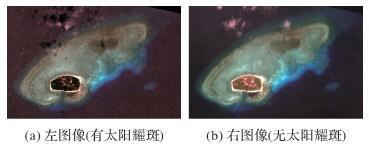
3.1 试验卫星影像及其特点综合考虑试验需要和遥感数据保障条件,选择海南省三沙市甘泉岛和珊瑚岛两个地区的WorldView-2[20]多光谱立体影像及其观测参数和定位模型参数进行试验。图 7和图 8分别为甘泉岛和珊瑚岛地区WorldView-2多光谱立体影像的局部重叠区域,而整幅图像对应的航向视角(即前视角或后视角)、侧视角、入视角等观测参数如表 1所示。实际试验中,图像上每个像素对应的航向视角、侧视角、入视角等观测参数用双线性内插方法计算得到。
|
| 图 7 甘泉岛WorldView-2多光谱立体影像(MS1的2、3、4波段合成) Fig. 7 WorldView-2 multispectral stereo images of Ganquan Island (compositing of MS1 bands2, 3 and 4) |
|
| 图 8 珊瑚岛WorldView-2多光谱立体影像(MS1的2、3、4波段合成) Fig. 8 WorldView-2 multispectral stereo images of Shanhu Island (compositing of MS1 bands 2, 3 and 4) |
| (°) | ||||||||||||
| 地点 | 立体影像 | 航向视角 | 侧视角 | 入视角 | ||||||||
| 最小 | 最大 | 平均 | 最小 | 最大 | 平均 | 最小 | 最大 | 平均 | ||||
| 甘泉岛 | 左影像 | 1.9 | 2.1 | 2.0 | -4.6 | -4.4 | -4.5 | 4.8 | 5.1 | 4.9 | ||
| 右影像 | -31.3 | -30.9 | -31.1 | -6.9 | -6.7 | -6.8 | 31.7 | 31.9 | 31.8 | |||
| 珊瑚岛 | 左影像 | 9.6 | 9.8 | 9.7 | -4.5 | -4.3 | -4.4 | 10.4 | 10.7 | 10.6 | ||
| 右影像 | -26.9 | -26.6 | -26.7 | -6.9 | -6.7 | -6.8 | 27.5 | 27.7 | 27.6 | |||
| 说明:航向视角即为文中的α1或α2(正值表示前视,负值表示后视),侧视角即为文中的ω1或ω2(正值表示右视,负值表示左视),入视角即为文中的r1或r2。 | ||||||||||||
虽然WorldView-2提供了全色立体影像和多光谱立体影像,但由于多光谱影像的分辨率已经很高(星下点分辨率已达1.85 m),完全能够满足摄影测量需要,并且其中蓝、绿波段影像的海底纹理特征比其他波段(包括全色)更清晰[21-22],更有利于海底纹理特征的检测和提取,这是本文选用WorldView-2多光谱立体影像的主要原因。
由于甘泉岛、珊瑚岛两个地区的WorldView-2立体影像的左图像都有严重的太阳耀斑,为了消除太阳耀光对水域影像质量、海底纹理特征提取和水下同名像点匹配等后续工作的影响,运用文献[23]的太阳耀斑消除的方法对甘泉岛、珊瑚岛两个地区WorldView-2立体影像的左图像进行了处理。
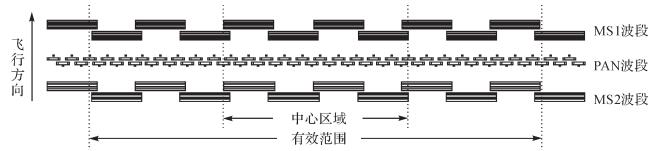
由于WorldView-2相机采用了图 9所示的交错拼接型长线阵探测器[24],所以WorldView-2影像(包括全色和多光谱)是由多个短线阵探测器推扫成像后经过拼接处理得到的,已不是严格意义上的原始影像,所以无法建立严格的物像关系模型。为此,WorldView-2提供了有理函数模型RFM(rational function model)以及相应的有理多项式系数RPC(rational polynomial coefficients)和坐标归一化参数作为近似的目标定位模型[25]。该模型考虑了光学相机镜头畸变、光行差(由卫星运动导致)、大气折射的影响,其表达式如下
|
| 图 9 WorldView-2焦平面上的探测器 Fig. 9 Detectors on WorldView-2 focal plane |
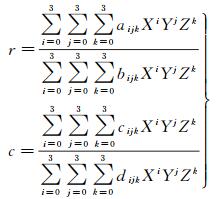 (20)
(20)
式中,(r, c)为相应像点的归一化像素坐标(即归一化的像点行、列号);(X, Y, Z)为相应地面点的归一化大地坐标(即归一化的地面点经度、纬度和高程);aijk、bijk、cijk、dijk为相应的多项式的系数。
在实际应用中,通常对式(20) 进行线性化并整理得到如下误差方程式
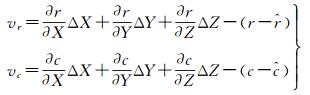 (21)
(21)
式中,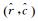
对于一对同名像点,依据式(21) 可以列出4个方程式,联立这4个方程式就可以求解出该同名像点对应的地面点的大地坐标(X, Y, Z)。
3.2 算法的合理性试验及理论误差测算本文算法的关键是利用水下目标的空中同名直线光线公垂线段的中点作为摄影测量交会点F的理论位置,并且近似地将摄影测量交会点F与线段F1F2中点视为同一点,在此基础上严格推导出从摄影测量交会点到水下物点的高程坐标折射改正公式。因此,本文算法的合理性和理论误差主要取决于摄影测量交会点F偏离线段F1F2中点的程度,即取决于摄影测量交会点F与线段F1F2中点之间的距离δ。
为此,利用WorldView-2立体影像的观测参数和其他信息,实际计算摄影测量交会点F到线段F1F2中点的距离δ(符号含义见图 6),并根据计算结果来分析“将摄影测量交会点F和线段F1F2中点视为同一点”的合理性以及由此造成的理论误差大小。
为了计算同名像点的δ,需要已知空中同名光线的航向视角、侧视角、入视角和水下目标点的水深值。虽然表 1给出了整幅图像航向视角、侧视角、入视角的最大值、最小值和平均值,图像上每个像素的航向视角、侧视角、入视角等观测参数也可以用线性内插方法得到。但由于每个像素航向视角、侧视角、入视角的差异都不大,由此引起的δ差异可以忽略不计,为使问题简单化,此处使用整幅图像航向视角、侧视角、入视角的平均值作为图像上每个像素的航向视角、侧视角、入视角,并假设水下目标点的水深hP分别为5 m、10 m、15 m来计算δ,其结果(包括中间结果)如表 2所示。
| 地名 | hp/m | θ/(°) | r1/(°) | r2/(°) | i1/(°) | i2/(°) | h1/m | h2/m | l1/m | l2/m | t1 | t2 | δ/m |
| 甘泉岛 | 5 | 33.013 | 31.8 | 4.9 | 23.288 | 3.674 | 3.471 | 3.745 | 4.084 | 3.759 | -0.003 3 | 0.069 7 | 0.123 |
| 珊瑚岛 | 5 | 36.297 | 10.6 | 27.6 | 7.933 | 20.340 | 3.723 | 3.545 | 3.788 | 4.001 | -0.035 9 | 0.011 9 | 0.051 |
| 甘泉岛 | 10 | 33.013 | 31.8 | 4.9 | 23.288 | 3.674 | 6.942 | 7.490 | 8.169 | 7.518 | -0.003 3 | 0.069 7 | 0.251 |
| 珊瑚岛 | 10 | 36.297 | 10.6 | 27.6 | 7.933 | 20.340 | 7.446 | 7.091 | 7.575 | 8.001 | -0.035 9 | 0.011 9 | 0.102 |
| 甘泉岛 | 15 | 33.013 | 31.8 | 4.9 | 23.288 | 3.674 | 10.413 | 11.236 | 12.252 | 11.277 | -0.003 3 | 0.069 7 | 0.377 |
| 珊瑚岛 | 15 | 36.297 | 10.6 | 27.6 | 7.933 | 20.340 | 11.169 | 10.636 | 11.362 | 12.002 | -0.035 9 | 0.011 9 | 0.153 |
从表 2可以看出:在θ、r1、r2一定的情况下,δ随hP的增大而线性增大,但δ/hP基本不变。例如,当水深hP为5 m、10 m、15 m时,甘泉岛的δ分别为0.123 m、0.251 m、0.377 m,δ/hP基本维持在2.5%左右;珊瑚岛的δ分别为0.051 m、0.102 m、0.153 m,δ/hP基本维持在1%左右。虽然甘泉岛的δ稍大一些,但δ/hP也只有2.5%左右,相对于双介质摄影测量的定位能力而言是不大的,可以忽略不计,因此将摄影测量交会点F与线段F1F2中点近似为同一点是合理的。
从表 2还可以看出:在水深hP分别为5 m、10 m、15 m的情况下,甘泉岛的|h1-h2|为0.274 m、0.548 m、0.823 m,珊瑚岛的|h1-h2|为0.178 m、0.355 m、0.533 m,均不为零,说明同名像点的空中成像光线延长线不相交。此时若按Murase算法[13](即假设同名像点的空中成像光线延长线相交)进行物方大地坐标折射改正,显然是不合理的。
仔细分析表 2还可以看出:在水深hP相同和交会角θ差别不大的情况下,甘泉岛的|h1-h2|和δ都明显大于珊瑚岛。究其原因,主要是甘泉岛的|r1-r2|为26.9°,而珊瑚岛的|r1-r2|为17°,即甘泉岛的同名成像光线关于L的对称性比珊瑚岛差一些。反过来,也正好说明:同名成像光线关于L的对称性越好,F、F1和F23点越接近重合,将摄影测量交会点F与线段F1F2中点视为同一点的误差越小。因此,在保证交会角θ合理的情况下,选择入视角对称性较好的立体像对进行双介质摄影测量,对提高位置精度是有利的。
3.3 算法的测量精度改善情况试验下面通过不同方法计算得到的浅海海底地形数据的比较,来验证本文算法对高程测量精度的改善能力。
首先分别按照本文方法和最有代表性的Murase算法[13]开发了相应的双介质立体摄影测量软件;然后分别运用每款软件对甘泉岛地区的WorldView-2多光谱绿色波段立体影像进行双介质立体摄影测量处理,共得到两组甘泉岛周围浅海海底地形数据(如图 10(a)和图 10(b)所示);接着再分别运用每款软件对珊瑚岛地区的WorldView-2多光谱绿色波段立体影像进行双介质立体摄影测量处理,共得到两组珊瑚岛周围浅海海底地形数据(图 11(a)和图 11(b))。

|
| 图 10 3种方法得到的甘泉岛周围浅海海底地形数据 Fig. 10 Three DEMs of Ganquan Island area derived from different methods |

|
| 图 11 两种方法得到的珊瑚岛周围浅海海底地形数据 Fig. 11 Two DEMs of Shanhu Island area derived from different methods |
本文方法的双介质立体摄影测量处理过程如下:
(1) 运用区域生长法提取遥感影像上的水域边界,将水域和陆地区分开来,以便对水域和陆地区域实施不同的摄影测量处理。
(2) 对陆地区域,按照特征点提取、同名像点匹配、目标点大地坐标立体摄影测量解算的流程,获得陆地区域内检测到的所有特征点的大地坐标,然后以离散陆地特征点为基础内插得到陆地区域规则格网的大地坐标。
(3) 对水域,按照太阳耀斑消除、特征点提取、同名像点匹配、目标点大地坐标立体摄影测量解算、双介质折射改正的流程,尽可能多地获得浅海区域海底特征点的大地坐标,然后以海底离散特征点为基础内插得到浅海区域规则格网的大地坐标。
Murase算法[13]的双介质立体摄影测量处理过程与本文方法完全一致,只是在物方坐标折射改正时所使用的公式不同。
为了客观进行精度比较,需要甘泉岛、珊瑚岛两个地区的高精度浅海海底地形数据作为参考基准。但由于数据资源和研究经费限制,仅购得甘泉岛周围浅海区域的高精度机载激光测深数据,如图 10(c)所示。该数据是采用加拿大Optech公司SHOALS-3000[26]测量得到的,测深精度为±0.3 m。由于仅有甘泉岛周围浅海区域的SHOALS-3000测深数据,所以精度比较试验只能针对甘泉岛地区。
精度试验方法是:以甘泉岛周围浅海区域为试验场,用SHOALS-3000测深数据作为基准,将本文方法得到的结果、Murase方法得到的结果与SHOALS-3000测深数据进行叠置比较,得到各个格网点高程坐标的误差,最后按式(22) 统计计算所有格网点高程值的均方根误差RMSE,结果如表 3所示。
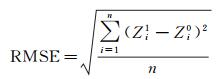 (22)
(22)
式中, n为本文方法获得的海底地形数据的格网点数;Zi1为本文方法或Murase方法获得第i个格网点的海底高程值;Zi0为SHOALS-3000测得的第i个格网点的海底高程值。
| m | |||
| 方法 | RMSE(全部点) | RMSE(水深大于4m的点) | 备注 |
| 本文方法 | 2.35 | 1.89 | 两种方法的双介质立体摄影测量处理过程完全相同,只是在物方坐标折射改正时所使用的公式不同 |
| Murase方法 | 3.13 | 2.31 | |
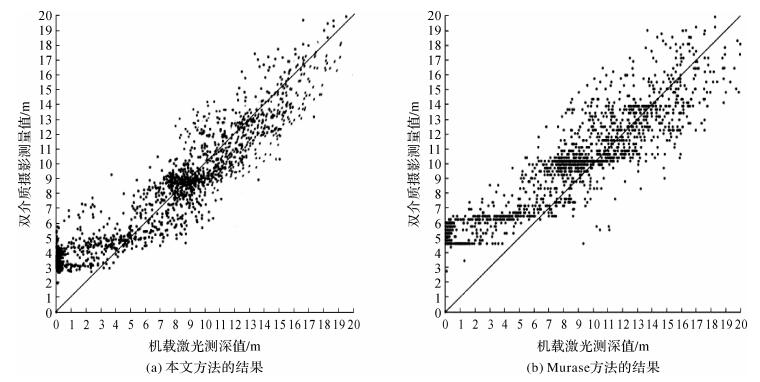
为了直观反映每个点的双介质摄影测量值(水深值)与机载激光测深值的偏离情况,对每种方法,以机载激光测深值作为平面直角坐标系的横轴、以双介质摄影测量值作为纵轴,将所有测量点绘制在该平面直角坐标系中,得到每种方法的双介质摄影测量值与机载激光测深值的偏离情况图,结果如图 12所示。
|
| 图 12 两种方法得到的甘泉岛周围浅海水深偏离情况图 Fig. 12 The relationships between our or Murase's results and SHOALS-3000's results |
从表 3可以看出:对所有格网点,本文方法的均方根误差为2.35 m,比Murase方法的3.13 m小0.78 m;对水深不低于4 m的格网点(即剔除水质较差区域的浅水点),本文方法的均方根误差为1.89 m,仍比Murase方法的2.31 m小0.42 m。由于测量精度的差异主要是物方坐标折射改正算法不同导致的,因此试验结果说明了本文方法对提高浅海海底的高程(或水深)测量精度有明显的效果。
从图 12(a)可以看出:本文方法的结果中,水深大于4 m的海底点基本分布在吻合线上或附近两侧(所谓吻合线是指通过坐标原点且斜率为1的直线,该线上所有点的双介质摄影测量值等于机载激光测深值)。从图 12(b)可以看出:Murase方法的结果中,虽然水深大于4 m的海底测量点也基本分布在吻合线上或附近两侧,但偏离吻合线的幅度明显大于本文方法的结果。图 12(a)与(b)的差异说明:本文方法获取的浅海海底地形更接近基准数据,即说明了本文方法优于Murase方法。
从图 12还可以看出:两种方法在水深小于4 m的浅水区域都有明显的系统性误差,主要原因是浅水区水质较差,水中杂质较多,提取到的特征点可能是水中杂质点而非海底特征点,从而导致水质较差的浅水区双介质摄影测量精度不高。另外,SHOALS-3000的测深能力为2~50 m,水深小于2 m的机载激光测深数据精度也不高。综合考虑这些因素,针对水深不低于4 m的测量点,统计得到的均方根误差RMSE更有参考价值。
4 结论提出了一种更严密的双介质立体摄影测量物方坐标折射改正算法。该算法用水下目标的空中同名直线光线公垂线段的中点作为摄影测量交会点的理论位置,在此基础上建立了摄影测量交会点与水下真实物点的相互位置关系,推导了水下目标点的水深和大地坐标计算公式(即折射改正公式)。理论研究和试验结果表明:
(1) 提出的双介质立体摄影测量物方坐标折射改正算法,除了合理地将摄影测量交会点F近似为线段F1F2中点以外,其余公式都是在严密的成像几何关系基础上推导出来的,比现有的双介质折射改正算法更严密。
(2) 无论空中同名直线光线延长线是否相交,本文的折射改正算法都是适用的。因此,在使用本文算法时,不需要考虑物像相对位置关系(如空中同名光线所在平面是否重合?空中同名光线关于L是否对称?)。
(3) 在空中同名直线光线的入视角r1和r2以及交会角θ一定的情况下,本文折射改正算法的理论误差δ随测量点的水深hP增大而线性增大,但δ/hP基本不变。另外,在交会角θ一定的情况下,选择入视角r1和r2对称性较好的立体像对进行双介质摄影测量,对降低本文折射改正算法的理论误差、提高水下目标的测量精度是有利的。
(4) 本文算法能显著提高水下目标的高程测量精度。以甘泉岛周围浅海海底地形测量为例,在水质清澈情况下,能将高程测量精度从Murase方法的2.31 m提高到1.89 m。
应当指出,利用航空航天遥感影像和双介质立体摄影测量方法进行水下目标定位,是建立在“空气和水体均为单一介质”、“空气与水体的分界面为平面”、“水下目标在遥感影像上清晰可见”等条件之上的。该方法仅适用于水体清澈、无海浪的浅海区域测绘,对影像质量和预处理技术(如太阳耀斑消除、水域影像增强等)也有更高要求。
| [1] | CHONG A K, SCHNEIDER K. Two-medium Photogrammetry for Bottlenose Dolphin Studies[J]. Photogrammetric Engineering and Remote Sensing, 2001, 67(5): 621–628. |
| [2] | TELEM G, FILIN S. Photogrammetric Modeling of Underwater Environments[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(5): 433–444. DOI:10.1016/j.isprsjprs.2010.05.004 |
| [3] | WIMMER M, MANDLBURGER G, RESSL C, et al. Estimation of High Resolution Shallow Water Bathymetry via Two-media-photogrammetry:A Case Study at the Pielach River[C]//Geophysical Research Abstracts vol. 18, EGU General Assembly 2016. Vienna, Austria:EGU, 2016:7197. |
| [4] | WESTAWAY R M, LANE S N, HICKS D M. Remote Survey of Large-scale Braided, Gravel-bed Rivers Using Digital Photogrammetry and Image Analysis[J]. International Journal of Remote Sensing, 2003, 24(4): 795–815. DOI:10.1080/01431160110113070 |
| [5] | LANE S N, WIDDISON P E, THOMAS R E, et al. Quantification of Braided River Channel Change Using Archival Digital Image Analysis[J]. Earth Surface Processes and Landforms, 2010, 35(8): 971–985. DOI:10.1002/esp.v35:8 |
| [6] | SHAN Jie. Relative Orientation for Two-media Photogrammetry[J]. The Photogrammetric Record, 1994, 14(84): 993–999. DOI:10.1111/phor.1994.14.issue-84 |
| [7] | TELEM G, FILIN S. Photogrammetric Modeling of the Relative Orientation in Underwater Environments[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013(86): 150–156. |
| [8] | 王有年, 韩玲, 王云. 水下近景摄影测量试验研究[J]. 测绘学报, 1988, 17(3): 217–224. WANG Younian, HAN Ling, WANG Yun. Experimental Research of Underwater Close-range Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 1988, 17(3): 217–224. |
| [9] | 常本义. 双介质摄影测量基本公式[J]. 测绘学报, 1991, 20(4): 288–294. CHANG Benyi. Basic Formulas of Two-media Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 1991, 20(4): 288–294. |
| [10] | 单杰. 双介质摄影测量的相对定向[J]. 测绘学院学报, 1993, 10(3): 38–44. SHAN Jie. Relative Orientation for Two-media Photogrammetry[J]. Journal of the Institute of Surveying and Mapping, 1993, 10(3): 38–44. |
| [11] | 周高伟, 李英成, 任延旭, 等. 低空无人机双介质水下礁盘深度测量试验与分析[J]. 测绘学报, 2015, 44(5): 548–554. ZHOU Gaowei, LI Yingcheng, REN Yanxu, et al. Research of Two-media Underwater Reefs Depth Measurement Experiment Based on Low-altitude UAV[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 548–554. DOI:10.11947/j.AGCS.2015.20140259 |
| [12] | 曹彬才, 邱振戈, 朱述龙, 等. 高分辨率卫星立体双介质浅水水深测量方法[J]. 测绘学报, 2016, 45(8): 952–963. CAO Bincai, QIU Zhenge, ZHU Shulong, et al. Shallow Water Bathymetry through Two-medium Photogrammetry Using High Resolution Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 952–963. DOI:10.11947/j.AGCS.2016.20150583 |
| [13] | MURASE T, TANAKA M, TANI T, et al. A Photogrammetric Correction Procedure for Light Refraction Effects at a Two-medium Boundary[J]. Photogrammetric Engineering & Remote Sensing, 2008, 74(9): 1129–1136. |
| [14] | GEORGOPOULOS A, AGRAFIOTIS P. Documentation of a Submerged Monument Using Improved Two Media Techniques[C]//Proceedings of the 18th International Conference on Virtual Systems and Multimedia. Milan, Italy:IEEE, 2012:173-180. |
| [15] | FRYER J G, KNIEST H T. Errors in Depth Determination Caused by Waves in Through-water Photogrammetry[J]. The Photogrammetric Record, 1985, 11(66): 745–753. |
| [16] | WESTAWAY R M, LANE S N, HICKS D M. Remote Sensing of Clear-water, Shallow, Gravel-bed Rivers Using Digital Photogrammetry[J]. Photogrammetric Engineering and Remote Sensing, 2001, 67(11): 1271–1282. |
| [17] | BUTLER J, LANE S, CHANDLER J, et al. Through-water Close Range Digital Photogrammetry in Flume and Field Environments[J]. The Photogrammetric Record, 2002, 17(99): 419–439. DOI:10.1111/phor.2002.17.issue-99 |
| [18] | MAAS H G. A Modular Geometric Model for Underwater Photogrammetry[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences:Volume XL-5/W5. Dresden, Germany:TSPRS, 2015:139-141. |
| [19] | DIETRICH J T. Bathymetric Structure-from-motion:Extracting Shallow Stream Bathymetry from Multi-view Stereo Photogrammetry[J]. Earth Surface Processes and Landforms, 2017, 42(2): 355–364. DOI:10.1002/esp.v42.2 |
| [20] | DigitalGlobe. WorldView-2 Overview[EB/OL].[2017-03-10]. http://content.satimagingcorp.com.s3.amazonaws.com/static/satellite-sensor-specification/WorldView-2-PDF-Download.pdf. |
| [21] | 曹斌, 邱振戈, 曹彬才. 四种遥感浅海水深反演算法的比较[J]. 测绘科学技术学报, 2016, 33(4): 388–393. CAO Bin, QIU Zhenge, CAO Bincai. Comparison among Four Inverse Algorithms of Water Depth[J]. Journal of Geomatics Science and Technology, 2016, 33(4): 388–393. |
| [22] | 曹斌, 邱振戈, 朱述龙, 等. BP神经网络遥感水深反演算法的改进[J]. 测绘通报, 2017(2): 40–44. CAO Bin, QIU Zhen'ge, ZHU Shulong, et al. Improvement of BPANN Based Algorithm for Estimating Water Depth from Satellite Imagery[J]. Bulletin of Surveying and Mapping, 2017(2): 40–44. DOI:10.13474/j.cnki.11-2246.2017.0045 |
| [23] | HEDLEY J D, HARBORNE A R, MUMBY P J. Technical Note:Simple and Robust Removal of Sun Glint for Mapping Shallow-water Benthos[J]. International Journal of Remote Sensing, 2005, 26(10): 2107–2112. DOI:10.1080/01431160500034086 |
| [24] | DigitalGlobe. Radiometric Use of WorldView-2 Imagery[EB/OL].[2017-03-10]. http://www.pancroma.com/downloads/Radiometric_Use_of_WorldView-2_Imagery.pdf. |
| [25] | DigitalGlobe. Imagery Support Data (ISD) Documentation[EB/OL].[2017-03-10]. http://www.docin.com/p-345895199.html. |
| [26] | Optech. SHOALS-3000 Product Brochure[EB/OL].[2017-03-10]. http://pdf.directindustry.com/pdf/optech/shoals-3000-product-brochure/25132-53146.html. |



