合成孔径雷达(synthetic aperture radar,SAR)具有监测范围广、分辨率高、全天时、全天候等优点,已被广泛应用于遥感、军事和水文等领域[1-3]。目前SAR图像处理算法开发及其应用日益成为遥感学界的研究难点和热点。边缘检测是提取图像中光谱测度跳变特征的过程,也是实现图像分割的重要手段之一[4-6]。图像分割主要分为区域分割与边缘分割,而边缘分割较区域分割简单快速,实用性较强[7-8]。
广泛使用的经典边缘检测算子,如Sobel、Prewitt、LOG等,仅利用邻近像素的梯度运算实现边缘检测,故对噪声非常敏感[9]。而Canny算子由于进行了最优化操作,在同类经典算子中取得了最好结果。但由于其仍是局部算子,且只有水平和垂直方向两个模板,故仍会受到噪声的影响而产生部分错检与漏检边缘[10]。
为了克服噪声影响,研究者不断提出新的方法。其中,最具代表性的当属文献[11]提出的均值比(ratio of averages,ROA)检测器。以待检测像素为中心,在0°、45°、90°和135° 4个方向上分别计算其两侧不重叠窗口内像素灰度均值并计算均值比,取在这4个方向上得到的最小值为边缘强度。由于考虑了一定范围内像素灰度均值信息,从而克服了经典算子对斑点噪声异常敏感的缺点,同时也顾及了边缘的方向性[12]。虽然文献[11]在理论上证明了该方法是一类恒虚警方法[13],但当窗口尺度增大或对某些特定的窗口形状,窗口内部许多采样点将偏离检测方向,或窗口内采样点数目相对较少,因此难以达到恒虚警的效果。在ROA检测器的基础上,文献[14]提出了MROA(modified ratio of averages)和RGOA(ratio and gradient of averages)检测器。虽然它们较之ROA检测器有一定的改进,但由于和ROA检测器具有相同的四方向窗口,故当噪声幅度过大时其对于任意方向边缘仍无法保障检测的完整性。
实际上,完整的边缘检测包括边缘定位与定向[4]。尽管指数加权均值比检测器(ratio of exponentially weighted averages,ROEWA)[15]是目前针对SAR图像的主流边缘检测器之一,但ROEWA也只能得到边缘强度而无法确定边缘方向[16]。为此,研究者在此基础上提出了一些边缘方向计算方法[17-20],但这些方法在得到边缘方向的同时也具有部分局限性,且最多只能在4个方向辨识边缘,对实际地物形状复杂的区域,有限的边缘方向难以满足边缘提取的精度要求。在多分辨率框架下,相继提出了多种基于小波变换的SAR图像边缘检测算法。文献[21—22]充分利用边缘的多方向性和小波变换的方向选择性,用边缘检测算子检测出小波变换系数在不同方向上所对应的边缘,然而算子的有限方向性限制了小波变换的能力。
在上述工作的基础上,文献[23—24]提出的方法可同时获得边缘强度与方向。该方法以窗口中变化最大方向上的灰度变化率为测度,以2个邻域窗口的最快变化率与中心像素所在窗口的最快变化率之差为边缘像素判别标准。由于该方法以差值为标准,符合梯度的定义,故可较好地保留边缘方向。但由于一定尺度窗口内的变化率并不显著,使得边缘与非边缘处的强度对比并不明显。
因前述方法具有不同程度的局限性,为此,提出任意方向对称差值核的SAR图像边缘提取算法,可为需要多方向性处理的算法提供一种新思路。
1 离散对称窗口与核函数 1.1 离散对称窗口灰度图像Z={zi(xi, yi), i=1, 2, …, n2}可视为三维曲面上的离散规则采样,其中, i为采样(像素)索引,(xi, yi)∈D为像素位置, D为图像域,zi为像素i的灰度值, n为图像行列数。在图像中,每个像素对应图像域中的一个样本点,对于任意检测中心(x, y),以图像域的x轴正方向为检测0方向,以逆时针旋转为正方向。对于任意检测方向θ∈[0, π),定义与检测方向相同的一侧窗口为前窗口W(x, y, θ),与检测方向相反的窗口为后窗口W(x, y, θ+π),两个窗口关于(x, y)成中心对称。此时两对称窗口应分别关于(x, y)逆时针旋转一个角度θ和θ+π。
为了在离散格点结构中得到窗口内样本点,提出任意方向上p×p(p为奇数)离散窗口构建算法。以(x, y)为起始点在θ方向上做射线rθ。对p×p窗口,沿射线方向rθ依次按行或按列选取与其相交的p个像素为窗口中轴线样本点集ma;以ma为基准沿rθ的垂线方向向两边各平行扩展(p-1)/2组,得到样本点集ma-1, ma-2, …, ma-(p-1)/2与ma+1, ma+2, …, ma+(p-1)/2,最终得到前窗口W(x, y, θ)={ma-(p-1)/2, …, ma, …, ma+(p-1)/2}。则同理可求与之对称的后窗口W(x, y, θ+π)。以θ∈[0, π/4]为例,具体操作如下:
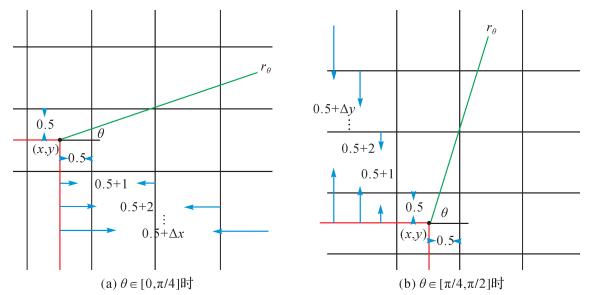
设单个像素的边长为1,令Δx和Δy分别为在(x, y)处的像素横坐标和纵坐标累加值。为得到p个窗口中轴线样本点,当θ∈[0, π/4]时,Δy由Δx确定。设Δx=0, 1, …, p-1,(0.5+Δx)tan θ为沿θ方向且随着像素横坐标的累加而增加的纵坐标值,与Δy的关系为:当0≤(0.5+Δx)tan θ < 0.5时,Δy=0;当0.5+k-1≤(0.5+Δx)tan θ < 0.5+k(k=1, 2, …, p)时,Δy=k。此时每个x+Δx+1均对应于y+Δy,即ma={(x+Δx+1, y+Δy); Δx=0, 1, …, p-1}。
图 1(a)为当θ∈[0, π/4]时确定ma的示意图,图 1(b)为当θ∈[π/4, π/2]时确定ma的示意图,其中格网代表像素,绿线为射线rθ,蓝色箭头指示代表半个像素的边长以及在该边长的基础上经像素横坐标和纵坐标累加后而产生的距离。
|
| 图 1 确定ma的过程 Fig. 1 Process of ma obtained |
按上述原则沿θ+π/2方向确定第j(j=1, 2, …, p)个中轴线样本点一边的(p-1)/2个点,则另一边与这(p-1)/2个点关于第j个中轴线样本点成中心对称的另(p-1)/2个点也可知,由此而最终得到前窗口W(x, y, θ)。
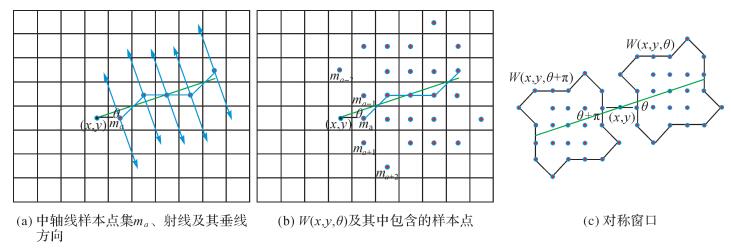
图 2所示为当θ∈[0, π/4]时的5×5窗口,沿射线方向rθ依次按列选取得到ma,再沿rθ的垂线方向向两边各平行扩展(5-1)/2组后得到W(x, y, θ)={ma-2, ma-1, ma, ma+1, ma+2}。图 2(a)为得到的中轴线样本点集ma与射线及其垂线方向示意图;图 2(b)为最终得到的前窗口W(x, y, θ)中包含的样本点示意图,其中格网代表像素,红点为样本点;图 2(c)为最终得到的对称窗口示意图,两窗口及内部样本点关于检测中心(x, y)成中心对称。窗口的形状使得在不同的窗口尺寸下,样本点总会沿着检测方向两侧均匀分布,从而可准确反映该检测方向下检测中心两侧的灰度跳变信息。
|
| 图 2 5×5对称窗口的确定过程 Fig. 2 Process of 5×5 symmetric windows obtained |
1.2 核函数
定义在对称窗口内包含的样本点上的二元核函数K(x, y)满足:① 核函数K(x, y)光滑且关于原点成中心对称,并越接近原点函数值越大;② 已知检测中心(x, y),则K(x, y)的定义域为F={(xu, yv); (xu, yv)∈W(θ)∪W(θ+π)};其中(xu, yv)是对称窗口内的样本;(3) 当(xu, yv)∈W(θ)∪W(θ+π)时,K(xu, yv)≥0。本文算法采用高斯核函数
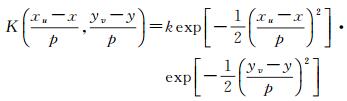 (1)
(1)
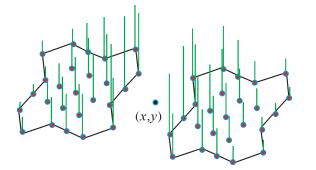
式中,k(>0) 用以调整(xu, yv)所获得的权重幅度。采用式(1) 可以将对称窗口内样本点的平均值进行加权,使越接近检测中心(x, y)的样本点(xu, yv)获得的核函数值(权重)越大,反之越小[25]。随着(x, y)由图像中的同质区域逐渐接近边缘,会使得两个窗口差值绝对值增大的速度呈现越来越快的非线性增长。最终可使检测出的边缘强度在靠近真实边缘时更大,远离时更小,使初始边缘更加靠近真实边缘。图 3为窗口内样本点获得的权重示意图,其中绿线代表权重大小,越长的权重越大,反之越小。
|
| 图 3 对称窗口内不同样本点的权重 Fig. 3 Weight of different sample points in symmetric windows |
2 边缘提取 2.1 初始边缘
以(x, y)为检测中心,其任意方向对称差值核检测模型为
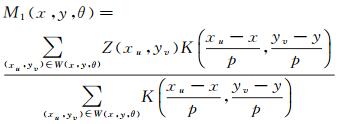 (2)
(2)
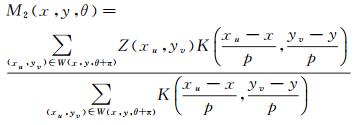 (3)
(3)
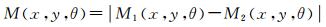 (4)
(4)
式(2) 表示(x, y)的前窗口W(x, y, θ)内样本点的加权平均值;式(3) 表示(x, y)的后窗口W(x, y, θ+π)内样本点的加权平均值;式(4) 表示两个窗口内加权平均值的差值绝对值。
相对于给定尺度的窗口,对远离边缘的像素,在任何检测方向上的两对称窗口总是位于同一同质区域,因此其M值较小;对靠近边缘的像素,存在某一窗口跨越不同同质区域,使得M值变大;而对于边缘像素,总会存在某一检测方向上的两个对称窗口分别位于不同的同质区域内,这时M取得最大值。由此,对给定像素可用所有检测方向上的最大M值为判据判断其是否为边缘像素
 (5)
(5)
式(5) 表示在(x, y)处的所有检测方向中最大M值所对应的方向,最大M值为
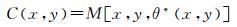 (6)
(6)
将(x, y)遍历D后得到C={C(x, y):(x, y)∈D},利用其得到值为0~255的像素边缘强度集为
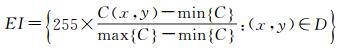 (7)
(7)
式中, T为一个在0~255内的阈值,进行二值化处理(边缘像素值为1),得到二值初始边缘H(x, y)。
2.2 边缘后处理通过下式对初始边缘进行消除非边缘处理
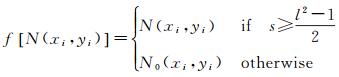 (8)
(8)
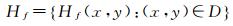 (9)
(9)
式中,N(xi, yi)表示以H或Hf中Hf(xi, yi)=1的像素(xi, yi)为中心的l×l邻域(本文算法取l=3);s表示N(xi, yi)中Hf(xi, yi)值为1的数目;N0(xi, yi)表示N(xi, yi)中Hf(xi, yi)值都为0。通过将式(8) 中的(xi, yi)遍历完图像域D后得到式(9) 中的Hf,再通过式(8) 对Hf处理后得到新的Hf,以此重复迭代,直到Hf不再发生变化为止。
当N(xi, yi)经过边缘主干时会使其中超过半数的像素都是检测到的初始边缘,故此时需保留;反之,当N(xi, yi)在主边缘外围或噪声点处则会将少于半数的初始边缘像素删去,最终留下边缘主干而滤除噪声点。
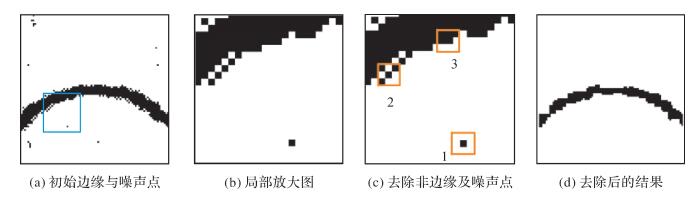
图 4为消除非边缘示意图,图 4(a)中的拱形黑色区域代表较粗的初始边缘,零散的黑点代表噪声点;图 4(b)为图 4(a)中蓝色方框所在区域的局部放大;图 4(c)表示利用邻域进行保留边缘主干,去除非边缘的处理,其中编号为1的黄色方框代表可消除零星的噪声点,编号为2的代表可消除边缘外围的不准确及错检边缘,编号为3的代表将边缘主干进行保留;图 4(d)表示对图 4(a)整体进行处理后的最终结果,保留了边缘主干,去除了错误边缘。
|
| 图 4 初始边缘去除非边缘及噪声点 Fig. 4 Non-edge and noise points of initial edge is removed |
初始结果去除噪声点以后,采用形态学对较粗的初始边缘进行细化处理,至此完成边缘提取。
3 试验结果与讨论为了能够全方位检测边缘,以Δθ为角度间隔使θ遍历[0, π),可产生[(π-Δθ)/Δθ]+1个不同的角度θk=(k-1)π/{[(π-Δθ)/Δθ]+1}(k=1, 2, …, [(π-Δθ)/Δθ]+1)。试验中采用5×5窗口产生16个不同的角度所对应的不同对称窗口来提取边缘。
3.1 模拟图像边缘提取将图 5(a)所示的模板图像添加独立同分布的高斯噪声后形成图 5(b)所示的256×256像素的模拟图像。

|
| 图 5 模板图像与模拟图像 Fig. 5 Template image and simulated image |
试验采用5种对比算法和本文算法提取其边缘,采用的对比算法包括:Canny算子、ROA检测器(5×5窗口)、文献[23]提出的方法(5×5窗口)、ROEWA检测器和小波变换。对所有算法结果均利用形态学细化处理。图 6中分别为ROA检测器、文献[23]提出的方法、ROEWA检测器、小波变换与本文算法提取模拟图像所产生的边缘强度。从图 6可知,ROA检测器、文献[23]提出的方法和小波变换都受到噪声的干扰而使得真实边缘与噪声背景的对比不明显;ROEWA检测器的真实边缘与噪声背景的对比虽然明显,但缺少多方向边缘强度的计算使得其检测性能受到了限制;与它们对比,本文算法的窗口均匀且其中包含相对较多的样本点,并通过很多方向的检测使得其受噪声的干扰尽可能减小,真实边缘与噪声背景的对比较为明显。

|
| 图 6 对比算法与本文算法的边缘强度 Fig. 6 Edge magnitude of compared algorithms and proposed algorithm in this paper |
图 7为本文算法提取模拟图像时每个像素所对应的C(x, y)及θk*(x, y)(k=1, 2, …, 16) 所构成的矢量场,其中矢量大小代表C(x, y)的值,矢量方向为θk*(x, y)所对应的方向。

|
| 图 7 C(x, y)和θk*(x, y)构成的矢量场 Fig. 7 Vector field made of C(x, y) and θk*(x, y) |
图 8为各对比算法对模拟图像提取的边缘结果,其中图 8(a)—(e)分别为Canny算子、ROA检测器、文献[23]提出的方法、ROEWA检测器和小波变换的边缘结果,且皆为人为选取的最佳阈值结果。

|
| 图 8 各对比算法的边缘结果 Fig. 8 Edge results of compared algorithms |
由图 8可知,Canny算子可以较好地克服噪声影像,但仍会有错检的边缘产生;ROA检测器由于窗口和方向的限制使得真实边缘与噪声的差异非常不显著,且其对于模拟图像中颜色较浅的区域抗噪性较好,但较深的区域则较差,即效果非恒虚警;由于文献[23]提出的算法中窗口内的变化率不很显著,故变化率之差检测出的边缘较噪声的差异不明显,仍然会有很多非边缘及噪声点存在;ROEWA检测器由于缺少多方向的计算而使得其抗噪能力受限,产生了部分噪声点;小波变换的抗噪能力也并不佳。
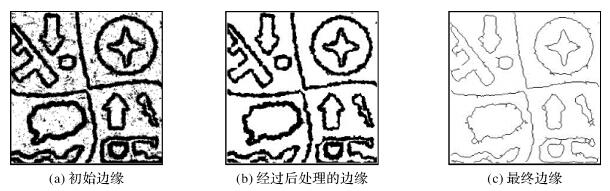
图 9(a)、(b)、(c)分别为本文算法提取的初始边缘与经过后处理去除了噪声点的边缘以及经过细化后的最终边缘。
|
| 图 9 初始边缘与最终边缘 Fig. 9 Initial edge and final edge |
为了判断本文算法的准确性,采用定性与定量评价。定性评价是将算法所提取的边缘与原图像进行叠加来进行目视评价。定量评价则采用缓冲区分析法,以模板图像的正确边缘为中心,3个像素为半径的范围作为缓冲区,计算出算法所提取的边缘分别落入不同半径的缓冲区内的百分比(Bi, i=1, 2, 3) 与累加百分比(Si, i=1, 2, 3)。图 10(a)—(f)分别为Canny算子、ROA检测器、文献[23]提出的方法、ROEWA检测器、小波变换与本文算法的定性评价结果。

|
| 图 10 各对比算法与本文算法的定性评价结果 Fig. 10 Results of qualitative evaluation of compared algorithms and proposed algorithm in this paper |
由于ROA检测器、文献[23]提出的方法和小波变换的结果目视效果较差,故不再对其进行定量评价,只对Canny算子、ROEWA检测器与本文算法进行对比定量评价,表 1为定量评价结果。由表 1可知,本文算法中,40%的提取边缘与正确边缘重合,84.29%的提取边缘落入到了1个像素宽度的缓冲区内,94.35%的提取边缘落入到了2个像素宽度的缓冲区内,97.08%的提取边缘落入到了3个像素宽度的缓冲区内。综合定量评价结果可知,本文算法的检测精度要优于Canny算子和ROEWA检测器。
| (%) | ||||||||
| B0 | S0 | B1 | S1 | B2 | S2 | B3 | S3 | |
| 本文算法 | 40.00 | 40.00 | 44.29 | 84.29 | 10.06 | 94.35 | 2.73 | 97.08 |
| Canny算子 | 54.97 | 54.97 | 24.91 | 79.88 | 5.83 | 85.71 | 4.69 | 90.40 |
| ROEWA检测器 | 38.79 | 38.79 | 42.10 | 80.89 | 7.14 | 88.03 | 5.03 | 93.06 |
3.2 真实SAR图像边缘提取
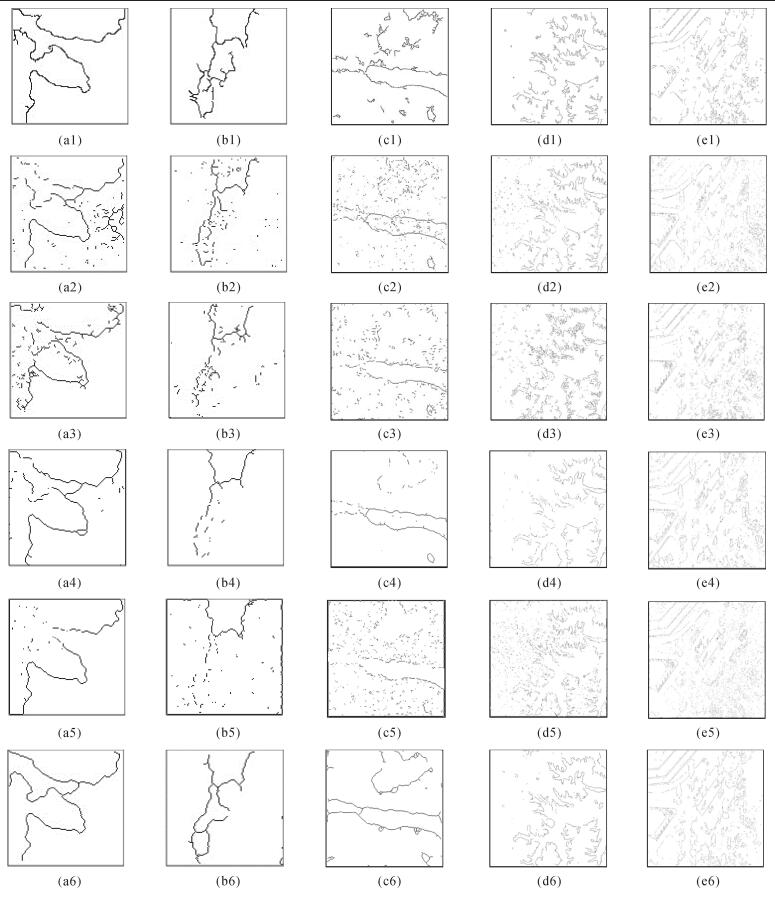
为进一步验证本文算法的性能,对图 11的真实SAR图像进行了试验。其中图 11(a)、(b)为128×128像素,图 11(c)为256×256像素,图 11(d)为512×512像素,图 11(e)为1024×1024像素。图 12(a1)—(e1)至(a5)—(e5)分别为Canny算子、ROA检测器、文献[23]提出的方法、ROEWA检测器和小波变换对真实SAR图像提取的边缘结果,图 12(a6)—(e6)为本文算法的结果。

|
| 图 11 真实SAR图像 Fig. 11 Real SAR images |
|
| 图 12 对比算法与本文算法的边缘结果 Fig. 12 Edge results extracted by compared algorithms and proposed algorithm in this paper |
4 结论
本文提出了一种任意方向对称差值核的SAR图像边缘提取算法。该算法克服了传统窗口形状固定不变以及采样点相对较少的特点,通过任意方向检测窗口会充分估计出边缘两侧的灰度跳变幅度与梯度方向,使得各个方向的边缘都会以同样的强度被检测出来;由于窗口内样本点的分布较为均匀,且数量相对较多,再经过本文的后处理算法就可以最大限度地消除噪声影响,反映真实边缘信息;以核函数加权的差值绝对值为标准来判别边缘会使得边缘与非边缘的对比更加明显,且结果更加精确,尤其对受噪声影响而边缘模糊的相近区域更为有效。但由于本文算法采用包含较多像素的窗口会将棱角分明的边缘变的平滑,从而丢失精细边缘处的细节信息,故后续会针对该问题做进一步的研究。
| [1] | 吴艳, 焦惊眉, 杨晓丽, 等. 基于Contourlet域HMT和D-S证据融合的SAR图像分割[J]. 测绘学报, 2011, 40(2): 148–155. WU Yan, JIAO Jingmei, YANG Xiaoli, et al. Segmentation Algorithm for SAR Images Based on Fusion of HMT in the Contourlet Domain and D-S Theory of Evidence[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 148–155. |
| [2] | 万红林, 焦李成, 辛芳芳. 基于交互式分割技术和决策级融合的SAR图像变化检测[J]. 测绘学报, 2012, 41(1): 74–80. WAN Honglin, JIAO Licheng, XIN Fangfang. Interactive Segmentation Technique and Decision-level Fusion Based Change Detection for SAR Images[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 74–80. |
| [3] | 吴诗婳, 吴一全, 周建江, 等. 利用倒数灰度熵和改进Chan-Vese模型进行SAR河流图像分割[J]. 测绘学报, 2015, 44(11): 1255–1262. WU Shihua, WU Yiquan, ZHOU Jianjiang, et al. SAR River Image Segmentation Based on Reciprocal Gray Entropy and Improved Chan-Vese Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1255–1262. DOI:10.11947/j.AGCS.2015.20140519 |
| [4] | 王庆, 曾琪明, 张海真, 等. 全极化SAR图像边缘检测的随机距离法[J]. 测绘学报, 2015, 44(7): 753–760. WANG Qing, ZENG Qiming, ZHANG Haizhen, et al. Edge Detection of PolSAR Image Based on Stochastic Distance[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 753–760. DOI:10.11947/j.AGCS.2015.20130810 |
| [5] | 李新娜, 王正明, 谢美华. SAR图像的核回归自适应相干斑抑制方法[J]. 测绘学报, 2013, 42(5): 729–737. LI Xinna, WANG Zhengming, XIE Meihua. The Adaptive Speckle Reduction Method Based Kernel Regression for SAR Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 729–737. |
| [6] | XIANG Yuming, WANG Feng, WAN Ling, et al. SAR-PC:Edge Detection in SAR Images via an Advanced Phase Congruency Model[J]. Remote Sensing, 2017, 9(3): 209. DOI:10.3390/rs9030209 |
| [7] | 隋立春. 主动式雷达遥感[M]. 北京: 测绘出版社, 2009. SUI Lichun. Active Radar and Lidar Remote Sensing[M]. Beijing: Surveying and Mapping Press, 2009. |
| [8] | WEI Qianru, FENG Dazheng. Extracting Line Features in SAR Images through Image Edge Fields[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(4): 540–544. DOI:10.1109/LGRS.2016.2523560 |
| [9] | WEI Qianru, FENG Dazheng, XIE Hu. Edge Detector of SAR Images Using Crater-Shaped Window with Edge Compensation Strategy[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(1): 38–42. DOI:10.1109/LGRS.2015.2493640 |
| [10] | YANG Haiyi, CAO Zongjie, PI Yiming, et al. Target Detection in High-Resolution SAR Images via Searching for Part Models[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 664–668. DOI:10.1109/LGRS.2017.2669945 |
| [11] | TOUZI R, LOPES A, BOUSQUET P. A Statistical and Geometrical Edge Detector for SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1988, 26(6): 764–773. DOI:10.1109/36.7708 |
| [12] | 刘俊怡, 李德仁, 李微, 等. 一种基于均值比率和最佳熵的SAR影像边缘检测方法[J]. 武汉大学学报(信息科学版), 2007, 32(6): 494–497. LIU Junyi, LI Deren, LI Wei, et al. A Method for SAR Imagery Edge Detection Based on Ratio of Averages and Optimal Entropy[J]. Geomatics and Information Science of Wuhan University, 2007, 32(6): 494–497. |
| [13] | 赵凌君, 贾承丽, 匡纲要. SAR图像边缘检测方法综述[J]. 中国图象图形学报, 2007, 12(12): 2042–2049. ZHAO Lingjun, JIA Chengli, KUANG Gangyao. Overview of Edge Detection in SAR Images[J]. Journal of Image and Graphics, 2007, 12(12): 2042–2049. DOI:10.11834/jig.20071202 |
| [14] | ZAMAN M R, MOLONEY C R. A Comparison of Adaptive Filters for Edge-Preserving Smoothing of Speckle Noise[C]//Proceedings of 1993 IEEE International Conference on Acoustics, Speech, and Signal Processing. Minneapolis, MN:IEEE, 1993:77-80. |
| [15] | LOPÈS A, FJØRTOFT R, DUCROT D, et al. Edge Detection and Segmentation of SAR Images in Homogeneous Regions[M]//CHEN C H. Information Processing for Remote Sensing. Singapore:World Scientific Publishers, 1999:139-166. |
| [16] | 杨道莲, 鲁昌华, 张金良, 等. 基于ROEWA与Hough变换的SAR图像边缘检测[J]. 电子测量与仪器学报, 2013, 27(6): 543–548. YANG Daolian, LU Changhua, ZHANG Jinliang, et al. Edge Detection in SAR Images Based on ROEWA and Hough Transform[J]. Journal of Electronic Measurement and Instrument, 2013, 27(6): 543–548. |
| [17] | 安成锦, 辛玉林, 陈曾平. 基于改进ROEWA算子的SAR图像边缘检测方法[J]. 中国图象图形学报, 2011, 16(8): 1483–1488. AN Chengjin, XIN Yulin, CHEN Zengping. Edge Detection Algorithm for SAR Image Based on Improved ROEWA[J]. Journal of Image and Graphics, 2011, 16(8): 1483–1488. DOI:10.11834/jig.100111 |
| [18] | 刘帅奇, 胡绍海, 肖扬, 等. 基于局部混合滤波的SAR图像边缘检测[J]. 电子与信息学报, 2013, 35(5): 1120–1127. LIU Shuaiqi, HU Shaohai, XIAO Yang, et al. SAR Image Edge Detection Based on Local Hybrid Filter[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1120–1127. |
| [19] | PAILLOU P. Detecting Step Edges in Noisy SAR Images:A New Linear Operator[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 191–196. DOI:10.1109/36.551947 |
| [20] | 吴禹昊, 陈天泽, 粟毅. 基于方向ROEWA算子的高分辨率SAR图像道路提取[J]. 计算机工程与科学, 2010, 32(8): 71–74. WU Yuhao, CHEN Tianze, SU Yi. Road Extraction from High Resolution SAR Images Based on the Directional ROEWA Detector[J]. Computer Engineering & Science, 2010, 32(8): 71–74. |
| [21] | 周树道, 王敏, 刘志华, 等. 基于多方向小波变换及形态学重构的SAR图像边缘检测[J]. 解放军理工大学学报(自然科学版), 2011, 12(5): 436–439. ZHOU Shudao, WANG Min, LIU Zhihua, et al. SAR Image Edge Detection Based on Multi-directional Wavelet Transform and Morphological Reconstruction[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2011, 12(5): 436–439. |
| [22] | 毛成林, 万寿红, 岳丽华, 等. 一种基于双树复小波变换的SAR图像边缘检测算法[J]. 中国科学院大学学报, 2014, 31(2): 238–248. MAO Chenglin, WAN Shouhong, YUE Lihua, et al. An Edge Detection Algorithm of SAR Images Based on Dual-Tree Complex Wavelet Transform[J]. Journal of University of Chinese Academy of Sciences, 2014, 31(2): 238–248. |
| [23] | QIU Peihua, YANDELL B. Jump Detection in Regression Surfaces[J]. Journal of Computational and Graphical Statistics, 1997, 6(3): 332–354. |
| [24] | QIU Peihua. Image Processing and Jump Regression Analysis[M]. Hoboken, New Jersey: John Wiley & Sons, 2005. |
| [25] | YANDELL B S. Kernel Smoothing[J]. Technometrics, 1996, 38(1): 75–76. |


