2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079
2. GNSS Research Center of Wuhan University, Wuhan 430079, China
哨兵卫星(Sentinel-1) 是继ERS和EnviSat之后,欧空局(European Space Agency,ESA)发射的又一颗具有划时代意义的C波段雷达SAR遥感卫星。该卫星选用TOPS(terrain observation by progressive scans)模式作为默认成像模式,该模式继承了ScanSAR模式的设计思路,在扫描成像过程中波束依次在各个测绘带间进行切换,通过牺牲方位向分辨率来增加影像覆盖面积[1],因此卫星可在12 d内环绕地球运行175周完成对地球表面的全部覆盖[2]。TOPS模式通过压缩目标的多普勒历程进行成像,与ScanSAR模式相比,不但提高了影像质量,更提高了干涉性能[3-4]。
欧空局在发射哨兵卫星之前进行了充分的星载TOPS成像模式理论和试验准备工作,分别基于TerraSAR-X和Radarsat-2卫星进行了拍摄试验,并进行了聚焦成像处理[5-6]。哨兵卫星在这些工作的基础上进一步提高了姿态和轨道的控制精度以提高卫星影像干涉性能。TOPS模式影像干涉理论论证和数据测试基本上由DLR(德空局)主导完成。文献[1]首先指出该模式影像需要较高的配准精度。文献[7]公布了TerraSAR-X卫星TOPS模式干涉图,并指出增强谱分集配准(enhanced spectral diversity)处理方法可以满足高精度配准的要求。文献[8]则论证了方位向重叠区域的增强谱分集算法的精度,并完成此类型影像的干涉和时序处理试验。随着哨兵卫星的成功发射,文献[9]在上述研究基础上完成了哨兵卫星TOPS模式干涉处理理论分析与试验验证。与此同时,其他研究团队针对哨兵卫星TOP模式影像也开发了相应的干涉处理软件,如Gamma、GMTSAR。这些软件各有特色,但主要算法均在几何配准和增强谱分集的框架中[10-11]。本文则基于开源软件DORIS在精密轨道条件下完成哨兵卫星TOPS模式的干涉处理。
1 TOPS模式影像配准TOPS模式在每组Burst扫描期间,波束由后向前摆动,使得波束覆盖区的移动速度大于卫星速度,卫星有足够时间进行多个子测绘带的成像。TOPS模式零多普勒聚焦成像后一组Burst影像点目标脉冲响应函数表示为
 (1)
(1)
式中,r0为点目标的零多普勒斜距;Vr为雷达传感器有效速度;kψ为天线波束旋转角速度。其中, sr和sa分别为距离向、方位向包络;τ、η分别为距离向、方位向时间;τ0、η0分别为距离向和方位向参考零多普勒时间;f0为雷达发射脉冲中心频率;c为电磁波速度;β为直线几何中波束中心斜视角。由式(1) 可知,在冲击响应峰值处,即η=η0,exp[j·2π·fηc·(η-η0)]相位贡献为零。但由于采样点一般不在峰值处,聚焦影像存在相位斜坡。距离向相位斜坡可以选择适当的成像几何予以消除,然而方位向相位斜坡代表目标到散射体中心的实际斜距,无法予以消除[12]。干涉处理时,方位向相位斜坡不但导致重采样时需进行方位线解斜或者内插核调制处理,还需要较高的配准精度,以降低多普勒中心变化带来的相位偏差[13]。根据式(1) 可以得到方位向配准误差Δη与干涉图相位偏差Δɸ的关系
 (2)
(2)
图 1为根据式(2) 计算的条带模式影像和TOPS模式影像方位向不同位置的点目标干涉相位偏差。条带模式影像由于方位向多普勒中心相同,其干涉相位偏差(红线)是一致的,通常配准精确度只要求达到0.1个像素以确保相干性不受影响;TOPS模式影像由于多普勒中心在方位向上的变化,导致其不同位置的干涉相位偏差并不相同。由于哨兵卫星TOPS模式影像多普勒中心变化范围一般在[-2500+2500] Hz内,为确保其干涉图在一组Burst中干涉相位偏差不超过3°,配准精确度要求达到0.001像素,相当于方位向零多普勒时间配准真误差小于2 μs。

|
| 图 1 配准误差引起的干涉图相位偏差 Fig. 1 Phase bias of interferogram caused by mis-coregistration |
由于地形起伏等原因,多项式难以准确拟合出主辅影像几何畸变的映射,无法满足哨兵卫星TOPS模式影像方位向0.001个像素的配准精度需要。本文则利用几何配准误差为系统误差的特点采用哨兵卫星精密轨道进行初配准,然后根据影像信息采用增强谱分集方法进一步做精配准处理,以获取正确的干涉图。
1.1 基于精密轨道的TOPS影像几何配准合成孔径雷达是通过多普勒频域算法将原始回波信号聚焦为斜距图像,其多普勒参数估计不仅依赖于卫星姿态传感器,还可以根据雷达回波多普勒频移特性进行估计,理论上其影像几何比光学影像更为严格[14-15]。欧空局对哨兵卫星TOPS模式影像聚焦时放弃“一步一停”聚焦模型,而是采用与卫星运动状态相符的“持续运动”模型,经过传感器延迟、地球固体潮、大气延迟校正后,其影像距离向绝对定位精度为1.5±0.37 m,方位向绝对定位精度为0.53±0.74 m[16-17]。SAR影像几何配准类似于光学摄影测量中物方影像匹配方法,根据DEM和卫星轨道信息基于零多普勒几何定位原理计算每个像元的相对偏移量。几何配准不依赖影像的相干性,可靠性较高,随着卫星轨道精度的提高,该方法逐步受到关注[18-20]。卫星轨道和DEM高程精度决定了几何配准精度[21-22]。卫星轨道对几何配准的影响通常以基线误差的形式呈现,其对距离向几何配准误差δ(p)的影响如式(3) 所示
 (3)
(3)
式中,Δr为距离向像素采样空间;p为影像距离向坐标;δSr为轨道距离向误差。欧空局提供的哨兵卫星精密轨道(precise orbit)精度约为5 cm,轨道距离向误差δSr导致的几何配准误差远远小于影像像元空间[23]。轨道误差对方位向配准误差δ(l)的关系如下
 (4)
(4)
式中,Δaz为方位向像素采样空间;l为影像方位向坐标;δSaz为轨道切向误差。从式(4) 可以看出,轨道误差对方位向配准的影响是由轨道切向误差δSaz引起的。哨兵卫星方位向配准精度要求为0.001个像元,相当于几何配准时轨道切向精度达到1 cm[24]。目前哨兵精密轨道无法满足这一条件,需要根据影像信息进一步优化方位向几何配准结果[25]。
除卫星轨道外,DEM高程精度与几何配准精度直接相关。DEM误差εh与距离向几何配准误差δ(p)关系如式(5) 所示
 (5)
(5)
式中, r0为影像零多普勒斜距;B⊥为干涉影像的垂直基线;θ为影像入射角。从式(5) 中可以看出垂直基线B⊥越短,距离向配准精确度越高。图 2为距离向配准精度0.1个像素时,垂直基线、雷达侧视角与DEM精度需求之间的关系。哨兵卫星垂直基线一般在150 m以内,入射角范围为19°~45°,如图中白色框线所示,此时DEM误差导致的距离向配准误差约为εh·10-4个像素。哨兵卫星距离向配准精度要求为0.1个像素,SRTM标称绝对高程精度是16 m,DEM对距离向配准误差的影响可以忽略不计。

|
| 图 2 DEM精度需求与轨道垂直基线、雷达侧视角的关系(距离向偏移量精度要求为0.1个像元) Fig. 2 Required DEM accuracy as a function of the incidence angle and perpendicular baseline (an accuracy of 0.1 pixel is required for range shift) |
对于雷达卫星重复干涉测量,其重复轨道之间并不是严格平行的,通常存在一定夹角。哨兵卫星轨道为准回归轨道,卫星运行175周后,理论上卫星应回到初始位置,然而受到各种摄动因素的影响,重复轨道之间必然存卫星位置、姿态、速率的差异,以及轨道间的不平行。卫星轨道夹角不但引起干涉影像间的多普勒频谱差异、时间同步问题,采用卫星轨道进行几何配准时还与DEM共同影响方位向几何配准精度,DEM高程误差与方位向几何配准误差接近于线性关系[26]。DEM误差εh对方位向几何配准误差δ(l)的影响如式(6) 所示
 (6)
(6)
式中,αg为轨道夹角,图 3为根据式(6) 得到的不同入射角和轨道夹角条件下所需的DEM高程精度。哨兵卫星多数情况下轨道夹角小于0.001°,白色框线范围内为哨兵影像干涉所需的DEM高程精度,可以看出SRTM可以满足大多数地区干涉处理的需要。一般条件下, DEM高程误差对配准误差的影响理论上优于0.000 1个像素量级,通常不对配准结果产生影响,方位向配准误差是由轨道切向误差引起的[27]。

|
| 图 3 DEM精度需求与雷达侧视角、轨道夹角的关系(方位向偏移量精度要求为0.001个像元) Fig. 3 Required DEM accuracy as a function of the incidence angle and orbit crossing angle (an accuracy of 0.001 pixel is required for azimuth shift) |
几何配准的优势是可以充分利用影像分辨率单元(resolution cell)估计影像残余偏移量。卫星轨道在一个时段内呈系统误差特性,轨道切向误差导致的方位向几何配准误差可视为系统误差[28-29]。哨兵卫星轨道基线控制在150 m的范围内,几何配准后的残余偏移量在每组Burst中通常认为是恒定值[30]。方位向配准偏移量可由式(7) 表示
 (7)
(7)
式中,F(l, p)为主辅影像间的方位向偏移量;f(l, p)为几何配准获得的方位向偏移量;V为几何配准残余偏移量;它们常以像素为单位。影像残余偏移量通常是根据影像信息进行估计,理论上影像分辨率单元数量越大,残余偏移量估计精度越高,几何配准可以充分利用影像中的分辨率单元以提高残余偏移量估计精度。如果采用多项式进行初配准,每个像素配准残余偏移量都不相同,则无法利用提高窗口的像元数来提高残余偏移量估计精度。图 4为采用不同方法估计几何配准残余偏移量的理论精度[31],其中横轴为影像相干系数,纵轴表示配准误差的标准差。根据哨兵影像参数,影像方位向过采样率约为1.3,距离向过采样率约为1.5,实相关(incoherent cross correlation)、复相关(coherent cross correlation)、谱分集(spectral diversity)处理窗口(一组Burst)设置为1502×21 549像素,而增强谱分集窗口为Burst间的重叠区域,设置为100×21 549像素。图中黑色横线为千分一个像素界限,可以看出增强谱分集配准精度最高,即使在相干性很低的时候,也满足0.001个像素精度要求。对于哨兵卫星,采用增强谱分集进行残余偏移量估计的前提是几何配准精度优于0.06个像素,防止增强谱分集相位出现缠绕现象。哨兵卫星精密轨道切向精度优于5 cm,几何配准时理论精度达到0.004个像素(置信度为68.3%),理论上精密轨道条件下几何配准后直接利用增强谱分集算法估计方位向配准误差发生相位缠绕的概率极低,精密轨道条件几何配准后无需采用相关配准进行校正,提高了干涉处理效率。当然其缺点是精密轨道相对于卫星数据发布时间较晚,无法满足准实时处理的需要。

|
| 图 4 SAR影像不同配准方法精度 Fig. 4 Accuracy of different methods for SAR image coregistration |
1.2 基于增强谱分集TOPS精配准
增强谱分集与传统谱分集原理上是一致的,不同的是增强谱分集利用Burst间的重叠区域来实现高精度配准。方位向相邻Burst分别视为增强谱分集上频带影像和下频带影像,其对应干涉图亦可视为上频带干涉图和下频带干涉图,最后利用重叠区域的上频带干涉图与下频带干涉图的相位差获取每组Burst的偏移量,实施高精度配准。增强谱分集提高了上下频带的多普勒中心频率基线,其对配准误差更为敏感,配准精度更高[32]。文献[33—34]利用增强谱分集估计精度较高的优势实现对哨兵卫星不同类型轨道精度进行了评估。
合成孔径雷达传感器发射的是相干脉冲,每个脉冲的起始相位和发射时间都受到精密的控制,而且雷达接收机和解调器均具有较高的时间定标精度。尽管哨兵卫星TOPS模式子测绘带中的每组Burst均独立成像,但在同一轨道面内进行零多普勒聚焦处理,理论上Burst方位向重叠区域几何投影和干涉图完全相同。图 5为哨兵卫星TOPS模式相邻两Burst间的频谱,可以看出Burst间多普勒中心分布并不连续,方位向的相位斜坡致使重叠区域的多普勒中心基线ΔfESD可视为谱分集中的上下频带多普勒中心差异,远大于影像的方位向带宽Baz。如果配准精度不够高,则重叠区域的干涉相位将呈现跳变现象[35]。增强谱分集正是利用这一原理进行方位向残余偏移量的估计以及配准精度的优化。

|
| 图 5 增强谱分集原理 Fig. 5 Principle of enhanced spectral diversity |
增强谱分集相位ɸESD与方位向配准时间误差Δη的关系为
 (8)
(8)
将式(8) 转换到以像素为单位的残余偏移量V,可进一步得到
 (9)
(9)
式中,Fa为方位向采样频率。理论上方位向重叠区域增强谱分集相位值是一致的, 然而受到失相干等噪声的影响,增强谱分集相位分布如图 6所示,每个像元相位值均存在差异,依靠单个像元难以获得准确的偏移量估计,需要优化增强谱分集相位值的估计。

|
| 图 6 增强谱分集相位分布 Fig. 6 Estimated phase from enhanced spectral diversity method |
理想点目标在SAR成像过程中被认为存在一致性的响应,具有无限大带宽,方位向子孔径分解后,点目标在上下频带影像中的响应依然存在相关性[36]。本文则根据上下频带干涉图的相干性选取点目标估计增强谱分集相位,提高增强谱分集相位估计的精度,估计方法如式(10) 所示,当然增强谱分集准确估计的前提是其相位不能出现缠绕现象
 (10)
(10)
式中,ɸESD为增强谱分集干涉图中的相位值; 
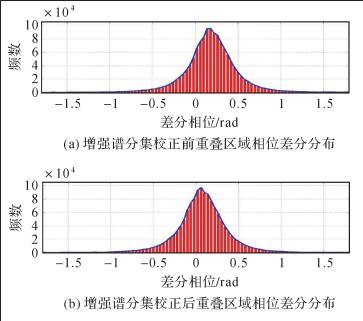
本文基于DORIS开源软件,完成哨兵卫星TOPS模式影像干涉处理模块,并对墨西哥地区影像进行干涉配准处理试验,影像拍摄时间分别为2015年2月12日和24日。本文首先对影像几何配准处理,此时方位向重叠区域差分相位分布如图 7(a)所示,相位均值为0.49°。然后采用增强谱分集进行精配准处理,此时方位向重叠区域差分相位分布如图 7(b)所示,相位均值为0.02°。图 8是与图 7所对应的几何配准和增强谱分集配准后的差分干涉图对比图,试验结果表明增强谱分集配准消除了重叠区域内的相位跳变,验证了精密轨道条件下几何配准之后采用增强谱分集用于精配准的可行性和有效性。试验也说明增强谱分集不但可以估计残余偏移量,也可用于配准精度的检验。
|
| 图 7 增强谱分集校正前后的重叠区域相位差分分布图 Fig. 7 Histogram of phase difference of overlap areas before and after ESD coregistration correction |

|
| 图 8 增强谱分集校正前后的干涉图结果对比 Fig. 8 Comparison of interferograms before and after ESD coregistration correction |
增强谱分集方法易受到地表方位向形变、电离层等因素的影响,其中地表方位向形变是最常见的现象[37-38]。TOPS模式天线波束视角在Burst方位向重叠区域存在较大的差异,尽管影像为零多普勒几何投影,当地表发生方位向形变时,其形变相位分量在上下频带干涉图中出现明显的差异。以模拟地震同震形变场为例,如图 9所示,方位向形变易导致哨兵卫星TOPS影像中方位向相邻两组Burst地震干涉图条纹无法闭合,而条带模式影像不会存在这种现象。方位向形变在干涉图产生的相位分量为

|
| 图 9 TOPS模式地震形变模拟差分干涉图 Fig. 9 Simulation differential interferogram of seismic deformation in TOPS mode |
 (11)
(11)
式中,Δx表示地表方位向形变;θsq星载雷达传感器在地球弯曲几何中的波束中心斜视角。又因为Δx=Vs·Δη,
 (12)
(12)
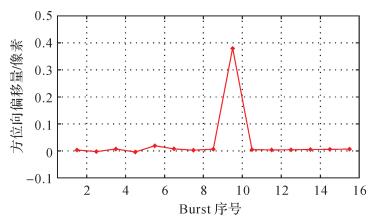
由于星载SAR成像时卫星轨道和地表都是弯曲的,而且地球独立于卫星轨道不停自转,其成像几何较为复杂,式(11) 和式(12) 中θsq、Vs参数与式(1) 中所对应的Vr、β参数意义并不等同。为了保证影像质量,聚焦成像时仍需对上述参数进行严格区分,但是这些参数相差不大,可忽略对形变监测结果的影响。式(13) 说明方位向形变将直接影响到增强谱分集结果,重叠区域的方位向形变信息不但造成Burst影像拼接时干涉相位的跳变,还将干扰增强谱分集结果,进一步影响多项式拟合结果。图 10为新疆皮山地震哨兵卫星干涉图,由于形变区域位于相邻影像中,本文对其子测绘带进行了拼接,共采用16组Burst残余增强谱分集处理,其干涉条纹在Burst 9与Burst 10结合处出现了明显的相位跳变,图 11即为与之相对应的增强谱分集估计残余偏移量结果,不难看出相位跳变处所对应的增强谱分集估计结果也出现异常。试验说明地表方位向形变信号类似于残余偏移量估计中的粗差,因此进行多项式拟合时应进行粗差探测,以避免方位向形变信号干扰配准精度[39]。当增强谱分集获得残余偏移量大于0.01个像素或者干涉结果出现跳变时,则表明增强谱分集中可能存在扰动信号。

|
| 图 10 新疆皮山地震同震形变差分干涉图(降轨) Fig. 10 The TOPS interferogram of Pishan earthquake in the Xinjiang Uygur Autonomous Region(descending) |
|
| 图 11 新疆皮山地震增强谱分集估计方位向残余偏移量结果 Fig. 11 Estimated residual offset in azimuth direction between consecutive bursts by ESD in Pishan earthquake in the Xinjiang Uygur Autonomous Region |
3 结论
哨兵卫星TOPS模式干涉时要求达到0.001个像元的配准精度。本文利用精密轨道和DEM进行几何配准,分析几何配准的适用条件,指出哨兵卫星精密轨道条件下几何配准精度可以确保增强谱分集相位不会出现缠绕现象,适合增强谱分集处理以实现系统性的配准偏差矫正。该方法具有运算效率较高、配准精度不依赖影像相干性的优势。本文在开源软件DORIS的基础上,增加增强谱分集配准模块,实现哨兵卫星TOPS数据的干涉处理。试验结果表明,即使是在地形起伏较大的区域,依然能够保持较高的精度。由于方位向形变等因素往往会干扰增强谱分集估计结果,本文通过粗差探测方法提高哨兵数据配准的可靠性。
本文提供的哨兵卫星干涉配准方案仅在精密轨道条件下使用,然而哨兵卫星精密轨道晚于影像数据发布,如果需要对哨兵数据进行近实时处理,还需考虑其他方法优化几何配准精度,以避免增强谱分集相位出现缠绕现象。
致谢: 特别感谢荷兰代尔夫特理工大学InSAR研究团队的帮助和密切合作。本文相关代码已通过DORIS软件发布。
| [1] | DE ZAN F, GUARNIERI A M M. TOPSAR:Terrain Observation by Progressive Scans[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(9): 2352–2360. DOI:10.1109/TGRS.2006.873853 |
| [2] | E SA. Sentinel-1:ESA's Radar Observatory Mission for GMES Operational Services[M]. [S.l.]: ESA, 2012. |
| [3] | XU Wei, HUANG Pingping, WANG R, et al. Processing of Multichannel Sliding Spotlight and Tops Synthetic Aperture Radar Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(8): 4417–4429. DOI:10.1109/TGRS.2013.2265306 |
| [4] | HUANG Pingping, LI Shenyang, XU Wei. Investigation on Full-aperture Multichannel Azimuth Data Processing in Tops[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(4): 728–732. DOI:10.1109/LGRS.2013.2278183 |
| [5] | PRATS P, SCHEIBER R, MITTERMAYER J, et al. A SAR Processing Algorithm for Tops Imaging Mode Based on Extended Chirp Scaling[C]//Proceedings of 2007 IEEE International Geoscience and Remote Sensing Symposium. Barcelona:IEEE, 2007:148-151. |
| [6] | DAVIDSON G, MANTLE V, BERNHARD R, et al. Implementation of Tops Mode on RadarSat-2 in Support of the Sentinel-1 Mission[C]//ESA Living Planet Symposium. London:ESA, 2013:1-22. |
| [7] | META A, PRATS P, STEINBRECHER U, et al. First TOPSAR Interferometry Results with TerraSAR-X[C]//Proceedings of the ESA FRINGE Workshop. Frascati, Italy:ESA, 2007. |
| [8] | PRATS P, MAROTTI L, WOLLSTADT S, et al. TOPS Interferometry with TerraSAR-X[C]//Proceedings of the 8th European Conference on Synthetic Aperture Radar. Aachen, Germany:IEEE, 2010:1-4. |
| [9] | YAGV-MARTÍEZ N, PRATS-IRAOLA P, GONZÁEZ F R, et al. Interferometric Processing of Sentinel-1 Tops Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2220–2234. DOI:10.1109/TGRS.2015.2497902 |
| [10] | WEGMVLER U, WERNER C, STROZZI T, et al. Sentinel-1 Support in the Gamma Software[C]//Geoscience and Remote Sensing Symposium. Frascati, Italy:ESA, 2015:23-27. |
| [11] | SANDWELL D, MELLORS R, TONG, Xiaopeng, et al. GMTSAR:An InSAR Processing System Based on Generic Mapping Tools[EB/OL]. UC San Diego:Scripps Institution of Oceanography. http://escholarship.org/uc/item/8zq2c02m. |
| [12] | BARA M, SCHEIBER R, BROQUETAS A, et al. Interferometric SAR Signal Analysis in the Presence of Squint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2164–2178. DOI:10.1109/36.868875 |
| [13] | Miranda N. Definition of the TOPS SLC Deramping Function for Products Generated by the S-1 IPF[R/OL]. https://earth.esa.int/documents/247904/165344%202/Sentinel-1-TOPS-SLC_Deramping.Paris, France:EuropeanSpaceAgency. |
| [14] | 程春泉, 张继贤, 黄国满, 等. 考虑定向参数精度信息的TerraSAR-X和SPOT-5HRS影像RFM联合定位[J]. 测绘学报, 2017, 46(2): 179–187. CHENG Chunquan, ZHANG Jixian, HUANG Guoman, et al. Combined Positioning of TerraSAR-X and SPOT-5 HRS Images with RFM Considering Accuracy Information of Orientation Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 179–187. DOI:10.11947/j.AGCS.2017.20160138 |
| [15] | CURLANDER J C, MCDONOUGH R N. Synthetic Aperture Radar:Systems and Signal Processing[M]. New York: Wiley, 1991. |
| [16] | SCHUBERT A, SMALL D, MEIER E, et al. Spaceborne SAR Product Geolocation Accuracy:A Sentinel-1 Update[C]//Proceedings of 2014 IEEE Geoscience and Remote Sensing Symposium. Quebec City:IEEE, 2014:2675-2678. |
| [17] | GEUDTNER D, YAGUE-MARTINEZ N, PRATS P, et al. Sentinel-1 InSAR Performance:Results from the Sentinel-1A In-orbit Commissioning[C]//Proceedings of the ESA FRINGE Workshop. Frascati, Italy:ESA, 2015. |
| [18] | ARIKAN M, VAN LEIJEN F, LIU Guang, et al. Improved Image Alignment under the Influence of Elevation[C]//Proceedings of the ESA FRINGE Workshop. Frascati, Italy:ESA, 2007. |
| [19] | PRATS-IRAOLA P, SCHEIBER R, MAROTTI L, et al. TOPS Interferometry with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3179–3188. DOI:10.1109/TGRS.2011.2178247 |
| [20] | YAGUE-MARTINEZ N, EINEDER M, BRCIC R, et al. TanDEM-X Mission:SAR Image Coregistration Aspects[C]//Proceedings of the 8th European Conference on Synthetic Aperture Radar. Aachen, Germany:IEEE, 2010:1-4. |
| [21] | SANSOSTI E, BERARDINO P, MANUNTA M, et al. Geometrical SAR Image Registration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2861–2870. DOI:10.1109/TGRS.2006.875787 |
| [22] | PRATS-IRAOLA P, RODRIGUEZ-CASSOLA M, DE ZAN F, et al. Role of the Orbital Tube in Interferometric Spaceborne SAR Missions[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(7): 1486–1490. DOI:10.1109/LGRS.2015.2409885 |
| [23] | FERNÁDEZ C, Sentinels POD Team, Sentinels POD Service File Format Specifications[R]. Paris, France:European Space Agency, 2011. |
| [24] | BAMLER R, EINEDER M, MONTI G A, et al. Session Summaries:InSAR Theory Session[C]//Proceedings of the ESA FRINGE Workshop.Frascati:ESA Publication, 2015. |
| [25] | POTIN P, ROSICH B, GRIMONT P, et al. Sentinel-1 Mission Status[C]//Proceedings of EUSAR 2016:11th European Conference on Synthetic Aperture Radar. Hamburg:IEEE, 2016:1-6. |
| [26] | BÄHR H. Orbital Effects in Spaceborne Synthetic Aperture Radar Interferometry[M]. Karlsruhe: KIT Scientific Publishing, 2013. |
| [27] | PRATS P, RODRIGUEZ-CASSOLA M, LÓEZ-DEKKER P, et al.Considerations of the Orbital Tube for Interferometric Applications[C]//Proceedings of the ESA FRINGE Workshop. Frascati, Italy:European Space Agency, 2015:23-27. |
| [28] | GRANDIN R.Interferometric Processing of SLC Sentinel-1 TOPS Data[C]//Fringe. Frascati, Italy:ESA, 2015. |
| [29] | XU Bing, LI Zhiwei, FENG Guangcai, et al. Continent-Wide 2-D Co-seismic Deformation of the 2015 Mw 8.3 Illapel, Chile Earthquake Derived from Sentinel-1A Data:Correction of Azimuth Co-registration Error[J]. Remote Sensing, 2016, 8(5): 376. DOI:10.3390/rs8050376 |
| [30] | GEUDTNER D, PRATS P, YAGUE-MARTINEZ N, et al. Sentinel-1 SAR Interferometry Performance Verification[C]//Proceedings of EUSAR 2016:11th European Conference on Synthetic Aperture Radar. Hamburg, Germany:IEEE, 2016:1-4. |
| [31] | BAMLER R, EINEDER M. Accuracy of Differential Shift Estimation by Correlation and Split:Bandwidth Interferometry for Wideband and Delta-K SAR Systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 151–155. DOI:10.1109/LGRS.2004.843203 |
| [32] | YAGUE-MARTINEZ N, BALSS U, BREIT H, et al. Operational Stacking OF TerraSAR-X ScanSAR and Tops Data[C]//Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium. Melbourne:IEEE, 2013:888-890. |
| [33] | MANCON S, TEBALDINI S, GUARNIERI A M, et al. Orbit Accuracy Estimation by Multi-squint Phase:First Sentinel-1 Results[C]//Proceedings of 2015 IEEE International Geoscience and Remote Sensing Symposium. Milan:IEEE, 2015:1276-1279. |
| [34] | MANCON S, GUARNIERI A M, GIUDICI D, et al. On the Phase Calibration by Multisquint Analysis in TOPSAR and Strip Map Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 134–147. DOI:10.1109/TGRS.2016.2598686 |
| [35] | RODRIGUEZ-CASSOLA M, PRATS-IRAOLA P, DE ZAN F, et al. Doppler-related Distortions in TOPS SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(1): 25–35. DOI:10.1109/TGRS.2014.2313068 |
| [36] | SCHNEIDER R Z, PAPATHANASSIOU K P, HAJNSEK I, et al. Polarimetric and Interferometric Characterization of Coherent Scatterers in Urban Areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(4): 971–984. DOI:10.1109/TGRS.2005.860950 |
| [37] | SCHEIBER R, JÄGER M, PRATS-IRAOLA P, et al. Speckle Tracking and Interferometric Processing of TerraSAR-X TOPS Data for Mapping Nonstationary Scenarios[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(4): 1709–1720. DOI:10.1109/JSTARS.2014.2360237 |
| [38] | PRATS-IRAOLA P, NANNINI M, SCHEIBER R, et al. Sentinel-1 Assessment of the Interferometric Wide-swath Mode[C]//Proceedings of 2015 IEEE International Geoscience and Remote Sensing Symposium. Milan:IEEE, 2015:5247-5251. |
| [39] | TEUNISSEN P J G, SIMONS D G, TIBERIUS C C J M. Probability and Observation Theory[M]. Amsterdam: Delft University of Technology, 2005. |



