2. 地理信息工程国家重点实验室, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
激光雷达测量(light detection and ranging, LiDAR)是近十几年迅猛发展起来的一种新型、高效的空间数据获取技术,在数字城市建设、植被检测、灾害处理和城市规划等领域都发挥着重要的作用[1]。建筑物作为城市中最基本、最主要的组成元素,其三维信息是重要的基础地理信息[2],基于机载激光雷达数据的建筑物三维模型重建已成为当前的研究热点[3]。屋顶面作为建筑物屋顶结构的基本组成元素,快速、准确地对其进行提取是基于机载LiDAR数据重建建筑物三维模型的关键步骤[4]。由于机载LiDAR点云分布不连续、不规则,点云中存在噪声,以及建筑物具有多层次空间复杂结构等因素的影响,从建筑物LiDAR点云中自动、高精度地提取屋顶面仍然面临较大的挑战。
目前,学者们围绕屋顶面提取进行了大量研究,提出了很多方法,主要可分为模型拟合法、区域增长法、聚类法、剖面分析法和能量最小化法[5-7]。模型拟合法利用局部范围内的点云拟合预定义模型的方程实现屋顶面的提取,较为经典的模型拟合法有随机采样一致性(random sample consensus, RANSAC)算法和三维Hough变换,其中RANSAC具有较好的稳健性,在有大量局外点时也能较好地估计出高精度的模型参数,但提取结果中容易出现伪平面,且在数据复杂的情况下,效率将显著降低,文献[5]提出了加权RANSAC,研究了多种权函数对提取结果的影响,较好地解决了提取结果中出现伪平面的问题,文献[8]改进了RANSAC的采样策略,较大地提高了其效率;三维Hough变换[9-10]将特征检测问题转换到参数空间,通过采样参数空间,并在参数空间进行简单累加统计得到参数聚类中心,但采样间隔大小对提取结果的精度有一定影响,通常采样间隔越小,提取结果越精确,但同时会使算法效率显著降低。区域增长法[11-14]简单易行,效率较高,但对初始种子点的要求较高,增长过程易受噪声点的影响,且对于过渡平缓的屋顶面难以设置停止增长条件,容易出现过增长。聚类法根据点之间的距离或点云密度等相似性测度,利用如k-means[15]、MeanShift[16]等聚类算法聚类点云,可得到较为稳定的提取结果,但由于受聚类参数、聚类策略等因素的影响,容易导致过提取和漏提取。剖面分析法将扫描线分析用于识别点云中的平面特征,其原理简单,具有分割结果好、速度快、效率高等优点,可实现大区域点云数据中平面特征的提取,文献[7]以规则格网组织方式索引点云,利用规则格网中高程最大点计算4个方向的扫描线,并由扫描线得到交叉线元,通过基于交叉线元和基于点的两种增长方式,实现了屋顶面快速准确提取,但由于仅利用了4个方向的扫描线,难以适应各种形状屋顶面的提取(如长条形屋顶面),且该算法利用规则格网中高程最大点计算扫描线,因此格网大小的设置对提取结果会有一定的影响,此外,交叉线元长度没有明确的含义,较难设置。能量最小化法通过定义包含数据项、平滑项等的能量函数,利用最小生成树、归一化割、图割等算法得到极小化解,从而将屋顶面提取问题转换成全局最优标记问题,文献[6]以区域增长的结果作为初始输入,利用α-expansion图割算法求得能量函数的极小化解,提高了提取完整率和正确率,但其提取结果中的屋顶面数不可能多于初始输入中的屋顶面数,因此无法通过后续优化过程提取部分漏提取的屋顶面,且迭代求解能量函数的极小化解效率较低。
针对现有方法提取复杂建筑物屋顶面适应性较差、精度较低等问题,本文提出一种利用点云邻域信息的建筑物屋顶面高精度自动提取方法。
1 算法描述本文算法通过预处理选取可靠聚类种子点,利用局部点云法向量分布密度聚类(local normal vector distribution density-based spatial clustering of applications with noise, LNVD-DBSCAN)提取初始屋顶面片,并在此基础上进行面片细化处理,可较好地提取不同复杂程度建筑物的屋顶面,具体技术流程见图 1。

|
| 图 1 屋顶面提取流程 Fig. 1 Flowchart of roof extraction |
1.1 预处理
建筑物屋顶一般由多个屋顶面构成,在屋顶面相交处会形成如屋脊线等尖锐特征,尖锐特征附近的点云法向量通常难以准确计算,尤其当点云较为稀疏或噪声较大时,计算的点云法向量可靠性更差[17]。为保证法向量分布密度聚类提取建筑物屋顶面的准确性,首先对建筑物点云进行预处理,得到可靠的聚类种子点。预处理过程包括以下两个步骤:
(1) 计算点云法向量与曲率特征。令点p代表建筑物点云中的任一点,p∈R3,其k邻域为Npk={p1, p2, …, pk},k为最近邻点数,则其法向量np和曲率Kp可通过计算邻域协方差矩阵Cp的特征值和特征向量得到[18]
 (1)
(1)
式中,λ0、λ1、λ2为Cp的3个特征值,且满足λ0≤λ1≤λ2;v0为λ0对应的特征向量。
(2) 统计曲率直方图,选取种子点,为后续处理提供可靠的初始数据。确定直方图采样间隔是构建直方图的首要步骤,由于点云分布不规则、建筑物屋顶面形状复杂多样等因素的影响,导致不同建筑物点云曲率的分布不同,设置固定的采样间隔难以得到较为准确的建筑物点云曲率分布,因此无法计算合适的曲率阈值。本文通过建筑物点数Nb设置统计区间个数,并根据建筑物点云曲率最大最小值动态计算采样间隔ΔK
 (2)
(2)
式中,KS代表所有建筑物点云的曲率;κmin为最小间隔,一般取10-3~10-5。
确定采样间隔后,通过累计直方图计算曲率阈值,得到种子点集seed
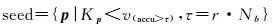 (3)
(3)
式中,accu为累计直方图的值;v(accu>τ)为accu大于τ时直方图横坐标对应的曲率值;r为非尖锐特征点数与屋顶面点云数的比值,一般取0.8~0.95。
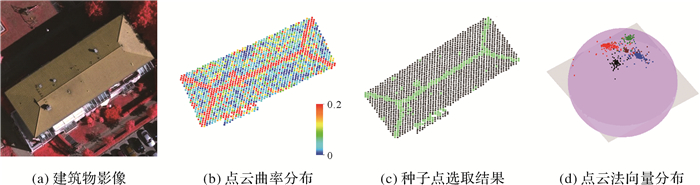
图 2(a)-(c)分别为建筑物影像、对应点云曲率分布和种子点选取结果,图 2(c)中黑色点代表选取的种子点。由图 2可知,算法较好地选取了可靠的聚类种子点。建筑物为典型的人工地物,屋顶面多为平面,屋顶面点云法向量整体上会指向多个方向,具有一定的相似性[19]。图 2(d)为图 2(a)所示建筑物的点云法向量空间分布(图 2中不同颜色代表不同的屋顶面点),由图 2可知,同一屋顶面点云法向量在法向量空间分布较为集中,因此可通过法向量分布密度聚类提取建筑物屋顶面。
|
| 图 2 点云特征分布及种子点选取结果 Fig. 2 Point cloud feature distribution and seeds selection result |
1.2 LNVD-DBSCAN聚类
聚类是一个无监督的分类过程,常见的聚类方法主要可以分为划分式聚类方法、层次聚类方法、基于密度和网格的聚类方法和其他聚类方法[20]。k-means作为一种经典的划分式聚类方法,应用较为广泛,但该方法需预先设定聚类个数或聚类中心,且只考虑单个聚类中心之间的距离[21],适用于类球形簇的聚类。层次聚类方法通过反复将数据进行分裂或聚合得到聚类结果,聚类个数难以确定且效率较低,适合小型数据集的聚类。DBSCAN(density-based spatial clustering of applications with noise)作为一种经典的基于密度的聚类方法[22],利用数据密度作为划分数据的准则,适用于聚类任意形状的数据,但仅使用单一距离度量数据间的相似性,难以顾及数据的多维特征[21],且方法对参数的设置比较敏感。目前已有学者利用DBSCAN从LiDAR数据中提取路灯[23]、建筑物[24]等地物点云,得到了较好的结果。
通过分析建筑物屋顶面点云法向量分布的特点和DBSCAN算法的聚类特性,本文提出一种点云局部法向量分布密度聚类(LNVD-DBSCAN)方法,将屋顶面点云在空间域和法向量特征域的特点融入DBSCAN,使用两个距离度量屋顶面点云之间的相似性,并结合建筑物同一屋顶面点云法向量夹角较小的特点,以解决DBSCAN算法参数难以设置的缺点。
LNVD-DBSCAN算法主要包括邻域扩充和面片验证两个步骤,下面对其主要原理进行介绍。
1.2.1 邻域扩充定义建筑物点p的ε邻域εp为
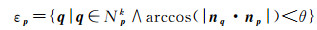 (4)
(4)
式中,q代表点p的ε邻域点;np、nq分别代表点p、q的单位法向量;θ为法向量夹角阈值,取值一般不大于10°。
邻域扩充流程如图 3所示,将所有建筑物点的处理状态置为未标记,算法依次处理种子点集中的未标记点,如果未标记点p的ε邻域点数|εp|大于形成屋顶面的最少点数m(m根据点云密度自适应设置),则判断为提取到屋顶面片M,将该点及其ε邻域点标记为屋顶面片M的点,并顺序处理M中的所有点。如果种子点集中满足条件的未标记点都已处理,则结束邻域扩充,得到多个初始屋顶面片。
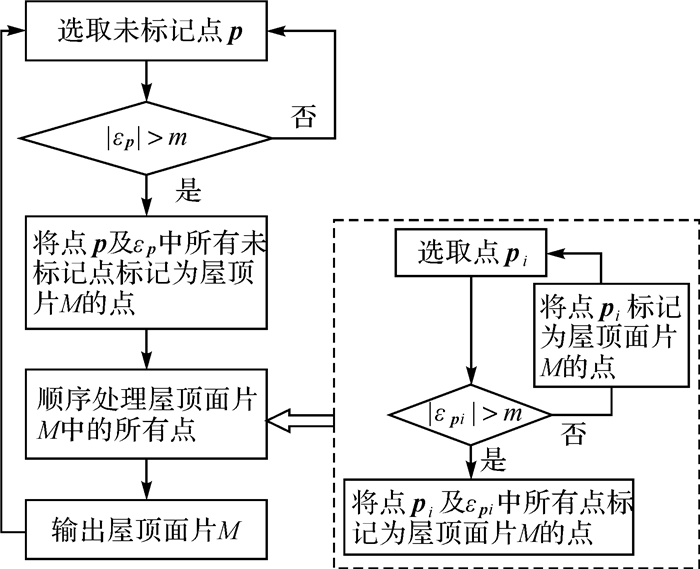
|
| 图 3 邻域扩充流程 Fig. 3 Illustration of neighborhood extension |
1.2.2 面片验证
建筑物可能包含多个平行屋顶面,虽然邻域扩充时加入了点云空间距离约束,但对于距离较小的平行屋顶面,如图 4(a)所示,屋顶面片A、B交界处点的k邻域点可能分布在A、B两个屋顶面片,导致算法在邻域扩充时将两个屋顶面片合并提取(如图 4(b)中红色点云所代表的屋顶面片),因此在邻域扩充后,需要判断提取的初始屋顶面片是否正确。
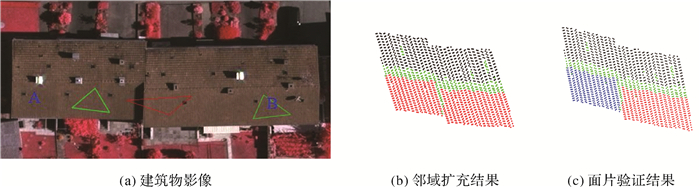
|
| 图 4 邻域扩充及面片验证结果 Fig. 4 Neighborhood extension and roof surface validation results |
由于相邻平行屋顶面的距离和法向量夹角较小,通过聚类或区域增长难以分离,因此采用随机抽样的方法构建虚拟屋顶面验证初始屋顶面片的正确性。面片验证流程如图 5所示,将初始屋顶面片M作为初始数据,通过随机选点构建虚拟屋顶面片N,如果存在相邻平行屋顶面(即M与N法向量夹角大于θ),则分离,并输出N,同时更新M的数据(即将属于N的点从M中去除)。相邻平行屋顶面数通常较少,因此只需设置较小的迭代次数t(根据单个建筑物相邻平行屋顶面数设置,取值一般不大于50) 即能分离所有相邻平行屋顶面,图 4(c)为面片验证结果,由图可知,算法较好地分离了相邻平行屋顶面。

|
| 图 5 面片验证流程 Fig. 5 Illustration of roof surface validation |
1.3 面片细化处理 1.3.1 面片合并
由于点云分布不规则、法向量计算存在偏差等因素的影响,部分屋顶面通过LNVD-DBSCAN聚类后可能形成多个面片,如图 6(a)中建筑物点云的聚类结果为图 6(b)。为得到完整的建筑物屋顶面,需合并属于同一屋顶面的初始屋顶面片。

|
| 图 6 屋顶面片合并 Fig. 6 Roof surface mergence |
初始屋顶面片只包含非尖锐特征区域的屋顶面点,在合并前需标记其余未标记点,即以初始屋顶面片平面外接矩形为基础,向四周扩展一定距离db形成缓冲区(根据屋顶面实际大小,db的取值范围为2~8 m);计算未标记点到各初始屋顶面片的距离,如果距离中的最小值小于δ0(由于噪声等因素影响,取值稍大,δ0一般不大于0.3 m),且未标记点在最小值对应的面片缓冲区内,则将未标记点标记为该初始屋顶面片点。
将未标记点标记后,根据以下3个原则合并初始屋顶面片:① 两屋顶面片相邻,即两屋顶面片之间的最小平面距离dh小于dhmin(dhmin取值范围为0~1.5 m);② 两屋顶面片夹角小于θ,面片夹角通过面片法向量计算;③ 两屋顶面片的垂距dv小于δ0。面片合并原则用式(5) 表示
 (5)
(5)
式中各符号的含义如图 6(c)面片合并示意图所示,其中p1、p2分别为屋顶面片A、B的任一点,平面A1、B1分别过屋顶面片A、B的质心p3、p4,且法向量满足式(6)
 (6)
(6)
图 6(d)为图 6(b)聚类结果的面片合并结果。由图 6可知,算法较好地合并了属于同一屋顶面的初始屋顶面片,得到了完整的屋顶面。
1.3.2 屋顶面竞争处理屋顶面竞争现象是指一些屋顶面点在数学意义上可同时归属为多个屋顶面,在多个屋顶面相交区域更为常见[14]。在图 7中,点p1、p2分别属于屋顶面A、C,但由于点p1、p2到屋顶面B的距离小于到屋顶面A、C的距离,因此在未标记点分类时点p1、p2被错误加入屋顶面B中,导致屋顶面边界不清晰。此外,在未标记点分类时,由于没有考虑建筑物屋顶面点云空间分布的连续性和规律性,导致部分点可能存在明显的错分现象,如图 7中的点p3。本文通过构建邻域投票模型解决上述问题。

|
| 图 7 屋顶面竞争示意图 Fig. 7 Illustration of roof competition |
建筑物点云中的任一点是否属于屋顶面M主要由两个因素决定:该点邻域点涉及的不同屋顶面点数和到屋顶面M的距离,且两个因素相互独立。令点p的k邻域点所涉及的屋顶面集合为Y,Y={Y1, Y2, …, Ym},m代表k邻域点涉及的屋顶面数,通过分析可知,点p属于屋顶面Yi的权值w(Yi)满足
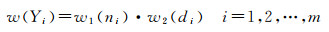 (7)
(7)
式中,ni、di分别代表点p的k邻域中属于屋顶面Yi的点数和到屋顶面Yi的距离;w1(ni)、w2(di)分别代表点p通过ni、di计算的权值。
权函数对确定点云所属屋顶面至关重要。通常,点p的k邻域点属于屋顶面Yi的点数ni越多,则点p为屋顶面Yi点的概率越大,即w1(ni)越大,且w1(ni)应随ni减小迅速减小;点p与屋顶面Yi的距离di越小,则点p属于屋顶面Yi的概率越大,即w2(di)越大,且w2(di)应随di增大迅速减小,当距离大于一定阈值时w2(di)接近于0,w1(ni)、w2(di)的曲线图应为图 8(a)、(b)所示,因此本文采用高斯函数进行描述。
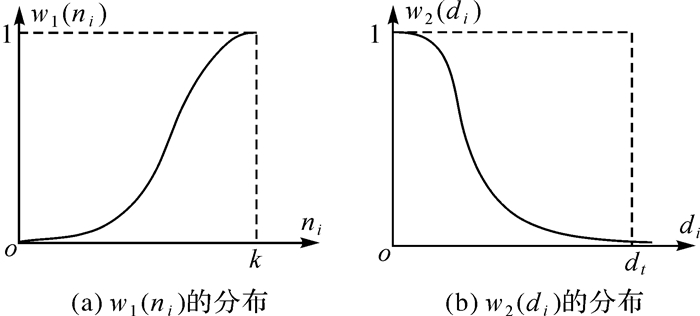
|
| 图 8 权函数分布示意图 Fig. 8 Illustration of weighted function distribution |
设ni、di服从方差为σni、σdi,均值为μni、μdi的高斯分布,通过分析及高斯分布3σ原则可得
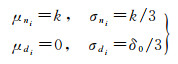 (8)
(8)
由于点p的邻域中可能存在距Yi较小但不属于屋顶面Yi的点,且当ni为0时,权值w1(ni)应为0,因此将w1(ni)乘以邻域中属于Yi的点数,得到权函数表达式。将点p标记为最大权值对应的屋顶面
 (9)
(9)
为了验证本文算法的提取精度及适应性,利用Vaihingen地区[26]和科罗拉多博尔德分校[27]的机载LiDAR数据集(分别记为数据集1和数据集2) 中的部分建筑物点云数据,在Visual Studio 2012 C++和Intel(R) CoreTM i7-4810MQ处理器、8 GB运行内存的软硬件环境下进行两组试验,分别记为试验1和试验2。由于本文研究重点是从建筑物点云中提取屋顶面,因此地面、墙面及植被等非建筑物地物点云已被剔除,本文所用数据集的基本信息如表 1所示。
| 数据集 | 采集年月 | 采集设备 | 点密度/(个/m2) | 建筑物特点 | 屋顶面特点 |
| Vaihingen地区 | 2008年8月 | Leica ALS 50 | 4 | 单个建筑物面积相对较小,且包含的屋顶面个数较少 | 包含倾斜和水平的屋顶面,附属屋顶面较多,屋顶面形状差异较大,屋顶面间拓扑关系较为复杂 |
| 科罗拉多博尔德分校 | 2010年5月 | Optech 3100 | 5 | 单个建筑物面积较大,且包含的屋顶面个数多 | 大部分为倾斜屋顶,倾斜角度差异较大,屋顶面大小、形状差异较大,屋顶面间拓扑关系十分复杂 |
试验与RANSAC[28]、M-采样一致性估计算法(M-estimators sample consensus, MSAC)[29]及结合主成分分析的区域增长(region growth+principal component analysis, RG_PCA)[11]算法进行对比,由于RANSAC和MSAC无法分离位于同一平面的屋顶面,因此本文将两种方法的提取结果经欧氏空间聚类(聚类距离设置为2 m)后与本文方法对比。根据前文列出的各阈值的范围,试验中本文算法阈值设置的情况如下:r=0.9,κmin=10-4,θ=4°,δ0=0.25 m,t=30,db=5 m,dhmin=1 m。
试验中建筑物标准屋顶面为结合影像人工提取,由于算法提取的屋顶面与标准屋顶面的关系可能为一对一、一对多或多对多,因此本文采用文献[25]的处理和评价方法,即通过计算提取的屋顶面与标准屋顶面的重叠率,根据最大重叠率确定提取的屋顶面与标准屋顶面的对应关系,按下式计算完整率comp、正确率corr和提取质量quality
 (10)
(10)
式中,‖TP‖为正确提取的屋顶面点数;‖FN‖为漏提取的屋顶面点数;‖FP‖为误提取的屋顶面点数。
2.2 试验结果及比较 2.2.1 试验1:单栋建筑物数据选取10栋屋顶面拓扑关系复杂的建筑物点云作为试验1数据,分别记为建筑物1-10(其中建筑物1-5选自数据集1,建筑物6-10选自数据集2)。不同算法屋顶面提取结果如图 9所示,其中绿色代表未提取的屋顶面点和屋顶附属物点,其他颜色分别代表提取的不同屋顶面。

|
| 图 9 试验1屋顶面提取结果 Fig. 9 Roof extraction results of the first experiment |
对比图 9中不同算法的提取结果可知,本文算法提取结果较好。对于过渡平缓的相邻屋顶面,如建筑物1和2影像中的蓝色矩形区域,RANSAC、MSAC及RG_PCA提取效果较差;对于曲率变化较小的曲面屋顶面,如建筑物2、4和9影像中的绿色矩形区域,RANSAC、MSAC提取结果较差,RG_PCA和本文算法能得到较好的提取结果;对于相邻屋顶面夹角适中的建筑物,如建筑物3,点云的法向量和曲率都能通过PCA较为准确地计算,4种算法均能得到较好的提取结果,但对于夹角较大的建筑物,如建筑物5,屋脊线附近点云法向量计算不准确且局部点云曲率变化较大,导致RG_PCA提取效果较差;本文算法漏提取了建筑物4和5中的部分屋顶面(如建筑物4、5影像红色矩形区域),主要原因是该部分屋顶面点数较少且位于多个屋顶面相交处,计算的点云曲率较大,因此选取的种子点不包含该屋顶面点云;对于存在多个重复结构的建筑物,如建筑物8,RANSAC提取结果中屋顶面竞争现象较为明显,导致提取结果效果较差,MSAC的提取效果在一定程度上有所提高,但存在过提取现象;对于屋顶面个数多、屋顶面大小形状差异大且拓扑关系极为复杂的建筑物,如建筑物6、9和10(屋顶面个数均大于30个),RANSAC、MSAC及RG_PCA均出现了不同程度的误提取,提取结果比较杂乱,难以用于构建屋顶面拓扑关系。本文方法主要为提取平面屋顶面,能较好地提取上述各建筑物的平面屋顶面,但对于曲率变化较大的曲面屋顶面,算法会将此类屋顶面提取为多个屋顶面片,如建筑物影像6和影像7红色矩形区域,提取效果较差。
2.2.2 试验2:区域建筑物数据选取6个区域建筑物点云作为试验2数据,分别记为area1-area6(其中area1-area3选自数据集1,area4-area6选自数据集2),所选区域影像如图 10(a)-(f)所示。由于篇幅限制,仅给出本文算法提取结果,如图 10(g)-(l)所示。

|
| 图 10 试验2建筑物影像及屋顶面提取结果 Fig. 10 Building image and roof extraction results of the second experiment |
由图 10可知,在建筑物屋顶面面积大小、形状变化较大,拓扑关系复杂程度不同的情况下,本文算法均能得到较好的提取结果。为更好地对比不同算法的提取结果,图 11给出了Area 1和Area 5中部分建筑物不同算法的提取结果。

|
| 图 11 试验2屋顶面提取结果对比 Fig. 11 Roof extraction results comparison of the second experiment |
对比图 11中A、B区域不同算法的提取结果可知,RG_PCA和本文算法均出现漏提取部分屋顶面现象,主要原因是漏提取的屋顶面点云法向量计算不准确且点云曲率较大,RANSAC和MSAC虽提取到B区域左侧屋顶面部分点,但难以提供可靠的屋顶面信息;RANSAC和MSAC较好地提取了C区域的建筑物屋顶面,但存在部分屋顶面过提取现象,由于该区域屋顶面较多且形成了较多的尖锐特征,导致点云曲率变化较大,因此RG_PCA漏提取了部分屋顶面和较多点云;D区域建筑物屋顶包含较多附属物(如烟囱等),屋顶面点云较为稀疏,相比其他3种算法,本文算法的提取结果较好;对于E、F区域的建筑物,RANSAC、MSAC和RG_PCA均存在明显的误提取,且RANSAC和MSAC存在明显的屋顶面竞争现象,而本文算法提取结果较好。
2.3 定量评价及分析为定量评价本文算法的提取性能,统计了两组试验的屋顶面提取精度及时间。屋顶面提取精度均按照式(10) 计算,统计结果如表 2所示。
| (%) | ||||||||||||||
| 编号 | 完整率 | 正确率 | 提取质量 | |||||||||||
| RANSAC | MSAC | RG_PCA | 本文方法 | RANSAC | MSAC | RG_PCA | 本文方法 | RANSAC | MSAC | RG_PCA | 本文方法 | |||
| 1 | 85.08 | 79.71 | 69.04 | 98.97 | 95.42 | 95.59 | 91.90 | 99.41 | 81.74 | 79.71 | 65.08 | 98.39 | ||
| 2 | 68.05 | 66.74 | 69.07 | 96.97 | 92.49 | 92.98 | 86.35 | 98.77 | 64.48 | 66.74 | 62.27 | 95.82 | ||
| 3 | 92.00 | 91.13 | 92.27 | 99.81 | 98.04 | 98.14 | 98.21 | 99.81 | 90.35 | 91.13 | 90.74 | 99.62 | ||
| 4 | 86.76 | 83.55 | 60.33 | 93.46 | 94.04 | 94.40 | 76.94 | 95.24 | 82.24 | 83.55 | 51.09 | 89.29 | ||
| 5 | 84.84 | 81.93 | 41.22 | 91.76 | 94.66 | 94.99 | 98.73 | 95.30 | 80.96 | 81.93 | 41.01 | 87.79 | ||
| 6 | 85.59 | 84.25 | 70.14 | 97.48 | 98.26 | 98.31 | 99.25 | 98.42 | 84.31 | 84.25 | 69.77 | 95.98 | ||
| 7 | 64.33 | 73.71 | 81.18 | 94.18 | 96.35 | 98.09 | 99.52 | 98.88 | 62.80 | 73.71 | 80.86 | 93.19 | ||
| 8 | 50.65 | 69.56 | 70.97 | 95.61 | 83.61 | 91.51 | 87.38 | 97.22 | 46.07 | 69.56 | 64.37 | 93.07 | ||
| 9 | 78.65 | 80.95 | 90.45 | 99.28 | 98.83 | 98.64 | 98.64 | 99.46 | 77.93 | 80.95 | 89.33 | 98.75 | ||
| 10 | 74.92 | 74.03 | 80.60 | 98.81 | 96.46 | 96.66 | 98.51 | 98.80 | 72.91 | 74.03 | 79.63 | 97.64 | ||
| area 1 | 86.97 | 88.20 | 67.07 | 95.15 | 95.15 | 95.48 | 93.63 | 97.05 | 83.28 | 84.67 | 64.14 | 92.48 | ||
| area 2 | 91.01 | 93.55 | 89.48 | 98.83 | 99.23 | 99.33 | 99.79 | 99.78 | 90.37 | 92.96 | 89.31 | 98.61 | ||
| area 3 | 94.71 | 94.98 | 83.58 | 98.72 | 98.44 | 98.32 | 97.80 | 99.27 | 93.31 | 93.47 | 82.03 | 98.01 | ||
| area 4 | 86.94 | 89.82 | 79.62 | 97.50 | 97.61 | 97.65 | 99.55 | 99.18 | 85.13 | 87.92 | 79.33 | 96.73 | ||
| area 5 | 83.28 | 84.34 | 72.81 | 98.13 | 96.98 | 96.96 | 99.06 | 98.73 | 81.18 | 82.16 | 72.32 | 96.91 | ||
| area 6 | 79.90 | 81.49 | 78.81 | 96.06 | 96.95 | 96.76 | 98.83 | 97.15 | 77.94 | 79.32 | 78.08 | 93.43 | ||
由表 2可知,RANSAC、MSAC、RG_PCA和本文方法屋顶面提取正确率相差不大,但本文方法相对于其他几种算法的完整率和提取质量有较大提高,即本文方法漏提取和误提取的屋顶面点相对较少。此外,对于屋顶结构相对简单的建筑物,如试验1中建筑物3和试验2中的area 2和area 3,4种算法都能比较准确地提取,但对于屋顶结构复杂的建筑物,本文方法提取精度有显著提高,该结果亦验证了2.2节的定性分析,同时也说明本文方法对不同复杂程度的建筑物屋顶面提取的适应性及准确性。
图 12为不同算法屋顶面提取时间统计结果。由图 12可知,整体上RANSAC和MSAC两种方法算法效率相近,且提取复杂建筑物屋顶面所需时间明显高于本文方法,RG_PCA算法效率较高,然而由2.2节和表 2可知,相较于其他3种算法,RG_PCA的屋顶面提取效果和精度较差,这也进一步说明本文方法提取复杂建筑物屋顶面的有效性。
|
| 图 12 屋顶面提取时间统计结果 Fig. 12 Roof extraction time statistics results |
通过试验结果对比和定量评价可知,对于屋顶结构简单的建筑物,本文方法稍优于其他3种算法,但对于屋顶结构复杂的建筑物,本文方法能显著降低误提取和漏提取屋顶面点云数,主要原因有:① 较好地综合利用了屋顶面点云的空间域和法向量特征域的特点,即对于法向量计算可靠的点云,利用LNVD-DBSCAN聚类得到较准确的初始屋顶面片,对于其他点云,通过计算点到面片距离进行处理;② 采用了由粗到细的处理方式,即先提取屋顶面部分点云(初始屋顶面片),然后通过面片细化处理得到建筑物所有完整屋顶面;③ 通过构建邻域投票模型,较好地解决了屋顶面竞争现象,保证了提取屋顶面的连续性。
本文方法本质上属于聚类法,与其他聚类法不同的是,本文方法依据点云聚类后能否得到可靠结果将其分为两部分进行处理,较好地解决了聚类法存在的过提取和漏提取问题。文献[6]作为一种能量最小化法,可同时得到所有屋顶面提取结果,但对于初始输入中漏提取的屋顶面,无法通过后续优化过程提取;本文算法通过聚类建筑物点也能同时得到所有屋顶面提取结果,且对于漏提取的屋顶面,可通过面片验证等步骤进行提取。文献[7]作为一种剖面分析法,具有较高的屋顶面提取效率和提取准确率,但难以适应各种形状屋顶面的提取(如长条形屋顶面),且算法涉及的部分参数(如格网大小和交叉线元的长度)没有明确的含义,如何设置这些参数得到最优结果需要进一步的探讨;本文方法利用点云特征提取初始屋顶面片,适用于任意形状屋顶面的提取,算法虽涉及多个参数,但各参数都有明确的含义,因此易于设置。
3 结论针对复杂建筑物屋顶面提取问题,本文提出了一种利用点云邻域信息的建筑物屋顶面高精度自动提取方法。试验结果表明,本文方法提取结果精度高,对复杂程度不同的建筑物屋顶面都能较好地提取;算法提取自动化程度较高,适应性较好。需要说明的是,本文方法虽涉及较多的参数,但都具有较好的适应性,文中针对不同数据集的多个区域建筑物屋顶面提取都设置相同的取值,均能得到较好的提取结果,因此参数较多并不影响本文方法的自动化程度和屋顶面提取精度。本文方法依赖于点云法向量,虽然通过选取种子点能得到法向量计算较为准确的点云,但法向量的计算精度对提取结果仍然有一定的影响,因此在后续工作中需对点云法向量的计算进行更多的讨论,以进一步提高屋顶面提取精度。
| [1] | 李怡静, 胡翔云, 张剑清, 等. 影像与LiDAR数据信息融合复杂场景下的道路自动提取[J]. 测绘学报, 2012, 41(6): 870–876. LI Yijing, HU Xiangyun, ZHANG Jianying, et al. Automatic Road Extraction in Complex Scenes Based on Information Fusion from LiDAR Data and Remote Sensing Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 870–876. |
| [2] | 徐文学, 杨必胜, 魏征, 等. 多标记点过程的LiDAR点云数据建筑物和树冠提取[J]. 测绘学报, 2013, 42(1): 51–58. XU Wenxue, YANG Bisheng, WEI Zheng, et al. Building and Tree Crown Extraction from LiDAR Point Cloud Data Based on Multi-marked Point Process[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 51–58. |
| [3] | 龚健雅, 崔婷婷, 单杰, 等. 利用车载移动测量数据的建筑物立面建模方法[J]. 武汉大学学报(信息科学版), 2015, 40(9): 1137–1143. GONG Jianya, CUI Tingting, SHAN Jie, et al. A Survey on Facade Modeling Using LiDAR Point Clouds and Image Sequences Collected by Mobile Mapping Systems[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1137–1143. |
| [4] | 黄先锋, SOHNG, 王潇, 等. 基于带权点法向量的LiDAR数据屋顶检测方法[J]. 武汉大学学报(信息科学版), 2009, 34(1): 24–27. HUANG Xianfeng, SOHN G, WANG Xiao, et al. Roof Detection Using LiDAR Data Based on Points' Normal with Weight[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 24–27. |
| [5] | XU Bo, JIANG Wanshou, SHAN Jie, et al. Investigation on the Weighted RANSAC Approaches for Building Roof Plane Segmentation from LiDAR Point Clouds[J]. Remote Sensing, 2016, 8(1): 5. |
| [6] | YAN Jixing, SHAN Jie, JIANG Wanshou. A Global Optimization Approach to Roof Segmentation from Airborne LiDAR Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014(94): 183–193. |
| [7] | WU Teng, HU Xiangyun, YE Lizhi. Fast and Accurate Plane Segmentation of Airborne LiDAR Point Cloud Using Cross-line Elements[J]. Remote Sensing, 2016, 8(5): 383. DOI:10.3390/rs8050383 |
| [8] | SCHNABEL R, WAHL R, KLEIN R. Efficient RANSAC for Point-cloud Shape Detection[J]. Computer Graphics Forum, 2007, 26(2): 214–226. DOI:10.1111/cgf.2007.26.issue-2 |
| [9] | TARSHA-KURDI F, LANDES T, GRUSSENMEYER P. Hough-transform and Extended RANSAC Algorithms for Automatic Detection of 3D Building Roof Planes from LiDAR Data[C]//International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences. Strasbourg:ISPRS, 2007:407-412. |
| [10] | VOSSELMAN G, DIJKMAN S. 3D Building Model Reconstruction from Point Clouds and Ground Plans[C]//International Archives of Photogrammetry and Remote Sensing. Annapolis, MD, USA:ISPRS, 2001:37-43. |
| [11] | RABBANI T, VAN DEN HEUVEL F A, VOSSELMAN G. Segmentation of Point Clouds Using Smoothness Constraint[C]//International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences. Delft:ISPRS, 2006:248-253. |
| [12] | 庞世燕, 刘亚文, 左志奇, 等. 结合区域增长法和TIN边缘分割的建筑物立面几何特征提取[J]. 武汉大学学报(信息科学版), 2015, 40(1): 102–106. PANG Shiyan, LIU Yawen, ZUO Zhiqi, et al. Combination of Region Growing and TIN Edge Segmentation for Extraction of Geometric Features on Building Facades[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 102–106. |
| [13] | VOSSELMAN G. Automated Planimetric Quality Control in High Accuracy Airborne Laser Scanning Surveys[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012(74): 90–100. |
| [14] | 高广, 马洪超, 张良. 利用合成算法从LiDAR数据提取屋顶面[J]. 武汉大学学报(信息科学版), 2014, 39(10): 1225–1230. GAO Guang, MA Hongchao, ZHANG Liang. Automatic Extraction of Building Roofs from LiDAR Data Using a Hybridized Method[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1225–1230. |
| [15] | SAMPATH A, SHAN Jie. Segmentation and Reconstruction of Polyhedral Building Roofs from Aerial LiDAR Point Clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1554–1567. DOI:10.1109/TGRS.2009.2030180 |
| [16] | FERRAZ A, BRETAR F, JACQUEMOUD S, et al. 3D Segmentation of Forest Structure Using a Mean-shift Based Algorithm[C]//Proceedings of the 17th IEEE International Conference on Image Processing. Hong Kong, China:IEEE, 2010:1413-1416. |
| [17] | LIU Xiuping, ZHANG Jie, CAO Junjie, et al. Quality Point Cloud Normal Estimation by Guided Least Squares Representation[J]. Computers & Graphics, 2015(51): 106–116. |
| [18] | PAULY M. Point Primitives for Interactive Modeling and Processing of 3D Geometry[D]. Zurich:ETH Zurich, 2003. |
| [19] | 胡伟. 机载LiDAR数据三维建筑物模型重建方法研究[D]. 焦作: 河南理工大学, 2012. HU Wei. Research on 3D Building Reconstruction from Airborne LiDAR Data[D]. Jiaozuo:Henan Polytechnic University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10460-1013030195.htm |
| [20] | 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48–61. SUN Jigui, LIU Jie, ZHAO Lianyu. Clustering Algorithms Research[J]. Journal of Software, 2008, 19(1): 48–61. |
| [21] | BIRANT D, KUT A. ST-DBSCAN:An Algorithm for Clustering Spatial-temporal Data[J]. Data & Knowledge Engineering, 2007, 60(1): 208–221. |
| [22] | BORDOGNA G, IENCO D. Fuzzy Core DBSCAN Clustering Algorithm[C]//LAURENT A, STRAUSS O, BOUCHON-MEUNIER B, et al. Information Processing and Management of Uncertainty in Knowledge-based Systems. Cham:Springer International Publishing, 2014:100-109. |
| [23] | YAN W Y, MORSY S, SHAKER A, et al. Automatic Extraction of Highway Light Poles and Towers from Mobile LiDAR Data[J]. Optics & Laser Technology, 2016, 77: 162–168. |
| [24] | 吕峰. 利用航空影像和LiDAR点云进行建筑物重建的方法研究[D]. 成都: 西南交通大学, 2013. LÜ Feng. Building Reconstruction Methods Study Based on Aerial Image and LiDAR Point Cloud[D]. Chengdu:Southwest Jiaotong University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10613-1013251251.htm |
| [25] | AWRANGJEB M, FRASER C S. An Automatic and Threshold-free Performance Evaluation System for Building Extraction Techniques from Airborne LiDAR Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(10): 4184–4198. DOI:10.1109/JSTARS.2014.2318694 |
| [26] | ISPRS. ISPRS Test Project on Urban Classification and 3D Building Reconstruction[DB/OL]. (2016-08-13)[2016-09-28]. http://www2.isprs.org/commissions/comm3/wg4/detection-and-reconstruction.html. |
| [27] | OpenTopography. NCALM Project. PI:Shane Grigsby, University of Colorado, Boulder[DB/OL]. (2016-09-10)[2016-12-10]. https://doi.org/10.5069/G9ZC80SR. |
| [28] | FISCHLER M A, BOLLES R C. Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381–395. DOI:10.1145/358669.358692 |
| [29] | TORR P H S, ZISSERMAN A. MLESAC:A New Robust Estimator with Application to Estimating Image Geometry[J]. Computer Vision and Image Understanding, 2000, 78(1): 138–156. DOI:10.1006/cviu.1999.0832 |


