2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉 430077;
3. 中国航天科技集团量子工程研究中心, 北京 100854
2. State Key Laboratory of Geodesy and Earth's Geodynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
3. Quantum Engineering Research Center, China Aerospace Science and Technology Corporation, Beijing 100854, China
卫星重力梯度测量(satellite gravity gradiometry,SGG)是恢复全球静态长波重力场的重要手段之一。2009年,ESA发射了人类第一颗基于SGG模式的卫星GOCE[1],通过搭载静电式重力梯度仪,采用差分加速度的测量原理获取了高分辨率的全球重力场信息。SGG直接测量轨道高度处重力位的二阶导--重力梯度值,可有效抑制重力场信号在高阶因轨道高度上升而快速衰减的问题,大大提升全球中长波重力场的测量分辨率。GOCE卫星设计的科学目标是将全球静态重力场恢复至200阶,国内外诸多机构利用GOCE卫星的在轨数据,同时结合2000年发射的高低卫卫跟踪模式的CHAMP卫星[2]以及2002年发射的低低卫卫跟踪模式的GRACE卫星的观测数据[3],联合反演出一系列高分辨率的全球重力场模型,如GOCO02s、GOCO05s、ITG-GOCE02等,最新的GOCE重力场模型分辨率已达到250~280阶[4]。
目前,CHAMP和GOCE卫星已结束任务,GRACE卫星也面临寿命到期、系统更新换代的问题,因此国际上推出了下一代低低跟踪重力卫星GRACE-Ⅱ计划[5-6],拟实现200阶左右的重力场及其时变测量,但仍无法满足大地测量、固体地球学、海洋学对200~360阶的全球重力场模型的迫切需求,且要求在该空间分辨率下获得厘米级的大地水准面误差和10-5 m/s2量级的重力异常误差[7],如图 1所示。因此通过SGG进一步提升全球重力场模型分辨率具有非常重要的科学意义。
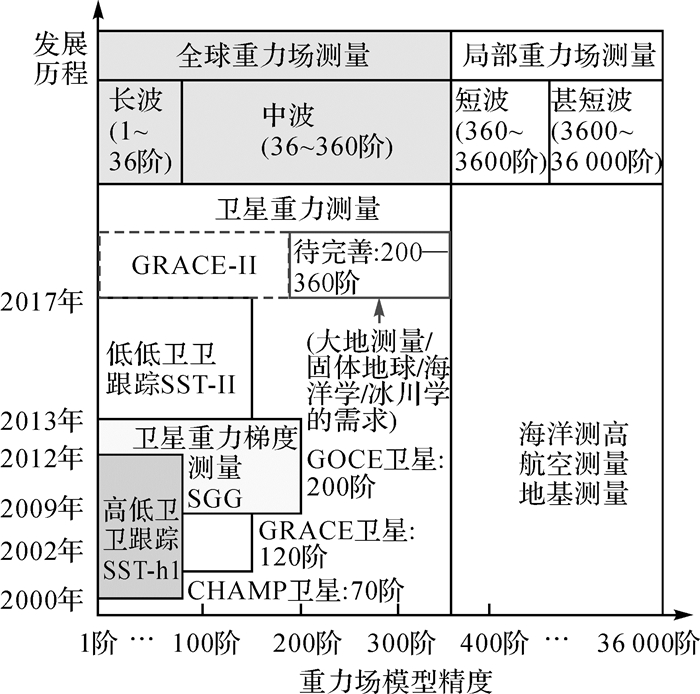
|
| 图 1 地球重力场各波段探测手段现状 Fig. 1 Measurement techniques of the Earth's gravity field for different wavelengths |
SGG的测量手段分为静电型、超导型、原子干涉型等。静电型已成功应用于GOCE卫星,目前在轨测量噪声10~20 mE/Hz1/2(1 E=10-9/s2)[8-9],未来性能提升空间有限[10-11];超导型依赖于低温环境,且体积庞大,结构复杂,离工程应用尚远[12];原子干涉型在空间微重力环境下可获得较长的干涉时间,具有很高的潜在测量灵敏度[13-15],被纳入下一代SGG的候选技术之一[10]。原子干涉SGG概念由JPL提出[16],由于在空间微重力环境下,原子失重接近自由悬浮状态,测量方法与测量结果与地面存在较大差异,为此NASA与ESA先后开展了星载便携式原子干涉重力梯度仪的设计、研制及相关落塔、机载飞行试验[17-19],根据测试结果预计原子干涉SGG对地球重力场的恢复精度比GOCE卫星(静电式SGG)至少高1~2个数量级[20-21]。
在该背景下,本文以200~360阶全球静态重力场测量的科学需求为背景,开展基于原子干涉技术的卫星重力梯度测量研究,文中提出一种自由悬浮式的原子干涉SGG测量方案,给出了关键参数的设计,在此基础上对该方法恢复重力场的预期精度进行了评估,本文的研究结果将为下一代更高分辨率的卫星重力梯度测量提供一种可能的技术途径。
1 原子干涉SGG方法与量测模型 1.1 基于差分原理求解重力梯度的理论分析SGG通过搭载星载重力梯度仪,结合定轨和卫星测姿,获取轨道高度处重力位V的二阶导数,也是重力加速度g的一阶导数,即重力梯度张量
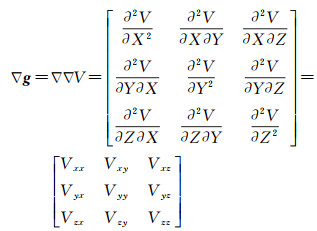 (1)
(1)
式中,∇为梯度算子,星载重力梯度仪主要基于差分加速度测量原理获取重力梯度。其由6个重力仪(或加速度计)构成,分别沿卫星质心对称放置(这里采用局部轨道坐标系,以卫星质心Osc为原点,X、Y、Z轴分别为卫星飞行方向、垂直轨道平面方向和地心径向方向),如图 2所示。
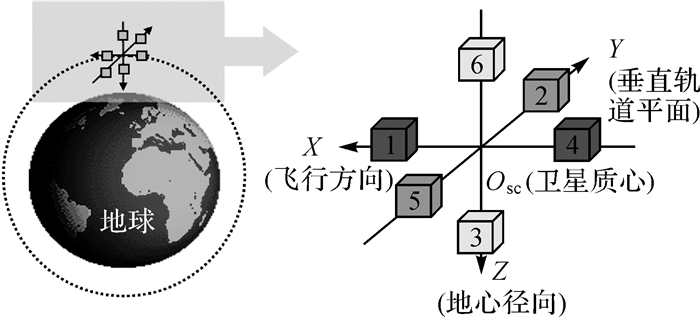
|
| 图 2 卫星重力梯度测量基本原理 Fig. 2 Principle of satellite gravity gradiometry |
每个重力仪由内部检验质量和外部框架(固连于卫星)构成,测量的是检验质量相对于卫星的加速度。当重力仪距离卫星质心r处时,重力仪输出aout可表示为[8]
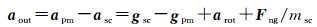 (2)
(2)
式中,apm与asc分别为检验质量与卫星的加速度;gpm与gsc分别为检验质量与卫星受到的重力加速度;Fng为卫星受到的大气阻力、太阳光压等非保守力;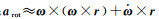
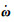
将gpm在卫星质心处(即原点Osc)泰勒展开为
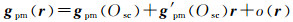 (3)
(3)
式中,gpm(Osc)=gsc表示卫星质心处受到的重力加速度;g′pm(Osc)=∇g表示卫星质心处的重力梯度值;o(r)是r的高阶无穷小。故将上式代入式(2) 可得重力仪的输出为
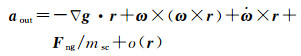 (4)
(4)
根据上式,对于某一基线方向上的一对重力仪而言,其差分输出Δa可表示为
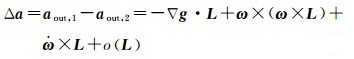 (5)
(5)
式中,L=r1-r2为两重力仪之间的基线长度。
由上式可以看出,在忽略重力位三阶导以上的高阶小项的情况下,差分加速度测量结果可等效于重力梯度Vij,但其引入两项主要误差,一是卫星角速度的影响,卫星角速度可由星敏感器、光纤陀螺等星上高精度姿态测量仪器获取,其引入的梯度误差将在最终的梯度数据提取中扣除[8]。二是重力加速度泰勒展开的高阶小项o(L)引入的梯度测量误差,该部分误差主要来源于重力位沿竖直方向上的三阶导数Vzzz[22],在0.5 m的基线长度下,其贡献的误差约为0.6 mE,在本文的重力梯度测量噪声分析结果下,该误差的影响可忽略不计。
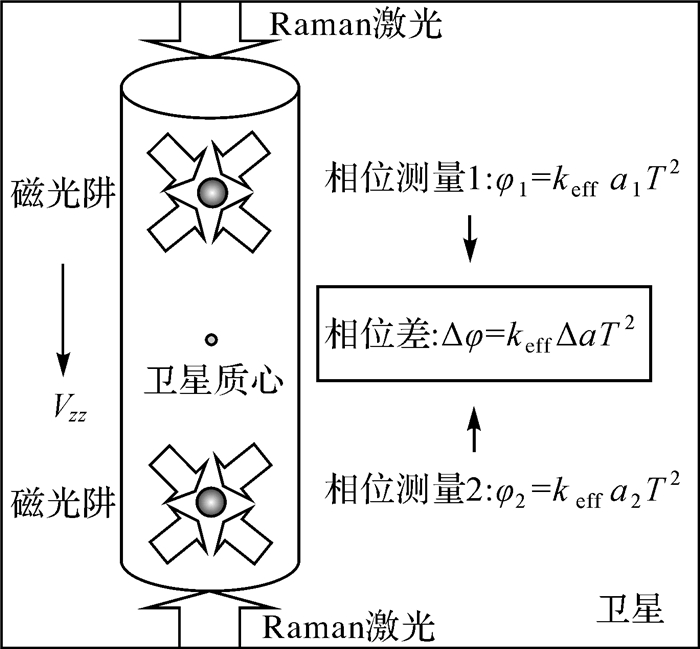
1.2 空间原子干涉重力梯度测量方法原子干涉SGG技术主要通过差分形式的原子干涉重力仪来实现重力梯度测量,其检验质量是冷却的原子。其采用磁光阱(magnetic optical trap,MOT)将原子冷却囚禁后释放,然后通过激光与原子相互作用,操控原子的内态变化,发生干涉,从相移中提取外界加速度信息。同一方向上相距L的一对原子干涉重力仪可构成原子干涉重力梯度仪,如图 3所示,通过测定两干涉重力仪的相移差Δφ获得同一方向上的差分加速度Δa,即[14]
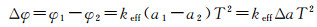 (6)
(6)
|
| 图 3 原子干涉重力梯度测量原理 Fig. 3 Principle of atom-interferometry gravity gradiometry |
式中,keff是Raman激光脉冲的有效波矢;T是激光脉冲间隔。
与地面不同的是,微重力环境下原子失重接近自由悬浮状态,仪器框架固连于卫星平台,因此原子干涉仪测量的是原子团相对于卫星本体的加速度之差。对于500 km以下的近地轨道,在测量基线L=0.5 m且采用无拖曳控制的情况下,原子团与卫星之间的相对加速度不超过1×10-6 m/s2[11]。
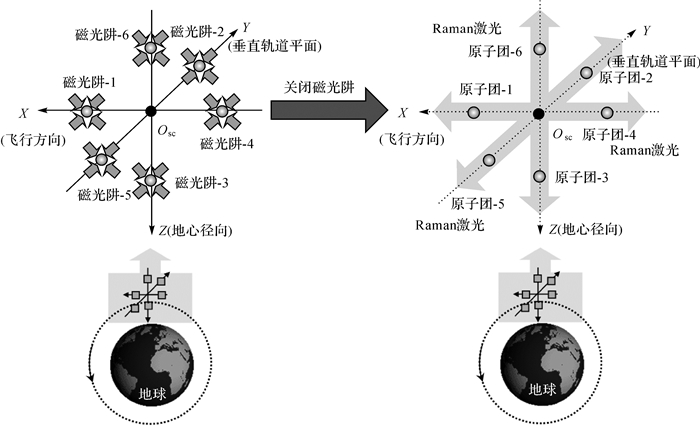
由此可知,空间中原子相对于仪器框架几乎静止,没有触碰容器壁的风险。在该情况下,笔者提出微重力环境下的自由悬浮式原子干涉SGG测量方法如下:X、Y、Z 3个方向上分别沿卫星质心对称放置3对MOT,每次测量先通过MOT将原子冷却囚禁,撤去MOT(关闭线圈电流)后原子接近自由悬浮状态,此时在每个方向上分别用同束Raman激光与自由悬浮的原子团相互作用,通过干涉测量相位差获取差分加速度信息。磁光阱1与4置于X轴基线上;磁光阱2与5置于Y轴基线上;磁光阱3与6置于Z轴基线上,如图 4所示。在空间环境下,该方案既可获得较大的干涉时间间隔,降低测量噪声,提升重力场恢复精度,又有利于星载梯度仪的小型化设计。
|
| 图 4 原子干涉SGG测量方案 Fig. 4 Measurement scheme of SGG based on atom interferometry |
值得注意的是,原子干涉重力梯度测量的方向与Raman激光打出的方向一致,此方案中,3束Raman激光分别沿X、Y、Z 3个基线方向打出,因此该方案主要用于测量沿基线方向的重力加速度的变化,即对角梯度分量Vxx、Vyy、Vzz。而对于静电式重力梯度仪而言,每个静电加速度计在三维正交坐标系下有3个平动轴的输出,其中一个轴沿所在基线方向放置,另外两个轴垂直于所在基线方向,因此静电梯度仪不仅可以测量沿基线方向的差分加速度(即对角梯度分量Vxx、Vyy、Vzz),还可测量垂直于基线方向上的差分加速度(即非对角梯度分量Vxy、Vyz、Vxz)。
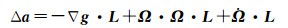 (7)
(7)
式中,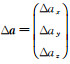
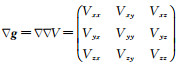
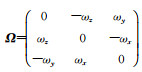
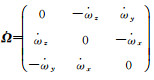
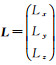
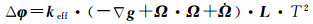 (8)
(8)
式中,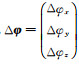
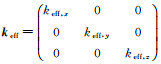
由式(8) 可知,对于自由悬浮式原子干涉SGG而言,在每个方向上由测量的差分相位扣除卫星角速度信息,便可得到全部的对角梯度分量。对角梯度分量Vxx、Vyy、Vzz的测量表达式如表 1所示。
| 测量方向 | 测量表达式 |
| X方向 | 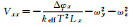 |
| Y方向 | 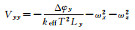 |
| Z方向 | 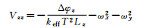 |
式中,Δφi表示i基线方向上(i=x, y, z)测量的相位差;keff表示Raman激光脉冲的有效波矢;T表示激光脉冲间隔;Li表示i方向的基线长度;ωi为卫星i轴的角速度。
2 原子干涉SGG关键参数分析关键参数的确定是原子干涉SGG方案设计中重要的工作之一。一方面,SGG测量地球重力场的空间分辨率直接取决于轨道高度、测量频带、梯度测量噪声等关键参数[23-24],因此为实现未来200~360阶重力场测量的科学目标,需对上述关键参数进行分析,并选取合适的设计值。另一方面,对于原子干涉型的SGG,干涉时间间隔与重力场恢复的空间分辨率、重力梯度仪噪声等参数之间相互制约,需权衡考虑与设计。NASA与ESA均明确指出这些关键参数选取对于未来开展原子干涉SGG方案设计的重要性[10, 16]。
2.1 轨道高度降低轨道高度可以增大重力场信息的感知程度,提升重力场测量的空间分辨率。仿真结果表明,阶数较高时,卫星轨道高度的作用随阶数增加越来越明显[24]。
轨道的设计一方面要考虑轨道高度的重力梯度信号的大小,另一方面要考虑大气阻尼对低轨航天器轨道维持及寿命的影响。
首先,重力梯度信号随高度衰减,对于3个对角梯度分量而言,Vxx≈Vyy≈Vzz/2,沿地心径向方向上的重力梯度信号Vzz最大,约为Vzz≈2GM/(R+h)3,其中GM为地球常数,R≈6378 km为地球的平均半径,h为轨道高度,在100~1000 km的轨道高度范围内,Vzz信号大小约在2000~3000 E,如图 5所示,比目前星载梯度仪mE量级的测量噪声高6个量级左右。
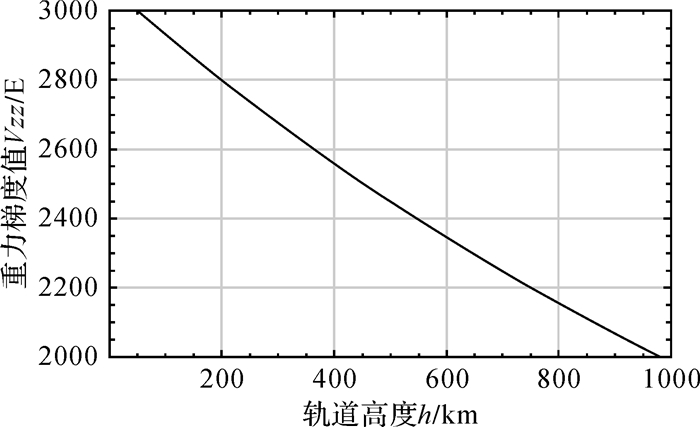
|
| 图 5 地心径向方向上重力梯度信号大小随轨道高度的变化 Fig. 5 Gravity gradient signal variances with orbit heights in radial direction |
其次,对于低轨航天器而言,飞行方向上的大气阻尼较大,在卫星面质比0.001的情况下,250 km的轨道高处大气阻尼可达10-6~10-5 m/s2,且轨道越低,阻尼增大的速度越快,如图 6所示。这对卫星的轨道维持和寿命设计提出了较高要求。正因如此,在综合考虑并采用无拖曳控制技术的前提下,GOCE选择了250 km的低轨轨道[8]。在250 km的轨道高度,3个对角梯度分量的值分别为Vxx≈Vyy≈1370E,Vzz≈2740 E[25]。
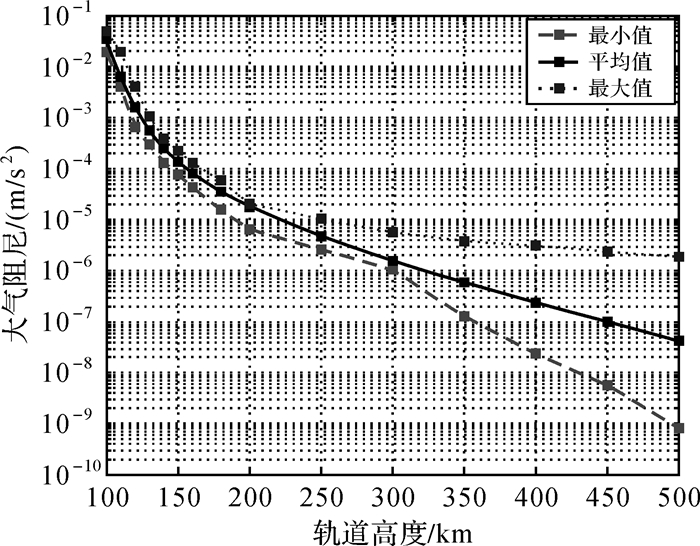
|
| 图 6 飞行方向大气阻尼随轨道高度的变化 Fig. 6 Air drag variance with orbit height along track |
因此参考GOCE,从重力场测量空间分辨率保证、卫星设计可行性以及工程实现技术成熟度的角度考虑,原子干涉SGG选择250 km的轨道高度为宜。
2.2 测量频带测量频带的选择主要根据地球重力场恢复的阶数。一般而言,测量频带的下限fmin设为轨道频率forbit的N倍(N≥1),测量频带的上限fmax则对应着重力场恢复的最大阶数Lmax,即
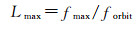 (9)
(9)
GOCE卫星设计的测量频带为5~100 mHz,轨道频率forbit=1/5384 s=1.86×10-4 Hz,理论上对应重力场球谐展开的阶数为26~538阶。但是实际在轨运行时,GOCE在轨测量噪声为10~20 mE/Hz1/2,38 mHz以上的重力梯度信号已经被测量噪声淹没[8],这对应着球谐展开的最大阶数约为203阶,与GOCE实际恢复的重力场模型阶数基本一致。
因此为满足200~360阶的全球静态重力场测量的需求,依据式(9),则要求原子干涉SGG测量频带的上限fmax的取值范围为37 mHz≤fmax≤67 mHz。在本文的设计中,为尽可能地提高重力场恢复阶数,取最大值67 mHz。
2.3 激光脉冲间隔由原子干涉重力梯度测量原理可知,完成一次原子干涉测量的时间主要由3段激光原子相互作用时间τ(很短)和两段激光脉冲间隔T(较长)组成,如图 7所示。
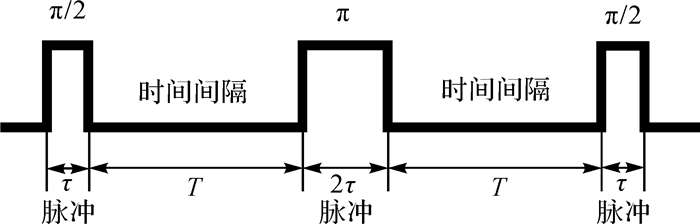
|
| 图 7 完成一次原子干涉测量的时间构成 Fig. 7 Total interaction time for a single measurement of atom interferometry |
因此完成一次原子干涉测量的时间Tatom可表示为
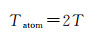 (10)
(10)
其对应着原子干涉测量的采样频率,即fatom=1/Tatom。
由表 1可知,原子干涉SGG测量噪声与激光脉冲间隔T的平方成反比。在空间微重力环境下,冷原子团失重接近悬浮状态,与仪器框架的相对运动非常微小,没有触碰容器壁的风险,因此激光脉冲间隔T可以很容易增大到数秒甚至十秒的量级,使得SGG测量噪声大大降低,重力场恢复的分辨率大大提高。但是较长的时间间隔T又限制着SGG的测量频段,即重力场测量的空间分辨率。根据奈奎斯特采样定理,为保证信号提取的不失真,采样频率fatom需为信号能够恢复的最大频率fmax的2倍,即fatom=2fmax,此时原子干涉SGG采样频率fatom可表示为
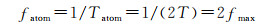 (11)
(11)
由(11) 式可知,fmax=1/(4T),因此重力场恢复的空间分辨率(半波长)与阶数之间的关系可表示为
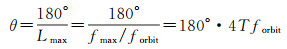 (12)
(12)
为满足地球物理等学科对200~360阶的重力场测量的需求,根据式(12),则要求激光脉冲间隔3.7 s≤T≤6.7 s,如图 8所示。由此可见,为保证重力场测量的空间分辨率,要求激光脉冲间隔T尽可能小。因此本文中取最严格的下限即T=3.7 s进行分析。
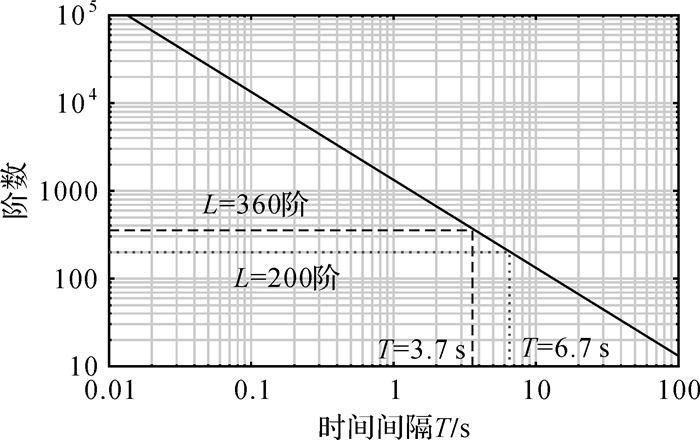
|
| 图 8 原子干涉时间间隔与重力场恢复阶数的关系 Fig. 8 Relationship between interrogation time of atom interference and degree of spherical harmonic series expansion in gravity field recovery |
2.4 重力梯度仪测量噪声
核心载荷重力梯度仪噪声是SGG最主要的误差源之一。ESA基于地面原子干涉重力梯度仪上抛下落式的测量原理,提出了另一种基于差分对抛式的星载原子干涉重力梯度仪方案,并估计其测量噪声谱密度可达到3.5 mE/Hz1/2[10],该方案可以同时测量对角梯度分量和卫星角速度信息,但是该类型的梯度仪测量噪声受限于仪器尺寸和原子抛出速度,并且为了测量卫星角速度,增大了系统结构的复杂度。
本文提出的自由悬浮式的重力梯度方案中,卫星角速度由星上高精度测姿系统获取,梯度仪仅用于测量Vxx、Vyy、Vzz 3个梯度分量,由于原子悬浮,干涉时间不受仪器尺寸限制,且结构简单,利于星载仪器的小型化设计。由前文可知,重力梯度值的获取通过测定干涉相位差Δφ来实现。相位差的测量噪声δ(Δφ)是原子干涉SGG噪声的根本限制。根据表 1,原子干涉重力梯度测量中,差分加速度由测量的相位差得到,因此相位差测量噪声δ(Δφ)直接影响差分加速度的测量噪声,进而贡献到对角梯度分量Vⅱ(i=x, y, z)测量噪声可写为ΔVⅱ=δ(Δφi)/(keffT2Li)。考虑完成一次干涉测量的积分时间约为Tatom=2T,则在频域中,梯度仪的测量噪声功率谱密度可表示为[10]
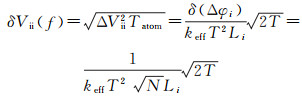 (13)
(13)
其中相位差的测量噪声δ(Δφ)根本上受限于量子投影噪声,即δ(Δφ)=1/N1/2[26],目前采集的原子数目N可达109个[13],按照选态时损失一个量级计算(即N=109)[27],则干涉仪的相移测量噪声可达到δ(Δφ)=0.03 mrad。Tatom=2T为噪声谱分析中完成单次测量的数据采样时长。由式(13) 可得,在测量基线L=0.5 m的情况下,自由悬浮式的星载原子干涉重力梯度仪测量噪声约为0.85 mE/Hz1/2,比静电式重力梯度仪在轨实测噪声降低1个量级,如表 2所示。
| 国外梯度仪 | 本方案梯度仪 | ||
| 测量原理 | 差分对抛 | 自由悬浮 | |
| 可测量的物理量 | 对角梯度分量、卫星角速度 | 对角梯度分量 | |
| 原子类型 | 87Rb | 87Rb | |
| 原子抛出速度/(cm/s) | 2.5 | - | |
| 测量基线长度/m | 0.5 | 0.5 | |
| 数据时长/s | 1 | 7.4 | |
| 干涉时间间隔/s | 5 | 3.7 | |
| 冷却状态 | 常规冷却 | 常规冷却 | BEC |
| 原子个数 | 106 | 109 | 106 |
| 梯度仪测量噪声 /(mE/Hz1/2) |
3.5 | 0.85 | 0.03 (潜在测量噪声) |
若未来进一步将原子冷却至玻色-爱因斯坦凝聚体(BEC)的状态,理论上其潜在测量噪声可进一步降低至0.03 mE/Hz1/2[27]。
2.5 小结综上所述,在自由悬浮式的星载测量方案下,本文分析得出,原子干涉SGG的轨道高度为250 km为宜,激光脉冲间隔设置为3.7 s,梯度测量噪声0.85 mE/Hz1/2,关键参数的选取及考虑因素如表 3所示。
| 参数 | 设计值 | 考虑因素 |
| 轨道高度h | 250 km | 既提升感测灵敏度,又利于工程实现,技术成熟度高(GOCE已实现) |
| 测量频带上限fmax | >67 mHz | 对应重力场恢复阶数360阶 |
| 激光脉冲间隔T | 3.7 s | 保证空间分辨率的前提下,尽可能选择较大的T,降低梯度仪噪声 |
| 梯度测量噪声δVⅱ | 0.85 mE/Hz1/2 | 根本受限于梯度仪量子投影噪声,且随T增大而显著提升 |
值得说明的是,上表中测量频带上限fmax与激光脉冲间隔T是以重力场恢复360阶的目标而设计的,但这并不意味着重力场就能恢复至360阶。一方面,重力场最终的恢复阶数是诸多关键参数综合贡献的结果,它不仅取决于激光脉冲间隔、测量频带,还取决于轨道高度、重力梯度仪噪声等,而轨道高度与梯度仪噪声的设计在考虑重力场恢复阶数的同时,还需考虑实际的工程实现,例如轨道高度的选取需考虑低轨大气阻尼对卫星寿命,重力梯度仪的噪声分析需考虑其噪声的根本限制。另一方面,参数之间相互制约,参数的选取是一个权衡的过程[16],例如这里激光脉冲间隔T的选取既要考虑重力场恢复的空间分辨率,又要考虑T对原子干涉重力梯度仪噪声的影响。最终参数的确定是一个折中的选取结果。
3 原子干涉SGG恢复地球重力场精度评估原子干涉SGG具有较低的测量噪声谱,对提升全球中长波重力场恢复精度具有重要意义。本文基于直接误差解析法[28],分别对静电型SGG与原子干涉型SGG恢复重力场的预期精度进行了仿真评估。仿真中设置轨道高度250 km,数据周期8个月,轨道倾角96.5°,数据采样频率0.135 Hz,频带内SGG测量噪声均设为白噪声,其中静电型SGG(即GOCE卫星)在轨实测噪声20 mE/Hz1/2,差分对抛式与自由悬浮式原子干涉SGG的噪声分别为3.5 mE/Hz1/2与0.85 mE/Hz1/2,得到重力场位系数的误差阶方差、全球大地水准面累积误差以及全球重力异常累积误差如图 9-图 11所示。
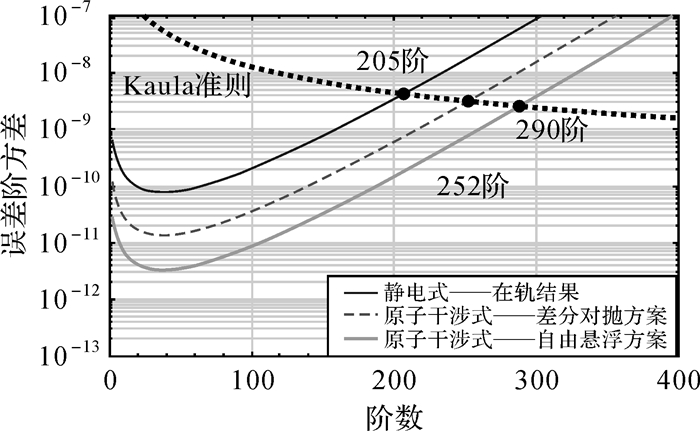
|
| 图 9 不同SGG噪声下的误差阶方差估计 Fig. 9 Expected error degree variance from different SGG noise |
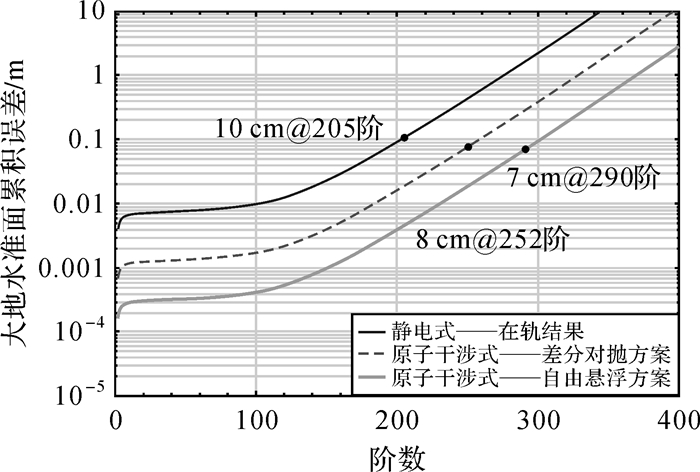
|
| 图 10 不同SGG噪声下的大地水准面累积误差估计 Fig. 10 Expected cumulative geoid height errors from different SGG noise |
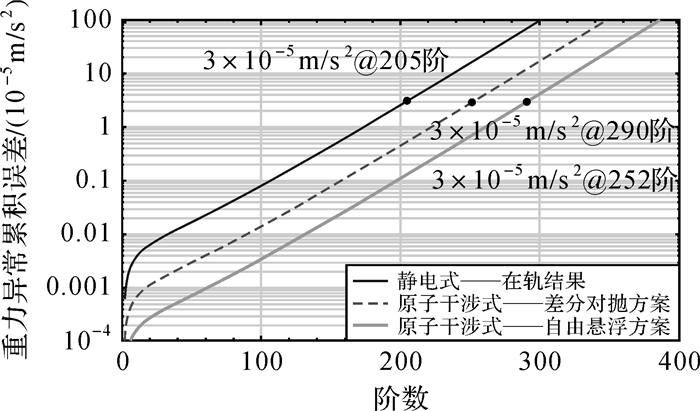
|
| 图 11 不同SGG噪声下的重力异常累积误差估计 Fig. 11 Expected cumulative gravity anomaly errors from different SGG noise |
从图中可以看出,静电式SGG恢复重力场阶数约为205阶(对应空间分辨率53′×53′),在该分辨率下累积大地水准面误差10 cm,累积重力异常误差3×10-5 m/s2;原子干涉型SGG可恢复250阶以上的高阶静态重力场,其中差分对抛式原子干涉SGG可将全球重力场恢复至252阶(对应空间分辨率43′×43′),在该分辨率下累积大地水准面误差8 cm,累积重力异常误差3×10-5 m/s2;本文提出的自由悬浮式原子干涉SGG可进一步将全球重力场恢复精度提升至290阶(对应空间分辨率37′×37′),在该分辨率下累积大地水准面误差7 cm,累积重力异常误差3×10-5 m/s2。静电型与原子干涉型SGG恢复高阶静态重力场的精度如表 4所示。
| SGG测量类型 | 测量原理 | 梯度测量噪声 /(mE/Hz1/2) |
大地水准面累积误差/cm | 重力异常累积误差/(m/s2) | |||||
| 205阶 | 252阶 | 290阶 | 205阶 | 252阶 | 290阶 | ||||
| 静电型 | 20 | 10 | - | - | 3×10-5 | - | - | ||
| 原子干涉型 | 差分对抛式 | 3.5 | 2 | 8 | - | 5×10-6 | 3×10-5 | - | |
| 自由悬浮式 | 0.85 | 0.5 | 2 | 7 | 1×10-6 | 7×10-6 | 3×10-5 | ||
值得注意的是,以上仅是基于SGG模式的仿真结果,若在低阶加入高低卫卫跟踪或低低卫卫跟踪模式对中长波重力场测量的贡献,高阶加入Kaula约束,则恢复阶数以及相应的大地水准面误差和重力异常误差将会进一步得到改善。这也是GOCE卫星当初设计指标200阶,实际模型反演结果达到250阶以上的原因。
4 总结基于原子干涉技术的卫星重力梯度测量在空间中具有很低的测量噪声谱,为未来完善200~360阶的全球高阶静态重力场模型提供了一种可能的技术途径。本文提出了一种适用于空间微重力环境下的原子干涉重力梯度测量方案,梯度测量噪声预计可达0.85 mE/Hz1/2。仿真结果表明,基于原子干涉技术的卫星重力梯度测量有望在现有技术的基础上,将全球重力场恢复阶数提升至252~290阶,累积大地水准面误差7~8 cm,累积重力异常误差3×10-5 m/s2,如表 5所示。
| 方案 | 静电型SGG | 原子干涉型SGG |
| 测量原理 | 电容位移传感+静电反馈控制 | 原子与激光干涉作用 |
| 测量方式 | 宏观(牛顿力学) | 微观(量子力学) |
| 检验质量 | 金属质量块 | 碱金属冷原子团 |
| 测量的梯度分量 | 对角梯度分量Vxx、Vyy、Vzz 非对角梯度分量Vxz、Vyz、Vxy |
对角梯度分量Vxx、Vyy、Vzz |
| 重力梯度测量噪声 | 设计:6~7 mE/Hz1/2 | 差分对抛式:3.5 mE/Hz1/2 |
| 在轨:10~20 mE/Hz1/2 | 自由悬浮式:0.85 mE/Hz1/2 | |
| 重力场反演精度 | 重力场模型恢复阶数:200阶 | 重力场模型恢复阶数:252~290阶 |
| 全球大地水准面误差:10 cm | 全球大地水准面误差:7~8 cm | |
| 全球重力异常误差:3×10-5 m/s2 | 全球重力异常误差:3×10-5 m/s2 |
值得说明的是,未来可通过提升原子冷却技术来进一步降低梯度仪噪声,原子冷却至BEC状态时,原子干涉SGG有望将全球重力场模型空间分辨率提升至360阶以上。值得注意的是,一方面,如此高的测量水平对磁场、振动等背景噪声抑制提出了较高要求,本文提出的自由悬浮式原子干涉SGG方案在每个方向上采用同样的Raman激光与两团原子相互作用,通过差分测量,可以获得很好的共模抑制效果,对卫星平台振动有80 dB~155 dB的抑制作用[13-14, 16];卫星平台磁场和空间磁场可通过高精度磁测以及卫星平台低剩磁设计以及磁屏蔽等手段进行控制[29]。同时对于本文提出的原子干涉SGG测量方案,理想情况下原子相对于仪器框架静止不动,但实际中由于大气阻尼等外界干扰力的存在,原子相对于仪器框架存在微小的加速度(10-6 m/s2以下),由于原子自由漂浮,在较长的干涉时间间隔下(秒量级),会引起两团原子之间的基线长度存在微米级的固定偏差,进而引入mE量级的梯度测量偏差,该偏差可通过梯度仪的共模加速度输出计算出,并在后续数据处理中扣除。
| [1] | FLOBERGHAGEN R, FEHRINGER M, LAMARRE D, et al. Mission Design, Operation and Exploitation of the Gravity Field and Steady-State Ocean Circulation Explorer Mission[J]. Journal of Geodesy, 2011, 85(11): 749–758. DOI:10.1007/s00190-011-0498-3 |
| [2] | REIGBER C, SCHWINTZER P, NEUMAYER K H, et al. The CHAMP-Only Earth Gravity Field Model EIGEN-2[J]. Advances in Space Research, 2003, 31(8): 1883–1888. DOI:10.1016/S0273-1177(03)00162-5 |
| [3] | 陈秋杰, 沈云中, 张兴福, 等. 基于GRACE卫星数据的高精度全球静态重力场模型[J]. 测绘学报, 2016, 45(4): 396–403. CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. GRACE Data-based High Accuracy Global Static Earth's Gravity Field Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 396–403. DOI:10.11947/j.AGCS.2016.20150422 |
| [4] | MARCHENKO A N, MARCHENKO D A, LOPUSHANSKY A N. Gravity Field Models Derived from the Second Degree Radial Derivatives of the GOCE Mission:A Case Study[J]. Annals of Geophysics, 2016, 59(6): S0649. |
| [5] | LOOMIS B D, NEREM R S, LUTHCKE S B. Simulation Study of a Follow-on Gravity Mission to GRACE[J]. Journal of Geodesy, 2012, 86(5): 319–335. DOI:10.1007/s00190-011-0521-8 |
| [6] | 宁津生, 王正涛, 超能芳. 国际新一代卫星重力探测计划研究现状与进展[J]. 武汉大学学报(信息科学版), 2016, 41(1): 1–8. NING Jinsheng, WANG Zhengtao, CHAO Nengfang. Research Status and Progress in International Next-generation Satellite Gravity Measurement Missions[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 1–8. |
| [7] | ESA. The Four Candidate Earth Explorer Core Missions-Gravity Field and Steady-State Ocean Circulation Mission (ESA SP-1233(1))[R]. Noordwijk:ESA Publications Division, 1999. |
| [8] | RUMMEL R, YI Weiyong, STUMMER C. GOCE Gravitational Gradiometry[J]. Journal of Geodesy, 2011, 85(11): 777–790. DOI:10.1007/s00190-011-0500-0 |
| [9] | 徐新禹, 赵永奇, 魏辉, 等. 利用先验重力场模型对GOCE卫星重力梯度观测值进行校准分析[J]. 测绘学报, 2015, 44(11): 1196–1201. XU Xinyu, ZHAO Yongqi, WEI Hui, et al. Calibration and Analysis of SGG Observations of GOCE Based on Prior Gravity Models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1196–1201. DOI:10.11947/j.AGCS.2015.20140414 |
| [10] | CARRAZ O, SIEMES C, MASSOTTI L, et al. A Spaceborne Gravity Gradiometer Concept Based on Cold Atom Interferometers for Measuring Earth's Gravity Field[J]. Microgravity Science and Technology, 2014, 26(3): 139–145. DOI:10.1007/s12217-014-9385-x |
| [11] | ZHU Zhu, ZHOU Zebing, CAI Lin, et al. Electrostatic Gravity Gradiometer Design for the Future Mission[J]. Advances in Space Research, 2013, 51(12): 2269–2276. DOI:10.1016/j.asr.2013.01.031 |
| [12] | PAIK H J. Superconducting Accelerometry:Its Principles and Applications[J]. Classical and Quantum Gravity, 1994, 11(6A): A133–A144. DOI:10.1088/0264-9381/11/6A/010 |
| [13] | MALEKI L, YU Nan, KOHEL J. Quantum Gravity Gradiometer for Sub-surface Imaging[C]//Space 2004 Conference and Exhibit. San Diego, California:AIAA, 2004. |
| [14] | YU Nan, KOHEL J M, KELLOGG J R, et al. Development of an Atom-Interferometer Gravity Gradiometer for Gravity Measurement from Space[J]. Applied Physics B, 2006, 84(4): 647–652. DOI:10.1007/s00340-006-2376-x |
| [15] | 翟振和, 吴富梅. 基于原子干涉测量技术的卫星重力梯度测量[J]. 测绘通报, 2007(2): 5–6, 36. ZHAI Zhenhe, WU Fumei. Satellite Gravity Gradiometry Based on Atom Interferometry Technique[J]. Bulletin of Surveying and Mapping, 2007(2): 5–6, 36. |
| [16] | YU Nan, KOHEL J M, ROMANS L, et al. Quantum Gravity Gradiometer Sensor for Earth Science Applications[C]//NASA Earth Science and Technology Conference 2002. Pasadena, CA:Jet Propulsion Laboratory, California Institute of Technology, 2002. |
| [17] | NYMAN R A, VAROQUAUX G, LIENHART F, et al. I.C.E.:A Transportable Atomic Inertial Sensor for Test in Microgravity[J]. Applied Physics B, 2006, 84(4): 673–681. DOI:10.1007/s00340-006-2395-7 |
| [18] | KÖNEMANN T, BRINKMANN W, GÖKLÜE, et al. A Freely Falling Magneto-Optical Trap Drop Tower Experiment[J]. Applied Physics B, 2007, 89(4): 431–438. DOI:10.1007/s00340-007-2863-8 |
| [19] | GEIGER R, MÉNORET V, STERN G, et al. Detecting Inertial Effects with Airborne Matter-Wave Interferometry[J]. Nature Communications, 2011(2): 474. |
| [20] | SORRENTINO F, BONGS K, BOUYER P, et al. The Space Atom Interferometer Project:Status and Prospects[J]. Journal of Physics:Conference Series, 2011(327): 012050. |
| [21] | 郑伟, 许厚泽, 钟敏, 等. 国际卫星重力梯度测量计划研究进展[J]. 测绘科学, 2010, 35(2): 57–61. ZHENG Wei, XU Houze, ZHONG Min, et al. Study Progress in International Satellite Gravity Gradiometry Programs[J]. Science of Surveying and Mapping, 2010, 35(2): 57–61. |
| [22] | 王谦身. 重力学[M]. 北京: 地震出版社, 2003. WANG Qianshen. Gravitology[M]. Beijing: Seismological Press, 2003. |
| [23] | RUMMEL R, BALMINO G, JOHANNESSEN J, et al. Dedicated Gravity Field Missions-principles and Aims[J]. Journal of Geodynamics, 2002, 33(1-2): 3–20. DOI:10.1016/S0264-3707(01)00050-3 |
| [24] | 蔡林, 周泽兵, 祝竺, 等. 卫星重力梯度恢复地球重力场的频谱分析[J]. 地球物理学报, 2012, 55(5): 1565–1571. CAI Lin, ZHOU Zebing, ZHU Zhu, et al. Spectral Analysis for Recovering the Earth's Gravity Potential by Satellite Gravity Gradients[J]. Chinese Journal of Geophysics, 2012, 55(5): 1565–1571. DOI:10.6038/j.issn.0001-5733.2012.05.014 |
| [25] | MVLLER J, WERMUT M. GOCE Gradients in Various Reference Frames and Their Accuracies[J]. Advances in Geosciences, 2003(1): 33–38. |
| [26] | AMELINO-CAMELIA G, APLIN K, ARNDT M, et al. GAUGE:The GrAnd Unification and Gravity Explorer[J]. Experimental Astronomy, 2009, 23(2): 549–572. DOI:10.1007/s10686-008-9086-9 |
| [27] | 祝竺, 白彦峥, 段小春, 等. 卫星重力梯度测量中星载重力梯度仪潜在测量精度研究[J]. 地球物理学进展, 2017, 32(2): 559–565. ZHU Zhu, BAI Yanzheng, DUAN Xiaochun, et al. Potential Resolution Research of Space-borne Gravity Gradiometer for Satellite Gravity Gradiometry[J]. Progress in Geophysics, 2017, 32(2): 559–565. DOI:10.6038/pg20170215 |
| [28] | CAI Lin, ZHOU Zebing, HSU H, et al. Analytical Error Analysis for Satellite Gravity Field Determination Based on Two-dimensional Fourier Method[J]. Journal of Geodesy, 2012, 87(5): 417–426. |
| [29] | HU Zhongkun, DUAN Xiaochun, ZHOU Minkang, et al. Simultaneous Differential Measurement of a Magnetic-field Gradient by Atom Interferometry Using Double Fountains[J]. Physical Review A, 2011, 84(1): 013620. DOI:10.1103/PhysRevA.84.013620 |


