2. 华东师范大学空间信息与定位导航上海高校工程研究中心, 上海 200241;
3. 中国科学院大学, 北京 100039
2. Shanghai Research Center for Space Information and GNSS, East China Normal University, Shanghai 200241, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
地面温度变化导致物质热胀冷缩是影响地壳形变的重要因素。温度变化引起的地表形变,最为显著的是周年性变化。近年来,许多学者针对温度变化对GPS台站垂直位移的影响展开研究[1-6]。文献[1]给出了基于半无限空间模型由地表温度变化引起的地壳垂向位移公式,结果表明温度变化引起的地表垂向周年性形变不足0.56 mm。文献[2]在此基础上,利用实测的温度数据,计算温度变化对地壳形变的影响,结果显示温度最大能引起~1.3 mm形变。文献[3]考虑中国区域GPS台站地下基岩以及地上安装GPS天线的水泥墩受温度变化的影响,计算温度变化引起的台站垂向位移最大周年振幅可达2.8 mm。但以上研究都基于半无限空间近似假定,因此水平向的位移恒为零,这显然是对实际地球过于简化的假定的结果。文献[4]将GPS测站垂直方向位移时间序列与温度变化进行相关性分析,结果显示二者高度相关,说明温度变化对测站的周年变化影响确实存在。文献[5]分别考虑了低、中、高纬度的测站温度变化对测站垂向位移的影响,结果显示中纬度地区测站受温度变化影响较大。然而,这些研究也仅限于垂直方向,没有讨论地表温度变化和水平位移的关系。
文献[6-7]研究了半无限空间模型下水平温度梯度场产生的水平方向的热弹性形变。但该模型有很大的局限性。因为实际地球是球形的,在球形地球上一个水平方向温度梯度的存在必然在绕地球表面的反向也存在水平温度梯度,必须计算来自各方面的温度梯度造成的热弹性形变才能得到正确的结果。文献[8]给出了在地心静止的约束下地表温度场引起的球形地球模型的热弹性形变解。该研究为笔者研究地表温度场引起的大陆地表三维周年形变提供了理论基础。随着陆态网络二期工程的建成,260个GPS连续台站广泛分布在中国大陆地区,其高时空分辨率的特性,为研究大陆地壳运动以及相应的地球物理机制提供了海量观测数据。本文利用陆态网络连续观测台站近3 a的GPS观测数据,计算了所有台站的坐标时间序列,分析了陆态网络GPS台站周年位移。为了对比温度变化与其他因素对GPS台站周年位移的影响,本文还联合GRACE重力观测数据,大气、海洋非潮汐、积雪与土壤水等负荷模型资料计算其对中国大陆地表三维周年变化的贡献。同时利用实测温度数据,研究温度变化对陆态网络GPS台站周年位移的影响。
1 方法与数据 1.1 温度数据及热弹性形变计算方法假设一个地心球面坐标系,半径为r=a,余纬为θ,经度为φ。在此坐标系下可以写出由频率为ω的周期性地表热能变化引起的温度传导方程,通过贝塞尔函数jn和球谐系数Ynm的形式,该方程可写成[6-7, 9-10]
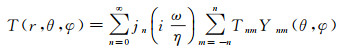 (1)
(1)
为了获取总的地表热弹性形变,需要确定Unm、Vnm同温度球谐系数Tnm之间的关系,在文献[8]的三维热膨胀模型中,垂向和水平向的热弹性形变完整解分别表示为式(2) 的形式
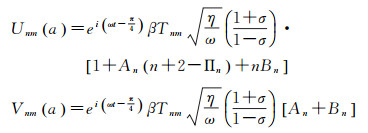 (2)
(2)
本文计算地表热弹性形变所采用的温度数据来自NOAA(http://esrl.noaa.gov),NASA提供的全球地表温度变化数据来源于卫星搭载的中型成像光谱仪MODIS表面排放,其温度数据不包括海平面温度变化数据。本文计算选用处于地面以下0~10 cm的温度数据,数据采样率为天,格网为0.5°×0.5°,时间跨度为2000年1月-2013年12月。根据以上介绍的三维热弹性形变模型,可以计算出由于温度变化引起的地表形变。
1.2 GPS、GRACE以及地球物理模型数据本研究基于陆态网络2011年2月-2013年12月,GPS连续观测台站在ITRF2008框架下的单日坐标序列进行。GPS台站坐标时间序列由上海天文台陆态网络数据处理中心提供,GPS数据的详细处理方法见文献[11]。利用QOCA(Quasi-observation combination analysis)软件(http://gipsy.jpl.nasa.gov/qoca)对测站坐标序列进行分析,通过时间序列拟合获取237个有效的GPS台站坐标季节性变化,本文取其中的周年变化。
本文利用CSR(Center for Space Research)提供的RL-05版本的GRACE 2011.0-2014.0年的60阶重力场球谐系数,计算地表形变。由于这里只使用GRACE前60阶重力系数,存在着高阶截断误差,笔者采用高斯平滑算子进行滤波计算,高斯平滑半径取500 km[12]。由于GRACE测定的二阶球谐系数不够准确,采用SLR(satellite laser ranging)技术得到的C20结果取代GRACE得到的C20系数进行运算[13]。GRACE与GPS处于不同的参考框架,需要加入地心的球谐系数,本文采用文献[14]提供的地心结果。由于GPS监测到的地形变中包含着大气和海洋非潮汐的影响,还需要加上大气和海洋非潮汐GAC模型数据,GAC模型取前60阶重力场球谐系数进行计算。
本文采用NCEP(National Centers for Envi-ronmental Prediction)(http://www.esrl.noaa.gov)提供的气压数据资料,GLDAS(Global Land Data Assimilation System)的Noah模型[15-16],ECCO(Estimating the Circulation & Climate of the Ocean)(http://ecco.jpl.nasa.gov/)非潮汐海洋模型计算大气,积雪和土壤水,海洋非潮汐质量负荷在陆态网络GPS连续台站站点位置的产生的地表形变。以上模型均选用2011.0-2014.0的数据,按照地表质量负荷引起地球弹性形变的格林函数方法计算地面形变[17]。
2 温度变化对大陆地表周年性形变的影响 2.1 中国大陆三维热弹性形变本文基于温度变化引起球形地球地表三维形变模型[8],计算了全球温度变化对中国大陆区域GPS连续台站基岩三维位移的影响(如图 1所示)。计算结果显示,大陆地区与温度相关的热弹性形变周年变化在东向的均值~0.239 mm,北向的均值~0.875 mm,垂向的均值~1.011 mm;温度变化引起的周年形变振幅东向最大的~1.332 mm,北向最大~1.230 mm,垂直~1.990 mm。陆态网络GPS台站中受地表温度变化影响最大的是台站HLAR(海拉尔),东向、北向以及垂向的周年形变振幅矢量和为~2.293 mm;影响最小的是台站是HIYS(永暑礁),东向、北向以及垂向的周年形变振幅矢量和为~0.177 mm。本文的计算结果与文献[8]的结果类似,温度变化引起的热弹性形变周年振幅在高程方向最大~2 mm,水平方向最大~1 mm。文献[3]计算的中国23个基准站受温度变化引起的垂向形变结果显示,周年形变最大的是BJFS,振幅~2.8 mm,最小的KMIN和XIAG,振幅~0.4 mm。与本文的结果存在差异。这是因为文献[3]不仅考虑了温度对地表岩石的影响,还计算了温度变化对地表以上安装GPS天线的水泥墩和金属杆的影响。此外,他们使用的是格网间距为2.5°的全球温度场数据,且只考虑基准站本地的温度变化对台站的影响。而本文考虑全球温度变化在陆态网络GPS连续台站上引起的形变。他们的计算方法是基于半无限空间的近似假定,而本文利用球状地球模型进行计算。因此二者的计算结果存在差异。
|
|
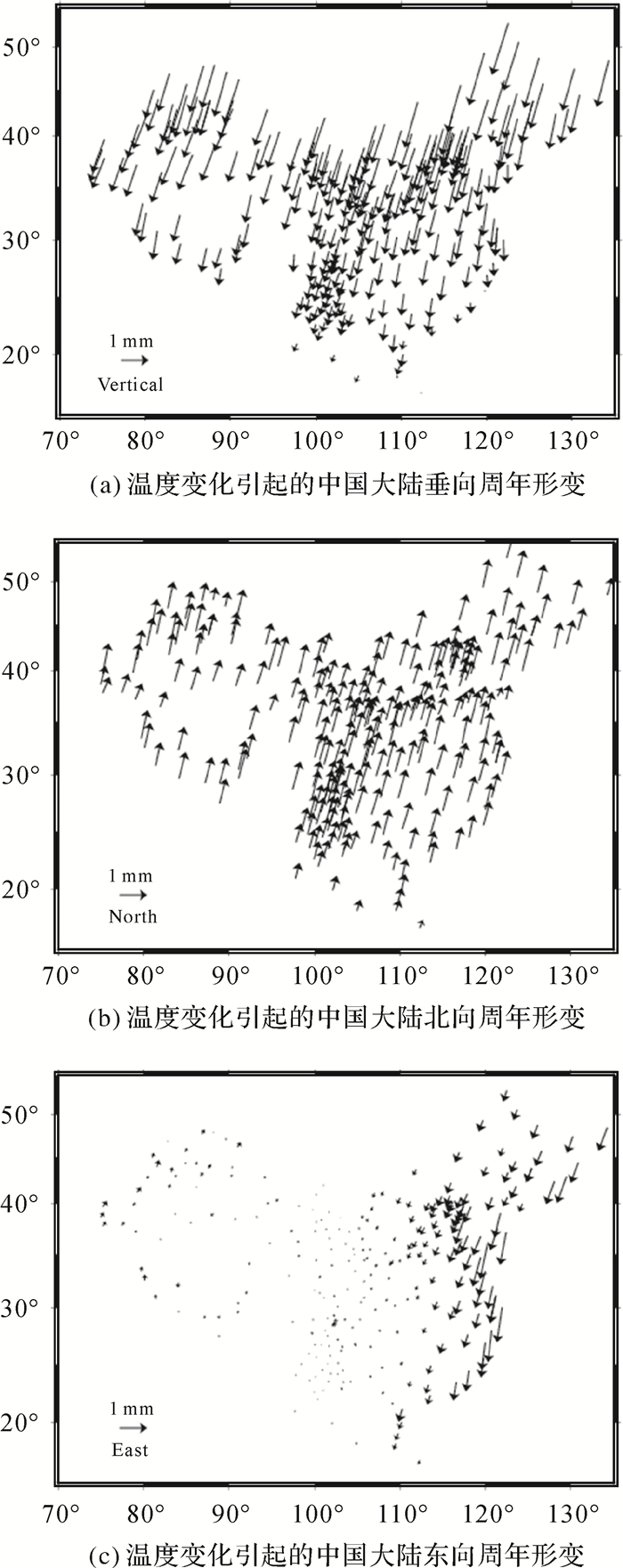
图 1
温度变化引起的中国大陆地表三维周年性形变
Fig. 1
Annual terms of the 260 sites in Chinese mainland for the thermoelastic seasonal deformation
注:周年振幅相位拟合模型:Asin(ω(t-t0)+ϕ),其中A是振幅ω是角频率,ϕ是相位。矢量长度表示地表形变周年性振幅(以下简称振幅),矢量的方向表示地表形变周年变化的初相位ϕ(以下简称相位) (本图为专题内容示意图,不涉及国家版图信息) |
图 1示意东向,北向,垂向3方向温度变化引起的陆态网络GPS台站周年形变。周年振幅相位拟合模型:Asin(ω(t-t0)+ϕ),其中,A是振幅,ω是角频率,ϕ是相位。矢量长度表示地表形变周年性振幅(简称振幅),矢量的方向表示地表形变周年变化的初相位ϕ(简称相位)。温度变化在垂向、北向上影响较大(见图 1(a)、图 1(b)),尤其在中高纬度地区,两个方向周年振幅~1 mm,这是因为温度场的分布在南北向显著。东向在中国东部沿海地区引起的地表形变较大,而在内陆地区引起的地形变较小(见图 1(c))。这是因为本文沿袭文献[3]的计算方案,假定海底和南极格陵兰冰盖底部陆地的温度场变化可以忽略的缘故。这个假定当然还有改进的空间,作为一级近似是可以接受的。由图 1(a)可知,垂直方向上温度变化引起的最大的形变发生在每年的7、8月份,此时正是北半球的夏季温度最高的时候。此时由于温度较高,地面膨胀,引起较为显著的地表形变。北向上,温度变化引起的最大形变在冬季,这是由于冬季南北半球温差显著受温度梯度影响,北半球地表由南向北运动[18]。
温度变化幅度是与纬度高度相关的,由温度变化引起的地表形变亦是。随着纬度的升高,三维地表形变由最小值0.177 mm,增加至2.293 mm。在中高纬度地区(40°N以上),温度变化引起的形变皆>1.5 mm,而在低纬度地区(25°N以下),温度变化引起的地表形变皆<1 mm。因此,温度变化引起的热弹性形变在中国北方影响较大。
2.2 热弹性形变对中国大陆三维地表周年性形变的贡献为了对比温度变化与其他地球物理因素对地表周年位移的影响,笔者首先分析了GPS、GRACE以及物质负荷模型(MODEL)获取的大陆地表三维的周年性形变信号,再探讨热弹性形变对大陆三维周年形变的贡献。
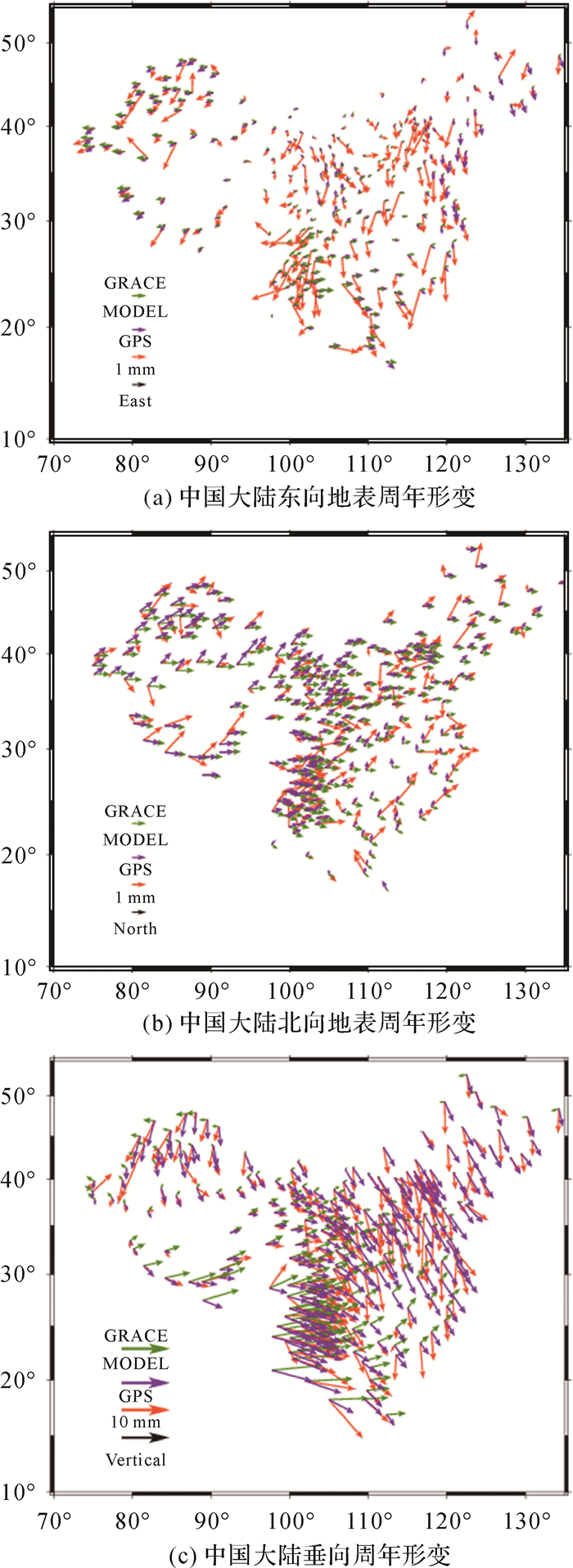
2.2.1 GPS、GRACE、MODEL获取大陆地表形变周年信号图 2为GPS、GRACE、MODEL 3种手段获取的陆态网络GPS台站东向、北向、垂向周年变化分布。垂直方向上,GPS监测到的中国区域地表周年形变平均振幅~5.452 mm(见表 1),其中振幅大于7 mm的形变主要集中在川滇区域。如图 2所示,中国大陆大部分区域垂向形变振幅最大在6月底,相位~270°。而川滇、西藏、青海等地,区域地形变最大值多在3月底,相位~0°。文献[19]等计算陆态网络23个基准站周年形变的结果显示,GPS获取的大陆周年振幅均值~5.98 mm。其中周年活动明显的台站分别是XIAG(9.43 mm),KMIN(9.13 mm),URUM(8.50 mm),LHAS(7.17 mm),这些台站均分布在云南(XIAG、KMIN), 新疆(URUM),西藏(LHAS)。此外,KMIN、XIAG两个台站周年振幅较其他区域存在明显的相位差。因此,本文的计算结果与文献[19]等的计算结果相近。同样,最新的陆态网络GPS观测结果[19]也与本文的计算结果相同。
|
| 图 2 利用GPS、GRACE、MODEL获取的中国大陆地表三维周年性形变 Fig. 2 The annual signals captured by GPS, GRACE and MODEL (此图为专题内容示意图,不涉及国家版图信息) |
| mm | |||||
| 平均振幅 | MODEL | 温度+MODEL | GRACE | 温度+GRACE | GPS |
| 垂向 | 4.313 | 4.941 | 4.567 | 5.216 | 5.452 |
| 北向 | 0.728 | 1.454 | 0.459 | 0.887 | 1.129 |
| 东向 | 0.451 | 0.598 | 0.514 | 0.652 | 1.059 |
将GPS获取的地表形变周年信号(记为GPS),与GRACE监测的质量重新分布反演获得的周年性信号(记为GRACE),以及由大气、海洋非潮汐、积雪与土壤水4种物质负荷引起GPS台站周年变化的综合效应(记为MODEL)进行对比(图 2),可以考察物质负荷部分对周年形变的贡献比例及其和观测结果的差异,便于进一步研究观测技术的系统误差和潜在的产生观测得到的周年形变的贡献源。
在垂直方向上(如图 2(c)),整个大陆东部和北部地区的相位在270°~290°,西藏、青海、川滇区域的相位超前了将近90°,在0°左右。川滇区域的垂直地形变周年振幅比其他区域地形变周年振幅大。总体而言,3种手段获取的地形变周年性变化在垂直方向上具有较好的一致性。GRACE获取的垂向形变振幅均值~4.567 mm,MODEL获取的垂向形变振幅均值~4.313 mm。GPS监测的地面形变垂直方向周年变化振幅偏大,相位与GRACE和MODEL计算的结果有一定差异。分析表明,振幅差在3 mm之内的台站占全部台站的80%。GPS与GRACE相位差值在40°范围内的台站占全部台站的75%,GPS与MODEL相位差值在40°范围内的台站占全部台站的90%。此外,与GPS相比,GRACE与MODEL周年信号吻合度更高。
与垂直方向相比较,水平方向上3种观测手段获取的周年形变信息吻合度较低(图 2(a),(b))。统计显示(表 1),东向上,MODEL给出的地表周年性形变均值~0.451 mm,只占GPS观测的形变~40%;而GRACE在东向周年振幅约占GPS观测的~50%。在北方向,GRACE和MODEL的结果分别是GPS观测结果的~40%、~64%。GPS获取的周年形变结果显示:北方向上,形变达到峰值时在每年的1-2月份;东向周年振幅最值多发生在夏季,约每年的5-6月。GPS获取的周年信号相位与GRACE、MODEL的周年相位差异较大。而与垂直方向相同的是,GRACE与MODEL相位和振幅吻合度较高,而二者与GPS的相位差都超过60°。
无论在垂直方向,还是水平方向,物质负荷能够解释部分GPS监测的周年信号,然而扣除负荷形变后GPS周年项仍有较大残余。这个结果与之前的计算结果一致[1, 18, 21]。目前,国内外针对GPS周年信号的残余项开展了很多研究,如文献[22]利用地下水资料,解释了美国加州地区周年信号异常的台站;文献[23]发现亚马逊河流域未能准确约束的地表水位变化是GPS残余项的重要原因。而这些解释只是针对某些特定区域的局部周年信号。在全球范围内,GPS残余项仍无法给出明确的解释,这极有可能源于观测手段的系统误差、地表负荷模型的模型误差,以及其他非物质负荷的策动源。
2.2.2 热弹性形变对大陆地表年形变的贡献温度场热弹性形变是很重要的非物质负荷形变源。由2.1节可知,热弹性形变是影响大陆地表形变一个不可忽略的因素。GPS直接观测地面形变,包括物质负荷和温度场变化等的贡献。然而,GRACE观测获取的是重力场系数,它仅与地表物质分布有关,温度场引起热弹性效应并不改变地表物质分布,不会改变重力场。因此,GRACE解不受温度变化热弹性效应的影响。物质负荷模型也仅推算物质负荷引起的那一部分形变,与温度变化无关。换言之,温度场热弹性形变信息不包括在GRACE和MODEL反演地表周年信号中,而GPS获取的地表周年信号中有。为了便于比较分析,笔者将温度变化引起的地表周年变化信息叠加到MODEL以及GRACE反演的地表周年信号中(图 3),详细讨论温度变化对GPS台站周年形变的贡献。

|
| 图 3 考虑温度变化前后GRACE和MODEL获取的大陆东向、北向、垂直方向周年性形变 Fig. 3 The annual deformation from GRACE and MODEL with or without the thermoelastic deformation (此图为专题内容示意图,不涉及国家版图信息) |
如图 3所示,考虑温度变化后,3种手段获取的地表形变周年信号相位和振幅上差异明显缩小。数值上(表 1),考虑地表温度变化引起的地表周年性形变后,GPS与GRACE以及MODEL的结果吻合程度更高。此外,笔者按照以下公式
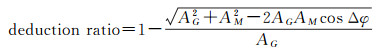 (3)
(3)
计算考虑温度变化后的MODEL(GRACE)计算的周年结果与GPS差别的扣除率。式中,AG、Am代表从GPS观测和MODEL(GRACE)的周年振幅;Δϕ表示GPS周年信号和MODEL(GRACE)相位差。式(3) 所定义的扣除率可能是负的,这意味着GPS的周年振幅经过物质负荷以及温度变化引起的形变修正后变得比原来的振幅大。经过计算得到,温度变化加上MODEL对GPS东向、北向、垂向的周年形变差别的扣除率约占GPS观测的36%、47%、59%;未加上温度变化贡献的MODEL对GPS差别的扣除率占GPS观测的30%、41%、57%。因此,温度变化对MODEL和GPS东向、北向、垂向的周年信号的吻合程度的改进率约为6%、6%、2%。温度变化加上GRACE对GPS北向、东向、垂向的周年形变差别的扣除率约占GPS观测的38%、45%、62%;而单纯的GRACE对GPS差别的扣除率占GPS的22%、40%、47%。因此,温度变化对GRACE和GPS东向、北向、垂向的周年信号的吻合程度的改进率约为16%、5%、15%。
此外,在川滇地区,考虑温度变化后的MODEL结果与GPS的周年信号相位差反而增大了;而GRACE的结果与GPS的周年信号吻合得更好。这表明很有可能有一些大尺度物质迁移在MODEL中缺少而实际上发生了,因而同时被GRACE和GPS观测到了。注意到川滇区域地处青藏高原边缘地区,每年春夏有大量的冰雪融化引起的强烈的地表径流,本文采用的MODEL中不包含地表径流信息,可能导致该项差异。
3 结论地表周年性形变研究是研究地表大规模物质迁移规律的重要方法。GPS、GRACE以及利用物质负荷模型模拟计算地表形变是分析地表三维周年形变的重要手段。通过提高3种手段的精度以及开展3种手段获取地形变的差异性研究,是更好的分析观测技术的系统误差以及潜在的地形变物理机制的重要手段。温度变化引起的热弹性形变也能引起地表的周年运动,但之前基于半无限空间热传导模型的研究,主要研究全球高程方向或者区域水平方向温度变化的影响,低估了温度变化对地表形变的影响。文献[8]推导的均匀热弹性位移解能够估计全球范围内三维地表位移。本文基于此,分析温度变化对陆态网络GPS台站三维位移的影响。
本研究利用全球温度变化数据,结合最新的三维全空间热弹性形变模型,计算中国大陆区域260个GPS台站由温度变化引起的三维周年地表形变。计算结果表明,温度变化对我国陆态网络GPS台站影响较明显,尤其是在25°N以上的区域,能引起~1 mm的周年形变。因此,温度变化引起的热弹性形变在中国区域的影响是不可忽略的,尤其在解释这些区域测站位移变化时,需要考虑温度变化才能更好地解释GPS观测到的形变的物理机制。
扣除已知的物质负荷和温度变化引起的周年形变,GPS观测的周年信号中仍有残余项。这可能源于以下原因:
(1) GPS获取的周年形变信号不仅包括大尺度物质迁移规律、温度变化的影响,还包括区域负载如局部地区河流、谷地及农田灌溉等负荷引起的地表形变[22-24]。而GRACE和MODEL反映的是大尺度物质负荷效应,GRACE对区域信息不敏感,MODEL中也不包括这些影响。
(2) 3种手段各自存在系统误差,如GPS周年信号包含draconitic项[25],地表物质负荷资料时空间分辨率不足,GRACE信号中存在条带误差等。本文的研究结果表明地表温度变化是引起地表季节形变的重要因素。事实上,还有很多因素等待进一步研究,如孔隙弹性变形,将在后面的工作中继续深入探讨。
| [1] | DONG D, FANG P, BOCK Y, et al. Anatomy of Apparent Seasonal Variations from GPS-Derived Site Position Time Series[J]. Journal of Geophysical Research(Solid Earth), 2002, 107(B4): ETG 9–1. |
| [2] | YAN Haoming, CHEN Wu, ZHU Yaozhong, et al. Contributions of Thermal Expansion of Monuments and Nearby Bedrock to Observed GPS Height Changes[J]. Geophysical Research Letters, 2009, 36(13): L13301. DOI:10.1029/2009GL038152 |
| [3] | 闫昊明, 陈武, 朱耀仲, 等. 温度变化对我国GPS台站垂直位移的影响[J]. 地球物理学报, 2010, 53(4): 825–832. YAN Haoming, CHEN Wu, ZHU Yaozhong, et al. Thermal Effects on Vertical Displacement of GPS Stations in China[J]. Chinese Journal of Geophysics, 2010, 53(4): 825–832. |
| [4] | 孙付平, 田亮, 门葆红, 等. GPS测站周年运动与温度变化的相关性研究[J]. 测绘学报, 2012, 41(5): 723–728. SUN Fuping, TIAN Liang, MEN Baohong, et al. Study on Correlation of Temperature Changes with GPS Stations's Non-Linear Movement[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 723–728. |
| [5] | 姜卫平, 王锴华, 邓连生, 等. 热膨胀效应对GNSS基准站垂向位移非线性变化的影响[J]. 测绘学报, 2015, 44(5): 473–480. JIANG Weiping, WANG Kaihua, DENG Liansheng, et al. Impact on Nonlinear Vertical Variation of GNSS Reference Stations Caused by Thermal Expansion[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 473–480. DOI:10.11947/j.AGCS.2015.20140296 |
| [6] | BERGER J. A Note on Thermoelastic Strains and Tilts[J]. Journal of Geophysical Research, 1975, 80(2): 274–277. DOI:10.1029/JB080i002p00274 |
| [7] | BEN-ZION Y, LRARY P. Thermoelastic Strain in a Half-space Covered by Unconsolidated Material[J]. Bulletin of the Seismological Society of America, 1986, 76(5): 1447–1460. |
| [8] | FANG Ming, DONG Danan, HAGER B H. Displacements due to Surface Temperature Variation on a Uniform Elastic Sphere with Its Centre of Mass Stationary[J]. Geophysical Journal, 2014, 196(1): 194–203. DOI:10.1093/gji/ggt335 |
| [9] | XU Xueqing, DONG Danan, FANG Ming, et al. Contributions of Thermoelastic Deformation to Seasonal Variations in GPS Station Position[J]. GPS Solutions, 2017, 21(3): 1265–1274. DOI:10.1007/s10291-017-0609-6 |
| [10] | ALTERMAM Z, JAROSCH H, PEKERIS C L. Oscillations of the Earth[J]. Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Sciences, 1959, 252(1268): 80–95. DOI:10.1098/rspa.1959.0138 |
| [11] | CHEN Junping, WU Bin, HU Xiaogong, et al.SHA:The GNSS Analysis Center at SHAO[C]//China Satellite Navigation Conference (CSNC) 2012 Proceedings.Berlin, Heidelberg:Springer, 2012:213-221. |
| [12] | KING M, MOORE P, CLARKE P, et al. Choice of Optimal Averaging Radii for Temporal Grace Gravity Solutions, a Comparison with GPS and Satellite Altimetry[J]. Geophysical Journal, 2006, 166(1): 1–11. DOI:10.1111/gji.2006.166.issue-1 |
| [13] | CHENG Minkang, TAPLEY B D. Variations in the Earth's Oblateness during the Past 28 Years[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B9): B09402. |
| [14] | SWESON S, CHAMBERS D, WAHR J. Estimating Geocenter Variations from a Combination of Grace and Ocean Model Output[J]. Journal of Geophysical Research:Solid Earth, 2008, 113(B8): B08410. |
| [15] | RODELL M, HOUSER P R, JAMBOR U, et al. The Global Land Data Assimilation System[J]. Bulletin of the American Meteorological Society, 2004, 85(3): 381–394. DOI:10.1175/BAMS-85-3-381 |
| [16] | CHEN Fei, MITCHELL K, SCHAAKE J, et al. Modeling of Land Surface Evaporation by Four Schemes and Comparison with FIFE Observations[J]. Journal of Geophysical Research:Atmospheres, 1996, 101(D3): 7251–7268. DOI:10.1029/95JD02165 |
| [17] | FARRELL W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761–797. DOI:10.1029/RG010i003p00761 |
| [18] | 魏娜, 施闯, 刘经南. 基于GPS和GRACE数据的三维地表形变的比较及地球物理解释[J]. 地球物理学报, 2015, 58(9): 3080–3088. WEI Na, SHI Chuang, LIU Jingnan. Annual Variations of 3-D Surface Displacement Observed by GPS and GRACE Data:A Comparison and Explanation[J]. Chinese Journal of Geophysics, 2015, 58(9): 3080–3088. DOI:10.6038/cjg20150906 |
| [19] | 王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045–1052. WANG Min, SHEN Zhengkang, DONG Danan. Effects of Non-tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045–1052. |
| [20] | GU Yanchao, YUAN Linguo, FAN Dongming, et al. Seasonal Crustal Vertical Deformation Induced by Environmental Mass Loading in Mainland China Derived from GPS, GRACE and Surface Loading Models[J]. Advances in Space Research, 2017, 59(1): 88–102. DOI:10.1016/j.asr.2016.09.008 |
| [21] | RAY J, COLLILIEUX X, REBISCHUNG P, et al.Consistency of Crustal Loading Signals Derived from Models and GPS:Inferences for GPS Positioning Errors[C].American Geophysical Union, Fall Meeting 2011.San Francisco:AGU, 2011. |
| [22] | TAN Weijie, DONG Danan, CHEN Junping, et al. Analysis of Systematic Differences from GPS-measured and GRACE-modeled Deformation in Central Valley, California[J]. Advances in Space Research, 2016, 57(1): 19–29. DOI:10.1016/j.asr.2015.08.034 |
| [23] | BEVIS M, ALSDORF D, KENDRICK E, et al. Seasonal Fluctuations in the Mass of the Amazon River System and Earth's Elastic Response[J]. Geophysical Research Letters, 2005, 32(16): L16308. DOI:10.1029/2005GL023491 |
| [24] | 王林松, 陈超, 邹蓉, 等. 利用GPS与GRACE监测陆地水负荷导致的季节性水平形变:以喜马拉雅山地区为例[J]. 地球物理学报, 2014, 57(6): 1792–1804. WANG Linsong, CHEN Chao, ZOU Rong, et al. Using GPS and GRACE to Detect Seasonal Horizontal Deformation Caused by Loading of Terrestrial Water:A Case Study in Himalayas[J]. Chinese Journal of Geophysics, 2014, 57(6): 1792–1804. DOI:10.6038/cjg20140611 |
| [25] | RAY J, ALTAMIMI Z, COLLILIEUX X, et al. Anomalous Harmonics in the Spectra of GPS Position Estimates[J]. GPS Solutions, 2008, 12(1): 55–64. DOI:10.1007/s10291-007-0067-7 |


