在多代卫星测高和卫星重力计划的支持下,海洋重力场的确定得到了迅速发展。所积累的大量卫星测高数据集,为地球物理学、大地测量学、海洋学的应用提供了丰富的信息源。而海洋区域的垂线偏差作为许多应用的基础数据,正受到越来越多的重视。传统的垂线偏差测定主要采用天文测量和大地测量结合的方法,数据稀疏、测量时间长、动用人力多。而卫星重力和卫星测高等空间技术的发展,对于占全球70%的海洋区域,从根本上改变了传统垂线偏差测定的缺陷,精度和分辨率显著提高,在地球物理和海洋学等方面,发挥着越来越重要的作用。
测定垂线偏差的方法一般可分为直接方法和间接方法[1-4]。天文大地测量方法和GPS方法可以对观测数据的简单计算获得垂线偏差,可称为直接方法;间接方法较多,如重力测量方法、地球重力场模型法、GNSS水准法以及卫星测高反演法等。但是由于海洋的特异性,在海洋上垂线偏差直接测量获取难度较大,通常采用间接方法并通过计算后得到大范围的格网化垂线偏差数据。
利用卫星测高数据计算海洋上的测高垂线偏差,国际上许多学者都进行了卓有成效的工作,主要侧重于间接垂线偏差解算方法,包括文献[5-7]提出的测高垂线偏差计算方法等。文献[5]的方法能计算海洋上测高卫星地面轨迹交叉点的垂线偏差,在交叉点计算的垂线偏差精度较高,但由于不同周期不同观测环境的影响,其空间分布不均匀且比较稀疏,各周期测高卫星地面轨迹在海洋上的有效交叉点数目不尽相同,不能满足反演高分辨率海洋垂线偏差要求;文献[6]的方法能够计算测高卫星逐个采样观测点和交叉点的垂线偏差,垂线偏差的空间分辨率很高,为利用卫星测高数据反演高分辨率海洋重力场提供了条件,但该方法沿轨迹于相邻交叉点之间各观测点处内插在垂直于轨迹方向的垂线偏差,影响了垂线偏差的精度;文献[7]的方法利用测高数据计算各观测点在沿轨迹方向的大地水准面梯度,然后根据大地水准面梯度及其方位角与垂线偏差的关系,在一定搜索区域内根据最小二乘原理计算测高垂线偏差在格网点上的均值。我国学者也利用卫星测高数据计算了中国海的垂线偏差结果[8-9]。综合国内外关于利用卫星测高数据求解垂线偏差的研究成果,由于一次差分法可以削弱径向轨道误差、长波海面地形等类似系统误差的影响,因而是当前由测高数据求解海域垂线偏差的最优方法之一。
1 联合多种测高数据的加权最小二乘方法通过理论分析和实际应用总结,沿轨迹加权最小二乘方法是当前测高垂线偏差计算最理想的方法之一,其理论严密,避免了计算测高卫星地面轨迹交叉点,而且直接利用沿轨迹方向的大地水准面梯度计算垂线偏差子午分量和卯酉分量在格网上的加权平均值,减少了中间计算过程,提高了格网平均垂线偏差的分辨率和精度,垂线偏差含有丰富的重力场高频成分,满足了反演高分辨率、高精度海洋重力场对测高垂线偏差的质量要求[10-12]。
本文采用T/P等6类测高数据进行联合处理,不同测高数据基本信息见表 1。卫星测高的误差源很多,包括大气介质误差、径向轨道误差、仪器偏差等,本文获得的数据是已经对上述误差进行处理后的数据。在进行垂线偏差解算前,对上述数据又做了进一步预处理,包括NAO99b全球海潮模型改正、参考椭球基准的统一与参考框架的转换(统一到T/P测高卫星的参考椭球与参考框架为基准),交叉点平差和共线平差的处理。
| 测高数据 | 时间跨度 | 周期数 | 轨道倾角/(°) | 跨赤道间距/km |
| GeoSat/GM | 1985-03-1986-09 | 25 | 108 | 4 |
| GeoSat/ERM | 1986-10-1989-12 | 68 | 108 | 164 |
| ERS1/ERM | 1992-10-1993-12 1995-03-1996-06 |
26 | 98.5 | 80 |
| ERS1/GM | 1994-04-1995-03 | 10 | 98.5 | 8 |
| T/P | 1993-10-2001-12 | 332 | 66 | 315 |
| ERS2 | 1995-04-2000-12 | 66 | 98.5 | 80 |
移去-恢复方法是卫星测高反演海洋重力场数据处理中一种常用的方法,本文使用分辨率为5′×5′的2160阶EGM2008模型作为参考场进行计算。先将观测到的沿轨迹海面高减去EGM2008模型重力场大地水准面起伏值以及DTU13模型海面地形,得到剩余大地水准面起伏值Nres,将Nres沿卫星轨迹作距离的微分,轨道误差将自动消除。
由式(1) 和式(2) 近似求得剩余大地水准面梯度ε和方位角α。沿着轨迹行进方向,后一个观测点减去前一个观测点。ε和α计算公式如下
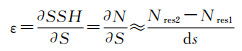 (1)
(1)
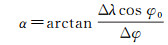 (2)
(2)
式中,ε和α对应位置为沿轨迹连续观测两点之间的中点位置;Δλ=λ2-λ1、Δφ=φ2-φ1、φ0=(φ2+φ1)/2分别为相邻两点的经度差、纬度差以及中间点纬度;ds为相邻两点间的球面距离。
根据观测方程式(3) 得到剩余大地水准面梯度的子午分量ξ和卯酉分量η在格网的平均值
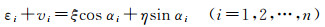 (3)
(3)
式中,n为该格网点及其邻近海域中沿轨迹海面高观测点的数目;vi、αi和εi分别为第i个观测点的残差、方位角和沿轨迹剩余大地水准面梯度。
参照星下点轨迹的空间分辨率以及计算稳定性和可靠性,每个待计算格网点采用的数据为半径3′的周围区域,根据最小二乘的基本原理,由式(4) 解出剩余垂线偏差分量ξ、η在格网1′×1′上的平均值
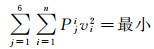 (4)
(4)
根据不同卫星测高的精度并考虑测点到网格中心的距离,采用比较可靠的先验值,设计了观测点距离和测高精度融合的定权方法,如式(5)-(6) 所示
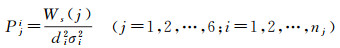 (5)
(5)
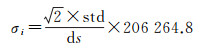 (6)
(6)
式中,j=1, 2, …, 6,分别代表 6颗不同卫星;i=1, 2, …, nj,表示第j颗卫星在半径3′的区域内的测点数。这里di是离散测点到计算网格中心点的距离;σi是大地水准面梯度的标准偏差;std为海面高噪声;Ws(j)为测高卫星定权。6类测高卫星具体定权参数见表 2。
| 测高卫星 | T/P | ERS2 | ERS1/ GM |
ERS1/ ERM |
GeoSat/ GM |
GeoSat/ ERM |
| 定权参数 | 1/2.51 | 1/4.5 | 1/8.6 | 1/6.7 | 1/15.3 | 1/8.0 |
由式(1)-(6) 计算得到剩余垂线偏差后,为了剔除精度不佳的观测值,本文采用3倍中误差理论,剔除对应观测值εi然后重新由剩余的εi观测点数计算剩余垂线偏差,进而恢复重力场模型的垂线偏差。每个待计算格网点垂线偏差计算时搜索半径一样,但不同格网点的搜索区域内测高数据个数以及数据质量存在不同,剔除的观测值比例会有一定差异,总体约0.3%~2%。考虑到海面高一次差分求解过程引入且放大了高频噪声,根据卫星测高数据沿轨迹的分辨率特征,选用滤波半径为18 km的Gaussian低通滤波器对解算的垂线偏差进行滤波,最后得到垂线偏差结果。
垂线偏差计算流程如图 1,其中E代表大地水准面梯度,A代表大地水准面梯度的方位角。

|
| 图 1 格网垂线偏差计算流程图 Fig. 1 Flow chart of vertical deflection grid models |
测高卫星不同, 测高精度也不同,进而导致求解的沿轨迹大地水准面梯度的精度不同。不同测高卫星数据融合时,除了通常考虑的距离因素外,在定权时有必要将距离和测高精度联合考虑。式(1)-(6) 设计的观测点距离和测高精度融合的定权方法,对后续更多测高卫星的有效融合反演海洋重力场具有借鉴意义。
2 基于重力异常的Vening-Meinesz方法这种方法的实质是利用大地水准面上的重力异常求出大地水准面垂线偏差。假如已知全球范围的重力异常,就可按斯托克司方法求得大地水准面上的垂线偏差。Vening Meinesz导出了大地水准面垂线偏差的计算公式[13-15]
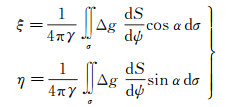 (7)
(7)
式中,ξ、η分别是垂线偏差的子午分量和卯酉分量;γ为全球正常重力平均值;Δg为格网平均重力异常;ψ为计算点到流动点的球面距离;α为计算点到流动点的方位角;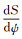
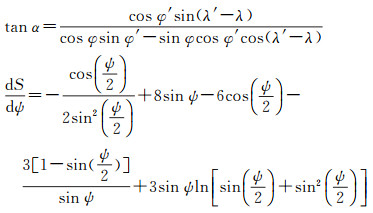
式中,φ、λ为计算点的大地纬度和经度;φ′、λ′为流动点的大地纬度和经度。
文献[16-18]在深入分析和比较二维平面和二维球面FFT算法特点和差异的基础上, 给出了二维球面FFT计算公式的改进形式, 并通过大量的数值计算, 详细讨论了参考场选取、积分球冠半径确定、边缘效应、积分元离散化误差以及计算点奇异积分处理对垂线偏差计算结果的作用和影响。本文在利用Sandwell团队的1′×1′格网重力异常计算垂线偏差时,使用2160阶次的EGM2008重力场模型参考场[19-20],为减弱边界效应,有效格网区域外扩展2°。
需要注意的是,Vening-Meinesz公式计算时需要覆盖全球的重力数据,而这往往难以实现,本文使用的移去-恢复方法能有效削弱这一影响,否则局部区域可能会产生2″~3″的垂线偏差系统差。
3 海洋垂线偏差网格化数值模型精度评估不论是本文构建的垂线偏差的两个数字模型,还是EGM2008模型垂线偏差,由于海洋的特殊性,目前还没有直接可靠的外部精度检核手段,因而这些不同方法得到的垂线偏差精度怎样,这是目前较难回答的问题[21]。对于沿海和有天文大地点的岛屿,可以利用沿海及岛屿已有高精度天文大地点进行该区域计算结果的精度估计,这种精度估计方法是目前最可靠的方法。对于远离海岸和海岛的海域来说,当前很难在其中固定点上进行高精度的天文测量。在目前很难获得其他更为可靠的海洋垂线偏差精度评估手段的前提下,本文采用国际上公认的EGM2008模型的垂线偏差[22]以及文献[23-24]的海洋重力异常作为垂线偏差精度评估的参考。从文献[23-24]全球海洋重力异常数据中截取出本文的西太平洋海域范围重力异常误差数据,结果为标准差4.69 mGal(1 Gal=10-2 m/s2)。根据文献[25-26],垂线偏差误差1″大约对应重力异常5 mGal误差,进而推导由文献[23-24]得到的重力异常经本文解算的垂线偏差误差在1″左右。
为了评估本文计算结果的有效性,将建立的垂线偏差模型与最新模型等结果进行比较。本文作为精度评估的3个垂线偏差结果分别命为:WHIGG(联合多种测高数据的加权最小二乘方法)、EGM2008、Sandwell(基于重力异常的Vening-Meinesz方法)。
为了更好地评估垂线偏差的精度,上述3个垂线偏差模型之间都进行了相互比较,作为例证,这里以WHIGG和EGM2008两个垂线偏差的比较方式进行说明。为了比较WHIGG和EGM2008的垂线偏差的差异,采用了常用的均值、标准偏差和均方根差作为衡量的标准。这里,Δξ=ξWHIGG-ξEGM2008、Δη=ηWHIGG-ηEGM2008,统计各点垂线偏差的差值(Δξ、Δη)的最大值、最小值、平均值、标准差和均方根差。
上述3种垂线偏差模型从图形宏观上而言总体特征相似度很高,从某种程度上也说明3种方式得到的垂线偏差结果从定性上看是合理的、有效的。为了更好地从定量上评判不同区域垂线偏差的精度,这里取2个代表性的区域进行垂线偏差的相互比较:A区(15°N-20°N, 130°E-135°E)、B区(12°N-17°N, 112°E-117°E)。3种垂线偏差在A、B两个区域的相互比较结果见表 3~表 6。
| arcsec | |||||
| 最小值 | 最大值 | 平均值 | 标准差 | 均方根差 | |
| WHIGG-EGM2008 | -3.32 | 2.53 | 0.02 | 0.38 | 0.38 |
| WHIGG-Sandwell | -3.21 | 3.13 | 0.06 | 0.42 | 0.43 |
| Sandwell-EGM2008 | -1.37 | 1.14 | -0.04 | 0.19 | 0.20 |
| arcsec | |||||
| 最小值 | 最大值 | 平均值 | 标准差 | 均方根差 | |
| WHIGG-EGM2008 | -9.01 | 6.47 | -0.02 | 0.99 | 1.00 |
| WHIGG-Sandwell | -8.85 | 6.48 | 0.01 | 1.02 | 1.02 |
| Sandwell-EGM2008 | -1.20 | 1.69 | -0.02 | 0.27 | 0.28 |
| arcsec | |||||
| 最小值 | 最大值 | 平均值 | 标准差 | 均方根差 | |
| WHIGG-EGM2008 | -4.64 | 5.61 | 0.07 | 0.57 | 0.58 |
| WHIGG-Sandwell | -6.88 | 6.25 | 0.10 | 0.75 | 0.76 |
| Sandwell-EGM2008 | -4.01 | 3.59 | -0.02 | 0.40 | 0.41 |
| arcsec | |||||
| 最小值 | 最大值 | 平均值 | 标准差 | 均方根差 | |
| WHIGG-EGM2008 | -13.37 | 12.25 | 0.06 | 1.25 | 1.26 |
| WHIGG-Sandwell | -13.31 | 10.92 | 0.01 | 1.36 | 1.36 |
| Sandwell-EGM2008 | -3.07 | 3.09 | 0.05 | 0.44 | 0.45 |
从表 3-表 6可以看出,总体而言,3种垂线偏差WHIGG、EGM2008、Sandwell的相互比较差异较小,但是在B区的差异性较A区更大,则可能是B区属于南海区域,海底地形复杂,岛屿较密集,对测高数据的质量产生较大影响,因而对垂线偏差的精度和可靠性导致了不稳定。WHIGG-EGM2008在A区垂线偏差均方根差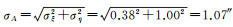

| arcsec | |||
| 区域 | WHIGG-EGM2008 | WHIGG-Sandwell | Sandwell-EGM2008 |
| A区 | 1.07 | 1.11 | 0.34 |
| B区 | 1.39 | 1.56 | 0.61 |
在西太平洋海域,尽管从图形定性看,三者的结果具有很高的一致性,但是通过选择A、B两个区域作定量比较,还是有一定的差异。但是相较而言,A区结果比B区结果更为稳定,与WHIGG相比,Sandwell和EGM2008的结果更为一致,这可能与Sandwell采用的数据源与EGM2008更为一致且更全面有关。但由于没有与天文大地点的实测垂线偏差等数据进行外部检核,表 7的符合度结果不具有完全的精度评估结论,但有一定的参考意义。总体而言,我国西太平洋海域垂线偏差计算精度比较理想,总体相对精度(均方根差)达到±1.56″(见表 7)。
但从表 5-表 6数据看出,南海代表区域B的模型垂线偏差计算精度相比之下较低,究其原因,主要是该区域岛屿众多导致精度不高,这一结果也基本符合实际情况。
在此基础上, 对由A、B区域1′×1′垂线偏差模型分析如下:
(1) A区:远离陆地和岛屿,水深较大,这些因素都有利于测高数据精度的改善。从表 3-表 4以及表 7可见,总体相对精度优于1.1″。
(2) B区:典型特征是岛屿较为密集,比如中沙群岛、黄岩岛、南沙群岛等,同时海底地形复杂,水深变化较大,这些因素对测高数据反演垂线偏差的精度产生了一定影响,从表 5-表 6以及表 7可见,相较A区,系统差变化不大。以均方根差而言,南海区域垂线偏差的相对精度优于1.6″。
(3) 依表 3-表 6,由卫星测高数据解算垂线偏差时,子午方向垂线偏差的精度优于卯酉方向垂线偏差的精度。测高卫星与赤道的轨道倾角都在66°以上,这一轨迹方向明显倾向于子午方向。从理论上来说,靠近子午方向的数据特征更丰富,由大地水准面梯度分解出子午垂线偏差和卯酉垂线偏差时,使得子午方向的垂线偏差精度优于卯酉方向的垂线偏差精度。
4 结语本文采用两种不同方法构建了不同的中国西太平洋海域1′×1′垂线偏差模型,并对其精度进行了初步评估,可以得到以下几点结论:
(1) 本文方法建立的我国西太平洋海域1′×1′垂线偏差(WHIGG模型),与地球重力场EGM2008垂线偏差模型和重力异常反演的垂线偏差模型在两个特征区域精度评估,以及在此基础上的分析结果,表明该模型在不同区域计算任意点垂线偏差的相对精度为:在南海代表海域均方根差优于1.6″,在远海区域均方根差为1.1″,卯酉分量η的均方根差大于子午分量ξ的均方根差,海底地形复杂的南海特征区域的垂线偏差均方根差大于西太平洋中部的均方根差。这一结果表明,本文研究并给出的卫星测高海域垂线偏差计算方法、精度估计方法以及模型的分辨率等,经大规模实际计算的检验,表明它们是正确合理的、可信的。
(2) 由于我国大部海洋区域尤其远海,尽管有一定数量的实测重力数据点,但由于密度和精度都不高,而且由于多种原因较难获取,这对联合多种数据反演并改善垂线偏差的精度造成了一定影响。在南海局部岛屿较多区域附近海域,如果岛上有可供控制拟合的天文大地点,当利用相应地区天文大地垂线偏差及分区二次曲面(或其他)方法进行控制拟合后,可消除部分系统误差,进而进一步提升垂线偏差的精度。目前国内外许多学者在这个领域做了大量的研究,随着卫星测高资料的不断补充和积累、波形重构等数据处理手段的提出和改进,以及宽刈幅技术、多星编队技术等卫星测高新手段的发展,解算海洋垂线偏差的数据源质量会逐步提高[27-29]。
本文在近海测高数据处理、高精度的船测重力融合、岛礁天文大地点垂线偏差的外部检核以及融合更多更新的海量测高数据等方面尽管做了大量研究,但还是存在很多不足,相信随着这些工作的积累,海洋垂线偏差的精度、分辨率和可靠性等会进一步改善。
| [1] | 郭金运, 宋来勇, 常晓涛. 数字天顶摄影仪确定垂线偏差及其精度分析[J]. 武汉大学学报(信息科学版), 2011, 36(9): 1085–1088, 1101. GUO Jinyun, SONG Laiyong, CHANG Xiaotao. Vertical Deflection Measure with Digital Zenith Camera and Accuracy Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1085–1088, 1101. |
| [2] | 彭富清, 夏哲仁. 卫星测高中的垂线偏差法[J]. 海洋测绘, 2004, 24(2): 5–9. PENG Fuqing, XIA Zheren. Vertical Deflection Theorem of Satellite Altimetry[J]. Hydrographic Surveying and Charting, 2004, 24(2): 5–9. |
| [3] | 张永毅, 张兴福. 垂线偏差的确定方法及精度分析[J]. 大地测量与地球动力学, 2016, 36(5): 395–399, 429. ZHANG Yongyi, ZHANG Xingfu. Determination and Accuracy Analysis of Vertical Deflection[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 395–399, 429. |
| [4] | BOYARSKY E A, AFANASIEVA L V, KONESHOV V N. Method to Compute the Vertical Deflection Components[C]//MERTIKAS S. Gravity, Geoid and Earth Observation. Berlin:Springer, 2010:415-420. |
| [5] | SANDWELL D T, SMITH W H F. Global Marine Gravity from Retracked GeoSat and ERS-1 Altimetry:Ridge Segmentation Versus Spreading Rate[J]. Journal of Geophysical Research:Solid Earth, 2009, 114(B1): B01411. |
| [6] | OLGIATI A, BALMINO G, SARRAILH M, et al. Gravity Anomalies from Satellite Altimetry:Comparison between Computation via Geoid Heights and via Deflections of the Vertical[J]. Journal of Geodesy, 1995, 69(4): 252–260. |
| [7] | HWANG C. Inverse Vening Meinesz Formula and Deflection-geoid Formula:Applications to the Predictions of Gravity and Geoid over the South China Sea[J]. Journal of Geodesy, 1998, 72(5): 304–312. DOI:10.1007/s001900050169 |
| [8] | 万剑华, 王莉娟, 范陈清, 等. 联合多卫星测高数据确定中国近海及其邻域垂线偏差[J]. 海洋学研究, 2012, 30(3): 86–91. WAN Jianhua, WANG Lijuan, FAN Chenqing, et al. Determination of Vertical Deflection over China Seas and Their Vicinity from the Multi-satellite Altimetric Data[J]. Journal of Marine Sciences, 2012, 30(3): 86–91. |
| [9] | 邓凯亮, 暴景阳, 章传银, 等. 联合多代卫星测高数据建立中国近海垂线偏差模型[J]. 海洋测绘, 2008, 28(3): 15–17. DENG Kailiang, BAO Jingyang, ZHANG Chuanyin, et al. Determination of Vertical Deflection over China Sea by Combination of Multi-satellite Altimeter Data[J]. Hydrographic Surveying and Charting, 2008, 28(3): 15–17. |
| [10] | 邢乐林, 李建成, 刘晓玲. ENVISAT测高卫星沿轨大地水准面梯度的海洋垂线偏差法研究[J]. 测绘科学, 2006, 31(5): 48–49, 53. XING Lelin, LI Jiancheng, LIU Xiaoling. Study on Ocean Vertical Deflection of EnviSat Satellite Altimetry Along-track Geoid Gradient[J]. Science of Surveying and Mapping, 2006, 31(5): 48–49, 53. |
| [11] | 张胜军, 李建成, 褚永海, 等. 基于CryoSat和Jason1 GM数据的垂线偏差计算与分析[J]. 武汉大学学报(信息科学版), 2015, 40(8): 1012–1017. ZHANG Shengjun, LI Jiancheng, CHU Yonghai, et al. Calculation and Analysis of the Deflection of Vertical Derived from CryoSat and Jason1 GM Data[J]. Geomatics and Information Science of Wuhan University, 2015, 40(8): 1012–1017. |
| [12] | WANG Hubiao, WANG Yong, LU Yang. High Precision Vertical Deflection over China Marginal Sea and Global Sea Derived from Multi-satellite Altimeter[J]. Geo-Spatial Information Science, 2008, 11(4): 289–293. DOI:10.1007/s11806-008-0122-8 |
| [13] | 海斯卡涅W A, 莫里兹H. 物理大地测量学[M]. 北京: 测绘出版社, 1979. HEISKANEN W A, MORITZ H. Physical Geodesy[M]. Beijing: Surveying and Mapping Press, 1979. |
| [14] | 聂琳娟, 超能芳, 金涛勇, 等. 卫星测高反演海洋重力异常的精度分析[J]. 测绘科学, 2016, 41(9): 1–6, 37. NIE Linjuan, CHAO Nengfang, JIN Taoyong, et al. Accuracy Analysis of Marine Gravity Anomaly Inferred by Satellite Altimetry Data[J]. Science of Surveying and Mapping, 2016, 41(9): 1–6, 37. |
| [15] | 黄谟涛, 翟国君, 欧阳永忠, 等. 利用多代卫星测高数据反演海洋重力场[J]. 测绘科学, 2006, 31(6): 37–39. HUANG Motao, ZHAI Guojun, OUYANG Yongzhong, et al. Recovery of Marine Gravity Field Using Integrated Data from Multi-satellite Missions[J]. Science of Surveying and Mapping, 2006, 31(6): 37–39. |
| [16] | 黄谟涛, 翟国君, 管铮, 等. 利用FFT技术计算垂线偏差研究[J]. 武汉测绘科技大学学报, 2000, 25(5): 414–420. HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. Determination of Vertical Deflections Using FFT Technique[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 414–420. |
| [17] | 翟振和, 任红飞, 孙中苗. 重力异常阶方差模型的构建及在扰动场元频谱特征计算中的应用[J]. 测绘学报, 2012, 41(2): 159–164. ZHAI Zhenhe, REN Hongfei, SUN Zhongmiao. Construction of Gravity Anomaly Degree Variance Model and Application in Computation of Spectral Sensitivity of Disturbing Gravity Functions[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 159–164. |
| [18] | 李厚朴, 边少锋. 利用垂线偏差计算大地水准面中央区效应的改进方法[J]. 测绘学报, 2011, 40(6): 730–735. LI Houpu, BIAN Shaofeng. The Improved Method of Calculating the Geoid Innermost Area Effects Using Deflections of the Vertical[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 730–735. |
| [19] | 章传银, 郭春喜, 陈俊勇, 等. EGM 2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283–289. ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283–289. |
| [20] | 齐显峰, 周巍, 崔吉春. EGM2008重力场模型计算中国地区垂线偏差分析[J]. 测绘技术装备, 2011, 13(1): 6–8. QI Xianfeng, ZHOU Wei, CUI Jichun. Analysis of Vertical Deflection in China Area Calculated with EGM2008 Gravity Model[J]. Geomatics Technology and Equipment, 2011, 13(1): 6–8. |
| [21] | 孙凤华, 吴晓平, 张传定. 中国陆海任意点垂线偏差的快速确定及精度分析[J]. 武汉大学学报(信息科学版), 2005, 30(1): 42–46, 50. SUN Fenghua, WU Xiaoping, ZHANG Chuanding. Fast Determination of the Vertical Deflection and Its Precision Analysis of Any Point on the Land and Sea in China[J]. Geomatics and Information Science of Wuhan University, 2005, 30(1): 42–46, 50. |
| [22] | EGM2008 Development Team.Users Handbook[EB/OL]. (2008-02-21).[2016-04-12]. http://earth-info.nga.mil.sixxs.org/GandG/wgs84/gravitymod/egm2008/anomalies_dov.html. |
| [23] | SANDWELL D T, MVLLER R D, SMITH W H, et al. New Global Marine Gravity Model from CryoSat-2 and Jason-1 Reveals Buried Tectonic Structure[J]. Science, 2014, 346(6205): 65–67. DOI:10.1126/science.1258213 |
| [24] | SANDWELL D, GARCIA E, SOOFI K, et al. Toward 1-mGal Accuracy in Global Marine Gravity from CryoSat-2, EnviSat, and Jason-1[J]. The Leading Edge, 2013, 32(8): 892–899. DOI:10.1190/tle32080892.1 |
| [25] | 彭富清, 陈双军, 金群峰. 卫星测高误差对海洋重力场反演的影响[J]. 测绘学报, 2014, 43(4): 337–340. PENG Fuqing, CHEN Shuangjun, JIN Qunfeng. Influence of Altimetry Errors on Marine Geopotential Recovery[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 337–340. |
| [26] | 李洋, 张润宁. 高度计测距精度对沿轨迹重力异常反演的影响[J]. 测绘学报, 2015, 44(4): 363–369. LI Yang, ZHANG Running. Inference of Altimeter Accuracy on Along-track Gravity Anomaly Recovery[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 363–369. DOI:10.11947/j.AGCS.2015.20140022 |
| [27] | 蒋涛, 李建成, 王正涛, 等. 联合Jason-1与GRACE卫星数据研究全球海平面变化[J]. 测绘学报, 2010, 39(2): 135–140. JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. Global Sea Level Variations from Combined Jason-1 and GRACE Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 135–140. |
| [28] | 金涛勇, 李建成, 姜卫平, 等. 基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报, 2011, 40(6): 723–729. JIN Taoyong, LI Jiancheng, JIANG Weiping, et al. The New Generation of Global Mean Sea Surface Height Model Based on Multi-altimetric Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 723–729. |
| [29] | 汪海洪, 罗志才, 杨元德, 等. 基于波形分类的近海卫星测高数据自适应重跟踪方法[J]. 测绘学报, 2012, 41(5): 729–734. WANG Haihong, LUO Zhicai, YANG Yuande, et al. An Adaptive Retracking Method for Coastal Altimeter Data Based on Waveform Classification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 729–734. |



