2. 长安大学, 陕西 西安 710054;
3. 中国科学院国家授时中心, 陕西 西安 710600;
4. 机械工业勘察设计研究院有限公司, 陕西 西安 710043
2. Chang'an University, Xi'an 710054, China;
3. National Time Service Center, Chinese Academy of Sciences, Xi'an 710600, China;
4. China J K Institute of Engineering Investigation and Design, Xi'an 710043, China
太阳和月亮的引潮力作用导致海面周期性的涨落,从而使海底负载发生变化及固体地球产生形变,这一现象称之为海潮负荷效应(ocean tide loading,OTL)[1-6]。研究表明,海潮负荷效应对沿海测站的影响已达厘米至分米量级[2-3, 7-8]。在高精度数据处理中,海潮负荷效应不容忽视,必须通过精确的模型予以扣除。目前发布的多个全球海潮模型,如TPXO72.2010(update of Egbert and Erofeeva(2010))[9];HAMTIDE11A.2011(Taguchietal.2012)[10];EOT11A.2011(update of Savcenko and Bosch(2008))[11],在公海地区精度高,在近海区域精度欠佳[12]。因此,国内外学者寻求利用最新的大地测量手段直接测定海潮作用地壳产生的质量负荷引起的地壳瞬时形变,反演得到海潮负荷位移建模参数(振幅与相位值),使其精度达到或优于模型估计的精度。
目前GPS技术反演海潮负荷位移得到了广泛应用[13]。常用的方法有两种,一种是静态定位方法,另一种是动态定位方法。在GPS精密单点定位(PPP)中增加48个海潮参数(3×2×8=48) 与其他未知参数(如测站坐标、对流层延迟等参数)一同求解称为静态定位方法[8]。该方法未知数过多,易降低估算强度,同时因采取24 h单天解方式,每天只得到一组估计值,将平均化一些海潮信息,使一些分潮波(1/3日潮)信号无法显示出来[14-17]。从高采样率(一般为1~4 h)的坐标时间序列中提取潮波振幅和相位值的方法称为动态方法[17-18]。动态PPP虽可反映每个观测间隔海潮负荷位移的变化和一些振幅较小的分潮波信号,但动态方法的反演精度低于静态方法,目前还未得到深入研究[17, 19, 20]。
本文基于GPS技术监测测站三维位移变化的灵敏度高于监测48个海潮参数的灵敏度这一现实,充分利用静态及动态估计方法的优势,改进了利用GPS静态PPP估计48个海潮参数的方法。提出将三维海潮负荷位移影响作为未知参数直接引入PPP模型中进行实时逐历元估计,可反映每个历元海潮负荷位移的变化,缩小动态时间序列的采样间隔,从而可有效提取各个潮波的振幅与相位值。选取香港连续运行参考站8年的GPS观测数据,采用本文提出的方法,精密测定了12个测站的三维OTL位移的振幅与相位值,比较分析了GPS技术求解的海潮负荷位移振幅值的收敛速度,并以中国近海海潮模型值为参考值,评价海潮负荷位移建模参数估值的精度,通过对比GPS与验潮站两种观测技术的结果及比较GPS海潮负荷位移建模估值与模型值的海潮负荷效应改正效果,得出了一些有益结论。
1 海潮负荷位移建模参数求解的基本原理 1.1 传统的静态PPP海潮负荷位移估计海潮负荷位移是海潮分潮的叠加,如式(1) 所示[2, 13]
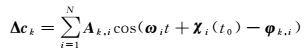 (1)
(1)
式中,Δck(k=1、2、3) 分别为海潮负荷在测站东西、南北和垂直方向的瞬时位移影响;N为叠加的潮波总数;ωi和χi(t0)分别为各个潮波的角速度和天文幅角初相;Ak, i和φk, i分别为每个潮波在k方向上的振幅和格林尼治相位。
在利用GPS技术反演海潮负荷位移参数时,为了方便参数建模,需要将式(1) 展开,并取8个主要潮波(忽略3个长周期潮波的影响,仅考虑8个主要潮波的影响),表达式如下
 (2)
(2)
式中
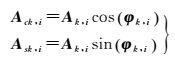 (3)
(3)
Ack, i和Ask, i为待求系数,其中每个潮波3个方向上共有6个未知参数,这样,对于每个测站就有48个海潮参数与测站坐标、接收机钟差、对流层延迟等待求参数。该方法未知数过多,易降低解算强度,同时每天只得到一组海潮估计值,这将平均化一些海潮信息,使得一些分潮波(1/3日潮)信号无法显示出来。
1.2 改进的PPP海潮负荷位移估计基于GPS技术监测测站三维位移变化的灵敏度高于监测48个海潮参数的灵敏度这一基本现实,本文改进了利用GPS PPP估计48个海潮参数的方法,直接逐历元求解三维海潮负荷位移参数。即在PPP求解中,增加三维海潮负荷位移参数,与测站坐标、接收机钟差,对流层延迟,模糊度等参数逐历元一并估计,可有效反映每个历元海潮负荷位移的变化,同时缩小动态时间序列的采样间隔[17]。改进后的海潮负荷位移估计模型如下:
利用IGS精密轨道和精密卫星钟差产品,对单台双频GPS接收机采集的相位和伪距观测值进行无电离层组合PPP定位测定海潮负荷位移,其简化的数学模型如下
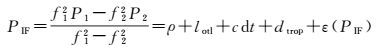 (4)
(4)
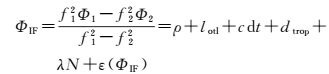 (5)
(5)
式中,PIF为组合码观测值;Pi(i=1、2) 为码观测值;ΦIF为组合载波相位观测值;Φi(i=1、2) 为载波相位观测值;fi(i=1、2) 为信号频率;ρ为站星几何距离;lotl为海潮负荷影响引起的等效距离误差,可分解为测站坐标系的东西E,南北N和垂直U方向位移,它是半日、周日、长周期潮波负荷位移的叠加;c为光速;dt为接收机的钟差;dtrop为对流层延迟误差;λ为波长, N为组合相位模糊度;ε(PIF)、ε(ΦIF)为测量噪声。其他观测误差如地球自转,固体潮,相对论效应,天线相位中心偏差,相位缠绕等采取对应的模型进行改正[21]。
式(4) 和(5) 中,lotl通常可用与测站坐标有关的三维分量形式表示。设在以测站(不考虑海潮负荷影响,用R表示)为原点的测站坐标系下卫星坐标为(Xi, Yi, Zi),考虑海潮负荷影响(用R′表示)坐标为(x, y, z),则对无电离层组合观测中海潮负荷改正前后引起的测站点位估值变化为RR′,(x, y, z)为其北、东、垂直分量;分别定义不考虑海潮影响与考虑其影响的接收机钟差参数估值的大小为δT与δT′;εi、ε′i为观测噪声;RR′(厘米级—分米级)相对于卫星两万多千米高度是个甚微量,因此海潮负荷对计算卫星相对测站的天顶距、方位角的影响可以忽略。令(θi)、(αi)分别为对应卫星的天顶距与方位角, 则可得站星距γi、γ′i的表达式
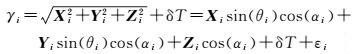 (6)
(6)
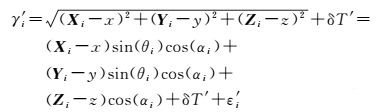 (7)
(7)
式(6) 与式(7) 相减,则海潮负荷对站星间几何距离观测的影响可表达为
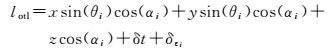 (8)
(8)
式中,δεi=εi-ε′i;δt=δT-δT′为海潮负荷引起的接收机钟差估值的变化。将式(8) 代入到式(4) 和(5),即可采用最小二乘参数估计实时求解海潮负荷位移变化。
最后利用调和分析方法[22]从海潮负荷位移时间序列中提取各潮波的海潮负荷位移振幅与相位值。
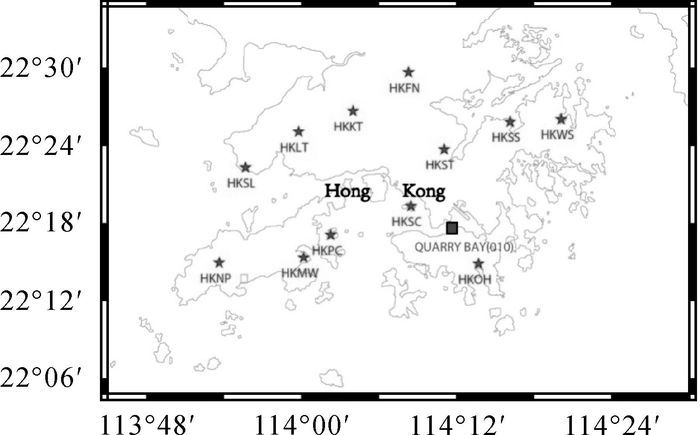
2 结果分析 2.1 数据选取与处理选取中国香港地区12个GPS连续运行参考站(CORS)站2006—2013年共8年的GPS观测数据,测站分布如图 2所示(QUARRY BAY(010) 是与HKSC测站最近的验潮站)。
|
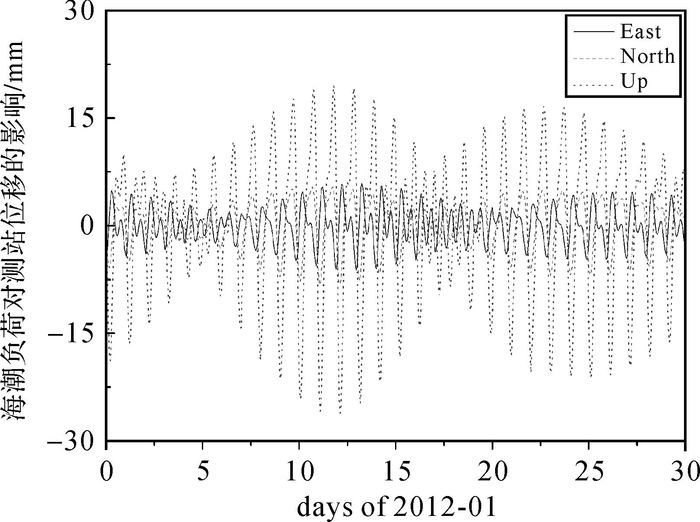
| 图 2 海潮负荷对HKOH测站位移的影响 Fig. 2 The effect of ocean tide loading on displacements of HKOH station |
具体处理策略分3步:
第1步,数据预处理,包括周跳探测和粗差剔除。
第2步,动态PPP求解三维海潮负荷位移时间序列。
第3步,调和分析,8个潮波振幅与相位值的提取。
本文采用的是静态CORS站数据,利用静态数据动态解,并附加先验坐标与历元约束实时逐历元获取海潮负荷位移影响,其中采用课题组研发的精密定位软件包[21],附加先验坐标与历元约束的动态PPP精度平面为4 mm,高程为14 mm[23],而海潮负荷对香港地区平面方向影响为10 mm,高程为25 mm(根据式(1) 及HAMTIDE2011.11A全球海潮模型提供的潮波振幅与相位值,计算海潮负荷对香港地区GPS测站位移的影响,本文以HKOH测站为例,计算海潮负荷对香港地区测站2012年第001—030 d共30 d的位移E、N、U方向的影响[2],如图 2所示)。
根据海潮负荷对测站位移的影响量级(厘米级—分米级)可说明:在本文改进的GPS估计海潮负荷位移算法中,海潮负荷对计算卫星相对测站的天顶距、方位等影响可忽略不计,因此可利用本文的方法获取海潮负荷位移时间序列。
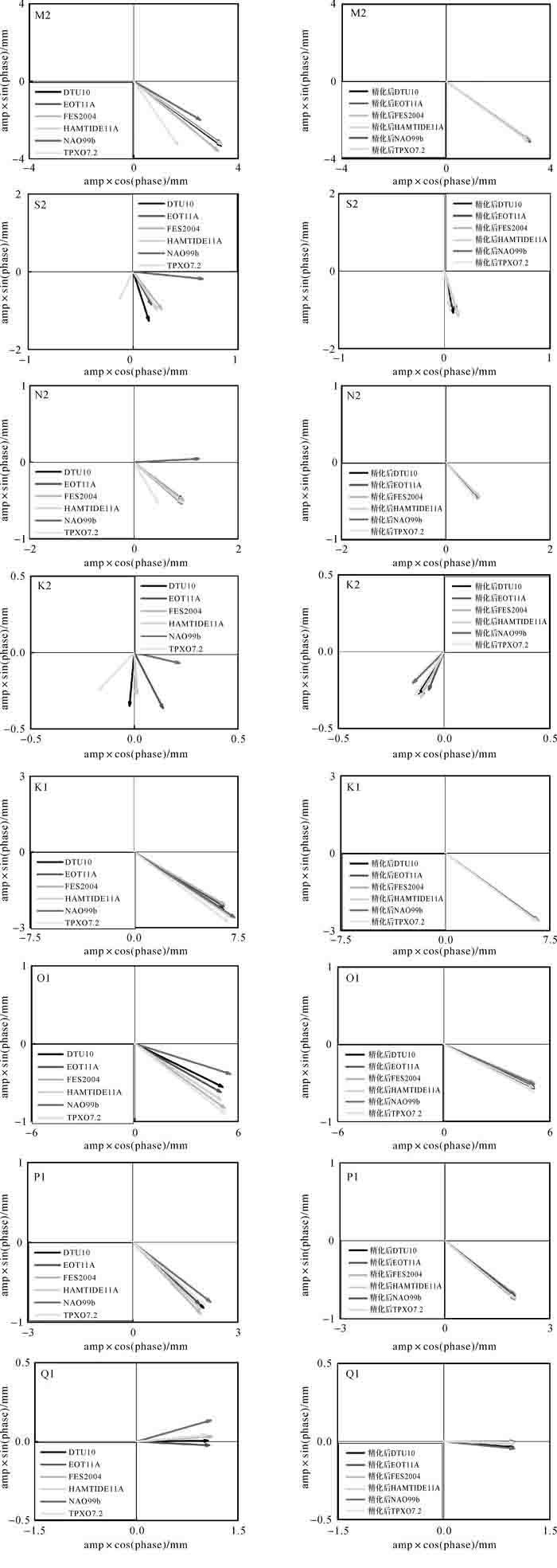
2.2 分潮波矢量对比为了获取香港地区是否受近海潮汐效应的影响及不同全球海潮模型在我国香港区域的适应性,本文首先利用SPOTL软件[24]计算了HAMTIDE11A[10]、EOT11A[11]、TPXO7.2[9]、DTU10[25]、FES2004[26]、NAO99b[27]这6个全球海潮模型在香港12个测站处的海潮负荷位移矢量。海潮模型的基本信息如表 1所示。海潮负荷对测站的影响主要体现在垂直分量,本文以HKKT测站8个潮波的垂直位移矢量为例。图 3列出了不同全球海潮模型的矢量结果,图中结果显示,6个全球海潮模型适应性在香港地区差异较大,尤其是TPXO7.2和NAO99b这两个全球海潮模型,这主要是受近海潮汐效应的影响。
|
| 图 3 HKKT测站8个潮波全球海潮模型精化前后的垂直位移矢量比较图 Fig. 3 Vertical phasors of 8 OTL displacements calculated from six global ocean tide models and six refined global ocean tide models |
本文利用中国近海高精度海潮模型(中国近海海潮模型(OSU.CHINASEA.2010) 为文献[9, 28]利用T/P卫星测高数据及我国台湾海峡、南海、泰国湾沿海的验潮站数据构建的,该模型包含了9个潮波M2、N2、S2、K2、K1、O1、P1、Q1、M4,模型分辨率为2′×2′,覆盖中国整个海域[9, 28])分别替换表 1中6个全球海潮模型的中国近海区域[24],得到精化后的各模型,对应的结果如图 3所示。对比图 3模型精化前后的8个潮波的矢量结果,可明显看出:经中国近海高精度海潮模型精化后的六大海潮模型结果一致,且中国近海海潮模型对香港区域11个CORS站均有相同的改善效果。可以看出:中国近海模型可改善不同全球海潮模型在我国香港地区的适应性。因此本文选择中国近海海潮模型作为参考值,评价海潮负荷位移建模参数估值的精度。
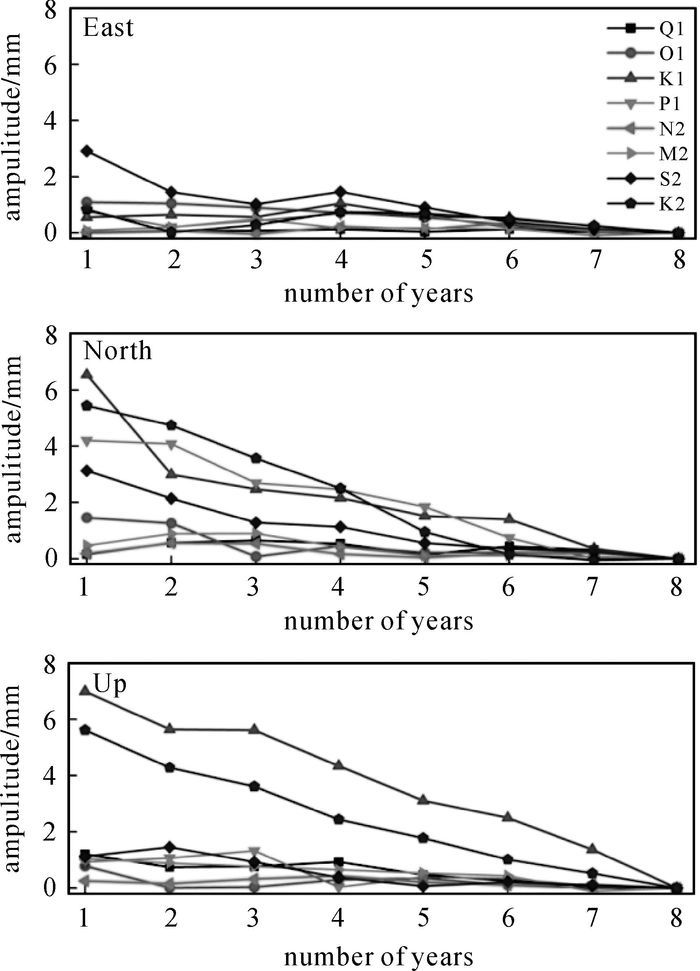
2.3 GPS海潮负荷位移振幅收敛性分析及与传统方法的收敛性比较为了分析GPS PPP提取测站的海潮负荷位移参数分别与观测时间的关系,图 4给出了HKKT测站随观测时间的增加,PPP海潮负荷位移振幅值和最终估计振幅值之间的差异。
|
| 图 4 GPS PPP提取HKKT测站海潮负荷位移参数的收敛性 Fig. 4 Convergence of the OTLD amplitude estimates of HKKT site |
由图 4中各潮波的收敛情况可看出:在东西方向,各潮波均在4~5年后趋于稳定值(波动小于1 mm);在南北方向,各潮波均在6~7年后趋于稳定值;在垂直方向,除K1与K2潮波在8年内未趋于稳定,其他潮波均在4~5年趋于稳定值。
传统方法(文献[13])中各潮波的收敛情况,在东西和南北方向上各潮波在6年左右趋于稳定值,在垂直方向上除K1与K2潮波在8年内未趋于稳定,其他潮波均在6年左右趋于稳定值。将本文各潮波的收敛情况与传统方法进行比较,发现本文各潮波的收敛情况与传统方法大体一致,且本文改进的方法可有效加速K1潮波在东西方向上的收敛,进一步说明本文方法的可靠性与先进性。
2.4 GPS PPP海潮负荷位移建模参数估值与中国近海海潮模型比较本文以中国近海海潮模型提供的潮波参数作为参考,采用均方根误差(root mean square(RMS)misfit)评价各个潮波海潮负荷位移建模参数估值的精度。对于各个潮波j,坐标分量k,所有测n=1、2、…、n站的GPS PPP估值与模型值之间的均方根误差可用式(9) 计算
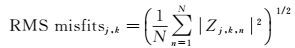 (9)
(9)
式中
 (10)
(10)
式中,LGPS、Lmodel为振幅;gGPS、gmodel为格林尼治相位。
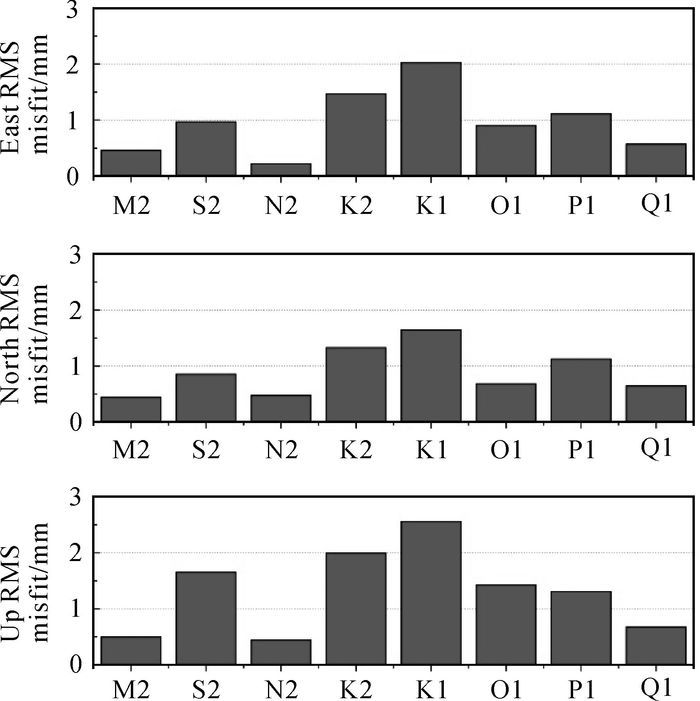
图 5给出了GPS海潮负荷位移建模参数估值相对于中国近海海潮模型的均方根误差。综合GPS海潮负荷位移估值东、北及垂直3个方向的均方根误差可得出:在水平方向,除K1潮波外,其他潮波的均方根误差均小于1.5 mm。在垂直方向,S2、K2和K1潮波的均方根大于其他潮波的均方根误差(1.5 mm)。
|
| 图 5 GPS海潮负荷位移建模参数估值相对于中国近海海潮模型的均方根误差 Fig. 5 RMS misfits between the GPS derived OTL displacement estimates and the osu.chinasea.2010 |
综合各潮波的均方根误差结果,可得出结论:GPS PPP海潮负荷位移建模参数估值与中国近海海潮模型之间的差异主要体现在S2、K2和K1潮波。其中与测站有关的多路径误差目前无法精确地靠模型扣除,且多路径效应的重复周期与K2潮波较接近,从而会影响K2潮波精度。卫星星座的重复周期与K1潮波一致,卫星轨道误差会影响K1潮波精度。与此同时S2潮波是与太阳有关的潮波,K2和K1是恒星日潮波,与太阳有关的电离层、对流层延迟、每日的温度变化等因素均会影响K2、K1与S2潮波精度,因此S2、K2和K1潮波的精度主要是受GPS观测技术中未建模的系统误差影响。
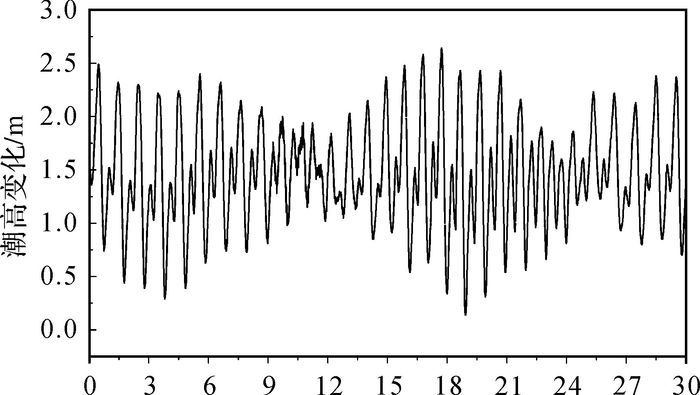
2.5 与验潮站结果比较为了进一步验证本文动态PPP估计的海潮负荷位移建模参数的准确性,选取香港区域离HKSC测站最近的验潮站QUARRY BAY(010),位置如图 1中所示,获取该验潮站2014年一年的潮高数据(http://www.psmsl.org/data/obtaining), 2014年1月的时间序列如图 6所示。利用本文建立的一次多项式模型从潮高数据的时间序列提取8个主要潮波的参数,再利用双线性插值法计算不同海潮模型在验潮站处的潮波参数值。最后计算HKSC测站的GPS海潮负荷位移建模参数估值相对不同海潮模型之间U方向的均方根误差,及验潮站数据反演的潮波参数值分别与模型之间的均方根误差,结果列于表 2、表 3及图 7。
|
| 图 1 香港地区GPS连续运行参考站分布图 Fig. 1 Distribution of the 12 GPS sites in Hong Kong |
|
| 图 6 验潮站2014年1月的潮高数据时间序列(以1 h为间隔) Fig. 6 The time series of tide gauge data spanning from 2008 to 2014(the interval is on hour) |
| mm | |||||||
| 潮波 | 模型 | ||||||
| OSU.CHINASEA.2010 | HAMTIDE2011.11A | EOT11A | FES2004 | DTU10 | TPXO7.2 | NAO99b | |
| M2 | 0.49 | 0.52 | 0.59 | 0.62 | 0.57 | 0.95 | 1.03 |
| S2 | 1.66 | 1.83 | 1.79 | 1.87 | 1.82 | 1.98 | 1.99 |
| N2 | 0.45 | 0.5 | 0.48 | 0.49 | 0.51 | 0.61 | 0.72 |
| K2 | 2.03 | 2.12 | 2.17 | 2.14 | 2.18 | 2.32 | 2.29 |
| K1 | 2.4 | 2.71 | 2.77 | 2.83 | 2.82 | 2.91 | 2.97 |
| O1 | 1.33 | 1.27 | 1.62 | 1.53 | 1.69 | 1.71 | 1.83 |
| P1 | 1.31 | 1.29 | 1.41 | 1.42 | 1.4 | 1.62 | 1.58 |
| Q1 | 0.68 | 0.65 | 0.67 | 0.59 | 0.62 | 0.67 | 0.66 |
| 总和 | 10.35 | 10.89 | 11.5 | 11.49 | 11.61 | 12.77 | 13.07 |
| cm | |||||||
| 潮波 | 模型 | ||||||
| OSU.CHINASEA.2010 | HAMTIDE2011.11A | EOT11A | FES2004 | DTU10 | TPXO7.2 | NAO99b | |
| M2 | 7.82 | 7.93 | 9.03 | 9.21 | 9.27 | 10.46 | 10.37 |
| S2 | 4.17 | 4.32 | 5.02 | 4.89 | 4.97 | 5.72 | 5.31 |
| N2 | 2.07 | 2.18 | 3.02 | 2.78 | 2.94 | 3.53 | 3.57 |
| K2 | 1.39 | 1.57 | 1.87 | 1.79 | 1.92 | 2.01 | 2.32 |
| K1 | 7.72 | 7.83 | 8.27 | 8.36 | 8.52 | 9.02 | 9.16 |
| O1 | 5.19 | 5.27 | 5.97 | 5.99 | 6.02 | 6.21 | 6.33 |
| P1 | 3.21 | 3.23 | 3.67 | 3.53 | 3.60 | 3.73 | 3.80 |
| Q1 | 1.17 | 1.36 | 1.42 | 1.47 | 1.43 | 1.51 | 1.57 |
| 总和 | 32.74 | 33.69 | 38.27 | 38.02 | 38.67 | 42.69 | 42.43 |

|
| 图 7 HKSC测站及验潮站与不同模型的均方根误差 Fig. 7 RMS misfits for HKSC and tide gauge stations |
分析表 2、表 4,同时比较图 7的(a)、(b)发现,HKSC测站及与它最近的验潮站结果均与中国近海海潮模型及HAMTIDE2011.11A模型符合的较好,其次是EOT11A、FES2004、DTU10全球海潮模型,与TPXO7.2及NAO99b全球海潮模型符合的较差,说明GPS PPP海潮负荷位移建模参数估值与验潮站的结论是一致的,进一步证明了GPS PPP求解海潮负荷位移建模参数方法的可靠性与准确性。
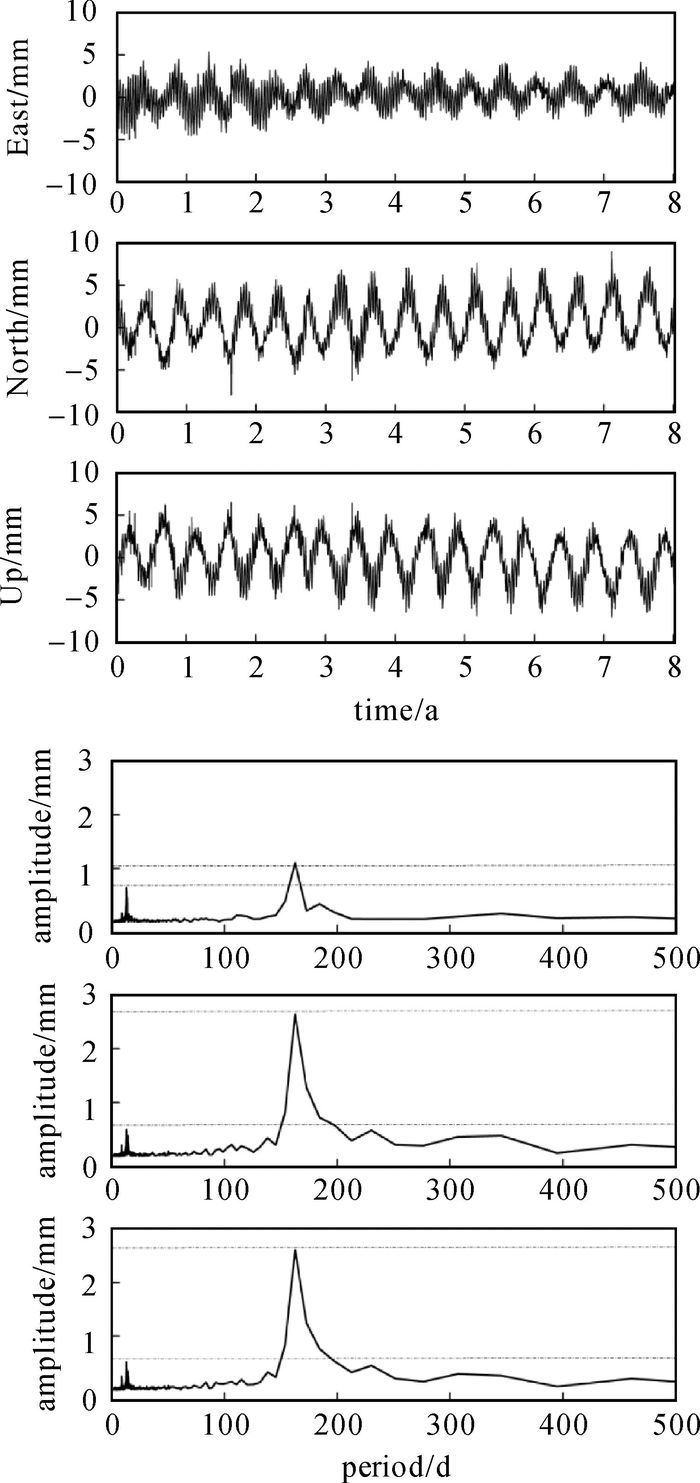
2.6 海潮负荷效应改正效果比较为了探究GPS PPP海潮负荷位移建模参数估值是否可进行海潮负荷效应改正,本文采用11个主要潮波进行海潮负荷效应改正,其中Mf,Mm,Ssa 3个长周期潮波由HAMTIDE2011.11A全球海潮模型提供,另外8个主要潮波分别来自GPS PPP海潮负荷位移建模参数估值与HAMTIDE2011.11A全球海潮模型,分别求解各测站对应的PPP单天解坐标时间序列:① GPS海潮负荷位移建模参数估值改正后的坐标时间序列;② 模型提供海潮负荷位移参数改正后的坐标时间序列。对坐标时间序列1与2作差,可消除两种坐标时间序列的共性误差,得到的仅是两种潮波参数改正效果的差异,并对其进行快速傅里叶变换(FFT)。以HKKT测站为例,图 8展示了两种不同坐标时间序列在ENU方向的差异,及其对应的振幅谱图。
|
| 图 8 HKKT测站GPS时间序列与模型时间序列在ENU方向的差异及其对应的振幅谱图 Fig. 8 Effects of different OTL-displacement corrections on daily GPS position time series of the HKKT site |
图 8结果显示:两种坐标时间序列在E方向的差异较小,变化在3 mm内,而在N、U方向的差异较E方向的大,变化在5 mm内。结合振幅谱图可明显看出,E、N、U方向的坐标时间序列差异均能探测出明显的半年周期信号,振幅分别为1.2 mm、2.6 mm、2.7 mm;同时3个方向还探测出微弱的两周周期信号,振幅均在0.5 mm左右。
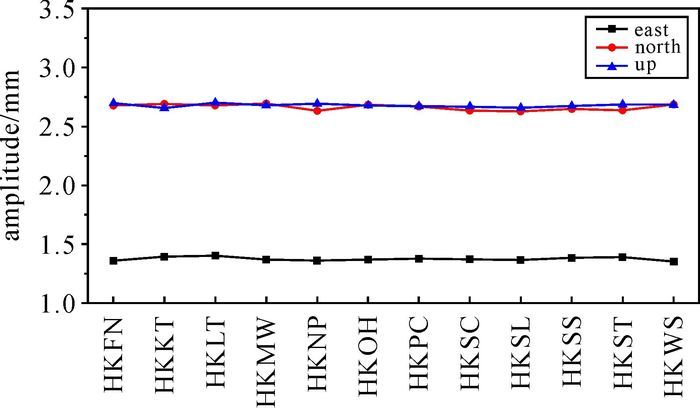
图 9提供了12个测站对应的两种坐标时间序列的差异均存在明显的半周年信号,E、N、U方向的振幅分别约为1.1 mm、2.7 mm、2.7 mm。本文已加入了长周期潮波改正,这可能是GPS海潮负荷位移参数估值受多种未建模误差影响,如多路径、卫星轨道这种周期性的影响。潮波结果包含了各种误差的影响,在进行海潮负荷效应改正时,可减弱其他误差的影响。因此若采用GPS PPP估计的8个主要潮波的振幅与相位值替换全球海潮模型中对应的潮波值,进行海潮负荷效应改正,可减弱GPS长时间序列中的半周年信号。
|
| 图 9 12个测站不同海潮负荷位移改正差异中存在的明显半周年信号ENU方向的振幅 Fig. 9 The amplitudes of the long period signal at the 12 CORS sites |
3 结论
本文基于GPS技术监测测站三维位移变化的灵敏度高于48个海潮参数这一基本思想,改进了利用GPS静态PPP技术估计48个海潮参数的方法,直接逐历元求解三维海潮负荷位移变化,再通过调和分析提取了8个主要潮波的振幅与相位值。利用香港连续运行参考站8年的GPS观测数据,采用本文方法计算了12个测站的三维海潮负荷位移建模参数。通过结果比较分析得出以下结论:
(1) 本文估计海潮负荷位移建模参数的方法较传统方法可有效加速K1潮波在东西方向上的收敛。
(2) 除S2、K2和K1潮波外,其他潮波GPS海潮负荷位移建模参数估值与中国近海海潮模型之间的均方根误差均小于1.5 mm。
(3) GPS与验潮站数据反演结果均与中国近海海潮模型及HAMTIDE2011.11A全球海潮模型符合较好,验证了GPS PPP反演海潮负荷位移的有效性。
(4) 采用GPS PPP估计的8个主要潮波的振幅与相位值替换全球海潮模型中对应的潮波值,进行海潮负荷效应改正,可减弱GPS长时间序列中的半周年信号影响。
| [1] | 周江存, 孙和平. 用东海和南海潮汐资料修正全球海潮模型对中国及邻区重力场负荷计算的影响[J]. 地震学报, 2005, 27(3): 332–338. ZHOU Jiangcun, SUN Heping. Influence of the Modified Global Ocean Tide Model with Local Tides of East and South China Seas on Load Gravity in China and Its Neighbor Area[J]. Acta Seismologica Sinica, 2005, 27(3): 332–338. |
| [2] | 赵红, 张勤, 黄观文, 等. 基于不同海潮模型研究海潮负荷对GPS精密定位的影响[J]. 大地测量与测量动力学, 2012, 32(5): 108–112. ZHAO Hong, ZHANG Qin, HUANG Guanwen, et al. Effect of Ocean Tide Loading on GPS Precise Positioning Based on Different Ocean Tide Models[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 108–112. |
| [3] | 张杰, 李斐, 楼益栋, 等. 海潮负荷对GPS精密定位的影响[J]. 武汉大学学报(信息科学版), 2013, 38(12): 1400–1404. ZHANG Jie, LI Fei, LOU Yidong, et al. Ocean Tide Loading Effect on GPS Precise Positioning[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1400–1404. |
| [4] | 刘友文, 姜卫平, 鄂栋臣, 等. 南极国际GPS联测的海潮位移改正[J]. 武汉大学学报(信息科学版), 2007, 32(10): 899–901. LIU Youwen, JIANG Weiping, E Dongchen, et al. Ocean Loading Tides Corrections of GPS Stations in Antarctica[J]. Geomatics and Information Science of Wuhan University, 2007, 32(10): 899–901. |
| [5] | 周旭华, 吴斌, 李军. 高精度大地测量中的海潮位移改正[J]. 测绘学报, 2001, 30(4): 327–330. ZHOU Xuhua, WU Bin, LI Jun. Ocean Tide Displacement Corrections in High Precision Geodesy[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 327–330. |
| [6] | 赵红, 张勤, 瞿伟, 等. 联合中国近海海潮模型与全球海潮模型分析海潮负荷对GPS精密定位的影响[J]. 武汉大学学报(信息科学版), 2016, 41(6): 765–771. ZHAO Hong, ZHANG Qin, QU Wei, et al. Effect Analysis of Ocean Tide Loading on GPS Precise Positioning Combining High Precision Local Tide Model with Global Ocean Tide Model[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 765–771. |
| [7] | VERGNOLLE M, BOUIN M N, MOREL L, et al. GPS Estimates of Ocean Tide Loading in NW-France:Determination of Ocean Tide Loading Constituents and Comparison with a Recent Ocean Tide Model[J]. Geophysical Journal International, 2008, 173(2): 444–458. DOI:10.1111/gji.2008.173.issue-2 |
| [8] | PENNA N T, CLARKE P J, BOS M S, et al. Ocean Tide Loading Displacements in Western Europe:1. Validation of Kinematic GPS Estimates[J]. Journal of Geophysical Research:Solid Earth, 2015, 120(9): 6523–6539. DOI:10.1002/2015JB011882 |
| [9] | EGBERT G D, EROFEEVA S Y. Efficient Inverse Modeling of Barotropic Ocean Tides[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 183–204. DOI:10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2 |
| [10] | TAGUCHI E, STAMMER D, ZAHEL W. Ocean Tides Obtained by Data Assimilative Hamtide Model[J/OL]. 2012. http://icdc.zmaw.de/hamtide.html?&L=l. |
| [11] | SAVCENKO R, BOSCH W. EOT08a:Empirical Ocean Tide Model from Multi-mission Satellite Altimetry[R]. Report No. 81. München:Deutsches Geodätisches Forschungs Institute (DGFI), 2008. |
| [12] | ALLINSON C R, CLARKE P J, EDWARDS S J, et al. Stability of Direct GPS Estimates of Ocean Tide Loading[J]. Geophysical Research Letters, 2004, 31(15): L15603. DOI:10.1029/2004GL020588 |
| [13] | YUAN Linguo, DING Xiaoli, SUN Heping, et al. Determination of Ocean Tide Loading Displacements in Hong Kong Using GPS Technique[J]. Science China Earth Sciences, 2010, 53(7): 993–1007. DOI:10.1007/s11430-010-3076-2 |
| [14] | SCHENEWERK M S, MARSHALL J, DILLINGER W. Vertical Ocean-loading Deformations Derived from a Global GPS Network[J]. Journal of the Geodetic Society of Japan, 2001, 47(1): 237–242. |
| [15] | VERGNOLLE M, BOUIN M N, MOREL L, et al. GPS Estimates of Ocean Tide Loading in NW-France:Determination of Ocean Tide Loading Constituents and Comparison with a Recent Ocean Tide Model[J]. Geophysical Journal International, 2008, 173(2): 444–458. DOI:10.1111/gji.2008.173.issue-2 |
| [16] | YUAN Linguo, CHAO B F, DING Xiaoli, et al. The Tidal Displacement Field at Earth's Surface Determined Using Global GPS Observations[J]. Journal of Geophysical Research:Solid Earth, 2013, 118(5): 2618–2632. DOI:10.1002/jgrb.50159 |
| [17] | 张小红, 马兰, 李盼. 利用动态PPP技术确定海潮负荷位移[J]. 测绘学报, 2016, 45(6): 631–638. ZHANG Xiaohong, MA Lan, LI Pan. Determination of Ocean Tide Loading Displacements Using Kinematic PPP[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 631–638. DOI:10.11947/j.AGCS.2016.20150327 |
| [18] | FARRELL W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761–797. DOI:10.1029/RG010i003p00761 |
| [19] | KHAN S A, TSCHERNING C C. Determination of Semi-diurnal Ocean Tide Loading Constituents Using GPS in Alaska[J]. Geophysical Research Letters, 2001, 28(11): 2249–2252. DOI:10.1029/2000GL011890 |
| [20] | MELACHROINOS S A, BIANCALE R, LLUBES M, et al. Ocean Tide Loading (OTL) Displacements from Global and Local Grids:Comparisons to GPS Estimates over the Shelf of Brittany, France[J]. Journal of Geodesy, 2008, 82(6): 357–371. DOI:10.1007/s00190-007-0185-6 |
| [21] | TU Rui, GE Maorong, ZHANG Hongping, et al. The Realization and Convergence Analysis of Combined PPP Based on Raw Observation[J]. Advances in Space Research, 2013, 52(1): 211–221. DOI:10.1016/j.asr.2013.03.005 |
| [22] | PAWLOWICZ R, BEARDSLEY B, LENTZ S. Classical Tidal Harmonic Analysis Including Error Estimates in MATLAB Using T_TIDE[J]. Computers & Geosciences, 2002, 28(8): 929–937. |
| [23] | 臧楠. BDS/GNSS精密单点定位算法研究[D]. 西安: 长安大学, 2015. ZANG Nan. A Study on the Algorithms of BDS and GNSS Precise Point Positioning[D]. Xi'an:Chang'an University, 2015. |
| [24] | AGNEW D C. NLOADF:A Program for Computing Ocean-tide Loading[J]. Journal of Geophysical Research, 1997, 102(B3): 5109–5110. DOI:10.1029/96JB03458 |
| [25] | CHENG Yongcun, ANDERSEN O B. Multimission Empirical Ocean Tide Modeling for Shallow Waters and Polar Seas[J]. Journal of Geophysical Research, 2011, 116(C11): C11001. DOI:10.1029/2011JC007172 |
| [26] | LYARD F, LEFEVRE F, LETELLIER T, et al. Modelling the Global Ocean Tides:Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394–415. DOI:10.1007/s10236-006-0086-x |
| [27] | MATSUMOTO K, TAKANEZAWA T, OOE M. Ocean Tide Models Developed by Assimilating TOPEX/POSEIDON Altimeter Data into Hydrodynamical Model:A Global Model and a Regional Model Around Japan[J]. Journal of Oceanography, 2000, 56(5): 567–581. DOI:10.1023/A:1011157212596 |
| [28] | 赵大江, 郭春喜, 张世娟, 等. 中国沿海不同海潮模型的倾斜负荷分析[J]. 大地测量学与地球动力学, 2015, 35(1): 34–39. ZHAO Dajiang, GUO Chunxi, ZHANG Shijuan, et al. Analysis of Tilt Loading with Different Ocean Tide Models in Coastal Areas of China[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 34–39. |



