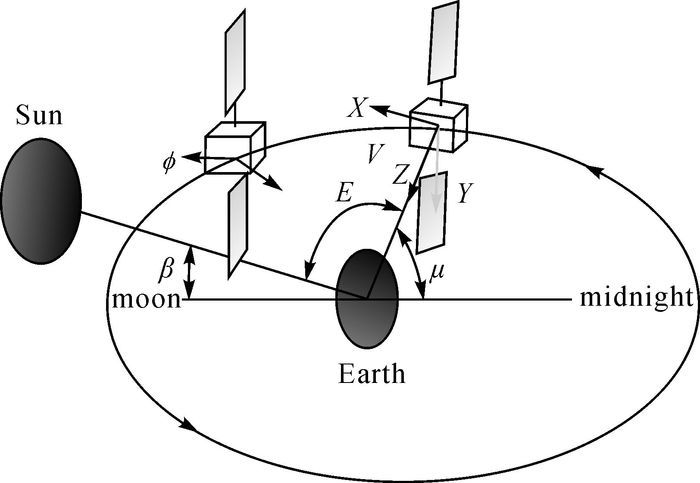
导航卫星在运行时要满足两个要求:① 为保证卫星信号有效传输到地面,卫星天线需指向地心;② 卫星太阳帆板尽量以最大面积面向太阳而获得更多太阳能。同时星固坐标系Z轴定义为卫星天线至地心方向, Y轴平行于太阳帆板, X轴始终指向或者背向太阳并与Y、Z轴组成右手的空间坐标系[1]。星固系在惯性系中的空间指向描述了卫星的飞行姿态,为了使卫星姿态满足这样的要求,需要在卫星运行中不断调整卫星偏航角φ,即如图 1所示的星固坐标系X轴与卫星速度V的夹角,这种卫星姿态的控制模式称为动偏。卫星偏航姿态异常有两个原因:一是当卫星运行至近日点或者远日点时,卫星航偏角发生近180°的剧烈转变,由于受卫星硬件的限制,航偏角速率无法达到理论航偏角速率,从而产生持续几分钟至数小时的卫星姿态异常,称为正午和子夜机动[2];二是卫星进入地影后,无法跟踪太阳的位置,星固坐标系的X轴无法正确指向太阳,卫星姿态将产生异常[3]。不合适的卫星姿态模型从两个方面影响高精度定位:① 引起相位缠绕和天线相位中心偏差(phase center offset, PCO)等几何型误差改正出现偏差;② 影响在卫星定轨时非保守力的计算,导致卫星轨道精度降低以及影响IGS联合钟差产品[4]。国内外学者对以GPS系统为代表的动偏姿态控制模式进行了系统研究,文献[5]提出GYM95模型,文献[6]基于GYM95模型进一步提出了针对GPS BLOCK IIR卫星的姿态模型,文献[7-8]针对GPS卫星姿态异常对动态PPP影响进行系统分析并给出相应的处理策略等。
|
| 图 1 卫星偏航姿态示意图 Fig. 1 The yaw-attitude control law of satellite |
我国北斗卫星导航系统姿态控制方式与国外导航系统不同,GEO卫星全时段采用零偏姿态控制,此时星固系X轴与卫星速度方向一致,即卫星偏航角φ=0。北斗IGSO和MEO卫星姿态控制采用”动-零-动”姿态模式控制,在太阳与卫星轨道面夹角较小时卫星姿态控制模式发生改变,一年发生两次姿态控制模式转变,零偏模式将持续8 d左右[9]。目前许多学者通过估计北斗卫星天线相位中心偏差的动态变化以估计北斗卫星的姿态, 并系统分析了北斗卫星不同偏航姿态和姿态转换期间对精密定轨的影响等[10-13],但目前在北斗PPP的处理中北斗卫星经常采用名义姿态计算相位缠绕和天线相位中心偏差,忽略或不考虑北斗卫星在零偏期间特殊的姿态改正问题[14-16]。因此,本文拟分析在北斗卫星零偏期间采用不同的姿态改正策略对天线相位中心偏差和相位缠绕改正计算以及PPP参数估计的影响。
1 BDS卫星姿态模型以及相关误差计算 1.1 GNSS卫星名义姿态计算动偏模式下卫星的太阳能帆板总是正对着太阳,即星固系Y轴总是平行于卫星的太阳帆板,则动偏模式下星固系坐标轴在地固系的指向(ex, ey, ez)可由式(1) 确定
 (1)
(1)
式(1) 中,rsat表示卫星在地固系下的位置矢量;rsun表示太阳在地固系下位置矢量。
或者采用式(2) 计算卫星偏航角φ。式(2) 中β、u分别是太阳高度角以及卫星轨道角;a tan 2(*)是FORTRAN语言中反正切函数。然后再将卫星速度绝对单位矢量v绕Z轴逆时针旋转φ,即得到星固坐标系X轴指向,进而确定动偏模式下星固系在ITRF中的指向。
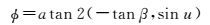 (2)
(2)
北斗GEO卫星全时段采用零偏姿态控制模式,北斗IGSO和MEO卫星姿态采用动偏和零偏相互转换的模式,当在太阳高度角|β|接近4°且名义姿态接近与实际偏航姿态接近时,IGSO卫星和MEO卫星姿态控制模式发生改变[17]。考虑到北斗卫星姿态转换时刻还与卫星轨道角、具体控制策略等复杂因素有关,且武汉大学分析中心已提供北斗卫星姿态产品,本文将利用武汉大学分析中心提供的北斗IGSO和GEO姿态产品判断北斗卫星姿态处于零偏的时间,在此期间可以通过式(3) 或令卫星偏航角φ=0以确定星固坐标系在ITRF中坐标轴的正确指向。
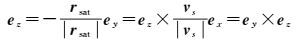 (3)
(3)
设BDS卫星天线相位中心在星固系中的偏差为Xpco, Xsa、Xsc分别为卫星天线和质心在惯性坐标系中的位置。卫星天线相位中心偏差对PPP的最直接影响是使测距产生偏差,可根据式(4) 进行卫星天线PCO的改正,将卫星质心改正到相位中心。
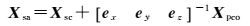 (4)
(4)
相位缠绕在PPP中是不可忽略的一项误差,设e′x、e′y、e′z是测站地平坐标系的坐标轴在地固系中指向的单位矢量;k是卫星至接收机中在地固系的单位矢量;d和d′是定义在卫星端和接收机端的偶极矢量;i、i-1分别表是当前历元和上一个历元。接收机端的天线旋转产生的相位缠绕被接收机钟差所吸收,则卫星端相位缠绕ΔΦi采用以下公式[18]计算
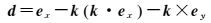 (5)
(5)
 (6)
(6)
 (7)
(7)
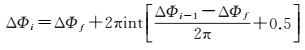 (8)
(8)
在针对北斗PPP研究中,经常采用名义姿态计算相位缠绕和卫星PCO改正,而忽略在北斗卫星零偏期间特殊的姿态改正问题。但由式(4) 和式(5) 可知,只有正确确定了BDS星固系X轴的指向或者BDS卫星姿态,用户才可正确进行相位缠绕和卫星PCO的改正计算,而错误的姿态模型将影响上述误差的改正计算,进而影响PPP解算精度。
2 基于不同姿态模型数据处理分析本文基于武汉大学分析中心提供的北斗卫星精密轨道钟差产品以及姿态产品,利用多个MGEX站的观测数据采用PPP传统无电离层组合模型进行解算[19]。所选测站信息如表 1所示,观测数据采样率为30 s,以MGEX提供的坐标参考值为真值,BDS天线相位中心改正采用ESA/ESOC模型[20-21],卫星截止高度角设为7°,忽略接收机端天线相位中心偏差改正。设计不同试验分析用户在不同卫星姿态改正策略下实施相位缠绕和卫星PCO改正对动静态PPP参数估计的影响(strategy1:处于动偏姿态模式的北斗卫星采用名义姿态,处于零偏姿态模式的北斗卫星使用纯零偏姿态改正;strategy2:所有北斗卫星采用名义姿态)。
| 测站 | 纬度 | 经度 | 天线类型 |
| GMSD | 30.6°N | 131.0°E | TRM59800.00 SCIS |
| CUTO | 32.0°S | 115.9°E | TRM59800.00 SCIS |
| JFNG | 30.5°N | 114.5°E | TRM59800.00 NONE |
| NNOR | 31.0°S | 116.2°E | SEPCHOKE_MC NONE |
| SEYG | 4.7°S | 55.5°E | TRM59800.00 NONE |
| KARR | 20.9°S | 117.1°E | TRM59800.00 NONE |
| POHN | 6.9°N | 158.2°E | TRM59800.00 NONE |
2.1 不同姿态模型下的北斗动态PPP精度分析
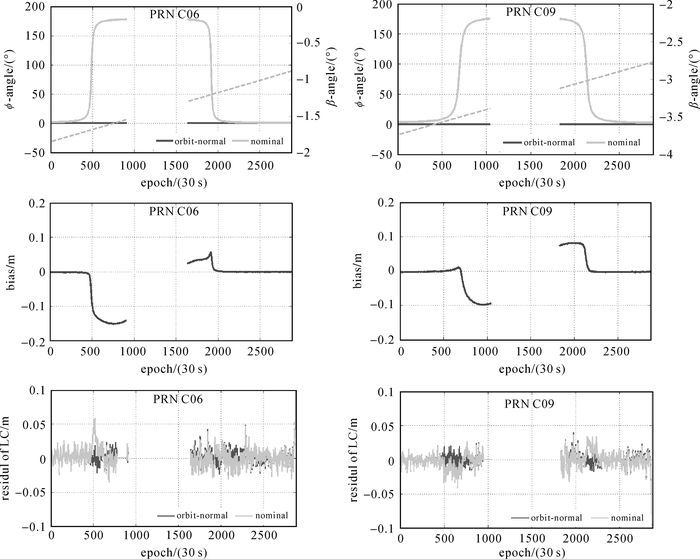
首先分析北斗卫星处于零偏期间时,不同姿态模型差异对相位缠绕和卫星PCO改正以及动态PPP参数估计的具体影响。选取2016年DOY93 d JFNG测站的观测数据, 其中GEO卫星和IGSO卫星的C06和C09一直处于零偏模式。为了突显IGSO卫星采用不同的姿态模型对PPP的影响,本试验将GEO卫星统一采用零偏姿态。图 2给出了在DOY93 d JFNG测站观测到的C06和C09卫星采用不同姿态模型(零偏姿态:orbit-normal;名义姿态:nominal)对相位缠绕和PCO改正的综合影响(bias)以及对LC载波组合观测值残差的影响。由图 2可知,卫星名义姿态接近于零偏姿态时,对相位缠绕和PCO改正的综合影响以及载波观测值残差的影响较小。当名义姿态与零偏姿态差异变大时,对相位缠绕和卫星PCO改正的综合影响逐渐变大,影响最大可超过15 cm,对滤波后载波相位观测值残差影响最大可达6 cm,这在高精度PPP定位中都是不可忽略的。图 3给出相应于图 2的JFNG站动态PPP解算位置误差示意图,当C06和C09卫星名义姿态与零偏姿态相差超过20°以后,动态PPP位置参数差异逐渐明显。由于错误的姿态模型对定位结果的持续影响,在部分时刻平面位置差异可达20~30 cm,天顶方向差异可达40~50 cm。此外,从图 3发现,最后15 min的坐标解算出现了较大偏差,这是由于在程序解算时采用连续两天的北斗精密轨道,而目前北斗精密轨道存在着明显的跨天不连续现象,使得内插的轨道精度降低进而影响定位结果[22]。
|
| 图 2 C06、C09卫星姿态变化以及对相位缠绕和天线相位中心偏差总影响、观测值残差变化 Fig. 2 Variation of C06 and C09 satellite attitude and the influence of the phase windup and phase center offset of the antenna, and the change of the residual value |

|
| 图 3 JFNG站(DOY93) 的动态PPP位置解算误差示意(标识有C06、C09的下划线短线分别表示C06、C09卫星名义姿态与零偏姿态差异大于20°时期) Fig. 3 ositioning error of JFNG station (DOY93) dynamic PPP(the underlines marked CO6, C09, respectively, represent an epoch that the difference between the C06, C09 satellite nominal attitude and the normal attitude is greater than 20°) |
为了进一步统计北斗卫星不同姿态改正策略对动态PPP定位结果的影响,选取在2015年DOY355—361期间7个MGEX站的观测数据,在此期间除了GEO卫星姿态处于零偏外,BDS卫星C11、C12(MEO)以及C08(IGSO)姿态也处于零偏模式。图 4给出了JFNG等7个MGEX站在此期间分别采用strategy1和strategy2策略进行相位缠绕等误差改正时的动态PPP定位误差统计结果。从图 4(左)可知,与strategy2策略相比,基于strategy1策略的动态PPP位置参数N、E、U收敛后的定位精度RMS分别提高53.2%、54.2%、39.3%,图 4(右)给出7个测站的定位结果具体提高幅度,通过图 4可知E方向相比N、U方向的定位精度提高程度稍大。因此,用户在此期间应使用零偏姿态进行相位缠绕和卫星天线偏差的改正计算,避免使用错误的姿态模型。
|
| 图 4 GEO/IGSO/MEO卫星零偏期间不同姿态改正策略动态PPP的RMS统计 Fig. 4 Positioning RMS of dynamic PPP in different attitude model during orbit-normal of GEO/MEO/IGSO satellite in different attitude correction strategy |
2.2 不同姿态模型下的北斗静态PPP精度分析
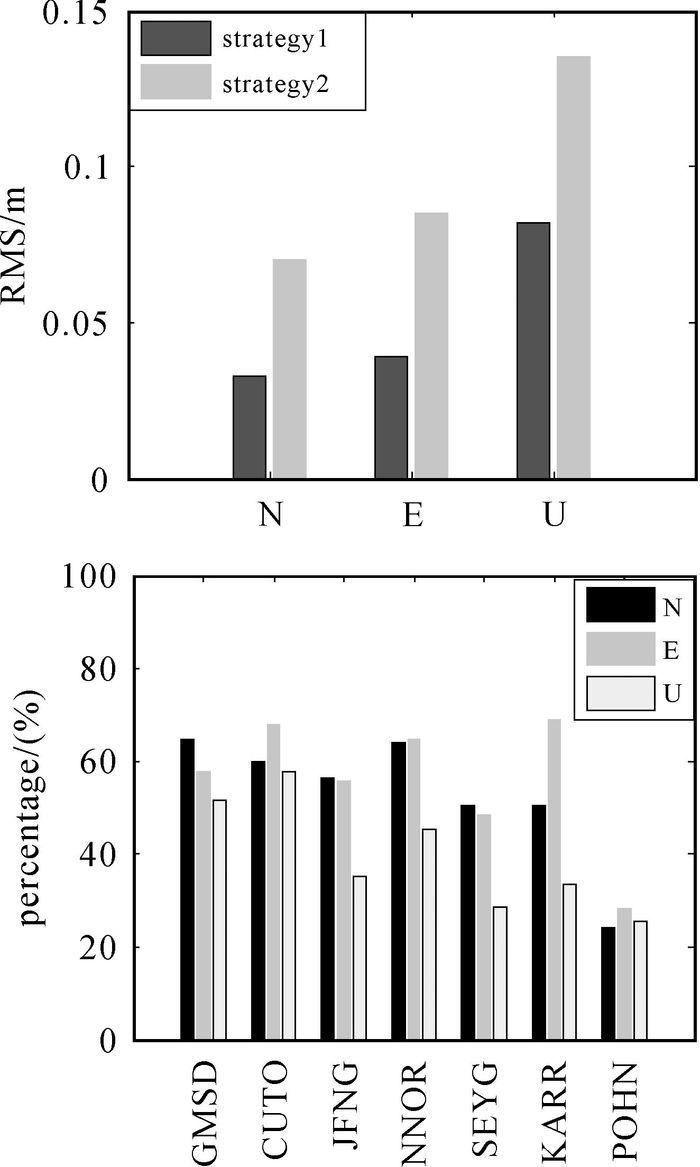
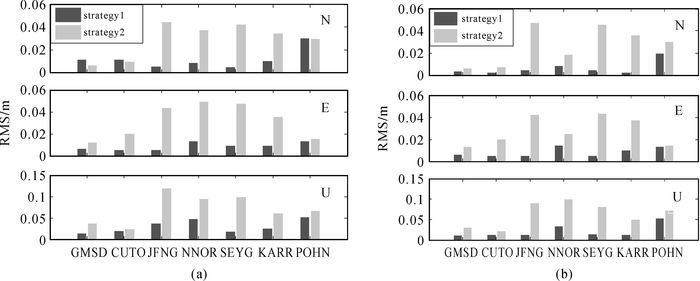
图 5(a)给出了2015年DOY355—361期间GMSD等7个MGEX站在不同姿态改正策略下静态PPP解算的N、E、U方向位置参数的RMS统计结果,图 5(b)给出了此期间7个MGEX站在不同姿态改正策略下静态PPP解算的N、E、U位置参数的点位重复精度STD统计结果。从图 5可知,与strategy 2策略相比,基于strategy 1策略静态PPP解算的N、E、U位置参数收敛后的点位重复精度STD和E、U方向的定位精度RMS整体得到了改善, N方向RMS在GMSD、CUTO、POHN测站略有降低(相差不超过5 mm)。基于strategy 1策略静态PPP解算的水平方向RMS和STD基本优于1 cm,高程方向RMS基本优于3 cm,最大不超过5 cm,STD平均优于2 cm。
|
| 图 5 不同姿态改正策略的静态PPP的定位结果统计 Fig. 5 Positioning RMS and STD of static PPP in different attitude strategies |
表 2是各站BDS PPP估计的天顶对流层延迟与IGS公布的对流层产品的比较结果,由于在该期间IGS未提供CUTO、SEYG的对流层产品,因而对剩余5个测站连续7 d的对流层天顶延迟进行统计。从表 2可知,与strategy 2策略相比,基于strategy 1策略的静态PPP天顶对流层延迟估计精度得到了改善,精度优于2 cm。
| GMSD | JFNG | NNOR | KARR | POHN | |
| strategy1 | 0.018 | 0.019 | 0.014 | 0.018 | 0.016 |
| strategy2 | 0.024 | 0.027 | 0.024 | 0.028 | 0.027 |
3 结论
本文通过分析不同姿态改正策略对相位缠绕等误差改正以及BDS PPP参数估计的影响得出以下结论:
(1) 在北斗卫星零偏期间,采用名义姿态导致星固坐标系X坐标轴指向出现偏差,进而影响卫星PCO和相位缠绕改正计算。基于仿动态PPP试验,名义姿态与零偏姿态相差超过20°时,卫星PCO和相位缠绕的改正计算差异逐渐明显,最大超过15 cm。对动态PPP位置参数的影响部分时刻平面位置达20~30 cm,高程方向达40~50 cm左右。
(2) 根据多个MGEX站的观测数据进行BDS仿动态PPP试验,针对处于零偏时期的BDS卫星采用纯零偏姿态改正后N、E、U方向的估计精度与采用名义姿态相比,可分别提高53.2%、54.2%、39.3%。
(3) 相比于采用名义姿态改正卫星天线偏差和相位缠绕的误差计算,针对处于零偏时期的BDS卫星采用纯零偏姿态,静态PPP的N、E、U位置参数解算精度可平均提高61.0%、72.3%、58.4%,天顶对流层延迟估计精度提高33.0%。因此,用户在此期间应采用零偏姿态改正相位缠绕等误差,避免使用名义姿态。
| [1] | LICHTEN S M, BORDER J S. Strategies for High-precision Global Positioning System Orbit Determination[J]. Journal of Geophysical Research:Solid Earth, 1987, 92(B12): 12751–12762. DOI:10.1029/JB092iB12p12751 |
| [2] | 范曹明, 王胜利, 欧吉坤. GPS/BDS卫星姿态异常对PPP相位缠绕的影响及其改正模型[J]. 测绘学报, 2016, 45(10): 1165–1170. FAN Caoming, WANG Shengli, OU Jikun. The Impact of Yaw Attitude of Eclipsing GPS/BDS Satellites on Phase Wind-up Solutions for PPP and Its Correction Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1165–1170. DOI:10.11947/j.AGCS.2016.20160126 |
| [3] | 毛悦, 宋小勇, 贾小林, 等. 北斗导航卫星地影状态分析[J]. 测绘学报, 2014, 43(4): 353–359. MAO Yue, SONG Xiaoyong, JIA Xiaolin, et al. Earth Eclipse Status Analysis of BeiDou Navigation Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 353–359. DOI:10.13485/j.cnki.11-2089.2014.0053 |
| [4] | MONTENBRUCK O, SCHMID R, MERCIER F, et al. GNSS Satellite Geometry and Attitude Model[J]. Advances in Space Research, 2015, 56(6): 1015–1029. DOI:10.1016/j.asr.2015.06.019 |
| [5] | BAR-SEVER Y E. A New Model for GPS Yaw Attitude[J]. Journal of Geodesy, 1996, 70(11): 714–723. DOI:10.1007/BF00867149 |
| [6] | KOUBA J. A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1): 1–12. DOI:10.1007/s10291-008-0092-1 |
| [7] | LOU Yidong, ZHENG Fu, GU Shengfeng, et al. The Impact of Non-nominal Yaw Attitudes of GPS Satellites on Kinematic PPP Solutions and Their Mitigation Strategies[J]. Journal of Navigation, 2015, 68(4): 718–734. DOI:10.1017/S0373463315000041 |
| [8] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Yaw Attitude of Eclipsing GPS Satellites and Its Impact on Solutions from Precise Point Positioning[J]. Chinese Science Bulletin, 2010, 55(32): 3687–3693. DOI:10.1007/s11434-010-4130-3 |
| [9] | WANG Wei, CHEN Gucang, GUO Shuren, et al. A Study on the BeiDou IGSO/MEO Satellite Orbit Determination and Prediction of the Different Yaw Control Mode[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin:Springer, 2013:31-40. |
| [10] | GUO Jing, ZHAO Qile, GENG Tao, et al. Precise Orbit Determination for Compass IGSO Satellites During Yaw Maneuvers[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin:Springer, 2013:41-53. |
| [11] | ZHU Jun, CHEN Jianrong, ZENG Guang, et al. Precise Orbit Determination for BeiDou Satellites During Eclipse Seasons[C]//China Satellite Navigation Conference (CSNC) 2014 Proceedings:Volume Ⅲ. Berlin:Springer, 2014:3-14. |
| [12] | 彭汉兵, 杨元喜, 王刚, 等. 星蚀期北斗卫星轨道性能分析——SLR检核结果[J]. 测绘学报, 2016, 45(6): 639–645. PENG Hanbing, YANG Yuanxi, WANG Gang, et al. Performance Analysis of BDS Satellite Orbits during Eclipse Periods:Results of Satellite Laser Ranging Validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 639–645. DOI:10.11947/j.AGCS.2016.20150637 |
| [13] | DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy, 2015, 89(10): 1005–1018. DOI:10.1007/s00190-015-0829-x |
| [14] | 丁赫, 孙付平, 李亚萍, 等. BDS/GPS/GLONASS组合精密单点定位模型及性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 303–307. DING He, SUN Fuping, LI Yaping, et al. Modeling and Performance Analysis of Combined BDS/GPS/GLONASS Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 303–307. |
| [15] | ZHAO X, WANG S, LIU C, et al. Assessing the Performance of Multi-GNSS Precise Point Positioning in Asia-Pacific Region[J]. Survey Review, 2017, 49(354): 186–196. DOI:10.1080/00396265.2016.1151576 |
| [16] | 朱永兴, 冯来平, 贾小林, 等. 北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377–383. ZHU Yongxing, FENG Laiping, JIA Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377–383. DOI:10.11947/j.AGCS.2015.20140082 |
| [17] | 郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014. GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan:Wuhan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm |
| [18] | 范磊. GPS/BDS精密单点定位算法及其应用研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2014. FAN Lei. Study on the Algorithm and Application of Precise Point Positioning Using GPS and BDS[D]. Wuhan:Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2014. |
| [19] | 叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002. YE Shirong. GPS Precise Point Positioning by Undifferenced Phase Observation[D]. Wuhan:Wuhan University, 2002. |
| [20] | DILSSNER F, SPRINGER T, SCHÖNEMANN E, et al. Estimation of Satellite Antenna Phase Center Corrections for BeiDou[C]//IGS Network, Data and Analysis Center Workshop. Pasadena, California:ESA, 2014. |
| [21] | 黄观文, 张睿, 张勤, 等. BDS卫星天线相位中心改正模型比较[J]. 大地测量与地球动力学, 2015, 35(4): 658–661. HUANG Guanwen, ZHANG Rui, ZHANG Qin, et al. Comparison and Analysis of Different Models of Antenna Phase Center Correction of BDS Satellites[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 658–661. |
| [22] | GUO Jing, XU Xiaolong, ZHAO Qile, et al. Precise Orbit Determination for Quad-constellation Satellites at Wuhan University:Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143–159. DOI:10.1007/s00190-015-0862-9 |


