2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
中国的北斗导航卫星系统(BDS)于2012年建成由5颗GEO、5颗IGSO和4颗MEO卫星构成的星座,当年12月27日开始正式向亚太区域提供定位和授时服务[1-3]。目前BDS在1 561.098 MHz(B1)、1 207.14 MHz(B2) 和1 268.51 MHz(B3) 共3个频点发播导航信号,成为国际上首个提供三频服务的导航卫星系统。BDS计划于2020年正式向全球用户提供服务,已成功发射了5颗新一代试验卫星,并计划于2017年7月开始陆续发射新一代工作卫星[3]。BDS的建设进展及各方面的性能受到国内外学者的广泛关注[4-6]。
文献[6]在分析BDS试验卫星M1的测量噪声和多径时发现伪距观测量存在长期慢变的系统性偏差。文献[5]在IGSO卫星多径和噪声分析中也发现类似问题,怀疑其原因可能与GPS SVN49星相似[7],作者将这一现象称为星内多径(spacecraft internal multipath,SIMP)[8]。文献[9]的研究表明北斗伪距的这种系统性偏差与观测仰角有关,但与接收机和天线类型、观测时间和视线方向无关,且MEO和IGSO卫星的SIMP明显分群。文献[9]利用全球分布的监测站数据采用分段线性模型对北斗卫星的SIMP进行建模,获得了IGSO和MEO卫星B1、B2和B3频点随高度角变化的SIMP改正值。文献[10]提出了通过估计星间差分小数偏差对GEO的SIMP进行建模的方法,构建了高度角在15°~75°范围的改正模型, 并分析了北斗卫星的SIMP对不同长度基线的超宽巷、宽巷和窄巷解算的影响。文献[11]分析了SIMP对MW组合及双差宽巷模糊度固定的影响。文献[12]采用多项式模型对SIMP进行建模。
由于GEO卫星相对于地面测站的位置几乎不变,利用地面站数据对其SIMP进行分析和建模非常困难。即使采用文献[10]的方法,也只能在有限高度角范围内进行描述。低轨卫星定轨也是BDS的一个重要应用领域,2013年10月发射的风云三号C(FY3C)气象卫星是国际上首颗搭载北斗双频接收机的低轨卫星[13]。由于低轨卫星的高速运动,其相对于北斗卫星(包括GEO卫星)的位置不断变化,可以利用FY3C星载观测数据对北斗3类卫星的SIMP进行分析和建模。已有的研究都将SIMP描述为随高度角变化的模型,这样得到的模型有时是不实用的(详见后文)。实际上,SIMP反映了伪距的偏差在导航信号不同空间区域的变化,因此采用接收机相对卫星的天底角作为自变量更加合适。
本文简要介绍采用多径组合进行SIMP建模的基本原理,然后说明应该采用天底角作为自变量描述SIMP的原因。在此基础上采用地面监测站数据给出新的北斗SIMP修正模型,最后利用FY3C星载双频数据对北斗3类卫星的SIMP进行分析和建模。然后分析SIMP对星端宽巷FCB解的影响,也作为对所构建模型的验证。最后总结本文的工作和主要结论。
1 北斗卫星SIMP建模和分析 1.1 基本原理北斗卫星的SIMP是在伪距和相位的多径组合中被人们注意到的[6, 8-9]。假设接收机r在频点i和k测量得到某一卫星的伪距和相位,则对应i频点伪距的多径组合Mi可利用频点i和k的伪距和相位的线性组合计算得,表示如下[14-15]
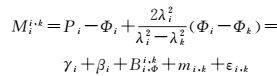 (1)
(1)
式中, P和Φ分别为以m为单位的伪距和相位观测量;γi和βi分别为卫星和接收机的伪距设备时延;λ为载波波长;Bi, Φi, k为组合相位偏差,包含了模糊度,卫星和接收机相位设备时延的组合;mi, k为接收机端的多径效应;εi, k为测量噪声。通常认识上,多径效应主要是信号经天线附近物体,如建筑物、地面、植被、水体等反射而引起的,因此与天线周边环境有很大关系。这导致不同测站的多径互不相同,无法通过差分技术消除。从而使得多径处理成为GNSS领域中一个比较棘手的问题,通常只能通过精心挑选测站位置或采用抗多径能力较强的接收机和天线设备尽量减少多径的影响。
式(1) 消去了几何相关项和电离层延迟的影响,前3项γi、βi、Bi, Φj, k一般情况下认为是稳定的不变量。由于载波的波长比伪距小得多,其噪声和多径可以忽略,因此式(1) 的mi, k和εi, k分别主要反映了伪距Pi的多径和噪声,故称为多径组合或MP组合。利用MP组合分析多径和噪声的好处就是仅需要单台接收机就可分析每颗卫星的伪距多径和噪声。该组合与几何延迟无关,适用于静态和动态的数据。
已有的研究表明,对于BDS观测数据,式(1) 中的星端伪距设备时延γi不是常数,而是随高度角或天底角缓慢变化的[8-10, 12, 16]。将式(1) 写成如下形式
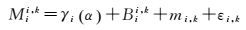 (2)
(2)
式中,Bii, k=βi+Bi, Φi, k为偏差参数,对于没有周跳的MP组合序列是一常量;γi(α)表示卫星端伪距设备时延是随参数α变化的函数,即所谓的星内多径SIMP,自变量α为卫星相对于测站的高度角或测站相对于卫星的天底角。因此MP组合包含了星内多径γi(α)、接收机噪声εi, k和测站本地多径mi, k的影响。严格地说,要从单个测站的MP组合中提取出SIMP信息需要完全抑制接收机端多径mi, k的影响[7]。现实中,只有少数装备有大口径天线的测站能够实现[7],而这样的测站往往数量非常有限,只能覆盖有限的观测弧段,特别是对IGSO和GEO卫星。由于测站多径取决于接收天线所处的环境及接收机和天线的抗多径性能,不同测站或不同类型接收机的多径效应的特性互不相同。因此可以利用大量的,分布范围广泛的,不同类型的高精度测量型接收机的观测数据,将测站本地多径作为随机误差处理。这样式(2) 可写成
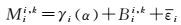 (3)
(3)
式中,εi包含了接收机的多径和测量噪声,这里视为随机误差。选择合适的模型对γi(α)进行模拟并进行线性化后就可以式(3) 为观测方程,采用最小二乘法对SIMP进行估计。例如文献[10, 12]采用了多项式模型。鉴于目前引起北斗SIMP的内部机制尚无定论,采用分段线性模型是比较合适的:只要节点足够密就可以模拟任何复杂模型。
1.2 SIMP模型自变量的选择SIMP反映了导航信号的延迟在不同空间区域的不一致性。现有的研究[9-10, 12]都习惯性地以高度角作为自变量给出北斗卫星SIMP的改正模型,这样做其实是不合适的甚至有时候是错误的。
如图 1所示,假设卫星S、测站A和地心O构成的三角形OAS,根据正弦定理有

|
| 图 1 高度角与天底角的几何关系 Fig. 1 Geometric relationship between elevation and nadir angle |
 (4)
(4)
将地球近似视为球体,则有
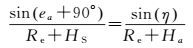 (5)
(5)
式中,Re为地球半径;Ha为测站的高程;地面ea为卫星S相对于测站A的高度角;HS为卫星S的高程;η为测站相对于卫星的天底角。对于连线AS上的另一点B,高度角eb和高程Hb有如下关系
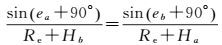 (6)
(6)
这说明,在同一视线方向SA上,处于不同位置的接收机观测同一卫星的高度角是不同的。图 2绘出北斗MEO和GEO/IGSO卫星相对于处于不同高程处的接收机的高度角随天底角变化的情况。可以看出,随着高程的增加,可观测到的天底角范围增大;对于同一天底角,卫星相对于测站的高度角随着测站高程的增加而增大;且随着天底角的增加,不同高程处的高度角差异加速增大。假设某MEO卫星相对于地面点(H≈0) 的高度角为0°,其相对于500 km、1000 km和3000 km高的接收机的高度角分别为21.98°、30.18°和47.15°。显然,此时如果直接采用类似文献[9-10, 12]那样利用地面站数据以高度角为自变量构建的SIMP改正模型必然会引入额外的误差。
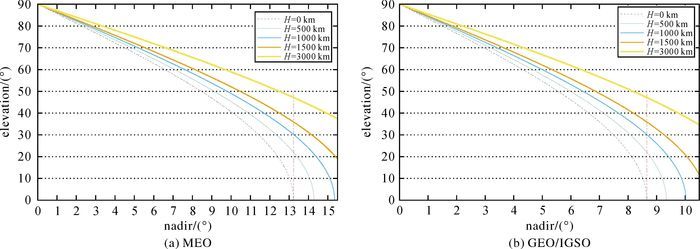
|
| 图 2 卫星相对于不同高程接收机的高度角随天底角的变化关系 Fig. 2 Elevation of satellites with respect to receivers at different altitude as a function of nadir angle |
通过以上分析,可以得到以下结论:
(1) 基于地面观测数据采用以高度角作为自变量的SIMP改正模型不能直接用于轨道高度较高(例如>1000 km)的低轨卫星。
(2) 仅用地面监测站数据,不能完全覆盖北斗卫星导航信号全部空域。只有包含了轨道高度1000 km以上的低轨卫星星载数据,才能构建覆盖北斗导航信号的全部波束范围(MEO:15°,GEO/IGSO:10°)的SIMP改正模型[17]。
(3) 只有采用天底角作为自变量,才能联合处于不同高程的接收机数据进行SIMP建模。
当然,已有的SIMP改正模型(如文献[9-10, 12])都可以通过关系式(5) 或(6) 将自变量进行变换后应用于不同高程的接收机。
1.3 北斗卫星的SIMP建模与分析为对北斗卫星的SIMP进行建模,收集了2015年DOY120—129、DOY250—259和DOY300—309共3个时间段,每个时段连续10 d的MGEX和iGMAS监测站的观测数据,以及2015年DOY060—073共14 d的FY3C的星载双频(B1/B2) 北斗数据。卫星的星下点轨迹和测站(接收机)分布如图 3所示。MGEX测站的接收机类型包括Trimble NETR9、Leica GR10、Septentrio PolaRx4、Javad TRE_G3TH,iGMAS测站的接收机类型包括CETC-54 GMR-4011、UNICORE UB4B0I、CETC-20。其中多数的Trimble NETR9接收机和所有的iGMAS测站可以同时获得北斗B1、B2和B3频点的数据。在3个时间段内平均每天分别约67、90和84个测站提供B1和B2频点数据,其中提供B3频点的测站分别约42、38和44个。
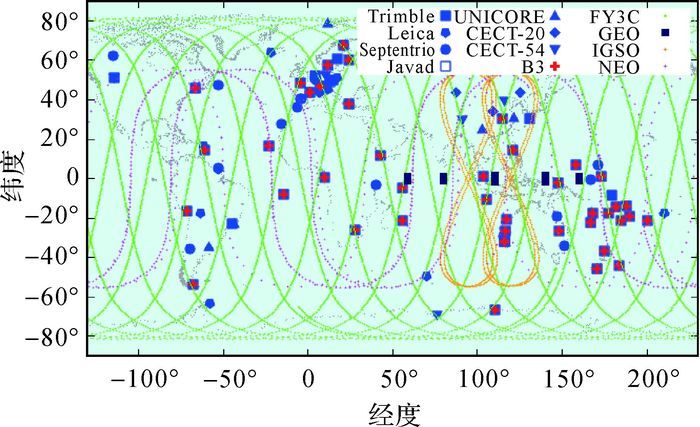
|
| 图 3 FY3C和北斗卫星星下点轨迹及地面测站分布(B3:提供B3频点观测数据的MGEX测站) Fig. 3 Ground track of FY3C and BDS satellites together with distribution of stations used in this study (B3:MGEX station with B3 observation) |
1.4 基于地面站数据的SIMP建模
为了能够适用于包括低轨卫星在内的不同用户,采用分段线性模型以天底角为自变量对SIMP进行估计,节点间隔为1°。由于所用数据量大,包含的偏差参数数量远大于节点参数个数,为了提高计算效率,数据处理采用法方程综合方法,每个频点的数据处理步骤如下:
(1) 对每颗卫星,分别利用3个数据段的MP组合进行最小二乘解算,消去偏差参数相关信息,保存SIMP节点参数估值及其协方差矩阵,这样每颗卫星可以得到3组估值。
(2) 对每颗卫星,利用第1步的3组估值和协方差矩阵作为虚拟观测量,平差得到3个时段平均的估值及对应的协方差矩阵。
(3) 利用步骤2的结果作为虚拟观测量进行平差得到按IGSO和MEO轨道分类的平均的SIMP估值。
图 4为利用步骤1得到的各颗卫星B1、B2和B3频点的伪距SIMP估值,每颗卫星有3条曲线。可以看出,同类轨道不同时段不同卫星的SIMP在多数节点上有非常好的一致性。由于观测数据量少,在天底角为0时各IGSO卫星SIMP的节点值差异较大。
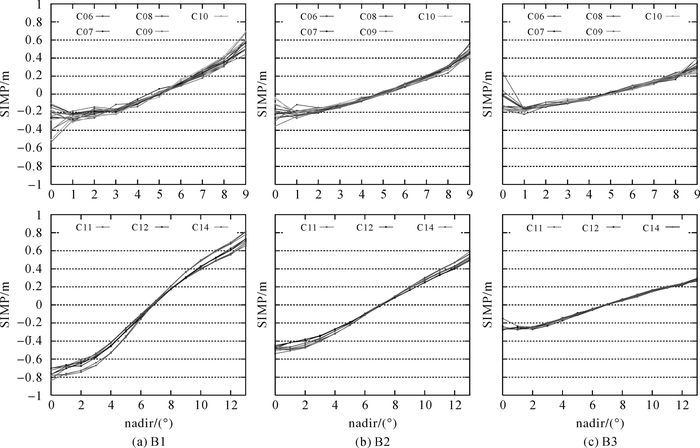
|
| 图 4 3个时段分别估计的IGSO和MEO各卫星各频点的SIMP值 Fig. 4 Estimated SIMP of individual IGSO and MEO satellites for each frequency band with different data arcs |
表 1给出了按轨道分类的SIMP节点值。需要说明的是,由于偏差参数的存在,为避免在解算中出现法方程奇异,对每个频点的SIMP节点值增加了一个松弛的约束条件:所有节点值之和为0。因此,每组SIMP估值都隐含有系统性偏差。
| m | |||||||
| 天底角/(°) | IGSO | MEO | |||||
| B1 | B2 | B3 | B1 | B2 | B3 | ||
| 0 | -0.27 | -0.21 | -0.15 | -0.78 | -0.50 | -0.26 | |
| 1 | -0.28 | -0.24 | -0.19 | -0.73 | -0.48 | -0.27 | |
| 2 | -0.24 | -0.20 | -0.14 | -0.69 | -0.44 | -0.27 | |
| 3 | -0.21 | -0.16 | -0.11 | -0.61 | -0.39 | -0.22 | |
| 4 | -0.13 | -0.09 | -0.06 | -0.48 | -0.31 | -0.17 | |
| 5 | -0.02 | -0.02 | -0.00 | -0.32 | -0.22 | -0.12 | |
| 6 | 0.09 | 0.07 | 0.06 | -0.15 | -0.12 | -0.07 | |
| 7 | 0.20 | 0.16 | 0.12 | 0.02 | -0.02 | 0.00 | |
| 8 | 0.33 | 0.26 | 0.18 | 0.17 | 0.07 | 0.04 | |
| 9 | 0.53 | 0.44 | 0.28 | 0.31 | 0.17 | 0.09 | |
| 10 | — | — | — | 0.42 | 0.25 | 0.14 | |
| 11 | — | — | — | 0.52 | 0.34 | 0.18 | |
| 12 | — | — | — | 0.60 | 0.42 | 0.22 | |
| 13 | — | — | — | 0.72 | 0.51 | 0.27 | |
1.5 基于FY3C星载BDS数据的SIMP分析
FY3C的轨道高度约为830 km,其搭载的GNSS掩星探测器(GNOS)可同时进行BDS和GPS定位和掩星测量,在国际上首次实现了星载BDS定位和接收BDS掩星信号的功能。GNOS输出北斗B1和B2频点的伪距和相位数据也可以用来分析北斗卫星的SIMP。由于FY3C相对于北斗卫星的高速运动,使得FY3C的观测数据还可以用于分析北斗GEO卫星的SIMP。本节利用FY3C星载双频北斗数据对GEO、IGSO和MEO卫星B1和B2频点的伪距SIMP进行估计。这一过程中,本研究约束天底角为4°时的SIMP值约束为0。
图 5绘出了北斗各颗卫星的SIMP随天底角的变化。可以看出,GEO卫星B1频点的SIMP的变化范围是-0.4~0.4 m,不同卫星之间有不小差异,最大差异达到0.5 m;B2的范围是-0.2~0.2 m,不同卫星的最大差异不超过0.2 m。IGSO卫星B1频点的范围为-0.1~0.5 m,不同卫星的差异小于0.2 m;B2的范围为-0.2~0.2 m,不同卫星之间有很好的一致性。MEO卫星B1频点的SIMP峰值范围是-0.4~1.4 m,值得注意的是,随着天底角的增大,C14星的SIMP曲线明显与C11、C12的偏离,最大的差异达到0.4 m。B2频点的SIMP峰值范围-0.2~0.6 m,不同卫星之间的最大差异不超过0.2 m。总体而言,GEO卫星的SIMP变化范围与IGSO卫星的比较接近;同类轨道的卫星中,B2频点的SIMP比B1频点具有更好的一致性。

|
| 图 5 FY3C数据得到的北斗各卫星的SIMP估值 Fig. 5 Estimated SIMP of individual GEO, IGSO and MEO satellite with BDS data from FY3C |
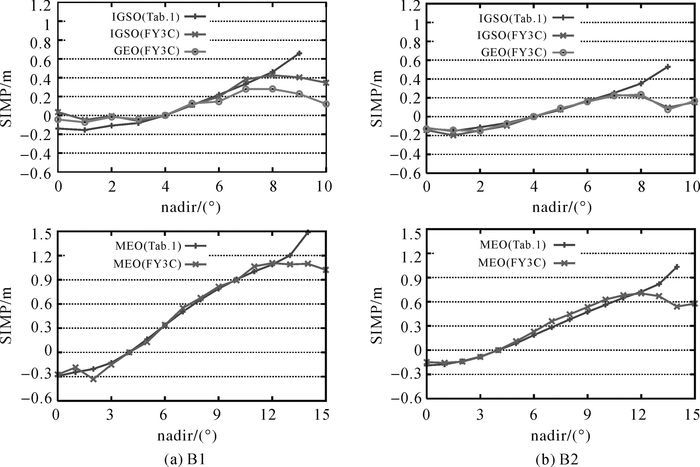
采用分段线性模型,对不同轨道类型的SIMP进行估计,可以得到按轨道类型平均的SIMP估值。图 6显示了利用FY3C数据估计的北斗3类轨道卫星B1和B2频点的SIMP估值。为了便于比较,将表 1的值进行适当平移调整(使得γi(4°)=0) 后也绘制在图中。可以看出,就FY3C数据估计的结果而言,对于B1频点,GEO卫星的SIMP在天底角小于7°时,与IGSO的差异都小与0.1 m;对于B2频点,GEO和IGSO卫星的SIMP估值有非常好的一致性,最大差异不超过0.06 m。由此或许可以认为GEO卫星可能与IGSO卫星有相似的SIMP变化规律。与表 1模型相比,IGSO卫星B1频点的SIMP在天底角为2°~8°时差异不超过0.1 m;B2频点在天底角小于7°时非常地一致。MEO星B1频点的SIMP在天底角为2°~12°时有非常不错的一致性;而B2频点,在小于12°时差异都小于0.2 m。总体而言,在天底角较大的区域,FY3C数据估算的SIMP与表 1结果差异较大。正如1.1节已经讨论的,当仅有FY3C唯一的低轨星时,其自身的多径是无法与北斗卫星的SIMP分离的。而在天底角较大时,对应的是FY3C的低高度角,接收机端的多径效应更加明显,由此造成这一区间的估计结果与表 1的值差异较大。鉴于这一状况,本文暂不将FY3C数据用于构建SIMP模型。
|
| 图 6 利用FY3C数据按轨道类型分组估计的SIMP分段线性模型 Fig. 6 Estimated SIMP for GEO-, IGSO-and MEO-satellite groups with piece-wise linear model and data from FY3C |
2 SIMP对宽巷FCB解算的影响
在高精度定位中,相位是主要观测量,但是伪距同样起到重要作用。例如双频伪距和相位的MW组合是进行长基线双差模糊度固定的重要数据,对于整数精密单点定位(IPPP)的模糊度固定更是至关重要[18-20]。目前已有的北斗IPPP方面的研究都是基于区域数据实现的[21],不同测站相对于同一卫星的天底角差异很小,也都没有考虑SIMP的影响。
为了分析在全球网的情况下SIMP对宽巷小数周偏差(FCB)解算的影响,收集2015年DOY230—249期间MGEX测站的北斗观测数据进行B1/B2频点星端宽巷FCB解算。SIMP改正采用表 1提供的数值,其中GEO卫星的SIMP改正采用IGSO的值。首先利用没有周跳且连续观测时间超过20 min的MW组合数据求得非差的宽巷模糊度,并以其为观测量进行星端FCB解算,每天解算一组。解算方法同文献[22]。
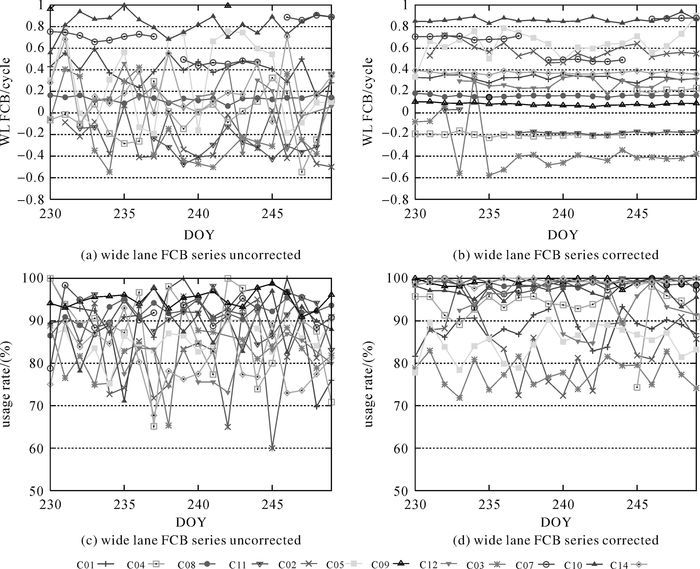
图 7(a)、(b)给出SIMP改正前后各颗卫星的宽巷FCB序列(以C06为参考),图中没有数据的点因当天广播星历标识该卫星不健康。可以看出SIMP修正之前,多数卫星的FCB序列极不稳定,而在修正之后,各颗卫星的FCB序列则要平稳许多,尤其是MEO和IGSO卫星。此外,容易看出:C07在DOY238和DOY245前后,C11在DOY235前后,C04在DOY245之后,C05在DOY249之后,FCB有明显的跳变,这可能是星上导航信号发生器重置引起的。还可以看出,C03星在DOY235之后FCB序列的稳定性有显著改善。图 7(c)、(d)给出宽巷模糊度的使用率,可以看出SIMP修正之后,使用率普遍大于70%,MEO和IGSO卫星的使用率则普遍高于90%。表 2统计了各卫星宽巷模糊度的平均使用率和FCB序列的重复性(STD)。可以看出在SIMP改正之后,对于IGSO和MEO卫星,平均使用率都有一定程度的提高,除了C12之外,都超过了97%。GEO卫星的使用率则未见有一致的改善,这可能与接收机端GEO卫星特有的多径效应影响有关[23]。在FCB序列的重复性方面,改正之前,IGSO的STD在0.02~0.1周,MEO的在0.2周左右,GEO的STD大于0.1周;改正之后,各颗卫星FCB序列的STD都有非常显著的提高,改进幅度都超过了60%,IGSO和MEO卫星的STD都减小到0.05周以内,其中MEO卫星的改进尤为明显。这是由于两个方面的原因:① MEO卫星的信号波束和SIMP范围比较大;② MEO卫星的星下点重复周期是7 d,而IGSO的是重复周期为1 d,SIMP的影响在跟踪弧段内被平均掉了。特别的,在GEO卫星当中,C01和C02的STD分别提高到了0.023和0.068周。
|
| 图 7 2015年宽巷FCB序列及宽巷模糊度的使用率 Fig. 7 The wide-lane FCB series and the usage rate of the wide-lane ambiguities in 2015 |
| PRN | 使用率/(%) | STD | |||
| 改正前/后 | 改进 | 改正前/后/cycle | 改进/(%) | ||
| C01 | 91.4/88.6 | -3.1 | 0.110/0.023 | 79.1 | |
| C02 | 82.0/84.6 | 3.2 | 0.180/0.068 | 62.2 | |
| C03* | 82.5/77.7 | -5.8 | 0.344/0.228 | 33.7 | |
| C04* | 88.1/92.9 | 5.4 | 0.203/0.179 | 11.8 | |
| C05* | 85.5/84.7 | -0.9 | 0.369/0.191 | 48.2 | |
| C06 | 94.4/99.4 | 5.3 | —/— | — | |
| C07* | 92.0/98.3 | 6.8 | 0.159/0.145 | 8.8 | |
| C08 | 91.9/98.8 | 7.5 | 0.026/0.009 | 65.4 | |
| C09 | 95.1/99.3 | 4.4 | 0.036/0.012 | 66.7 | |
| C10 | 88.4/97.1 | 9.8 | 0.100/0.023 | 77.0 | |
| C11* | 91.3/99.0 | 8.4 | 0.191/0.074 | 61.3 | |
| C12 | 81.4/93.8 | 15.2 | 0.218/0.046 | 78.9 | |
| C14 | 80.8/99.3 | 22.9 | 0.232/0.011 | 95.3 | |
| *这些卫星的FCB序列存在着明显的跳变,统计得到的FCB序列的STD指标不具有参考意义 | |||||
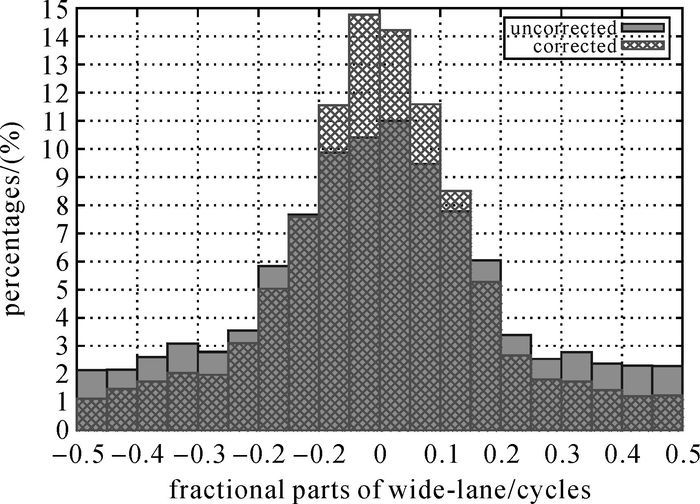
图 8给出了非差宽巷模糊度的残差分布。可以看出经SIMP改正之后,分布在±0.1周以内的比例明显增加:从40.8%提高到52.1%;对于IGSO/MEO卫星,这一比例从43.7%提高到62.1%;对于GEO,这一比例只是从33.5%略微提高到35.1%。绝对值超过0.3周的比例则从19.7%减少到12.0%,特别的,对于IGSO/MEO卫星,这一比例从16.0%降低到4.6%;而对于GEO卫星,SIMP改正前后,这一比例变化不大,分别为25.8%和25.0%。
|
| 图 8 宽巷模糊度残差分布 Fig. 8 Distribution of wide-lane ambiguity residuals |
以上试验表明,SIMP的存在将显著影响FCB解算,通过SIMP改正可以有效提高FCB解算序列的稳定性,这也验证了本文的SIMP模型的正确性和有效性。特别的,对于GEO卫星,当采用IGSO的SIMP模型进行改正时,虽然对于非差宽巷模糊度的使用率及残差分布情况的改善不大,但是显著地提高了FCB序列的稳定性,这在一定程度上验证了1.5节的观点,说明IGSO卫星的SIMP模型可在一定程度上适合于GEO卫星。
3 结论本文简要介绍了采用多径组合观测量进行北斗卫星SIMP建模和分析的基本原理,通过分析天底角和高度角的关系,提出并强调应该采用天底角而不是高度角作为SIMP建模的自变量。这样才能联合不同高程的接收机数据进行SIMP建模,所建模型才可普适地应用于处在不同高程的接收机。指出应该联合轨道高度达到1000 km以上的低轨卫星星载数据才能构建覆盖北斗空间信号全部波束范围的SIMP改正模型。利用iGMAS和MGEX地面站观测数据构建了以天底角为自变量的北斗IGSO和MEO两类卫星B1、B2和B3频点的SIMP改正模型。利用FY3C星载北斗双频数据进行了GEO、IGSO和MEO卫星的SIMP估计试验。结果表明,GEO与IGSO的SIMP非常相似。这说明地面数据解算得到的IGSO卫星的SIMP可在一定程度上适用于GEO卫星,这点在后续的FCB解算试验中得到验证。比较发现,对于MEO和IGSO卫星,在天底角分别小于12°或7°时,星载数据与地面数据获得的SIMP模型有很好的一致性。由于目前仅有FY3C一颗低轨星,其自身的多径和噪声无法分离,本文没有也不建议将其数据用于联合构建SIMP改正模型。基于全球网数据的北斗星端宽巷FCB解算试验表明,SIMP的存在将显著影响解算结果。通过SIMP改正,可显著提高GEO、IGSO和MEO卫星的星端宽巷FCB序列的重复精度,相对改善幅度都超过了60%,其中IGSO和MEO的星端FCB重复精度达到0.05周以内。特别的,对于GEO卫星,采用IGSO卫星的SIMP进行改正后,C01和C02星的FCB重复精度分别达到了0.023和0.067周。以上结果说明在进行FCB解算时需要考虑SIMP的影响。
致谢: 感谢中国科学院空间中心提供FY3C星载北斗数据;感谢IGS和iGMAS提供BDS观测数据。
| [1] | 杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(2): 2813–2819. YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Sience Bulletin, 2011, 56(2): 2813–2819. |
| [2] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [3] | 陈金平, 胡小工, 唐成盼, 等. 北斗新一代试验卫星星钟及轨道精度初步分析[J]. 中国科学:物理学力学天文学, 2016, 46(11): 119502. CHEN Jinping, HU Xiaogong, TANG Chengpan, et al. Orbit Determination and Time Synchronization for New-generation BeiDou Satellites:Preliminary Results[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2016, 46(11): 119502. |
| [4] | SHI Chuang, ZHAO Qile, HU Zhigang, et al. Precise Relative Positioning Using Real Tracking Data from Compass GEO and IGSO Satellites[J]. GPS Solutions, 2013, 17(1): 103–119. DOI:10.1007/s10291-012-0264-x |
| [5] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the Compass/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211–222. DOI:10.1007/s10291-012-0272-x |
| [6] | HAUSCHILD A, MONTENBRUCK O, SLEEWAEGEN J M, et al. Characterization of Compass M-1 Signals[J]. GPS Solutions, 2012, 16(1): 117–126. DOI:10.1007/s10291-011-0210-3 |
| [7] | HAUSCHILD A, MONTENBRUCK O, THOELERT S, et al. A Multi-technique Approach for Characterizing the SVN49 Signal Anomaly, Part 1:Receiver Tracking and IQ Constellation[J]. GPS Solutions, 2012, 16(1): 19–28. DOI:10.1007/s10291-011-0203-2 |
| [8] | BLEWITT G, BERTIGER W, WEISS J P. Ambizap3 and GPS Carrier-range:A New Data Type with IGS Applications[M]. Newcastle: IGS Workshop 2010, 2010. |
| [9] | WANNINGER L, BEER S. BeiDou Satellite-induced Code Pseudorange Variations:Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639–648. DOI:10.1007/s10291-014-0423-3 |
| [10] | LOU Yidong, GONG Xiaopeng, GU Shengfeng, et al. Assessment of Code Bias Variations of BDS Triple-Frequency Signals and Their Impacts on Ambiguity Resolution for Long Baselines[J]. GPS Solutions, 2017, 21(1): 177–186. DOI:10.1007/s10291-016-0514-4 |
| [11] | ZHANG Xiaohong, HE Xiyang, LIU Wanke. Characteristics of Systematic Errors in the BDS Hatch-Melbourne-Wübbena Combination and Its Influence on Wide-lane Ambiguity Resolution[J]. GPS Solutions, 2017, 21(1): 265–277. DOI:10.1007/s10291-016-0520-6 |
| [12] | YANG Wenke, TONG Haibo, PAN Lei, et al. Analysis and Correction of BDS Code Multipath Bias[C]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. Proceedings of the China Satellite Navigation Conference (CSNC) 2016:Volume Ⅲ.[S.l.]:Springer, 2016. |
| [13] | WANG Shuzhi, ZHU Guangwu, BAI Weihua, et al. For the First Time FengYun3 C Satellite-global Navigation Satellite System Occultation Sounder Achieved Spaceborne BeiDou System Radio Occultation[J]. Acta Physica Sinica, 2015, 64(8): 089301. |
| [14] | KLEUSBERG A, TEUNISSEN P J G. GPS for Geodesy[M]. Berlin: Springer-Verlag, 1996: 407. |
| [15] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Three's the Challenge:A Close Look at GPS SVN62 Triple-frequency Signal Combinations Finds Carrier-phase Variations on the New L5[J]. GPS World, 2010, 21(8): 8–19. |
| [16] | CHEN Hua, JIANG Weiping, GE Maorong, et al. An Enhanced Strategy for GNSS Data Processing of Massive Networks[J]. Journal of Geodesy, 2014, 88(9): 857–867. DOI:10.1007/s00190-014-0727-7 |
| [17] | 李振海, 焦文海, 黄晓瑞, 等. GNSS服务空域空间信号可用性比较与分析[J]. 宇航学报, 2013, 34(12): 1605–1613. LI Zhenhai, JIAO Wenhai, HUANG Xiaorui, et al. Comparison and Analysis of Signal Availability in the GNSS Service Volume[J]. Journal of Astronautics, 2013, 34(12): 1605–1613. DOI:10.3873/j.issn.1000-1328.2013.12.010 |
| [18] | GE M, GENDT G, SHI M, et al. Resolution of GPS Carrier-Phase Ambiguity in Precise Point Positioning[M]. Vienna: EGU Assembly, 2007. |
| [19] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation, 2009, 56(2): 135–149. DOI:10.1002/navi.2009.56.issue-2 |
| [20] | COLLINS P, LAHAYE F, HEROUX P, et al. Precise Point Positioning with Ambiguity Resolution Using the Decoupled Clock Model[M]//Proceedings of ION GNSS 2008. Savannah, Georgia:Institute of Navigation, 2008. |
| [21] | LIU Yanyan, YE Shirong, SONG Weiwei, et al. Integrating GPS and BDS to Shorten the Initialization Time for Ambiguity-Fixed PPP[J]. GPS Solutions, 2017, 21(2): 333–343. DOI:10.1007/s10291-016-0525-1 |
| [22] | LI Xingxing, ZHANG Xiaohong. Improving the Estimation of Uncalibrated Fractional Phase Offsets for PPP Ambiguity Resolution[J]. The Journal of Navigation, 2012, 65(3): 513–529. DOI:10.1017/S0373463312000112 |
| [23] | WANG Min, CAI Hongzhou, PAN Zongpeng. BDS/GPS Relative Positioning for Long Baseline with Undifferenced Observations[J]. Advances in Space Research, 2015, 55(1): 113–124. DOI:10.1016/j.asr.2014.10.001 |


