2. 中国科学院地质与地球物理研究所, 北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Science, Beijing 100029, China
21世纪以来,卫星重力观测技术的进步,为观测地球重力场变化提供了关键技术,在地球外部约500 km高度的空间轨道上,GRACE、GOCE卫星提供了覆盖全球范围的重力观测数据。通过对卫星重力数据解算获得的月尺度球谐模型,已经成功用于研究陆地水迁移、冰川融化速率、与地震和地球动力学过程相关的重力变化等一系列科学问题[1-5]。与卫星重力测量方式不同,地表重力测量通常采用绝对和相对重力仪通过定期同点位重复观测来获得重力场变化信号。地表测量的优点在于观测点距离场源近、测量精度高、观测位置重复性好,观测信号的高阶分量更精确,但受地表环境限制,测点空间分布不均匀。相比卫星重力能提供的全球范围球谐模型结果,陆地观测的数据覆盖和密度都很难达到球谐函数解算要求,因此,基于陆地重力场观测获得模型结果通常需通过离散点插值实现。但由于观测手段和数据处理方法差异,很难在一定时-频尺度上定量对比卫星重力与陆地重力的观测结果。本文研究应用局部球谐函数解算方法,对陆地重力测量的离散点进行模型解算,获得有限阶的时空局部球谐模型,给出不同阶的重力图像,用于信号对比和混合模型构建等。
以“中国大陆构造环境监测网络”项目(简称“陆态网络”)为主导的重力测网是目前世界上最大的陆地重力观测系统,包含23个绝对重力测量基准点和近400个相对重力测量点,实现对中国大陆内主要构造单元和断裂系统的覆盖。其中,绝对重力测量精度优于5×10-8 m/s2;相对重力测量段差精度优于10×10-8 m/s2。在1998—2008年间,已经产出5期观测结果,有效重复测点数超过300个,平均点值精度优于16×10-8 m/s2[6]。“陆态网络”项目的建设和持续监测,主要目的是监测地壳形变、板块运动几何模式,为构建地震孕育模型等提供数据服务[7-9]。近年来的众多研究结果表明,陆地重力观测获得的重力场结果可用于研究与地震孕育过程相关的地球物理场变化[10-13]。同时,也为研究中国大陆板内构造变形和深部物质运移及岩石圈动力学过程提供非常难得的科学观测数据。受中国大陆复杂地形和地表测量条件所限,实际重力测点空间分布并不均匀,测点空间位置的统计结果显示,相邻重力测点间最大间距为2.07°,平均间距为0.71°。因此,要通过该测网数据结果恢复整个中国大陆的重力场变化,并基于不同球谐函数来解算一定阶次的重力模型存在一定难度。
重力位场问题,可用拉普拉斯方程描述,该方程的解可表示为面球谐函数形式。对于数据覆盖程度高的卫星重力数据解算等全球尺度问题,面球谐展开可用于表示不同时空尺度的重力场,如著名的EGM2008全球重力异常模型[14]。但在地球两极,卫星数据具有“极空白”问题,即在高纬度地区缺少数据有效覆盖,若要进一步进行球谐展开系数计算,则会遇到面球谐函数不正交问题,Slepian函数是从原理上解决卫星测量“极空白”问题的有力工具之一。Slepian问题最早的提出,主要用于解决有限信号截断问题和提高信号功率谱密度的估算等应用[15-16]后来进一步完善推广到二维球面区域,形成了“时空局部谱方法”[17]。该方法与其他空间平滑方法的不同在于可以保证在球面上局部区域范围内获得最优的谱平滑解[18-20],通过使用Slepian函数作为球谐基函数,引入“聚集因子”对不同阶次的Slepain函数进行排序,在有限区域内的频率能量最优,并可保证其展开与同阶次的球谐函数具有同等意义。该方法已应用于解算局部重力场模型问题[21-22]。
1 时空局部谱方法和中国大陆本征函数计算球坐标系下的拉普拉斯方程解可用球谐函数来表示,引用球谐方法可将任意复杂的信号用一系列不同阶次的系数来描述,即球面上的傅里叶变换。其优点是将空间域任意复杂的信号展开为具有固定频率特征的一系列信号的组合,通过指定阶截断,保留足够观测精度的有限阶模型解。
在单位球面上,任意平方可积函数f(r),可以表示为如式(1) 所示的级数展开形式
 (1)
(1)
式中,θ为经度;φ为余纬;Y为面球谐函数;Ylm为m次、l阶函数,可表示为
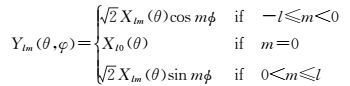 (2)
(2)
式(2) 中,Xlm(θ)可以进一步表示为
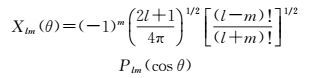 (3)
(3)
式(3) 中,Plm(x)可以表示为
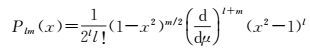 (4)
(4)
根据球谐函数的正交特性,由式(1)—(3) 可以得出式(5)
 (5)
(5)
对于球面上任何一个封闭区域R,引入s(θ, φ)函数来表示一个带限信号,可以将面球谐函数Y等价表示为式(6)[20]
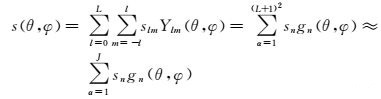 (6)
(6)
式中,gn(θ, φ)即为第n阶Slepian基函数;sn为Slepian展开系数;J为截断阶数。一般对于球面上的一个有限封闭区域R,Slepian基函数具有很好的局部能量集中特性。如果仅考虑表示有限区域R内信号的Slepian函数解算,可以采用J阶近似来获得带限信号在区域内的能量最大形式。一般为了在球面上任意区域R,将带限函数能量限制在有限球带之内,可以引入参数λ来度量集中程度,这里称为聚集因子(concentration factor),如式(7) 所示
 (7)
(7)
式(7) 中的λ值最大化问题,通常称作“Slepian”问题。该问题的求解可以表示为频率域内的特征值方程组形式
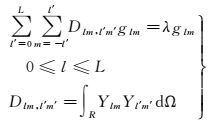 (8)
(8)
相应的空间域特征值方程可以表示为
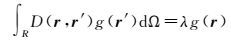 (9)
(9)
 (10)
(10)
式(7) 中,λ为一系列0到1之间的比例系数,λ越接近于1,表示Slepian基函数的线性组合在区域R内部的能量集中度越高,也就是说信号在区域R内可以得到有效的近似分解。如果对λ的值进行排序,接近于0的λ值,被认为是无效特征值,意味着在球面的R区域上,该基函数没有贡献。通常只取某一段λ接近于1的J组Slepian基函数计算球谐系数,即可以得到球面上区域R范围内的一个带限信号的最佳函数展开。由于这种改进的局部球谐方法对于L阶展开,仅选取(L+1)2项中的J项具有最佳λ值的Slepian基函数组合来最佳近似表示s(θ, φ)函数,因此,该方法也被认为是一种具有稀疏(sparse)特性的时空局部谱方法。但是,对于球面区域R内的信号近似,与相同阶次的球谐展开具有同样的意义。
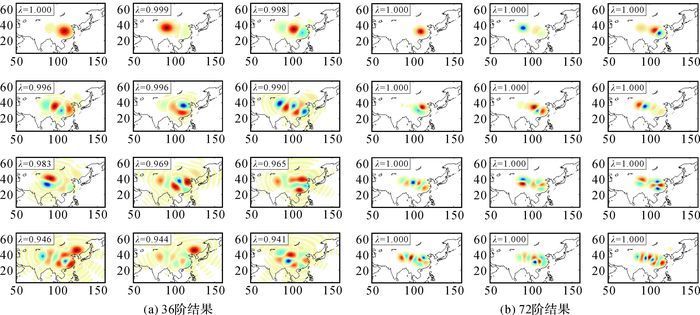
对于中国大陆区域,首先从计算Slepian基函数形式入手,以大陆具有重力观测点分布的闭合区域为边界分别计算了18阶、36阶、72阶和120阶的内部基函数形式,结果如图 1所示。在图 1中依据计算Slepian函数结果的λ值进行排序后,仅表示了36和72阶展开的前12个Slepian基函数分布情况。通过计算不同阶Slepain函数在中国大陆范围内的形式,并计算聚集因子λ,按从大到小形式进行排序,选取局部集中度最好的一组函数用于本征值计算,图 1(a)是36阶结果,图 1(b)是72阶结果,展开阶数越高本征函数数目越多。
从图 1的Slepian函数结果可以看出,同样是前12个Slepian基函数的λ值排序结果,72阶的λ值在区域内的能量聚集度结果优于36阶结果。如36阶结果随着λ值减小,在区域外部能量出现泄漏。随着阶数的增加,可得到更多的具有较高聚集因子的本征基函数。且随着展开阶数增加,本征函数能表示的信号频率和空间分辨率都得到增加。该方法对解算数据并不要求在空间上规则分布,但数量上必须要大于选取的有效λ值截断数,以确保本征值计算过程中求解线性方程组的稳定性。
|
| 图 1 中国大陆Slepian本征函数计算结果(图中实线为水陆分界线) Fig. 1 The eigen function of Slepian localized method in Chinese mainland(the solid lines are water and land boundary) |
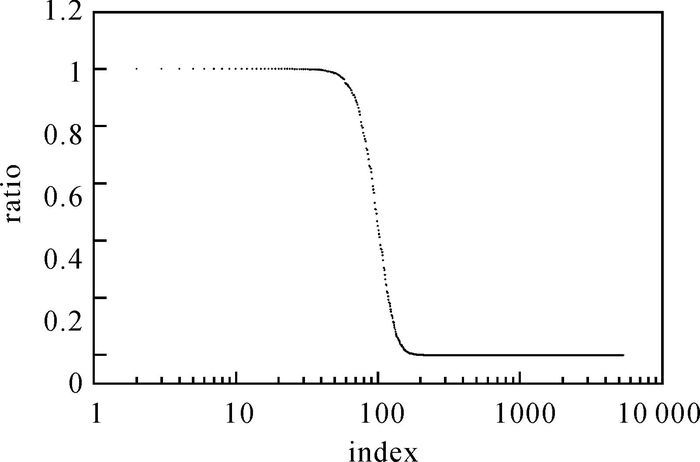
图 2显示基于Slepian函数的72阶局部球谐展开后,对λ值的排序结果。在本文研究区域λ值的计算共计可以得到73×73=5329个。其中,大于λ>0.1的值有130个,而剩余的5199项本征函数,由于λ值较小,对于表征区域内的信号在能量上贡献很小,因此,可以对其进行截断处理,而如何选取最优的截断项数J将在下一部分基于实际数据情况进一步讨论。
|
| 图 2 Slepian函数的聚集因子排序分布形式 Fig. 2 The sorted concentrated factor of Slepian function |
2 应用Slepian函数解算GOCE卫星重力异常
已有学者针对重力异常阶方差模型[22]和大地水准面的确定于精度估计展开了研究[23-25]。在有限区域内不均匀分布的地面重力观测数据,Slepian局部谱方法可以从数学上解决正交性问题,但测点的不均匀分布仍会对于模型解算精度产生一定影响。研究由实际测点不均匀分布和模型解算精度关系,需要选取一个已知的模型作为研究对象,通过离散化采样获得已知模型值,再通过对比已知值和解算值之间的差异,讨论优选参数和适用性等问题。
本文选取欧空局发射的GOCE(gravity field and steady-state ocean circulation explorer)卫星的Level 2级重力异常球谐模型(EGM_GOC_2) 产品作为测试对象(GOCE卫星携带重力梯度仪,设计识别重力异常的空间分辨率约为100 km,重力异常精度1 mGal(1 Gal=10-2 m/s2),大地水准面精度1 cm)。以GOCE卫星球谐模型解为已知输入,对其分别在空间上以均匀和非均匀两种方式进行采样,来对比局部球谐方法的有效性和最优参数选取问题。利用欧空局提供的球谐模型,选取GOCE静态自由空气重力异常的72阶球谐模型数据,提取中国大陆及其周边地区(65°N—140°N,15°E—55°E)的异常值,最大异常值为115.42 mGal,最小值为-113.86 mGal,变化范围约为230 mGal。其次,在中国大陆区域范围内分别进行等间距均匀采样和依据实际流动重力测点位置进行非均匀采样,得到对应节点上的重力异常作为已知信号。然后通过调整截断参数J,计算Slepain局部谱方法构建的模型结果在对应节点位置与已知信号的差异。通过对已知阶次重力场模型数据的分析,研究实际测点空间分布不均匀可能对模型解算误差的影响,进而优化截断参数J。最后,获得与实际地面观测分辨能力相一致的最优重力场模型解。
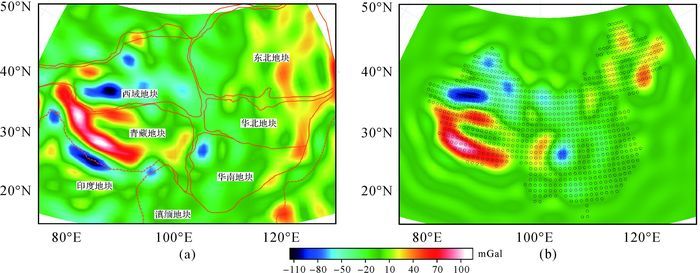
基于GOCE卫星数据计算的72阶球谐自由空气重力异常模型,模型数据范围包括了中国大陆和其周边地区,并将该球谐重力异常模型作为已知解,结果如图 3(a)所示。中国大陆及其周边的主要构造块体和卫星数据解算的自由空气重力异常模型结果,从异常特征来看,在构造变形较大的块体边界地区,自由空气重力异常多呈现高梯度变化特征。自由空气重力异常主要反映地壳由于构造变形引起物质重新分布后的质量盈亏情况,在构造运动变形较强的地区,这种质量运移或构造变形作用相对较强,常常与构造边界运动相对应的高异常梯度特征。
|
| 图 3 中国大陆自由空气重力异常场和Slepian局部谱模型 Fig. 3 The free-air gravity anomaly of Chinese mainland and the Slepian local spectrum model |
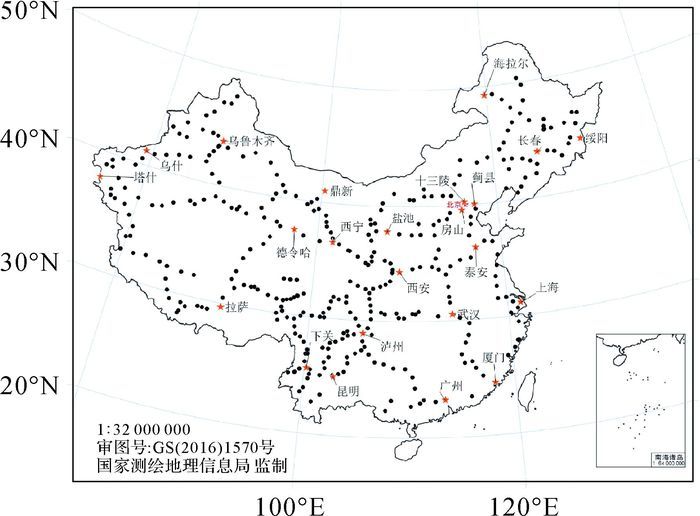
在中国大陆内部,对GOCE卫星重力异常模型数据,首先以1°为间隔进行等间距数据采样(最小曲率插值),具体采样点位置如图 3(b)中的黑色圆圈所示和如图 4所示的“陆态网络”项目实际重力观测点。通常球谐函数的空间异常分辨率一般与展开的阶数相关,72阶球谐函数理论上表示的异常空间分辨率约为2.5°,而Slepian局部谱方法的阶数定义与球谐函数等价,阶数L的定义如式(6) 所示。因此,本文采用72阶Slepian函数来测试在中国大陆内部局部球面内重采样后的重力场模型计算问题。
|
| 图 4 中国大陆实际流动重力观测网络测点分布 Fig. 4 The distribution of mobile gravity survey in Chinese mainland 注:黑色圆点为流动重力测点,红色五角星为绝对重力观测基点, 蓝色实线为海陆边界 |
图 3(b)是以1°为间隔对72阶模型均匀采样后,恢复的重力异常结果。根据Slepian函数性质,以聚集因子大小排序后,可以得到有限截断项数的近似解。通过模型试验,对于均匀采样点的模型解算,误差的均方差随截断数J值的增大而减小。本文选取的72阶GOCE卫星重力异常模型,如果取λ>0.1,即J=130的情况下,应用Slepian基函数进行局部拟合结果,均方误差为3.78 mGal;取λ>0.01的前J=161情况下,均方误差为0.749 mGal。从图 3(b)可以看出在中国大陆区域内部重力异常形态与图 3(a)异常基本相同,区域外部有少量能量泄漏,这与J的截断数有关。从均匀采样的Slepian局部谱方法解算结果看,在区域内部信号的主要能量成份都已经恢复出来,在不依赖与边界外部信号约束的情况下,该方法完全可以实现球面局部数据的球谐模型解算。
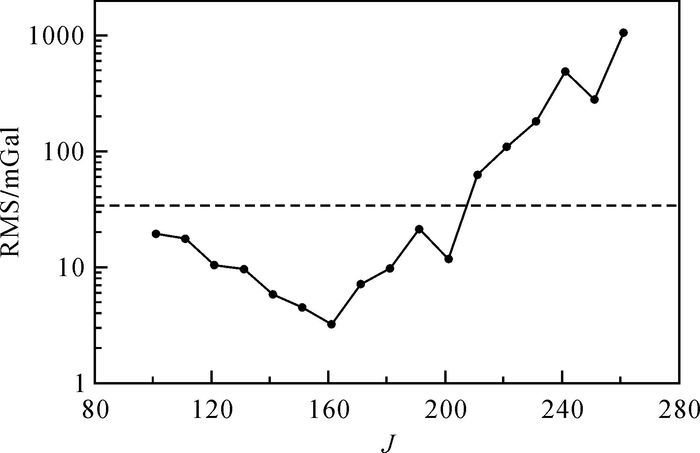
但是,对于实际非均匀分布采样点的异常解算问题,与均匀采样计算试验结果不同。通过模型测试发现J参数的选取变化与异常的解算误差之间呈现非线性变化特征,也就是说与均匀采样时误差随J值的增加而减小不同。本文统计了截断项数从J=80至J=280的多组试验。根据对采样点已知值和解算值相比,均方误差在J=161时最小,为3.1 mGal,误差与J项数的变化规律如图 5所示。为了突出结果之间的差异,采取如图 6所示的色标表示采用非均匀采样数据解算后的异常特征。图 6(a)为解算得到的J=161时的异常模型,在区域内与已知重力异常模型之间的残差分布如图 6(b)所示。图 6(a)中恢复得到的重力异常场特征与图 3(b)具有一定差异,其差异特点与实际测点空间覆盖不均匀相关。对比图 6(b)给出的与拟合剩余误差分布特征,可以看出在中国大陆的东北部由于测点距离边境较远,剩余误差较大。另外,在中国华南和青藏高原西南部、新疆等地区由于测点覆盖出现空区,而产生了较大的剩余误差。因此,针对这些地点进行适当的测点加密是十分必要的。而在中国大陆内部华北地区和南北地震带地区由于测点分布空间较密,解算模型误差都低于3 mGal。针对GOCE卫星提供的静态自由空气重力异常模型测试结果,在异常变化幅值约为230 mGal情况下,非均匀采样拟合误差可以实现3 mGal精度,解算的异常精度约为变化幅值的1.3%。表 1给出了两种采样情况恢复的模型统计参数结果(J=161)。
|
| 图 5 测点非均匀分布的Slepian基函数局部球谐展开截断系数与误差关系 Fig. 5 The relationship between the truncated parameter and fitting error with the non-uniformed measured points |

|
| 图 6 基于非均匀分布重力测点解算的区域重力异常场模型结果 Fig. 6 The regional gravity anomaly model based on the non-uniformed gravity points |
| mGal | |||||
| 异常变化幅度 | 最大值 | 最小值 | 平均值 | 标准差 | |
| 模型数据 | 229.27 | 115.39 | -113.88 | -5.24 | 32.42 |
| 均匀采样 | 210.47 | 104.80 | -105.68 | -5.44 | 31.58 |
| 非均匀采样 | 221.20 | 111.62 | -109.58 | -4.47 | 32.08 |
此外,从图 6(b)的误差分布特点上看,非均匀采样结果与已知模型之间的误差分布特征含有一定的周期性成分,这是由于采样点缺失而产生的频率泄漏,即解算的高阶Slepian函数系数存在误差。对于在实际测点分布不均匀,应该根据测点分布对照已知模型结果来研究截断阶数、测点分布特征与误差变化规律之间的关系,以确定最优参数,并确保获得与实际观测情况精度相互一致的模型结果。而对于截断阶数J客观上是由于Slepian局部谱方法与传统球谐展开采用了不同的球谐基函数形式,在保证正交化的同时,可以实现在无外部边界数据约束的情况下,使解算的模型在球面局部区域内部信号能量达到最大化,具体是根据λ值的排序实现。一般情况下,如果仅考虑球面局部内的信号恢复问题,截断项数J通常远远小于(L+1)2值,即具有稀疏特性。
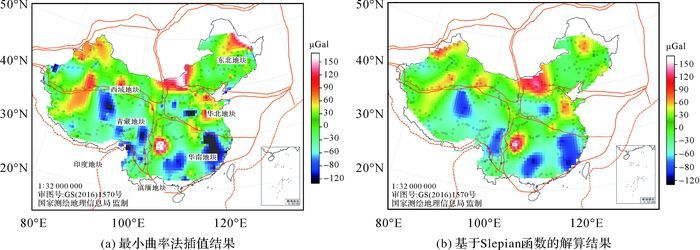
3 中国大陆重力场变化的Slepian局部谱方法解算中国大陆地区的重力场变化主要是通过定期流动重力测量获得,以每期观测的绝对重力结果为基准,对相关联测重力进行平差,可以获得每个空间测点位置的重力场。本文根据“陆态网络”项目数据库,选取了2005年和2008年两期测量获得的重力点值数据,通过差分获得测点位置的重力场变化(分别对每个测量点用2008年的测量值减去2005年测量值)。对此数据,采用Slepian局部谱方法进行球谐解算,在计算过程中参数选取依据第2节的试验结果,得到了72阶中国大陆内部重力场变化信号,结果如图 7所示。图 7中橙色实线为中国大陆块体边界,图(b)中的红色圆圈为2000—2012年间6级以上地震震中位置。
|
| 图 7 中国大陆2005—2008年重力场变化对比与地震活动分布 Fig. 7 The gravity variation from 2005 to 2008 and large earthquakes in Chinese mainland |
图 7(a)所示的2005—2008年间重力场差分变化信号是采用最小曲率插值方法,而图 7(b)是采用Slepian局部谱方法解算获得的72阶模型解。对比可知,图 7(b)相比图 7(a)信号更光滑,这是由于两种方法恢复的重力变化信号频率成分不同,从原理上最小曲率插值属于空间域算法,而Slepian局部谱方法属于频率域算法。插值方法更侧重对空间局部点值变化的拟合,而频率域方法是从频率上合成异常信号,对局部的高频干扰具有明显的压制作用。其优点在于若测网中个别测点测量误差较大,插值算法通常以拟合搜索半径内的测点值最优为标准,这样在恢复模型解的过程中不但拟合了信号,同时也拟合了误差。而Slepian局部球谐解算技术,可以从直接依据展开阶数的选取来控制拟合异常的频带范围,并获得频域最优的信号估计,因此,具有一定抗干扰性。
从图 7(b)中与中国大陆主要活动地块边界的对比可以看出,重力场变化与构造之间具有一定相关关系,青藏地块内部以重力减小为主,华南地块与青藏地块交界位置存在正负变化梯度带,3年期间的重力变化达到百微伽量级。当然这些重力场变化的信号成分也十分复杂,除了测量误差外,还与地下水储量变化、地表形变和深部构造变形相关。而近年来利用区域重力场变化来研究地震活动的研究也很多[8-9]。
4 结论与讨论本文采用Slepian局部谱分析方法解算中国大陆范围内的实测重力场变化数据,以GOCE卫星球谐函数解作为已知模型来评估实际陆地重力测点非均匀分布对球谐函数解的误差影响。首先计算了多个阶次中国大陆局部范围的Slepian基函数分布;然后采用GOCE卫星获得重力场模型的前72阶球谐系数作为已知结果,评价重力实际测点非均匀分布的解算有效性,并针对中国大陆地区采用Slepian基函数进行解算,通过模型对比选择最优截段项数;最后针对2005—2008年中国大陆地区流动重力测量获得的重力场变化信号进行解算,获得72阶重力场变化模型。本文采用Slepian局部谱方法解算中国大陆重力场变化,主要研究结论如下:
(1) 对于球面局部空间分布不均匀的地表重力测量数据,利用GOCE球谐模型解作为已知输入,试验表明在均匀采样的情况下,Slepian方法可以获得局部最优解。但由于测点空间分布不均匀,会降低球谐解模型解算精度。对于中国大陆实际流动重力测点数据,采用72阶Slepian函数解算时,在同取截断参数J=161时,由于测点分布不均匀误差相差约4.1倍。
(2) 应用Slepian函数为基的局部球谐展开技术,可以在球面任意区域范围内,实现局部球谐展开,从原理上可对任意重力位场信号进行求解。本文的模型试验和实际数据测试计算得到了中国大陆的重力场变化特征。该方法相比经典球谐函数解算方法,对同阶模型解算要求的数据点数更少,而且不要求数据点空间严格均匀分布,即可获得球谐模型解。这对于开展陆地和空间不同途径的重力测量数据对比,构建联合球谐模型等方面可以提供更多的技术保障。
(3) 应用该方法对中国大陆2005—2008年重力场变化数据进行处理,计算得到了72阶球谐展开结果,相比直接插值获得的重力场空间变化结果,球谐函数解具有全局最优、谱光滑、高频噪声源干扰小等特点,是一种具有最高截断频率特性的最优模型估计。
(4) 从恢复的72阶重力变化信号特征与已知构造边界对比表明,低频空间重力场变化与构造运动具有较好的一致性,特别是在青藏地块内部和围绕其边界的主要构造活动区,重力场变化程度较大。这种以Slepian局部谱方法为基础的球谐模型解,恢复的短期数年尺度的低频重力场变化信号可以在一定程度上反映地壳介质的运动规律和短时间区域构造变形等动力学过程。
本文旨在采用Slepian局部谱方法解算中国大陆内部流动重力测量数据,并获得的重力场变化信号。与球冠谐方法、空间插值方法等不同之处在于其可以针对任何几何边界区域,并且不需要数据扩边、预插值等前处理工作,且该方法获得的不同阶球谐展开模型与面球谐方法获得的同阶模型具有相同意义。进一步应用该方法还可以获得其他不同阶模型的重力场变化,研究不同空间尺度范围的重力异常信号,提供重力变化异常源提取的可能。此外可与卫星重力等球谐模型结果进行合成,各取优势频段获得混合模型解。
| [1] | CHEN J L, WILSON C R, TAPLEY B D, et al. GRACE Detects Coseismic and Postseismic Deformation from the Sumatra-andaman Earthquake[J]. Geophysical Research Letters, 2007, 34(13): L13302. |
| [2] | CHEN J L, WILSON C R, TAPLEY B D, et al. 2005 Drought Event in the Amazon River Basin as Measured by GRACE and Estimated by Climate Models[J]. Journal of Geophysical Research, 2009, 114(B5): B05404. |
| [3] | 邹正波, 罗志才, 吴海波, 等. 日本Mw9.0地震前GRACE卫星重力变化[J]. 测绘学报, 2012, 41(2): 171–176. ZOU Zhengbo, LUO Zhicai, WU Haibo, et al. Gravity Changes Observed by GRACE before the Japan Mw9.0 Earthquake[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 171–176. |
| [4] | 王武星, 顾国华, 陈石. 利用GRACE观测资料分析日本Mw9.0地震前区域重力变化特征[J]. 地震地质, 2014, 36(2): 523–535. WANG Wuxing, GU Guohua, CHEN Shi. Study on Regional Gravity Changes Before the MW9.0 Japan Earthquake Detected by Grace[J]. Seismology and Geology, 2014, 36(2): 523–535. |
| [5] | 郑秋月, 陈石. 应用GRACE卫星重力数据计算陆地水变化的相关进展评述[J]. 地球物理学进展, 2015, 30(6): 2603–2615. ZHENG Qiuyue, CHEN Shi. Review on the Recent Developments of Terrestrial Water Storage Variations Using GRACE Satellite-based Datum[J]. Progress in Geophysics, 2015, 30(6): 2603–2615. DOI:10.6038/pg20150619 |
| [6] | 祝意青, 梁伟锋, 湛飞并, 等. 中国大陆重力场动态变化研究[J]. 地球物理学报, 2012, 55(3): 804–813. ZHU Yiqing, LIANG Weifeng, ZHAN Feibing, et al. Study on Dynamic Change of Gravity Field in China Continent[J]. Chinese Journal of Geophysics, 2012, 55(3): 804–813. |
| [7] | 滕吉文, 白登海, 杨辉, 等. 2008汶川MS8.0地震发生的深层过程和动力学响应[J]. 地球物理学报, 2008, 51(5): 1385–1402. TENG Jiwen, BAI Denghai, YANG Hui, et al. Deep Processes and Dynamic Responses Associated with the Wenchuan MS8.0 Earthquake of 2008[J]. Chinese Journal of Geophysics, 2008, 51(5): 1385–1402. |
| [8] | 祝意青, 闻学泽, 张晶, 等. 华北中部重力场的动态变化及其强震危险含义[J]. 地球物理学报, 2013, 56(2): 531–541. ZHU Yiqing, WEN Xueze, ZHANG Jing, et al. Dynamic Variation of the Gravity Field in Middle North China and Its Implication for Seismic Potential[J]. Chinese Journal of Geophysics, 2013, 56(2): 531–541. DOI:10.6038/cjg20130217 |
| [9] | 祝意青, 徐云马, 吕弋培, 等. 龙门山断裂带重力变化与汶川8.0级地震关系研究[J]. 地球物理学报, 2009, 52(10): 2538–2546. ZHU Yiqing, XU Yunma, LV Yipei, et al. Relations between Gravity Variation of Longmenshan Fault Zone and Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2009, 52(10): 2538–2546. DOI:10.3969/j.issn.0001-5733.2009.10.012 |
| [10] | 高倩, 陈石. 基于欧拉反褶积方法计算川滇交界重力变化场源特征[J]. 地球物理学进展, 2015, 30(2): 503–509. GAO Qian, CHEN Shi. Based on the Euler Deconvolution Technique to Determine the Field Source Characteristics of Gravity Variation in the Boundary of Sichuan and Yunnan[J]. Progress in Geophysics, 2015, 30(2): 503–509. DOI:10.6038/pg20150205 |
| [11] | 陈石, 徐伟民, 蒋长胜. 中国大陆西部重力场变化与强震危险性关系[J]. 地震学报, 2015, 37(4): 575–587. CHEN Shi, XU Weimin, JIANG Changsheng. Relationship between Gravity Variation and Seismic Hazards in the Western China[J]. Acta Seismologica Sinica, 2015, 37(4): 575–587. DOI:10.11939/jass.2015.04.005 |
| [12] | CHEN Shi, JIANG Changsheng, ZHUANG Jiancang. Statistical Evaluation of Efficiency and Possibility of Earthquake Predictions with Gravity Field Variation and Its Analytic Signal in Western China[J]. Pure and Applied Geophysics, 2016, 173(1): 305–319. DOI:10.1007/s00024-015-1114-x |
| [13] | CHEN Shi, LIU Mian, XING Lelin, et al. Gravity Increase before the 2015 Mw7.8 Nepal Earthquake[J]. Geophysical Research Letters, 2016, 43(1): 111–117. DOI:10.1002/2015GL066595 |
| [14] | 章传银, 郭春喜, 陈俊勇, 等. EGM 2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283–289. ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283–289. |
| [15] | SLEPIAN D. Some Comments on Fourier Analysis, Uncertainty and Modeling[J]. SIAM Review, 1983, 25(3): 379–393. DOI:10.1137/1025078 |
| [16] | THOMSON D J. Spectrum Estimation and Harmonic Analysis[J]. Proceedings of the IEEE, 1982, 70(9): 1055–1096. DOI:10.1109/PROC.1982.12433 |
| [17] | SIMONS F J, VAN DER HILST R D, ZUBER M T. Spatiospectral Localization of Isostatic Coherence Anisotropy in Australia and Its Relation to Seismic Anisotropy:Implications for Lithospheric Deformation[J]. Journal of Geophysical Research (Solid Earth), 2003, 108(B5): 2250. |
| [18] | DAHLEN F A, SIMONS F J. Spectral Estimation on a Sphere in Geophysics and Cosmology[J]. Geophysical Journal International, 2008, 174(3): 774–807. DOI:10.1111/gji.2008.174.issue-3 |
| [19] | WIECZOREK M A, SIMONS F J. Localized Spectral Analysis on the Sphere[J]. Geophysical Journal International, 2005, 162(3): 655–675. DOI:10.1111/gji.2005.162.issue-3 |
| [20] | SIMONS F J, DAHLEN F A, WIECZOREK M A. Spatiospectral Concentration on a Sphere[J]. SIAM Review, 2006, 48(3): 504–536. DOI:10.1137/S0036144504445765 |
| [21] | 朱广彬, 李建成, 文汉江, 等. 卫星重力梯度数据确定地球重力场的Slepian局部谱分析方法[J]. 测绘学报, 2012, 41(1): 1–7. ZHU Guangbin, LI Jiancheng, WEN Hanjiang, et al. Slepian Localized Spectral Analysis of the Determination of the Earth's Gravity Field Using Satellite Gravity Gradiometry Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 1–7. |
| [22] | 孙雪梅, 李斐, 鄢建国, 等. Slepian函数在月球局部重力场分析中的适用性分析[J]. 测绘学报, 2015, 44(3): 264–273. SUN Xuemei, LI Fei, YAN Jianguo, et al. An Analysis of the Applicability of Slepian Function in Analyzing Lunar Local Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 264–273. DOI:10.11947/j.AGCS.2015.20130728 |
| [23] | 翟振和, 任红飞, 孙中苗. 重力异常阶方差模型的构建及在扰动场元频谱特征计算中的应用[J]. 测绘学报, 2012, 41(2): 159–164. ZHAI Zhenhe, REN Hongfei, SUN Zhongmiao. Construction of Gravity Anomaly Degree Variance Model and Application in Computation of Spectral Sensitivity of Disturbing Gravity Functions[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 159–164. |
| [24] | 许曦, 朱建军. 区域重力大地水准面确定的相对精度估计[J]. 测绘学报, 2009, 38(5): 383–390. XU Xi, ZHU Jianjun. Relative Accuracy Estimation for Determining Regional Gravimetric Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 383–390. DOI:10.3321/j.issn:1001-1595.2009.05.002 |
| [25] | 申文斌. 论确定全球大地水准面的斯托克斯方法[J]. 测绘学报, 2012, 41(5): 670–675, 689. SHEN Wenbin. On Stokes' Approach for Determining Global Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 670–675, 689. |



