地面点的正高h定义为
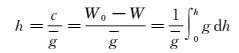 (1)
(1)
式中,g、g分别为地面点到大地水准面间的流动点重力和平均重力;W、W0分别为地面点和大地水准面的重力位;c=W0-W为重力位数。
由于不能测量地球内部重力,通常假设地面点到大地水准面的地壳密度为常数,采用珀雷归算公式计算平均重力gH[1-3]
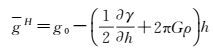 (2)
(2)
式中,g0为地面点的实测重力;G为万有引力常数;ρ为地壳密度;∂γ/∂h为正常重力梯度。
利用式(2),由水准测量高差和水准路线上的重力值计算得到的正高,称为赫尔默特(Helmert)正高hH=c/gH。采用不同重力归算公式确定平均重力,可得到不同形式的正高。
在式(1) 中,将流动点重力g用流动点正常重力γ替换,得到正常高h*定义如下[1, 2, 7]
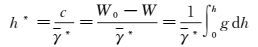 (3)
(3)
式中,γ*为地面点到大地水准面间的平均正常重力。
1.2 解析正高与Molodensky正常高 1.2.1 解析正高若直接由地球外部重力场数据,按解析延拓法计算地面点到大地水准面间的流动点重力g,则平均重力可按式(4) 确定
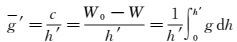 (4)
(4)
本文将按解析平均重力g′确定的正高暂称为解析正高h′。由式(4) 得解析正高定义如下
 (5)
(5)
与Helmert正高相比,解析正高可适用于近地空间的非地面点,利用解析正高公式,易于建立不同类型高程之间的重力学关系。
1.2.2 Molodensky正常高如图 1所示,从地面点A向下量取其高程异常ζ后得到似地形面上的Q点(在一定海拔高度的大陆地区,ζ<0,似地形面在地面上方)。令Q到对应地球椭球面上G点之间的平均正常重力为γG,用γG替换式(1) 或式(3) 中A点到大地水准面上O点之间的平均(正常)重力,得到Molodensky理论中重力学定义[3]的正常高hγ=c/γG。

|
| 图 1 Molodensky正常高的几何意义 Fig. 1 Geometric interpretation for Molodensky normal height |
设U0=W0,由Molodensky基本条件U0-UQ=W0-W得
 (6)
(6)
式中,U0、UQ分别为地球椭球面和Q点的正常重力位;W为A点的重力位。
式(6) 中,通过引入Molodensky基本条件,只是将计算重力位数c的积分变量由难以测定的实际重力g变换为可解析计算正常重力γ,但仍然有c=W0-W。
由式(5) 和式(6) 可得
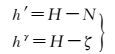 (7)
(7)
式中, H为A点的大地高;ζ为A点的高程异常;N为A点处的大地水准面高。
由于γG≠γ*,gH≠g′,因此对于正常高h*和Helmert正高hH有
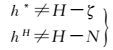 (8)
(8)
本文测试不同类型高程系统地面点高程之间的差异,分析GNSS代替水准与实际水准测量成果的一致性,研究高精度GNSS代替水准算法。
2 高程基准面的重力等位性质传统的高程基准由水准原点(高程基准零点)和高程控制网实现,水准点正(常)高的起算面称为高程基准面或零高程面。为保证GNSS代替水准测定的正(常)高与水准测量成果一致,要求GNSS代替水准中采用的高程基准面与水准点正(常)高的起算面完全一致。
2.1 由高程系统定义分析高程基准面的等位性质各种类型高程系统的通用高程定义可表示为:hG=c/G=W0-W/G,而高程系统的差别视如何选定分母中的G值而定。将大地水准面重力位W0用区域高程基准零点重力位WR代替,区域高程基准中通用高程定义为:hG=cR/G=(WR-W)/G。
在区域高程基准中,水准点的重力位数cR等于高程基准零点重力位WR与该点重力位W之差,水准点高程的起算重力位等于高程基准零点重力位WR,水准点零高程面的重力位唯一,处处都等于WR,因此,区域高程的零高程面(高程起算面)是过高程基准零点的重力等位面。
对于任一地面点,不论是用正高、正常高还是力高来表示其海拔高程,该点的重力位数c或cR都是唯一的,高程基准面的重力位处处都等于高程基准零点重力位,高程基准面的这种重力等位性质与采用的高程系统类型无关。
总之,不论是正高系统、正常高系统、力高系统,还是重力位数系统,高程基准面是唯一不变的,都是过高程基准零点的大地水准面。
2.2 非地面点的高程异常及其正常高起算面由式(3) 或式(6) 可知,正常高定义适合非地面点,而由重力方法确定的似大地水准面是相对计算者选定、用于表示地面的特定数字高程模型而言。设在似大地水准面模型计算时用2′×2′数字高程模型代表地面,若某地面点A的正常高为h,由2′×2′数字高程模型内插得到该点在数字高程模型面上的正常高为h0,由对应的2′×2′似大地水准面模型内插得到该点在数字高程模型面上的高程异常为ζ0,则A点的实际高程异常ζ为[1]
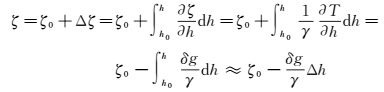 (9)
(9)
式中,T、δg、γ分别为地面点到对应数字高程模型面间流动点的扰动位、扰动重力和正常重力。
中国大陆2′×2′数字高程模型的高程最大值一般只有6 km,而珠峰地区的实际地面高程超过8 km。若令δg=-100 mGal,γ≈10 m/s2,Δh=2000 m,则Δζ=100×10-5/10×2000 m=20 cm。即在珠峰地区,若将2′×2′重力似大地水准面直接作为正常高的基准面,则由GNSS代替水准测定的正常高要比实际正常高大20 cm。
当A点不在地面上,如在地面下方或低空高度上,Δζ的绝对值还会进一步增大。因此,将似大地水准面作为正常高的起算面是不严密的。
综上所述,在严格意义上所有类型高程系统的基准面都是重力等位面。中国国家1985高程基准采用正常高系统,高程基准面是过青岛零点的大地水准面。
3 不同类型高程系统地面点高程之间的差别测试分析 3.1 地面点正常高h*与Molodensky正常高hγ的差别任意地面点的正常高h*与Molodensky正常高hγ的差异可表示为
 (10)
(10)
式中,∂γ/∂h=0.308 6×10-5s-2为正常重力梯度。
在一定海拔高度的大陆地区,ζ<0,因此似地形面在地面上方,由式(10) 可得:hγ>h*。
令ζ=-50 m,h*=6000 m,则h*-hγ=-0.308 6×10-6×50×6000 m≈-0.09 m。Molodensky正常高hγ与正常高h*的差异在中国大陆东部地区约为0~3 cm,中部2~5 cm,西部4~10 cm。
利用Eigen6C4地球重力场模型分别按Molodensky正常高定义hγ=(W0-W)/γG和正常高定义h*=(W0-W)/γ*计算2′×2′数字高程模型面上的正常高值,得到hγ-h*结果见图 2。

|
| 图 2 地面点Molodensky正常高hγ与正常高h*之差 Fig. 2 Differences between Molodensky normal height hγ and normal height h* at ground points |
在中国《国家一、二等水准测量规范》中,用于计算两水准点i、i+1间水准高差正常水准面不平行改正ε的平均正常重力公式为[8]
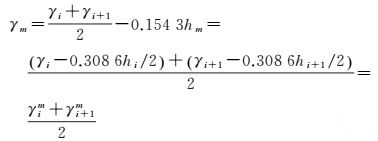 (11)
(11)
式中,γi、γi+1分别为水准点i、i+1在地球椭球面上的正常重力(单位为mGal);hi为水准点i的概略高程;hm=(hi+hi+1)/2;γim为水准点i(处)的平均正常重力。
式(11) 中,γim=γi-0.308 6hi/2,是水准点i处似地形面到地球椭球面间正常重力平均值的线性近似,可见在中国国家水准网成果中,水准点的正常高属于Molodensky正常高系统。
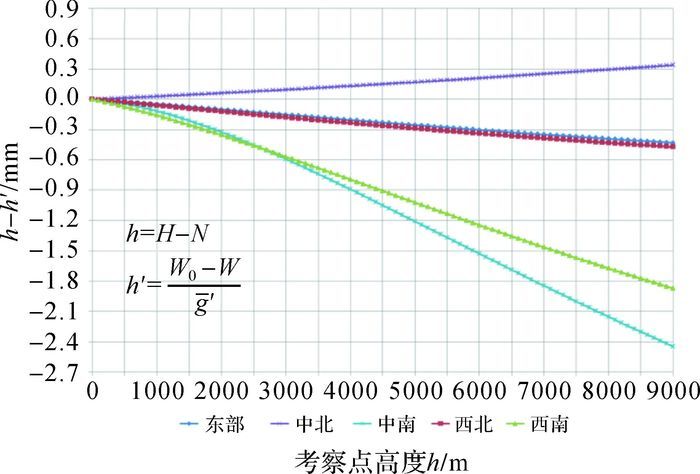
3.2 解析正高h′与H-N的差别测试分析在中国大陆东部、中部北方和南方、西部北方和南方各取1点,分别从大地水准面起算,以大地高每增加100 m为考察点,用Eigen6C4重力场模型计算考察点的重力位W、大地水准面的重力位W0、以及考察点到大地水准面间流动点的重力g,按定义计算解析正高h′=W0-W/g′。以h=H-N为x轴,以h与解析正高h′之差h-h′为y轴绘图,见图 3。
|
| 图 3 GNSS直接代替水准测定的正高h与解析正高h′的差别 Fig. 3 Differences between orthometric height h determined by GNSS replacing leveling and actual orthometric height h′ |
由图 3可知,在整个中国大陆地区,GNSS直接代替水准测定的正高h=H-N与解析正高h′相差不到2 mm。忽略由地球重力场模型计算其对应大地水准面上重力位W0的计算误差,则有:h′=H-N。可见,等解析正高面与大地水准面平行,GNSS代替水准能直接测定地面点的解析正高。
采用同样方法,可以测试验证:hγ=H-ζ。
3.3 Molodensky正常高hγ与H-N的差别测试分析顾及地面点解析正高h′=H-N,则h=H-N与Molodensky正常高hγ的差异可表示为
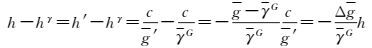 (12)
(12)
式中,Δg为地面点到大地水准面间的平均空间重力异常。
令Δg=-100 mGal,h=6000 m,则h-hγ=100×10-6×6000 m=0.6 m。
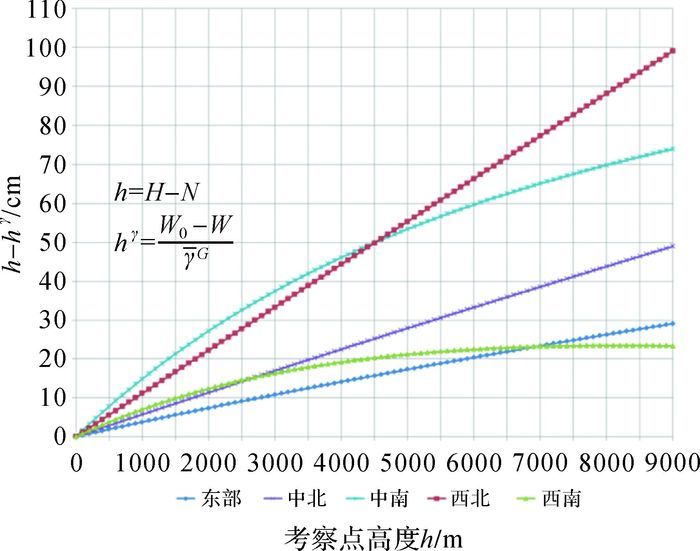
在中国大陆东部、中部北方和南方、西部北方和南方各取1点,由Eigen6C4地球重力场模型按定义计算Molodensky正常高hγ=(W0-W)/γG和有关模型参数。令h=H-N,以h为x轴,以h与Molodensky正常高hγ之差h-hγ为y轴绘图,见图 4。
|
| 图 4 Molodensky正常高hγ与(H-N)的差别 Fig. 4 Differences between Molodensky normal height hγ and (H-N) |
由图 4可知,h-hγ随高度增大而增大,在大地水准面附近接近零,在中国西部北方超过0.5 m;在中国东部地区,h-hγ一般小于0.15 m。
实际上,由式(7) 可得
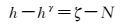 (13)
(13)
设GNSS定位测得地面点大地高为H,地面点到大地水准面的大地高差为h=H-N,由地球重力场知识可知,该点的重力位W=T+U=ζγ+U,其中,T、ζ、U分别为地面点的扰动位、高程异常和正常重力位,顾及通用高程定义hG=c/G,得
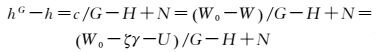 (14)
(14)
令
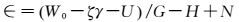 (15)
(15)
类比水准测量中正常高的水准面不平行改正,这里仍将∈作为GNSS代替水准中通用高程的水准面不平行改正。
当G=g′时,hG=c/G=c/g′=h′为解析正高,此时∈=c/g′-H+N=h′-H+N=0。因此在GNSS代替水准中,解析正高h′的水准面不平行改正恒等于零。
当G=gH、γ*或γG时,∈≠0。因此在GNSS代替水准中,Helmert正高hH、正常高h*、Molodensky正常高hγ和力高hd(力高中G为常量,力高系统可看成是与重力位数系统等价的一种特殊类型正常高系统),都需要增加水准面不平行改正∈。
由于大地水准面重力位W0已知,地面点高程异常ζ可由大地水准面模型按Possion积分计算,正常重力位U、正常重力γ和平均正常重力γ*(或γG)可严密计算,因此在GNSS代替水准中,正常高(h*或hG)水准面不平行改正∈能由GNSS定位和大地水准面模型按式(15) 计算。
由于不能测量地球内部重力,Helmert正高hH的水准面不平行改正也难以准确计算。
若用GNSS代替水准传递高差,也需对高差增加水准面不平行改正Δ∈。即
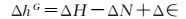 (16)
(16)
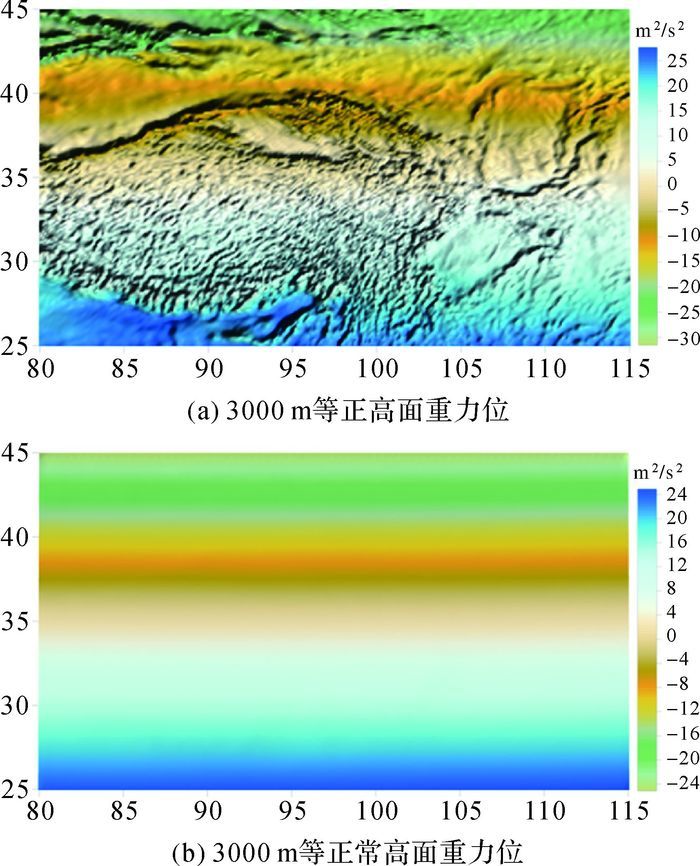
由图 2可知,等解析正高面相互之间平行,且都与大地水准面平行;但由图 3可以看出,等正常高面相互之间不平行,等正常高面与大地水准面也不平行。利用等高程面上的重力位差大小和空间分布情况可以评价高程系统的力学性质。图 5是用Eigen6C4重力场模型计算的3000 m等正高面的重力位(图 5(a))和3000 m等正常高面的重力位(图 5(b))。
由图 5可知,等正高面的重力位(已扣除了平均值)随空间变化复杂,等正常高面沿卯酉圈方向具有等位性质。考察卯酉圈上正常高等于3000 m的两点A、B,其重力位差ΔWAB≈0.308 6×10-5ΔNABh*≈9.2×10-3ΔNAB m2/s2(ΔNAB为两点处大地水准面高之差),是小量。图 5(b)中各卯酉圈方向的重力位标准差均小于0.03 m2/s2。可见,正常高系统更有利于描述地势和地形起伏。
|
| 图 5 重力位对比图 Fig. 5 Gravitational potential contrast |
5 GNSS代替水准测定正常高的新算法 5.1 GNSS代替水准测定近地点正常高的统一算法
当忽略大陆水负荷、非潮汐海平面和非潮汐大气负荷等变化引起的大地水准面形变(GRACE监测结果显示,非潮汐大地水准面形变达到厘米量级)时,大地水准面高不随时间变化,是稳态的。本文只讨论稳态大地水准面情况下GNSS代替水准测定正常高算法。
设GNSS测定近地点A(可以是地面点,也可以是非地面点)的大地高为H,忽略厘米量级的地心运动影响,则GNSS代替水准测定正常高h*(或hγ)的公式可统一写为如下形式
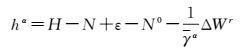 (17)
(17)
式中,hα=h*或hγ;γα=γ*或γG;N0为大地水准面零阶项;ΔWr为区域高程基准位差。
实际作业中,可不额外计算水准面不平行改正∈,直接由正常高定义导出GNSS代替水准测定A点正常高hα的统一算法公式为
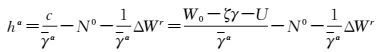 (18)
(18)
式中,W0为大地水准面重力位;γ、U分别为A点正常重力与正常重力位;ζ为A点高程异常,能由大地水准面模型按Possion公式精确计算。GNSS大地高H以ζ、γ、U自变量的形式代入。
不难发现,式(18) 也适合于GNSS代替水准测定力高hd的高精度计算。
5.2 高精度GNSS代替水准测定正常高的误差分析对GNSS代替水准测定正常高的通用算法式(18) 进行变分,省略γ上标,顾及高程基准位差ΔWr为小量,以及W0、N0和ΔWr为常数,其变分都等于零,得
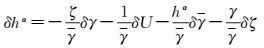 (19)
(19)
式中,δγ、δU分别为A点正常重力变分和正常重力位变分;δγ为平均正常重力变分;δζ为A点高程异常变分。
对于误差分析目的,不失一般性,可采用如下线性近似
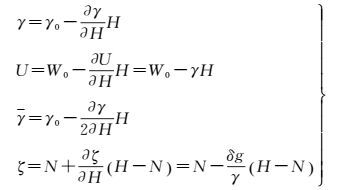 (20)
(20)
对式(20) 进一步进行变分,顾及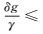

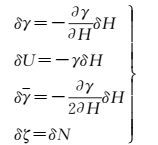 (21)
(21)
将式(21) 代入式(19),并顾及
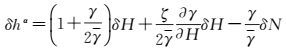 (22)
(22)
令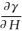
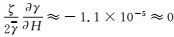
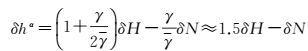 (23)
(23)
式(23) 中,GNSS代替水准测定正常高(h*或hγ)的误差δhα由两项构成:大地高误差δH和大地水准面误差δN,误差影响因子分别为τH≈1.5(<1.5) 和τN≈1(<1)。这表明,1倍大地高误差会导致近1.5倍的正常高误差,1倍大地水准面误差会导致近1倍的正常高误差。
在GNSS代替水准测定力高hd时,由于不存在γ误差,因此有
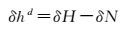 (24)
(24)
本文从高程系统定义出发,探讨高程基准面的重力等位性质,测试分析不同类型高程系统地面点高程之间的差异,考察GNSS代替水准与实际水准测量成果的一致性,进而提出新的GNSS代替水准算法。主要结论包括:
(1) 当精度要求达到厘米级水平时,正常高的基准面也应是大地水准面。中国国家1985高程基准采用正常高系统,其高程基准面是过青岛零点的大地水准面。
(2) 近地空间中等解析正高面与大地水准面平行,GNSS代替水准能直接测定地面点的解析正高,但正常高系统更有利于描述地势和地形起伏。
(3) 本文给出的GNSS代替水准测定近地点正常高算法,大地高误差对正常高结果的影响比大地水准面误差大,前者影响约为后者的1.5倍。
致谢: 本文是在许厚泽院士、宁津生院士、晁定波教授、魏子卿院士、杨元喜院士、李建成院士、吴晓平教授、黄谟涛高工、李斐教授、翟国君高工、张传定教授、申文斌教授、罗志才教授与几位审稿专家的许多建设性意见基础上逐步完善的,在此特别致谢。
| [1] | 党亚民, 章传银, 陈俊勇, 等. 现代大地测量基准[M]. 北京: 测绘出版社, 2015. DANG Yamin, ZHANG Chuanyin, CHEN Junyong, et al. Modern Geodetic Datum[M]. Beijing: Surveying and Mapping Press, 2015. |
| [2] | 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 2版. 武汉: 武汉大学出版社, 2010. KONG Xiangyuan, GUO Jiming, LIU Zongquan. Foundation of Geodesy[M]. 2nd ed. Wuhan: Wuhan University Press, 2010. |
| [3] | HOFMANN-WELLENHOF B, MORITZ H. Physical Geodesy[M]. New York: Springer, 2006. |
| [4] | ARDALAN A A, SAFARI A. Global Height Datum Unification:a New Approach in Gravity Potential Space[J]. Journal of Geodesy, 2005, 79(9): 512–523. DOI:10.1007/s00190-005-0001-0 |
| [5] | BALASUBRAMANIA N.Definition and Realization of a Global Vertical Datum[R].Ohio:Department of Geodetic Science and Surveying, the Ohio State University, 1994:112. |
| [6] | BLEWITT G. Self-consistency in Reference Frames, Geocenter Definition, and Surface Loading of the Solid Earth[J]. Journal of Geophysical Research, 2003, 108(B2): 2103. |
| [7] | FILMER M S, FEATHERSTONE W E, KUHN M. The Effect of EGM2008-based Normal, Normal-orthometric and Helmert Orthometric Height Systems on the Australian Levelling Network[J]. Journal of Geodesy, 2010, 84(8): 501–513. DOI:10.1007/s00190-010-0388-0 |
| [8] | 国家测绘局. GB/T 12897-2006国家一、二等水准测量规范[S]. 北京: 中国标准出版社, 2006. National Bureau of Surveying and Mapping.GB/T 12897-2006 Specifications for the First and Second Order Leveling[S].Beijing:China Standard Press, 2006. |
| [9] | IHDE J, SÁNCHEZ L. A Unified Global Height Reference System As a Basis for IGGOS[J]. Journal of Geodynamics, 2005, 40(4-5): 400–413. DOI:10.1016/j.jog.2005.06.015 |
| [10] | 李建成. 最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651–660. LI Jiancheng. The Recent Chinese Terrestrial Digital Height Datum Model:Gravimetric Quasi-geoid CNGG2011[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 651–660. |
| [11] | LAVALLÉE D A, VAN DAM T, BLEWITT G, et al. Geocenter Motions from GPS:A Unified Observation Model[J]. Journal of Geophysical Research, 2006, 111(B5): B05405. |
| [12] | MORITZ H. Geodetic Reference System 1980[J]. Journal of Geodesy, 2000, 74(1): 128–133. DOI:10.1007/s001900050278 |



