2. 中国地质调查局发展研究中心, 北京 100037
2. Development and Research Centre, China Geological Survey, Beijing 100037, China
空间关系是空间数据组织、查询、分析和推理的基础,一直受到国内外地理信息系统(GIS)研究方面的广泛关注[1-3]。拓扑关系是其中最重要的一种空间关系,描述两个空间对象在连续空间变换(旋转、缩放、平移等)下的拓扑不变性[3-5]。许多方法被用来描述空间对象之间的拓扑关系,比如9交模型[5-6]和区域链接法(region connection calculus,RCC)[7-8]。这些方法最初只是描述简单点、简单线和简单区域等空间对象之间的拓扑关系。随着空间信息获取与更新能力的飞速发展,空间数据的复杂程度也在增加。复杂区域对象定义已有大量研究[9-13],主要包括有确定边界的区域对象和带不确定边界的区域对象(模糊对象)。本文主要讨论有确定边界区域对象间的拓扑关系计算问题。
针对复杂区域拓扑关系的描述,9交模型仍是广泛使用的一种方法,并被OpenGIS采用[12]。文献[13-14]给出了确定边界复杂区域间的33种9交拓扑关系。同时,研究人员也提出了大量扩展9交模型的方法,比如9+交集模型[15],V9I模型[16-17]、扩展9交模型[18-20]、25交模型[21]等。这些方法根据复杂对象的特点改变9交矩阵中各个元素的含义进而形成新矩阵。文献[4, 22]采用关系矩阵表精细描述复杂区域间的拓扑关系,主要将复杂区域分解为有限个简单区域,这些简单区域按一定关系组合构成复杂区域的表达形式,例如带一个洞区域,可以分解为两个简单区域,一是洞区域,另一个是包含洞的广义区域。关系矩阵表详细描述了分解后两两简单区域间的拓扑关系,简单区域间仅存在8种基本拓扑关系。然而,在空间查询中,关系矩阵表不能像其他拓扑关系描述模型一样方便使用,需要将其转化为目前GIS领域熟知的拓扑查询谓词或者其他交集模型[23]。如OpenGIS中提供了两种查询方法[12],一种是面向语义的查询谓词,比如Overlap等;另一种是基于9交矩阵的查询。其核心问题是如何利用简单区域间的8种基本拓扑关系计算出复杂区域间的拓扑关系。文献[24—25]利用8种基本拓扑关系谓词形成推理组合表来计算复杂区域间的拓扑关系谓词,但是此类方法不能直接计算出9交矩阵。
本文提出了基于9交矩阵的拓扑关系计算方法,将复杂区域分解有限个简单区域,采用正则表达式描述其多部分和洞构成,通过定义两个9交关系矩阵操作算子,利用分解区域间的拓扑关系直接计算复杂区域间的9交关系矩阵。
1 相关定义 1.1 复杂区域本文定义基于文献[11]、OpenGIS[12]和文献[13]中相关描述。复杂区域对象是定义在二维空间ℜ2上带确定边界的正则闭集合,由有限个连通子集构成,其结构定义如下:
定义1:简单区域同胚于一个圆盘,具有完全连通的内部、边界和外部,如图 1(a)。

|
| 图 1 复杂区域对象定义 Fig. 1 Definition of complex region |
定义2:带洞简单区域A是由一个外部广义区域A0减去n(n>0) 个洞区域Ai构成,如图 1(b)。设A0, …,An是n+1个简单区域,∀i,j∈{1,…, n},i≠j,则Aj和Ai相离而且A0包含Aj和Ai。带洞简单区域A定义为
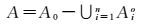
定义3:多部分区域A是n(n≥1) 个相离的简单区域或者带洞简单区域的构成,如图 1(c)。设A1、…、An是n个简单区域或者带洞简单区域,∀i,j∈{1,…,n},i≠j,则Aj和Ai相离。多部分区域A定义为
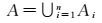
复杂区域既可以是简单区域,也可以是带洞简单区域或者多部分区域及其组合。
1.2 复杂区域的正则表达式定义4:如果一个复杂区域A由两个区域对象A1和A2构成且A1与A2相离,记A=A1+A2,表示A是A1和A2的并集,“+”称为区域加算子,并且A1o=A1o∩A2o,∂A=∂A1∪∂A2和A+=A+∪A2+。
定义5:如果一个复杂区域A由两个区域对象A1和A2构成且A1包含A2,记A=A1-A2,表示A是A1减去A2的差集,“-”称为区域差算子,并且A2o=A1o∩A+,∂A=∂A1∪∂A2和A1+=A+∪A2o。
一个复杂区域的结构构成形式可由“+”和“-”形成一个正则表达式。定义2带洞简单区域可表示为A=A1-A2,定义3多部分区域可记为A=A1+…+An。表 1是不同区域对象的表达方式,采用正则表达式可以使用语法树对表达式进行不同方式的遍历,本文采用先序遍历方法,将复杂区域逐层级进行分解。此外,根据本文复杂区域定义,一个复杂区域可能对应多个正则表达式,如表 1实例C,C1-(C2-C4)-C3、(C1-C2-C3)+C4以及(C1-(C2+C3))+C4均可表达该复杂区域的结构。为了可以从表达式中分析出不同对象的层次关系和包含关系,建议选择此类信息的表达式,如C1-(C2-C4)-C3显然更能反映出各个简单对象之间的包含关系(比如C2包含C4)以及相离关系(C4与C3相离)。
| 实例 | A | B | C |
| 结构构成 |  |  |  |
| 正则表达式 | A1-(A2-(A3-A4)) | (B1-B2-B3)+(B4-B5) | C1-(C2-C4)-C3 |
| 语法树 |  |  |  |
1.3 9交模型
9交模型[5-6]是通过两个复杂区域A、B的内部(°)、边界(∂)和外部(+)的交集来描述拓扑关系。由一个3×3的0/1型9交矩阵R9(A,B)表示

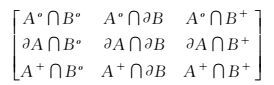
R9(A,B)是所能表达的拓扑关系总数为33种[13]。若A和B均为简单区域,如图 2,仅可推导出8种拓扑关系,依次定义为:disjoint、meet、contain、cover、inside、coverby、equal和overlap。
2 基于9交矩阵的拓扑关系计算
本文拓扑关系计算的主要方法是利用分解区域间的已知拓扑关系推导复杂区域间的拓扑关系。复杂区域的分解是根据其正则表达采用先序遍历的方式逐层分解,每次分解得到两个新的正则表达式,直至全为简单对象。如图 3,计算A、B的拓扑关系为:先序遍历B, B分解为简单对象后,R9矩阵转置再逐层分解A。整个拓扑关系的计算层次表现为8种基本拓扑关系进行组合的形式。可以看出,拓扑关系计算的核心是根据区域“+”和“-”操作进行拓扑关系的组合,该组合即为本文提出的两种9交关系矩阵操作算子。

|
| 图 3 拓扑关系的分层计算 Fig. 3 Hierarchical computation of 9-instesection |
2.1 多部分区域对象分解和加布尔操作
定义6:9交关系矩阵的加布尔操作∨
若复杂区域B=B1+B2,B1与B2相离,则复杂区域A和B的9交关系矩阵加布尔操作∨为
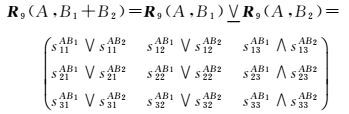
不成立条件:(∂A⊆B∨Ao⊆Bo)∧∂A∩B1+≠φ∧∂A∩B2+≠φ
显然,∨满足交换律,即R9(A,B1)∨R9(A,B2)=R9(A,B2)∨R9(A,B1)。
证明:由于B=B1+B2,由定义4可得

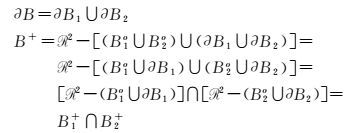
设Ma={Ao,∂A,A+},∀a∈Ma可得
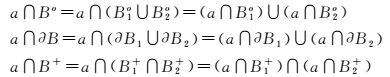
由于R9(A,B)是0/1布尔型矩阵,需要将上述集合的并和交操作转化为逻辑或和逻辑与。显然,集合的并和逻辑或对应,运算不会产生歧义,故:a∩Bo→si1AB1∨ri1AB2,a∩∂B→si2AB1∨si2AB2,其中, i是R9(A,B)矩阵的行号。
集合的交和逻辑与运算对应,故a∩B+→si3AB1∧si3AB2。然而,集合的交转化为逻辑与是会产生歧义的,如图 4。

|
| 图 4 集合运算和逻辑运算的差异 Fig. 4 Differences of set and logical Boolean operators |
下面论证加布尔操作不能成立的情况。
B的内部(边界)是B1和B2内部(边界)的并集,不会出现A与B1和B2的内部(边界)相交,而与B的内部(边界)不相交的情况,也不会出现A与B1和B2的内部(边界)都不相交,而与B的内部(边界)相交的情况,故第1列和第2列为逻辑或操作恒成立。
B的外部是B1和B2外部的交集,由于B1和B2相离且均不为空,则B1+=B+∩B2+⊂B1+且B1+∩B2+⊂B2+,交集运算转为逻辑与运算会出现a∩(B1+∩B2+)≠(a∩B1+)∧(a∩B2+)的情况。由于A+∩B+≠φ,只需考虑加布尔操作公式Ao∩B+和∂A∩B+的计算正确性。
(1) 若Ao∩B1+=φ且A2o∩B+=φ,则∂A∩B1+=φ且∂A∩B2+=φ。由Ao∩B1+=φ和∂A∩B1+=φ可得A=Ao∪∂A⊆ ℜ2-B1+,即A⊆B1,同理可得A⊆B2,则与B1∩B2=φ矛盾。此种情况不存在。
(2) 若Ao∩B1+=φ且Ao∩B2+≠φ,则∂A∩B1+=φ,可得A⊆B1⊂B,加布尔操作公式恒成立。同理,若Ao∩B2+=φ且Ao∩B1+≠φ,加布尔操作公式恒成立。
(3) 若Ao∩B1+≠φ且Ao∩B2+≠φ,分3种情况。
当∂A∩B1+=φ且∂A∩B2+=φ。由∂A∩B1+=φ可得∂A⊆B1,同理可得∂A⊆B2,与B1∩B2=φ矛盾,此情况不存在。
当∂A∩B1+=φ且∂A∩B2+≠φ。由∂A∩B1+=φ可得∂A⊆B1⊂B,公式恒成立。同理,当∂A∩B1+≠φ且∂A∩B2+=φ,公式恒成立。
当∂A∩B1+≠φ且∂A∩B2+≠φ时,假设加布尔操作公式不成立,可穷举出两种情况:① Ao∩B+=φ且∂A∩B+=φ,说明Ao∩B1+⊆B2o且Ao∩B2+⊆B1o,此时Ao⊆Bo,如表 2实例1、2此种情况存在,加布尔操作公式不成立;② Ao∩B+≠φ且∂A∩B+=φ,说明∂A∩B1+⊆B2且∂A∩B2+⊆B1,此时∂A⊆B,如表 2实例3、4此种情况存在,加布尔操作公式不成立。综上分析,加布尔操作∨公式当∂A∩B1+≠φ∧∂A∩B2+≠φ∧(∂A⊆B∨Ao⊆Bo)时不成立。
| 序号 | A,B | 实例 | R9(A,B) | R9(A,B1) | R9(A,B2) |
| 1 | A=A1+A2 B=B1+B2 |  |  |  |  |
| 2 | A=A1+A2 B=B1+B2 |  |  |  |  |
| 3 | A=A1+A2 B=B5-B3+B2 B1=B5-B3 |  |  |  |  |
| 4 | A=A1-A3+A2 B=B1+B6-B4 B2=B6-B4 |  |  |  |  |
推论1:R9(B1+B2,A)=[R9(A,B1+B2)]T=[R9(A,B1)∨R9(A,B2)]T。
推论2:R9(A,B1+B2…+Bn)=R9(A,B1)∨R9(A,B2)…∨R9(A,Bn)=
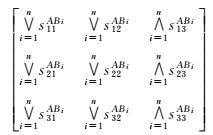
式中,A、B1、…、Bn均为简单区域,n>1,∀i,j=1, …, n,且i≠j, Bi与Bj相离。

定义7:9交关系矩阵的差布尔操作∧
若复杂区域B=B1-B2,B1包含B2,则复杂区域A和B的9交关系矩阵差布尔操作∧为
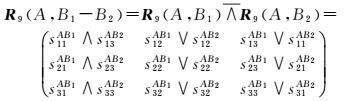
不成立条件
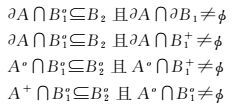
∧不满足交换律,即R9(A,B1)∧R9(A,B2)≠R9(A,B2)∧R9(A,B1)。
证明:由于B=B1-B2,由定义5可得
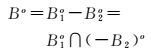
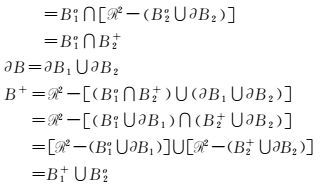
设Ma={Ao,∂A,A+},∀a∈Ma可得
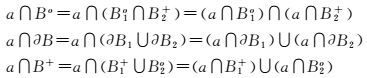
R9(A,B1-B2)的第2列和第3列为R9(A,B1)和R9(A,B2)两个分解关系矩阵的逻辑或,第1列为两个分解关系矩阵的逻辑与。
下面论证差布尔操作不能成立的情况。
B的外部(边界)是B1和B2补集的外部(边界)的并集,不会出现A与B1和B2补集的外部(边界)相交,而与B的外部(边界)不相交的情况,也不会出现A与B1和B2补集的外部(边界)都不相交,而与B的外部(边界)相交的情况,故第2列和第3列逻辑或操作恒成立。
B的内部是B1和B2补集内部的交集,由于B1包含B2,Bo=B1o-B2o,则Bo⊂B1o且Bo⊂B2+,交集运算转为逻辑与运算会出现a∩(B1o∩B2+)≠(a∩B1o)∧(a∩B2+)的情况。下面逐一分析差布尔操作公式不成立的条件。
(1) 当Ao∩B1o=φ,由Bo⊂B1o可知不存在Ao∩Bo≠φ的情况,公式中Ao∩Bo=φ计算成立。
(2) 当Ao∩B1o≠φ,若Ao∩B2+=φ,说明A⊆B2,由于Bo⊂B2+,公式中Ao∩Bo=φ计算恒成立;若Ao∩B2+≠φ,假设公式不成立,即Ao∩Bo=φ,由于Bo=B1o-B2o,说明Ao∩B1o⊆B2o且Ao∩B1+≠φ,如表 3第4种实例,公式不成立。
| 序号 | A,B | 实例 | R9(A,B) | R9(A,B1) | R9(A,B2) |
| 1 | A=A1-A2 B=B1-B2 |  |  |  |  |
| 2 | A=A1-A2 B=B1-B2 |  |  |  |  |
| 3 | A=A1-A2 B=B1-B2 |  |  |  |  |
| 4 | A=A1+A2 B=B1-B2 |  |  |  |  |
(3) 当A+∩B1o=φ,且A+∩B2+≠φ,由Bo⊂B1o可知公式中A+∩Bo=φ计算恒成立,此时B1⊆A。
(4) 当A+∩B1o≠φ,假设公式不成立,即A+∩Bo=φ,由于Bo=B1o-B2o,说明A+∩B1o⊆B2o且Ao∩B1o≠φ,如表 3第1、第2和第3种实例,公式不成立。
(5) 当∂A∩B1o=φ,由Bo⊂B1o可知∂A∩Bo=φ计算恒成立。
(6) 当∂A∩B1o≠φ,若∂A∩B2+=φ,由于Bo⊂B2+,公式中∂A∩B2o=φ计算恒成立;若∂A∩B+≠φ,假设公式不成立,即∂A∩B1o=φ,说明∂A∩B1o⊆B2且∂A∩∂B1≠φ或者∂A∩B+≠φ,如表 3第1和第4种实例,此时上述公式不成立。
综上分析,差布尔操作公式在∂A∩B1o⊆B2且∂A∩∂B1≠φ,∂A∩B1o⊆B2且∂A∩B1+≠φ,Ao∩B1o⊆B2o且Ao∩B1+≠φ或者A+∩B1o⊆B2o且Ao∩B1o≠φ 4个条件之一满足时不成立。
推论3:R9(B1-B2,A)=[R9(A,B1-B2)]T=[R9(A,B1)∧R9(A,B2)]T。
推论4:R9(A,B1-B2…-Bn)=
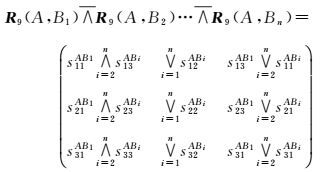
式中,A、B1、…、Bn均为简单区域,n>1,∀i=1, …, n, B1包含Bi。

从9交关系矩阵操作算子的证明看出,其不成立原因是集合运算和逻辑布尔运算之间的差异。布尔运算是对集合运算的简化,一个0/1型矩阵可表示很多种交集可能性。由于从9交矩阵无法获知复杂区域间的真实交集形式,故加和差布尔操作公式直接计算得到的矩阵可能对应多种拓扑关系,产生表 2、表 3所示歧义问题。
根据9交模型的特点以及转置矩阵RT的性质,可知R9(A,B)=[R9(B,A)]T。然而,从加和差布尔操作公式不成立条件可以看出,公式发生歧义时,分别计算R9(A,B)和R9(B,A),存在R9(A,B)≠[R9(B,A)]T的情况。因为不成立条件影响两个矩阵元素的位置不一样,当不成立条件对计算R9(A,B)造成影响时,并不对R9(B,A)的计算造成影响。因此,根据这一特性可消除公式的歧义性。即利用这两个矩阵的逻辑与运算得到最终的正确结果。修正公式为
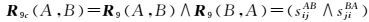
式中,sijAB是R9(A,B)的矩阵元素,sjiBA是R9(B,A)的矩阵元素。
2.4 计算实例如图 5中两个带洞区域。绿化用地区域有3个简单面域构成A=A1-B1-B2,建筑用地区域也有3个简单面域构成B=B1+(B2-C1)。其构成简单区域间的拓扑关系如图 5所示。分别根据A和B的正则表达式先序遍历逐层分解,同时由于算子存在不成立情况,计算中还需要进行不成立条件的消除。R9(A,B)的计算如下(方框内为分解后的拓扑关系,需要修正后才能参与计算)

|
| 图 5 计算实例 Fig. 5 An example for complex regions with holes |
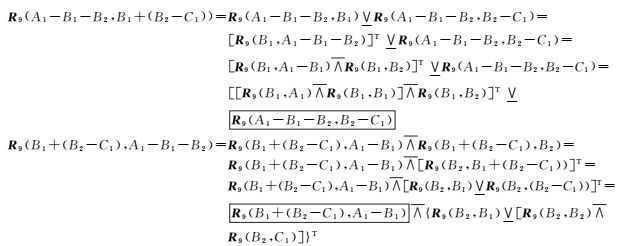
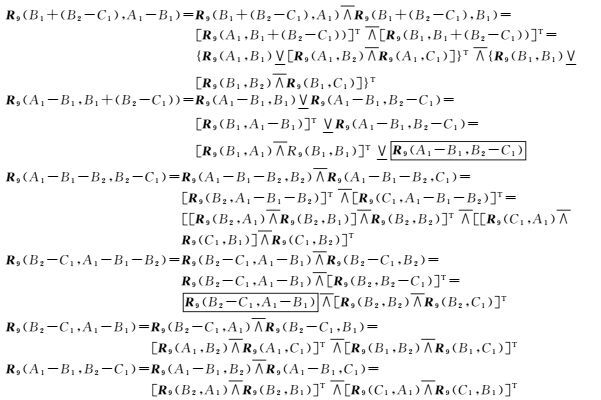
从以上过程可以看出,分解过程从上向下进行,计算过程从下向上进行。计算过程中,方框内的拓扑关系可能存在计算错误的情况,需要按2.3节的方法进行修正,修正后方可进行下一步计算。需要修正的关系主要包括先序遍历A和B后分解得到的复杂区域,如表 4,根据计算的先后顺序进行修正。本实例中只有最后一步,即R9(A1-B1-B2,B1+(B2-C1))与R9(B1+(B2-C1),A1-B1-B2)存在计算问题。修正过程如表 5所示,R9(A,B)与[R9(B,A)]T在计算有误的位置处得到的结果不一致,按逻辑与运算进行修正后得到正确的结果。
| A1-B1-B2 | A1-B1 | |
| B1+(B2-C1) | R9≠[R9]T | R9=[R9]T |
| B2-C1 | R9=[R9]T | R9=[R9]T |
| R9(A1-B1-B2, B1+(B2-C1)) 修正结果 | R9(A1-B1-B2, B1+(B2-C1)) 计算结果 | R9(B1+(B2-C1), A1-B1-B2) 计算结果 |
 |  |  |
3 推导已知结构区域对象间的9交拓扑关系
利用以上两个算子可计算出已知结构区域对象间所有可能的9交拓扑关系。首先利用关系矩阵表[11]描述复杂区域间的精细拓扑关系,然后将关系矩阵表转化为9交拓扑关系。
设复杂区域A的简单区域集合为WA={A1,A2,…,Ai,…,Am};B的简单区域集合WB={B1,B2,…,Bi,…,Bn},其中m≥1,n≥1。关系矩阵表,如表 6,描述A与B间所有可能的拓扑关系。
基于关系矩阵表的拓扑关系计算和推理已有研究[22]。利用A、B与B、C的关系矩阵表推理A、C关系矩阵表的公式为
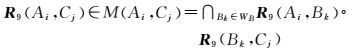
式中,M(Ai,Cj)为推理出的基本关系集合,R9取值均为为基本关系,Cj∈WC, Ai∈WA。
分析复杂区域的9交拓扑关系可利用关系矩阵表转化为9交关系矩阵,推导和推理任意复杂区域的9交拓扑关系。表 6中有m×n个基本拓扑关系,其能描述的拓扑关系个数为8m×n,其中存在大量不合理的情况,需要设定一定的条件剔除这些不合理的拓扑关系。根据本文复杂区域的定义,简单对象间的关系是明确的,且仅存在包含和相离两种关系,可以设置如下限定条件
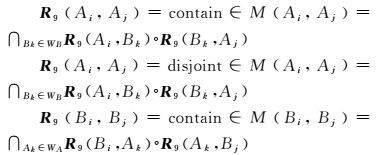

例如,当已知A=A1-A2,B=B1+(B2-B3)和C=C1+(C2-C3),从8m×n种关系中剔除不合理情况后,可以得到关系矩阵表和9交模型的可能关系数如表 7。
| A | B | C | |
| A | 14/152 | 16/950 | 16/950 |
| B | 16/950 | 21/11 066 | 21/11 066 |
| C | 16/950 | 21/11 066 | 21/11 066 |
当A、B与B、C的拓扑关系已知,如图 6所示,可推理出A, C的可能拓扑关系为15种,如表 8所示,进而可得到9交拓扑关系为5种,如图 7。注意的是,这里不是基于9交矩阵的推理,利用图 6中的9交矩阵得到的关系会更多,此处推理计算出的5种关系,仅是在已知A、B与B、C的具体拓扑关系下得到的。

|
| 图 6 A、B与B、C的拓扑关系 Fig. 6 Topological relations of A and B, and B and C |
| C1 | C2 | C3 | |
| A1 | {d,m,ct,cb,o} | {d,m,o} | {d} |
| A2 | {d} | {d} | {d} |

|
| 图 7 A、C推理结果:5种9交拓扑关系 Fig. 7 Reasoning results: 5 relations based on 9I |
4 局限性
加和差布尔操作公式的局限性主要表现为两点:
(1) 公式不是完全成立的,其本质原因是集合操作和逻辑操作的差异性。应用此公式一方面需要小心仔细地消除不成立条件,另一方面消除过程也使得计算过程变得复杂,这在计算实例(2.4节)中有所体现。
(2) 公式与复杂区域的定义有关。本文对复杂区域的限定条件是比较严格的。比如B=B1+B2要求B1与B2相离,保证了B1与B2不能出现1-meet的拓扑关系,故对于一些由相邻区域的组合比如被断层切断的地层或者多尺度分析中的区域合并,无法直接使用加布尔操作公式,如图 8(a)所示。同理B=B1-B2,当广义区域与洞存在公共边界,差布尔操作公式无法使用,如图 8(b)所示。

|
| 图 8 存在公共边界的复杂区域 Fig. 8 Complex regions with common boundaries |
5 结论
本文将复杂区域分解为有限个简单区域并采用正则表达进行结构描述,为了利用分解后的简单区域间精细拓扑关系计算出复杂区域间的拓扑关系,定义了两个9交关系矩阵操作算子,通过分解部分的拓扑关系直接计算出两个复杂区域的9交关系矩阵。并证明和分析了两个操作算子的不成立条件以及消除不成立条件的方法。该算子是基于9交矩阵的拓扑关系计算方法,结合关系矩阵表法[4]拓扑关系的推导和推理过程,在已知复杂区域结构的情况下,可以推导出其所有可能9交拓扑关系。
本文提出的9交关系矩阵操作算子也存在一定的局限性,一方面由于要消除不成立条件,计算过程显得较为复杂;二是与复杂区域的定义有关,不适用于所有区域对象。
由于布尔型9交矩阵对真实空间关系进行了简化,仅依赖矩阵运算存在信息不足问题,需进一步研究如何补充信息(如对图 11公共边及其相邻外部进行区分)扩展本方法适用于诸如多尺度分析中区域对象聚合操作等应用[26];同时后续研究可考虑将定义操作算子的方法扩展到其他类型空间对象(如点、线)以及其他交集模型,如25交[21]、E9I交模型[9]等。
| [1] | FRANK A U. Qualitative Spatial Reasoning about Distance and Directions in Geographic Space[J]. Journal of Visual Languages & Computing, 1992, 3(4): 343–371. |
| [2] | CLEMENTINI E, SHARMA J, EGENHOFER M J. Modelling Topological Spatial Relations:Strategies for Query Processing[J]. Computers & Graphics, 1994, 18(6): 815–822. |
| [3] | 陈军, 赵仁亮. GIS空间关系的基本问题与研究进展[J]. 测绘学报, 1999, 28(2): 95–102. CHEN Jun, ZHAO Renliang. Spatial Relations in GIS:A Survey on Its Key Issues and Research Progress[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2): 95–102. |
| [4] | EGENHOFER M J, CLEMENTINI E, DI FELICE P. Research Paper:Topological Relations between Regions with Holes[J]. International Journal of Geographical Information Systems, 1994, 8(2): 129–142. DOI:10.1080/02693799408901990 |
| [5] | EGENHOFER M J, FRANZOSA R D. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information Systems, 1991, 5(2): 161–174. DOI:10.1080/02693799108927841 |
| [6] | EGENHOFER M J, HERRING J R. Categorizing Binary Topological Relations between Regions, Lines and Points in Geographic Databases[R]. Orono:University of Maine, 1991. |
| [7] | RANDELL D A, CUI Z, COHN A G. A Spatial Logic Based on Regions and Connection[C]//Proceedings of the 3rd International Conference on Knowledge Representation and Reasoning. Los Altos:Morgan Kaufman, 1992:165-176. |
| [8] | LI Sanjing, YING Mingsheng. Extensionality of the RCC8 Composition Table[J]. Fundamenta Informaticae, 2002, 55(3-4): 363–385. |
| [9] | CLEMENTINI E, DI FELICE P. Spatial Model for Complex Objects with a Broad Boundary Supporting Queries on Uncertain Data[J]. Data & Knowledge Engineering, 2001, 37(3): 285–305. |
| [10] | TANG Xinming, KAINZ W, WANG Hongyan. Topological Relations between Fuzzy Regions in a Fuzzy Topological Space[J]. International Journal of Applied Earth Observation and Geoinformation, 2010, 12(S2): S151–S165. |
| [11] | WORBOYS M F, BOFAKOS P. A Canonical Model for a Class of Areal Spatial Objects[C]//Proceedings of the Third International Symposium on Advances in Spatial Databases. London:Springer-Verlag, 1993:36-52. |
| [12] | OpenGIS® Implementation Specification for Geographic Information:Simple Feature Access:Part 2:SQL Option[R]. Reference Number:OGC 06-104r4, 2006. |
| [13] | SCHNEIDER M, BEHR T. Topological Relationships between Complex Spatial Objects[J]. ACM Transactions on Database Systems, 2006, 31(1): 39–81. DOI:10.1145/1132863 |
| [14] | LI Sanjiang. A Complete Classification of Topological Relations Using the 9-intersection Method[J]. International Journal of Geographical Information Science, 2006, 20(6): 589–610. DOI:10.1080/13658810600661383 |
| [15] | KURATA Y. The 9+-Intersection:A Universal Framework for Modeling Topological Relations[M]//COVA T J, MILLER H J, BEARD K, et al. Geographic Information Science. GIScience 2008. Lecture Notes in Computer Science. Berlin:Springer, 2008:181-198. |
| [16] | CHEN Jun, LI Chengming, LI Zhilin, et al. Voronoi-based 9-intersection Model for Spatial Relations[J]. International Journal of Geographical Information Science, 2001, 15(3): 201–220. DOI:10.1080/13658810151072831 |
| [17] | LONG Zhiguo, LI Sanjiang. A Complete Classification of Spatial Relations Using the Voronoi-based Nine-intersection Model[J]. International Journal of Geographical Information Science, 2013, 27(10): 2006–2025. DOI:10.1080/13658816.2013.781607 |
| [18] | 欧阳继红, 霍林林, 刘大有, 等. 能表达带洞区域拓扑关系的扩展9-交集模型[J]. 吉林大学学报(工学版), 2009, 39(6): 1595–1600. OUYANG Jihong, HUO Linlin, LIU Dayou, et al. Extended 9-intersection Model for Description of Topological Relations between Regions with Holes[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(6): 1595–1600. |
| [19] | 李健, 欧阳继红, 王振鑫. 带双洞区域与简单区域间的拓扑关系[J]. 吉林大学学报(工学版), 2012, 42(5): 1214–1218. LI Jian, OUYANG Jihong, WANG Zhenxin. Topological Relations between a Region with Two Holes and a Simple Region[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(5): 1214–1218. |
| [20] | 陈占龙, 冯齐奇, 吴信才. 复合面状对象拓扑关系的表达模型[J]. 测绘学报, 2015, 44(4): 438–444. CHEN Zhanlong, FENG Qiqi, WU Xincai. Representation Model of Topological Relations between Complex Planar Objects[J]. Acta Geodaeticaet Cartographica Sinica, 2015, 44(4): 438–444. DOI:10.11947/j.AGCS.2015.20130708 |
| [21] | 沈敬伟, 周廷刚, 朱晓波. 面向带洞面状对象间的拓扑关系描述模型[J]. 测绘学报, 2016, 45(6): 722–730. SHEN Jingwei, ZHOU Tinggang, ZHU Xiaobo. Topological Relation Representation Model between Regions with Holes[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 722–730. DOI:10.11947/j.AGCS.2016.20150352 |
| [22] | DU Shihong, GUO Luo, WANG Qiao, et al. Efficiently Computing and Deriving Topological Relation Matrices between Complex Regions with Broad Boundaries[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(6): 593–609. DOI:10.1016/j.isprsjprs.2008.02.004 |
| [23] | EGENHOFER M J. Deriving the Composition of Binary Topological Relations[J]. Journal of Visual Languages & Computing, 1994, 5(2): 133–149. |
| [24] | TRYFONA N, EGENHOFER M J. Consistency among Parts and Aggregates:A Computational Model[J]. Transactions in GIS, 1996, 1(3): 189–206. DOI:10.1111/tgis.1996.1.issue-3 |
| [25] | NGUYEN V H, PARENT C, SPACCAPIETRA S. Complex Regions in Topological Queries[C]//Proceedings of the International Conference on Spatial Information Theory:COSIT97. Laurel Highlands:Springer-Verlag, 1997:175-192. |
| [26] | DU Shihong, FENG Chenchen, GUO Luo. Integrative Representation and Inference of Qualitative Locations about Points, Lines, and Polygons[J]. International Journal of Geographical Information Science, 2015, 29(6): 980–1006. DOI:10.1080/13658816.2015.1004333 |



