2. 地理信息工程国家重点实验室, 陕西 西安 710000
2. State Key Laboratory of Geo-information Engineering, Xi'an 710000, China
惯性导航系统(inertial navigation system,INS)是目前导航领域内重要的定位方法,具有高度自主性、全参数导航(可提供载体位置、速度、航向等9维导航参数)、短时导航精度高等众多优势[1]。但其定位误差会随着时间推移而不断发散,因此通常需要利用一些其他辅助导航方式引入外部信息,采用相关算法校正惯性导航系统,从而提高导航的精度[2]。
卫星导航定位作为辅助导航手段已被广泛地应用在各个领域,但在遇到高层建筑物、林荫道或者立交桥时,其信号会受到影响甚至出现中断现象,使导航定位精度降低[3-4]。此外在战时或者非常规条件下,卫星信号会受到干扰和屏蔽,严重影响了组合导航系统的正常工作。而运动载体通常行驶在道路上,因此矢量道路也能够提供准确的位置信息,且与惯性导航轨迹在空间位置上具有一一对应性。矢量数据具有无损变换、数据量小、空间效率高等优势,所以利用高精度矢量道路的路径匹配方法可以作为一种辅助导航手段来辅助惯性导航系统[5-6],有效地解决卫星导航定位“盲区”等无源环境下的轨迹校正和位置更新问题。
国内外关于路径匹配方法的研究较为深入和广泛,但大多是针对卫星信号良好环境下的导航校正,常用的有直接投影法、概率统计法、相关性算法、最近点迭代法等。直接投影法是利用载体轨迹点在当前最近道路的投影点进行位置校正,原理简单,操作方便,但匹配过程存在大量的距离运算,大大降低了匹配效率,遇到平行道路或者复杂交叉口等特殊道路时,容易出现误匹配[7-8]。概率统计法是以导航传感器得到的坐标位置为中心设置误差置信区,寻找最优待匹配道路的方法[9]。该算法能够剔除无效和冗余道路,匹配准确度较高,但却过度依赖于道路数据和导航系统精度,而惯性导航误差随时间发散,会对匹配过程造成干扰[10]。相关性算法是利用特殊形状(拐角、交叉等)对行驶轨迹进行校正,根据各个信息参数的权值,筛选出与运动载体轨迹相关性最高的道路作为其真实行驶轨迹[11]。该算法对交叉口和转弯拐角匹配具有良好的效果,但相关性的定权问题一般采用经验值,没有统一的标准和依据,会对导航结果造成不良的影响[12]。最近点迭代算法最初来源于图像配准,主要是通过反复刚性变换(旋转和平移)减小匹配对象和目标对象间的距离,使得匹配对象尽可能地接近目标对象[13-14]。该算法被广泛应用在辅助惯性导航系统中,能够有效抑制误差的发散,且具有较高的精度,但匹配过程中需要保证矢量道路就在惯性导航轨迹附近,若初始误差较大则迭代时间变长,增加了匹配结果的不确定,因此该算法更适合于小误差下的精匹配[15-16]。
基于上述路径匹配方法的研究成果,本文提出了一种粗精匹配结合的矢量道路辅助惯性导航算法。算法将路径匹配过程分为两个阶段:粗匹配阶段和精匹配阶段。首先,根据特征标示点,利用改进的概率统计算法和相关性算法快速确定待匹配道路集合,并通过粗匹配保证待匹配道路在惯导轨迹点附近;之后,利用最近点迭代算法进行精匹配,确定运动载体所处的具体位置以及定位误差,通过匹配方差以及历史匹配轨迹的评价比较,输出最终的匹配结果,以实现粗精匹配的结合。最后,本文针对算法的可行性、与其他算法的匹配效果对比以及算法中阈值的选取进行了仿真试验验证。
1 基于特征标示点的粗匹配粗匹配的目的是快速缩小匹配搜索区域并确定待匹配的道路点集合,概率统计法能够缩小搜索范围,而相关性算法能够有效剔除非相关道路,因此本文结合概率统计法和相关性算法的优点,提出一种基于特征标示点算法进行快速粗匹配。
1.1 特征标示点的提取(1) 由于受红绿灯、交叉口以及转弯离心力的干扰影响,车辆在这些路段行驶时经常会出现走走停停的现象,其行驶速度一般低于普通道路的车速[17],因此这些路段的匹配基础条件基本一致。
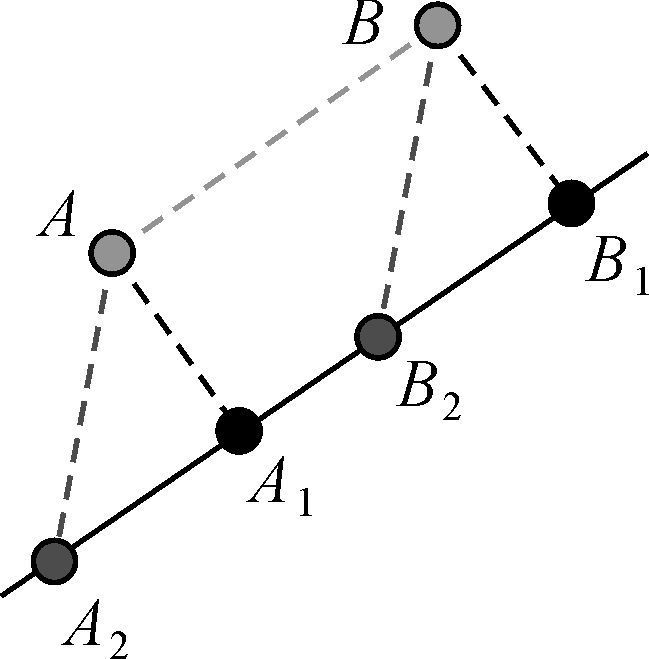
(2) 惯性导航的定位误差一般分解为沿道路行进方向的定位误差和与道路垂直方向的定位误差[18-19]。如果只按照轨迹点行进方向法线方向寻找最近点,将只能获得与道路垂直方向的定位误差而无法获取沿道路方向的定位误差。如图 1所示,AB为车辆的导航轨迹,但是如果只考虑垂直于道路方向的误差,将会得到A1B1的匹配结果,而A2B2才是AB对应的真实轨迹,这样就增大误差累积。因此在粗匹配算法中主要针对具有转弯特征或者交叉口路段进行匹配。
|
| 图 1 直线道路与轨迹匹配造成误差 Fig. 1 Matching error caused by linear path and track |
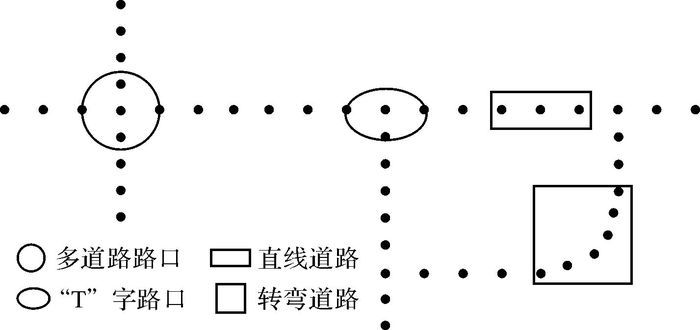
本文采用笔者在文献[20]中提出的顾及轨迹趋势变化的特征提取算法,将道路特征按照顺序点集合的形式提取出来,并将矢量道路划分为3种类型:直线道路、弯曲特征道路和交叉路口。图 2是一个小区域内的矢量道路网,从图中可以看出,矢量道路都是以坐标点集的形式进行表达,因此本文设计的矢量点的数据结构见表 1,道路类型中0表示的是直线道路点,1表示的是路口交点,2表示的是弯曲特征道路点。方位角是指当前点与道路方向后一点之间连线方向与正北方向之间的夹角。
| ID(int型) | 经度坐标(double型) | 纬度坐标(double型) | 高程(double型) | 方位角(double型) | 道路类型(int型) |
| 0 | 116.255 867 | 39.911 662 | 49.412 000 | 270.016 626 | 0 |
| 125 | 116.827 245 | 40.345 484 | 55.040 000 | 166.373 005 | 1 |
| 32 | 116.819 722 | 40.566 610 | 175.140 000 | 13.760 785 | 2 |
|
| 图 2 矢量道路网中的几种道路情况 Fig. 2 Several conditions in vector road network |
根据上述矢量道路的数据结构和几何形状特征,本文给出如下定义:
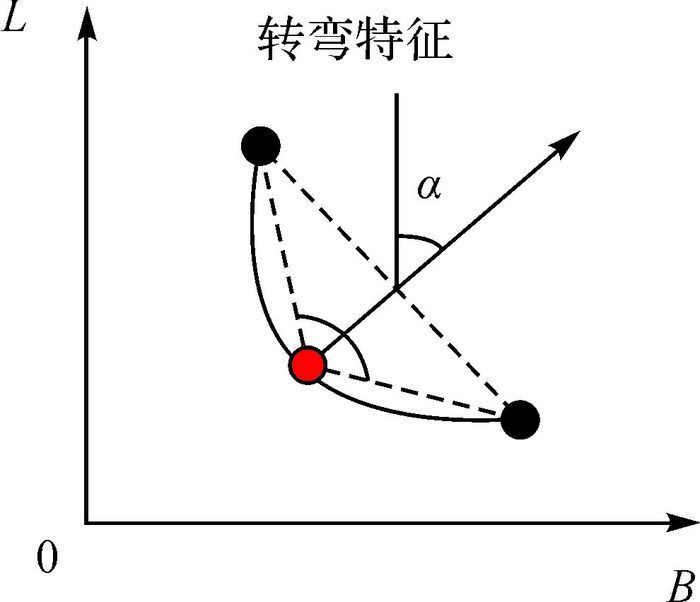
定义1:弯曲道路特征上曲率最大的一点,称为该道路特征的特征标示点;该点切线的法线方向与正北方向的逆时针夹角,称为该道路特征的曲线开口方向。
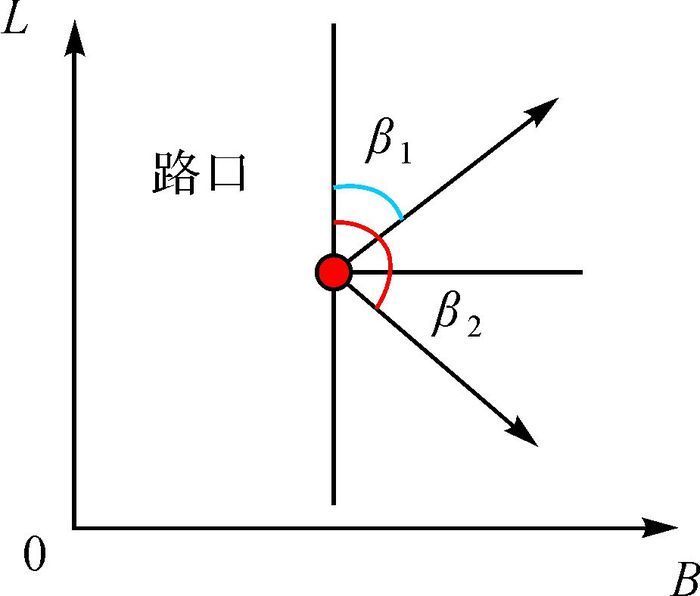
定义2:道路的丁字、十字或者更复杂的相交道路的唯一相交点,称为该交叉口的特征标示点。各道路夹角的角平分线的指向(由顶点向外)与正北方向的逆时针夹角,称为该路口的开口方向(集合)。
如图 3、图 4所示,红色点表示当前路段的特征标示点;弯曲特征道路的开口方向为α,有且只有一个;而路口道路的开口方向集合中元素的数量由相交道路的数量确定,可表示为β1、β2、…、βn,可将计算后获取的开口方向逐一储存在集合中以备后续粗匹配使用。
|
| 图 3 路口特征标示点及开口方向的定义 Fig. 3 Label point of feature and open direction in the intersection |
|
| 图 4 转弯特征标示点及开口方向的定义 Fig. 4 Label point of feature and open direction in the corner |
特征标示点是弯曲特征道路和道路交叉口的重要控制点,表示着矢量道路网的整体结构。弯曲特征道路反映着道路的形状起伏和方向变化,是道路网中直线道路之间过渡连接的重要纽带,而道路交叉口是道路网的交汇点,是行人、车辆的汇合、转向、分流的地方,也是道路网灵活性的关键所在[21]。因此,本文根据道路交叉口以及弯曲道路的不同情况进行了分类,并针对每种类型道路的特征标示点进行了判断和提取,其具体步骤方法见表 2。
| 编号 | 道路名称 | 特征标示点示意图 | 提取方法 |
| 1 | 十字路口 |  | 根据相交直线道路直接计算出交点坐标 |
| 2 | “T”字路口 | 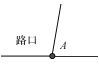 | 根据相交直线道路直接计算出交点坐标 |
| 3 | “K”字路口 |  | 根据相交直线道路直接计算出交点坐标,若交点多于一个,取所有交点的经纬度平均值作为交点坐标 |
| 4 | 环岛型路口 | 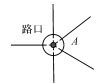 | 计算环岛内所有直线道路延长线的交点并取平均值,或者取环岛环中心点 |
| 5 | 转弯道路 | 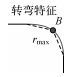 | 计算曲线中曲率最大的一点或者距曲线首末点距离相等点 |
| 6 | 立体相交“非路口” |  | 一般存在于立交桥中,先判断道路高程差,若超过阈值,不做特征标示点提取处理 |
| 7 | 延长线相交“非路口” | 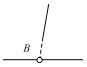 | 根据两条道路之前的最近距离进行阈值判断,如果小于阈值则认为相交,计算交点;否则,不做处理 |
1.2 待匹配道路点集合的搜索范围确定
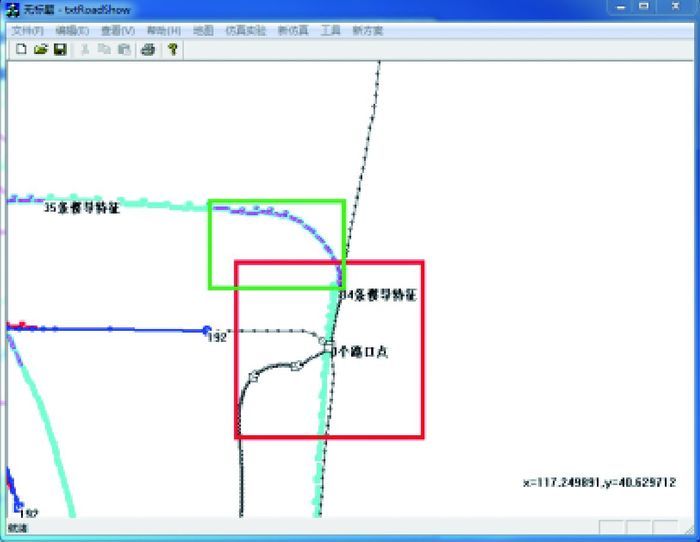
根据1.1节提取到的特征标示点,以其为中心,作一个边长为d的正方形,将正方形区域内包含的所有道路矢量点作为待匹配道路点集合存储起来。以双向八车道的城市道路为例,按照道路设计规范[22],每个车道宽约为3.5~3.75 m,运动载体在道路交叉口完成转弯动作时,其最大转弯半径约为20~30 m(考虑到存在绿化带以及非机动车道,约6个车道宽),因此可令正方形的边长d=60 m,以保证能包含整个道路交叉口或者转弯特征。如图 5、图 6所示,红色正方形框内的道路点集合即为待匹配道路点集合。
|
| 图 5 基于特征标示点的交叉口待匹配道路点集合 Fig. 5 Road point set to be matched in intersection based on label point of feature |
|
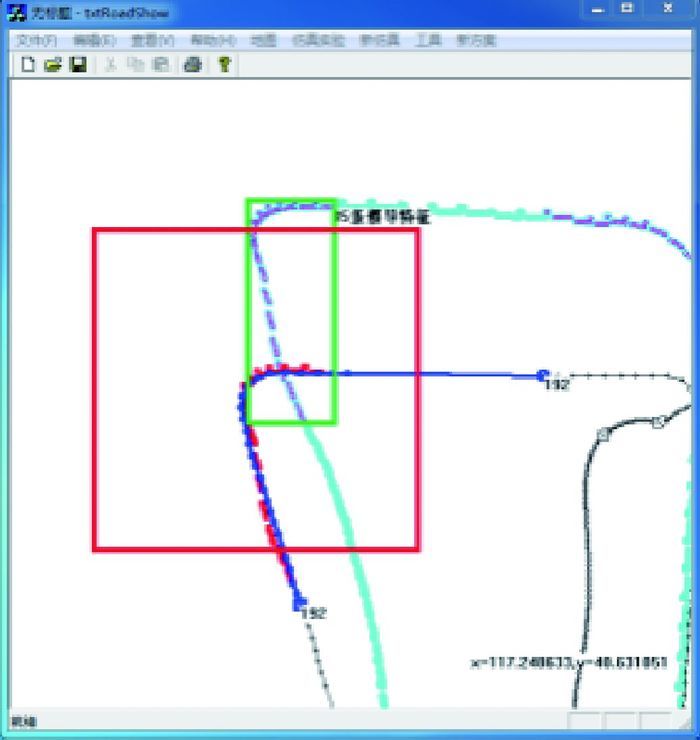
| 图 6 基于特征标示点的弯曲特征道路待匹配道路点集合 Fig. 6 Road point set to be matched in corner based on label point of feature |
按照文献[20]中提出的顾及轨迹趋势变化的特征提取算法,亦可将导航轨迹的转弯特征点集合及其特征标示点提取出来,并可以计算出轨迹特征所对应的最小外接矩形,如图 5,图 6所示,绿色矩形框即为轨迹特征的最小外接矩形。考虑惯性导航存在一定的累积误差,需要将提取出的边界进行适当的放大。而轨迹特征的搜索范围大小由组合导航定位误差椭圆确定[23-24]。
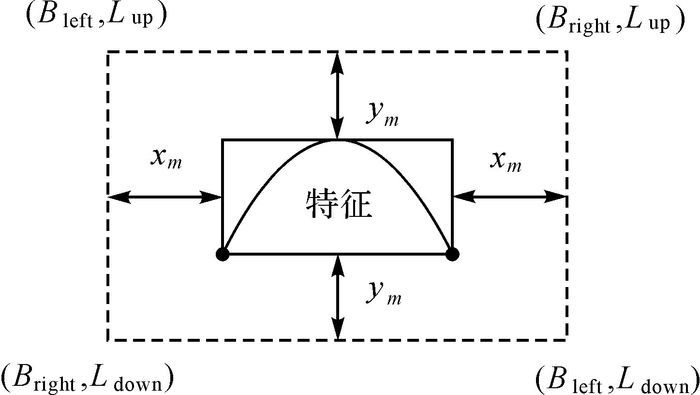
如图 7所示,虚线外界边框为轨迹特征搜索待匹配道路点集合的区域大小。
|
| 图 7 轨迹特征搜索区域 Fig. 7 Search area of trajectory feature |
1.3 粗匹配策略
相比交于误差椭圆相交需要进行距离量算,判断矩形相交只需要进行简单一元计算,其计算量简化了不少,效率也相对较高。此外,考虑到一些道路曲线形状的不规则性,传统曲线拟合算法存在难以线性化或者曲线的维数较多等问题,都需要通过大量计算分析才能完成相关度判断,一定程度上影响了匹配的效率。因此本文采用搜索矩形区域相交原则和道路开口方向的相关性来对待匹配道路点集合进行粗匹配,从计算量和判断方法上进一步简化匹配过程,以提高整体匹配效率。
粗匹配过程大致分为3个步骤:
步骤1:根据1.2节的轨迹特征搜索区域内按照矩形相交原则,搜索满足相交条件的基于特征标示点的道路点集合,设符合条件的基于特征标示点的道路点集合数量为N,则可按照如下规则进行判断。
规则1:若N=0,运动载体不在道路上或者存在矢量道路网没有更新的新增道路,退出当前轨迹特征匹配,以当前轨迹作为运动载体的当前实际位置,并跳至下一个轨迹特征重新进行粗匹配判断。
规则2:若N=1,该待匹配道路点集合即为轨迹特征对应的匹配道路点集合,直接进入步骤3。
规则3:若N>1,存在多个待匹配道路点集合,进入步骤2继续判断处理后,再进入步骤3。
步骤2:根据2.1节中定义的道路开口方向进行限差判断,可设αP、αQ分别为轨迹特征和道路特征的开口方向,则有
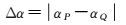 (1)
(1)
公式(1) 中·表示取绝对值。若该道路点集合为弯曲特征道路,则只需要计算一次开口方向限差;若是交叉口道路点集合,则需要逐一计算当前轨迹特征开口方向与各条道路开口方向的限差,至少有一个满足限差即可。
由于运动载体在行驶过程中,会受到紧急避让或驾驶员习惯等因素的影响,因此轨迹和道路的开口方向会有一定差异,本文取最大道路的开口方向限差为Δα=10°。所以,当且仅当Δα≤10°时,该待匹配道路点集合即是轨迹特征相对应的匹配道路点集合。此时,若N=1,该道路即为轨迹对应道路点集合,进入步骤3完成粗匹配修正;若N>1,也进入步骤3完成粗匹配修正,保留这N个道路点集合,通过后续的精匹配重新对匹配结果进行评价判断。
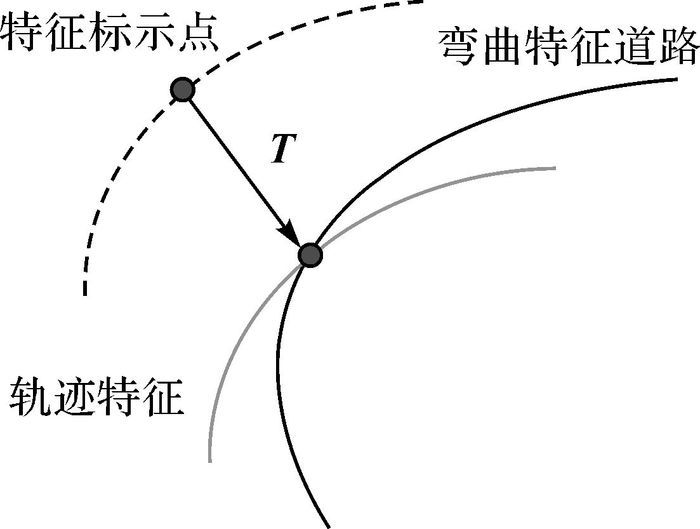
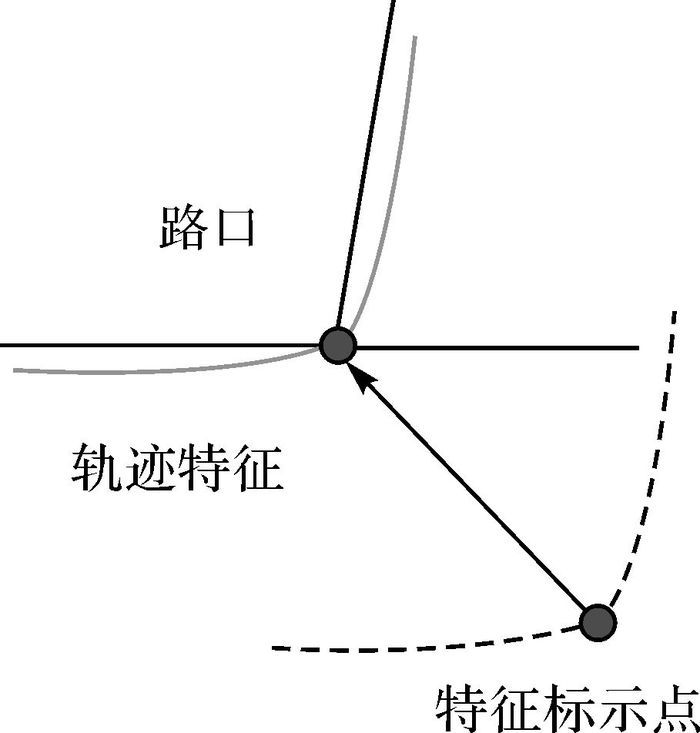
步骤3:按照道路特征标示点与轨迹特征标示点之间的偏差T进行粗匹配修正,将轨迹特征点集合按照偏差T整体平移至道路点集合附近,并进入精匹配阶段。
如图 8、图 9所示,经过粗匹配偏差修正后,轨迹特征标示点和道路标示点重合,轨迹特征点集合基本位于匹配道路的附近,为精匹配寻找最近点提供了有利条件。
|
| 图 8 轨迹特征与弯曲道路粗匹配 Fig. 8 Rough match of trajectory feature and corner |
|
| 图 9 轨迹特征与路口粗匹配 Fig. 9 Rough match of trajectory feature and intersection |
2 基于最近点迭代算法精匹配
精匹配是要获取运动载体的行驶轨迹和矢量道路数据之间定位误差,抑制定位误差的发散,并按照一定方法将该误差修正,使行驶轨迹和矢量道路基本吻合。最近点迭代算法完全基于匹配对象间的几何形状,具有很高的匹配准确度,文献[15-16, 25]中都采用该算法作为精匹配算法进行辅助导航,且取得了良好的匹配结果。因此,本文根据粗匹配的结果,采用最近点迭代算法进行精匹配,从而进一步减小并修正导航定位误差。
最近点迭代算法起初用于图像配准,ICCP算法则是该算法的特例,通过搜索最近点、迭代变换,实现匹配对象之间的最优匹配,从而修正定位误差获取导航位置信息[26]。
2.1 最近点的搜索一般ICCP算法都是基于等值线匹配单元进行最近点搜索和迭代计算,但考虑到行驶轨迹和矢量道路数据并没有明显的等值线信息,所以需要通过其他有效信息来确定最近点的搜索规则。文献[27-28]采用基于法向量的最近点确定思想,在图像配准中取得了良好的效果。而惯性导航轨迹能够提供以航向角为主的较为准确的姿态信息,且行驶轨迹和待匹配矢量道路点集合在形状上具有一定的相似性,为了保证航向角的一致性和轨迹形状的完整性,本文根据航向角法线方向来搜索最近点。
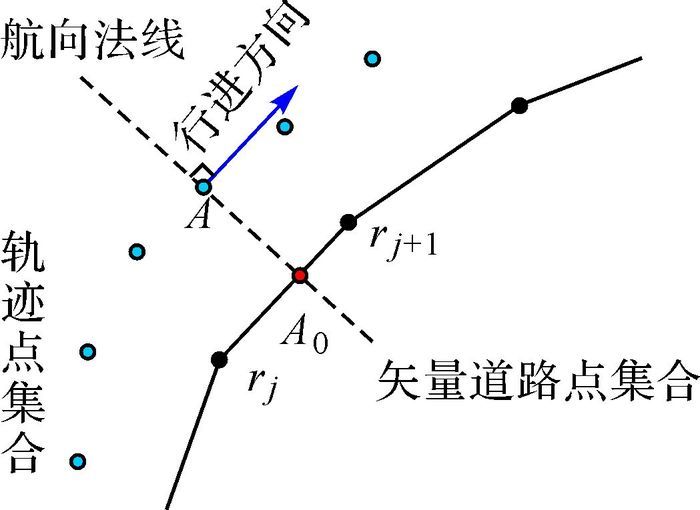
由于矢量道路是由一系列坐标点集合构成,所以可以将矢量道路抽象为首尾端点相接的折线段。每个线段以待匹配道路点集合中相邻两个点作为端点,记为{rj, rj+1}。如图 10所示,蓝色点集为轨迹特征点集合,其对应的黑色点集为经过粗匹配后获得的待匹配道路特征点集合。记轨迹点A的当前航向法线与{rj, rj+1}的交点作为其在道路上的对应最近点,记为A0。若该法线与{rj, rj+1}没有交点,则忽略该轨迹点,继搜索下一个轨迹点的对应最近点;若交点多于1个,则取距离最小的交点作为有效的最近点,其坐标记为(xi,yi)。遍历整个轨迹特征,依次求取各个轨迹点对应的最近点,得到最近点集合。
|
| 图 10 最近点的搜索 Fig. 10 Search of the closest point |
2.2 迭代变换的计算
由2.1节可知,进行精匹配就是要找到一个刚性变换T,使行驶轨迹特征点集合和最近点集合之间的距离最小,以达到最优匹配。其中刚性变换是由两个平移分量以及一个旋转分量组成的,即
 (2)
(2)
式中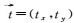
理论上旋转变换和平移变换是不可交换的,因此必须首先确定两种变换的先后顺序。文献[29]、文献[30]在重力和地磁辅助导航中都采用了先旋转变换后平移变换的方法,也有文献[31]和文献[32]提出先平移后旋转以及并行运算平移和旋转变换的方法,但其计算量巨大,也未表现出较为突出的匹配效率和性能。因此,本文仍采用先旋转后平移的传统刚性变换方法。
最近点集合N与经过刚性变换后的轨迹特征点集合的距离可表示为
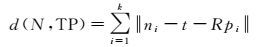 (3)
(3)
根据文献[33]的计算方法可求解出平移矩阵
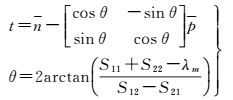 (4)
(4)
根据公式(4) 的结果,可以对轨迹特征点集合进行一次刚性变换,得到新的轨迹点集合P′,即P′=TP,此时第一次匹配结束。迭代匹配需要将新的轨迹点集合P′作为初始的点集合继续进行2.1节的最近点搜索和本节的刚性变化,直到T收敛后跳出迭代过程。经过最后一次迭代刚性变换后获得的集合TP即为最终精匹配的匹配结果。
2.3 迭代结束条件的确定迭代匹配算法需要经过多次迭代计算才能达到系统要求, 本文通过最小误差和最优迭代次数两个指标作为判定迭代结束的条件。考虑到计算机的内存要求以及系统效率,本文取迭代平移30次为迭代上限,超过30次,则匹配修正结束;此外,当轨迹点的逼近程度基本与道路点吻合时,即经度或者纬度偏差小于导航允许的基本误差范围内,也认为匹配成功,此时有
 (5)
(5)
式中,dmax为组合导航的要求的最大误差,参照一般导航的误差要求设置为1.363 51×10-4°(大约15 m)。
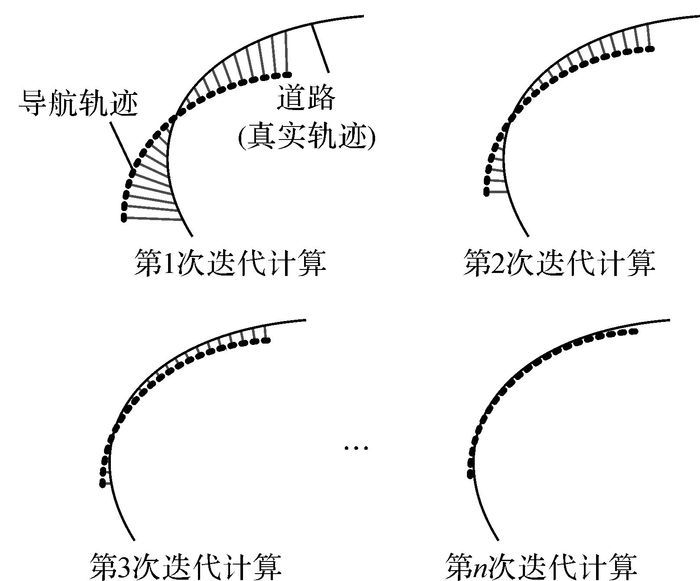
如图 11所示,经过满足迭代条件的匹配修正,轨迹点与道路点基本吻合,达到了导航匹配的要求。
|
| 图 11 迭代匹配的过程 Fig. 11 Process of iterative matching |
2.4 匹配结果的分析评价
根据1.3节中会出现不止一个待匹配道路点集合的情况,本文采用匹配方差对其进行进一步的判断。匹配方差主要描述了通过粗精匹配后得到的行驶轨迹与矢量道路之间的匹配程度,其大小直接反映出匹配结果的好坏;如果存在多个匹配结果的情况,可以根据匹配方差筛选出最优匹配结果。
匹配方差δ2的一般计算公式为
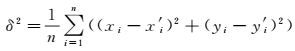 (6)
(6)
式中,(xi, yi)为精匹配阶段中经过最后一次迭代后轨迹特征点的坐标;(x′i, y′i)为该轨迹特征点在矢量道路上的对应最近点。由2.1节可知,最近点搜索过程中可能存在一些轨迹点没有找到道路对应最近点,因此匹配方差其具体的计算方法为:
(1) 如果特征轨迹点有道路对应最近点,则计算迭代变换后该轨迹点与其对应最近点的距离平方,记为DIS2;否则,没有对应最近点轨迹点的个数加1,记没有对应最近点的轨迹点总数为m。
(2) 找到DIS2的最大值,记为设Dmax2。
(3) 当迭代变换匹配完成后,计算所有轨迹点到其对应最近点的距离平方和,若轨迹点没有找到匹配点,则将其距离平方统一规定为Dmax2,则
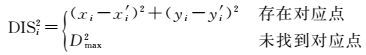 (7)
(7)
那么匹配方差的计算公式可表示为
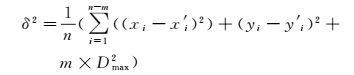 (8)
(8)
式中, n为轨迹特征点集合中轨迹点的总数;m为未找到对应最近点的轨迹点数。δ2值越小,表示匹配后的轨迹点与真实轨迹点越接近,匹配结果较好。
2.5 匹配结果的反馈判断由于1.3节中存在待匹配道路特征点集合个数N>1的情况,为了保证匹配结果的正确性,可将2.4节中的最终匹配结果暂时缓存起来不进行输出,其匹配规则如下:
规则1:若迭代匹配结束后,有且只有一个δ2最小,则取该道路特征点集合的匹配结果作为最终结果。
规则2:如迭代匹配结束后,存在不止一个最小且相近的δ2,则进入二次反馈判断。
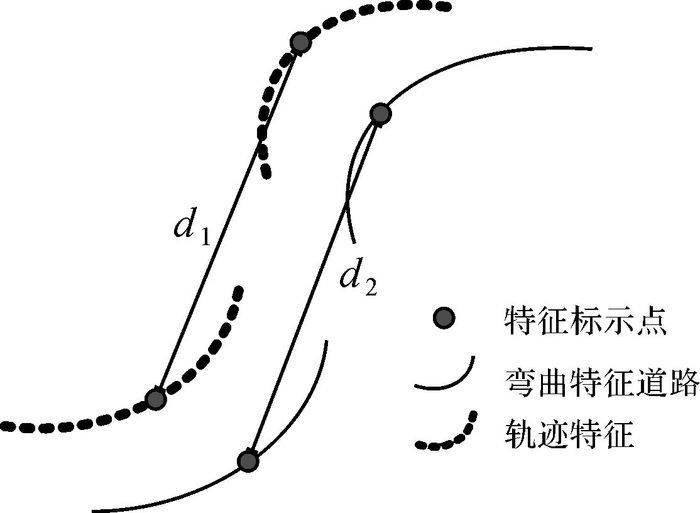
由于运动载体的行驶轨迹与矢量道路在几何形状上具有一定相似性,受文献[34]的启发,本文根据历史匹配结果对后续的匹配结果进行二次反馈判断,以获取准确度更高的匹配结果。如图 12所示,二次反馈判断需要比较两次匹配的轨迹特征段的特征标示点之间距离和两次对应矢量道路的特征标示点之间距离是否相近,即
|
| 图 12 匹配结果的反馈判断 Fig. 12 Feedback judgment of match results |
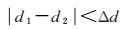 (9)
(9)
式中,Δd为距离误差阈值;d1表示前后两个行驶轨迹特征标示点之间的直线距离;d2表示与行驶轨迹对应的前后两个矢量道路特征标示点之间的直线距离。若两次匹配的特征标示点距离之差能够满足误差阈值条件,则认为本次匹配无误,可以输出匹配结果作为修正轨迹;若其中一个匹配结果距离误差很大,不满足误差阈值,则将舍弃该匹配结果,将误差较小且满足距离误差阈值的作为最终匹配结果;若所有匹配结果都不满足阈值条件,证明出现误匹配,扩大粗匹配的搜索范围,寻找正确的轨迹点位置,然后再次进行相同的精匹配计算,直到匹配结果满足阈值条件,如果仍旧没有找到合适的匹配结果,则跳出本次匹配,不进行修正结果输出。
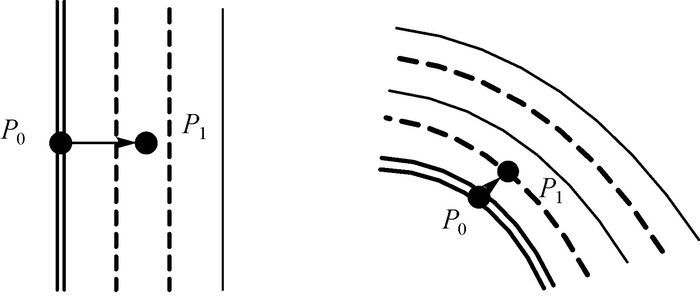
考虑到道路宽度和车道数等因素,尤其是宽度较大的道路,本文算法利用矢量道路中心线数据进行匹配,会对匹配修正结果造成一定的影响。针对此问题需要,通过结合矢量道路的自身属性如车道数和单车道宽度进行误差判定和修正,其具体判定修正方法为:如果路段右侧车道数量为奇数,则选择中间一条为参考车道,如果为偶数,则选择中间靠近中心线一条为参考车道,而后将中心线的轨迹点根据车道数和单个车道宽度沿着法线方向平移到参考车道即可完成匹配,如图 13所示。
|
| 图 13 道路宽度修正 Fig. 13 Correction of road width |
3 算法整体流程
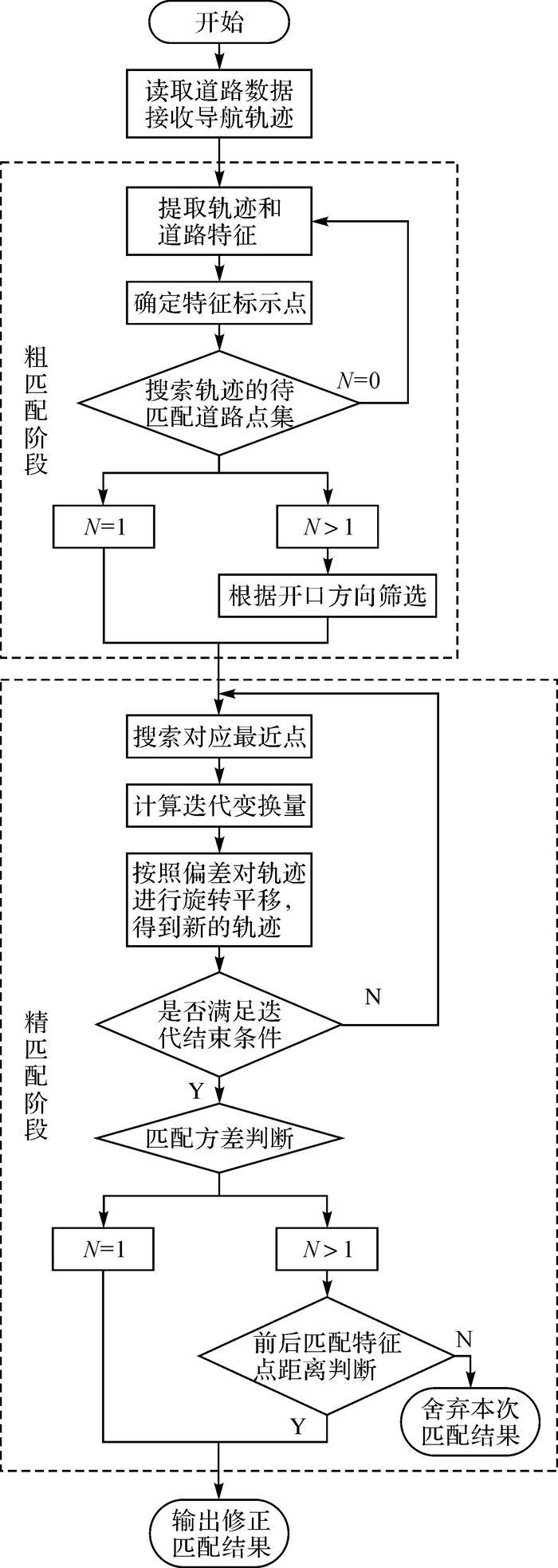
综合上述第1、2节的分析讨论,总结得到本文提出的精粗匹配结合的矢量道路辅助导航算法的总体流程如图 14所示。
|
| 图 14 算法整体流程 Fig. 14 Integrated process of algorithm |
4 算法的试验与分析 4.1 算法试验数据说明
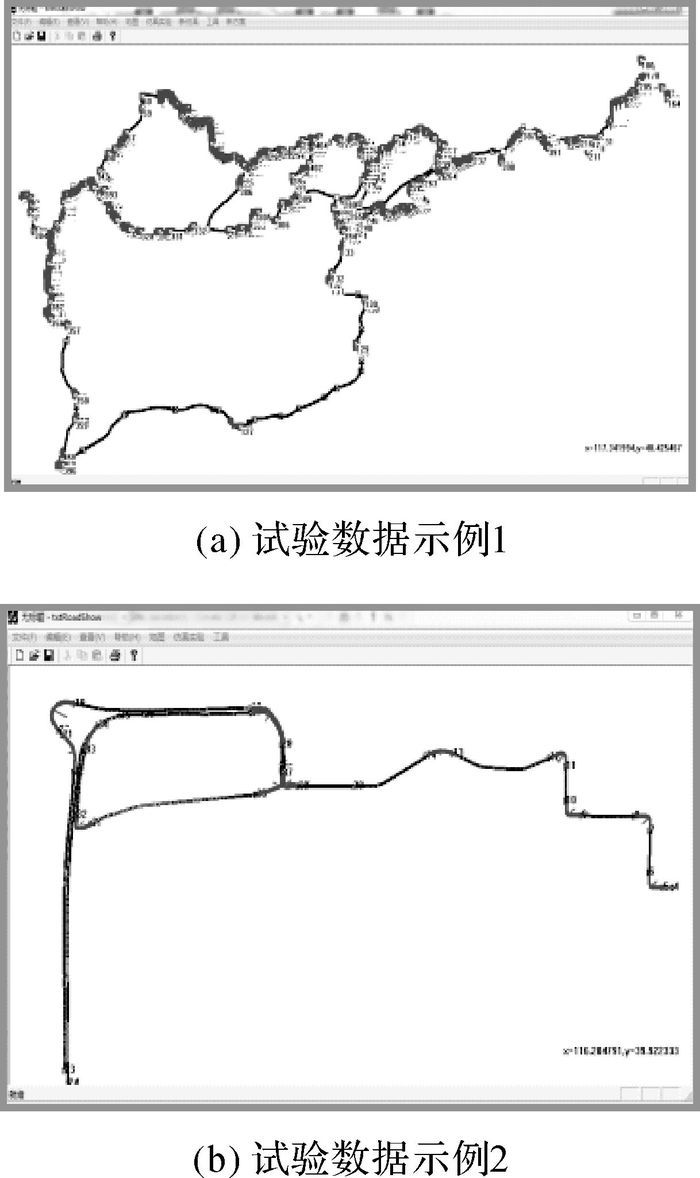
为了验证上述算法的可行性,本文将算法用Visual C++ 6.0编程实现,集成到文献[12]设计的算法测试系统中。仿真所用的道路数据为txt格式的矢量数据,2014年实地跑车测量北京市“西五环晋元桥”路段(如图 15(a)所示)以及密云地区路段(如图 15(b)所示),道路数据包含直行、平行路段、交叉路口和匝道等城市复杂道路,能够全面有效验证算法的可行性,检测整体算法的匹配效果。
|
| 图 15 试验数据 Fig. 15 Samples of experimental data |
本文使用的行驶轨迹数据为纯惯性导航实测轨迹数据,行驶过程不开启卫星信号设备,以便于仿真过程中模拟卫星信号干扰或者卫星导航“盲区”情况下的轨迹修正效果。其中平均车速为60 km/h,惯性导航中陀螺常值漂移量为0.05°/h,随机漂移量为0.01°/h,加速度计的初始零偏均值取为10-4g,随机零偏值为0.5×10-4g,东向、北向和方位失准角的初始值取为1°[35]。由于导航数据轨迹点是差分后得到的结果,所以暂不考虑由于采样频率较低时造成的影响。
本文通过试验首先对基于精粗匹配算法的导航误差收敛性进行分析,验证算法的可行性;并与文献[12]提出的类似算法以及传统垂直投影算法进行对比仿真试验,验证算法在匹配精度和稳定性上的提高;最后,通过多次试验确定本文算法提出的各项阈值,证明在当前阈值下算法的性能达到了最优。
4.2 算法可行性分析本文算法采用了精粗匹配结合的方式,匹配采用了多级筛选验证条件,以进一步提高算法的适应性、匹配准确率。结合各阶段独立匹配过程,本文单独使用粗匹配算法分别进行了仿真试验,并对不同匹配结果进行计算其匹配标准差,获得了不同条件下的匹配方差见表 3。
| 匹配标准差 | 匹配方法 | ||
| 无匹配 | 粗匹配 | 精粗匹配 | |
| δ(×10-4) | 4.063 51 | 1.636 21 | 0.954 18 |
由表 3可知,采用精粗匹配结合的方法比单独使用粗匹配具有更好的修正效果,进一步缩小了导航过程的误差。
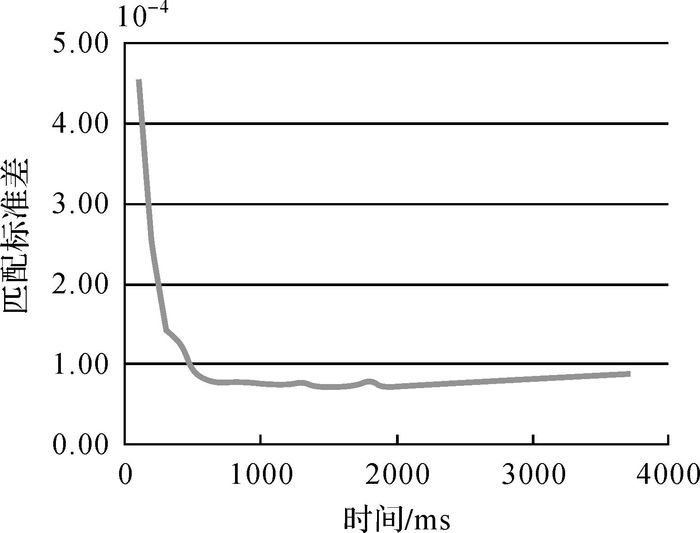
图 16给出了车辆的实际航迹、行进的道路以及经过本文算法修正后的匹配轨迹,图中蓝色轨迹为惯性导航轨迹,可以看出红色匹配轨迹可较好地定位跟踪到黑色的矢量道路上。从图 16(b)、图 16(c)局部放大图可以看出,在完成了多次迭代变换后,匹配轨迹和行进道路的形状基本吻合,即算法达到了收敛。图 16(b)给出的是一个道路交叉口(丁字路口)的匹配效果图,通过匹配的结果可以看出本文算法不但在道路转弯处能够完成匹配,在复杂道路交叉口同样有不错的匹配效果。图 17表示的是迭代匹配过程中匹配标准差的变化情况,随着时间的增加,匹配标准差逐渐减小并达到了收敛。通过以上仿真试验可以得出本文算法用于矢量道路辅助导航是完全可行的。

|
| 图 16 算法匹配效果 Fig. 16 Match results of algorithm |
|
| 图 17 匹配标准差随时间变化图 Fig. 17 Match standard deviation with time |
4.3 算法对比试验
现行热门的百度地图、高德地图等知名导航电子地图软件在道路匹配上大多采用由GIS软件厂商(如ArcInfo或Mapinfo)提供的高级综合算法,如卡尔曼滤波、模糊逻辑模型、隐式马尔科夫等[36-37]。本文对北京密云地区不同路段的5条轨迹分别利用本文算法、直接投影法、文献[12]算法和高级综合算法进行匹配修正仿真实验,并分别计算出4种方法的匹配准确度,其中匹配准确度的定义如下。
匹配准确度=正确匹配的轨迹特征点数量/导航轨迹的总特征点数量
试验统计结果如表 4所示。
| 匹配算法 | 评价标准 | 轨迹序号 | |||||
| 1 | 2 | 3 | 4 | 5 | 平均 | ||
| 本文算法 | 准确度/(%) | 86.7 | 91.0 | 88.5 | 94.0 | 90.7 | 90.2 |
| 匹配时间/s | 9.75 | 2.55 | 3.75 | 1.65 | 7.05 | 4.95 | |
| 投影算法 | 准确度/(%) | 77.2 | 83.5 | 79.7 | 80.9 | 78.7 | 80.0 |
| 匹配时间/s | 8.12 | 2.1 | 3.22 | 1.4 | 5.88 | 4.20 | |
| 文献[12]算法 | 准确度/(%) | 88.4 | 83.3 | 85.3 | 81.7 | 85.6 | 84.9 |
| 匹配时间/s | 12.87 | 3.41 | 4.95 | 2.20 | 9.35 | 6.60 | |
| 高级综合算法 | 准确度/(%) | 92.3 | 93.7 | 92.5 | 94.4 | 97.1 | 95.0 |
| 匹配时间/s | 10.04 | 2.63 | 3.86 | 1.70 | 7.26 | 5.10 | |
| 轨迹点个数 | 5490 | 1293 | 1722 | 782 | 3840 | 2625 | |
由表 4分析可得,本文算法的平均匹配准确度可以达到90.2%,相对于传统的垂直投影算法和文献[12]算法有了提高,有效地减少了误匹配概率。虽然相比较于高级综合算法在准确率上有所差距,但本文在粗匹配阶段就进行了待匹配道路点集合的范围确定和开口方向筛选,缩短了整体遍历匹配的时间,同时精匹配阶段的二次反馈判断,将正确匹配的结果作为有效匹配信息,因此参与匹配的轨迹点越多,准确率就越高,再次降低了出现误匹配的概率。而投影算法针对平行路段或者复杂路段效果往往不佳,文献[12]算法也考虑了趋势状态,但出现相似路段无法有效地甄别出正确匹配路段。
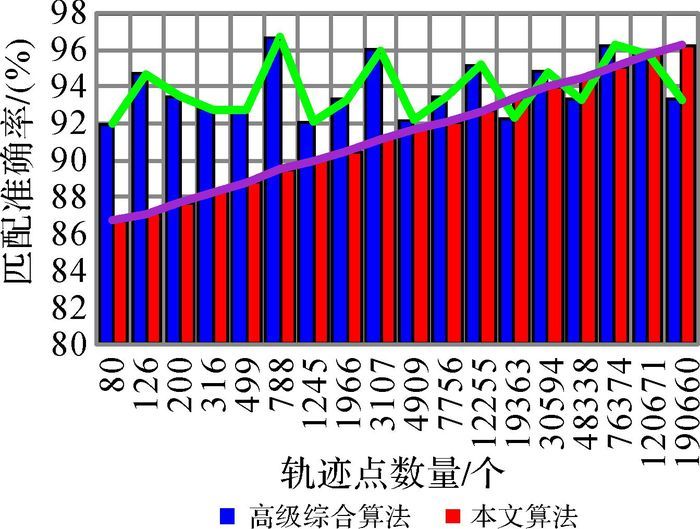
图 18给出了本文算法与高级综合算法在试验数据区域内准确率的柱(线)状图比较分析。从整体上看本文算法的匹配准确率在90%以上,尤其是随着轨迹点数量增多,匹配准确率稳定上升。相比较而言,高级综合算法虽然具有较高的匹配准确率,随着轨迹点样本数量的增多或者路况的复杂性增加,出现误匹配的概率会有所提高。
|
| 图 18 试验区域内惯导轨迹匹配结果比较 Fig. 18 Match results of INS trajectory in experimental area |
4.4 算法阈值设定分析
本文算法中涉及一些阈值的确定,例如1.3节中的开口方向、2.3节的迭代次数以及2.5节中距离阈值等,它们的取值通常都采用算法原理计算或者理论经验的方法来确定,其试验结果往往达不到最优的效果。本文以2.5节的距离阈值为例,对北京五环晋元桥地区5条导航轨迹进行了不同阈值下的匹配仿真试验,分别设置了不同距离阈值,通过分析最后的误匹配率和漏匹配率,以确定最优阈值。
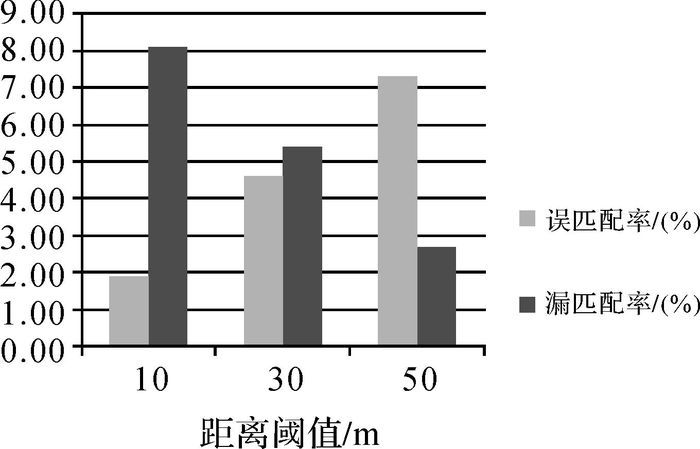
图 19给出了本文算法在不同距离阈值下误匹配率和漏匹配的柱状比较分析图。整体上来,当Δd=10时,由于判断距离过小,会将一些正确匹配的结果通过二次反馈判断舍弃,造成漏匹配现象;当Δd=50时,阈值条件过于宽松,算法会将许多误匹配结果一并输出,因此造成误匹配率相对较高;当Δd=30时,误匹配率和漏匹配率相对较低并趋于稳定,匹配结果达到最优。综上所述,取距离阈值为30 m时,算法匹配结果最佳。
|
| 图 19 不同距离阈值下匹配结果的柱状示意 Fig. 19 Histogram of match results with different distance thresholds |
5 结论
本文提出了一种精粗匹配结合的矢量道路辅助惯性导航算法,是对构建辅助惯性导航算法的一种新的尝试,能够有效应对摆脱卫星信号情况下惯性导航轨迹的校正工作。首先,通过基于特征标示点的改进概率统计法来确定待匹配矢量道路点集合,并根据开口方向信息进行了筛选判断,提高了算法的性能效率,完成了粗匹配;其次,按照迭代最近点算法对行驶轨迹进行迭代变换完成精匹配,并以匹配方差和距离阈值作为评价标准对匹配结果进行二次反馈判断,保证了匹配的准确率。最后,通过仿真试验验证了本文算法的可行性,同时与传统的投影算法、文献[12]算法以及高级综合算法进行匹配结果分析比较,并根据多次试验确定了算法中相关阈值最优取值。试验结果表明,利用本文提出的精粗匹配结合的矢量道路辅助导航算法能够在无源环境下有效修正运动载体的行驶轨迹误差,给出良好的匹配结果,并在一定程度提高了匹配的准确度。但本文算法对矢量道路数据的几何形状特征要求较高,文中仅对一些道路特征明显的区域进行匹配和分析,未来的研究应该结合更多辅助导航信息,如里程计、激光雷达、运动学模型等,使可供参考的数据信息多元化,进一步提高定位精度和可靠性。
| [1] | 宋磊. 基于熵和ICCP的多级地磁辅助惯性导航算法研究[J]. 华北科技学院学报, 2014, 11(10): 70–74. SONG Lei. Research on the Multi-level Geomagnetic Match Algorithm Aided Inertial Navigation Based on Entropy/ICCP Algorithm[J]. Journal of North China Institute of Science and Technology, 2014, 11(10): 70–74. DOI:10.3969/j.issn.1672-7169.2014.10.014 |
| [2] | 寇义民. 地磁导航关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. KOU Yimin.Research of Key Technologies in Geomagnetic Navigation[D]. Harbin:Harbin Institute of Technology, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10213-2011012768.htm |
| [3] | 李清泉, 黄练. 基于GPS轨迹数据的地图匹配算法[J]. 测绘学报, 2010, 39(2): 207–212. LI Qingquan, HUANG Lian. A Map Matching Algorithm for GPS Tracking Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 207–212. |
| [4] | 王美玲, 程林. 浮动车地图匹配算法研究[J]. 测绘学报, 2012, 41(1): 133–138. WANG Meiling, CHENG Lin. Study on Map-matching Algorithm for Floating Car[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 133–138. |
| [5] | 孙永荣, 黄斌, 王丽娜, 等. 抗尺度变换的矢量地图匹配导航方法[J]. 中国惯性技术学报, 2013, 21(1): 89–92, 111. SUN Yongrong, HUANG Bin, WANG Lina, et al. Vector Map Matching Navigation Method with Anti-scale Transformation[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 89–92, 111. |
| [6] | 黄斌. 惯性/地磁/地图组合导航系统研究[D]. 南京: 南京航空航天大学, 2013. HUANG Bin. Research on INS/Geomagnetic/Map Integrated Navigation System[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2013. |
| [7] | 郭黎, 李宏伟, 张泽建, 等. 道路网信息投影匹配方法研究[J]. 武汉大学学报(信息科学版), 2013, 38(9): 1113–1117. GUO Li, LI Hongwei, ZHANG Zejian, et al. Geometry Matching Method for Transportation Road Network Data Based on Projection[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1113–1117. |
| [8] | CHAWATHE S S. Segment-based Map Matching[C]//Proceedings of 2007 IEEE Symposium on Intelligent Vehicles. Istanbul:IEEE, 2007:1190-1197. |
| [9] | 李洋, 张晓冬, 鲍远律. 多权值概率论实时地图匹配[J]. 电子测量与仪器学报, 2012, 26(2): 166–170. LI Yang, ZHANG Xiaodong, BAO Yuanlv. Algorithm on Real-time Map-matching of Multi-weight Probability[J]. Journal of Electronic Measurement and Instrument, 2012, 26(2): 166–170. |
| [10] | 彭飞, 柳重堪, 张其善. 基于代价函数的组合导航系统地图匹配算法[J]. 北京航空航天大学学报, 2002, 28(3): 261–264. PENG Fei, LIU Zhongkan, ZHANG Qishan. Cost Function Based Map Matching Algorithm for GPS/DR Integrated Navigation Systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(3): 261–264. |
| [11] | BERNOULLI T, KRAMMER M, WALDER U, et al. Improvement of Inertial Sensor Based Indoor Navigation by Video Content Analysis[C]//Proceedings of 2011 International Conference on Indoor Positioning and Indoor Navigation. Guimaraes:IEEE, 2011:1-9. |
| [12] | 李翔. 基于路网特征的惯性导航辅助定位算法的研究与实现[D]. 郑州: 信息工程大学, 2013. LI Xiang. Research and Implementation on Aided Inertial Navigation Positioning Algorithm Based on Road Networks Feature[D]. Zhengzhou:Information Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-90005-1013353623.htm |
| [13] | 王志刚, 边少锋. 基于ICCP算法的重力辅助惯性导航[J]. 测绘学报, 2008, 37(2): 147–151, 157. WANG Zhigang, BIAN Shaofeng. ICCP Algorithm for Gravity Aided Inertial Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 147–151, 157. |
| [14] | 刘锐, 张江水, 李翔. 基于路网惯导载体路径匹配的ICCP算法改进[J]. 测绘科学技术学报, 2016, 33(1): 82–87. LIU Rui, ZHANG Jiangshui, LI Xiang. The Research on the Improvement of ICCP Algorithm for the Route-matching of Initial Navigation Vehicles in Road Network[J]. Journal of Geomatics Science and Technology, 2016, 33(1): 82–87. |
| [15] | 赵建虎, 张红梅, 王爱学, 等. 利用ICCP的水下地磁匹配导航算法[J]. 武汉大学学报(信息科学版), 2010, 35(3): 261–264. ZHAO Jianhu, ZHANG Hongmei, WANG Aixue, et al. Underwater Geomagnetic Navigation Based on ICCP[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 261–264. |
| [16] | 谌剑, 张静远, 查峰. 一种改进ICCP水下地形匹配算法[J]. 华中科技大学学报(自然科学版), 2012, 40(10): 63–67. SHEN Jian, ZHANG Jingyuan, ZHA Feng. Improved ICCP Algorithm for Underwater Terrain Matching Method[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2012, 40(10): 63–67. |
| [17] | OCHIENG W Y, QUDDUS M, NOLAND R B. Map-matching in Complex Urban Road Networks[J]. Brazilian Journal of Cartography, 2003, 55(2): 1–14. |
| [18] | 许建国, 张志利, 周召发. 交互式地图匹配算法在组合导航中的应用[J]. 上海交通大学学报, 2013, 47(8): 1323–1328. XU Jianguo, ZHANG Zhili, ZHOU Zhaofa. Application of Interactive Map Matching Algorithm in SINS/Odometer Integrated Navigation[J]. Journal of Shanghai Jiao Tong University, 2013, 47(8): 1323–1328. |
| [19] | 崔留争. MEMS-SINS/GPS组合导航关键技术研究[D]. 长春: 中国科学院大学(长春光学精密机械与物理研究所), 2014. CUI Liuzheng. Research on the Key Technologies of MEMS-SINS/GPS Integration Navigation System[D]. Changchun:Changchun Institute of Optics, Fine Mehcanics and Physics, Chinese Academy of Sciences, 2014. |
| [20] | 李翔, 张江水, 马健, 等. 顾及轨迹趋势变化的特征提取算法[J]. 计算机辅助设计与图形学学报, 2016, 28(8): 1341–1349. LI Xiang, ZHANG Jiangshui, MA Jian, et al. Feature Extraction Algorithm in Consideration of the Trend Changing of Track[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(8): 1341–1349. |
| [21] | 马小龙, 李成名, 赵占杰. 道路交叉口自动检测与基于OpenSceneGraph的三维自动建模方法[J]. 测绘学报, 2014, 43(10): 1083–1091. MA Xiaolong, LI Chengming, ZHAO Zhanjie. Three-dimensional Road Intersection Automatic Inspection and Robotization Modeling Based on OpenSceneGraph[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1083–1091. DOI:10.13485/j.cnki.11-2089.2014.0158 |
| [22] | 胡云岗, 陈军, 赵仁亮, 等. 地图数据缩编更新中道路数据匹配方法[J]. 武汉大学学报(信息科学版), 2010, 35(4): 451–456. HU Yungang, CHEN Jun, ZHAO Renliang, et al. Matching of Roads under Different Scales for Updating Map Data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 451–456. |
| [23] | VELAGA N R, QUDDUS M A, BRISTOW A L. Developing an Enhanced Weight-based Topological Map-matching Algorithm for Intelligent Transport Systems[J]. Transportation Research Part C, 2009, 17(6): 672–683. DOI:10.1016/j.trc.2009.05.008 |
| [24] | 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008: 161-163. SHENG Zou, XIE Shiqian, PAN Chengyi. Probability Theory and Mathematical Statistics[M]. 4th ed. Beijing: Higher Education Press, 2008: 161-163. |
| [25] | 王志刚, 边少锋. 基于ICCP算法的重力辅助惯性导航[J]. 测绘学报, 2008, 37(2): 147–151, 157. WANG Zhigang, BIAN Shaofeng. ICCP Algorithm for Gravity Aided Inertial Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 147–151, 157. |
| [26] | 黄晓颖, 童余德, 边少锋. 基于Matcom混合编程的ICCP算法仿真实现[J]. 测绘科学技术学报, 2011, 28(3): 186–189. HUANG Xiaoying, TONG Yude, BIAN Shaofeng. Implementation for Simulation of ICCP Based on Matcom[J]. Journal of Geomatics Science and Technology, 2011, 28(3): 186–189. |
| [27] | 李世飞, 王平, 沈振康. 迭代最近点算法研究进展[J]. 信号处理, 2009, 25(10): 1582–1588. LI Shifei, WANG Ping, SHEN Zhenkang. A Survey of Iterative Closest Point Algorithm[J]. Signal Processing, 2009, 25(10): 1582–1588. DOI:10.3969/j.issn.1003-0530.2009.10.017 |
| [28] | BERNARDINI F, MITTLEMAN J, RUSHMEIER H, et al. The Ball-pivoting Algorithm for Surface Reconstruction[J]. IEEE Transactions on Visualization and Computer Graphics, 1999, 5(4): 349–359. DOI:10.1109/2945.817351 |
| [29] | 张悦. 水下机器人地磁组合导航中ICCP算法的改进[D]. 哈尔滨: 哈尔滨工程大学, 2011. ZHANG Yue. Improvement of ICCP Algorithm in Geomagnetic Integrated Navigation for Underwater Robot[D]. Harbin:Harbin Engineering University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012517509.htm |
| [30] | 闫利, 崔晨风, 谢洪. ICCP算法在重力匹配中的应用[J]. 遥感信息, 2009(1): 16–19. YAN Li, CUI Chenfeng, XIE Hong. The Application of ICCP Algorithm to Gravity Matching[J]. Remote Sensing Information, 2009(1): 16–19. |
| [31] | 张红梅, 赵建虎, 王爱学, 等. 预平移简化ICCP匹配算法研究[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1432–1435. ZHANG Hongmei, ZHAO Jianhu, WANG Aixue, et al. Pre-translation Simplified ICCP Algorithm[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1432–1435. |
| [32] | 徐克虎, 沈春林. 地形特征匹配辅助导航方法研究[J]. 东南大学学报(自然科学版), 2000, 30(3): 113–117. XU Kehu, SHEN Chunlin. Study of Terrain Feature Matching Aided Navigation Method[J]. Journal of Southeast University (Natural Science Edition), 2000, 30(3): 113–117. DOI:10.3969/j.issn.1001-0505.2000.03.025 |
| [33] | 刘承香. 水下潜器的地形匹配辅助定位技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2003. LIU Chengxiang. A Study on Terrain Matching Assistant Positioning Technology for Underwater Vehicle[D]. Harbin:Harbin Engineering University, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10217-2003114797.htm |
| [34] | 李强, 曹鹏, 缪立新. 针对探测车历史数据的离线地图匹配算法[J]. 武汉大学学报(信息科学版), 2013, 38(2): 244–247. LI Qiang, CAO Peng, MIAO Lixin. Offline Map-matching for Archived Probe Vehicle Data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(2): 244–247. |
| [35] | 李翔, 张江水, 杨柏欣, 等. 基于航向角变化的趋势集合轨迹特征划分算法[J]. 地球信息科学学报, 2015, 17(10): 1172–1178. LI Xiang, ZHANG Jiangshui, YANG Baixin, et al. An Extraction Algorithm of Track Features Based on Trend Set of Heading Angle Variable[J]. Journal of Geo-information Science, 2015, 17(10): 1172–1178. |
| [36] | 百度地图API[EB/OL]. [2017-02-05] http://developer.baidu.com/map/index.html. |


