地球静止轨道卫星具有对地观测位置相对固定、时间分辨率高、观测范围广等特点,是航天对地观测成像技术的重要组成部分,是对低轨观测的有益补充。GF-4是我国第1颗民用面阵静止轨道光学成像卫星,具有凝视成像、机动巡查、区域成像等多个模式,能够满足减灾、气象、地震、林业等多个领域的不同需求[1]。
GF-4采用面阵凝视成像模式,搭载有一台10 240×10 240的面阵CMOS探测器和一台1024×1024的面阵碲镉汞探测器。在可见光近红外通道,GF-4可以提供全色影像与多光谱影像,空间分辨率为50 m,重复成像周期为15 s,单帧影像区域大小为500 km×500 km;在中波红外通道,提供光谱范围为3.5 μm~4.1 μm的中波红外影像,空间分辨率为400 m,重复成像周期为1 s,单帧区域大小为400 km×400 km。GF-4可以对地面进行连续观测,提供高时间分辨率的多帧序列影像。相较于低轨推扫式卫星,GF-4的空间分辨率依然较低,有必要利用其高时间分辨率的数据特点对其进行超分辨率重建,提高其空间分辨率,增强影像的可判读能力,扩大数据的使用范围。
超分辨率重建(super resolution,SR)的概念是由文献[2-3]于20世纪60年代提出的,指用若干张低分辨率图像重建生成一幅高分辨率图像,可以分为频率域与空间域两种。频率域方法主要是基于傅里叶变换的位移特性,通过在频率域消除频谱混叠现象来改善图像的空间分辨率的[4]。频率域方法原理简单,计算方便,但是难以建立复杂的运动模型与降质模型,造成其复原效果不佳[5]。空间域方法可以建立较为复杂的运动模型,使用范围广,具有较强的先验知识包含能力,使其逐渐取代了频率域方法。空间域方法主要包括非均匀样本内插法(non-uniform interpolation)[6]、迭代反向投影(iterative back projection, IBP)[7]、最大后验概率估计(maximum a posteriori, MAP)[8]、凸集投影[9-10]、混合MAP/POCS[11]多尺度细节增强[12]等。近年来,基于学习的超分辨率重建方法[13-14]在试验与实际应用中取得了较好的效果。
本文基于凸集投影对GF-4序列影像进行超分辨率重建。利用能量连续降减法构造参考帧,以减少迭代次数,提高计算效率;利用Vandewalle配准法进行运动估计以确定低分图像在高分网格中的精确位置;利用高斯模型生成的点扩散函数(point spread function, PSF)对参考帧进行修正。试验表明,该方法可以有效提高图像清晰度,增加细节信息,提升图像的判别能力,扩展数据的应用范围。
1 原理与方法 1.1 凸集投影凸集投影是一种空间域超分辨率算法[15],原理直观,算法简单。超分辨率重建是一个病态求逆的过程,一般是通过正则化方法,利用图像的约束条件与先验信息来约束可行解的范围。低分序列影像的每一帧都可以认为是由高分图像经过一系列降质因素得到的,即每一帧低分图像都构成一个约束条件。低分图像的获取模型可以由下式表示
 (1)
(1)
式中,gl(m1, m2)是第l帧低分图像;f(n1, n2)是高分图像;hl(m1, m2; n1, n2)是相应的降质函数,一般描述为点扩散函数;η1(m1, m2)是加性噪声。
凸集投影的基本原理就是求解闭合凸集的交集。假设有m个先验知识或约束条件,则对应有m个闭合凸集Ci, i=1, 2, …, m。对于每个闭合凸集Ci,记对应的投影算子为Pi,假设交集C0是非零解空间,那么理想高分图像f∈C0。因为影像超分重建结果包含于解空间,所以POCS算法得到的结果是不唯一的。其迭代过程可以表示为
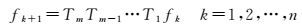 (2)
(2)
式中,Ti是第i个先验知识所对应的松弛投影算子,定义为
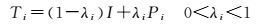 (3)
(3)
式中,0<λi<2是松弛投影算子。
在考虑噪声影响时,需要在模型中加入噪声的先验知识。假设图像中的噪声是方差为σv2 的高斯噪声,先验边界为cσv(c≥0),决定了其统计置信度。对于图像中的各个像素应当满足以下公式
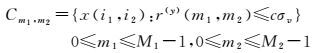 (4)
(4)
式中,r(y)(m1, m2)表示x(i1, i2)和g(m1, m2)的残差,与噪声统计特性相同。对于任意一个x(i1, i2),它在Cm1, m2上的投影[16]可以表示如下
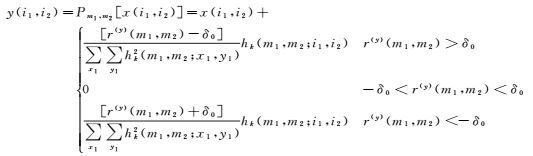 (5)
(5)
GF-4采用10 bit存储,将振幅也作为一个限制条件,如下式所示
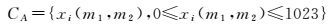 (6)
(6)
根据以上原理,凸集投影的实现主要可以分为3个步骤。第1步是对初始值的预估,即构造参考帧;第2步是寻找低分图像的各个像素在参考帧上的具体位置,即运动估计;第3步是根据低分序列图像对参考帧进行迭代修正[17-18]。本文利用能量连续降减法来构造参考帧,使用Vandewalle配准法进行运动估计。其技术路线图如图 1所示。

|
| 图 1 总体技术路线图 Fig. 1 Overall technology |
1.2 能量连续降减法
能量连续降减法是一种基于频率域的外推方法[19-20],也被称为Papoulis-Gerchberg。该方法能够消除下采样后信号的频率混叠现象。文献[21]提出了一维信号混叠的外推恢复算法。一维原始信号f(t)的傅里叶频谱为
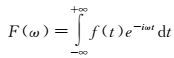 (7)
(7)
对原始信号抽样得到的实际信号为
 (8)
(8)
式中,rect为矩形函数;a用于调整采样频率。
 (9)
(9)
用截止频率为ω0低通滤波,得到
 (10)
(10)
于是
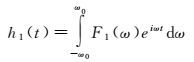 (11)
(11)
再将信号h0(t)加载在h1(t)上,得到
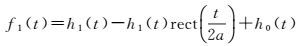 (12)
(12)
在对图像这种二维信号进行操作时,将低分序列影像的各个像素放置于对应的高分网格中作为已知点,其余点赋值为零。对图像进行低通滤波后(空间域操作时可以使用均值滤波),把已知点重新加载覆盖到图像上,这样的操作作为一次迭代。这一方法的实质是将已知点的信息向周围点进行扩散,以填充未知点。以一定准则退出迭代后,即可产生一幅具有较高分辨率的图像。
1.3 Vandewalle配准法Vandewalle配准法是一种频率域配准方法[22]。它使用图像的低频信息进行配准,因为噪声主要包含在高频信息中,而低频信息不包含走样信息[23],具有更强的鲁棒性。记参考图像为f1(x),待匹配图像为f2(x),两者关系可表示为
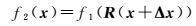 (13)
(13)
式中,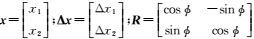
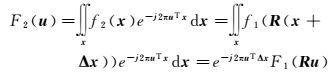 (14)
(14)
因为|F1(u)|和|F2(u)|之间的关系与旋转角度有关,而与平移量无关,所以先进行旋转角度估计,再进行平移参数估计。在进行旋转角度估计时,定义一个关于旋转角度α的函数
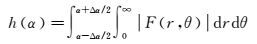 (15)
(15)
由于|F(r, θ)|是一个离散信号,可以把h(α)每隔0.1°进行一次计算。此时只考虑ερ<r<ρ的圆形区域,其中ρ为图像半径,ε设为0.1。因为低频信息的值相对很大,所以可以忽略r<ερ的值。
在进行平移参数估计时,平移参数是通过频率域中的一个线性相位移动来表示的,即
 (16)
(16)
相位差∠(F2(u)/F1(u))是关于u的线性函数,斜率为2πΔx。平移参数Δx可以通过计算相位差平面斜率来获得。
1.4 超分辨率具体实现在处理大幅图像时,因内存等因素限制,需要对图像进行分块操作。本文的分块大小设置为64×64。因为PSF的大小是5×5。在参考帧修正的过程中,图像块边缘的两个像素的处理与中间像素不一致,这会导致图像块边缘的清晰度没有得到充分改善,使得拼接后图像产生明显的格网。因此,需要在图像块之间设置一定像素的重叠,以消除格网现象,本文设置了4个像素的重叠。
对于参考帧构造,首先选取低分序列图像中的一帧P1,利用双线性内插法进行上采样,得到底图P′,使得其分辨率提高两倍。双线性内插法是一种重采样方法,使用投影位置周围4个像素作为采样数据,在x、y方向上分别进行一次插值,即
 (17)
(17)
式中, F是输出图像;f是输入图像;(i+u, j+v)是(m, n)在输入影像上的映射坐标,i、j是整数坐标,u、v是0到1之间的小数坐标。同时建立一个大小与P′相同的高分网格Ptemp。分别计算其余各帧与P′的偏移量,并根据偏移量将P2、P3、…、Pn的像素填入Ptemp。将P′用以下规则更新
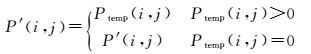 (18)
(18)
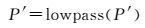 (19)
(19)
对上述步骤进行多次迭代操作后,即可得到参考帧Pref。
对于运动估计,首先对图像进行傅立叶变换,并提取其低频信息,利用低频信息计算图像之间的旋转参数与平移参数。根据旋转参数与平移参数计算P2、P3、…、Pn在Pref上的准确位置。
对于参考帧修正,首先应用高斯模型生成一个大小为5×5的模拟点扩散函数。高斯模型为
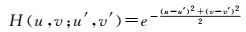 (20)
(20)
式中,u′、v′是PSF中心点的坐标值。归一化后,PSF如表 1所示。
| 0.018 3 | 0.082 1 | 0.135 3 | 0.082 1 | 0.018 3 |
| 0.082 1 | 0.367 9 | 0.606 5 | 0.367 9 | 0.082 1 |
| 0.135 3 | 0.606 5 | 1.000 0 | 0.606 5 | 0.135 3 |
| 0.082 1 | 0.367 9 | 0.606 5 | 0.367 9 | 0.082 1 |
| 0.018 3 | 0.082 1 | 0.135 3 | 0.082 1 | 0.018 3 |
根据运动估计得到的具体坐标,提取5×5的图像块,以式(21)、(22) 计算像素的理想灰度值
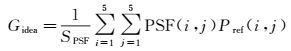 (21)
(21)
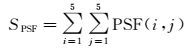 (22)
(22)
误差E定义为
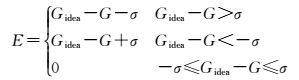 (23)
(23)
式中,σ是噪声水平的估计,本文设置为3。根据式(24) 对图像块进行修正
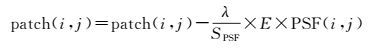 (24)
(24)
式中,λ用于调整步长,本文设置为6。
2 试验与分析 2.1 试验数据试验数据为5帧GF-4可见光近红外影像,拍摄于2016年3月6日,左上角坐标为100.440 9°E,37.382 8°N,右下角坐标为106.214 7°E,31.743 8°N。在图幅中,分布有山川、城镇、冰山、湖泊等多种地形地貌。从中截取2000×2000的图像作为输入数据,如图 2所示。

|
| 图 2 试验数据 Fig. 2 Experiment data |
2.2 评价标准
本文通过平均梯度(average gradient,AG)、信息熵(information entropy,IE)、信噪比(signal-noise ratio,SNR)等指标对试验结果进行评价。平均梯度是图像的灰度变化率,反映了图像微小细节的反差变化的和纹理变化[24],表示图像的清晰程度,其数值越大表明图像越清晰。平均梯度的定义为
 (25)
(25)
式中,M、N是图像的长度与宽度;f是测试图像。
信息熵代表图像信息量,数值越大越好。其定义为
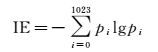 (26)
(26)
式中,pi表示灰度值为i的像素数量占整幅图像的比例。
信噪比通过局部平均值与标准差法测量[25-26],其值越大越好。信噪比的测量步骤为:① 求图像平均值M;② 对图像进行分块,求取局部均值与标准差;③ 得到局部标准差的最大值STDmax;④ 求解信噪比
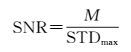 (27)
(27)
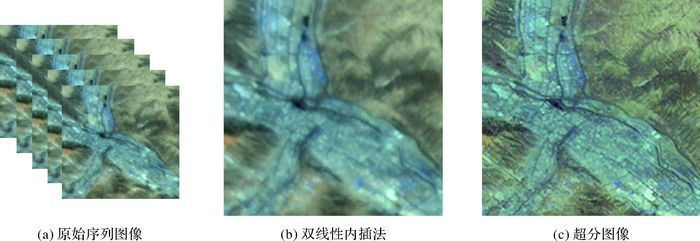
图 3分别是输入的序列图像、双线性内插图像和超分图像的局部区域。
|
| 图 3 超分辨率重建结果图 Fig. 3 Super resolution results |
| 评价参数 | 图像 | band1 | band2 | band3 | band4 | band5 | mean |
| 平均梯度 | original | 8.374 | 4.155 | 7.319 | 11.309 | 7.858 | 7.803 |
| bilinear | 6.266 | 4.178 | 5.806 | 7.367 | 6.011 | 5.926 | |
| SR | 14.303 | 9.008 | 11.260 | 23.004 | 14.355 | 14.386 | |
| 信息熵 | original | 8.827 | 7.920 | 8.821 | 8.737 | 8.679 | 8.597 |
| bilinear | 8.827 | 7.920 | 8.820 | 8.734 | 8.679 | 8.596 | |
| SR | 8.831 | 7.921 | 8.825 | 8.742 | 8.683 | 8.600 | |
| 信噪比 | original | 3.258 | 4.397 | 3.622 | 2.846 | 2.932 | 3.411 |
| bilinear | 3.703 | 4.948 | 4.080 | 3.212 | 3.379 | 3.865 | |
| SR | 3.167 | 4.346 | 3.547 | 2.695 | 2.927 | 3.336 |
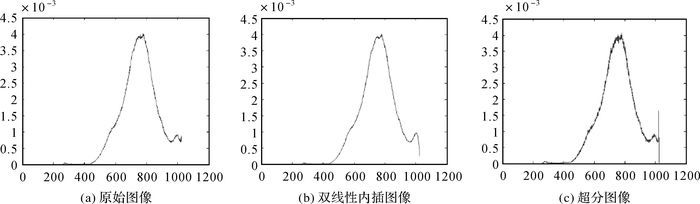
如表 2所示,原始图像,双线性内插图像,超分图像的信息熵没有明显差别。这是因为信息熵是对全图信息量的体现,而原始图像,双线性内插图像,超分图像三者的差异主要体现在图像细节上,而非图像的整体特性上。图 4是三者的灰度直方图分布,可以看到三者的灰度分布几乎是一致的,仅在灰度极值附近有所差异,而这一差异无法在信息熵这一指标上有明显反映。
|
| 图 4 灰度直方图比较 Fig. 4 Comparison of three gray level histograms |
平均梯度体现了图像的清晰度,就平均梯度而言,双线性内插图像最小,平均为5.926;原始图像居中,平均为7.803;超分图像最大,平均为14.386。这说明经过超分重建后,图像的清晰度得到明显提高,图像细节更为丰富。从图 3(b)、(c)的对比中可以明显看出超分图像具有更为清晰的地物特征。
就信噪比而言,双线性内插图像最高,平均为3.865;原始图像其次,平均为3.411;超分图像最低,平均为3.336。双线性内插法模糊了图像的细节结构,相当于在理想高分图像上做了低通滤波。因为噪声主要分布在图像的高频部分,所以双线性内插图像的信噪比会较原始图像有较大提高。凸集投影对噪声较为敏感,迭代次数越多,噪声放大情况越为严重。因为本文只进行一次迭代,所以其噪声放大情况较为轻微。反映在信噪比上,可以看到超分图像的信噪比虽然较原始图像有所降低,但是幅度较小,在可控范围内。就视觉效果而言,图 3(c)中未出现大量影响视觉效果的明显噪点。
超分辨率重建的效果与序列影像帧数有直接关系,图 5是不同帧数的超分辨率重建结果。

|
| 图 5 不同帧数的影像超分重建结果 Fig. 5 Super resolution results processed by different input frame amount |
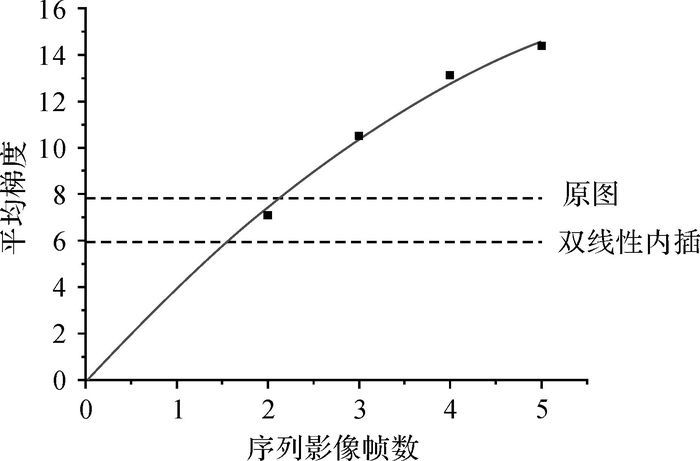
表 3是图 5中各幅子图的评价参数,图 6是序列影像帧数与影像超分重建结果平均梯度的关系图,图 7是序列影像帧数与影像超分重建结果信噪比的关系图。
| 评价参数 | 帧数 | band1 | band2 | band3 | band4 | band5 | mean |
| 平均梯度 | 2 | 7.156 | 4.789 | 6.466 | 10.300 | 10.296 | 7.801 |
| 3 | 9.428 | 6.504 | 8.412 | 14.084 | 14.092 | 10.504 | |
| 4 | 11.511 | 7.717 | 9.543 | 18.292 | 18.527 | 13.118 | |
| 5 | 14.303 | 9.008 | 11.260 | 23.004 | 14.354 | 14.386 | |
| 信息熵 | 2 | 8.828 | 7.922 | 8.822 | 8.738 | 8.733 | 8.609 |
| 3 | 8.829 | 7.921 | 8.823 | 8.739 | 8.739 | 8.610 | |
| 4 | 8.830 | 7.921 | 8.824 | 8.740 | 8.740 | 8.611 | |
| 5 | 8.831 | 7.921 | 8.825 | 8.742 | 8.683 | 8.600 | |
| 信噪比 | 2 | 3.487 | 4.458 | 3.849 | 3.017 | 3.017 | 3.566 |
| 3 | 3.369 | 4.445 | 3.734 | 2.901 | 2.901 | 3.470 | |
| 4 | 3.269 | 4.462 | 3.641 | 2.798 | 2.798 | 3.394 | |
| 5 | 3.167 | 4.346 | 3.547 | 2.695 | 2.927 | 3.336 |
|
| 图 6 帧数-平均梯度关系图 Fig. 6 Relationship between frame amount and average gradient |
|
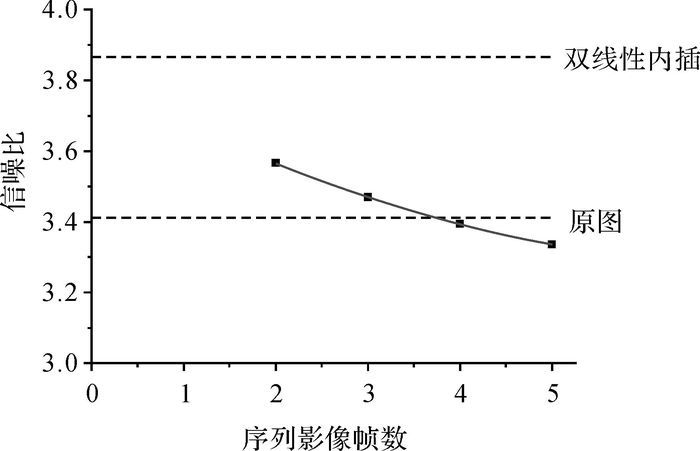
| 图 7 帧数-信噪比关系图 Fig. 7 Relationship between frame amount and SNR |
就视觉效果而言,图 5中,随着序列图像帧数的增加,影像超分重建结果的清晰度在不断提高,但噪点也在不断增多。从表 3和图 6可以看出,影像超分重建结果的清晰度与序列图像的帧数呈正相关,但平均梯度的增长幅度随着帧数增加而降低。通过二次多项式拟合,在一定范围内,序列影像帧数与平均梯度满足y=-0.332 6x2+4.558x-0.009 518。从表 3和图 7可以看出,影像超分重建结果的信噪比与序列图像的帧数呈负相关,但信噪比的下降幅度随着帧数的增加而降低。通过二次多项式拟合,在一定范围内,序列影像帧数与信噪比满足公式y=0.009 5x2-0.143 1x+3.814 1。从图 5、图 6与图 7的对比可以发现,在采用4帧影像进行超分辨率重建时,其结果有较好的清晰度与较少的噪点。平均梯度从原图的7.803提高到13.118;信噪比则与原图保持基本一致,原图为3.411,重建结果是3.395。所以本文建议采用4帧影像进行超分辨率重建以得到清晰度和信噪比都较为平衡的结果。
3 结论本文研究了基于凸集投影的高分四号超分辨率重建方法,利用有限数量的低分辨率图像来重建得到一幅高分辨率的图像。本文应用能量连续降减法来构建参考帧以减少迭代次数,提高运算效率;利用Vandewalle配准法来进行运动估计以方便分块操作。试验表明序列影像帧数与超分重建效果有密切关系。重建图像清晰度与帧数呈正相关,信噪比与帧数呈负相关。本文方法经过一次迭代即可重建出一幅清晰度良好,细节信息更为丰富的高分辨率图像,提高了GF-4卫星影像的可判读能力,对扩展数据的应用范围具有一定的实际意义。该方法依然存在一些值得研究与改进的方面,比如怎样进一步减弱噪声的影响,以及减弱分块操作时出现响应不一致而产生的颜色差异等。
| [1] | 徐文, 龙小祥, 李庆鹏, 等. "高分四号"卫星影像辐射与几何精度评价[J]. 航天返回与遥感, 2016, 37(4): 16–25. XU Wen, LONG Xiaoxiang, LI Qingpeng, et al. Image Radiometric and Geometric Accuracy Evaluation of GF-4 Satellite[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(4): 16–25. |
| [2] | HARRIS J L. Diffraction and Resolving Power[J]. Journal of the Optical Society of America (1917-1983), 1964, 54(7): 931–936. DOI:10.1364/JOSA.54.000931 |
| [3] | GOODMAN J W. Introduction to Fourier Optics[M]. New York: McGraw-Hill, 1968. |
| [4] | TSAI R Y, HUANG T S. Multiple Frame Image Restoration and Registration[C]//Advances in Computer Vision and Image Processing. Greenwich, CY:JAI Press Inc., 1984. |
| [5] | 陈健. 基于POCS的红外弱小目标超分辨率复原算法研究[D]. 长春: 长春光学精密机械与物理研究所, 2014. CHEN Jian. Research on Infrared Dim-small Target Super-resolution Arithmetic Based on POCS[D]. Changchun:Changchun Institute of Optics, Fine Mechanics and Physics, 2014. http://cdmd.cnki.com.cn/Article/CDMD-80139-1014263816.htm |
| [6] | UR H, GROSS D. Improved Resolution from Subpixel Shifted Pictures[J]. CVGIP:Graphical Models and Image Processing, 1992, 54(2): 181–186. DOI:10.1016/1049-9652(92)90065-6 |
| [7] | IRANI M, PELEG S. Improving Resolution by Image Registration[J]. CVGIP:Graphical Models and Image Processing, 1991, 53(3): 231–239. DOI:10.1016/1049-9652(91)90045-L |
| [8] | SCHULTZ R R, STEVENSON R L. A Bayesian Approach to Image Expansion for Improved Definition[J]. IEEE Transactions on Image Processing, 1994, 3(3): 233–242. DOI:10.1109/83.287017 |
| [9] | STARK H, OSKOUI P. High-resolution Image Recovery from Image:Plane Arrays, Using Convex Projections[J]. Journal of the Optical Society of America A, 1989, 6(11): 1715–1726. DOI:10.1364/JOSAA.6.001715 |
| [10] | YOULA D C, WEBB H. Image Restoration by the Method of Convex Projections:Part 1:Theory[J]. IEEE Transactions on Medical Imaging, 1982, 1(2): 81–94. DOI:10.1109/TMI.1982.4307555 |
| [11] | ELAD M, FEUER A. Restoration of a Single Superresolution Image from Several Blurred, Noisy, and Undersampled Measured Images[J]. IEEE Transactions on Image Processing, 1997, 6(12): 1646–1658. DOI:10.1109/83.650118 |
| [12] | 朱红, 宋伟东, 谭海, 等. 多尺度细节增强的遥感影像超分辨率重建[J]. 测绘学报, 2016, 45(9): 1081–1088. ZHU Hong, SONG Weidong, TAN Hai, et al. Remote Sensing Images Super Resolution Reconstruction Based on Multi-scale Detail Enhancement[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1081–1088. DOI:10.11947/j.AGCS.2016.20150451 |
| [13] | YANG Jianchao, WRIGHT J, HUANG T, et al. Image Super-resolution as Sparse Representation of Raw Image Patches[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, AK:IEEE, 2008:1-8. |
| [14] | 钟九生, 江南, 胡斌, 等. 一种遥感影像超分辨率重建的稀疏表示建模及算法[J]. 测绘学报, 2014, 43(3): 276–283. ZHONG Jiusheng, JIANG Nan, HU Bin, et al. A Super-resolution Model and Algorithm of Remote Sensing Image Based on Sparse Representation[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 276–283. DOI:10.13485/j.cnki.11-2089.2014.0040 |
| [15] | FAN Chong, ZHU Jianjun, GONG Jianya, et al. POCS Super-resolution Sequence Image Reconstruction Based on Improvement Approach of Keren Registration Method[C]//Proceedings of the 6th International Conference on Intelligent Systems Design and Applications. Jinan:IEEE, 2006:333-337. |
| [16] | 庞亚红, 毛幼菊. 一种基于凸集投影(POCS)的数字图像超分辨率重建算法[J]. 计算机工程与应用, 2005, 41(4): 69–71. PANG Yahong, MAO Youju. A Super-resolution Image Reconstruction Algorithm on the Theory of Projection Onto Convex Sets(POCS)[J]. Computer Engineering and Applications, 2005, 41(4): 69–71. |
| [17] | 张砚, 徐昆, 李勇. 基于外存和凸集投影法的遥感图像超分辨率方法[J]. 清华大学学报(自然科学版), 2010, 50(10): 1743–1746, 1756. ZHANG Yan, XU Kun, LI Yong. Remote Sensing Image Super-resolution Based on POCS and Out-of-core[J]. Journal of Tsinghua University (Science & Technology), 2010, 50(10): 1743–1746, 1756. |
| [18] | SU Binghua, JIN Weiqi. POCS-MPMAP Based Super-resolution Image Restoration[J]. Acta Photonica Sinica, 2003, 32(4): 502–504. |
| [19] | PAPOULIS A. A New Algorithm in Spectral Analysis and Band-limited Extrapolation[J]. IEEE Transactions on Circuits and Systems, 1975, 22(9): 735–742. DOI:10.1109/TCS.1975.1084118 |
| [20] | 穆绍硕, 张叶, 贾平. 一种改进Papoulis-Gerchberg的多幅超分辨重构方法[J]. 哈尔滨工业大学学报, 2015, 47(10): 118–123. MU Shaoshuo, ZHANG Ye, JIA Ping. An Improved Papoulis-Gerchberg Algorithm for Multiframe Super-resolution Reconstruction[J]. Journal of Harbin Institute of Technology, 2015, 47(10): 118–123. DOI:10.11918/j.issn.0367-6234.2015.10.023 |
| [21] | GERCHBERG R W. Super-resolution Through Error Energy Reduction[J]. Optica Acta:International Journal of Optics, 1974, 21(9): 709–720. DOI:10.1080/713818946 |
| [22] | VANDEWALLE P, SÜSSTRUNK S, VETTERLI M. A Frequency Domain Approach to Registration of Aliased Images with Application to Super-resolution[J]. EURASIP Journal on Advances in Signal Processing, 2006, 2006(1): 071459. |
| [23] | 陈岳军, 孙广玲, 姚恒. 结合小波金字塔的空频域亚像素图像配准[J]. 上海大学学报(自然科学版), 2012, 18(4): 342–348. CHEN Yuejun, SUN Guangling, YAO Heng. Hybrid Spatial-frequency Domain Sub-pixel Image Registration with Wavelet Pyramid[J]. Journal of Shanghai University (Natural Science), 2012, 18(4): 342–348. |
| [24] | 陈超, 江涛, 徐文学. 基于平均梯度的多聚焦图像融合方法研究[J]. 山东建筑大学学报, 2009, 24(2): 133–137. CHEN Chao, JIANG Tao, XU Wenxue. Research on Multi-focus Image Fusion Methods Based on Mean Gradient[J]. Journal of Shandong Jianzhu University, 2009, 24(2): 133–137. |
| [25] | 吴琼. 可见光图像超分辨率客观评价方法研究[D]. 北京: 首都师范大学, 2009. WU Qiong. Scientific Super-resolution Objective Evaluation Index and Method System[D]. Beijing:Capital Normal University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10028-2009130183.htm |
| [26] | 傅鹏, 孙权森, 纪则轩, 等. 一种遥感图像信噪比评估和度量准则[J]. 测绘学报, 2013, 42(4): 559–567. FU Peng, SUN Quansen, JI Zexuan, et al. A Method of SNR Estimation and Comparison for Remote Sensing Images[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 559–567. |



