地震是影响人类的最严重自然灾害之一,为最大限度降低在地震灾害中人员和财产的损失,灾后第一时间掌握和评估受灾区域损毁建筑物信息,对灾后应急响应和救援极其重要[1]。
随着遥感技术的不断发展, 遥感影像已经成为获取灾情的重要数据源,利用地震前后的遥感影像进行变化检测已经成为获取震害信息的研究热点[2-5]。从特征选取角度来看,可分为两类:基于单特征的震后建筑物变化检测方法和基于多特征的震后建筑物变化检测方法。基于单特征的方法通常选用某种单一特征作为变化检测判别依据,如利用影像灰度信息差值[6]、颜色特征[7]、纹理特征[8]、高度信息[9]、线特征[10]及边缘特征[11]等。但随着遥感影像分辨率的提高,基于单特征的方法往往对地物信息描述不够完备,可靠性不强。因此,许多学者在上述工作基础上进一步研究结合多特征的方法以提高算法的精度和可靠性。例如结合多特征的单类支持向量机[12]、模糊推理[13-14];机器学习[15]、构建知识规则集[16]等进行损毁建筑物检测。但总体来看,目前该类方法仍然是多种特征的简单组合决策,如何在统一的框架中充分利用多种互补特征以获得更稳定、可靠的检测结果仍需进一步探索。
文献[17]首次将图割算法引入到图像分割领域,该方法将图像分割问题转化为图的最小割问题,且能在一个最优化框架下同时考虑影像多种互补信息(如颜色、梯度、纹理信息),因此在分割性能上较传统影像分割方法有较大优势[18-19]。受此启发,本文利用图割算法能同时利用影像多种互补特征、且能获得全局最优解的优势,将图割算法引入到变化检测中。结合地震前后的高分辨率遥感影像和震前GIS辅助数据,融合影像的多种特征对震后影像构造能量函数,将能量函数最小值作为地震前后建筑物相似性的度量指标,实现损毁建筑物的自动检测。试验结果表明,本文提出的方法能充分利用多种特征,有效检测损毁建筑物。
1 建筑物变化检测原理图割理论的基本思想是将图像分割表达为能量函数最小化的问题,并据此构建网络图,通过相应的优化算法求解最小割。图割算法构造包括区域项和边界项的能量函数,将图像映射成一个s-t网络图。其中区域项定义像素节点与源点s(汇点t)间连接的能量,称为t连接;边界项定义相邻像素节点间连接的能量,称为n连接,像素之间的相似度决定了连接能量的大小。图割的能量函数为
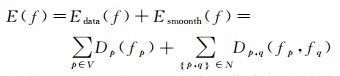 (1)
(1)
式中,Dp为区域项,用来衡量像素与为其分配的标签的一致性;Dp, q为边界项,用来惩罚分割的边界;V表示源点与汇点的集合;N表示相邻节点对。s-t网络图构建完成后,通过网络流理论,使用最大流-最小割算法即可求解能量函数的最小值Emin,实现图的最优分割。
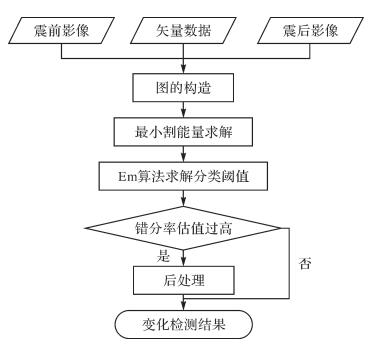
本文依据图割的最小割能量度量地震前后建筑物的相似性,从而区分变化和未变化的建筑物。算法主要流程:首先,利用震前建筑物线划图确定建筑物的最小外接矩形,在震前和震后影像上分别提取包含建筑物的局部影像。然后,结合建筑物的位置、形状、边缘、角点等信息选取了4个约束条件,据此对震后的每个局部影像构造能量函数,并依据能量函数将局部影像映射为网络图,能量函数的各项则对应网络图中的连接权值。利用最大流/最小割算法求得网络图的最小割能量,以最小割能量作为判断建筑物是否变化的指标。建筑物变化检测可视为对震后建筑物的二分类问题,利用EM算法求得最小割能量的分类阈值,对震后的建筑物进行分类。最后根据分类的错分率估值执行后处理,若错分率估值较高,则对易错分的样本利用支持向量机(support vector machine,SVM)进行再次分类,获得最终的变化检测结果。整体流程如图 1。
|
| 图 1 变化检测流程 Fig. 1 Flow chart of the proposed method |
2 建筑物变化检测算法 2.1 图的构造 2.1.1 局部影像
局部影像定义为影像中每栋建筑物对应的局部区域。根据震前建筑物线划图确定该建筑物的最小外接矩形,考虑到两时相影像的成像角度与配准误差,将最小外接矩形向四周扩展6个像素,扩展后的矩形在两时相影像上对应的区域即构成一对局部影像。
2.1.2 能量函数的构造常规的图割算法通过最小化能量函数得到实际问题的解。本文已知震前局部影像中包含建筑物,需判断震后建筑物的变化情况。利用相应的约束条件构造能量函数,将震后局部影像映射成s-t网络图,通过求解最小割实现对局部影像的分割。若震后局部影像中建筑物未变化,则能得到最满足约束条件的图分割结果,对应的最小割能量值较小;否则,若建筑物变化,则其最小割能量值较大。故本文不关注最小割对应的划分方式,而是将最小割能量值作为判断建筑物是否变化的指标。
根据建筑物在遥感影像中的特征,若震后建筑物未变化,应满足以下约束条件:
(1) 该建筑物在震后影像中的位置应与建筑物线划图标记的位置基本吻合;
(2) 含建筑物的局部影像的形状特征与不含建筑物的有显著差异;
(3) 该建筑物的轮廓位置在震后影像中是较为明显的边缘;
(4) 该建筑物的顶点位置在震后影像中是比较显著的角点;
为实现上述约束,通过建筑物线划图对震后局部影像进行标记,建立Eprevious项;利用基于方向梯度直方图(histogram of oriented gradient, HOG)[20]的SVM分类器,计算局部影像的HOG特征类别响应值,建立Ehog项;选取基于熵的超像素分割法[21]对震后局部影像进行分割,基于超像素分割结果建立Eedge项;使用Harris算子[22]计算震后局部影像中的建筑物顶点附近的角点响应强度,建立Ecorner项。对于每个局部影像,构造图割能量函数
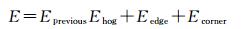 (2)
(2)
式中,Eprevious和Ehog项的乘积构成函数的区域项,对应s-t网络图中的t连接权值;Eedge和Ecorner项的和构成函数的边界项,对应网络图中的n连接权值。
2.1.2.1 Eprevious项通过约束图割的最小割的位置,定义区域项的主体部分Eprevious项
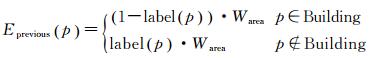 (3)
(3)
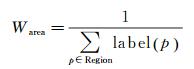 (4)
(4)
式中,p∈Building表示像素p被检测为建筑物。label是震前影像的标记函数,直接由建筑物线划图获得。p为建筑物像素时,label(p)=1;p为背景像素时,label(p)=0。Warea用于归一化能量值, 使得最小割能量的取值不受建筑物面积的影响,其中,p∈Region表示p为局部影像中的像素。震后局部影像的图割结果与震前建筑物位置越吻合,该项能量越小。
2.1.2.2 Ehog项Ehog项将HOG特征与SVM分类器结合,利用建筑物形状特征,计算震后某局部影像包含建筑物的可能性。首先,根据建筑物线划图在震前影像中选取包含建筑物的局部影像为正样本,选取不含建筑物的局部影像为负样本;然后,将所有样本重采样为相同尺寸(本文使用所有样本的平均尺寸),计算样本的HOG特征,并用于训练线性SVM分类器;最后,将震后局部影像重采样为所需尺寸并计算其HOG特征,用线性SVM分类器参数计算其HOG特征的类别响应值score+。Ehog项与像素位置无关,即对某一局部影像而言Ehog项是一个常数。因此,可以将Ehog项视为Eprevious项的系数,其计算公式如下
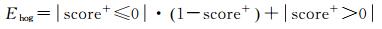 (5)
(5)
式中,|·|为取逻辑值运算。若|·|中的表达式为真,则返回1;否则,返回0。
2.1.2.3 Eedge项为实现对建筑物边缘特征的约束,本文先使用基于熵率的超像素分割算法来对震后影像进行分割,获取超像素。基于局部影像的超像素分割结果,定义各像素之间的能量项Eedge。针对两个相邻像素p1和p2
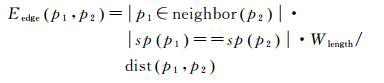 (6)
(6)
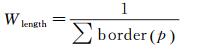 (7)
(7)
式中,运算|·|与上一节定义相同。函数neighbor(p)取像素p的邻域集合,即p1是p2的相邻像素时,p1∈neighbor(p2)为真,本文中统一取四邻域。函数sp(p)返回像素p所属的超像素编号,当p1和p2属于同一超像素时, sp(p1)=sp(p2)为真。dist(p1, p2)计算像素p1与p2之间的欧氏距离,由于neighbor函数取4邻域,实际计算时直接取distp1, p2≡1。Wlength用于归一化该项能量值。局部影像的border函数根据建筑物线划图直接获得,判断像素p是否位于震前影像中的建筑物边界上,是则返回1,否则返回0。
由定义知,当两相邻像素位于不同超像素时,表明两像素很可能位于边界位置,此时Eedge项能量为0;反之,能量值不为0。
2.1.2.4 Ecorner项一般而言,建筑物的顶点都会具有很强的角点响应,而建筑物消失后相应位置的角点响应往往会显著降低。使用Harris算子计算震后局部影像的角点响应,评价其为角点的可能性。然后,基于像素的角点响应来区分不同边界的可靠性,定义超像素边界处的能量项Ecorner项。针对位于超像素边界处的像素p定义
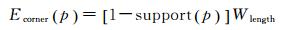 (8)
(8)
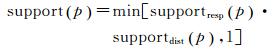 (9)
(9)
式中,Wlength与式(7) 中的定义相同,min函数返回两个参数中的最小值,此处将support的取值限定为[0, 1]。函数supportdist和supportresp分别称为距离支持度和响应支持度,根据建筑物顶点的角点响应,从不同角度描述像素p处边界的可靠性。
通过震前建筑物线划图获得建筑物的每个顶点V和边B的位置。给定像素p,求得与其距离最短的一条边B(p),称作支持边,该最短距离记为d(p)。支持边B的两个顶点为V1(p)、V2(p),称作支持顶点。据此定义距离支持度和响应支持度
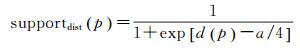 (10)
(10)
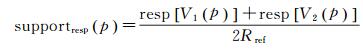 (11)
(11)
式中,d(p)为像素p到支持边的最短距离;a是超像素平均边长。此处supportdist的取值范围是(0, 1),d(p)值越小,表明超像素边界与支持边越接近,获得的距离支持度越高。resp(V)为点V的角点响应强度。鉴于两时相影像的配准偏差,在点V周围半径为5个像素的范围内计算Harris角点响应,并取最大值作为resp(V)。Rref为参考角点响应强度,用于将角点响应强度标准化。
合适的Rref值可以更好地保留角点响应值对建筑物与背景的可分性,其选取步骤如下:
(1) 忽略能量函数中的Ecorner项,构建震后局部影像的网络图,并根据最大流/最小割方法求解最小割能量Emin;
(2) 使用EM算法估计Emin分布中两个正态分量的参数,使两类样本错分率相等选择分类阈值,对样本进行分类,并称正样本的顶点为正顶点,负样本的顶点为负顶点;
(3) 计算每个顶点的Harris角点响应值resp(V),选择Rref值,使得
 (12)
(12)
步骤(1) 和(2) 避开Rref值的选定问题,通过Eprevious项、Ehog项和Eedge项构成的能量函数求解最小割能量,完成不精确的分类,对每个顶点进行类别标记;步骤(3) 将Rref值视为分类阈值,利用正负样本错分率相等的约束求得Rref值。
2.2 震后建筑物变化检测 2.2.1 最小割求解通过构造网络图,能量函数最小化即转化为求解网络图的最小割问题。针对构造的图使用任意一种最小割求解算法即可得到图分割结果,其对应的能量即为最小割能量Emin。本文通过求解最大流/最小割算法,可保证得到全局最优解,即最小割可收敛至最符合建筑物4项约束的位置。
2.2.2 确定分类阈值本文构造的能量函数,使得建筑物变化的局部影像对应的最小割能量较大,建筑物未变化的局部影像对应的最小割能量较小。以能量函数的最小割能量Emin为分类指标,若最小割能量Emin大于阈值Eseg,则将建筑物分为变化,否则,分为未变化。将包含建筑物的局部影像x标记为建筑物未变化或建筑物变化,分别记为Y(正类别)和N(负类别)。假设两类建筑物的最小割能量Emin的频数分布都近似服从高斯分布,则震后局部影像的最小割能量Emin近似为两个子高斯分布的叠加。EM算法能够在不完全的数据中寻找局部极大似然值,能有效估计混合高斯分布模型参数[23]。采用EM算法估计这两个正态分布的参数,令两类样本的错分率估值相等以选定分类阈值。给定任意正样本x∈Y,其最小割能量为Emin(x),对于选定的阈值Eseg,该正样本被错分的概率为
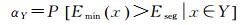 (13)
(13)
同理,负样本被错分的概率为
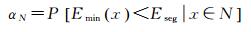 (14)
(14)
选定合适的阈值Eseg使得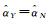
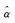
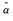
当两组样本的正态分布混淆严重时,错分率估值较高,此时可以对混叠区间内的样本进行后处理,过程概括为以下4步:
(1) 利用EM算法得到两类样本的正态分布参数,计算样本的可分度β,并认为β高于阈值β0的样本已被正确分类,将这些样本构成可靠样本集合(包括正负样本)。可分度计算公式为
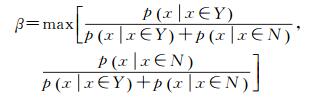 (15)
(15)
(2) 若可靠样本集合中的正负样本比例不均匀,则根据线划图标记的建筑物位置,在震前影像中随机选取正样本,或在震后影像中随机选取负样本,将其加入可靠样本集,使正负样本比例均匀;
(3) 将可靠样本重采样为所有样本的平均尺寸,计算其HOG特征,训练SVM分类器;
(4) 用所得SVM分类器对可分度低于β0的样本分类,接受该分类结果。
为了确保训练样本的可靠性,本文始终固定β0=0.99。
3 试验与分析 3.1 数据与研究区域本文选取了2011年3月东日本地震后受灾严重的石卷港的3组影像数据,如图 2。分别为2010年6月25日地震前GeoEYE-01全色影像(0.5m空间分辨率),和2011年4月6日的WorldView-1全色影像(0.5m空间分辨率),数据1和数据2的影像大小为1000×700像素,数据3的影像大小为557×378像素。震前GIS辅助数据,建筑物矢量线划图通过人工目视判读在震前影像上标记获得。

|
| 图 2 震前和震后影像 Fig. 2 Pre-and post-earthquake remote sensing images |
3.2 变化检测 3.2.1 变化检测精度
本文选取的精度评定指标包括总体精度(overall accuracy,OA)、Kappa系数、生产者精度(producer accuracy, PA)、用户精度(user accuracy, UA)、误检率(commission)、漏检率(omission)。其中,生产者精度(PA)为变化和未变化建筑物的生产者精度的平均值,用户精度(UA)为变化和未变化房屋的用户精度的平均值。误检率(commission)是实际未变化、检测为变化的建筑物占实际未变化建筑物的比例;漏检率(omission)是实际变化、检测为未变化的建筑物占实际变化建筑物的比例,误检率和漏检率计算公式如下
 (16)
(16)
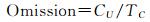 (17)
(17)
式中,UC表示实际未变化、检测为变化的建筑物,TU表示实际未变化的建筑物,CU表示实际变化、检测为未变化的建筑物,TC表示实际变化的建筑物。
3.2.2 试验结果与分析在将本文算法应用于试验影像进行损毁建筑物检测时,设置超像素平均边长a为10像素,高错分率阈值α0=5%,参考角点响应强度Rref值则由算法自动选定。采用的试验平台为Matlab 2016a,CPU为Intel i5-2400,RAM为8GB。
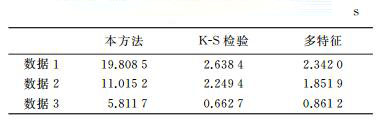
试验结果的精度如表 1所示。3组试验的总体精度分别为85.79%、81.62%和85.12%,Kappa系数分别为71.61%、59.14%、68.96%。其中,数据1的用户精度(85.98%)和生产者精度(85.86%)均最好,对损毁房屋和未损毁房屋的检测精度都较高,误检率(10.36%)最低,数据2的用户精度(78.75%)、生产者精度(80.75%)最低,误检率(16.88%)、漏检率(21.62%)最高。
3组数据试验的目视结果如图 3所示。其中红色部分表示正确检测的损毁房屋,蓝色部分表示正确检测的未损毁房屋,绿色部分表示误检为损毁房屋,黄色部分表示漏检。3组数据的大部分损毁房屋被正确检测,存在少许误检和漏检区域。数据1的右下角漏检较多,数据2的中间区域误检和漏检较多,数据3的左侧漏检和误检较多。漏检或误检原因为:本方法主要利用建筑物的边缘和角点特征进行损毁建筑物检测。对于建筑物实际损毁,但留下明显的轮廓;或由于周围紧邻的建筑物未变化,能检测到明显的边缘特征,容易检测为建筑物未损毁,造成漏检。对于建筑物完好,但被周围建筑物遮挡;或由于成像角度不同,建筑物在两时相影像上的成像位置偏差较大;太阳高度角不同导致的建筑物阴影不同,以及周围建筑物的阴影遮挡,可能会检测为建筑物已经损毁,造成误检。

|
| 图 3 检测结果 Fig. 3 Results of detection |
3.3 建筑物变化检测方法对比分析
将本文方法与基于K-S双样本检验的面向对象变化检测[24]和融合多特征的面向对象变化检测[25]进行比较试验。基于K-S的双样本检验将每一组样本看作一对概率分布样本,对光谱统计特征进行差分,计算对象在不同时相影像中的吻合度,判断对象是否发生变化。融合多特征的面向变化检测方法利用G统计量计算两时相对象的光谱和纹理距离,并对特征进行自适应加权获得对象的异质性从而实现变化检测。
3种方法试验精度如表 2所示。与另外两种方法相比,本文提出的方法在总体精度、Kappa系数、用户精度、生产者精度4项指标上均取得最好的效果,误检率和漏检率最低。总体上,本方法的检测结果最好,融合多特征的方法精度次之,基于K-S双样本检验的检测结果最差。分析原因如下:高分辨率遥感影像光谱混淆严重,而且不同时相影像的光照条件、太阳高度角、成像角度等导致地物在不同影像上灰度值不同,因此只利用了对象灰度特征的K-S双样本检测算法精度较低。融合多特征的方法可以自适应地调节灰度特征和纹理特征的权值,对特征进行了有效融合,因而能获得较好的检测效果。而本文提出的方法综合利用了建筑物的位置、形状、边缘及角点信息,建立了更稳健的检测模型,故能获得更好的检测结果。
3种方法的实验时间如表 3所示,本文提出的方法耗时最多,K-S检验耗时次之,融合多特征的方法效率最高、耗时最短。本文算法运行时间由HOG特征响应值计算、角点响应参考强度计算、超像素分割、图割算法求解和后处理等时间组成。由于本方法综合利用了多种特征,而且角点响应参考强度的确定也需运行一次图割算法,导致本文算法复杂度较高,运行时间也高于其他两种方法。
4 结论
本文针对高分辨率遥感影像信息丰富的特点,提出了一种图割框架下融合多特征的建筑物变化检测方法。利用建筑物线划图,结合建筑物的形状、边缘和角点等特征,构造震后局部影像的网络图;根据图割的最小割能量进行两时相局部影像的相似性度量,实现对损毁建筑物的检测。试验结果表明,本方法能有效检测出震害损毁建筑物。然而,对于建筑物实际损毁但轮廓清晰的区域,本方法较易检测为建筑物未损毁。下一步可以考虑在图的构建中加入其它特征,减少对边缘特征的依赖,提高检测的精度。对于本文算法耗时较长的问题,可以考虑训练一个新的模型,根据样本的其他特征计算其角点响应参考强度值,来提高计算效率。
另外,本文根据建筑物在高分辨率光学影像上的特征构造能量函数,故本文方法只适用于光学影像。考虑到实验数据的多源化,结合多源异质数据进行损毁建筑物检测也是后续的研究方向。
| [1] | JANALIPOUR M, MOHAMMADZADEH A. Building Damage Detection Using Object-based Image Analysis and ANFIS from High-resolution Image (Case Study: BAM Earthquake, Iran)[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(5): 1937–1945. DOI:10.1109/JSTARS.2015.2458582 |
| [2] | ADAMS B J, EGUCHI R T, HUYCK C K, et al. Using Optical and Synthetic Aperture Radar Remote Sensing Technology to Detect Earthquake Damage Following the 1999 Marmara, Turkey Earthquake[C]//Proceedings of the 9th Biennial Conference on Engineering, Construction, and Operations in Challenging Environments. Houston, Texas: American Society of Civil Engineers, 2014: 239-246. |
| [3] | CAO Chunxiang, LIU Di, SINGH R P, et al. Integrated Detection and Analysis of Earthquake Disaster Information Using Airborne Data[J]. Geomatics, Natural Hazards and Risk, 2016, 7(3): 1099–1128. DOI:10.1080/19475705.2015.1020887 |
| [4] | TONG Xiaohua, LIN Xiaofei, FENG Tiantian, et al. Use of Shadows for Detection of Earthquake-induced Collapsed Buildings in High-resolution Satellite Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013(79): 53–67. |
| [5] | KAHRAMAN F, IMAMOGLU M, ATES H F. Disaster Damage Assessment of Buildings Using Adaptive Self-similarity Descriptor[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(8): 1188–1192. DOI:10.1109/LGRS.2016.2574960 |
| [6] | YUSUF Y, MATSUOKA M, YAMAZAKI F. Damage Assessment after 2001 Gujarat Earthquake Using Landsat-7 Satellite Images[J]. Journal of the Indian Society of Remote Sensing, 2001, 29(1-2): 17–22. DOI:10.1007/BF02989909 |
| [7] | YAMAZAKI F, SUZUKI D, MARUYAMA Y. Detection of Damages due to Earthquakes Using Digital Aerial Images[J]. 2008. |
| [8] | EHRLICH D, BIELSKI C. Texture Based Change Detection of Built-up on Spot Panchromatic Imagery Using PCA[C]//Proceedings of 2011 Joint Urban Remote Sensing Event. Munich, Germany: IEEE, 2011: 77-80. |
| [9] | SUSAKI J. Region-based Automatic Mapping of Tsunami-damaged Buildings Using Multi-temporal Aerial Images[J]. Natural Hazards, 2015, 76(1): 397–420. DOI:10.1007/s11069-014-1498-4 |
| [10] | ROWE N C, GREWE L L. Change Detection for Linear Features in Aerial Photographs Using Edge-Finding[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(7): 1608–1612. DOI:10.1109/36.934092 |
| [11] | HUYCK C K, ADAMS B J, CHO S, et al. Towards Rapid Citywide Damage Mapping Using Neighborhood Edge Dissimilarities in Very High-resolution Optical Satellite Imagery—Application to the 2003 Bam, Iran, Earthquake[J]. Earthquake Spectra, 2005, 21(S1): S255–S266. DOI:10.1193/1.2101907 |
| [12] | LI Peijun, XU Haiqing, LIU Shuang, et al. Urban Building Damage Detection from Very High Resolution Imagery Using One-Class SVM and Spatial Relations[C]//Proceedings of the 2009 IEEE International, IGARSS 2009 Geoscience and Remote Sensing Symposium. Cape Town, South Africa: IEEE, 2010: V-112-V-114. |
| [13] | YE Xin, QIN Qiming, LIU Mingchao, et al. Building Damage Detection From Post-quake Remote Sensing Image Based on Fuzzy Reasoning[C]//Proceedings of 2014 IEEE International Geoscience and Remote Sensing Symposium. Quebec City: IEEE, 2014: 529-532. |
| [14] | SAMADZADEGAN F, RASTIVEISI H, VⅢ W G. Automatic Detection and Classification of Damaged Buildings, Using High Resolution Satellite Imagery and Vector Data[J]. Journal of Food Science, 2011, 78(7): M1049–M1056. |
| [15] | PEYKHERFEH M, SHAHBAHRAMI A. Evaluation of Adaptive Boosting and Neural Network in Earthquake Damage Levels Detection[J]. International Journal of Computer Applications, 2014, 100(3): 23–29. DOI:10.5120/17507-8058 |
| [16] | GONG Lixia, LI Qiang, ZHANG Jingfa. Earthquake Building Damage Detection with Object-Oriented Change Detection[C]//Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium. Melbourne, VIC, Australia: IEEE, 2013: 3674-3677. |
| [17] | BOYKOV Y Y, JOLLY M P. Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images[C]//Proceedings of the Eighth IEEE International Conference on Computer Vision, 2001. ICCV 2001. Vancouver, BC, Canada: IEEE, 2001(1): 105-112. |
| [18] | 刘毅, 黄兵, 孙怀江, 等. 利用视觉显著性与图割的图像分割算法[J]. 计算机辅助设计与图形学学报, 2013, 25(3): 402–409. LIU Yi, HUANG Bing, SUN Huaijiang, et al. Image Segmentation Based on Visual Saliency and Graph Cuts[J]. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(3): 402–409. |
| [19] | 王涛, 纪则轩, 孙权森. 结合非局部信息与图割的图像分割算法[J]. 计算机辅助设计与图形学学报, 2015, 27(5): 783–791. WANG Tao, JI Zexuan, SUN Quansen. A Segmentation Algorithm Combined with Non-Local Information and Graph Cut[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(5): 783–791. |
| [20] | DALAL N, TRIGGS B. Histograms of Oriented Gradients for Human Detection[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA: IEEE, 2005(1): 886-893. |
| [21] | LIU Mingyu, TUZEL O, RAMALINGAM S, et al. Entropy Rate Superpixel Segmentation[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2011: 2097-2104. |
| [22] | HARRIS C, STEVENS M. A Combined Corner and Edge Detector[C]//Proceedings of the 4th Alvey Vision Conference. Manchester, UK: [s.n.], 1988: 147-151. |
| [23] | 骆剑承, 王钦敏, 马江洪, 等. 遥感图像最大似然分类方法的EM改进算法[J]. 测绘学报, 2002, 31(3): 234–239. LUO Jiancheng, WANG Qinmin, MA Jianghong, et al. The EM-based Maximum Likelihood Classifier for Remotely Sensed Data[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 234–239. DOI:10.3321/j.issn:1001-1595.2002.03.010 |
| [24] | TANG Yuqi, ZHANG Liangpei, HUANG Xin. Object-oriented Change Detection Based on the Kolmogorov-Smirnov Test Using High-resolution Multispectral Imagery[J]. International Journal of Remote Sensing, 2011, 32(20): 5719–5740. DOI:10.1080/01431161.2010.507263 |
| [25] | 李亮, 舒宁, 王凯, 等. 融合多特征的遥感影像变化检测方法[J]. 测绘学报, 2014, 43(9): 945–953. LI Liang, SHU Ning, WANG Kai, et al. Change Detection Method for Remote Sensing Images Based on Multi-features Fusion[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 945–953. DOI:10.13485/j.cnki.11-2089.2014.0138 |