2. 地球空间信息协同创新中心, 湖北 武汉 430079;
3. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
4. 武汉大学遥感信息工程学院, 湖北 武汉 430072
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
4. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430072, China
当前,随着航天遥感技术的不断发展,人类已经能够在较短时间内快速获取地球表面的海量卫星影像数据。通过这些卫星影像数据进行测图,可以获取地球表面高精度的数字正射影像DOM和数字表面模型DSM,为各行各业提供必要的高精度空间参考数据。在利用光学卫星影像进行测图时,区域网平差是其中的一项关键环节,平差结果的好坏通常直接决定了最终DOM和DSM产品的几何精度,长期以来是摄影测量工作关注的重点,并取得了一定的理论与实践成果。根据所采用的平差模型,目前光学卫星区域网平差方法主要包括基于严格几何成像模型[1-3]和单景影像RPC模型[4-7]两种。其中,前者是基于影像几何误差与成像时间满足一定的变化关系,在严格几何成像模型中引入相应的误差补偿模型,如姿轨多项式模型[8]、姿轨定向片模型[9]、EFP模型[10]等,在平差过程中对影像的几何误差进行补偿。后者则是以单景影像为平差单元,通过在RPC模型的像方附加合适的数学模型,如仿射变换模型,在平差过程中求解该模型参数,实现对待平差影像几何误差的修正与补偿[11-12]。相较而言,基于单景影像RPC模型的平差方法因具有数据易组织、模型通用简单的优点,在实际应用中使用更为广泛,特别是当区域网规模较大时,优势更为明显,因此本文的研究同样基于RFM[13]。
随着全球测图工程的开展,作为大区域测图的一项重要手段,大规模区域网平差技术得到越来越多的重视。然而,由于大区域平差中影像数量较大,区域网内结构复杂,导致大规模平差在实际应用中难以实现。针对于大区域的平差,国内外学者同样进行相应的研究,其中,文献[14]提出一种基于DEM辅助的区域网平差的方法来提高大区域影像的测图精度,使用覆盖江西省的ZY-3号和GF1号影像数据进行了区域网平差的实验,并验证了实验的精度和效率。文献[15]在RFM的基础上提出了一个相似的方法来改善覆盖意大利北部区域的414个立体像对的几何精度。针对于QuickBird影像的大区域平差测图,文献[16]基于严格几何成像模型研究了在大区域平差中的最佳控制点分布,并针对不同点位分布给出了定量的精度分析。然而,上述方法主要针对控制点约束下的大区域测图进行了研究,因此这些方法并不适用于全球测图工程中遇到的环境恶劣的无人区、境外军事敏感区等无控制区域,此外上述方法所针对的区域一般只包含几百景影像,对于上万景影像覆盖区域的超大规模的区域网平差难以适用。
在无控制点条件下进行超大规模平差时,由于缺少控制点的约束,平差模型的自由度较高,直接将待平差参数作为自由未知数会导致法方程矩阵的病态,进而使得平差精度不稳定以及误差容易过度累积而引起网的扭曲变形[17]。针对该问题,本文提出一种基于虚拟控制点的超大区域无控制区域网平差。该方法利用各景待平差影像的初始RPC模型生成虚拟控制点,将虚拟控制点作为带权观测值引入到平差模型中以改善平差模型的状态。与传统方法相比,本文方法通过引入虚拟控制点代替待平差参数作为附加观测值,避免了对各项复杂的待平差参数构建平差模型并确定其权值,具有模型简单、易于定权的优点,具有较强的实用性。
1 基本原理 1.1 RPC模型有理多项式模型(RFM)是从数学意义上对严格几何成像模型的高精度拟合[18],较于严格几何成像模型,由于其形式简单、使用方便而更适合于大规模区域网平差处理中,如式(1) 所示
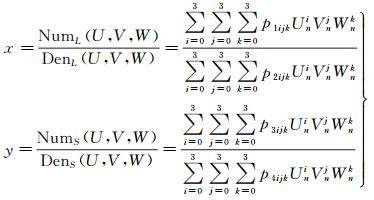 (1)
(1)
式中,(U, V, W)与(x, y)分别代表为正则化的地面点大地坐标与正则化的影像像点坐标;p1ijk、p2ijk、p3ijk、p4ijk(i=1, 2, 3;j=1, 2, 3;k=1, 2, 3) 代表RFM的有理多项式系数(rational polynomial coefficients, RPC)。正则化的坐标与非正则化的坐标的关系如式(2) 所示
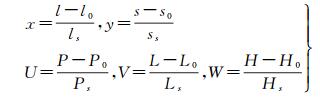 (2)
(2)
式中,(l0, s0)为像点坐标的重心化参数;(P0, L0, H0)为地面点大地坐标的重心化参数;(ls, ss)为像点坐标的归一化参数;(Ps, Ls, Hs)为地面点大地坐标的归一化参数[19]。
利用单景影像的RPC模型进行区域网平差时,需要根据影像几何误差的特性,选择合适的数学模型并附加到RPC模型的像方,如式(3) 中Δl和Δs
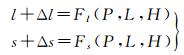 (3)
(3)
在平差过程中对该模型进行求解,以补偿各景影像中存在的几何误差。
以资源三号卫星为例,经过严格的在轨几何定标及传感器校正处理后,其单景影像产品的几何误差主要为低阶线性误差[20-22],因此,其像方附加模型Δl和Δs选择仿射变换模型即可,如式(4) 所示
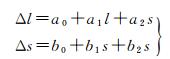 (4)
(4)
在有控制条件下,基于上述平差模型可将待平差参数作为自由未知数进行平差求解。然而,在无控制点条件下,由于缺少控制点的约束,平差模型的自由度较高,直接将待平差参数作为自由未知数求解会导致法方程矩阵的病态,进而造成平差精度不稳定以及误差容易过度累积等问题。对此,传统方法通过将待平差参数根据先验信息处理成带权观测值引入到平差模型中来改善平差模型的状态,但该方法由于需要对多类不同物理意义且相互之间存在相关性的参数构建误差方程并定权,因此在实际应用中受到一定的局限。针对于传统方法的不足,本文方法通过在模型中引入虚拟控制点来约束区域网的自由度,从而达到改善平差模型的状态的目的。下面将对虚拟控制点的生成及其观测方程的构建进行阐述。
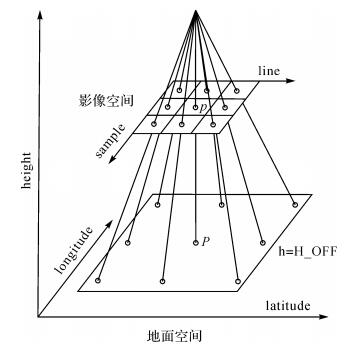
对各景待平差影像,在其像平面上按一定间距均匀划分规则格网,对每个格网的中心点p(smp, line),利用该影像的初始RPC模型,在物方局部任一高程基准面(本文取为影像初始RPC模型中的H_OFF)上通过前方交会得到一物方点P(Lat, Lon, H_OFF),此时,像点p与物方点P构成一组虚拟控制点,如图 1所示。
|
| 图 1 虚拟控制点生成 Fig. 1 The generation of virtual control points |
一般情况下, 基于影像间自动匹配获取的连接点信息和人工半自动量测获取的控制点信息构建区域网平差模型时, 其原始观测值包括连接点像点坐标和控制点像点坐标两类.对于控制点像点而言, 由于其对应的物方点坐标精确已知, 因此, 所构建的误差方程式中未知参数仅包括该像点所在影像的RPC模型像方附加参数, 显然, 对于RPC模型像方附加参数而言, 此时视为线性方程而无需进行线性化处理, 如式(5)
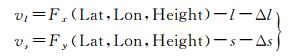 (5)
(5)
对于连接点而言,由于其未知参数除了包括该像点所在影像的RPC模型像方附加参数外,还包括其对应的物方坐标(Lat, Lon, Height),由连接点构建的误差方程为一非线性方程,需要对其赋予合适的初值(Lat, Lon, Height)0并进行线性化处理,如式(6) 所示
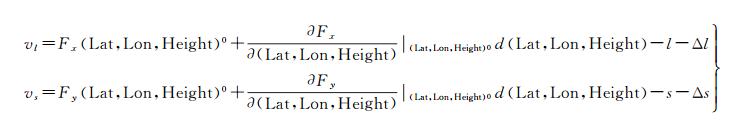 (6)
(6)
各连接点物方坐标的初值可由相应待平差影像初始RPC模型通过前方交会计算得到。将由所有连接点像点以及虚拟控制点像点构建的观测误差方程组分别写成矩阵形式,如式(7) 和式(8) 所示
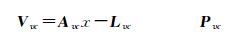 (7)
(7)
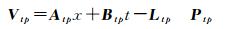 (8)
(8)
式(7) 为所有虚拟控制点像点构建的观测误差方程组矩阵;式(8) 为所有连接点像点构建的观测误差方程组矩阵。其中,x和t为平差待解参数,分别代表待平差影像RPC模型的像方附加参数向量和连接点物方坐标改正数向量。A、B则分别为相应未知数的偏导数系数矩阵,L和P则分别为相应的常向量和权矩阵,其中连接点像点的权值可根据连接点匹配精度确定。将两类误差方程矩阵合并,如式(9) 所示
 (9)
(9)
式中, 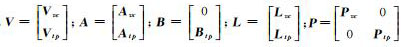
在上述平差模型中,其观测值仅包含虚拟控制点像点与连接点像点两类,它们之间相互独立,可分别根据各自的观测精度进行定权,而无需考虑两者之间的相关性。其中,连接点像点观测值的权值可依据同名像点的匹配精度进行设定,对于光学卫星影像而言,采用高精度匹配算法[23]通常可达到子像素级的匹配精度。而对于虚拟控制点像点观测值,其权值可根据待平差影像无控几何定位精度的先验信息来确定。以资源三号卫星下视影像为例,长期在轨测试表明,其无控几何定位中误差约为15m[24],根据其几何分辨率换算至像方约7.5像素,据此可将其虚拟控制点像点观测值的权值pvc设为1/(7.5)3。
为了避免虚拟控制点与连接点之间由于数量比例失衡导致平差模型局部出现“弱”连接、“强”控制的情况,给平差后相邻影像之间的相对几何精度带来不利影响,本文方法中对各景影像均单独统计其两类点数量的比例因子,即μ=Ntp/Nvc,其中Ntp和Nvc分别代表该景影像上连接点和虚拟控制点的个数,然后对其中所有虚拟控制点像点观测值的权值pvc均乘以该比例因子。
从上述可以看出,与传统方法相比,本文方法通过引入虚拟控制点代替待平差参数作为附加观测值,在改善平差模型状态的同时,避免了对各类复杂的待平差参数构建平差模型并进行定权,具有模型简单、易于定权的优点,具有较强的实用性。
1.4 平差求解与精度验证根据最小二乘平差原理,对误差方程式(9) 进行法化,可得到法方程如式(10) 所示
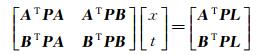 (10)
(10)
对于一个较大规模的测区而言,通过自动匹配获取的连接点数量一般情况下高达上万个,同时解算x和t这两类未知数,所需的内存与时间开销是难以满足的。考虑到连接点数量一般远大于影像数量,更重要的是法方程系数矩阵中BtpTPtpBtp为一分块对角矩阵,在矩阵存储、运算等方面具有优良的性质。根据这一特点,摄影测量中常采用的方法是首先通过消元法消去连接点物方坐标这一类待解参数,构建出仅包含待解参数x的等价方程组先求解x,如式(11) 所示
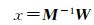 (11)
(11)
式中,M=ATPA-ATPB(BTPB)-1BTPA;W=ATPL-ATPB(BTPB)-1BTPL。区域网平差的解算是一个迭代的过程,当两次平差解算的结果小于限差时,迭代结束,在此基础上,利用各景影像的初始RPC模型和已求解的附加模型参数x,通过空间前方交会即可逐个计算各连接点的物方坐标。
区域网平差后通常需要对平差结果的精度进行验证,绝对几何定位精度与拼接精度是表征区域网平差质量的两项重要指标。对于影像产品的绝对几何定位精度,可以将覆盖测区范围的高精度外业控制点作为独立检查点,通过统计检查点的物方坐标与前方交会获取的相应点的物方坐标的差值来对其进行验证,拼接精度则可以通过统计相邻影像之间匹配的同名像点的像方残差来进行验证,本文同样采用上述方法验证绝对几何定位精度与拼接精度来评价本方法的有效性。
2 试验与结果 2.1 试验数据基于本文方法对资源三号卫星获取的覆盖中国整个大陆的8802景三线阵立体像对(共26406景影像)进行了无控制区域网平差试验。每景影像均附带RPC参数文件,相邻影像之间具有一定的重叠度,影像数据量约20TB。测区覆盖面积约900万km2,约占中国国土面积93%以上,仅在广西、贵州等局部区域由于天气原因而缺少有效影像数据。测区内包含高原、山地、丘陵、平原等以及沙漠多类地形,最大最小高程起伏达8000m以上。为了对平差结果的几何精度进行分析与验证,在全国范围内通过GPS外业测量,共获取了约8000余个高精度控制点(平面和高程精度均优于0.1m)。
对上述ZY-3卫星影像数据,利用100个高性能计算节点组成的集群计算环境(该环境由中国资源卫星应用中心提供,每个节点均配置了一个6核Xeon-L7455的CPU和128GB的内存),约耗费2h在整个测区内自动匹配了约300万个均匀分布且可靠性较高的连接点。并对各景影像在像方均匀划分3×3格网,对每个格网的中心点按前述方法生成虚拟控制点,每景影像生成9个虚拟控制点,共生成237654个虚拟控制点。按照本文方法将生成的虚拟控制点与连接点一起进行联合平差,平差过程在个人普通PC机(CPU为双核Intel-i5,内存空间为8GB)上完成,仅需两次迭代解算就已收敛,共耗时约15min。这表明,在常规自由网平差模型中,通过引入虚拟控制点作为带权观测值,能够有效改善平差模型的状态,使平差模型具有良好的收敛性。为了对于平差结果的精度进行评价,下面分别对于平差后生产的DOM产品的绝对几何定位精度和拼接精度分别进行验证。
2.2 绝对几何定位精度验证本试验中利用覆盖全国范围的高精度外业控制点作为独立检查点,分别对DOM和DSM产品的平面和高程几何精度进行了验证。为了更加科学地分析区域网几何精度,特别是内部几何精度的均匀性,不仅对所有检查点整体统计其几何误差的均值、中误差和最大值等精度指标,还根据检查点的分布情况将全国划分为5个子区域,分别统计各子区域内的检查点几何误差的精度指标。
从表 1中可以得出以下结论:① 不论是平面还是高程方向,各子区域检查点误差的均值和中误差基本相当,无明显差异;② 各子区域平面和高程的误差均值均接近于0,区域网整体在空间中无明显的偏移性系统误差;③ 各子区域内检查点的平面和高程最大误差值均控制在3倍中误差以内。以上结论说明:① 虚拟控制点能够对区域网内部的误差累积起到一定的约束作用,避免了区域网的扭曲变形而使得中心与边缘精度不一致,保证了区域网内部几何精度的均匀性;② 每个虚拟控制点相当于一个具有一定精度的控制点观测值,根据平差理论,大量的虚拟控制点能够显著提高待平差参数的估计精度,从而实现网的无偏估计,为无控制点条件下达到有控制点的测图精度提供了一种简单实用的方法;③ 虚拟控制点的引入能够有效改善平差模型的状态,避免了无控制点时由于平差模型病态而导致解算结果不稳定、几何精度异常的问题,保证了平差结果具有高可靠性。
2.3 拼接精度验证
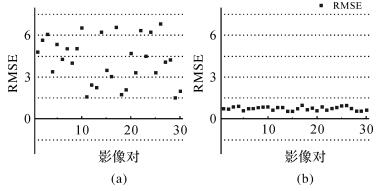
作为测图作业中的一项关键指标,DOM拼接精度表征了相邻DOM同名地物之间几何定位精度的一致性。为此,本文试验中在全国范围内均匀选取了平差前后的30对相邻DOM产品进行验证。在每对相邻DOM产品的重叠区域内,通过影像匹配自动获取一定数量、均匀分布的同名像点,统计这些同名像点几何坐标差值的中误差,以此对其几何拼接精度进行定量化评价,如图 2所示。图中纵坐标为各对相邻DOM同名像点几何坐标差值的均方误差RMSE,横坐标代表各对相邻DOM的编号。
|
| 图 2 DOM几何拼接误差 Fig. 2 Errors of DOM geometric mosaic |
此外,对每对相邻DOM产品采用人工目视检查的方式对其几何拼接精度进行直观评价。图 3中(a)、(b)分别为城市和山地在原始2m分辨率的基础上放大2倍后人工目视检查的情况。

|
| 图 3 DOM拼接图 Fig. 3 The sketch map of mosaic DOM |
从图 2和图 3可以看出,基于本方法平差后,相邻影像之间的拼接精度得到明显的改善,目视效果良好,相邻DOM产品之间的几何拼接精度均优于1个像素,满足无缝拼接的要求。
在平差完成后,基于平差后的26406景三线阵立体像自动生产了5m分辨率的DSM产品以及2m分辨率的DOM产品[25],DOM和DSM产品的数据量共约20TB,图 4为利用本方法所生产的测区内局部区域的DSM产品。

|
| 图 4 局部DSM示意图 Fig. 4 The sketch map of local DSM |
3 结论
本文提出了一种以单景影像为平差单元,基于虚拟控制点的光学卫星影像超大规模无控制区域网平差方法。该方法利用待平差影像的初始RPC模型生成虚拟控制点,并将其作为带权观测值引入平差模型中,实现对各项待平差参数的稳健估计。与传统将待平差参数作为带权观测值的方法相比,本文方法通过引入虚拟控制点代替待平差参数作为附加观测值,在改善平差模型状态的同时,避免了对各类复杂的待平差参数构建平差模型并进行定权,具有模型简单、易于定权的优点。基于本文方法对资源三号卫星获取的覆盖中国全国的26406景三线阵立体影像进行了无控制区域网平差,并利用中国全国分布的约8000个高精度控制点对平差后自动生产的DOM和DSM产品几何精度进行了验证,其平面和高程中误差均达到4m以内,同时,区域网内部几何精度均匀,相邻模型之间的几何拼接精度优于1个像素,满足无缝拼接的要求,实现了资源三号卫星影像中国全国无控制测图精度优于5m的目标。目前,本文方法已在商业化卫星影像区域网平差软件中得到成功应用。
| [1] | 程春泉, 邓喀中, 孙钰珊, 等. 长条带卫星线阵影像区域网平差研究[J]. 测绘学报, 2010, 39(2): 162–168. CHENG Chunquan, DENG Kazhong, SUN Yushan, et al. Study of Block Adjustment for Long-strip Satellite CCD Images[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 162–168. |
| [2] | ROTTENSTEINER F, WESER T, LEWIS A, et al. A Strip Adjustment Approach for Precise Georeferencing of ALOS Optical Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 4083–4091. DOI:10.1109/TGRS.2009.2014366 |
| [3] | 邵巨良, 王树根, 李德仁. 线阵列卫星传感器定向方法的研究[J]. 武汉测绘科技大学学报, 2000, 25(4): 329–333. SHAO Juliang, WANG Shugen, LI Deren. Determination of Satellite Sensor Orientation[J]. Journal of Wuhan Technical University of Surveying and Mapping (WTUSM), 2000, 25(4): 329–333. |
| [4] | GRODECKI J, DIAL G. Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 59–68. |
| [5] | 李德仁, 张过, 江万寿, 等. 缺少控制点的SPOT-5 HRS影像RPC模型区域网平差[J]. 武汉大学学报(信息科学版), 2006, 31(5): 377–381. LI Deren, ZHANG Guo, JIANG Wanshou, et al. SPOT-5 HRS Satellite Imagery Block Adjustment Without GCPS or with Single GCP[J]. Geomatics and Information Science of Wuhan University, 2006, 31(5): 377–381. DOI:10.3321/j.issn:1671-8860.2006.05.001 |
| [6] | 刘军, 张永生, 王冬红. 基于RPC模型的高分辨率卫星影像精确定位[J]. 测绘学报, 2006, 35(1): 30–34. LIU Jun, ZHANG Yongsheng, WANG Donghong. Precise Positioning of High Spatial Resolution Satellite Images Based on RPC Models[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 30–34. DOI:10.3321/j.issn:1001-1595.2006.01.007 |
| [7] | TAO C V, HU Yong. A Comprehensive Study of the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(12): 1347–1357. |
| [8] | POLI D. General Model for Airborne and Spaceborne Linear Array Sensors[C]//Proceedings of ISPRS Commission I Symposium on Integrating Remote Sensing at the Global, Regional and Local Scale. Denver: [s.n.], 2012: 177-182. |
| [9] | FRASER C S, RAVANBAKHSH M. Precise Georefrencing of Long Strips of ALOS Imagery[J]. Photogrammetric Engineering & Remote Sensing, 2011, 77(1): 87–93. |
| [10] | 王任享. 卫星摄影三线阵CCD影像的EFP法空中三角测量(二)[J]. 测绘科学, 2002, 27(1): 1–7. WANG Renxiang. EFP Aerial Triangulation for Triple Linear-array CCD Satellite Images[J]. Science of Surveying and Mapping, 2002, 27(1): 1–7. |
| [11] | 张力, 张继贤, 陈向阳, 等. 基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J]. 测绘学报, 2009, 38(4): 302–310. ZHANG Li, ZHANG Jixian, CHEN Xiangyang, et al. Block-adjustment with SPOT-5 Imagery and Sparse GCPs Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 302–310. |
| [12] | ZHANG Guo, WANG Taoyang, LI Deren, et al. Block Adjustment for Satellite Imagery Based on the Strip Constraint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 933–941. DOI:10.1109/TGRS.2014.2330738 |
| [13] | 皮英冬, 杨博, 李欣. 基于有理多项式模型的GF4卫星区域影像平差处理方法及精度验证[J]. 测绘学报, 2016, 45(12): 1448–1454. PI Yingdong, YANG Bo, LI Xin. Block-adjustment and Accuracy Validation for GF4 Patch-images Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1448–1454. DOI:10.11947/j.AGCS.2016.20160262 |
| [14] | ZHENG Maoteng, ZHANG Yongjun. DEM-aided Bundle Adjustment With Multisource Satellite Imagery: ZY-3 and GF-1 in Large Areas[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(6): 880–884. DOI:10.1109/LGRS.2016.2551739 |
| [15] | D'ANGELO P, REINARTZ P. Dsm Based Orientation of Large Stereo Satellite Image Blocks[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012, XXXIX-B1: 209–214. DOI:10.5194/isprsarchives-XXXIX-B1-209-2012 |
| [16] | PASSINI R M, BLADES A, JACOBSEN K. Handling of Large Block of High Resolution Space Images[J]. 2005. |
| [17] | 李德仁. 论自检校区域网平差中的信噪比[J]. 测绘学报, 1982, 11(3): 170–184. LI Deren. On the Signal-to-noise Ratio in Self-calibrating Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 1982, 11(3): 170–184. |
| [18] | MADANI M. Real-time Sensor-independent Positioning by Rational Functions[C]//Proceedings of ISPRS Workshop on Direct Versus Indirect Methods of Sensor Orientation. Barcelona: ISPRS, 1999: 25-26. |
| [19] | 胡芬, 杨博, 唐新明, 等. ZY-3卫星异轨立体影像几何定位精度分析[J]. 航天返回与遥感, 2016, 37(1): 71–79. HU Fen, YANG Bo, TANG Xinming, et al. Geo-positioning Accuracy Analysis Validation of ZY-3 Cross-track Stereo-images[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(1): 71–79. |
| [20] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191–198. TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191–198. |
| [21] | WANG Mi, YANG Bo, HU Fen, et al. On-orbit Geometric Calibration Model and Its Applications for High-resolution Optical Satellite Imagery[J]. Remote Sensing, 2014, 6(5): 4391–4408. DOI:10.3390/rs6054391 |
| [22] | ZHANG Yongjun, ZHENG Maoteng, XIONG Jinxin, et al. On-orbit Geometric Calibration of ZY-3 Three-line Array Imagery With Multistrip Data Sets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 224–234. DOI:10.1109/TGRS.2013.2237781 |
| [23] | 张力, 张继贤. 基于多基线影像匹配的高分辨率遥感影像DEM自动生成[J]. 测绘科学, 2008(S2): 35–39. ZHANG Li, ZHANG Jixian. Multi-image Matching for DEM Generation from Satellite Imagery[J]. Science of Surveying and Mapping, 2008(S2): 35–39. |
| [24] | WANG Mi, YANG Bo, HU Fen, et al. On-orbit Geometric Calibration Model and Its Applications for High-resolution Optical Satellite Imagery[J]. Remote Sensing, 2014, 6(5): 4391–4408. DOI:10.3390/rs6054391 |
| [25] | 张静, 杨博, 王密, 等. 基于资源3号影像的全国DOM快速制作方法[J]. 测绘地理信息, 2016, 41(6): 70–74. ZHANG Jing, YANG Bo, WANG Mi, et al. Rapid Manufacturing Method of Nationwide Digital Orthophoto Map Based on ZY-3 Satellite Imagery[J]. Journal of Geomatics, 2016, 41(6): 70–74. |




