2. 辽宁工程技术大学测绘与地理科学学院, 辽宁 阜新 123000;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079
2. School of Surveying, Mapping and Geoinformation Science, Liaoning Technology University, Fuxin 123000, China;
3. GNSS Research Center, Wuhan University, Wuhan 430079, China
2016年5月30日,我国资源三号02星首次搭载了一台试验性激光测高仪,用于开展地表高程信息获取试验[1]。星载激光测高仪是一种精确的主动式测距载荷,其获取的高精度地表高程信息可与光学立体影像联合实现复合测绘[2]。由于受火箭推力力矩变化、平台振动、外界环境变化、时统误差等因素影响,激光测高仪的指向、测距等参数较发射前实验室测量值均会发生一定变化,从而影响了激光测高仪自身测量几何精度以及与光学立体影像复合测绘的精度,因此,有必要在资源三号02星上天后开展激光测高仪在轨几何检校试验,消除其激光载荷的指向、测距等系统误差[3-4]。在资源三号02星发射前,只有美国ICEsat(ice, cloud and land elevation satellite)卫星上搭载了对地观测激光测高仪(geo-science laser altimetry system, GLAS)[5]。针对GLAS在轨几何检校,国内外学者已有一些研究[6-7]。根据参考源不同,可归纳为基于地面探测器检校[8-13]和基于自然地形检校[6-7, 14]两大类。自然地形检校方法主要依赖卫星机动或者波形数据,然而由于我国资源三号02星首次搭载的激光测高仪为试验性载荷,只有测距数据,不下传波形;同时卫星采用三轴姿态稳定大平台,仅具备左右侧摆能力,无法实现圆锥扫描等复杂姿态机动能力,因此,资源三号02星激光测高仪主要通过地面探测器检校法来实现在轨几何检校[8-11]。
基于地面探测器检校法也是GLAS主要的几何检校手段之一。该方法需要提前预知星载激光测高仪足印的位置,并在卫星过境前在该位置布设地面红外探测器阵列,精确捕获卫星过境时激光足印光斑能量并确定中心位置,然后将光斑质心坐标作为地面控制实现激光测高仪在轨几何检校解算。因此,激光足印位置预报是星载激光测高仪地面探测器检校试验的第一步,预报的精度不仅关系着探测器阵列布设的大小,甚至决定着试验的成败。对于美国GLAS而言,由于其脉冲重频高,为40 Hz,按照卫星飞行速度,沿轨方向相邻激光足印间距为170 m左右,即只要沿轨方向上探测器阵列布设范围大于该距离,就能顺利捕获到光斑[15],因此其试验成功率高,实施难度较小。对于资源三号02星激光测高仪而言,其脉冲发射频率为2 Hz,沿轨方向相邻足印质心相距为3.5 km左右。如果不开展激光足印位置精确预报,需要布设超过3.5 km的探测器阵列才能捕获激光光斑。不仅探测器数量及耗费巨大,而且卫星过境前短时间内难以完成布设任务,不具备工程可实施性。因此,亟需开展资源三号02星激光足印位置预报方法研究,为激光载荷在轨几何检校试验实施提供技术支撑。
本文针对资源三号02星激光测高仪在轨几何检校试验需求,在分析光学遥感卫星姿态变化和轨道运行规律的基础上,利用了大平台卫星在轨运行姿轨高稳定度的特点,构建了一套在轨道坐标系下的严密激光足印位置预报模型,该模型充分借鉴了激光测高仪光束定位几何原理,采用了基于地形匹配的指向预估、基于经验加速度的轨道预报和基于频域分析的姿态预报方法,获取过境时刻对应预报参数的计算。最后,利用卫星在轨测试期间成功捕获的激光足印数据,与预报的足印位置进行对比分析,全面评价模型的预报精度。
1 激光足印严密几何预报模型基于单光束几何定位的原理,综合考虑卫星平台质心、激光器发射位置、GPS天线质心以及地球椭球面的相对位置偏移和旋转几何关系,并充分顾及星体在轨道坐标系下的几何物理意义[16],构建的严密几何预报模型如式(1) 所示
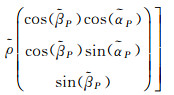 (1)
(1)
式中,
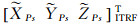
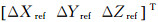
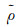

卫星质心轨道位置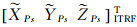
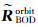

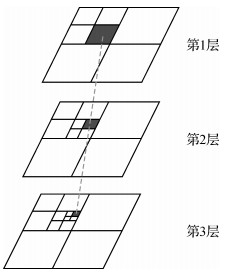
由于采用不同的激光指向计算的地面高程值都不同,理论上,只有正确的激光指向计算出来的激光点高程值才与真实的地形最接近。基于该原理,提出了一种基于金字塔地形匹配策略的指向预估方法。其计算原理如图 1所示。
|
| 图 1 基于金字塔策略地形匹配的指向预估原理图 Fig. 1 Established angle prediction by pyramid |
基本流程是依次累加不同的指向,通过计算整轨甚至多轨激光对应地面区域的高程信息,将得到的高程信息与真实的地形高程信息进行对比,计算高程值与真实地形高程最接近时,对应的指向为最优指向估计值。由于计算量大,本文提出采用金字塔分层搜索方法可以提高搜索效率,从而较短时间内获取较高精度的指向预估值。计算公式为
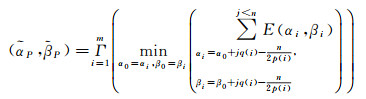 (2)
(2)
式中,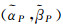
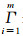
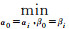
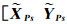
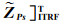
利用卫星下传双频GPS原始观测数据,结合快速发布的GPS轨道和钟差产品计算卫星过境前一段时间里的精密轨道,再利用拟合经验加速度的方法进行轨道预报[18]。
基于经验加速度的轨道预报公式为
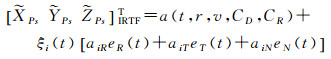 (3)
(3)
式中
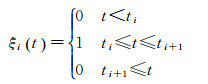
待估参数Y包括卫星初值位置和速度y0、CD、CR及经验加速度
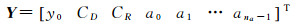 (4)
(4)
式中,CD和CR作为常值估计。
1.3 基于频域拟合预报姿态roll、pitch和yaw利用过境前一段时间累积的原始姿态数据,估计卫星平台姿态抖动的一系列固有频率,引入了一般多项式和三角多项式对累积姿态进行外推,能够较好的保证姿态精度,其中姿态频域分析预报的公式为(以roll为例)
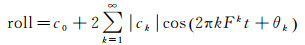 (5)
(5)
式中,roll预报的横滚姿态结果;c0为常量;k为频率区段的个数;ck为第k个频率段的振幅值;Fk为频率值;t为时间;θk为初相位。
2 试验验证与分析 2.1 激光足印位置预报试验在资源三号02星在轨测试期间,利用本文构建的激光足印位置预报模型,分别于2016年8月9日、14日、29日开展了3次激光在轨检校试验。其中,2016年8月9日为卫星上天后激光测高仪第一次检校试验,因此,采用的指向、轨道和姿态等数据均为预报的结果。后面试验中指向均采用前次检校的结果。
下面以2016年8月9日试验为例,给出指向、轨道和姿态的预报结果及最终预报误差。
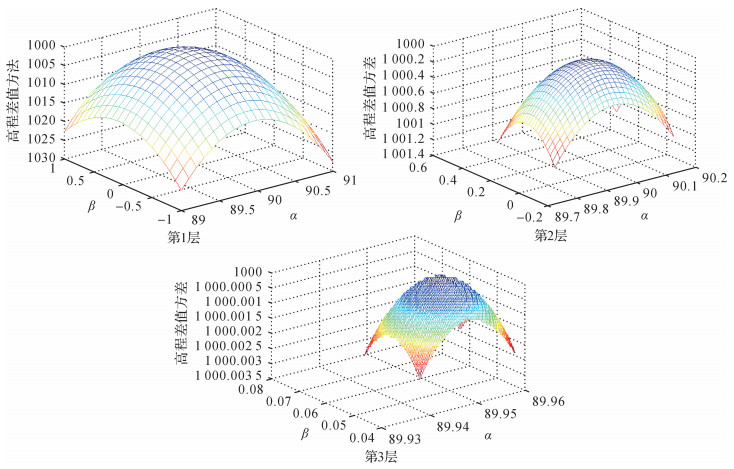
2.1.1 基于地形匹配的指向预报结果根据本文所提方法,在指向预估时,第1层金字塔的遍历间隔为0.1°,第2层为1′,第3层为1″,3层搜索的结果分别如图 2所示;地面参考地形数据采用30 m格网的AW3D30数据[21],指向预估结果与在轨几何检校的最终指向的差值为Δα=-0.005 358 9°,Δβ=-0.003 465°,可见具有较高的预估精度。
|
| 图 2 指向预估的计算 Fig. 2 Pointing prediction |
2.1.2 基于经验加速度的轨道预报结果
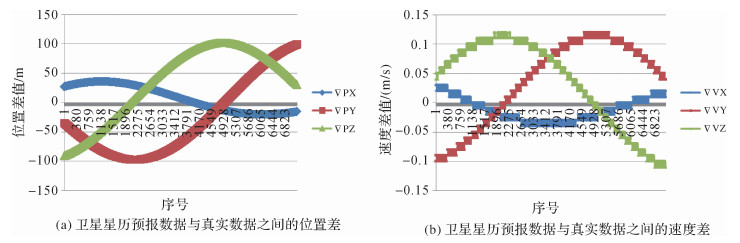
以2016年8月8日卫星过境前24 h事后处理的精密星历为初始数据,利用经验加速度方法来预报未来24 h即包含8月9日卫星过境时刻的卫星轨道参数,预报得到轨道数据(PX1,PY1,PZ1,VX1,VY1,VZ1)。利用卫星过境检校区域后下传的原始GPS数据进行事后精密轨道确定算法处理的精密轨道参数(PX2,PY2,PZ2,VX2,VY2,VZ2),对比两者可评估预报轨道精度。如图 3所示,图中显示了包含检校试验时间在内的1 h的轨道数据差值,横轴表示轨道数据的序号,纵轴表示卫星预报轨道与真实轨道(事后精密轨道,误差在5 cm以内)之间的位置差值,(ΔPX,ΔPY,ΔPZ,ΔVX,ΔVY,ΔVZ)为预报轨道参数与精密轨道参数的差值。24 h以内轨道预报的最大位置误差在100 m以内,最大速度差在0.1 m/s以内。
|
| 图 3 卫星星历预报数据与真实数据之间的差值 Fig. 3 The difference between prediction ephemeris and real ephemeris |
2.1.3 基于频域拟合的姿态预报结果
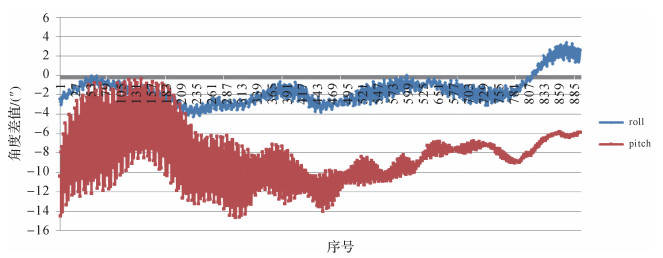
顾及卫星姿态平台的固定频率抖动,采用基于频域拟合的卫星姿态预报方法,由于偏航角yaw对地面定位的影响很小,几乎可以忽略。下面仅给出预报的横滚角roll和俯仰角pitch与事后精密定姿处理的精密姿态数据之间的差值,如图 4所示,图中显示了包含检校试验时间点在内的4.2 min的姿态数据差值,横轴表示姿态值的序号,纵轴表示角度差值,横滚角roll能够控制在4″以内,俯仰角pitch能够控制在15″以内。
|
| 图 4 卫星姿态预报数据与真实数据之间的差值 Fig. 4 The difference between prediction attitude and real attitude |
2.1.4 激光足印位置预报结果
将预估指向、预报姿态和轨道数据分别代入激光足印严密几何预报模型中,即可得到激光足印的预报位置,卫星实际过境后,探测器捕获并确定的足印中心即为激光足印实际位置,计算该值与之前预报的足印地面平面位置差值,用于评价预报模型的整体精度,它综合反映了指向预估误差、轨道预报误差、姿态预报误差等引起的激光足印预报的位置误差,称之为“综合误差”。为了更好地分析预报误差,将综合误差分解为沿轨误差和垂轨误差,分别为综合误差在沿轨和垂轨两个方向上的误差分量。相对于足印质心真实位置而言,预报误差偏北和偏西为正,偏南和偏东为负。
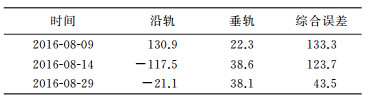
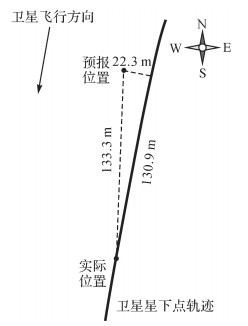
以2016年8月9日的第一次检校试验为例,将预估的指向和预报的姿态轨道数据计算激光足印地面位置,与通过地面探测器捕获的激光足印实际位置进行比对,如图 5所示,预报综合误差即两点地面距离为133.3 m,沿轨和垂轨误差分别为130.9 m和22.3 m。同样方法,2016年8月14日及2016年8月29日综合误差结果如表 1所示。
|
| 图 5 激光足印预报位置与真实位置偏差图 Fig. 5 Error graph between prediction and true-value |
2.2 各误差项对激光足印预报影响分析
为了进一步分析各误差项对激光足印预报定位误差,考虑到事后检校的指向、事后定姿和定轨精度都很高,对地面误差影响均在米级,本文视其为参考理论值,采用独立分析法对各误差项影响进行分解。即在统一的预报模型中,其他参数保持一致,分别拟比较的预报参数和事后处理参数代入计算两种情况下的激光足印地面坐标,将两种情况下的激光足印地面坐标的差值,作为该参数误差引起的激光足印位置偏差。
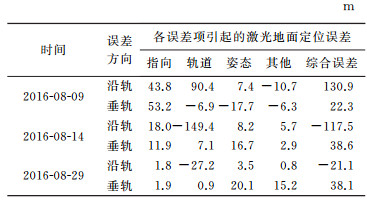
以2016年8月9日的第一次检校试验为例,将2.1节预估的指向和预报的姿态轨道数据和事后检校的指向、事后处理的轨道和姿态等分别对应代入到预报模型计算得到的地面位置。在姿轨参数不变的情况下,指向预估误差引起的激光足印地面距离差为68.9 m,沿轨和垂轨的误差分别为43.8 m和53.2 m;在指向和姿态不变情况下,轨道预报误差引起激光足印地面距离差为90.7 m,沿轨误差为90.4 m,垂轨误差为-6.9 m;在指向和轨道参数不变的情况下,姿态预报误差引起的激光足印地面差为19.2 m,沿轨和垂轨分别为7.4 m和-17.7 m;由于预报过程包含一些随机误差和模型尚未考虑到的误差量,这部分误差统称为“其他”误差,结合上述分析的预报参数预报的位置与地面探测器得到真实位置差,其综合误差为133.3 m,沿轨和垂轨误差分量分别为130.9 m和22.3 m,可计算得到沿轨和垂轨方向的误差分量,分别为-10.7 m和-6.3 m。3次试验各误差项分解情况如表 2所示。
从表 2中3次试验结果来看,指向误差引起的激光足印地面位置误差逐渐变小,说明指向精度逐渐提高,其中,第1次试验采用地形匹配预估的指向,第2次检校试验的指向则是采用第1次捕获的光斑进行精确检校的结果,第3次试验的指向则是采用第1、2次捕获的光斑进行联合检校的结果。这说明,基于多场的联合检校的指向结果较单场检校更优。从最终指向误差引起的沿轨和垂轨足印地面位置误差来看,检校后的精度优于2″。
轨道预报是激光足印预报的主要误差源,误差大小与方向均具有较强的随机性,这是因为轨道预报结果主要与卫星所处的空间环境有关,无法通过试验减小或消除。由于近地卫星轨道的特性,沿轨预报误差要大于垂轨误差,且误差相差一个数量级。姿态预报引起的激光足印位置偏差较小,总体上垂轨误差要大于沿轨误差,这主要是由于资源三号02星在轨飞行过程中,其俯仰角pitch比横滚角roll的稳定性要差,姿态预报模型难以较好反映稳定性较差的姿态数据。大气、潮汐等其他误差引起的激光地面足印位置误差较小,总体上不具系统性。
从总体上看,尽管轨道预报误差呈现随机性,但随着多次检校试验对指向等系统误差量进行有效的修正,综合预报误差呈逐渐减小的趋势。对比表 1和表 2发现,3次试验的姿态、轨道和指向预报等引起的激光足印位置沿轨和垂轨误差的绝对值之和均大于最终地面的综合误差,这说明各项误差方向存在耦合关系。为了确保试验成功,在外业试验中,探测器布设范围取决于各类预报误差绝对值之和,以确保探测器阵列顺利捕获光斑。
3 结论本文针对资源三号02星激光测高仪在轨几何检校需求,充分顾及卫星平台的空间运行规律以及激光与平台的相对几何关系,构建了一种轨道系下严密激光足印位置预报模型,该模型通过激光指向预估、轨道和姿态预报,实现激光足印中心位置的预报。该预报模型成功应用于资源三号02星激光测高仪3次在轨几何检校试验中。本文利用地面探测器捕获的足印实际位置为基准,对3次试验的总体预报精度进行了评估,并对指向、姿态和轨道预报等各误差项引起的激光足印位置误差进行了分解,充分验证了模型的有效性。相关结论如下:
(1) 经过3次试验各误差项分解与定量分析可以看出,指向误差为系统误差,可以通过检校试验加以消除,最终精度可达3 m左右;尽管姿态误差可用建模方法进行抑制,由于平台稳定性问题,拟合残差属于随机误差无法消除,引起的足印预报误差在30 m以内;轨道预报误差优于150 m,呈现随机性。姿态、轨道和指向预报等误差项引起的激光足印位置误差存在耦合关系,最终综合预报误差均小于各项误差绝对值之和。
(2) 构建的激光足印位置预报模型在3次试验中综合预报精度均优于150 m,大大缩小了探测器阵列布设范围,解决了资源三号02星激光测高仪在轨几何检校试验中的地面探测器布设位置的预报问题,并可应用于高分七号、陆地生态碳卫星等携带的国产低脉冲重频激光测高仪在轨几何检校工程试验中。
| [1] | 唐新明, 李国元, 高小明, 等. 卫星激光测高严密几何模型构建及精度初步验证[J]. 测绘学报, 2016, 45(10): 1182–1191. TANG Xinming, LI Guoyuan, GAO Xiaoming, et al. The Rigorous Geometric Model of Satellite Laser Altimeter and Preliminarily Accuracy Validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1182–1191. DOI:10.11947/j.AGCS.2016.20150357 |
| [2] | LI Guoyuan, TANG Xinming, GAO Xiaoming, et al. Improve the ZY-3 Height Accuracy Using Icesat/glas Laser Altimeter Data[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, XLI-B1: 37–42. DOI:10.5194/isprsarchives-XLI-B1-37-2016 |
| [3] | 范大昭. 航天线阵传感器在轨几何标定的理论和技术[D]. 北京: 北京大学, 2010: 6-20. FAN Dazhao. Theory and Techniques for On-orbit Geometric Calibration of Space Linear Sensors[D]. Beijing: Peking University, 2010: 6-20. |
| [4] | 蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523–529, 553. JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523–529, 553. |
| [5] | SCHUTZ B E, ZWALLY H J, SHUMAN C A, et al. Overview of the ICESat Mission[J]. Geophysical Research Letters, 2005, 32(21). DOI:10.1029/2005GL024009 |
| [6] | LUTHCKE S B, ROWLANDS D D, WILLIAMS T A, et al. Reduction of ICESat Systematic Geolocation Errors and the Impact on Ice Sheet Elevation Change Detection[J]. Geophysical Research Letters, 2005, 32(21). DOI:10.1029/2005GL023689 |
| [7] | MARTIN C F, THOMAS R H, KRABILL W B, et al. ICESat Range and Mounting Bias Estimation over Precisely-surveyed Terrain[J]. Geophysical Research Letters, 2005, 32(21): L21S05. |
| [8] | MAGRUDER L A, SCHUTZ B E, SILVERBERG E C. Laser Pointing Angle and Time of Measurement Verification of the ICESat Laser Altimeter Using a Ground-based Electro-optical Detection System[J]. Journal of Geodesy, 2003, 77(3-4): 148–154. DOI:10.1007/s00190-003-0319-4 |
| [9] | MAGRUDER L A, SULEMAN M A, SCHUTZ B E. ICESat Laser Altimeter Measurement Time Validation System[J]. Measurement Science and Technology, 2003, 14(11): 1978–1985. DOI:10.1088/0957-0233/14/11/016 |
| [10] | MAGRUDER L A, SILVERBERG E, Webb C, et al. In Situ Timing and Pointing Verification of the ICESat Altimeter Using a Ground-based System[J]. Geophysical Research Letters, 2005, 32(21). DOI:10.1029/2005GL023504 |
| [11] | MAGRUDER L A, WEBB C E, URBAN T J, et al. ICESat Altimetry Data Product Verification at White Sands Space Harbor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(1): 147–155. DOI:10.1109/TGRS.2006.885070 |
| [12] | SCHUTZ B E. GLAS Altimeter Post-launch Calibration/Validation Plan[D]. Texas: University of Texas, 2001: 45-53. |
| [13] | MAGRUDER L A, RICKLEFS R L, SILVERBERG E C, et al. ICESat Geolocation Validation Using Airborne Photography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2758–2766. DOI:10.1109/TGRS.2010.2040831 |
| [14] | 马跃, 阳凡林, 易洪, 等. 对地观测星载激光测高仪在轨姿态系统误差检校方法[J]. 红外与激光工程, 2015, 44(8): 2401–2405. MA Yue, YANG Fanlin, YI Hong, et al. Calibration Method of On-orbit Attitude Systematic Error for Spaceborne Laser Altimeter of Earth Observation[J]. Infrared and Laser Engineering, 2015, 44(8): 2401–2405. |
| [15] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191–198. TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear Array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191–198. |
| [16] | MAGRUDER L A. Pointing Angle and Timing Verification of the Geoscience Laser Altimeter Using a Ground-based Detection System[D]. Texas: University of Texas, 2001: 14-39. |
| [17] | 汤靖师, 刘林. 低轨航天器长期轨道预报的初步研究[J]. 飞行器测控学报, 2014, 33(1): 59–64. TANG Jingshi, LIU Lin. On Long-term Prediction for Low Earth Orbit Spacecraft[J]. Journal of Spacecraft TT&C Technology, 2014, 33(1): 59–64. |
| [18] | 王文彬, 刘荣芳. 基于经验加速度的低轨卫星轨道预报新方法[J]. 空间科学学报, 2015, 35(6): 715–720. WANG Wenbin, LIU Rongfang. A New Method of Orbit Prediction for LEO Satellites Using Empirical Accelerations[J]. Chinese Journal of Space Science, 2015, 35(6): 715–720. |
| [19] | TONG Xiaohua, XU Yusheng, YE Zhen, et al. Attitude Oscillation Detection of the ZY-3 Satellite by Using Multispectral Parallax Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3522–3534. DOI:10.1109/TGRS.2014.2379435 |
| [20] | TONG Xiaoua, YE Zhen, XU Yusheng, et al. Framework of Jitter Detection and Compensation for High Resolution Satellites[J]. Remote Sensing, 2014, 6(5): 3944–3964. DOI:10.3390/rs6053944 |
| [21] | TADONO T, ISHIDA H, ODA F, et al. Precise Global DEM Generation by ALOS PRISM[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, Ⅱ-4: 71–76. |