2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 江西省数字国土重点实验室, 江西 南昌 330013
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, Nanchang 330013, China
总体最小二乘[1]是顾及了系数矩阵误差的平差方法,是Errors-in-Variables(EIV)[2-3]模型的严密估计方法。在EIV模型的基础上,文献[4]将系数矩阵中不同的随机元素提取并作为参数进行求解,提出了Partial Errors-in-Variables(Partial EIV)模型。文献[5]将Partial EIV模型进行转换,进行两步间接平差法得到参数估值,在形式上比文献[4]简单。文献[6]分析了Partial EIV模型算法与一般算法的优势分别为:① Partial EIV模型是EIV模型的更一般的表达式;② Partial EIV模型是将系数矩阵中不同的随机元素提取并作为参数进行求解,因此Partial EIV模型系数矩阵中待改正量的个数要小于或等于对应EIV模型中待改正量的个数,提高了计算效率;③ 便利了后续的精度评定。总体最小二乘法在近年来发展迅速[7-13],在平差时随机模型的不准确对参数估值有很大的影响,方差分量估计可以对随机模型进行修正从而得到更加合理的参数估值。方差分量估计(VCE)方法主要有赫尔默特估计[14-15](Helmert)、最小范数二次无偏估计[16](MINQUE)、最优不变二次无偏估计[17-18](BIQUE)及最小二乘方差分量估计[19-22](LS-VCE);最小二乘方差分量估计(LS-VCE)方法是Teunissen提出,该方法使用的是最小二乘准则,经过转换将方差分量作为参数进行解算,得到的方差分量估值具有无偏性,且便利了后续工作。文献[20]给出了不同情形下的最小二乘方差分量估计方法并探索其特性。文献[21]将最小二乘方差分量估计应用于EIV模型中,将加权总体最小二乘参数解的表达式写成标准化的最小二乘形式,结合最小二乘方差分量估计方法确定方差分量估值,然而算例部分函数模型的系数矩阵既有随机元素又有非随机元素,使用更具有一般性的Partial EIV模型解算更具有代表性。与其他方差分量估计方法相似,在计算中可能出现负方差,函数模型多余观测量的不足和随机模型结构的不正当是出现负方差的主要原因,在最小二乘方差分量估计方法的基础上,文献[22]结合非负最小二乘理论,将非负最小二乘方差分量估计应用到GPS时间序列中,方差分量估计方法在本质上是相同的。文献[15]指出由MINQUE可以导出严密的Helmert估计公式。文献[23]针对概括函数平差模型进行公式推导,总结了不同方差分量估计方法并指出最小二乘方差分量估计方法的一般性,通过公式推导得到了MINQUE、Helmert和BIQUE方法均是最小二乘方差分量估计的特例。相比于其他方法的方差分量计算公式推导,LS-VCE方法过程更加简单、易于理解、具有较强的应用价值。
本文在文献[5]参数估计方法的基础上,结合最小二乘方差分量估计方法计算系数矩阵与观测向量的方差分量估值,在迭代过程中更新协因数阵,从而达到修正参数估值的效果。针对估计中出现的负方差,增加非负约束条件,使用非负最小二乘方差分量估计方法计算方差分量估值。通过算例试验对本文方法进行验证,并与已有方差分量估计方法进行比较。与文献[14]相比,本文方法不需要引入权比因子,在计算参数估值时迭代次数要更少,且方便了后续方差分量估值的精度评定,当计算中出现负方差时,文献[14]的方法则会出现不可估的现象。与文献[21]相比,本文方法继承了原有Partial EIV模型的优势。
1 Partial EIV模型算法在某些实际应用中,EIV[24-25]模型中系数矩阵由一些非随机元素与随机元素组成,文献[4]对系数矩阵进行处理,提取了系数矩阵中的随机元素,将EIV模型改写成Partial EIV模型[4]
函数模型
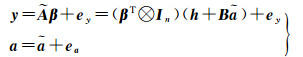 (1)
(1)
随机模型
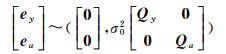 (2)
(2)
式中,
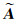
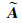
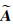
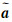
文献[5]对式(1) 进行变形得到
 (3)
(3)
式中,令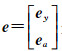
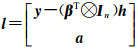
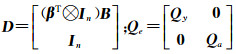
将观测值a作为参数进行平差,计算得到[5]
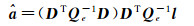 (4)
(4)
用参数估值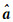
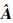
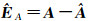
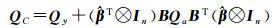 (5)
(5)
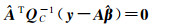 (6)
(6)
为将法矩阵变成对称正定矩阵,对式(6) 加上和减去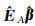
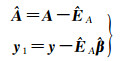 (7)
(7)
式中,根据协方差传播律可得到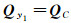
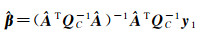 (8)
(8)
进而得到观测量估值及残差[21]
 (9)
(9)
式中,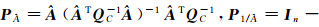
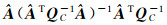
最小二乘方差分量估计[19-23]由Teunissen提出,使用的是最小二乘准则,解算出的方差分量估值具有无偏性;文献[14]在Partial EIV模型中引入权比因子,使用赫尔默特方差分量估计方法确定权比因子,并通过算例验证了与其他方差分量估计方法的等价性。文献[14]在参数计算过程中使用的是文献[4]的算法,在表达形式上相对较复杂,且文献[5]指出该算法收敛较慢,影响计算效率;方差分量估计的本质是相同的,都是对随机模型进行修正,即修正观测值的权,从而达到修正参数估值的效果,最小二乘方差分量估计是更为一般的方差分量估计方法,而且最小二乘方差分量估计有利于后续对方差分量估值的精度评定及其他方面的应用,如出现负方差时可以增加约束条件使其成为附有约束条件的最小二乘平差,处理出现负方差的情况,而出现负方差时,其他方差分量估计方法会出现不可估的情况。针对总体最小二乘中系数矩阵与观测量有不同方差分量的情况,使用LS-VCE对随机模型进行修正更加合理。
由式(1)、式(2) 及式(8) 可知,期望可以表示为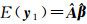


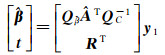 (10)
(10)
式中,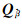
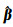
由式(10) 可知,根据协因数传播律可得到向量t的协因数阵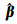
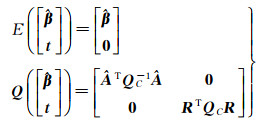 (11)
(11)
式中,协因数阵QC如式(5) 所示,经过相应的变换可以得到方差分量的关系[19-22]为
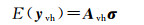 (12)
(12)
式中,Avh和yvh均表示对矩阵进行vh[21]操作后的矩阵和向量,σ表示方差分量组成的向量。根据文献[20]可得
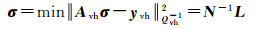 (13)
(13)
式中,σ为方差分量组成的向量;Qvh-1为σ的协因数阵;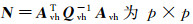
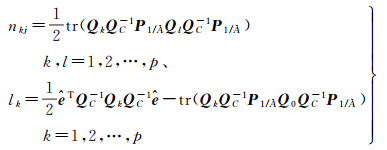 (14)
(14)
式中,nkj、lk分别表示矩阵N, L中的某一元素;Qk、Ql都表示为系数矩阵或观测量的协因数阵;Q0为已知的矩阵,一般为零矩阵。
在Partial EIV模型中,观测向量和系数矩阵在某些情况具有不同的方差分量,对于式(2) 的随机模型存在
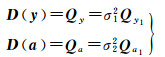 (15)
(15)
式中,σ1、σ2分别为观测向量和系数矩阵误差的方差分量;Qy1、Qa1为给定的观测量和系数矩阵的协因数阵。
将式(5) 改写成线性求和形式,即
 (16)
(16)
Partial EIV模型是顾及了系数矩阵误差的总体最小二乘模型,文献[20]从经典的Gauss-Markov模型出发分析了最小二乘方差分量估计方法,相比于Partial EIV模型的数学模型,Gauss-Markov的数学模型可以表示为
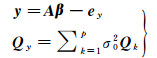 (17)
(17)
对式(17) 进行平差解算可得到参数的表达式
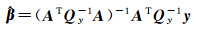 (18)
(18)
误差向量ey可以表示成多个分量求和的形式。在Partial EIV模型的解算中,式(8) 和式(18) 与Gauss-Markov模型解算得到的参数表达式及协因数阵的形式相同,这与文献[21]中EIV模型的最小二乘方差分量估计是一致的。
迭代计算分为参数估计和方差分量估计,具体的迭代步骤为:数据准备:A、y、Qy、Qa、h、a、B、收敛条件ε=10-10。
(1) 用最小二乘法求解模型参数初值
(2) 给定方差分量初值σ(0)=[σ12(0) σ22(0)]T;设计迭代次数i=0;
外循环:
(3) 用式(15) 更新Qy和Qa;设计迭代次数j=0;
内循环:
(1) 更新Qe,由式(4) 计算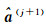
(2) 由式(5) 更新QC;
(3) 由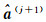
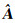
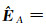
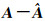
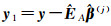
(4) 由式(8) 计算参数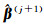
(5) 重复步骤① 至步骤④ 直至满足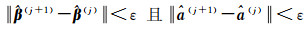
(4) 更新
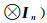
(5) 由式(16) 更新QC;
(6) 计算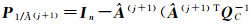
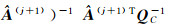
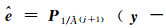
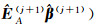
(7) 由式(14) 更新N和L,计算σ(i+1)=N-1L,i=i+1;
(8) 重复步骤(3) 到步骤(7) 直至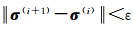
最小二乘方差分量估计方法是根据最小二乘准则使得其误差平方和取最小,与其他方差分量估计方法类似,在进行方差分量解算时也会出现负方差,这与方差分量的自身含义是相互冲突的,出现负方差的原因有两种[22]:① 函数模型观测量的不足,即多余观测量的不足。多余观测量也叫自由度,增加模型的多余观测量可以提高数据解算精度。② 结构不正当的随机模型,随机模型又表现在观测值的权中,然而观测数据初始的权往往是不精确的,严重影响了平差结果的精度。非负最小二乘方法[27-28]是在最小二乘准则下增加非负约束条件而得,在最小二乘方差分量估计的基础上增加约束条件使得方差分量非负,因此可以将非负最小二乘方差分量估计作为附有约束条件的最小二乘问题,其准则[22, 28]为
 (19)
(19)
令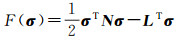
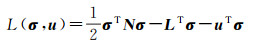 (20)
(20)
式中,u是拉格朗日乘子,对式(20) 求偏导计算得到
 (21)
(21)
采用文献[28]的非负最小二乘方法,令σk是向量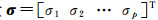
 (22)
(22)
式中,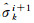
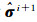
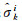

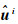
对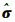
 (23)
(23)
式中,n(:, k)表示矩阵N的第k列。
由式(23) 可以看出,迭代计算出的方差分量估值,若某一分量出现负值,通过式(23) 进行约束。非负最小二乘方差分量估计可以当成附有约束条件的最小二乘方差分量估计,其约束条件可以表达成
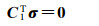 (24)
(24)
式中,C1T是z×p的矩阵;z表示σ中0元素的个数。
在计算参数协因数阵时,根据附有约束条件的平差方法,由协因数传播律可得到方差分量估值的协因数阵为
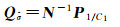 (25)
(25)
式中,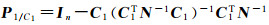
具体迭代步骤为:
数据准备同最小二乘方差分量估计,在计算出参数估值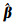
(1) 给定方差分量初值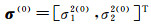
外循环:
(2) 计算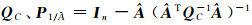
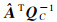
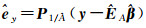
(3) 用式(14) 更新N和L;令σ(0)=0,u(0)=-L;设计迭代次数j=0;
内循环:
(1) 用式(22) 计算σ(j+1);式(23) 计算u(j+1);
(2) 更新u(j)=u(j+1),j=j+1;
(3) 重复步骤① 到② 直至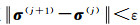
(4) 更新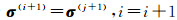
(5) 重复步骤(2) 到(4) 直至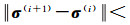
(6) 计算矩阵C1T和P1/C1;
(7) 由式(25) 计算方差分量估值的协因数阵。
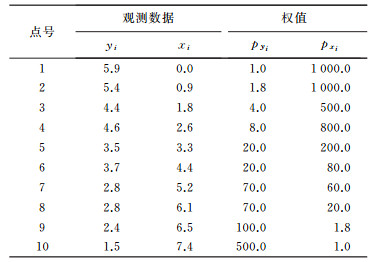
3 算例与分析 3.1 算例1数据采用文献[5, 21]直线拟合数据,已知坐标观测值(xi, yi)和相应的权值(pxi, pyi),见表 1。
 (26)
(26)
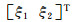
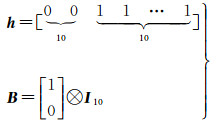 (27)
(27)
权阵pa=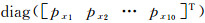

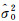
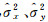
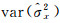

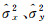
|
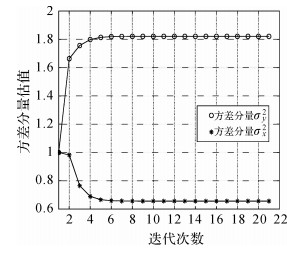
| 图 1 算例1的方差分量估值变化图 Fig. 1 The changes of estimates variance components of the first example |
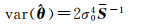 (28)
(28)
式中, 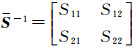
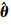
 (29)
(29)
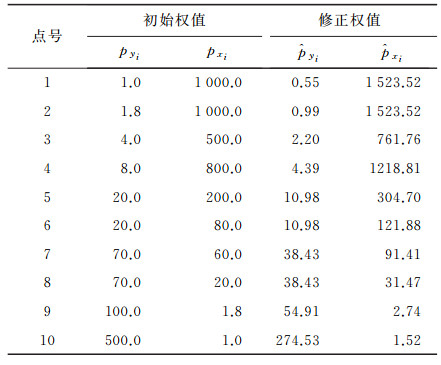
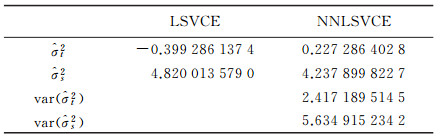
方差分量估计是针对随机模型不准确进而修正随机模型并再次平差的方法,本文以Partial EIV模型为基础的的最小二乘方差分量估计方法重新确定了两类观测值的权阵,得到的权值见表 3,可以发现与文献[14]和文献[21]重新确定的权值是相等的。
3.2 算例2
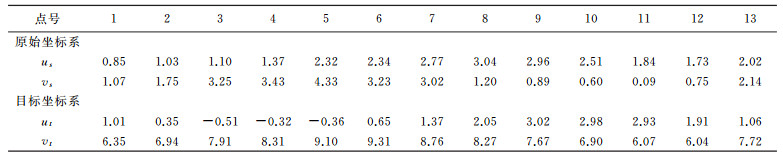
模拟一个二维仿射变换,对文献[29]的数据进行改化,已知6个转换参数真值a1=0.9,b1=-0.8,c1=1,a2=0.6,b2=0.7,c2=0.5和原始坐标、目标坐标的真值,相应的协因数阵为Qa=0.005·diag([1 1 2 2 3 3 1 1 5 5 4 4 2 2 7 7 1 1 8 8 3 3 6 6]T),Qy=0.005·diag([1 1 3 3 6 6 1 1 1 1 8 8 4 4 3 3 6 6 5 5 4 4 5 5 2 2]T),用Matlab软件mvnrnd函数给真值加上均值为0,协方差分别为Qy和3Qa的随机误差,得到随机一组坐标值见表 4。
二维仿射变换模型[29]为
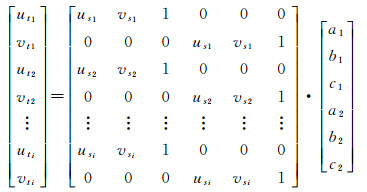 (30)
(30)
表 4中提供了26组坐标,向量h和确定矩阵B、y、a的形式分别为
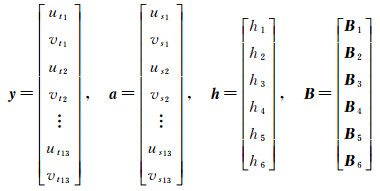 (31)
(31)
式中,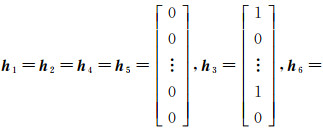

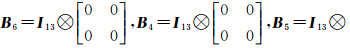
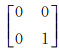
数据准备:h、B、y、a、pa、py,权阵为协因数阵的逆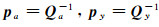
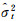

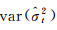
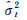
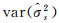

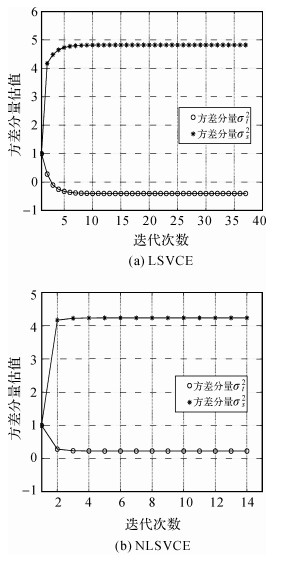
|
| 图 2 算例2的方差分量估值变化图 Fig. 2 The changes of estimates variance components of the second example |
图中,LS-VCE的迭代次数都为37次,NNLSVCE的迭代次数为14次,而在使用文献[14]方法进行求解时,因为方差分量出现负值的现象,计算时则出现不收敛的情况。
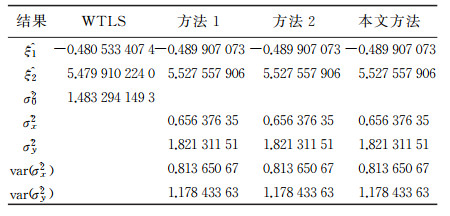
3.3 算例分析(1) 由表 2可以看出本文方法与文献[14、21]得到的待估参数结果及方差分量估值相等,对应的方差分量估值方差也相等,图 1显示了方差分量估值的变化图,两种方法的迭代次数都为21次,表 3显示了修正方差分量所对应的权值。在不考虑方差分量估计情况下,文献[5]的参数估计需要迭代7次,文献[30]需要迭代8次;文献[14]计算中进行参数估计时需要迭代267次,而本文只需要94次,在一定程度提高了计算效率,且在计算方差时本文只需要根据协方差传播律获得,如式(25),相对更简单。
(2) 用最小二乘方法计算算例2方差分量估值时出现负值,而文献[14]的方法则出现不可估的情况,使用非负最小二乘理论得到的方差分量估值变化图见图 2。在非负约束下,通过解算其余方差分量估值从而达到准则下的整体最优解。非负最小二乘方差分量估计可以看成为附有限制条件的间接平差,在结合LS-VCE后,非负方差分量估计实质上就为非负最小二乘估计,因此本文方法与文献[22]方法是等价的。
(3) Partial EIV模型是将系数矩阵中的重复的随机元素提取,使得模型需要改正的待改正量个数相对更少。对于Partial EIV模型的随机模型,其协因数阵构造简单,更具有一般性的Partial EIV模型在解算海量数据时更能体现其优势。在式(5) 计算协因数阵时,BQaBT与EIV模型的系数矩阵的协因数阵QA相等,与文献[30]求解公式一致,相应的在进行方差分量估计时是等价的。
4 结论本文以Partial EIV模型为基础,当观测数据的随机模型不准确时,结合最小二乘方差分量估计方法对随机模型进行修正,推导了以Parial EIV模型为基础的最小二乘方差分量估计公式,将观测向量误差和系数矩阵误差分别作为一类数据,从而计算出两个方差分量估值;并且当方差分量估值出现负的时候,使用非负最小二乘理论,增加非负约束条件,可以处理方差分量出现负值的现象。计算过程分为参数估计与方差分量估计,Partial EIV模型的优势是减少了待估参数的个数,如算例1直线拟合在不考虑方差分量估计时Partial EIV模型解算的迭代次数比EIV模型少,虽然对Partial EIV模型进行解算之后参数的表达式与文献[29]等价,但是使用更具一般性的Partial EIV模型更能体现其代表性。将Partial EIV模型与最小二乘方差分量估计结合可以得到与EIV模型一样的结果,但在参数估计上使用Partial EIV模型一定程度上提高运算效率,该方法继承了Partial EIV模型原有的优点,对总体最小二乘理论进行了必要的完善。本文只讨论了Partial EIV模型系数矩阵与观测向量不相关时出现负方差的处理,而针对相关观测情况及负方差产生的具体原因及分析是今后需要研究的工作。
| [1] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883–893. DOI:10.1137/0717073 |
| [2] | 王乐洋. 基于总体最小二乘的大地测量反演理论及应用研究[J]. 测绘学报, 2012, 41(4): 629. WANG Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 629. |
| [3] | 王乐洋, 许才军. 总体最小二乘研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(7): 850–856. WANG Leyang, XU Caijun. Progress in Total Least Squares[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 850–856. |
| [4] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661–675. DOI:10.1007/s00190-012-0552-9 |
| [5] | 王乐洋, 余航, 陈晓勇. Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22–29. WANG Leyang, YU Hang, CHEN Xiaoyong. An Algorithm for Partial EIV Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22–29. DOI:10.11947/j.AGCS.2016.20140560 |
| [6] | 刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5): 505–512. LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505–512. |
| [7] | 王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575–581. WANG Leyang, YU Dongdong. Virtual Observation Method to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575–581. DOI:10.13485/j.cnki.11-2089.2014.0091 |
| [8] | 王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报(信息科学版), 2010, 35(11): 1346–1350. WANG Leyang, XU Caijun, LU Tieding. Ridge Estimation Method in Ill-posed Weighted Total Least Squares Adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1346–1350. |
| [9] | 王乐洋, 于冬冬, 吕开云. 复数域总体最小二乘平差[J]. 测绘学报, 2015, 44(8): 866–876. WANG Leyang, YU Dongdong, LV Kaiyun. Complex Total Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 866–876. DOI:10.11947/j.AGCS.2015.20130701 |
| [10] | FANG Xing. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8): 733–749. DOI:10.1007/s00190-013-0643-2 |
| [11] | FANG Xing. Weighted Total Least Squares Solutions for Applications in Geodesy[D]. Germany: Leibniz Universität Hannover, 2011. |
| [12] | SNOW K. Topics in Total Least-squares Adjustment within the Errors-in-variables Model: Singular Cofactor Matrices and Prior Information[D]. Ohio: The Ohio State University, 2012. |
| [13] | SCHAFFRIN B, WIESER A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [14] | WANG Leyang, XU Guangyu. Variance Component Estimation for Partial Errors-in-Variables Models[J]. Studia Geophysica et Geodaetica, 2016, 60(1): 35–55. DOI:10.1007/s11200-014-0975-2 |
| [15] | 崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2005. CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2005. |
| [16] | XU Peiliang, LIU Jingnan. Variance Components in Errors-in-Variables Models: Estimability, Stability and Bias Analysis[J]. Journal of Geodesy, 2014, 88(8): 719–734. DOI:10.1007/s00190-014-0717-9 |
| [17] | 刘志平, 张书毕. 方差-协方差分量估计的概括平差因子法[J]. 武汉大学学报(信息科学版), 2013, 38(8): 925–929. LIU Zhiping, ZHANG Shubi. Variance-covariance Component Estimation Method Based on Generalization Adjustment Factor[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 925–929. |
| [18] | 王乐洋, 许才军, 张朝玉. 一种确定联合反演中相对权比的两步法[J]. 测绘学报, 2012, 41(1): 19–24. WANG Leyang, XU Caijun, ZHANG Chaoyu. A Two-step Method to Determine Relative Weight Ratio Factors in Joint Inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 19–24. |
| [19] | AMIRI-SIMKOOEI A. Least-squares Variance Component Estimation: Theory and GPS Applications[D]. Delft: Delft University of Technology, 2007. |
| [20] | TEUNISSEN P J G, AMIRI-SIMKOOEI A R. Least-squares Variance Component Estimation[J]. Journal of Geodesy, 2008, 82(2): 65–82. DOI:10.1007/s00190-007-0157-x |
| [21] | AMIRI-SIMKOOEI A R. Application of Least Squares Variance Component Estimation to Errors-in-Variables Models[J]. Journal of Geodesy, 2013, 87(10-12): 935–944. DOI:10.1007/s00190-013-0658-8 |
| [22] | AMIRI-SIMKOOEI A R. Non-negative Least-squares Variance Component Estimation with Application to GPS Time Series[J]. Journal of Geodesy, 2016, 90(5): 451–466. DOI:10.1007/s00190-016-0886-9 |
| [23] | 赵俊, 郭建锋. 方差分量估计的通用公式[J]. 武汉大学学报(信息科学版), 2013, 38(5): 580–583, 588. ZHAO Jun, GUO Jianfeng. Auniversal Formula of Variance Component Estimation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 580–583, 588. |
| [24] | VAN HUFFEL S, VANDEWALLE J. The Total Least Squares Problem: Computational Aspects and Analysis[M]. Philadelphia: Society for Industrial and Applied Mathematic, 1991. |
| [25] | 曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013. ZENG Wenxian. Effect of the Random Design Matrix on Adjustment of An EIV Model and Its Reliability Theory[D]. Wuhan: Wuhan University, 2013. |
| [26] | 许光煜. Partial EIV模型的总体最小二乘方法及应用研究[D]. 南昌: 东华理工大学, 2016. XU Guangyu. The Total Least Squares Method and Its Application of Partial Errors-in-variables Model[D]. Nanchang: East China University of Technology, 2016. |
| [27] | LAWSON C L, HANSON R J. Solving Least Squares Problems[M]. Philadelphia: SIAM, 1995. |
| [28] | FRANC V, HLAVÁČ V, NAVARA M. Sequential Coordinate-wise Algorithm for the Non-negative Least Squares Problem[C]//Proceedings of the 11th International Conference on Computer Analysis of images and Patterns. Berlin Heidelberg: Springer, 2005: 407-414. |
| [29] | MAHBOUB V. On Weighted Total Least-Squares for Geodetic Transformations[J]. Journal of Geodesy, 2012, 86(5): 359–367. DOI:10.1007/s00190-011-0524-5 |
| [30] | AMIRI-SIMKOOEI A, JAZAERI S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Journal of Geodetic Science, 2012, 2(2): 113–124. |