2. 信息工程大学, 河南 郑州 450052;
3. 火箭军工程大学, 陕西 西安 710025
2. Information Engineering University, Zhengzhou 450052, China;
3. Xi'an High-Tech Institute, Xi'an 710025, China
在过去20多年中,多个国家和组织不断积极建设和发展卫星导航定位系统,使得GNSS数据处理将迎来成千上万个GNSS观测站、多个导航卫星系统带来的超过120颗导航卫星和多频信号的时代。采用合理的处理策略对多频多系统GNSS数据进行整体解算能够得到更精确可靠的结果[1],但海量GNSS数据整体解算面临巨大的计算挑战,国内外学者对GNSS大网数据解算提出很多改进的算法或方法[2-5]。其中关于大网数据的利用率与利用方法一直受到关注,如文献[6]建议在无法提高单机计算机性能的前提下,通过增加超大网络多GNSS数据的采样间隔以降低计算压力,但增大采样间隔导致数据使用率和精度有所降低,如不同采样间隔的轨道、钟差产品下GPS非差定位精度在高程方向变化达到6 mm。
双差模型是GNSS数据处理中常见的数学模型之一,它能够消除大部分的观测误差和具有模糊度为整数的特性,因而一直在GNSS应用领域中得到广泛应用。对多测站同步网采用双差模型解算时首先需组建双差观测值,而观测值组建应满足两个条件[7]:一是双差观测值之间的函数独立性;另一个是在满足前一个条件的基础上定义出所有可能的双差观测值,即充分利用观测值。然而,采用双差模型处理GNSS数据时,独立双差观测值组建与后续双差网解计算的时间随测站数目增加而呈指数级增长,得到并解算全网最优独立双差观测值并不是一件容易的事。文献[8]提出一种先基线层后网层的分层独立双差模糊度选取方法,该方法比路径最短法选取的GPS双差独立模糊度平均多300个,提高了模糊度固定率和测站坐标东方向的重复性精度。文献[9]进一步提出了改进的分层独立双差模糊度选取方法,有效降低了双差模糊度选取的时间。由于双差网解的计算时间随测站数目增加而呈指数级增长,传统的集中式串行解算策略无法同时快速处理全网所有双差观测数据,通常将大网划分为若干个子网单独处理,然后再采用子网联合平差的方法得到最终结果[10]。但子网划分没有统一原则,公共点的数据质量与分布直接影响最终的解算精度。
以云计算、分布式计算等为代表的高性能计算技术逐渐成为大地测量数据处理的首选方式[11-17]。由于高性能计算技术的本质是并行计算,将传统的GNSS数据处理模型分解并设计合理的并行算法是实现GNSS数据快速处理的首要问题。因此,本文针对GNSS大网双差解算时双差观测值组建与网解计算的时效性差的问题,从观测值选取、基线解算等方面提出相应的并行改进方法,采用多核并行与网络并行的双层策略编程实现了双差网解的并行处理,以提高GNSS大网数据双差解算的效率。
1 双差观测值并行选取选取双差观测值的原则是尽可能的包含网中所有的独立双差观测值,但在每个历元或时段内组建双差观测值需要巨大的计算量,从效率角度考虑,一般采用基线模式(baseline mode)解算GNSS数据,而不是时段模式(session mode)[18]。通常,是以“基线长度”为标准采用图论中从连通图中产生最小生成树的Kruskal算法[19]等选择路径最短的独立基线,对每一条独立基线简单地通过选取参考星确定独立双差观测值,所有独立基线的双差观测值进而构成全网的独立双差观测值集[20]。这种以“路径最短原则”选取独立双差观测值的方法计算效率高且算法实现简单,然而,由于地面遮挡等干扰因素,路径最短原则所选取的独立基线并不一定是观测值最多的基线。
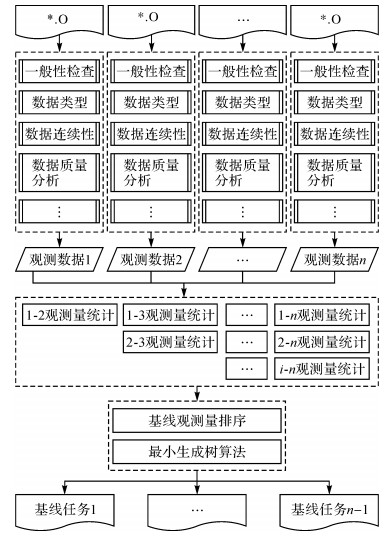
为了获取同步网中所有可能的独立双差观测值,本文以“观测值数量”为标准选取观测值最多的独立基线,即以“观测值最多原则”选取独立基线。该方法需要遍历读取每条基线对应的观测文件,统计全网的每条基线的同步观测值数量,导致该方法计算效率很低。由于同步网中每个测站的数据预处理、每条基线的观测量统计具有良好的并行特征,因此,设计基于观测量最多原则的独立基线并行选取流程,如图 1所示。首先设置观测数据类型、连续同步观测时段等信息,对n个观测文件并行的进行一般性检查、数据类型筛选、数据连续性筛选、数据质量分析等预处理,剔除质量较差的观测数据弧段。然后,任意两个未组合过的观测数据组成一条基线数据,采用嵌套并行循环对所有基线数据进行逐历元并行匹配运算,统计每条基线的共视卫星数目。最后,对n(n-1)/2个基线的观测值按照观测数量从大到小进行排序,以观测值数量为权值采用Kruskal算法生成最小生成树,得到n-1条独立基线。
|
| 图 1 独立基线并行选取流程 Fig. 1 The selection of independent baselines in parallel |
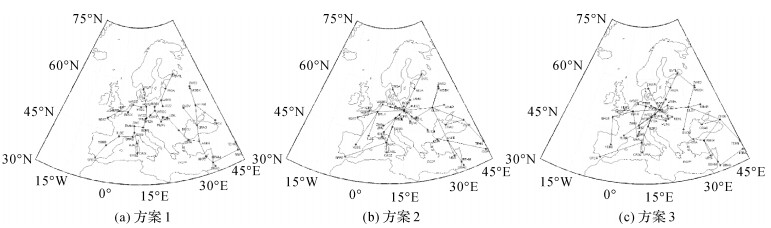
数据类型、数据连续性、卫星高度截止角等参数影响每条基线的实际观测值数量的统计,如为了消除电离层影响,通常采用双频消电离层组合载波相位作为主要观测量;为了剔除无效数据,通常只保留连续观测超过一定时段的卫星;为了降低噪声和多路径影响,卫星高度角通常取高一点,而对于中长基线,较高的高度截至角导致共视卫星数减少。因此,设置不同参数统计每条基线的共视卫星数目是不相同的,导致选择的独立基线也不唯一。如选取欧洲区域46个IGS测站2013年第1天的GPS数据,采样间隔为30 s,设置同时观测到某卫星双频载波和伪距的数据为一个有效观测量,只统计每颗卫星连续观测大于10 min以上的数据,分别设置3种方案选取独立基线:方案1是截止高度角为5°的路径最短法;方案2是截止高度角为5°的观测量最多法;方案3是截止高度角为7°的观测量最多法。图 2为不同方案选取的独立基线分布图。
|
| 图 2 欧洲46个IGS测站不同方案选取的独立基线分布图 Fig. 2 Distribution of independent baselines under different selection schemes for Europe stations |
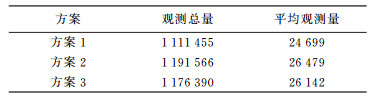
统计不同方案所选独立基线的观测量情况见表 1,其中平均观测量是指平均每条基线的观测量,即全网观测总量除以全网的独立基线个数。方案1路径最短原则所选独立基线平均观测量为24 699个,而方案2和方案3所选独立基线平均观测量为26 479个和26 142个,总观测量比方案1所选独立观测量多出80 111个和64 935个。
|
2 独立基线并行计算
原始GNSS观测值之间通常认为是不相关的,但通过矩阵变换组建双差观测值时导致双差观测值存在了相关性,反映到解算的局部参数之间存在了相关性。由于顾及双差观测值之间的相关性,会大大增加计算的工作量,而忽略基线相关性对基线解算的精度量级影响很小,通常采用单基线解算模式[20]。而且由于基线之间相关性随测站规模的增大而逐渐降低[21-22]。GNSS网解中测站坐标等局部参数之间通过轨道、卫星钟差、地球自转参数等全局参数联系起来的,当全局参数精度很高,将轨道等全局参数视为真值求解局部参数,局部参数之间是不相关的[23]。因此,本文将n个测站组成的n-1条独立基线采取并行解算策略,得到n-1条基线向量,再通过网平差得到测站坐标参数。
对GNSS同步观测网采用双差模型解算时,通常首先进行基线解算获得基线向量,再引入坐标基准进行网平差得到测站的绝对坐标。忽略观测噪声和多路径等误差,采用无电离层组合值组双差进行基线解算,则测站r、s观测到卫星i、j的双差无电离层组合观测方程可表示为
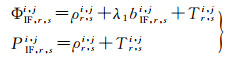 (1)
(1)
式中,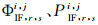
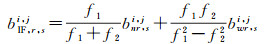 (2)
(2)
通过先固定宽巷后固定窄巷的顺序固定双差无电离层模糊度。首先双差宽巷模糊度的估值bwr, si, j及标准差δwr, si, j通过观测时段内多历元取平均[24-25]
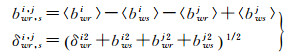 (3)
(3)
式中,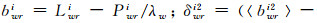
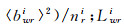
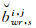
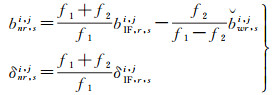 (4)
(4)
采用模糊度固定判定函数对窄巷模糊度的估值与标准差进行检验,最后利用固定的宽巷与窄巷模糊度得到固定的无电离层组合的双差模糊度。当双差模糊度固定到正确解之后,双差解算可以达到厘米到毫米级的定位精度。在模糊度固定过程中,有效观测值的样本数越多,通过多历元的平滑或取平均后,能降低模糊度参数的偏差误差,增大模糊度成功固定的概率和个数,参数求解更稳定、可靠。
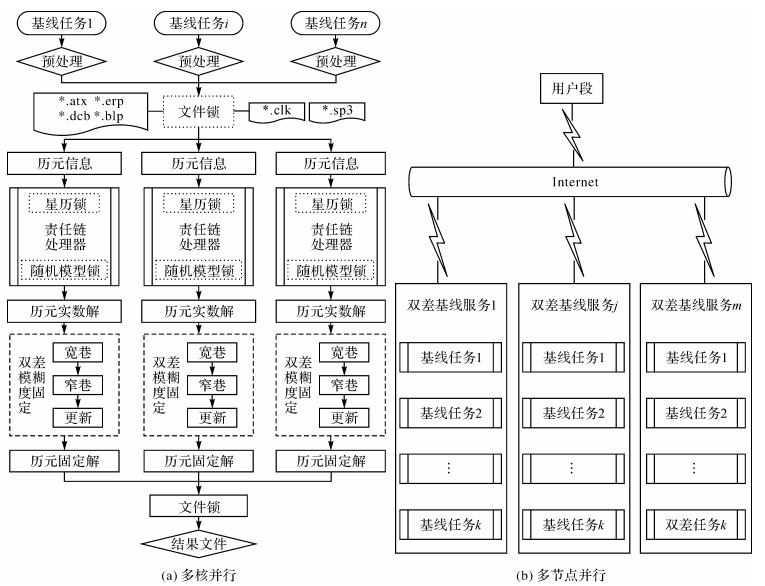
对于多个独立基线计算任务,以基线作为基本计算单元,在多核多节点环境下采用并行计算技术设计其并行计算流程见图 3,其中图 3(a)为内存共享环境的多核并行计算流程,图 3(b)为网络环境下多节点的并行计算流程。多核环境下首先将n个基线任务并行进行预处理后形成各自的任务信息,通过加载外部文件进行相关误差模型的改正,然后各自建立双差误差方程进行并行计算,得到基线历元解信息,循环至所有历元完成计算,得到基线的最终计算结果。
|
| 图 3 独立基线并行计算流程 Fig. 3 Parallel computing of independent baselines |
由于多核环境下影响数据访问效率的主要因素是锁竞争,即全部线程存在共同操作的共享部分,因此,为了抑制并发性的数据共享访问可能导致的不可预知的结果,对公共临界访问部分,如多个测站对精密星历产品信息、部分误差改正模型文件的并发访问等,使用互斥锁(如图 3(a)中的文件锁、星历锁等)提供的同步对象访问机制进行高并发的同步数据访问与处理。每个独立基线解算时添加模糊度固定模块,该模块先宽巷后窄巷的顺序进行计算,采用部分模糊度固定原则,当窄巷模糊度也成功固定后,即可利用固定的无电离层模糊度更新坐标等参数信息。图右侧的网络环境下并行计算采用Web等服务技术建立面向对象的双差多核计算服务,将双差基线多核计算服务发布在m个网络节点中,用户端通过指令发布k个基线计算任务至每个双差基线服务节点上,然后通过网络调用多个双差服务实现GNSS双差网络多核多节点并行计算,因此,具有松散耦合、粗粒度、可重用性等特点。
在基线解算过程中,当数据质量或其他异常原因导致某些独立基线无法成功固定解算时,采取舍弃这些基线,再从剩余的基线中选择新的独立基线的方法,然后对重新选取的独立基线进行并行解算,循环直到得到全网成功解算的n-1条独立基线为止。
为了得到绝对坐标值,需以基线向量值作为观测值进行网平差,但由于存在秩亏,需要引入基准条件或进行自由网平差。常见方法有已知点固定法、已知点加权法、最小约束条件法等。如采用最小约束条件法,可保证不同时期解算的坐标值之间的连续性和一致性[18]。由于大网平差涉及大型法方程解算,采用文献[14]所提方法,通过对大型矩阵进行矩阵分块,实现分块并行网平差。
3 试验与分析采用IGS测站第1810周的7 d GPS数据,年积日(DOY)为2014年第257—263天,采样间隔为30 s,卫星高度截止角统一设置为5°。以伪距和载波相位双差消电离层组合值作为观测值,精密星历和钟差分别采用IGS发布的15 min和5 min的最终产品,对流层改正采用GMF模型,每个测站的对流层天顶湿延迟逐历元估计。所有厘米级以上的误差均进行改正。
周跳采用MW组合与LG组合探测并标记,由于数据预处理不可能探测出所有的周跳,再通过验后残差迭代分析确定观测值中的粗差或未剔除的周跳。双差消电离层模糊度固定采用部分模糊度固定策略,先利用MW组合取整固定宽巷模糊度,再利用固定的宽巷模糊度与消电离层组合模糊度实数解计算窄巷模糊度,采用LAMBDA算法固定窄巷模糊度,最终得到固定的消电离层模糊度,将部分固定的消电离层模糊度作为约束条件平差更新坐标等参数。仅考虑同步观测时长超过20 min的模糊度,固定成功概率的门限取99.9%。为保持连续性,选取IGS核心测站作为约束条件,采用最小约束条件法进行基线网平差。在基于Visual Studio平台C#语言自主开发的GNSS数据处理软件平台Gnsser(www.gnsser.com)基础上,采用TPL(task parallel library)并行编程技术实现单机多核的双差并行解算,采用WCF(Windows communication foundation)网络并行编程技术实现网络多节点的双差并行计算服务。
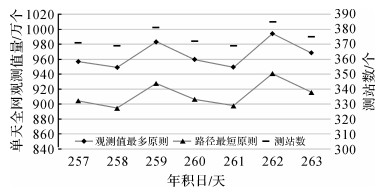
首先对年积日257—263的全球IGS站GPS观测数据,分别采用路径最短法和观测值最多法组建单天全网独立双差观测值,单天观测值总量与测站数统计见图 4。
|
| 图 4 不同方案选取的单天全网观测值总量 Fig. 4 Number of observations of different schemes in IGS stations |
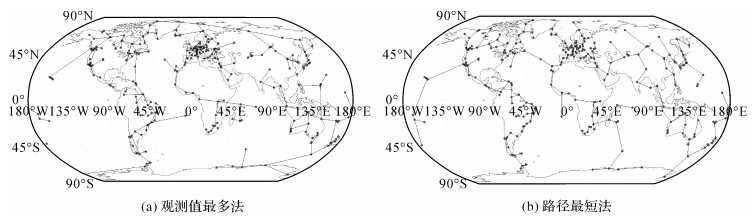
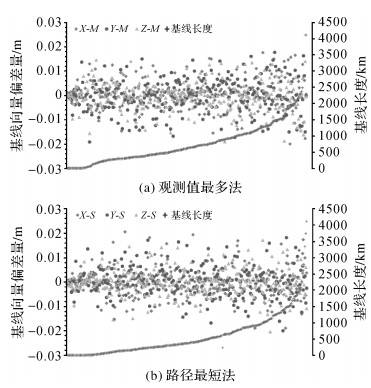
由于IGS测站的可用站数每天都不一致,本文选取的1810周全网每天测站数变化如图 4右侧所示,平均每天有375个测站。测站数目的变化导致每天所选基线数和基线分布也不断变化,图 5给出了1810周第1天371个IGS站采用观测值最多原则和路径最短原则所选独立基线分布情况。进一步分析图 4,基于路径最短原则选取的全网观测值总量平均每天9 124 898,而基于观测值最多原则选取的全网观测值总量平均每天9 660 453个,即平均每天比基于路径最短原则多了535 555个,平均每天每条基线多了1432个观测值。分别对两个方案选取的独立基线进行基线解算,将每个方案所算独立基线向量与IGS发布的坐标产品反算的基线向量作差,验证两个方案的计算精确性和一致性,其中第一天的基线偏差如下图 6所示,图中十字丝表示基线的长度。
|
| 图 5 1810周第1天不同方案选取的独立基线分布图 Fig. 5 Distribution of independent baselines under different selection schemes for global stations |
|
| 图 6 不同方案的偏差统计图 Fig. 6 Deviation statistical figure of different schemes |
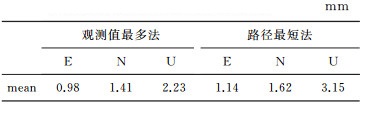
图 6(a)为观测量最多法所得基线偏差,X、Y、Z方向的偏差的标准差为(6.0, 6.1, 5.3),单位为mm,而图 6(b)路径最短法所得基线偏差在X、Y、Z方向的偏差的标准差为(6.2, 6.6, 5.8),单位为mm,两者计算结果的精度基本相当,一致性较好,观测量最多法稍优于路径最短法。进一步将得到的基线向量以IGb08的核心站为约束条件,采用最小约束法平差得到测站坐标,统计每个测站E、N、U 3个方向的坐标重复性,则所有测站坐标重复性的平均值见表 2。
|
由表 2可知,观测值最多原则所选独立基线的坐标重复性为(0.98, 1.41, 2.23)(单位为mm)优于路径最短原则所选基线的坐标重复性(1.14、1.62、3.15)(单位为mm),E、N、U 3个方向平均提升了14.0%、12.9%和29.2%。
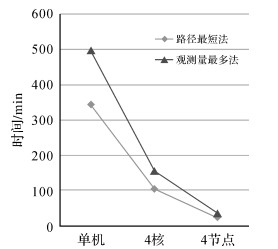
为了验证并行计算的效率,在局域网中利用4台计算机搭建网络并行计算环境。4台计算机的配置基本相同,均为4核台式机(内存4 GB,主频2.2~2.8 GHz),每台计算机作为硬件平台发布双差多核并行计算服务,其中1台作为用户端,用户端通过指令调用每台计算机提供的双差计算服务,然后4个节点同时自动多核并行处理基线计算任务,用户端汇总所有的基线解算结果后再进行网平差得到测站坐标。数据统一放在局域网中的FTP上。分别采用单机串行、单机4核并行、4节点并行方案对7 d的数据进行双差解算,由于1810周每天的测站数相差不大,统计不同解算方案下7 d的平均计算开销时间,见图 7。
|
| 图 7 不同方案的解算时间统计图 Fig. 7 Calculating time of different schemes |
采用传统的单机串行解算方案时,独立基线法平均消耗342.11 min,而由于基于观测量最多算法选取独立基线需要统计观测量,观测量最多法解算时间比独立基线法多增加了150 min。但采用单机多核并行解算方案时,路径最短法和观测量最多法的4核的并行加速比达到了3.79和3.72,而进一步采用网络4节点多核并行解算方案后,虽然网络通信等造成一定的计算耗时,但路径最短法和观测量最多法的4节点的并行加速比仍达到了14.39和13.92,即4节点计算效率比单机串行方案提高了14.39倍和13.92倍,分别仅需23.84 min和35.62 min。可见,不论是算法更复杂的观测量最多原则还是传统的路径最短法,并行方案均有效提高了计算效率,而且两种方案的计算时间随着并行计算节点数的增加而逐渐趋近。可见,在并行计算平台和并行编程技术支持下,可实现算法模型更复杂的GNSS大网数据的整体快速解算。
4 结论本文提出了一种适用于多核多节点网络环境下的改进独立双差观测值构建与独立基线并行解算的方法。改进的基于观测值最多原则构建全网独立双差观测值比传统路径最短法提高了GNSS网中观测值的利用率,而有效观测值越多越有利于提供更稳定可靠的解算精度。通过对IGS测站1810周的数据构建独立双差观测值,平均每天375个测站组成的同步观测网采用观测值最多原则选取的独立双差观测值比基于路径最短原则多了约53万个,解算7 d数据的坐标重复性在ENU方向比路径最短原则平均分别提升了14.0%、12.9%和29.2%。
针对大网双差观测值构建与整网解算效率低的问题,设计了观测值并行构建与独立基线并行解算方法,利用多核并行和网络并行编程技术实现了GNSS大网数据在多核多节点计算平台下自动并行处理,具有无需分区、自动化、并行扩展性强等优点。通过对1810周全球分布的IGS测站进行并行计算试验,4核4节点的并行方案比传统单机串行方案的计算效率提升了14倍左右,如基于观测值最多原则的双差整网解算的单机串行方案需要492 min,而并行方案仅需要35.62 min,显著提高了整网双差解算的效率。
随着GNSS测站规模不断扩大以及多频多系统时代的到来,GNSS逐渐面临更大的计算压力,本文采用并行算法设计与并行编程技术初步实现了GNSS大网双差模型的快速解算。随着云计算、大数据等新兴计算技术与理论不断发展,充分利用多核CPU/众核GPU等新的硬件搭建云平台,为GNSS大规模数据的处理提供新的解决途径,将是下一步重点研究的方向。
| [1] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al. IGS-MGEX: Preparing the Ground for Multi-constellation GNSS Science[J]. Inside GNSS, 2014, 9(1): 42–49. |
| [2] | CHEN Hua, JIANG Weiping, GE Maorong, et al. An Enhanced Strategy for GNSS Data Processing of Massive Networks[J]. Journal of Geodesy, 2014, 88(9): 857–867. DOI:10.1007/s00190-014-0727-7 |
| [3] | GE M, GENDT G, DICK G, et al. A New Data Processing Strategy for Huge GNSS Global Networks[J]. Journal of Geodesy, 2006, 80(4): 199–203. DOI:10.1007/s00190-006-0044-x |
| [4] | BOOMKAMP H.Distributed Processing for Large Geodetic Solutions[M]//ALTAMIMI Z, COLLILIEUX X. Reference Frames for Applications in Geosciences. Berlin Heidelberg, Germany: Springer, 2013: 13-18. |
| [5] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005–5017. DOI:10.1029/96JB03860 |
| [6] | 陈俊平, 张益泽, 谢益炳, 等. 超大观测网络及多GNSS系统的快速数据处理[J]. 武汉大学学报(信息科学版), 2014, 39(3): 253–257. CHEN Junping, ZHANG Yize, XIE Yibing, et al. Rapid Data Processing of Huge Networks and Multi-GNSS Constellation[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3): 253–257. |
| [7] | 葛茂荣. GPS卫星精密定轨理论及软件研究[D]. 武汉: 武汉测绘科技大学, 1995. GE Maorong. Study on Theory and Software of Precise Orbit Determination for GPS Satellite[D]. Wuhan, China: Wuhan Technical University of Surveying and Mapping, 1995. |
| [8] | GE M, GENDT G, DICK G, et al. Improving Carrier-phase Ambiguity Resolution in Global GPS Network Solutions[J]. Journal of Geodesy, 2005, 79(1-3): 103–110. DOI:10.1007/s00190-005-0447-0 |
| [9] | 阮仁桂. SPODS软件GPS/GNSS网解的模糊度解算方法[J]. 测绘学报, 2015, 44(2): 128–134. RUAN Rengui. Ambiguity Resolution for GPS/GNSS Network Solution with SPODS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 128–134. DOI:10.11947/j.AGCS.2015.20130461 |
| [10] | 程传录, 蒋光伟, 聂建亮, 等. 利用双差的超大GNSS基准站网解算方法改进[J]. 武汉大学学报(信息科学版), 2014, 39(5): 596–599. CHENG Chuanlu, JIANG Guangwei, NIE Jianliang, et al. Improving the Processing Stragegy Based on Double-differenced Observations for Huge GNSS Network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 596–599. |
| [11] | SERPELLONI E, CASULA G, GALVANI A, et al. Data Analysis of Permanent GPS Networks in Italy and Surrounding Regions: Application of a Distributed Processing Approach[J]. Annals of Geophysics, 2006, 49(4-5): 897–928. |
| [12] | BOOMKAMP H. Global GPS Reference Frame Solutions of Unlimited Size[J]. Advances in Space Research, 2010, 46(2): 136–143. DOI:10.1016/j.asr.2010.02.015 |
| [13] | 崔阳, 陈正生, 吕志平, 等. 非差模式的GNSS数据并行解算设计及实现[J]. 测绘科学技术学报, 2015, 32(6): 565–569. CUI Yang, CHEN Zhengsheng, LV Zhiping, et al. Design and Implementation of Parallel Processing Strategy for GNSS Data Based on the Undifferenced Method[J]. Journal of Geomatics Science and Technology, 2015, 32(6): 565–569. |
| [14] | 崔阳, 吕志平, 陈正生, 等. 多核环境下的GNSS数据并行处理研究[J]. 测绘学报, 2013, 42(5): 661–667. CUI Yang, LV Zhiping, CHEN Zhengsheng, et al. Research of Parallel Data Processing for GNSS Network Adjustment Under Multi-core Environment[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 661–667. |
| [15] | 王成, 施闯, 段兵兵, 等. 利用位置与云计算建立电离层TEC主动式播发平台[J]. 武汉大学学报(信息科学版), 2016, 41(3): 304–309. WANG Cheng, SHI Chuang, DUAN Bingbing, et al. Ionosphere Total Electron Content Active Broadcasting Platform Using Location and Cloud Computing[J]. Geomatics and Information Science of Wuhan University, 2016, 41(3): 304–309. |
| [16] | 邹贤才, 李建成, 汪海洪, 等. 基于OpenMP的并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636–641. ZOU Xiancai, LI Jiancheng, WANG Haihong, et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636–641. |
| [17] | BABOULIN M, GIRAUD L, GRATTON S, et al. Parallel Tools for Solving Incremental Dense Least Squares Problems. Application to Space Geodesy[J]. Journal of Algorithms & Computational Technology, 2006, 3(1): 117–133. |
| [18] | DACH R, LUTZ S, WALSER P, et al. User Manual of the Bernese GPS Software Version 5.2[M]. Bern: Astronomical Institute, University of Bern, 2015. |
| [19] | 王海英, 黄强, 李传涛, 等. 图论算法及其MATLAB实现[M]. 北京: 北京航空航天大学出版社, 2010. WANG Haiying, HUANG Qiang, LI Chuantao, et al. Graph Theory Algorithm and Its Implemention Based on MATLAB[M]. Beijing: Beijing Univeristy of Aeronautics and Astronautics Press, 2010. |
| [20] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010. LI Zhenghang, HUANG Jingsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2010. |
| [21] | BLEWITT G. Fixed Point Theorems of GPS Carrier Phase Ambiguity Resolution and Their Application to Massive Network Processing: Ambizap[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B12): B12410. DOI:10.1029/2008JB005736 |
| [22] | 陈宪冬. Ambizap方法在大规模GPS网处理中的应用及结果分析[J]. 武汉大学学报(信息科学版), 2011, 36(1): 10–13. CHEN Xiandong. Application of Ambizap Algorithm in Large GPS Network and Its Test Results[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 10–13. |
| [23] | 刘焱雄, 彭琳, 周兴华, 等. 网解和PPP解的等价性[J]. 武汉大学学报(信息科学版), 2005, 30(8): 736–738, 743. LIU Yanxiong, PENG Lin, ZHOU Xinghua, et al. Equivalence of Network-solution and PPP-solution[J]. Geomatics and Information Science of Wuhan University, 2005, 30(8): 736–738, 743. |
| [24] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines Up to 2000 km[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B8): 10187–10203. DOI:10.1029/JB094iB08p10187 |
| [25] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |



