2. 千寻位置网络有限公司, 上海 200438
2. Qian Xun Wei Zhi Network Co. Ltd., Shanghai 200438, China
我国于2012年底建成了具备导航定位授时能力的北斗卫星导航定位系统(BeiDou navigation satellite system,BDS)。截至2015年12月,北斗导航卫星系统包括5颗Geostationary Orbit(GEO)卫星,5颗Inclined Geosynchronous Orbit(IGSO)卫星,4颗Medium Earth Orbit(MEO)卫星[1]。许多学者对北斗系统在标准单点定位[2]、精密单点定位[3-4]、双频([5-6])以及多频相对定位[7]等多种模式下的定位性能进行了分析评价,验证了北斗系统的可用性。
近年来一些研究表明[8-12],BDS伪距观测值和相位观测值之间存在系统性差异,该差异在高高度角情况下达到0.4 m,在低高度角情况下甚至超过1 m。该系统性偏差可分为两类:一类是IGSO/MEO卫星随高度角变化的伪距系统性偏差;另一类是GEO卫星(高度角仅微小变化)明显的伪距系统性偏差。该系统性偏差对单点定位、宽巷模糊度固定、单频PPP定位等都有显著的影响。针对此问题,文献[13]提出了一种基于高度角的伪距改正模型,该模型可应用于北斗IGSO卫星和MEO卫星的伪距观测值改正,其测试结果表明,该改正模型可显著改善单频PPP的定位精度。
对于GEO卫星的系统性偏差[14-15],因单个测站的GEO卫星高度角几乎不变,文献[13]未对此建立模型。文献[16]基于多个测站的观测值建立了GEO卫星的高度角改正模型。对于单个静态站或低动态观测,由于GEO卫星高度角几乎不变,其修正值是恒定的。
文献[13]及文献[16]所给出的改正模型,更多地是对北斗卫星端的多路径系统误差(星内多径)进行建模。本文的分析表明,虽然GEO卫星高度角几乎不变,但是由于受到测站端多路径影响较为严重,其MP序列存在若干分米量级的抖动,已有改正模型难以准确描述卫星伪距偏差变化。因此,本文针对GEO卫星伪距偏差问题,提出了一种基于卡尔曼滤波的修正方法。滤波模型兼顾GEO卫星观测值卫星端和接收机端多路径的影响,将两部分误差统一进行处理。
单频接收机具有低成本优势,以单频接收机实现用户高精度单机定位已成为近年来的研究热点[17]。单频PPP是其中一种重要的技术方法,目前已有不少学者开展了GPS单频PPP方面的研究工作,取得了丰富的成果[18-20]。基于伪距相位组合的单频PPP(precise point positioning,PPP)技术的伪距权重较大,会受到上文提到的北斗伪距偏差的影响。本文分析了该偏差对单频PPP水平和高程方向精度的影响,并对比了改正伪距偏差后的效果。
1 BDS伪距多路径系统误差Multipath(MP)组合观测值常用于评估伪距观测值的多路径特征,其计算公式如下[21-22]
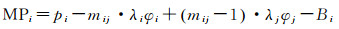 (1)
(1)
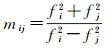 (2)
(2)
式中,p和φ分别表示伪距和相位观测值;f和λ分别表示信号的频率和波长;下标i, j(i, j=1, 2, 3, i≠j)用于标识不同的信号频率。偏差项Bi包含了相位模糊度以及硬件延迟和多路径误差的常数部分。
MP组合消除了观测值的电离层延迟和几何相关项(如对流层延迟、几何距离、钟差等),剩余项包括相位观测值模糊度、信号硬件延迟差、多路径以及观测噪声。通常情况下,信号硬件延迟在一定时间内保持稳定,而相位观测值模糊度在未发生周跳和失锁的情况下同样保持不变,因此B值中包含硬件延迟和模糊度。对MP组合进行长时间平均,可确定B值的大小。MP原始组合减去B值后仅剩下观测噪声和多路径误差变化部分。由于观测噪声通常表现为高斯白噪声特性,因此通过MP组合可以分析伪距观测值的多路径系统误差特性。
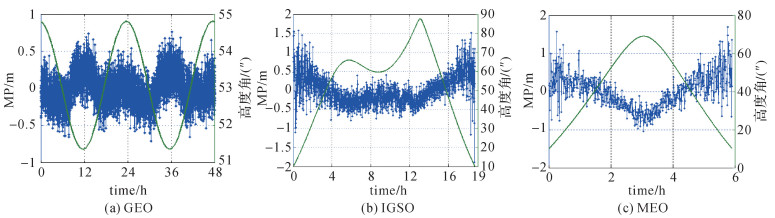
图 1给出了基于GMSD测站数据计算的北斗3种不同类型卫星B1频率伪距观测值多路径系统误差的典型示例,数据观测时间为2016年8月1日—2016年8月2日(DOY 213—DOY 214)。GEO卫星给出了连续2 d的MP序列,IGSO卫星和MEO卫星则给出了一个观测弧段的MP序列。由图 1可知,3种类型卫星观测值的多路径误差均存在较为明显的系统性偏差,波动量级从几个分米到1 m左右。观测值的多路径与信号高度角存在较强的相关性,GEO卫星的多路径同时还呈现出约1 d为周期的变化。
|
| 图 1 北斗多路径误差特征 Fig. 1 Characteristics of BeiDou multipath |
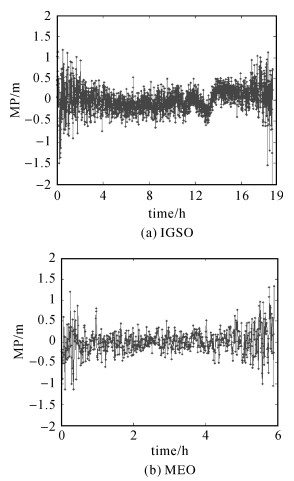
IGSO卫星和MEO卫星伪距观测值的系统多路径误差可采用Wanninger和Beer的模型进行改正。图 2给出了IGSO卫星和MEO卫星修正多路径误差后的MP序列。从图中可以看到,经过模型修正后,IGSO卫星和MEO卫星MP序列的系统性误差被明显削弱或消除。
|
| 图 2 修正多路径误差后的MP序列 Fig. 2 MP series after multipath correction |
2 GEO卫星观测值多路径滤波方法
本节主要研究如何对GEO伪距观测值多路径进行修正。有关多路径的研究方法有多种,如小波变换法[23-24]、恒星日滤波法[25-26],本文拟采用卡尔曼滤波方法对多路径偏差进行分析和修正。
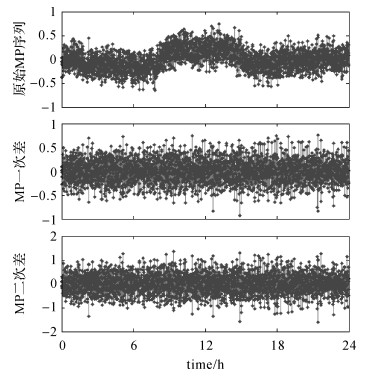
2.1 特征分析MP序列反映了多路径的量级,但同时受到噪声的影响。本文首先采用卡尔曼滤波对MP序列进行拟合,以去除噪声的影响,进而得到多路径修正量,对伪距观测值进行修正。图 3给出了基于GMSD站2015年8月1日(年积日213) 数据获得的GEO C01卫星MP组合的原始序列、历元一次差序列和历元二次差序列。从图中可以看出,经过一次差或者二次差后的MP序列,趋近于白噪声。因此,采用常加速模型可表达出GEO多路径系统偏差。
|
| 图 3 C01观测值MP原始序列、一次差序列、二次差序列 Fig. 3 Original, first-order differenced and second-order differenced MP series for C01 satellite mesurements |
2.2 滤波方法
常加速模型的状态方程为
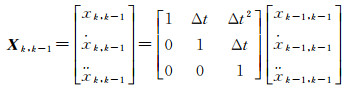 (3)
(3)
式中,Δt为时间差。假定加速度是一个具有常量谱密度的白噪声过程,系统噪声(过程噪声)的协方差矩阵为
 (4)
(4)
式中,I为单位阵;σa2为加速度常量方差,本文依据经验设定为σa2=10-102·Δt。
对于MP序列,其滤波状态为MP系统偏差量、及其随时间变化的速度和加速度。采用该滤波模型,可提取出MP序列的多路径系统偏差,进而对伪距观测值进行修正。由于该系统偏差存在约一天周期的变化,因此可基于前一天数据获取的修正对当天的伪距观测值进行修正。
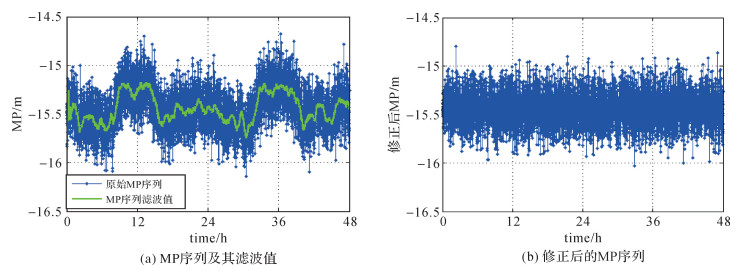
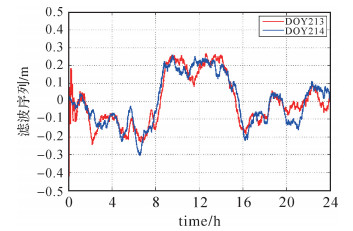
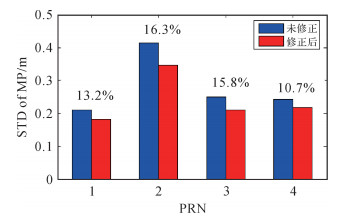
2.3 修正效果图 4(a)给出了GMSD站C01卫星的MP序列滤波示例,数据观测时间为2015年8月1日(年积日213);图 4(b)给出了经过修正后的MP序列。可以看出,本文的滤波方法可以较好地滤波出多路径系统偏差项,经过修正后的MP序列非常接近于白噪声特性。图 5给出了DOY 213和DOY 214相邻两天多路径偏差项对比,相邻两天的修正量非常类似,进一步证实可基于前一天数据获取的修正量对当天的伪距观测值进行修正。根据文献[27]的研究,GEO卫星多路径周期约为86 160 s,修正时依据该周期进行。图 6给出了GMSD测站2015年8月2日4颗GEO卫星观测值MP序列修正前后的标准偏差统计值,修正值基于2015年8月1日数据计算得到。经过修正后,MP序列的标准偏差下降了10%~16%。
|
| 图 4 C01卫星观测值MP序列滤波值及修正后序列 Fig. 4 MP series before and after multipath correction for C01 satellite mesurements |
|
| 图 5 滤波修正值对比(DOY 213 VS DOY 214) Fig. 5 Comparison of filtered values for two consecutive days (DOY 213 vs DOY 214) |
|
| 图 6 MP序列标准偏差对比 Fig. 6 Comparison of Standard deviation for MP series before and after correction 注:图中百分比表示修正多路径系统误差后的MP序列相比未改正的MP序列的标准偏差改进程度。 |
3 修正伪距多路径系统误差改善单频PPP定位精度
本节分析伪距多路径偏差对单频PPP的影响及修正伪距多路径偏差后的改善效果。
3.1 单频PPP模型单频PPP的一种形式为伪距相位组合模型[18],该模型利用伪距和相位一阶电离层延迟符号相反、大小相同的特性,消除了一阶电离层延迟的影响;其缺点在于伪距在观测方程中占了较大的权重。当伪距噪声或多路径较大时,如上文的BDS伪距多路径系统偏差,该模型精度将受到影响。
3.2 处理策略采用GFZ提供的精密星历和精密卫星钟差产品、以及MGEX的北斗DCB产品进行单频PPP解算。估计参数包括测站坐标、接收机钟差、天顶对流层延迟参数、相位观测值模糊度。采用卡尔曼滤波方式进行数据处理。接收机钟差参数采用白噪声模型,对流层参数初值采用Saastamonien模型确定[28],估计参数采用随机游走模型,投影函数为NMF模型[29],位置参数当作常数估计(静态模型),模糊度参数在未失锁和未发生周跳情况下认为不变,发生周跳或失锁时间过长则重置。伪距与相位验前标准差之比为1:100。截止高度角取为15°。
采用第2节的滤波方法消除GEO卫星伪距观测值的多路径误差:基于B1频率伪距观测值和B1和B2频率的相位观测值计算MP序列,由前一周期提取的多路径误差模型,对当前观测值进行多路径误差改正。IGSO和MEO卫星的系统性偏差采用Wanninger和Beer的高度角模型进行修正。
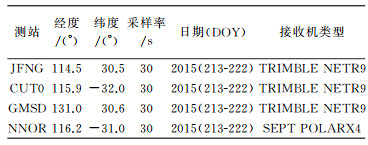
3.3 数据处理与分析为了测试改正多路径系统误差前后北斗单频PPP的定位精度情况,选择MGEX网亚太地区的4个测站进行分析,所用数据的具体信息见表 1。由于需要基于前一天数据计算修正值,同时获取了所有测站2015(212) 的观测数据用于计算2015(213) 的修正值。
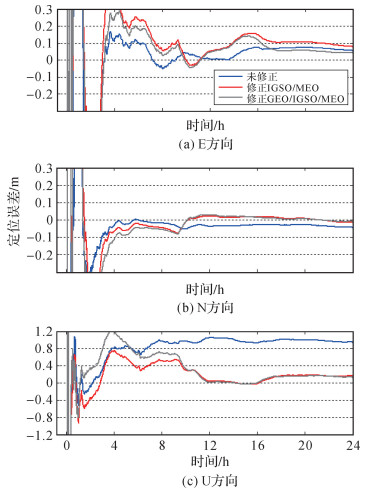
图 7给出了GMSD站2015(213) 的单频PPP定位结果在N、E、U 3个方向的定位误差。由图 7可以看出,在收敛之后,修正IGSO和MEO多路径系统偏差的定位结果在E方向略差于未修正多路径系统偏差的定位结果,在N方向和高程方向则优于未修正多路径系统偏差的定位结果,尤其在高程方向,定位精度得到了显著改善。修正GEO、IGSO和MEO多路径系统偏差的定位结果则在N、E、U 3个方向均略优于修正IGSO和MEO多路径系统偏差的定位结果。对表 1 4个测站共39组数据(GMSD存在1 d无法获取观测数据)的定位结果进行统计分析表明,大部分测站均呈现出上述规律。需要指出的是,存在少数几组数据的计算结果在进一步修正GEO卫星的系统偏差后,结果甚至差于未对GEO卫星的系统偏差进行修正的结果,该原因可能是部分数据GEO卫星的多路径误差经过弧段平均后,其仍存在较大系统性偏差。该系统性偏差将被吸收到式(1) 中的常数项部分中,导致计算的修正值不准确。
|
| 图 7 定位误差对比 Fig. 7 Comparison of positioning errors |
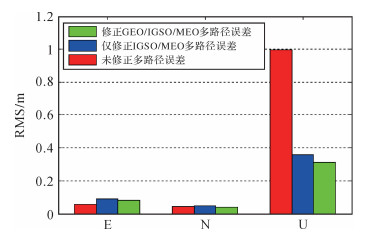
图 8给出了4个测站2015(213—222) 所有计算结果的坐标误差在各个方向的坐标误差RMS统计值。由图 8可以看出,未修正多路径误差时,水平方向定位精度在10 cm以内,而高程方向则达到1 m。修正IGSO和MEO卫星观测值的多路径误差后,虽然水平方向的精度有略微下降,但高程方向的精度得到了极大的改善,从1 m下降到3.5 dm左右,改善了65%。进一步修正GEO卫星的多路径误差后,相比仅修正IGSO和MEO卫星观测值多路径误差的定位结果,其在平面和高程方向都有一定程度的改善,尤其在高程方向,从3.5 dm下降到了3.0 dm左右,改善了约15%。相比不修正多路径的情形,高程精度总体改善了75%左右。
|
| 图 8 定位误差RMS值对比 Fig. 8 Comparison of RMS values of positioning errors |
本文中对GEO卫星的修正采用的是后处理的方式,且需要用到双频的载波相位观测值。当采用单频接收机进行实时单频PPP定位时,该方法并不适用。本文主要侧重于研究GEO卫星观测值系统多路径偏差对单频PPP定位的影响。
4 结论北斗伪距观测值存在特有的系统性偏差,偏差的数量级达到几分米到米。该系统偏差可分为两类:一类是IGSO/MEO卫星随高度角变化的伪距系统性偏差;另一类是GEO卫星(高度角仅微小变化)明显的伪距系统性偏差。
本文对该系统偏差对单频PPP的影响进行了分析,表明该系统性偏差将导致单频PPP定位结果高程方向产生约1m的偏差。针对GEO卫星伪距偏差,本文提出了一种基于卡尔曼滤波的修正方法,对卫星端和接收机端多路径误差进行统一处理,修正后的GEO卫星MP序列的标准偏差下降了10~16%。
结合Wanninger和Beer的高度角模型对IGSO/MEO伪距偏差进行修正,本文分析了同时修正IGSO/MEO及GEO卫星伪距偏差后对单频PPP的改善情况。采用4个MGEX站10 d的数据进行了处理,分析结果表明:仅改正和卫星多路径误差,高程方向定位结果精度可改善65%左右;采用本文方法对GEO卫星的多路径修正后,该方向定位结果精度改善比例将进一步提高至75%左右。
| [1] | 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件[EB/OL]. 2. 0版. 北京: 中国卫星导航系统管理办公室, [2016-10-23]. http://www.beidou.gov.cn/2013112127.html. CSNO. BeiDou Navigation Satellite System Signal in Space Interface Control Document, Open Service Signal[EB/OL]. (Version 2.0). Beijing: China Satellite Navigation Office[2016-10-23]. http://www.beidou.gov.cn/2013112127.html. |
| [2] | 肖国锐, 隋立芬, 刘长建, 等. 北斗导航定位系统单点定位中的一种定权方法[J]. 测绘学报, 2014, 43(9): 902–907. XIAO Guorui, SUI Lifen, LIU Changjian, et al. A Method of Determining the Weight Matrix for BeiDou Navigation Satellite System Single Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 902–907. DOI:10.13485/j.cnki.11-2089.2014.0165 |
| [3] | 张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250–256. ZHANG Xiaohong, ZUO Xiang, LI Pan, et al. Convergence Time and Positioning Accuracy Comparison Between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250–256. DOI:10.11947/j.AGCS.2015.20130771 |
| [4] | 朱永兴, 冯来平, 贾小林, 等. 北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377–383. ZHU Yongxing, FENG Laiping, JIA Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377–383. DOI:10.11947/j.AGCS.2015.20140082 |
| [5] | HE Haibo, LI Jinlong, YANG Yuanxi, et al. Performance Assessment of Single-and Dual-Frequency BeiDou/GPS Single-epoch Kinematic Positioning[J]. GPS Solutions, 2013, 18(3): 393–403. |
| [6] | TEUNISSEN P J G, ODOLINSKI R, ODIJK D. Instantaneous BeiDou+GPS RTK Positioning with High Cut-off Elevation Angles[J]. Journal of Geodesy, 2014, 88(4): 335–350. DOI:10.1007/s00190-013-0686-4 |
| [7] | ZHANG Xiaohong, HE Xiyang. Performance Analysis of Triple-Frequency Ambiguity Resolution with BeiDou Observations[J]. GPS Solutions, 2016, 20(2): 1–13. |
| [8] | HAUSCHILD A, MONTENBRUCK O, SLEEWAEGEN J M, et al. Characterization of Compass M-1 Signals[J]. GPS Solutions, 2012, 16(1): 117–126. DOI:10.1007/s10291-011-0210-3 |
| [9] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. A COMPASS for Asia: First Experience with the BeiDou-2 Regional Navigation System[C]//Poster at IGS Workshop. Olsztyn, Poland, 2012. |
| [10] | MONTENBRUCK O, RIZOS C, WEBER R, et al. Getting a Grip on Multi-GNSS—the International GNSS Service MGEX Campaign[J]. GPS World, 2013, 24(7): 44–49. |
| [11] | WANG G, DE JONG K, LI X, et al. Analysis of Characteristics of BDS Observable Combinations for Wide-lane Integer Ambiguity Resolution[C]//SUN J, JIAO W, WU H, et al. Proceedings of China Satellite Navigation Conference (CSNC). Berlin, Heidelberg: Springer, 2014. |
| [12] | ZHANG Xiaohong, HE Xiyang, LIU Wanke. Characteristics of Systematic Errors in the BDS Hatch-Melbourne-Wübbena Combination and Its Influence on Wide-lane Ambiguity Resolution[J]. GPS Solutions, 2016, 21(1): 265–277. |
| [13] | WANNINGER L, BEER S. BeiDou Satellite-induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639–648. DOI:10.1007/s10291-014-0423-3 |
| [14] | WANG Guangxing, DE JONG K, ZHAO Qile, et al. Multipath Analysis of Code Measurements for BeiDou Geostationary Satellites[J]. GPS Solutions, 2014, 19(1): 129–139. |
| [15] | HE Xiyang, ZHANG Xiaohong. Characteristics Analysis of BeiDou Melbourne-Wübbena Combination[C]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. Proceedings of the China Satellite Navigation Conference (CSNC) 2015. Berlin, Heidelberg, Germany: Springer, 2015: 587-593. |
| [16] | LOU Yidong, GONG Xiaopeng, GU Shengfeng, et al. Assessment of Code Bias Variations of BDS Triple-frequency Signals and Their Impacts on Ambiguity Resolution for Long Baselines[J]. GPS Solutions, 2017, 21(1): 177–186. DOI:10.1007/s10291-016-0514-4 |
| [17] | 张小红, 李星星, 郭斐, 等. GPS单频精密单点定位软件实现与精度分析[J]. 武汉大学学报(信息科学版), 2008, 33(8): 783–787. ZHANG Xiaohong, LI Xingxing, GUO Fei, et al. Realization and Precision Analysis of Single-frequency Precise Point Positioning Software[J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 783–787. |
| [18] | CHOY S, ZHANG K, SILCOCK D. An Evaluation of Various Ionospheric Error Mitigation Methods Used in Single Frequency PPP[J]. Journal of Global Positioning Systems, 2008, 7(1): 62–71. DOI:10.5081/jgps |
| [19] | 涂锐, 黄观文, 张勤, 等. 利用单基准站改正信息和电离层参数估计的单频PPP算法[J]. 武汉大学学报(信息科学版), 2012, 37(2): 170–173, 182. TU Rui, HUANG Guanwen, ZHANG Qin, et al. PPP Algorithm of Single Frequency Based on Corrections of Single-Base Station and Ionospheric Parameters Estimation[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 170–173, 182. |
| [20] | 王利, 张勤, 涂锐, 等. 基于原始观测值的单频精密单点定位算法[J]. 测绘学报, 2015, 44(1): 19–25. WANG Li, ZHANG Qin, TU Rui, et al. A Kind of Single-frequency Precise Point Positioning Algorithm Based on the Raw Observations[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 19–25. DOI:10.11947/j.AGCS.2015.20130315 |
| [21] | KEE C, PARKINSON B W. Calibration of Multipath Errors on GPS Pseudorange Measurements[C]//Proceedings of the 7th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake City, UT: [s.n.], 1994: 353-362. |
| [22] | ESTEY L H, MEERTENS C M. TEQC: the Multi-Purpose Toolkit for GPS/GLONASS Data[J]. GPS Solutions, , 3(1): 42–49. DOI:10.1007/PL00012778 |
| [23] | SATIRAPOD C, RIZOS C. Multipath Mitigation By Wavelet Analysis for GPS Base Station Applications[J]. Survey Review, 2005, 38(295): 2–10. DOI:10.1179/sre.2005.38.295.2 |
| [24] | SOUZA E M, MONICO J F G, POLEZEL W G C, et al. An Effective Wavelet Method to Detect and Mitigate Low-Frequency Multipath Effects[C]//XU P, LIU J, DERMANIS A. Proceedings of International Association of Geodesy Symposia. Berlin, Heidelberg, Germany: Springer, 2008: 413-417. |
| [25] | BORRE K, DE JONG K, PICHOT C. Subsidence Monitoring System Using Real-time GPS Sensors[C]//Proceedings of ION-GNSS-2001, The Institute of Navigation. Salt Lake City, Utah: [s.n.], 2001: 362-367. |
| [26] | CHOI K, BILICH A, LARSON K M, et al. Modified Sidereal Filtering: Implications for High-Rate GPS Positioning[J]. Geophysical Research Letters, 2004, 31(22): L22608. DOI:10.1029/2004GL021621 |
| [27] | MA X, SHEN Y. Multipath Analysis of COMPASS Triple Frequency Observations[C]//The International Symposium on GPS/GNSS. Xi'an: [s.n.], 2012. |
| [28] | SAASTAMOINEN J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[M]//HENRIKSEN S W, MANCINI A, CHOVITZ B H. The Use of Artificial Satellites for Geodesy. Virginia: AGU, 1972: 274-251. |
| [29] | NIELL A E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227–3246. DOI:10.1029/95JB03048 |