2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054;
4. 长安大学, 陕西 西安 710054;
5. 解放军理工大学, 江苏 南京 210007
2. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Changan'an University, Xi'an 710054, China;
5. PLA University of Science & Technology, Nanjing 210007, China
我国北斗卫星导航系统(BDS)精密轨道确定精度受光压模型建模、姿态模式切换、测站分布等多重因素的影响相比GPS仍有较大差距,为此许多学者作了相关研究工作[1-10]。目前BDS尚处于提供亚太服务能力阶段,受地理等其他因素制约,BDS全球地面监测站仍然分布不均匀且测站个数不足GPS的1/4,严重影响北斗卫星定轨精度。因此有必要研究在当前测站布局情况下BDS精密定轨的增强方法。使用低轨卫星(LEO)的星载观测数据联合地面测站同时解算导航星轨道、低轨卫星轨道、钟差参数等进行星地一体定轨是一个较为有效的解决办法。文献[11]分析了在使用星地一体定轨策略下LEO的定轨精度改善情况。文献[12]基于星地一体定轨试验结果,首次分析并得出星载数据的加入可以提高GPS轨道精度,且对地球自转参数等也有一定的改进。此后,多人作了相关的试验分析[13-16],表明低轨卫星的加入可以获得不同于地面测站的可观性观测量,其定轨解算得到的整体结果是仅使用地面测站定轨不能比拟的。文献[17]通过数据仿真分析了定轨增强中的一项关键技术——低轨卫星模糊度固定,指出对于星载接收机观测数据,由于低轨卫星运动速度快、连续观测时间短(15~25 min)、基线更长且含电离层延迟等问题,不能沿用地面测站模糊度固定方法。提出在函数模型中使用电离层加权模型,并给出了部分模糊度固定方法。文献[18]分析了联合121个IGS测站在有/无JASON-2卫星的星载GPS、SLR、DORIS观测数据进行定轨时,多种观测技术的组合观测量对GPS轨道的增强程度。结果表明星载观测数据不仅有助于提升单独解算地面测站模糊度的固定率,且对轨道约有7 mm量级的精度改善。
目前北斗事后精密产品主要使用GPS/BDS双系统定轨或者“两步法”定轨策略。“两步法”即首先使用精密单点定位网解得到地面测站坐标、天顶对流层延迟、接收机钟差参数等,然后将这些参数固定,进行BDS精密定轨试验。搭载有双模接收机的风云三号C星(GNOS)于2013年发射以后[19],文献[20]通过使用“两步法”评定了GNOS卫星对BDS卫星的轨道精度改善情况,但未评定钟差比较结果。我国BDS 3类卫星GEO、IGSO、MEO并存,其中GEO卫星由于几何变化缓慢,单独地面测站定轨时轨道元素、光压参数、模糊度参数等相互依赖,分离不彻底[5]。由于低轨卫星迅速变化的特性,GNOS的加入将会对北斗GEO卫星的定轨精度产生较大幅度的提升,其他类型卫星的改善程度有待试验论证。
基于低轨卫星的BDS星地一体“一步”定轨增强试验目前尚未有学者分析。联合GNOS星载双模接收机观测数据及地面测站数据,本文首次基于实测数据分析在进行星地一体定轨时,低轨卫星的加入对BDS卫星轨道精度及钟差的改善情况。在全球测站、区域测站情况下进行BDS单系统及GPS/BDS双系统定轨增强试验,使用重叠弧段的方法对轨道及钟差精度进行评估。细致分析3类卫星3个方向的精度改善情况,并统计可视弧段内的钟差重叠精度。进行星地一体定轨前对星载接收机观测数据进行了数据质量分析。
1 GNOS介绍及数据质量分析属于太阳同步轨道的风云极轨气象卫星(FY3 C)的轨道高度为836 km,轨道倾角98.75°,主要功能是实现掩星探测[19]。借助导航卫星发播的信号,FY3 C上搭载的掩星探测仪GNOS可获取大气层的信息,能够近实时、高精度、多数量地提供掩星廓线,广泛应用于天气预报、气候分析、电离层研究等领域[19]。GNOS仪器由中科院空间中心研制,包含3类天线:定位天线、前向掩星接收天线、后向掩星接收天线。搭载的GPS接收机有14个通道,8个用于定位,6个用于掩星探测;搭载的BDS接收机有8个通道,4个用于定位,4个用于掩星探测[19]。
1.1 数据统计选取2013年10月10日—16日GNOS 7 d 1 Hz观测数据和2013年5月11日—30日海洋二号(HY2A)20 d 1 Hz观测数据,统计有效卫星数及观测码的丢失率。表 1统计了可见卫星个数、有效卫星个数(同时包含两个伪距、两个载波相位观测量)的百分比及观测码与总观测个数的百分比(以每个观测量为单位)。分析见表 1。
(1) GNOS卫星单历元有效可见卫星数大于等于4颗情况BDS、GPS分别为11.54%、79.95%,相应的HY2A卫星中的GPS为99.0%。说明GNOS受接收机设备通道限制可观测到的卫星个数较少,尤其是BDS卫星。BDS有效卫星个数0颗的情况平均占27.1%,小于3颗的情况接近90%。说明由于BDS目前为区域导航系统,对GNOS在轨运行时可视弧段极其受限。
(2) 相较于HY2A卫星,GNOS可见卫星数与有效卫星数占比差别较大。从表中观测量丢失率统计可知,GNOS包含4个观测码的占比仅60%左右,而HY2A为94%,说明GNOS相比HY2A数据丢失率大。
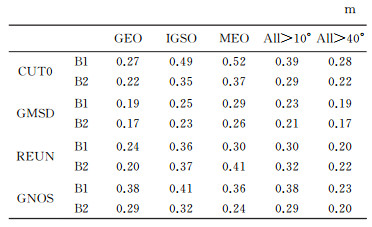
1.2 BDS伪距测量精度使用码减载波相位组合(CC组合)历元间差分的方法分析GNOS卫星北斗观测量的伪距测量精度[21-23],并选取位于不同区域的CUT0、GMSD、REUN 3个地面测站比较。选取同1.1时段一周的GNOS、3个地面测站观测数据,GNOS采样间隔为10 s,地面测站采样间隔为30 s。对所有BDS卫星CC组合历元间差分值序列按高度角排列,每隔10°换算为非差伪距噪声相对于零均值的RMS,结果绘于图 1,整体精度见表 2。按BDS卫星类型分类,统计3类卫星伪距噪声RMS(取截止高度角大于10°),见表 2。

|
| 图 1 伪距测量精度RMS Fig. 1 Pseudorange measuring precision RMS |
分析图 1、表 2,GNOS的伪距测量精度与3个地面测站相当,地面测站3类卫星伪距测量精度大小GEO < IGSO < MEO,GNOS两个频点都为MEO < GEO < IGSO。GNOS中北斗卫星伪距测量精度B1、B2频点分别为0.38 m、0.29 m,在截止高度角大于40°情况下则分别为0.23 m、0.20 m。试验结果表明,尽管星载BDS数据丢失率大且分配的通道数少,但实测伪距测量精度仍然较好,且与卫星标称精度相当[19]。
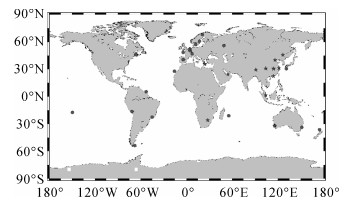
2 试验结果与分析 2.1 全球测站网增强试验试验选取2013年10月10日—16日共7 d GNOS、37个地面测站GPS/BDS双模观测数据。地面观测站包含24个Multi-GNSS Experiment(MGEX)测站及13个武汉大学建立的北斗卫星观测实验网(BeiDou experimental tracking stations, BETS)测站。测站分布如图 2所示,地面站总体上全球分布但并不均匀。在该观测时段我国北斗二代导航系统包括:5颗GEO卫星(C01-C05,G类卫星)、5颗IGSO卫星(C06-C10,I类卫星)、4颗MEO卫星(C11-C14,M类卫星)。
|
| 图 2 测站分布图 Fig. 2 Tracking stations 注:圆圈为MGEX测站,五角星为BETS测站。 |
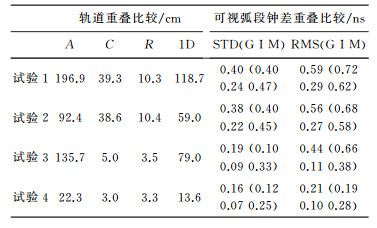
定轨弧长为3 d,共5个定轨弧段,力学模型和观测模型见表 3。由于该时段只有wum精密轨道产品发布,且其定轨精度不可知,因此使用相邻弧段之间的重叠时段进行轨道、钟差的精度评估。每个重叠时段为2 d,共4个重叠弧段。其中卫星钟差统计的是卫星可见测站数大于等于4的情况,在此称为可视弧段钟差重叠精度,选取C10卫星作为基准钟。

|
2.1.1 有GEO卫星试验
试验选取的时段中C06、C09卫星正处于姿态模式切换时期,且通过广播星历卫星健康标识发现C02卫星处于不健康状态,因此在定轨时不添加这些卫星。进行的试验如下:
试验1:37个地面测站BDS单系统定轨;
试验2:37个地面测站+GNOS BDS星地一体定轨;
试验3:37个地面测站GPS/BDS双系统定轨,添加速度脉冲;
试验4:37个地面测站+GNOS GPS/BDS双系统星地一体定轨,添加速度脉冲。
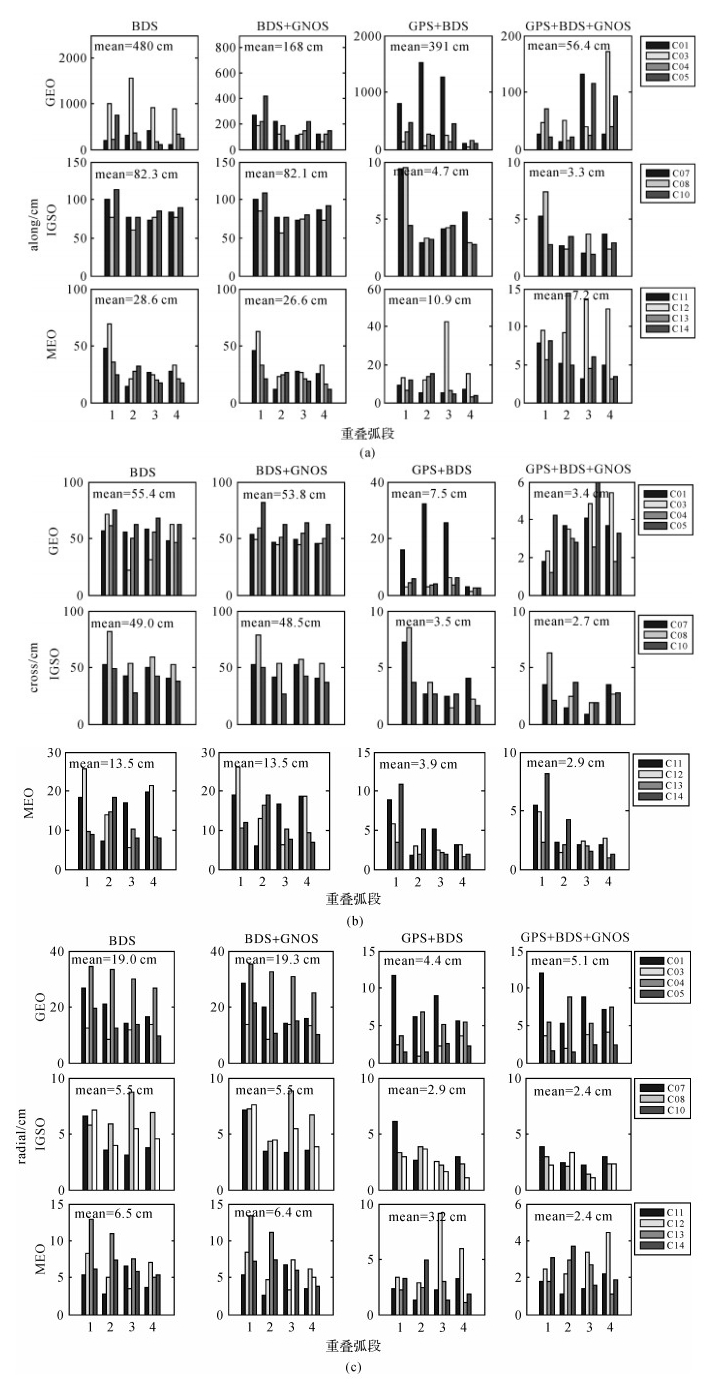
图 3分别为4组试验切向、法向、径向各弧段各颗卫星定轨重叠精度,图中给出了3类卫星重叠精度的平均值。表 4统计了整体轨道及可视弧段钟差重叠精度。图 3、表 4分析如下:
|
| 图 3 BDS各颗卫星3个方向轨道重叠精度 Fig. 3 The orbit overlapping precision of BDS each satellite in three direction |
(1) 轨道整体精度一维RMS在单、双系统加入GNOS后分别提高50.3%、82.8%。双系统定轨精度由79 cm提高至13.6 cm。钟差重叠精度单、双系统STD由0.40 ns、0.19 ns提升至0.38 ns、0.16 ns,改善不大;RMS由0.59 ns、0.44 ns提升至0.56 ns、0.21 ns,M类卫星提升最明显,双系统相较单系统改善幅度更大。
(2) GNOS的加入对BDS卫星轨道精度切向提高程度最大,法向次之。BDS单系统切、法、径向分别提高了1.0 m、0.7 cm、-0.1 cm,提高53.1%、1.8%、-1.0%。双系统切、法、径向分别提高了1.1 m、2 cm、0.2 cm,提高83.6%、40.0%、5.7%。
(3) 切向精度改善主要集中在G类卫星,且有量级性的提高,单系统从4.8 m减小至1.7 m,双系统3.9 m减小至0.6 m;I、M类卫星单系统有微小改善,双系统分别提高29.8%、33.9%。法向精度单系统G、I、M类卫星均有微小提升,双系统分别改善54.7%、22.9%、25.6%。径向精度单系统I、M类卫星改善微弱,双系统分别改善17.2%、25.0%,G星精度稍有下降。
(4) 单、双系统加入GNOS均出现BDS卫星个别弧段定轨精度稍有下降情况,主要表现在径向G类卫星上。分析主要有如下几个原因(后文试验同样出现精度稍有下降情况,原因类似):
BDS目前尚处于区域系统服务能力阶段,对于星载观测数据要保证全弧段连续且充足的观测量较为困难。由第二部分内容可知,GNOS对BDS卫星观测有效卫星数大于等于四颗情况平均仅占11.54%,观测到零颗卫星的情况占27.1%。这意味着联合GNOS星地一体定轨时,由于观测量的限制无法对GNOS进行有效动力学建模并取得相当精度。BDS卫星对GNOS卫星可视弧段受限是造成精度下降的最主要原因。
目前BDS定轨的许多关键技术仍在研究中,北斗的整体定轨精度相比GPS仍有较大差距,包括3类卫星的光压模型、GEO卫星定轨精度较差等因素制约了低轨卫星的增强效果。
GNOS自身定轨精度限制,如GNOS的PCO使用的是出厂标定值、观测量丢失率较大等。
另外参与定轨试验的北斗卫星只有11颗,相对较少,这也是导致精度稍有下降的原因。
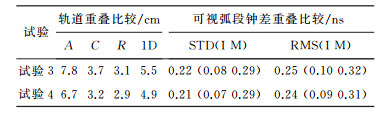
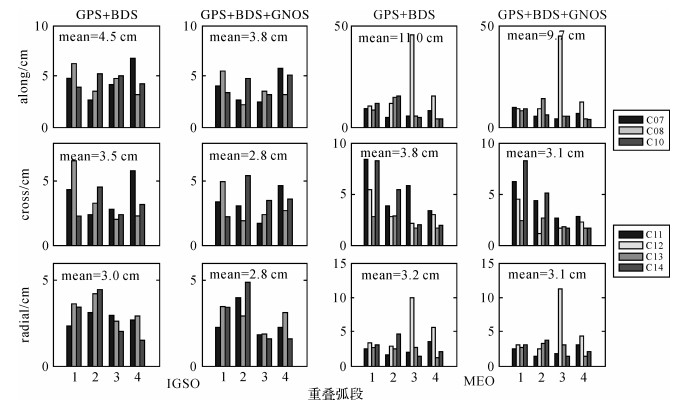
2.1.2 无GEO卫星试验由于北斗GEO卫星定轨精度较差,为进一步分析另外两类卫星的增强情况,并考虑到排除GEO卫星后总的BDS卫星个数较少,因此只进行双系统定轨增强试验。同样进行2.1.1节中的定轨试验3、4,但不包含GEO卫星,相关结果见图 4、表 5。
|
| 图 4 BDS各颗卫星3个方向重叠精度 Fig. 4 The orbit overlapping precision of BDS each satellite in three direction |
(1) 不添加GEO卫星情况下,两组试验轨道整体精度均提升明显,加入GNOS定轨精度提升11.6%。
(2) I类卫星A、C、R 3方向精度改善分别为16.3%、6.0%、7.3%,相应地M类卫星分别改善12.3%、17.3%、2.9%。比较2.1.1节中双系统I、M类卫星增强情况,不添加GEO卫星情况下GNOS的加入对轨道精度虽有一定改善,但幅度更小,其原因有待进一步分析讨论。
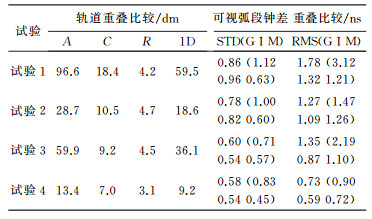
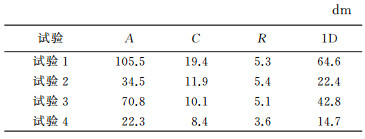
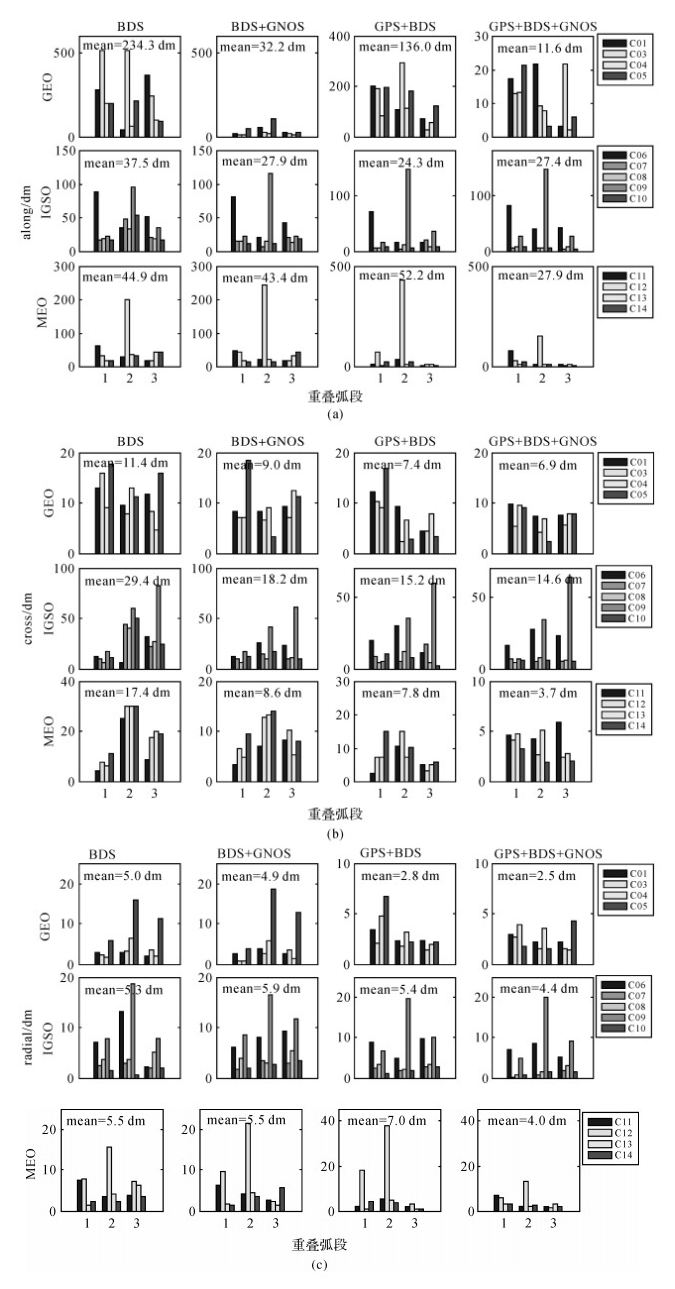
2.2 区域监测网增强试验及轨道预报为分析GNOS在区域测站布局情况下对BDS的增强效果,以期为BDS系统建设提供参考。选取BETS国内7个观测站组成区域监测网进行精密定轨增强试验,并对轨道作12 h的预报[26]。考虑到地面测站个数较少,因此除C02卫星以外,其他北斗卫星均参与试验。试验数据及相关定轨模型同上,但试验3、4不添加速度脉冲。限于篇幅,不绘出各颗卫星定轨结果,卫星轨道、可视弧段钟差重叠精度整体情况见表 6,各颗卫星各弧段3个方向轨道预报精度如图 5,轨道预报整体情况见表 7。分析图 5、表 6、表 7。
|
| 图 5 BDS各颗卫星3个方向预报重叠精度/dm Fig. 5 The orbit overlapping precision of BDS each satellite in three direction /dm |
(1) 单、双系统添加GNOS轨道1D RMS分别由5.95 m、3.61 m提升至1.86 m、0.92 m,分别提高72.9%、74.5%。轨道预报精度由6.46 m、4.28 m提升至2.24 m、1.47 m,分别提高65.3%、65.7%。钟差重叠精度STD改善不大,RMS分别由1.78 ns、1.35 ns提升至1.27 ns、0.73 ns,分别提高24.2%、45.9%。
(2) 单系统轨道预报精度切向G类卫星提升最显著,预报精度由10 m级下降至m级;其次是切向I类,法向I、M类卫星,均有接近1 m量级的提升;径向I类卫星存在精度稍有下降的情况。双系统轨道预报精度切向G类卫星提升最显著,预报精度由10 m级下降至m级;其次是M类卫星切向、法向、径向和I类卫星径向,均有dm~m量级的提升;切向I类卫星存在精度下降情况(C09正处于姿态模式切换时期)。
(3) 区域测站布局轨道精度改善G类卫星切向提升幅度最大,其次是法向和其他类型卫星切向,但相比全球测站试验改善程度更大。说明处于当前区域系统服务能力阶段的BDS,仍然是区域测站布局相比全球测站布局加入低轨卫星的增强效果更好。
(4) 钟差重叠精度G类卫星RMS值改善最为显著,单、双系统分别由3.12 ns、2.19 ns提升至1.47 ns、0.90 ns;I、M类卫星也有亚纳秒量级精度提升。
总结GNOS增强北斗区域星座时轨道精度改善提升的主要原因:
对于BDS GEO卫星,相较于地面测站,GNOS可极大增强GEO卫星的几何强度,从而显著提升北斗GEO卫星定轨精度。
考虑到目前BDS测站分布仍然是全球布设但并不均匀,低轨卫星的加入可显著增加地面测站无法跟踪到BDS卫星的弧段,从而整体提升北斗轨道精度。
由于低轨卫星的运行特点,相较于地面测站,GNOS对BDS卫星的观测特性具有较大差异,从而得到不同于地面测站的观测量。比如由于低轨卫星的高速运动,对北斗卫星轨道的切向、法向观测将比地面测站更加灵敏。
3 结束语本文针对搭载有GPS/BDS双模接收机的低轨卫星GNOS首先进行了星载观测数据统计及伪距测量精度分析。然后基于MGEX测站及BETS测站观测数据,在全球37个、区域7个地面测站布局情况下,进行有/无GNOS的BDS单系统、GPS/BDS双系统定轨试验。首次分析星地一体定轨策略下低轨卫星对BDS卫星轨道精度的增强效果。主要有以下结论:
(1) 受可视弧段及接收机通道限制GNOS观测的北斗卫星数据量较少,且相比海洋二号卫星部分观测量丢失率更大,但未对伪距测量精度产生影响,接近卫星标称精度0.3 m,且与地面测站相当。
(2) 全球测站情况下,GNOS主要对BDS GEO卫星切向精度提升显著,其次是法向和其他类型卫星切向;切向提升程度60%以上,法向双系统下达40%;单系统可视弧段钟差重叠精度改善微弱,双系统MEO卫星钟差RMS改善显著。
(3) 区域测站情况下,GNOS对GEO卫星轨道预报精度切向提升85%以上,其余方向及卫星有较大改善,平均改善幅度为21.7%,双系统下MEO卫星法向提升达53.3%;可视弧段钟差重叠精度RMS值三类卫星均改善显著,整体0.5 ns的改进。
致谢: 特别感谢IGS的MGEX项目以及武汉大学的BETS为本文提供数据。
| [1] | GUO Rui, HU Xiaogong, LIU Li, et al. Orbit Determination for Geostationary Satellites with the Combination of Transfer Ranging and Pseudorange Data[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(9): 1746–1754. DOI:10.1007/s11433-010-4092-0 |
| [2] | ZHOU Shanshi, HU Xiaogong, WU Bin, et al. Orbit Determination and Time Synchronization for a GEO/IGSO Satellite Navigation Constellation with Regional Tracking Network[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1089–1097. DOI:10.1007/s11433-011-4342-9 |
| [3] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the COMPASS/Beidou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211–222. DOI:10.1007/s10291-012-0272-x |
| [4] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–486. DOI:10.1007/s00190-013-0622-7 |
| [5] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515–525. DOI:10.1007/s00190-013-0625-4 |
| [6] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of Beidou Constellation Based on BETS and MGEX Network[J]. Scientific Reports, 2014(4): 4692. |
| [7] | 刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132–1138. LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellites System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132–1138. DOI:10.13485/j.cnki.11-2089.2014.0186 |
| [8] | GUO Rui, ZHOU Jianhua, HU Xiaogong, et al. Precise Orbit Determination and Rapid Orbit Recovery Supported by Time Synchronization[J]. Advances in Space Research, 2015, 55(12): 2889–2898. DOI:10.1016/j.asr.2015.03.001 |
| [9] | GUO Jing, CHEN Guo, ZHAO Qile, et al. Comparison of Solar Radiation Pressure Models for BDS IGSO and MEO Satellites with Emphasis on Improving Orbit Quality[J]. GPS Solutions, 2017, 21(2): 511–522. DOI:10.1007/s10291-016-0540-2 |
| [10] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of Beidou Constellation: Method Comparison[J]. GPS Solutions, 2016, 20(2): 259–268. DOI:10.1007/s10291-014-0436-y |
| [11] | RIM H J, SCHUTZ B E, ABUSALI P A M, et al. Effect of GPS Orbit Accuracy on GPS-determined TOPEX/Poseidon Orbit[C]//Proceedings of ION GPS-95. California: Palm Springs, 1995: 613-617. |
| [12] | ZHU Shengyuan, NEUMAYER K H, MASSMANN F H, et al. Impact of Different Data Combinations on the CHAMP Orbit Determination[M]//REIGBER C, LVHR H, SCHWINTZER P. First CHAMP Mission Results for Gravity, Magnetic and Atmospheric Studies. Berlin, Heidelberg: Springer, 2003: 92-97. |
| [13] | HUGENTOBLER U, JÄGGI A, SCHAER S, et al. Combined Processing of GPS Data from Ground Station and LEO Receivers in a Global Solution[C]//Proceedings of the International Association of Geodesy Symposia. Berlin, Heidelberg: Springer, 2003: 169-174. |
| [14] | KÖNIG R, REIGBER C, ZHU S Y. Dynamic Model Orbits and Earth System Parameters from Combined GPS and LEO Data[J]. Advances in Space Research, 2005, 36(3): 431–437. DOI:10.1016/j.asr.2005.03.064 |
| [15] | 匡翠林. 利用GPS非差数据精密确定低轨卫星轨道的理论及方法研究[D]. 武汉: 武汉大学, 2008: 30-33. KUANG Cuilin. Research on Precise Orbit Determination Theory and Methods of Lower Earth Orbit Satellites Using Zero-difference GPS Data[D]. Wuhan: Wuhan University, 2008: 30-33. |
| [16] | 刘伟平. 北斗卫星导航系统精密轨道确定方法研究[D]. 郑州: 解放军信息工程大学, 2014: 91-92. LIU Weiping. Research on Precise Orbit Determination of BeiDou Navigation Satellite System[D]. Zhengzhou: The PLA Information Engineering University, 2014: 91-92. |
| [17] | NARDO A, LI Bofeng, TEUNISSEN P J G. Partial Ambiguity Resolution for Ground and Space-Based Applications in a GPS+Galileo Scenario: A Simulation Study[J]. Advances in Space Research, 2016, 57(1): 30–45. DOI:10.1016/j.asr.2015.09.002 |
| [18] | ZOULIDA M, POLLET A, COULOT D, et al. Multi-technique combination of space geodesy observations: Impact of the Jason-2 satellite on the GPS satellite orbits estimation[J]. Advances in Space Research, 2016, 58(7): 1376–1389. DOI:10.1016/j.asr.2016.06.019 |
| [19] | BAI Weihua, SUN Yueqiang, DU Qifei, et al. An Introduction to the FY3 GNOS Instrument and Mountain-Top Tests[J]. Atmospheric Measurement Techniques, 2014, 7(6): 1817–1823. DOI:10.5194/amt-7-1817-2014 |
| [20] | ZHAO Qile, WANG Chen, GUO Jing, et al. Enhanced orbit determination for BeiDou satellites with FengYun-3C onboard GNSS data[J]. GPS Solutions, 2017. DOI:10.1007/s10291-017-0604-y |
| [21] | DE BAKKER P F, VAN DER MAREL H, TIBERIUS C C J M. Geometry-Free Undifferenced, Single and Double Differenced Analysis of Single Frequency GPS, EGNOS and GIOVE-A/B Measurements[J]. GPS Solutions, 2009, 13(4): 305–314. DOI:10.1007/s10291-009-0123-6 |
| [22] | DE BAKKER P F. On User Algorithms for GNSS Precise Point Positioning[D]. Netherlands: Delft University of Technology, 2016: 118-145. |
| [23] | 赵齐乐, 戴志强, 孙宾姿, 等. 方差分量估计分析北斗伪距信号精度[J]. 测绘科学, 2016, 41(2): 182–186. ZHAO Qile, DAI Zhiqiang, SUN Binzi, et al. Analysis of BDS Pseudorange Accuracy and Time Correlation Using the Least-Squares Variance Component Estimation Method[J]. Science of Surveying and Mapping, 2016, 41(2): 182–186. |
| [24] | 刘伟平, 郝金明, 田英国, 等. 北斗卫星导航系统双差动力法精密定轨及其精度分析[J]. 测绘学报, 2016, 45(2): 131–139. LIU Weiping, HAO Jinming, TIAN Yingguo, et al. Solution Method and Precision Analysis of Double-difference Dynamic Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 131–139. DOI:10.11947/j.AGCS.2016.20150190 |
| [25] | CERRI L, BERTHIAS J P, BERTIGER W I, et al. Precision Orbit Determination Standards for the Jason Series of Altimeter Missions[J]. Marine Geodesy, 2010, 33(S1): 379–418. |
| [26] | 周善石, 胡小工, 吴斌. 区域监测网精密定轨与轨道预报精度分析[J]. 中国科学:物理学力学天文学, 2010, 53(6): 1130–1138. ZHOU Shanshi, HU Xiaogong, WU Bin. Orbit Determination and Prediction Accuracy Analysis for A Regional Tracking Network[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(6): 1130–1138. |