2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079;
3. 桂林理工大学广西空间信息与测绘重点实验室, 广西 桂林 541006
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China;
3. Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin University of Technology, Guilin 541006, China
随着空间技术的不断发展,GNSS技术实现了全球平面位置基准统一,其测定的平面位置,即地面点大地经度和纬度,能直接应用于地理信息系统、工程建设和国防建设,可满足测绘、地球科学等学科和行业的需求。但GNSS技术并未解决全球高程基准统一问题,GNSS定位技术提供的高程是相对于参考椭球面的高度,即大地高h,是地球空间的几何高度,不含重力位信息。而地形图标示的高程和工程建设所需的高程信息,是与大地水准面或似大地水准面对应的正高H或正常高H*。正高或正常高是工程建设必需的基础信息,在长距离、跨境跨国大型工程建设中,需要统一的高程信息,才能确保工程项目联合施工作业与对接。例如我国南水北调工程、中俄油气输送管网工程以及计划中的欧亚高铁、中俄加美高铁。因此实现全球高程基准与区域高程基准的统一,对相关跨国工程建设开展国际合作有重要意义。目前,实现全球高程基准与区域高程的统一,主要方法是确定全球各国家或地区现行局部高程基准面与全球大地水准面之间的重力位差[1-4],从而获得两者之间的高程差。全球大地水准面是全球高程基准最适宜的参考面,全球大地水准面重力位通常采用2010年国际地球自转服务(The International Earth Rotation and Reference Systems Service, IERS)公布的62 636 856.0 m2s-2[5]。局部或区域现行高程基准重力位的确定依据各地区的实际情况采取不同的方法。例如美国、加拿大等区域的高程基准由多验潮站观测的长时间平均海面确定,且拥有可实用的、精度较高的局部大地水准面模型,可以利用沿海多个验潮站数据、海洋数据、GNSS/水准数据以及大地水准面模型确定该区域高程基准重力位[6-9]。而希腊、中国等地区是依据单验潮站观测的长时间平均海面确定高程基准,采用的平均海面只是某一区域的平均海面,其中中国1985国家高程基准所依据的黄海平均海面是采用青岛验潮站1952—1979年共28年的验潮数据,并用中数法的计算值推算出来的。因此不能利用多个沿海验潮站数据和海洋数据确定大陆沿海区域平均海面重力位作为该区域高程基准重力位,通常只能联合重力场模型和GNSS/水准数据确定高程基准重力位[10-11]。
随着新一代卫星重力探测计划CHAMP(Challenging Mini-satellite Payload)、GRACE(Gravity Recovery and Climate Experiment)、GOCE(Gravity and Ocean Circulation Explorer)的实施,使得利用卫星数据获得的重力场模型精度有了明显提升。其中GRACE和GOCE卫星数据对确定重力场模型中长波部分具有重要贡献,GRACE卫星采用高-低(satellite to satellite tracking in the high-low model, SST-hl)和低-低(satellite to satellite tracking in the low-low model, SST-ll)卫星跟踪卫星观测方式,其中SST-ll观测模式可观测重力位二阶导数,弥补了高-低卫星跟踪卫星观测模式对沿轨重力变化不敏感和不能提供近轨空间重力场精细结构信息的不足,大幅度提高重力场中长波部分的精度[12-14]。GRACE计划主要用于探测重力场的中长波分量及其随时间的变化,因此,基于GRACE数据可确定高时间分辨率的重力场模型,但空间分辨率只有100~200 km(半波长)。GOCE卫星是第一颗装载卫星重力梯度仪直接测定引力位二阶导数的低轨重力卫星,重力梯度数据在一定程度上弥补了重力信号随卫星高度增加而衰减带来的影响。除此之外, GOCE卫星还可以对卫星进行三维空间内的连续跟踪;对大气阻力、辐射压力等非保守力进行连续补偿,使得观测不受作用在卫星上的保守力的影响;轨道较低可以感应更强的重力场信号。因此,基于GOCE卫星数据恢复重力场的能力大大提高,尤其是恢复中、高频部分重力场信息的能力,空间分辨率达100 km(半波长)[15-16]。因此,利用GRACE/GOCE卫星重力场模型,可以提高确定局部高程基准重力位和(似)大地水准面的精度[17-19]。
基于GRACE/GOCE卫星数据反演的重力场模型中、长波部分精度高,但短波部分还需要局部地形数据或地面重力数据的补充和完善。当前的超高阶重力场模型(例如EGM2008) 使用了大量的局部重力数据,能有效的表示短波信息,但长波精度略低于最新的卫星重力场模型。为此,本论文联合卫星重力场模型的中长波信息和EGM2008模型的短波信息,利用EGM2008模型高阶次球谐系数扩展GRACE/GOCE卫星重力场模型,利用组合模型确定的我国高程基准重力位与文献[20-21]确定的重力位结果一致。
1 理论部分我国采用的高程基准为1985国家高程基准,是由青岛验潮站1952—1979年观测的黄海平均海面利用移动平均处理得到,属于局部高程基准。我国高程采用正常高,对应的参考面为似大地水准面,似大地水准面是地面点沿正常重力线量取的正常高所得端点构成的闭合曲面,可以由Molodensky理论确定,代表了地面扰动位大小。但似大地水准面并不是重力等位面,对应的正常高没有明确的物理意义。但大地水准面不同于似大地水准面,它不仅是与全球平均海面最佳密合的重力等位面,且具有明确的几何物理意义,求取局部区域的高程基准重力位时,计算的重力位应为局部区域高程基准对应局部大地水准面的重力位,因此,利用重力场模型和GPS/水准数据计算的我国高程基准面重力位时,应将GPS/水准数获得的高程异常ζ转化为大地水准面高N,实现似大地水准面到大地水准面的转换,从而确定我国高程基准重力位W0LVD。
1.1 似大地水准面与大地水准面的转换地面任一点P的大地高hP与该点的正高HP和8正常高HP*之间的关系如下
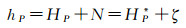 (1)
(1)
由此得大地水准面起伏N与高程异常ζ之间的关系为
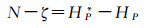 (2)
(2)
依据正高与正常高的定义可知
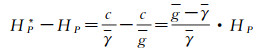 (3)
(3)
式中,c为地面点P与起始大地水准面之间的位能差;g为地面点P沿重力线到大地水准面之间的平均重力值;γ为似地形面Σ上与P点对应的Q点沿正常重力线到正常椭球面之间的平均正常重力值。由似大地水准面转换为大地水准面的主要困难是难以严密求出g,它涉及地球内部密度问题,一般采用近似计算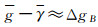
GPS/水准数据可获得地面点高程异常ζ,将高程异常ζ转化为对应的大地水准面高N,同时利用重力场模型也可以确定该点大地水准面高NGGM,但两者对应的高程基准面不同,前者对应的参考面为局部高程基准面,由局部平均海面确定,而后者对应的参考面为全球大地水准面,全球大地水准面与局部平均海面存在差异,该差异称之为局部高程基准与全球高程基准之间的垂直偏差,从而得到两者之间的重力位差。已知大地水准面重力位W0取2010年IERS公布的数值:W0=62 636 856.000 0 m2s-2,则我国高程基准重力位W0LVD为
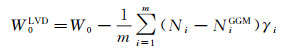 (4)
(4)
利用重力场模型确定的大地水准面高为
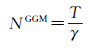 (5)
(5)
该式成立的前提条件是参考水准椭球与大地水准面有同样的位W0=U0,且参考水准椭球与地球有同样的质量M=M0,否则, T和N要分别加常数T0、N0[22]
 (6)
(6)
本文参考水准椭球选取为WGS-84,对应的地心引力位常数GM与正常重力位U0分别为:GM=3 986 004.415×108 m3s-2, U0=62 636 851.714 6 m2s-2;重力场模型地心引力常数GM0=3 986 004.418×108 m3s-2,大地水准面重力位W0=62 636 856.0 m2s-2,椭球半径R为参考椭球WGS-84平均半径R=6 378 137 m,由此确定的N0为-0.442 1 m。
GRACE、GOCE卫星数据对重力场模型中长波部分贡献突出,但GRACE/GOCE重力场模型最高阶次有限,为提高高阶项对确定大地水准面高的贡献,本文采用高阶重力场模型EGM2008扩展GRACE/GOCE重力场模型,使组合后的重力场模型不仅满足高精度的低阶项,同时拥有超高阶次的优势。利用组合后的重力场模型确定的大地水准面高NEGM为
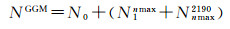 (7)
(7)
利用超高阶重力场模型EGM2008扩展GRACE/GOCE重力场模型时需要考虑模型之间参数的一致性,基于公式(8) 统一两重力场模型参数[23]
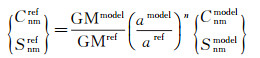 (8)
(8)
利用重力场模型计算地面点大地水准面高NEGM与GPS/水准数据确定的地面点大地水准面高N参考框架不统一,利用上式将组合后的重力场模型位系数转换到WGS-84椭球上,最终将重力场模型和GPS数据统一到同一参考框架下。
本文重力场模型采用的潮汐系统为无潮汐系统(tide free),而GPS/水准数据采用的潮汐系统为平均潮汐系统(mean tide),利用公式(9) 将GPS/水准数据潮汐系统统一到平均潮汐系统,单位为m
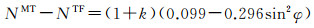 (9)
(9)
式中,k表示地球形变造成的附加潮与平衡潮高度之比,称为勒夫数,一般取0.3,经过上述一系列的改正后,利用公式(4) 确定的我国高程基准重力位W0LVD。
重力场模型不同潮汐系统的准换,只与C20项有关,基于公式(10) 将重力场模型统一到平均潮汐系统[23],单位为m
 (10)
(10)
式中,k=0.3;重力场模型地心引力常数GM,半径r取值均采用ICEGM网站提供的数据;a为WGS-84参考椭球长半轴a=6 378 137 m。具体数值如表 1所示。
2 计算结果及分析
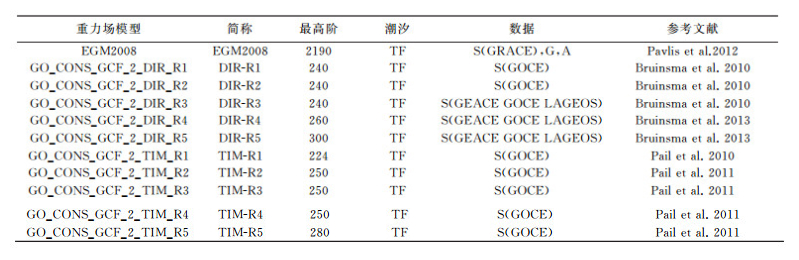
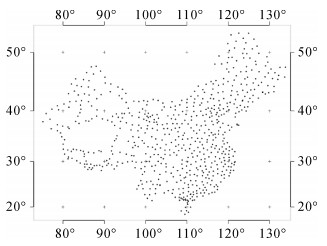
本文联合地球重力场模型(如表 2所示[24-28])和我国均匀分布的649个GPS/水准数据(如图 1所示)基于公式(4) 确定我国1985国家高程基准的重力位W0LVD。
|
| 图 1 GPS/水准数据分地理布图 Fig. 1 Geographical distribution of GPS/levelling benchmarks in China |
随着重力卫星计划的实施,目前可以提供高精度全球重力场模型,对应大地水准面精度也不断提高。其中,GRACE卫星可以更加有效地恢复重力场的中长波部分。GRACE卫星采用SST-ll观测模式,观测数据为重力位的二阶导数,不同于观测数据为低轨卫星处重力位的一阶导的CHAMP卫星,很好地克服了CHAMP卫星的不足,大幅度提高中、长波重力场精度;GOCE卫星不仅克服了CHAMP卫星的不足,还添加了无阻尼控制系统和卫星梯度测量系统SGG(Satellite Gravity Gradiometry),无阻尼控制系统可以很好地补偿大气阻力,卫星梯度测量系统,可以提供高精度地球重力场高频信号,最终提供高精度、高分辨率的地球重力场和大地水准面模型。且GOCE卫星的任务之一为提供分辨率达100 km,精度为1~2 cm的全球大地水准面模型,从而实现全球高程基准统一。因此本文采用纯GOCE或GRACE/GOCE联合重力场模型确定我国高程基准重力位。
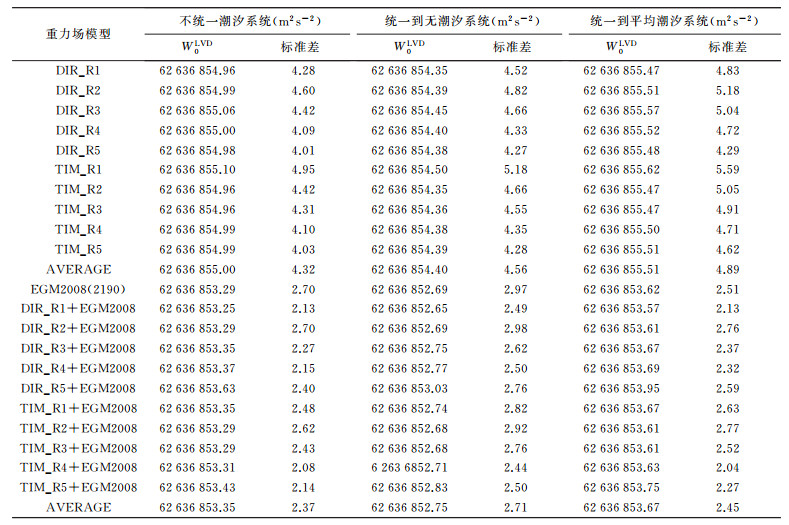
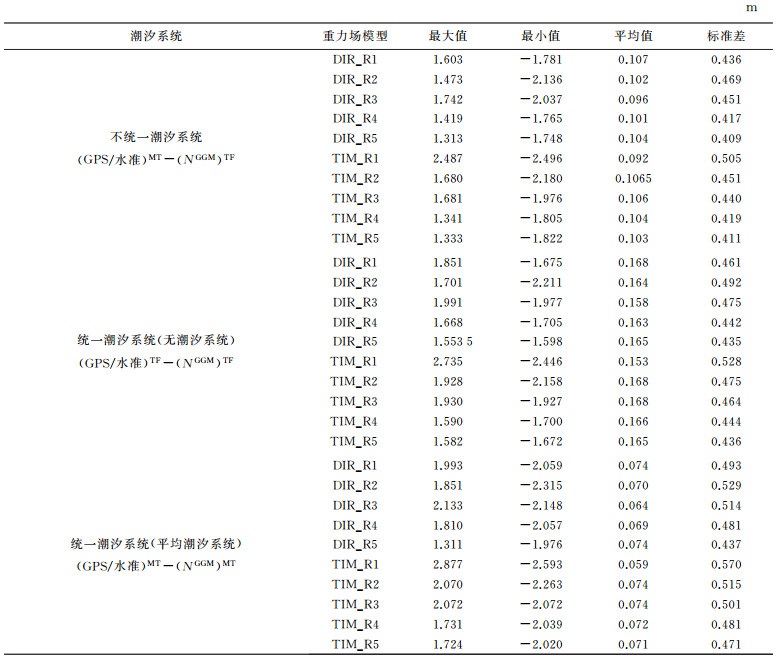
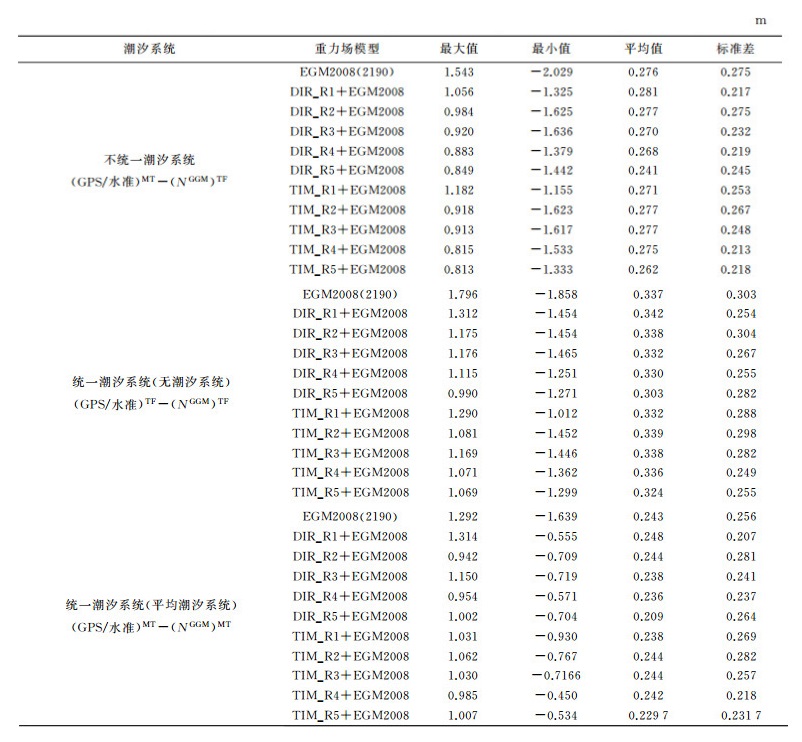
表 3为利用GPS/水准数据确定的大地水准面与GRACE/GOCE重力场模型确定的大地水准面之间的差异,表 3从上到下一共3组数据,第1组数据为没有统一潮汐系统计算的结果,即重力场模型和GPS/水准数据分别采用无潮汐和平均潮汐系统;第2组计算结果为将GPS/水准数据和重力场模型统一到平均潮汐系统;第3组计算结果为将GPS/水准数据和重力场模型统一到无潮汐系统。计算结果显示将两者潮汐系统统一到无潮汐系统时,潮汐系统对确定大地水准面高在我国区域内的影响约为6 cm,而将两者潮汐系统统一到平均潮汐系统时,潮汐系统对确定大地水准面高在我国区域内的影响约为4 cm,此时假设GPS/水准数据获得的大地水准面高无误差,表 4中同样可以得到同样的结果。本文采用基于GRACE/GOCE卫星数据反演的重力场模型中、长波部分精度高,但短波部分还需要局部地形数据或地面重力数据的补充和完善,当前的超高阶重力场模型(例如EGM2008) 使用了大量的局部重力数据,能有效的表示短波信息,但长波精度略低于最新的卫星重力场模型。GPS/水准数据获得的大地水准面高包含全波段信息,因此联合GPS/水准数据与重力场模型确定重力位时需考虑重力场模型的截断误差。因此本文利用超高阶重力场模型EGM2008扩展GRACE/GOCE重力场模型至2190阶,此时已将EGM2008模型与GRACE/GOCE重力场模型参数统一,表 4为计算结果。从表 4中可以看出重力场模型截断误差对确定大地水准面高的影响约为16 cm,同时考虑重力场模型截断误差后确定的大地水准面高精度提高约20 cm。因此在确定我国区域大地水准面高时需考虑重力场模型截断误差的影响,利用超高阶重力场模型计算更为合理。
|
|
利用组合重力场模型计算的结果显示,除利用EGM2008模型扩张DIR_R2模型后计算的结果精度低于EGM2008模型,其他组合模型计算的结果精度均高于EGM2008模型计算的结果,说明利用EGM2008模型扩展GRACE/GOCE重力场模至2190阶后不仅弥补了GRACE/GOCE重力场模阶次受限的劣势,同时保证了组合模型低阶项的精度。因此利用组合模型确定的大地水准面精度不仅优于GRACE/GOCE重力场模,同时优于EGM2008取2190阶计算的结果。
表 5为利用GRACE/GOCE重力场模型和组合重力场模型确定的我国1985国家高程基准重力位,将GPS/水准数据与重力场模型潮汐系统统一到平均潮汐系统后,利用GRACE/GOCE重力场模型确定的我国1985国家高程基准重力位均值为62 636 855.51 m2s-2;利用组合重力场模型确定的我国1985国家高程基准重力位均值为62 636 853.67 m2s-2。将GPS/水准数据与重力场模型潮汐系统统一到无潮汐系统后,利用GRACE/GOCE重力场模型确定的我国1985国家高程基准重力位均值为62 636 854.40 m2s-2。利用组合重力场模型确定的我国1985国家高程基准重力位均值为62 636 852.75 m2s-2。其中利用EGM2008模型扩展TIM_R4模型至2190阶后建立的组合模型确定的我国1985国家高程基准重力位精度最高。
我国高程基准面是由青岛验潮站测得的黄海平均海面定义,利用重力场模型和海面高模型可确定平均海面重力位,利用重力场模型EGM2008和海面高模型DTU13_MSS计算的黄海海域(35°N—45°N, 120°E—123°E)平均海面重力位分别为62 636 852.71±1.83 m2s-2(无潮汐系统),62 636 853.55±1.83 m2s-2(平均潮汐系统)。本文组合模型TIM_R4+EGM2008计算的我国1985国家高程基准重力位精度最高,利用该组合模型和DTU13_MSS模型计算的黄海海域平均海面重力位为62 636 852.73±1.55 m2s-2(无潮汐系统),62 636 853.56±1.52 m2s-2(平均潮汐系统)。与本文利用重力场模型和GPS/水准数据计算的结果一致,由此验证本文计算结果的合理性。
3 总结GRACE和GOCE卫星数据对确定重力场模型的中、长波部分具有重要贡献,大幅度提高中、长波重力场精度,相应重力场模型计算的大地水准面精度明显提高,因此本文采用的重力场模型为纯GOCE模型或GRACE/GOCE联合模型。
我国采用的高程是正常高,对应的参考面为似大地水准面,似大地水准面是非等位面。因此,利用GPS、水准数据和重力场模型确定我国1985国家高程基准重力位时应先将我国似大地水准面转化为相应的大地水准面,此时确定的我国1985国家高程基准重力位为62 636 854.395 3 m2s-2。
基于GRACE/GOCE卫星数据建立的重力场模型中长波部分精度较高,但分辨率有限。为获得可靠的重力位结果,需要考虑重力场模型截断误差对重力位的影响。本文利用超高阶重力场模型EGM2008扩展GRACE/GOCE重力场模型至2190阶,组合重力场模型时将不同模型参数统一,利用扩展后的重力场模型确定的我国1985国家高程基准重力位为62 636 852.75 m2s-2,其中利用EGM2008模型扩展TIM_R4模型计算的结果精度最高。重力场模型截断误差对确定我国高程基准重力位的影响约为1.6 m2s-2(~16 cm)。
本文利用的重力场模型采用的潮汐系统为无潮汐系统,而GPS数据采用的是平均潮汐系统,是否统一潮汐系统对确定我国大地水准面高存在一定影响,其中将两者潮汐系统统一到无潮汐系统时,潮汐系统对确定我国大地水准面高的影响约为6 cm,对确定我国1985国家高程基准重力位的影响约为0.6 m2s-2;将潮汐系统统一到平均潮汐系统时,潮汐系统对确定我国大地水准面高的影响约为4 cm,对确定我国1985国家高程基准重力位的影响约为0.4 m2s-2。
统一潮汐系统后,利用EGM2008模型扩展TIM_R4模型至2190阶确定的我国高程基准重力位值62 636 852.71 m2s-2(无潮汐系统),62 636 853.63 m2s-2(平均潮汐系统)精度最高,本文将该值作为我国高程基准重力位,并利用确定我国高程基准的黄海平均海面重力位值进行验证,验证结果显示两者计算结果一致。
| [1] | TOCHO C, VERGOS G S. Estimation of the Geopotential Value W0 for the Local Vertical Datum of Argentina Using EGM2008 and GPS/Levelling Data W0LVD[C]//International Association of Geodesy Symposia. Cham, Germany: Springer, 2015, 143: 271-279. |
| [2] | VERGOS G S, ANDRITSANOS V D, GRIGORIADIS V N, et al. Evaluation of GOCE/GRACE GGMs Over Attica and Thessaloniki, Greece, and Wo Determination for Height System Unification[C]//International Association of Geodesy Symposia. Cham, Germany: Springer, 2015, 144: 101-109. |
| [3] | BARZAGHI R, CARRION D, REGUZZONI M, et al. A Feasibility Study on the Unification of the Italian Height Systems Using GNSS-leveling Data and Global Satellite Gravity Models[M]//RIZOS C, WILLIS P. IAG 150 Years. Berlin Heidelberg, Germany: Springer, 2015. |
| [4] | KOTSAKIS C, KATSAMBALOS K, AMPATZIDIS D. Estimation of the Zero-height Geopotential Level WoLVD in A Local Vertical Datum from Inversion of Co-located GPS, Leveling and Geoid Heights: A Case Study in the Hellenic Islands[J]. Journal of Geodesy, 2012, 86(6): 423–439. DOI:10.1007/s00190-011-0530-7 |
| [5] | SÁNCHEZ L, DAYOUB N, ČUNDERLÍK R, et al. W0 Estimates in the Frame of the GGOS Working Group on Vertical Datum Standardisation[C]//International Association of Geodesy Symposia. Cham, Germany: Springer, 2014, 141: 203-210. |
| [6] | HAYDEN T, RANGELOVA E, SIDERIS M G, et al. Evaluation of W0 in Canada Using Tide Gauges and GOCE Gravity Field Models[J]. Journal of Geodetic Science, 2012, 2(4): 290–301. |
| [7] | HAYDEN T, AMJADIPARVAR B, RANGELOVA E, et al. Estimating Canadian Vertical Datum Offsets Using GNSS/Levelling Benchmark Information and GOCE Global Geopotential Models[J]. Journal of Geodetic Science, 2012, 2(4): 257–269. |
| [8] | WOODWORTH P L, HUGHES C W, BINGHAM R J, et al. Towards Worldwide Height System Unification Using Ocean Information[J]. Journal of Geodetic Science, 2012, 2(4): 302–318. |
| [9] | RÜLKE A, LIEBSCH G, SACHER M, et al. Unification of European Height System Realizations[J]. Journal of Geodetic Science, 2012, 2(4): 343–354. |
| [10] | 翟振和, 魏子卿, 吴富梅, 等. 利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差[J]. 大地测量与地球动力学, 2011, 31(4): 116–118. ZHAI Zhenhe, WEI Ziqing, WU Fumei, et al. Computation of Vertical Deviation of Chinese Height Datum from Geoid By Using EGM2008[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 116–118. |
| [11] | GRIGORIADIS V N, KOTSAKIS C, TZIAVOS I N, et al. Estimation of the Reference Geopotential Value for the Local Vertical Datum of Continental Greece Using EGM08 and GPS/Leveling Data[C]//International Association of Geodesy Symposia. Cham, Germany: Springer, 2014, 141: 249-255. |
| [12] | 周旭华, 许厚泽, 吴斌, 等. 用GRACE卫星跟踪数据反演地球重力场[J]. 地球物理学报, 2006, 49(3): 718–723. ZHOU Xuhua, XU Houze, WU Bin, et al. Earth's Gravity Field Derived from GRACE Satellite Tracking Data[J]. Chinese Journal of Geophysics, 2006, 49(3): 718–723. |
| [13] | 邹贤才, 李建成. 单加速度计模式下的GOCE卫星重力场建模方法研究[J]. 地球物理学报, 2016, 59(4): 1260–1266. ZOU Xiancai, LI Jiancheng. Study on the Earth Gravity Modeling by GOCE in Individual Accelerometer Mode[J]. Chinese Journal of Geophysics, 2016, 59(4): 1260–1266. DOI:10.6038/cjg20160408 |
| [14] | 钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉: 武汉大学, 2010. ZHONG Bo. Study on the Determination of the Earth's Gravity Field from Satellite Gravimetry Mission GOCE[D]. Wuhan, China: Wuhan University, 2010. |
| [15] | 宁津生, 王正涛, 超能芳. 国际新一代卫星重力探测计划研究现状与进展[J]. 武汉大学学报(信息科学版), 2016, 41(1): 1–8. NING Jinsheng, WANG Zhengtao, CHAO Nengfang. Research Status and Progress in International Next-generation Satellite Gravity Measurement Missions[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 1–8. |
| [16] | RUMMEL R. Height Unification Using GOCE[J]. Journal of Geodetic Science, 2012, 2(4): 355–362. |
| [17] | ČUNDERLíK R, MINARECHOVÁ Z, MIKULA K. Realization of WHS Based on the Static Gravity Field Observed By GOCE[M]//MARTI U. Gravity, Geoid and Height Systems. Cham, Germany: Springer, 2014. |
| [18] | GRUBER T, GERLACH C, HAAGMANS R. Intercontinental Height Datum Connection with GOCE and GPS-Levelling Data[J]. Journal of Geodetic Science, 2012, 2(4): 270–280. |
| [19] | GODAH W, KRYNSKI J. A New Gravimetric Geoid Model for the Area of Sudan Using the Least Squares Collocation and a GOCE-Based GGM[C]//International Association of Geodesy Symposia. Cham, Germany: Springer, 2015. |
| [20] | 焦文海, 魏子卿, 马欣, 等. 1985国家高程基准相对于大地水准面的垂直偏差[J]. 测绘学报, 2002, 31(3): 196–200. JIAO Wenhai, WEI Ziqing, MA Xin, et al. The Origin Vertical Shift of National Height Datum 1985 with Respect to the Geoidal Surface[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 196–200. DOI:10.3321/j.issn:1001-1595.2002.03.003 |
| [21] | 郭海荣, 焦文海, 杨元喜. 1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[J]. 测绘学报, 2004, 33(2): 100–104. GUO Hairong, JIAO Wenhai, YANG Yuanxi. The Systematic Difference and Its Distribution Between the 1985 National Height Datum and the Global Quasigeoid[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 100–104. DOI:10.3321/j.issn:1001-1595.2004.02.002 |
| [22] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco, California: Freeman, 1967. |
| [23] | BARTHELMES F. Definition of Functionals of the Geopotential and Their Calculation from Spherical Harmonic Models. Theory and Formulas Used By the Calculation Service of the International Centre for Global Earth Models (ICGEM)[EB/OL]. http://gfzpublic.gfz-potsdam.de/pubman/faces/viewItemOverviewPage.jsp?itemId=escidoc:8786. |
| [24] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008)[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4): B04406. |
| [25] | BRUINSMA S L, MARTY J C, BALMINO G, et al. GOCE Gravity Field Recovery By Means of the Direct Numerical Method[C]//Proceedings at the ESA Living Planet Symposium. Bergen, Norway: ESA, 2010. |
| [26] | BRUINSMA S L, FÖRSTE C, ABRIKOSOV O, et al. The New ESA Satellite-Only Gravity Field Model Via the Direct Approach[J]. Geophysical Research Letters, 2013, 40(14): 3607–3612. DOI:10.1002/grl.50716 |
| [27] | PAIL R, GOIGINGER H, MAYRHOFER R, et al. GOCE Gravity Field Model Derived from Orbit and Gradiometry Data Applying the Time-Wise Method[C]//Proceedings at the ESA Living Planet Symposium 2010. Bergen, Norway: ESA, 2010. |
| [28] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived By Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11): 819–843. DOI:10.1007/s00190-011-0467-x |