2. 海军大连舰艇学院海洋测绘工程军队重点实验室, 辽宁 大连 116018;
3. 海军出版社, 天津 300450;
4. 92403部队, 福建 福州 350501
2. Key Laboratory of Hydrographic Surveying and Mapping of PLA, Dalian Naval Academy, Dalian 116018, China;
3. Navy Press, Tianjin 300450, China;
4. 92403 Troop, Fuzhou 350501, China
数字水深模型(digital depth model,DDM)是反映水深变化的数字化模型,也是用深度表达海底基本地貌特征的一种常用三维数字模型[1]。按照数据结构的不同,DDM可分为规则格网DDM和不规则格网DDM。本文所指DDM为规则格网DDM,并简称为DDM。作为海洋地理空间信息框架的基本内容和其他各种相关信息的载体,DDM不但是保证舰船海上航行安全的主要信息源之一,而且也是进行海洋地学研究和海上工程建设、考古活动等的重要信息平台[1-2]。随着我国数字海洋等海洋环境工程建设的发展,DDM的应用领域日益扩大,从而导致了对多尺度DDM的需求。受技术制约,长期以来主要采用重复数字化的方法来建立不同尺度的DDM。这种方法耗资巨大、效率低,不但数据采集与建库工作繁重,且数据不稳定[3-6]。尽管高密度多波束测深技术的应用为DDM精细化建模提供了良好的数据基础,且相关水深测量数据处理软件(如CARIS HIPS等)也提供了多种可实现海量测深数据滤波与抽稀的算法,但DDM的多尺度表达不完全等同于同一数据源不同分辨率的数据导出,还需结合DDM应用领域的特殊需求[1, 7-10]。
等深线作为数字水深模型可视化表达的一种重要形式,其与DDM的多尺度表达具有相同的约束原则[1, 8, 19]。因而现有的DDM多尺度表达算法大都是对二维等深线图形综合算法的三维扩展。比较典型的有点面距法、滤波法、三维Douglas-Peucker法、分形法、小波变换法等化简算法[5-6, 11-13]。这些算法都是从DDM的几何特性出发,通过删除DDM上的某些格网点而同时保留特征点来进行化简的。然而DDM综合不是一个简单格网点取舍的几何操作过程,应充分考虑DDM的地理特征和尺度特性,维护其空间认知与抽象程度的一致性[4, 14-15]。近年来,由于二维双向缓冲区变换(正向滚动圆变换)对平面线要素几何特征具有严密的定量调控特性,已被广泛应用于等深线等线要素的制图综合中[16-20]。文献[21]提出了基于正向滚动圆变换的等深线形状化简算法,可充分顾及等深线综合中的“安全性”原则,保留等深线中具有航海意义的凸部特征点,并依据阈值(缓冲距)大小对各类凹部特征点进行合理移位,实现对等深线的多尺度表达。文献[22]进一步对正向滚动圆变换的应用范围进行了扩展,研究了基于正向滚动圆变换的海图多要素自动制图综合方法。针对新一代电子海图对于航海表面(navigation surface, NS)的应用需求,文献[1, 21]通过对二维双向缓冲区变换的维数扩展,提出了三维双向缓冲区变换(正向滚动球变换)的概念,并将其应用于DDM的制图综合,通过保留DDM中浅点水深初步实现了航海表面的自动构建。文献[23]结合尺度因子的概念分析了三维正向滚动球变换的尺度依赖特性,提出了DDM多尺度表达的正向滚动球变换算法,从保障舰船海上航行安全的角度实现了综合尺度严密可控的DDM多尺度表达[23]。
然而,等深线(DDM)的应用领域并不局限于舰船海上航行的安全保障,对于海洋地学研究和海上工程建设、考古活动等应用领域,更为关注的是海底地形的真实性[1, 7-10, 23]。相比于DDM,数字高程模型(DEM)的精度及地形保真度的研究较为深入。文献[24]研究了DEM地形描述误差的成因、影响因素、量测方法及误差的数学模拟途径。文献[25]对DEM地形描述精度作了进一步的细化研究,定量分析了地形描述误差(均方差)与空间分辨率、平均剖面曲率、坡度的函数关系。文献[26]首次在地形形态层面构建了高保真DEM的基本概念,指出了DEM高保真的关键在于对原有对象高程序列的有效维护。文献[27]分析了DEM地形模拟失真的5类现象,指出了高保真DEM应能准确描述地形的宏观地貌特征与局地形态信息、有效维护地形的三维有序系统以及可正确恢复原始地形的三维形态。
上述研究为高保真DDM多尺度表达提供了建模思路与评价方法:即顾及“保真性”原则的DDM多尺度表达采用的模型和方法需有效区分和识别DDM中的骨架和细部地貌、维护水深的严密有序性及不同尺度下地形信息的等级嵌套性,并以DDM地形描述不确定度对DDM多尺度表达的真实性进行定量评估。为此,本文针对航海以外各相关领域对不同尺度DDM的应用需求,在分析DDM滚动球变换原理实质的基础上,利用DDM双向滚动球变换结合尺度因子对海底地貌进行定量分析,并顾及DDM格网点起伏程度的统计特性,建立DDM多尺度表达中细部(骨架)地貌的判定准则。在此基础上,通过对给定尺度下的细部地貌进行DDM双向滚动球变换的等距离面提取,以及不同尺度下地形信息等级单元逻辑包含关系的分析论证,提出一种符合“保真性”要求的基于双向滚动球变换的DDM多尺度表达算法。
1 DDM正向滚动球变换存在问题分析参照文献[4, 15, 27-28]关于高保真DEM多尺度表达评价标准,可以将顾及“保真性”原则的DDM多尺度表达评价标准归纳为水深值的准确性、严密有序性及不同尺度下地形信息的等级嵌套性。此处,水深值的准确性主要针对DDM中的骨架地貌而言,即通过保留一定尺度下DDM中骨架地貌,以保持海底地形的整体变化趋势[1, 4, 15];水深值的严密有序性则是针对DDM中的细部地貌而言,即在保留DDM中骨架地貌的基础上,通过维护DDM中细部地貌的相对高度以实现海底地形局部起伏形态的保持[1, 4, 28];而不同尺度下地形信息的等级嵌套性,实质上就是要求多尺度变换过程不破坏原始DDM地形信息等级单元的逻辑包含关系,从而保证DDM多尺度表达的准确稳定性及逆向还原的正确有效性[27, 29-30]。
文献[23]通过对DDM正向滚动球变换中尺度因子λ与原始DDM格网单元大小ξ逻辑相关性的分析与论证,已揭示了不同尺度下DDM地形信息等级单元的层次结构关系,可保证地形信息等级(层次)单元逻辑包含关系的一致性[1, 23]。然而高保真DDM的多尺度表达还需进一步确保多尺度表达的水深值准确性和严密有序性。文献[4]指出,实现DDM多尺度表达的水深值准确性和严密有序性的关键在于有效区分DDM中骨架地貌与细部地貌。而DDM中对于骨架地貌与细部地貌的区分除了考虑海底地貌的横向分布范围(长度和宽度)外,还需进一步考虑其纵向分布高度(矢高)。DDM正向滚动球变换中尺度因子由于仅从横向分布范围对海底地貌进行了限定(负向地貌的凹部长度、宽度小于等于2λξ)[1, 23],无法有效区分DDM中骨架地貌与细部地貌,使得DDM中纵向分布高度不同的负向地貌由于其横向分布范围相同而进行了同样的填平处理,无法满足DDM多尺度表达中对海底骨架地貌水深值准确性的要求。
此外,由于海底地貌纵向分布的相对高度在一定程度上反映了DDM中海底地形的起伏形态,从而DDM中海底地形起伏形态的保持关键在于维护海底地貌纵向分布的相对高度。由于DDM正向滚动球变换的几何特性仅保留了DDM中正向地貌纵向分布的高度信息[1, 23],并未顾及负向地貌特征值的保留,从而导致DDM海底地貌纵向分布的相对高度发生了变化,破坏了DDM多尺度表达中水深值严密有序性的原则。
由上述分析看出,DDM正向滚动球变换尽管在一定程度上解决了面向航海应用中顾及“安全性”原则的DDM多尺度表达,但同时也破坏了原始海底地貌信息。这主要是由于DDM正向滚动球变换所涉及的尺度仅从三维空间分量中的X、Y轴方向对海底地貌特征进行度量,并未考虑Z轴方向的海底地貌特征,从而导致海底地貌在Z轴方向存在综合尺度过大的倾向。
如图 1所示,(a)、(b)子图分别为原始DDM和正向滚动球变换后一定尺度下DDM沿X轴方向的剖面图。α、β、γ为原始DDM中相邻负向地貌,各负向地貌的横向分布范围(X、Y轴方向的海底地貌特征描述)均等于2λξ;hα、hβ、hγ为负向地貌α、β、γ的纵向分布高度(Z轴方向的海底地貌特征描述),且hβ>hγ>hα。由DDM正向滚动球变换的尺度依赖特性可知,经由缓冲距
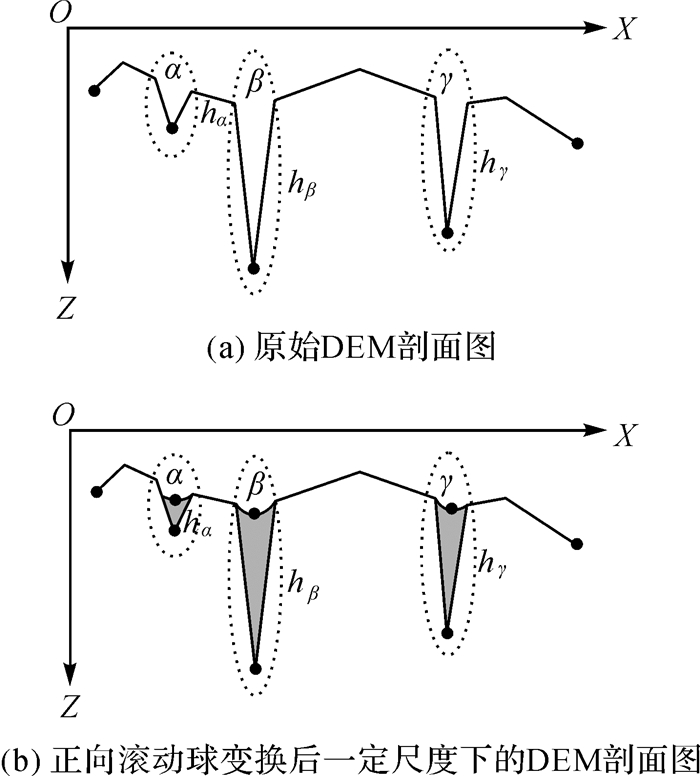
|
| 图 1 DDM正向滚动球变换的局限性 Fig. 1 The deficiency of positive direction rolling ball transform |
2 DDM双向滚动球变换及多尺度表达 2.1 DDM双向滚动球变换
由于DDM正向滚动球变换中的尺度因子λ并未考虑Z轴方向的海底地貌特征,因而破坏了DDM格网点水深值准确性与严密有序性。因此,研究如何利用DDM滚动球变换获得DDM在Z轴方向的海底地貌特征描述成为解决问题的关键。由文献[23]可知,DDM正向滚动球变换VU(r)具有保持正向和平坦地貌不变、缩小或填平负向地貌的几何特性,且曲面T·VU(r)中包含了正向和平坦地貌特征点与缩小或填平后负向地貌特征点的水深值信息,从而DDM中负向地貌的纵向分布高度可由曲面T·VU(r)与原始DDM在Z轴方向的差值来确定
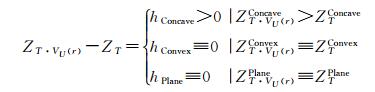 (1)
(1)
式中,ZT·VU(r)表示曲面T·VU(r)格网点水深值;ZT表示原始DDM格网点水深值;hConcave、hConvex、hPlane分别表示DDM中负向地貌、正向地貌、平坦地貌的纵向分布高度;ZT·VU(r)Concave、ZT·VU(r)Convex、ZT·VU(r)Plane分别表示曲面T·VU(r)中负向地貌、正向地貌、平坦地貌的特征点水深值;ZTConcave、ZTConvex、ZTPlane分别表示原始DDM中负向地貌、正向地貌、平坦地貌的特征点水深值。与之相反,DDM负向滚动球变换VD(r)具有保持负向和平坦地貌,缩小或削平正向地貌的几何特性,且曲面T·VD(r)中包含了负向和平坦地貌特征点与缩小或削平后正向地貌特征点的水深值信息[1, 23],从而DDM中正向地貌的纵向分布高度可由原始DDM与曲面T·VD(r)在Z轴方向的差值来确定
 (2)
(2)
式中,ZT·VD(r)表示曲面T·VD(r)格网点水深值;ZT·VD(r)Concave、ZT·VD(r)Convex、ZT·VD(r)Plane分别表示曲面T·VD(r)中负向地貌、正向地貌、平坦地貌的特征点水深值。结合式(1)、(2),本文提出DDM双向滚动球变换的概念,即通过对原始DDM分别进行正向和负向滚动球变换,得到曲面T·VU(r)与T·VD(r),由于上述曲面分别包含了原始DDM中负向地貌与正向地貌特征点的水深值信息(ZT·VD(r)Concave≡ZTConcave且ZT·VU(r)Convex≡ZTConvex),且相对于原始DDM,平坦地貌保持不变(ZT·VU(r)Plane≡ZTPlane≡ZT·VD(r)Plane),从而DDM在Z轴方向的海底地貌特征描述可以由曲面T·VU(r)与T·VD(r)在Z轴方向的差值来确定
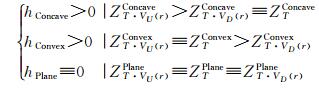 (3)
(3)
如图 2所示即为双向滚动球变换原理图,原始DDM经由DDM正(负)向滚动球变换得到曲面T·VU(r)(以黑色格网表示)和T·VD(r)(以白色格网表示),而海底地貌在2轴方向的海底地貌特征描述可由图 2中黑色格网与白色格网在Z轴方向的差值来实现。在此基础上,通过下文所述方法建立DDM多尺度表达中细部(骨架)地貌判定准则,即可确定出各DDM格网点的地貌特征值(用于标识骨架地貌或细部地貌)。对于DDM中骨架地貌予以保留(以绿色格网表示),以满足DDM多尺度表达的水深值准确性要求;对于DDM中细部地貌则通过对曲面T·VU(r)和T·VD(r)进行等距离面提取(以红色格网表示),以满足DDM多尺度表达中水深值严密有序性的要求。

|
| 图 2 DDM双向滚动圆变换原理图 Fig. 2 Theory map of double direction rolling ball transform |
2.2 DDM多尺度表达中细部(骨架)地貌判定准则的建立
由2.1中分析可知,实现DDM多尺度表达中水深值准确性与严密有序性的关键在于有效区分DDM中细部地貌与骨架地貌,即能否在给定参数条件下,利用DDM双向滚动球变换对海底地貌进行定量分析,依据DDM格网点起伏程度的统计特性,建立DDM多尺度表达中细部(骨架)地貌的判定准则。为便于问题的叙述,此处以负向地貌为例。如图 3所示,负向地貌分别由DDM格网单元GFPH、FEDP、PDCB和PBAH构成。其中,P为海底地貌特征点,其余格网点水深值相等;Pu为滚动球球心;Pud、Pdu分别为海底地貌特征点P经由DDM正(负)向滚动球变换VU(r)(VD(r))所对应的海底地貌特征点,PudPdu的大小可理解为海底地貌特征点P处起伏程度的定量描述;PuPud与平面ACEG相交于P′ud, PudP′ud的大小反映了负向地貌的填平程度,即海底地貌特征点P处起伏程度的定量描述精度。

|
| 图 3 DDM双向滚动球变换中细部(骨架)地貌的判定 Fig. 3 Identifying detail (skeleton) reliefs through double direction rolling ball transform |
由图 3中分析不难看出:DDM双向滚动球变换的过程中,海底地貌特征点P的空间位置发生了改变。在给定λ、σ的前提下,PudPdu的大小反映了海底地貌特征点P相对其周围格网点的起伏程度。令Skeleton(QT)代表DDM格网点QT的地貌特征值(0表示细部地貌;1表示骨架地貌),在海底地形变化光滑连续、平缓的假设下,本文建立如下细部(骨架)地貌判定准则
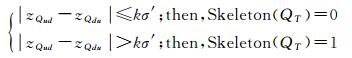 (4)
(4)
式中,Qud(xT, yT, zQud)表示DDM格网点QT经由DDM正向滚动球变换VU(r)后所对应的格网点;Qdu(xT, yT, zQdu)表示DDM格网点QT经由DDM负向滚动球变换VD(r)后所对应的格网点;|zQud-zQdu|表示DDM格网点QT处海底地形的起伏程度;k表示骨架地貌判定因子;σ′表示DDM内格网点起伏程度的中误差,可由下式解算获得
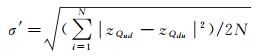 (5)
(5)
式中,N表示DDM内格网点数目。如图 1所示,经由缓冲距
为了最大限度减小因DDM尺度变换引起的海底地貌失真,要求在DDM多尺度变换过程中,所用方法、概念不能破坏原始DDM水深值的严密有序性,借鉴文献[28]定义它为DDM多尺度表达的水深序同构问题。即:对于序集T到序集T′上的映射H:T→T′,若a<b,则必有H(a)<H(b),则称为序集的同态或序同态,且当H是一一对应,而H-1也是T′到T上的同态时,则H称为同构或序同构。
对于任意DDM格网点QT,依据DDM多尺度表达中细部(骨架)地貌判定准则,标记DDM格网点QT的地貌特征值Skeleton(QT)。若Skeleton(QT)=1,则保留该地貌特征点,以满足DDM多尺度表达中水深值准确性的要求;若Skeleton(QT)=0,则对原始DDM经双向滚动球变换后所得到的曲面T·VU(r)、T·VD(r)进行等距离面提取,以得到顾及水深序同构原则的DDM。
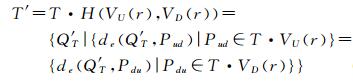 (6)
(6)
式中,H(VU(r), VD(r))表示等距离面变换;T′表示曲面T·VU(r)、T·VD(r)的等距离面;Q′T(xT, yT, z′T)表示等距离面T′上任意格网点。参照文献[1]和[23],曲面T·VU(r)、T·VD(r)均为单值曲面。在原始DDM格网点QT数量足够大的前提下,等距离面T′的解算可近似简化为[1, 33-34]
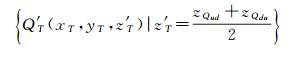 (7)
(7)
如图 4所示,(a)、(b)子图分别为原始DDM和双向滚动球变换后一定尺度下DDM沿X轴方向的剖面图。P、Q为原始DDM中相邻地貌特征点,且zP>zQ。在阈值(缓冲距r)满足
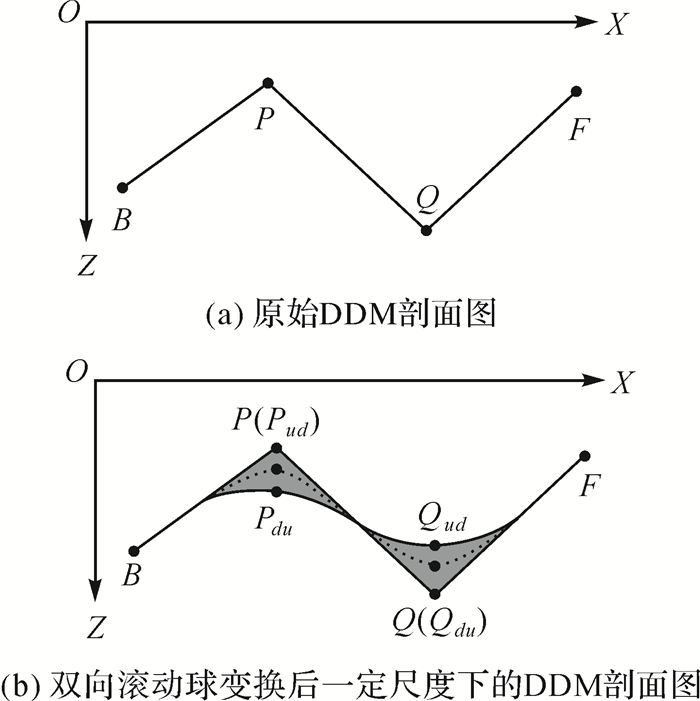
|
| 图 4 DDM双向滚动球变换的水深序同构特性 Fig. 4 The depth order isomorphism characteristic of double direction rolling ball transform |
2.4 DDM多尺度表达中地形信息等级的嵌套性分析
顾及“保真性”原则的DDM多尺度表达不仅要求DDM具有较高的水深数值精度(宏观地貌特征与局地形态信息的准确描述)和地形形态精度(地形三维有序系统的有效维护),而且要求DDM多尺度表达的地形模拟结果与DDM格网的具体布设位置无关(准确稳定的DDM地形模拟)以及能够正确、有效地恢复原始地形的三维形态(正确有效的DDM地形还原)[24-27]。文献[27]将此类地形模拟(还原)要求定义为不同尺度下地形信息的等级嵌套性。地形信息的等级嵌套是地形的固有属性,对于原始DDM构成的曲面T,其等价于原始DDM中各类不同等级地形信息单元的并集[4, 14]
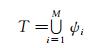 (8)
(8)
式中, i表示地形信息单元的等级;ψi表示指定等级的地形信息单元;M表示地形信息单元的等级数量。对于T中任意不同等级的地形信息单元ψi、ψj(j>i),地形信息的等级嵌套性要求高等级的地形信息单元范围包含低等级的地形信息单元范围。即:Ω(ψi)⊆Ω(ψj)(Ω表示地形信息单元的范围)。
图 5为原始DDM沿X轴方向的剖面图。P1、P2、P3、…、P11为原始DDM中相邻地貌特征点;ψ1(P3, P4, P5, P6, P7, P8, P9)、ψ2(P2, P3, P9, P10)、ψ3(P1, P2, P10, P11)分别表示不同等级的地形信息单元;原始DDM沿X轴方向的剖面TX等价于地形信息单元ψ1、ψ2、ψ3的并集。即TX=ψ1∪ψ2∪ψ3,且不同等级地形信息单元的范围间存在Ω(ψ1)⊆Ω(ψ2)⊆Ω(ψ3)的逻辑包含关系。

|
| 图 5 原始DDM中不同等级地形信息的嵌套关系 Fig. 5 Different hierarchical nesting relationship of terrain information in original DDM |
DDM多尺度表达的实质是在不同尺度条件下对原始DDM中相应等级的地形信息单元进行综合和处理。DDM多尺度表达中地形信息等级的嵌套性包含两方面内容[15, 24-27]:一方面要求由尺度变换引起的地形信息单元形态变化不能破坏原始DDM中地形信息等级的嵌套关系,即DDM中地形信息等级的嵌套关系与尺度相互独立,以保证DDM地形模拟的准确稳定性;另一方面要求某一尺度下的地形信息单元综合结果不能违背其后续尺度下的地形信息等级的嵌套关系,即大尺度地形信息等级的嵌套关系优先于小尺度地形信息等级的嵌套关系,以保证DDM地形还原的正确有效性。DDM多尺度表达中地形信息等级的嵌套性表述如下[27, 29]
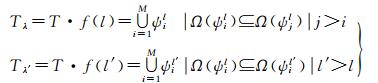 (9)
(9)
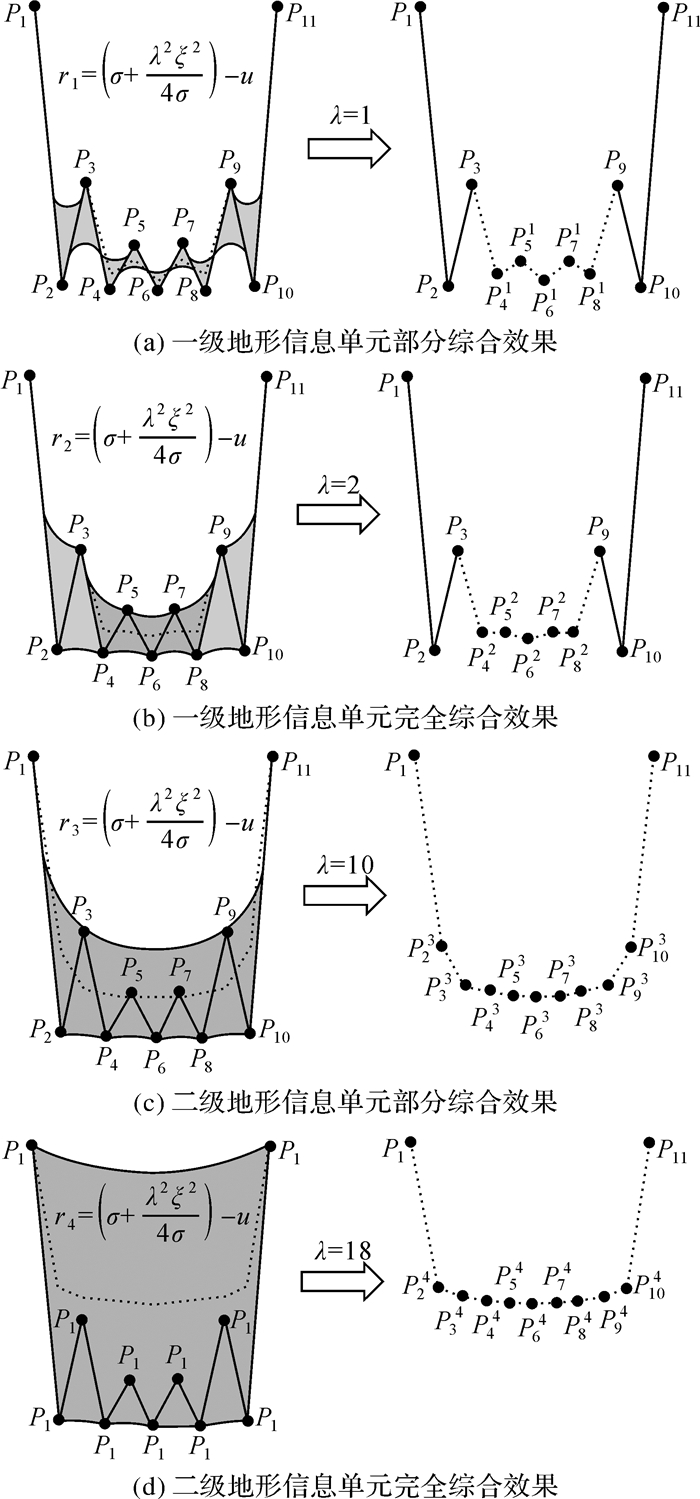
式中,f表示多尺度变换函数;ψil、ψil′分别表示不同尺度(l、l′)下DDM中的地形信息单元。图 6为基于双向滚动球变换中不同尺度因子条件下的DDM综合效果剖面图。其中:尺度因子λ取值分别为1、2、10、18,对应的滚动球半径取值分别为r1、r2、r3、r4;

|
| 图 6 不同尺度下DDM中地形信息等级的嵌套关系 Fig. 6 Hierarchical nesting relationship of terrain information in different scale DDM |
如图 6(a)所示,经DDM双向滚动球变换(λ=1) 后,TX中一级地形信息单元ψ1被部分综合(P4、P5、P6、P7、P8被判定为细部地貌特征点并进行等距离面的提取,构成尺度因子λ=1条件下的一级地形信息单元ψ11),二、三级地形信息单元(ψ2、ψ3)予以保留(P1、P2、P3、P9、P10、P11被判定为骨架地貌特征点,构成尺度因子λ=1条件下的二级地形信息单元ψ21(ψ21=ψ2)和三级地形信息单元ψ31(ψ31=ψ3)),综合后的TX由地形信息单元ψ11、ψ21、ψ31共同构成。即:TX1=ψ11∪ψ21∪ψ31,且各等级的地形信息单元范围间存在Ω(ψ11)⊆Ω(ψ21)⊆Ω(ψ31)的逻辑包含关系。此外,由于DDM双向滚动球变换仅改变了地貌特征点的水深值,并未改变其水平位置信息,故尺度因子λ=1条件下的各级地形信息单元范围等价于原始DDM中的相应等级的地形信息单元范围。即:Ω(ψi)=Ω(ψi1)(i∈[1, 3])。与图 6(a)中情形类似,图 6(b)中TX的二、三级地形信息单元予以保留(ψ22=ψ2且ψ32=ψ3),仅一级地形信息单元的形态发生了变化,故综合后TX中各级地形信息等级的嵌套关系与图 6(a)中结论一致。即:TX2=ψ12∪ψ22∪ψ32、Ω(ψ12)⊆Ω(ψ22)⊆Ω(ψ32)、Ω(ψi)=Ω(ψi2)(i∈[1, 3])。
DDM双向滚动球变换过程中,尺度因子取值的持续增大将导致高级别的地形信息单元形态发生改变,图 6(c)中TX的一级地形信息单元被完全综合,二、三级地形信息单元被部分综合,综合后的TX表示为TX10=ψ110∪ψ210∪ψ310,且Ω(ψ110)⊆Ω(ψ210)⊆Ω(ψ310)。然而,尺度因子取值的剧烈变化(尺度因子λ由2增至10) 并未影响大尺度DDM与原始DDM间相应等级的地形信息单元范围等价关系。图 6(c)各级地形信息单元范围同样等价于原始DDM中对应等级的地形信息单元范围。即:Ω(ψi)=Ω(ψi10)(i∈[1, 3])。以此类推,图 6(d)中TX18的各级地形信息等级的嵌套关系与图 6(c)中结论一致。
综上所述,DDM双向滚动球变换中,尺度因子取值变化引起的地形信息单元的综合和处理并未破坏原始DDM中地形信息等级的嵌套关系,且任意尺度因子条件下DDM中相应等级的地形信息范围始终与原始DDM保持一致。
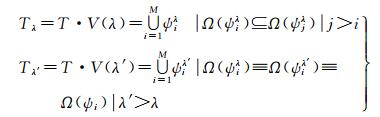 (10)
(10)
式中,V表示DDM双向滚动球尺度因子变换函数。对比式(9) 中关于DDM多尺度表达中地形信息等级的嵌套性描述,DDM双向滚动球变换中的尺度因子与该尺度下DDM中地形信息等级单元的逻辑包含关系不存在相关性,保证了DDM多尺度表达的准确稳定性;不同尺度因子条件下相应等级的地形信息范围始终等价,保证了DDM多尺度表达中逆向还原的正确有效性。
3 试验结果与分析为验证算法的正确性和有效性,本文借助于文献[34]提出的单值曲面缓冲体边界生成算法的构建原理,通过VC++编程实现了基于双向滚动球变换的DDM多尺度表达算法,并利用Surfer8.0软件对生成的试验结果进行了可视化显示与分析。试验采用的数据为我国东海某海区的格网DDM数据,水深测量的中误差为0.5 m。格网DDM数量为900×783,初始分辨率ξ为5 m,骨架地貌判定因子k为2。
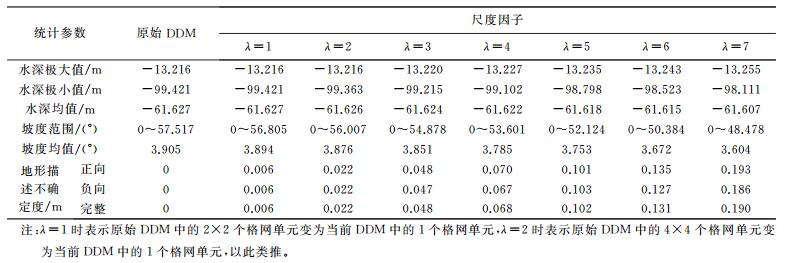
试验共分7组,基于不同的尺度因子利用本文算法与文献[23]中提出的DDM多尺度表达的正向滚动球变换算法对原始DDM进行了多尺度表达。如表 1所示分别为原始DDM与不同尺度因子(λ=1、λ=3、λ=5和λ=7) 条件下DDM的海底地形表面及等深线(等深距为5 m)对比图。从表中不难看出,DDM双向滚动球变换能较好地区分出反映海底地形特征的基本骨架地貌数据以及相对应的细部地貌数据,且随着尺度因子的增大,细部地貌数据呈现逐渐减少直至滤除的趋势,而基本骨架地貌数据则得以保留。借助Surfer8.0软件的坡度分析功能,并参照文献[10]中DDM地形描述不确定度的计算方法,本文对双向滚动球变换的7组试验结果进行了量化分析,试验结论见表 2。

|
|
试验结果表明:① DDM双向滚动球变换能基本保持原始数据的特性,山脊与山谷的骨架地貌没有发生大的变化,仅局部细部地貌被适当地进行了平滑;② 随着尺度因子的增大,水深极大值呈现逐渐减小的趋势、水深极小值呈现逐渐增大的趋势,说明双向滚动球变换具有减少或滤除DDM中的细部地貌数据的特性;③ 水深均值相对于原始DDM基本保持不变,说明DDM双向滚动球变换具有保持原始DDM中基本骨架地貌数据的特性;④ 坡度的变化表现为在一定范围内的震荡,但坡度的范围呈现出逐渐减小的变化,结合坡度均值的变化可以发现,不同尺度间变化较大的是相邻尺度间的细部地貌特征点,随着尺度的减小和数据压缩量的增大,DDM整体则呈现逐步平缓的变化趋势,这与DDM多尺度表达的原则是相吻合的;⑤ 正向地貌综合与负向地貌综合引起的地形描述不确定度在数值上近似相等,且随着尺度因子的增大,相邻尺度间的地形描述不确定度差异逐渐增大,说明双向滚动球变换对于正、负向地貌的综合程度基本一致,且遵循由细部到骨架的地貌综合顺序;⑥ 3类地形描述不确定度的变化规律基本一致,均呈现出与尺度因子的正相关关系,结合各类地形描述不确定度的变化程度不难看出,地形描述不确定度与尺度因子的相关性相对较弱,且试验中未超出水深测量的中误差,说明双向滚动球变换具有较好的地形保真性。
为更为直观地验证基于双向滚动球变换的DDM多尺度表达算法在地形保真方面的优势,对本文算法与文献[23]算法就表 2中的相关统计参数进行对比分析。分析结论见图 7(图中红色、蓝色折线分别为经本文算法与文献[23]算法获得的数据统计结果;横轴的含义为尺度因子,当尺度因子为0时,表示原始DDM)。

|
| 图 7 多尺度表达统计参数对比分析 Fig. 7 Contrast analysis of multi-scale representation statistics parameters |
对比分析表明:① 文献[23]算法的水深极大值相对于原始DDM保持不变,而水深极小值相对于本文算法以及原始DDM变化较大,这主要是由于文献[23]算法所采用DDM正向滚动球变换所具有的几何特性决定的,同时也证明了DDM正向滚动球变换以牺牲“保真性”来换取满足舰船航行的“安全性”为原则的;② 经由本文算法处理后的DDM水深均值相对于原始DDM基本保持不变,说明DDM双向滚动球变换相对于文献[23]算法在保持DDM骨架地貌数据方面具有一定的优势;③ 两类算法处理后的海底地形表面坡度均呈现在一定范围内的震荡,且坡度的范围从总体上呈现出逐渐减小的变化,这说明海底地形表面呈现逐步平缓的变化趋势,这与DDM多尺度表达的原则是相吻合的;④ 相对于文献[23]算法,本文算法的坡度范围与坡度均值变化明显较弱,说明DDM双向滚动球变换可较好地保持原始DDM的水深值严密有序性;⑤ 文献[23]算法的正向地形描述不确定度相对于原始DDM保持不变,说明DDM正向滚动球变换能较好地保留原始DDM中的正向地貌,从地形形态精度的层面验证了文献[23]算法的“安全性”原则;⑥ 相对于本文算法,文献[23]算法的负向、完整地形描述不确定度随尺度因子变化的程度更加剧烈,且试验中部分尺度因子条件下的负向、完整地形描述不确定度已超出水深测量的中误差,说明DDM正向滚动球变换在负向地貌及完整地形形态的保持方面相对较差,同时也验证了本文算法的在地形保真方面的相对优势。
最后,为验证DDM双向滚动球变换中地形信息等级的嵌套性,利用本文算法与文献[23]算法对不同尺度因子条件下DDM等深线与原始DDM等深线的套合程度进行了分析。如表 3所示,红色部分表示某一尺度因子条件下DDM的等深线,黑色部分表示原始DDM的等深线,红色与黑色部分的差异表示不同尺度下DDM等深线的套合程度。不难看出,在尺度因子较小(λ=1) 的情况下,两类算法的等深线套合程度均表现相对较好,这主要是由于DDM正向滚动球变换的尺度依赖特性决定的,即小尺度因子条件下,两类算法仅针对小尺度的微型地貌进行了综合处理,相关综合原则和方法的差异在等深线套合程度方面的表现并不明显;随着尺度因子的增大,两类算法的等深线套合程度均表现出不同程度的弱化,但相对于本文算法,文献[23]算法中等深线的套合程度的弱化趋势明显,尤其在尺度因子较大(λ=7) 的情况下,表现出大范围等深线无法套合的情况。

|
综上所述,DDM双向滚动球变换能够有效区分和识别DDM中的骨架和细部地貌、维护水深的严密有序性及不同尺度下地形信息的等级嵌套性,且在同等尺度下具有较小的地形描述不确定度,有效地保证了DDM的地形形态精度,实现了高保真DDM的多尺度表达。
4 结束语实现顾及“保真性”原则的DDM多尺度表达核心是建立满足一定条件的抽象模型,多个尺度空间数据集间的变换应该是尺度依赖的,且应满足高保真DDM多尺度表达评价标准对水深值准确性、严密有序性及不同尺度下地形信息的等级嵌套性的要求。本文从DDM滚动球变换的构建原理出发,首先利用DDM双向滚动球变换对于海底地貌的定量分析特性,建立DDM多尺度表达中细部(骨架)地貌的判定准则;然后通过DDM中骨架地貌的保留和细部地貌的等距离面提取,以满足高保真DDM多尺度表达对水深值准确性与严密有序性的要求;最后,结合尺度因子分析论证了不同尺度下地形信息等级单元逻辑包含关系的变化规律,证明了DDM双向滚动球变换中地形信息的等级嵌套性。试验结果表明该算法可有效保留DDM中骨架地貌并综合细部地貌,在有效维护地形信息等级嵌套性的同时具有较小的地形描述不确定度,实现了顾及“保真性”原则的DDM多尺度表达。但需要指出的是,算法解算过程中,所涉及的骨架地貌判定因子由于采用的是经验参数,理论性和通用性有待加强,需进一步研究如何根据实际DDM格网点水深分布情况进行自适应估计的问题。
| [1] | 董箭. 格网水深插值优化及滚动球变换处理方法研究[D]. 大连: 海军大连舰艇学院, 2013. DONG Jian. Research on Grid Depth Interpolation and Rolling Ball Transform Processing[D]. Dalian: Dalian Naval Academy, 2013. |
| [2] | 贾帅东, 张立华, 宋国大, 等. 基于区域平均垂直不确定度的自适应网格水深建模方法[J]. 测绘学报, 2012, 41(3): 454–460. JIA Shuaidong, ZHANG Lihua, SONG Guoda, et al. A Method for Constructing an Adaptive Grid Digital Depth Model Based on Mean Vertical Uncertainty of Area[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 454–460. |
| [3] | 刘鹏程, 艾廷华, 杨敏. 基于傅里叶级数的等高线网络渐进式传输模型[J]. 测绘学报, 2012, 41(2): 284–290. LIU Pengcheng, AI Tinghua, YANG Min. The Internet Progressive Transmission Model for Contour Based on Fourier Series[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 284–290. |
| [4] | 艾廷华, 成建国. 对空间数据多尺度表达有关问题的思考[J]. 武汉大学学报(信息科学版), 2005, 30(5): 377–382. AI Tinghua, CHENG Jianguo. Key Issues of Multi-scale Representation of Spatial Data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 377–382. |
| [5] | 费立凡, 何津, 马晨燕, 等. 3维Douglas-Peucker算法及其在DEM自动综合中的应用研究[J]. 测绘学报, 2006, 35(3): 278–284. FEI Lifan, HE Jin, MA Chenyan, et al. Three Dimensional Douglas-Peucker Algorithm and the Study of Its Application to Automated Generalization of DEM[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3): 278–284. |
| [6] | 万刚, 朱长青. 多进制小波及其在DEM数据有损压缩中的应用[J]. 测绘学报, 1999, 28(1): 36–40. WAN Gang, ZHU Changqing. Application of Multi-band Wavelet on Simplifying DEM with Lose of Feature Information[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 36–40. DOI:10.3321/j.issn:1001-1595.1999.01.007 |
| [7] | 贾帅东, 张立华, 彭认灿, 等. 确保水深模型航海安全性的深度保证率控制方法[J]. 交通运输工程学报, 2015, 15(5): 101–109. JIA Shuaidong, ZHANG Lihua, PENG Rencan, et al. Control Method of Probability of Adequate Depth Ensuring Navigation Safety of Depth Model[J]. Journal of Traffic and Transportation Engineering, 2015, 15(5): 101–109. |
| [8] | 张立华, 贾帅东, 元建胜, 等. 一种基于不确定度的水深控浅方法[J]. 测绘学报, 2012, 41(2): 184–190. ZHANG Lihua, JIA Shuaidong, YUAN Jiansheng, et al. A Method for Controlling Shoal-bias Based on Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 184–190. |
| [9] | 张立华, 贾帅东, 王涛, 等. 深度保证率和表达度指标的定义及评估方法[J]. 武汉大学学报(信息科学版), 2015, 40(5): 695–700. ZHANG Lihua, JIA Shuaidong, WANG Tao, et al. Definitions and Estimating Methods of a Probability of an Adequate Depth and Representiveness[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 695–700. |
| [10] | 贾帅东. 航海DDM的构建理论与方法[D]. 大连: 海军大连舰艇学院, 2015. JIA Shuaidong. The Theory and Methods for Constructing Digital Depth Model Serving for Navigation[D]. Dalian: Dalian Naval Academy, 2015. |
| [11] | 吴凡, 祝国瑞. 基于小波分析的地貌多尺度表达与自动综合[J]. 武汉大学学报(信息科学版), 2001, 26(2): 170–176. WU Fan, ZHU Guorui. Multi-scale Representation and Automatic Generalization of Relief Based on Wavelet Analysis[J]. Geomatics and Information Science of Wuhan University, 2001, 26(2): 170–176. |
| [12] | 杨族桥, 郭庆胜, 牛冀平, 等. DEM多尺度表达与地形结构线提取研究[J]. 测绘学报, 2005, 34(2): 134–137. YANG Zuqiao, GUO Qingsheng, NIU Jiping, et al. A Study on Multi-scale DEM Representation and Topographic Feature Line Extraction[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 134–137. DOI:10.3321/j.issn:1001-1595.2005.02.008 |
| [13] | 李精忠, 艾廷华, 王洪. 一种基于谷地填充的DEM综合方法[J]. 测绘学报, 2009, 38(3): 272–275. LI Jingzhong, AI Tinghua, WANG Hong. The DEM Generalization Based on the Filing Valley Coverage[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 272–275. DOI:10.3321/j.issn:1001-1595.2009.03.013 |
| [14] | 李志林. 地理空间数据处理的尺度理论[J]. 地理信息世界, 2005, 3(2): 1–5. LI Zhilin. A Theoretical Discussion on the Scale Issue in Geospatial Data Handling[J]. Geomatics World, 2005, 3(2): 1–5. |
| [15] | 胡鹏, 高俊. 数字高程模型的数字综合原理研究[J]. 武汉大学学报(信息科学版), 2009, 34(8): 940–942. HU Peng, GAO Jun. The Digital Generalization Principle of Digital Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2009, 34(8): 940–942. |
| [16] | CHRISTENSEN A H J. Cartographic Line Generalization with Waterlines and Medial-axes[J]. Cartography and Geographic Information Science, 1999, 26(1): 19–32. DOI:10.1559/152304099782424893 |
| [17] | CHRISTENSEN A H J. Two Experiments on Stream Network Generalization[C]//Proceedings of the 21st International Cartographic Conference. Durban: The International Cartographic Associatio, 2003. |
| [18] | International Hydrographic Bureau. A Manual on Technical Aspects of the United Nations Convention on the Law of the Sea-1982[M].4th ed. Monaco: International Hydrographic Bureau, 2006. |
| [19] | 董箭, 彭认灿, 陈轶, 等. 一种基于缓冲区边界相向逼近求交模型的曲线间中心线生成算法[J]. 武汉大学学报(信息科学版), 2011, 36(9): 1120–1123. DONG Jian, PENG Rencan, CHEN Yi, et al. An Algorithm for Centre Line Generation Based on Model of Approaching Intersection of Buffering Borderline from Reciprocal Direction[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1120–1123. |
| [20] | 董箭, 彭认灿, 张立华, 等. 利用滚动圆变换的多波束测深数据滤波算法[J]. 武汉大学学报(信息科学版), 2016, 41(1): 86–92. DONG Jian, PENG Rencan, ZHANG Lihua, et al. An Algorithm of Filtering Noises in Multi-beam Data Based on Rolling Circle Transform[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 86–92. |
| [21] | SMITH S M. The Navigation Surface: A Multipurpose Bathymetric Database[D]. Durham: University of New Hampshire, 2003. |
| [22] | 高王军. 双向缓冲区模型在海图自动制图综合中的应用研究[D]. 大连: 海军大连舰艇学院, 2009. GAO Wangjun. Research of the Double Direction Buffering Model and Its Application on Chart Generalization[D]. Dalian: Dalian Naval Academy, 2009. |
| [23] | 董箭, 彭认灿, 张立华, 等. 滚动球变换的数字水深模型多尺度表达[J]. 地球信息科学学报, 2012, 14(6): 704–711. DONG Jian, PENG Rencan, ZHANG Lihua, et al. Multi-scale Representation of Digital Depth Model Based on Rolling Ball Transform[J]. Journal of Geo-Information Science, 2012, 14(6): 704–711. |
| [24] | 汤国安, 龚健雅, 陈正江, 等. 数字高程模型地形描述精度量化模拟研究[J]. 测绘学报, 2001, 30(4): 361–365. TANG Guoan, GONG Jianya, CHEN Zhengjiang, et al. A Simulation on the Accuracy of DEM Terrain Representation[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 361–365. DOI:10.3321/j.issn:1001-1595.2001.04.016 |
| [25] | 王光霞, 朱长青, 史文中, 等. 数字高程模型地形描述精度的研究[J]. 测绘学报, 2004, 33(2): 168–173. WANG Guangxia, ZHU Changqing, SHI Wenzhong, et al. The Further Study on the Accuracy of DEM Terrain Representation[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 168–173. DOI:10.3321/j.issn:1001-1595.2004.02.014 |
| [26] | 胡鹏, 杨传勇, 吴艳兰, 等. 新数字高程模型:理论方法标准和应用[M].北京: 测绘出版社, 2007. HU Peng, YANG Chuanyong, WU Yanlan, et al. New DEM Theories Methods Standards and Application[M].Beijing: Surveying and Mapping Press, 2007. |
| [27] | 王春, 刘学军, 汤国安, 等. 格网DEM地形模拟的形态保真度研究[J]. 武汉大学学报(信息科学版), 2009, 34(2): 146–149. WANG Chun, LIU Xuejun, TANG Guoan, et al. The Morphologic Fidelity of Grid Digital Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 146–149. |
| [28] | 胡鹏, 白轶多, 胡海. 数字高程模型生成中的高程序同构[J]. 武汉大学学报(信息科学版), 2009, 34(3): 352–357. HU Peng, BAI Yiduo, HU Hai. Elevation Order Isomorphism Characteristics of DEM[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 352–357. |
| [29] | 张锦明, 游雄. DEM保真精度定量化描述模型[J]. 中国图象图形学报, 2013, 18(9): 1206–1214. ZHANG Jinming, YOU Xiong. Quantitative Descriptive Model of DEM Fidelity Accuracy[J]. Journal of Image and Graphics, 2013, 18(9): 1206–1214. DOI:10.11834/jig.20130920 |
| [30] | 吴艳兰, 胡海, 胡鹏, 等. 数字高程模型误差及其评价的问题综述[J]. 武汉大学学报(信息科学版), 2011, 36(5): 568–574. WU Yanlan, HU Hai, HU Peng, et al. A Review on the Issues in DEM Error and DEM Quality Assessment[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5): 568–574. |
| [31] | 刘雁春, 肖付民, 暴景阳, 等. 海道测量学概论[M].北京: 测绘出版社, 2006. LIU Yanchun, XIAO Fumin, BAO Jingyang, et al. Introduction to Hydrogrophy[M].Beijing: Surveying and Mapping Press, 2006. |
| [32] | 张立华, 贾帅东, 吴超, 等. 顾及不确定度的数字水深模型内插方法[J]. 测绘学报, 2011, 40(3): 359–365. ZHANG Lihua, JIA Shuaidong, WU Chao, et al. A Method for Interpolating Digital Depth Model Considering Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 359–365. |
| [33] | 郭仁忠. 空间分析[M].2版. 武汉: 武汉测绘科技大学出版社, 2000. GUO Renzhong. Spatial Analysis[M].2nd ed. Wuhan: Wuhan Technical University of Surveying and Mapping Press, 2000. |
| [34] | 董箭, 彭认灿, 郑义东, 等. 基于滚动球模型的单值曲面缓冲体边界生成算法[J]. 计算机辅助设计与图形学学报, 2013, 25(7): 996–1004. DONG Jian, PENG Rencan, ZHENG Yidong, et al. An Algorithm of 3D-buffer Boundary Generation for Singular Value Surface Based on Rolling Ball Model[J]. Journal of Computer-aided Design & Computer Graphics, 2013, 25(7): 996–1004. |



