尺度是地理数据的重要特征[1]。不同尺度的数据在形态特征、细节信息和抽象程度上存在差异,使得空间数据的多尺度表达成为制约GIS应用的难点之一[2-4]。空间数据多尺度表达的目的在于,解决离散数据与连续显示之间的矛盾。目前多尺度表达数据库的建立机制主要有两种:一是静态多版本方法,二是动态在线的方式[2, 5]。理想的多尺度表达方法是由单一大比例尺矢量数据直接自动综合生成任意小比例尺矢量数据,但是由于自动综合这一国际难题仍未取得突破性进展,因此现有条件下多尺度表达数据库的建立主要是基于静态多版本机制[6-7]。传统基于关键比例尺的多尺度表达,数据间跳跃程度大,不能给用户以连续的视觉感受,随着研究日益深入,为了解决这一问题,基础比例尺数据参与中间比例尺的新数据的生成被认为是更合理的方式,实现的手段是在相邻比例尺数据之间进行插值,生成中间比例尺的表达。生成的插值数据要同时反映两端比例尺数据的特征,因此需要建立两端比例尺数据之间的联系,从而出现了多尺度匹配的问题。建立两端比例尺数据之间的联系,必须借助空间数据匹配技术。空间数据匹配是空间数据集成与更新的核心技术,是指通过对目标的几何、拓扑和语义进行相似性度量,识别出同一地区不同来源空间数据集中的同一地物[8-9]。
道路网作为最重要的地理要素之一,是多尺度表达研究的重点。长期以来,许多研究人员都对道路匹配算法进行了研究,文献[10]基于概率统计的基本思想,对道路数据进行了几何匹配,其核心是计算一定范围内候选目标的匹配概率,取概率最大者为匹配结果,属于典型的缓冲区增长法(buffer growing)[11-13];文献[14—15]用迭代几何匹配算法对GDF导航数据和德国ATKIS道路数据进行了匹配,属于迭代最近点法(iterative closest point)。前者是一种基于道路弧段的道路网匹配方法,后者是一种基于道路节点的道路网匹配方法,现有道路网匹配基本上都属于这两类方法,或者是基于这两类方法的合并与改进。文献[16]采用层次分析法进行道路网整体分析,自动对道路的相似评价指标分配权值,评价道路的整体相似度完成道路的自动匹配。文献[17]提出基于多尺度道路网距离的匹配算法,将复杂的折线与折线之间的几何相似度计算转化为求节点到折线的距离,并通过建立格网索引提高了计算效率。文献[18]提出全局寻优的矢量道路网自动匹配方法,综合利用道路弧段和节点的特征信息,建立最优化模型,利用概率松弛法求解最优解,获得道路弧段之间的匹配关系。文献[19]针通过对道路交叉口的结构化描述,提取道路节点的局部网络模式特征,计算节点之间的形态相似性进行道路匹配。
传统方法多是基于对同尺度的道路之间的整体相似度进行评价,而在多尺度条件下,同名道路之间的形态具有明显差异,在属性信息缺失条件下,利用几何特征提取道路整体往往会出现错误,不能保证不同比例尺的道路数据提取出完全相同的道路整体,因此利用多指标建立的相似性评价体系可能无法得到满意的匹配效果。针对这一难题,本文提出一种基于小比例尺道路网眼约束下的多尺度道路自动匹配算法,先建立大比例尺道路网眼与小比例尺道路网眼之间的匹配关系,然后利用道路网眼的匹配关系作为约束条件完成不同比例尺同名道路之间的匹配。
1 道路网眼多尺度匹配模型本文的匹配研究主要是针对简单形态的多尺度道路网数据,不考虑具有复杂结构体以及双线道路的道路网数据之间的匹配。
1.1 道路网眼的定义地图中道路纵横交错,将地图分割成若干个相互独立的面状区域,这些面状区域构成了道路网眼。道路网眼并不是一种具体的地理要素,而是人们在研究道路网智能选取、多尺度矢量空间数据匹配、道路自动综合算法等过程中为了方便表达与描述道路网空间结构特征而抽象出的一种对象[20]。
道路的层次性决定了道路围成的道路网眼的层次性。高等级道路对空间区域形成主要分割,形成较高等级的网眼,低等级道路对空间区域形成次要分割,形成低等级网眼。最典型的实例就是“城市街区系统”。为了区分道路网眼的层次性,根据其复杂性的不同将道路网眼划分为基本道路网眼和复合道路网眼。基本道路网眼是道路网形态结构分解的最小单元,如图 1中的a、b、c、d,它的基本特征是网眼内部不存在其他道路对其产生有效分割。复合道路网眼的内部则存在多条道路对道路网眼所在区域进行分割,形成其他的道路网眼。实际上也就是复合道路网眼是由两个或者两个以上的道路网眼组合而成。如道路网眼A、B和C,它们都是由图 1中较小的网眼进一步合并而成。复合网眼并不是随意由相邻任意基本网眼简单组合而成,形成复合网眼的边界道路,对空间区域形成主要分割,与复合网眼内部道路相比,具有更高的等级。
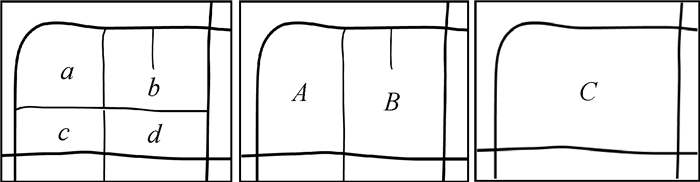
|
| 图 1 道路网眼及其分类示例 Fig. 1 The classification sample of road meshes |
为了保证道路网眼的构成符合人的认知习惯,在构成上必须遵循下列原则[21]:
(1) 道路网眼的边界由顶点和边构成,边实际对应一条道路(stroke)的一部分(路段),顶点则是不同道路的交点。
(2) 复合道路网眼边界道路的等级不能低于其内部网眼边界道路的等级。
道路网眼边界道路的等级由道路本身的属性等级、结构重要性以及长度来决定,具体判断方法参考文献[22]。
1.2 多尺度道路网眼的对应关系反映同一地区的小比例尺道路网数据和大比例道路网数据中存在着同名道路,这些道路在大比例尺路网数据中具有较高的等级,它们构成了大比例尺道路网的“骨架”网络。小比例尺道路网将空间区域划分为若干较大的网眼区域,大比例尺道路往往对这些大道路网眼所对应的区域做进一步细分,从而产生较小网眼,显然这些较小的网眼包含于小比例尺道路网的大网眼之中,即大比例尺的小网眼处于小比例尺大网眼的约束之下,这是本文匹配方法的思想基础。图 2是某一区域1:5万和1:25万道路数据,反映了大小比例尺数据的道路网眼之间可能的对应情况。
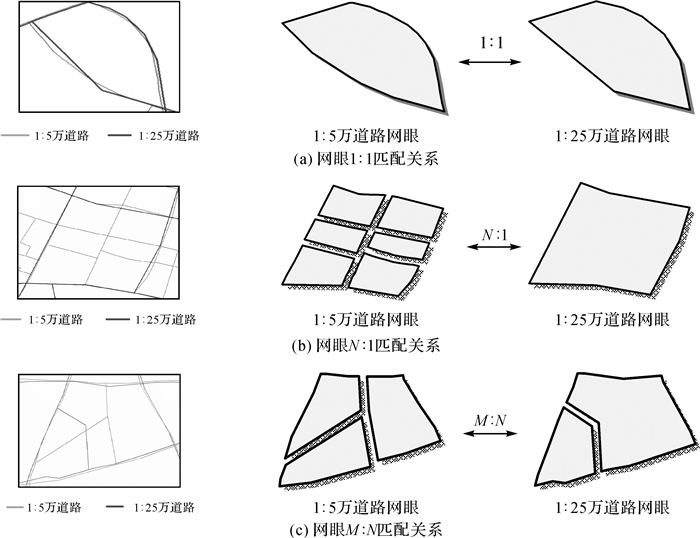
|
| 图 2 同一地区不同比例尺道路网眼的对应关系 Fig. 2 Matching relationships of road networks meshes of different scales in the same area |
对同一地区的道路网数据,大比例尺道路将小比例尺道路网眼内部空间进一步划分为若干较小网眼,使大比例尺和小比例尺同名道路网眼之间以构成N:1(N>1) 的匹配关系,显而易见,在多尺度网眼匹配关系中以N:1匹配为主。除此之外,也存在着少量的M:N(M>1, N>1) 和1:1匹配关系。
1.3 基本思想由于大比例尺数据道路密度较大,同时存在位置误差,导致小比例尺中的道路容易与同名实体道路附近道路发生错误匹配。利用道路网眼进行匹配可以突出道路结构的重要性,削弱位置误差对匹配造成的影响,并且道路网眼越大,对位置误差的容错能力越强。其基本思想是:通过建立道路之间的拓扑关系,构建道路网眼,道路网眼将整个道路网划分为不同的道路子集,首先利用道路网眼匹配实现网眼边界道路的匹配,再对网眼内部道路实施匹配,这样不但缩小了匹配搜索的范围,而且增加了匹配道路的相关性,便于匹配道路对象的快速准确查找。
大比例尺道路网眼与小比例尺道路网眼的N:1和M:N的匹配关系反映的是网眼边界路段之间的N:1和M:N匹配关系。在道路要素的匹配关系中,N:1和M:N匹配关系要比1:1关系复杂的多。理想的方法是将道路之间的N:1和M:N匹配关系转化为1:1匹配关系,从而提高匹配效率和准确率。实际上,小比例尺数据中的道路在大比例尺数据中的同名实体道路往往是大比例尺道路网中的骨架道路,从大比例尺道路网眼中提取与小比例尺网眼或其组合构成为“1:1”匹配关系道路网眼或复合网眼,根据网眼间的“1:1”匹配关系实现匹配网眼间对应边界道路的“1:1”匹配,然后根据一致性原则对网眼内部道路进行合并处理,再进行网眼内部道路匹配。
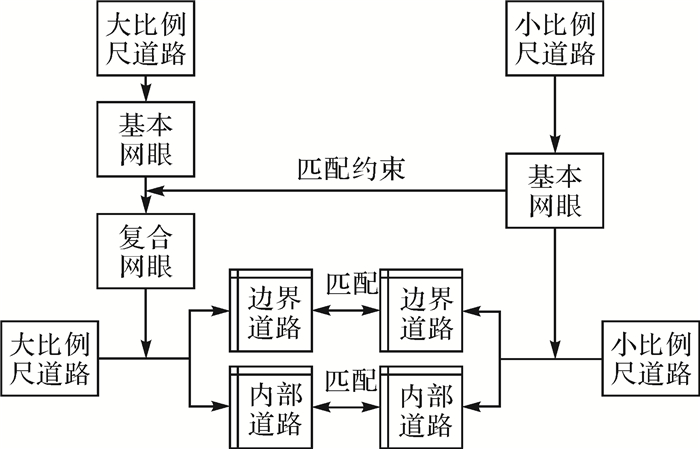
|
| 图 3 多尺度路网匹配 Fig. 3 Matching of multi-scale road networks |
2 多尺度道路匹配的实现方法 2.1 根据匹配关系提取复合网眼 2.1.1 提取N:1和1:1匹配关系的复合网眼
利用道路网眼实现多尺度道路匹配的关键在于分别从大小比例尺道路网数据中提取出构成匹配关系的道路网眼(或复合道路网眼)。大比例尺路网与小比例尺路网构成N:1(N>1) 和1:1匹配关系的道路网眼的提取步骤为:
(1) 计算大比例尺基本道路网眼与小比例尺网眼的重叠率。大比例尺基本网眼与小比例尺网眼的重叠率很大程度上决定了在提取复合网眼时受小比例尺数据上哪一个网眼的约束,从而影响复合网眼提取的准确性。重叠率计算公式为
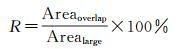 (1)
(1)
式中,Areaoverlap是大比例尺基本道路网眼与小比例尺网眼相交部分的面积;Arealarge为大比例尺道路网眼面积。设阈值R0,当R≥R0,该小比例尺道路网眼为约束网眼。
(2) 搜索大比例尺基本道路网眼中被同一个小比例尺网眼约束的所有网眼,放入同一个候选集。
(3) 合并同一个候选集中的网眼,提取出初始复合网眼,如图 4(c)所示。
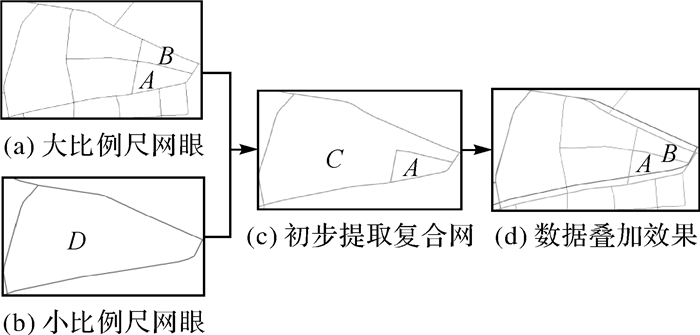
|
| 图 4 复合网眼的初步提取 Fig. 4 Extraction of composite meshes in the first step |
不同比例尺数据的同名道路之间存在位置偏差,导致复合道路网眼的提取产生偏差,表现为大比例尺道路网眼不在对应的小比例尺网眼区域内(具有较低的重叠率),甚至位于相邻的网眼区域内。为了更准确地提取复合网眼,需要对提取的初始复合网眼进行评估修正,识别遗漏的网眼并与初始复合网眼合并,同时将错误加入的网眼从初始复合网眼中剔除,得到正确的提取结果。
以图 4为例,说明初始复合网眼修正的基本过程。图 4中C是在网眼D约束下初步提取的复合网眼,网眼A由于重叠率低于阈值在初步提取时没被选中,B为被正确提取组成的C的大比例网眼,与A相邻且面积最小。对A进行分析,判定是否要与初始复合网眼C合并生成新的复合网眼。判定过程如下:
(1) 搜索初始复合网眼C内部与A相邻的网眼,选择其中重叠率最高且面积最小的网眼B作为候选对象。如果重叠率最大与面积最小出现冲突,规定优先考虑重叠率指标。
(2) 将A与候选对象B合并,按式(2) 求合并后整体的重叠率
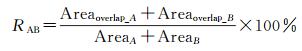 (2)
(2)
式中,RAB为AB作为整体时的重叠率,Areaoverlap_A和Areaoverlap_B分别为A、B与小比例尺网眼的重叠面积,AreaA和AreaB分别为网眼A、B的面积。
(3) 比较RAB与R0,如果RAB≥R0,则网眼C作为与网眼A合并的候选对象。对与A相邻的下一个复合网眼进行同样的判定,直到与A相邻的所有复合网眼判定完毕,从网眼A的所有候选对象中选择重叠率最高的复合网眼与网眼A合并。如果按照上述方法找不到可合并的复合网眼,则网眼A保持独立现状。
除了上述重新加入遗漏的道路网眼外,还需剔除错误加入的网眼,如图 5所示。
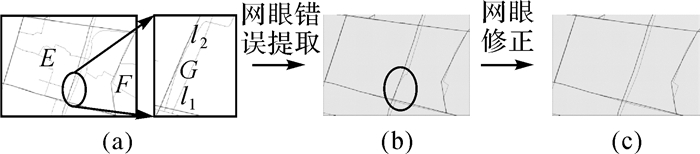
|
| 图 5 网眼错误提取及修正 Fig. 5 Wrong extraction of meshes and correction |
根据认知判断,大比例尺道路网眼中的基本网眼G与小比例尺道路网眼E对应,成为在网眼E约束下生成的复合网眼的候选对象,然而根据重叠率判断,网眼G却与网眼E的相邻网眼F对应,成了网眼F约束下的复合网眼的候选对象。针对这种错误,需要进行修正。根据道路网眼的定义,道路网眼边界道路的等级应比内部道路的等级要高,据此对错误匹配的小网眼进行剔除。将初始复合网眼的边界道路与内部网眼的边界道路进行等级比较,如图 5(a)中,对基本网眼G的边界道路l1和l2的属性等级进行判定,l1为高速公路,l2为等外公路,显然,l1的等级要高于l2,说明前面得到的初始复合网眼F是存在问题的,应将网眼G从复合网眼F中剔除,并入网眼E,完成对复合网眼的修正。
经过上述步骤,完成不同比例尺道路网眼的匹配关系,最后必须判断它们在大小上的相似,避免出现伪匹配,大小相似性计算为
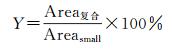 (3)
(3)
式中,Y为相似性指标,设定Y的阈值为ε0≤Y≤ε1;Area复合为初始复合网眼面积,Areasmall为与之匹配的小比例尺网眼面积。当Y大于阈值时,最终确认二者匹配。
通过小比例尺道路网眼的约束提取大比例尺网眼中与之相对应的复合网眼,通过网眼之间的匹配关系实现道路的匹配。该方法了避免大比例尺道路数据中不相关的道路数据对匹配过程产生干扰,简化了匹配过程,提高匹配的效率和准确率。提取复合网眼的流程如图 7所示。
|
| 图 6 网眼伪匹配关系 Fig. 6 Fake matching relationship of meshes |

|
| 图 7 复合网眼提取流程 Fig. 7 Extraction of composite meshes |
2.1.2 提取M:N匹配关系的复合网眼
在多尺度网眼匹配关系中,对1:1和N:1匹配关系处理后,剩下的还可能存在未匹配网眼,这部分网眼属于M:N匹配关系。存在M:N匹配关系的网眼在空间上呈现“群落”的特点,即若干未匹配网眼往往聚集在一起,通过对群落区域中邻近网眼的合并处理来识别网眼M:N匹配关系。
对呈现群落特点的网眼聚集区域逐个区域处理,处理的过程如下:
(1) 将一个网眼聚集区域整体合并为一个复合网眼,然后对大小比例尺合并后的复合网眼进行匹配,再根据前一节的匹配条件判定这对复合网眼是否匹配,如果匹配,则转入下一个网眼聚集区域的处理,直至完成所有未匹配网眼的匹配,匹配过程停止;如果不匹配,则转到步骤(1)。
(2) 任意选取小比例尺中两个相邻的网眼合并为一个复合网眼,将大比例尺中与之相交且重叠率达到阈值R0的网眼合并为一个复合网眼,判定二者是否匹配,若匹配,则用同样的方法进行余下的网眼匹配处理;若余下的任意两个网眼的合并得到的复合网眼都不能完成匹配,则转入步骤(3)。
(3) 任意选取小比例尺中3个相邻的网眼合并为一个复合网眼,将大比例尺中与之相交且重叠率达到阈值R0的网眼合并为一个复合网眼,判定二者是否匹配,若匹配,则用同样的方法进行余下的网眼匹配处理;若余下的任意3个网眼的合并得到的复合网眼都不能完成匹配,则依次逐个增加相邻的网眼按步骤(3) 重新进行,直至最后完成匹配。然后转入下一个网眼聚集区域的处理,直至所有的网眼匹配判定完成。
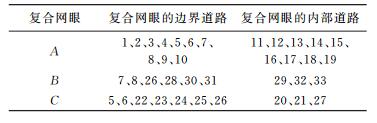
2.2 利用道路网眼匹配进行道路分类处理网眼匹配完成后,根据道路与网眼的拓扑关系进行分类匹配,待匹配道路按类别被划分为网眼边界道路和网眼内部道路。原始道路数据经过拓扑处理后,会在道路交点处被分段,形成节点和弧段。由于道路网眼之间构成的匹配关系不仅仅只有1:1,还存在N:1和M:N,因此需要对复合网眼中的边界道路弧段和内部道路弧段分别进行合并处理,按照Gestalt视觉感知中的良好延续性(good continuation)原则将弧段合并为stroke[23-24]。为了提高道路匹配的效率,需要建立复合网眼与网眼道路之间的拓扑映射关系。如图 8所示为某个尺度的道路网经过网眼匹配识别后,提取得到若干复合网眼,复合网眼与其边界道路以及内部的拓扑映射关系见表 1。

|
| 图 8 道路网及匹配识别的复合网眼 Fig. 8 The road network and composite meshes by matching |
根据网眼匹配结果和道路与网眼的拓扑映射关系,可以快速确定匹配道路所在的网眼,从而大大缩小匹配搜索的范围,提高道路匹配的效率和准确性。
2.3 道路匹配的实现建立匹配关系是将匹配数据映射到参考数据的过程。本文利用网眼匹配约束实现道路匹配,流程为:首先对大比例尺和小比例尺道路网眼进行网眼匹配识别,得到相匹配的道路网眼(复合道路网眼),然后对识别的匹配网眼的边界道路进行匹配,最后对网眼的内部道路进行匹配。首先对网眼边界道路进行匹配。对于已匹配的两个道路网眼,确定网眼边界道路的匹配很容易实现。取小比例尺已匹配道路网眼的某条边(路段),它的匹配对象一定是对应的大比例尺相匹配的道路网眼中的某条边(路段),避免了大范围的搜索,并且一旦确定了某条边的匹配对象,其他边的匹配对象可以根据网眼边的连接次序通过推导得到。
由于网眼的匹配约束,网眼边界道路的匹配判断不需要复杂的相似性计算就可以实现。本文利用Hausdorff距离[25]对已匹配道路网眼的边界道路进行匹配判断,选择距离最小的道路作为匹配对象。
Hausdorff距离最初是用来测定点集之间的距离。设有两个点集合A={a1, a2, …, am}和B={b1, b2, …, bn},则点集A与B之间的Hausdorff距离定义为
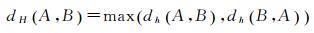 (4)
(4)
式中
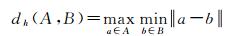 (5)
(5)
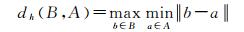 (6)
(6)
dh(A, B)表示点集合A中每一个点到点集合B最小距离的最大值。
线要素可以看作一组有序的点集,因此可以利用Hausdorff距离来衡量线要素之间距离。它反映的是线要素之间的整体距离,比单纯使用欧式距离更加合理,常被用于线要素之间的匹配判断。
已匹配网眼的内部道路,存在两种类型,一种是能够对网眼形成剖分的道路,另一种是未对网眼形成剖分的道路。第1种类型的内部道路,没有匹配对象,不做处理。第2种类型的道路,主要是一些悬挂道路,这类道路的匹配,在对应的匹配网眼内部搜索可能与之匹配的道路。
3 试验与分析 3.1 试验数据本文的试验,选取宁波市的1:25万和1:5万部分道路数据进行匹配试验。首先将两个不同比例尺的道路网数据进行投影、坐标统一变换后叠加显示,如图 9所示,其中1:25万道路网,其数据量为80 KB,382个对象;1:5万道路网,数据量为594 KB, 1588个对象。

|
| 图 9 多尺度道路网数据 Fig. 9 The multi-scale road networks data |
3.2 匹配试验结果
对1:5万和1:25万道路网数据网眼匹配识别,从而提取出两个数据集中构成匹配关系的道路网眼。根据式(1) 初步建立多尺度网眼间的匹配关系,将大比例尺中与同一小比例尺网眼具有匹配关系的网眼进行合并生成初步的复合网眼,经过多次试验,由于试验数据位置误差较小,经试验设定重叠率R0=0.9时较为合适,生成结果如图 10的初步复合网眼,红色区域为待进一步处理的网眼。

|
| 图 10 复合网眼初步提取 Fig. 10 Preliminary extraction of composite meshes |
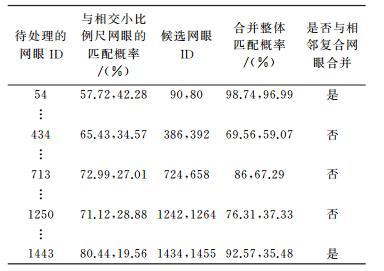
1:5万目标数据中的网眼数为1473,首先进行复合网眼的粗提取,处理掉大部分的大比例尺网眼,得到初步的复合网眼,剩余79个网眼在初步提取复合网眼过程中不满足阈值条件,需要进一步判定处理,如图 10(c)。这部分网眼的判定结果如表 2。
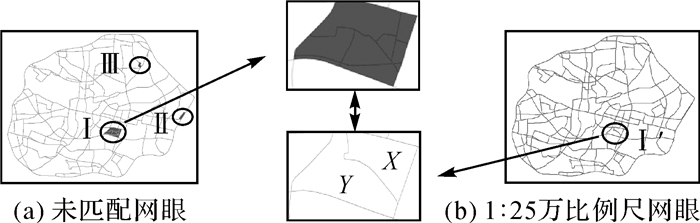
经过进一步的提取,79个待处理网眼中有75个经判定符合合并条件,与相邻的最优复合网眼进行合并处理,然后根据相似性指标Y进行检验,设定的阈值为0.9≤Y≤1.1,7个网眼被解除匹配关系,最终得到11个未匹配网眼,如图 11(a)。在此基础上,在剩下的未匹配网眼中进行M:N匹配。
|
| 图 11 网眼M:N匹配实例 Fig. 11 An example of many-to-many matching of meshes under different scales |
在提取的复合网眼中,Ⅰ处的未匹配网眼形成聚集区域,对应在小比例尺网眼中Ⅰ′处存在未匹配网眼X和Y,根据2.1.2节中的匹配思想,小比例尺中Ⅰ′处的未匹配网眼X和Y组成的复合网眼与大比例尺中Ⅰ处的所有网眼组成的复合网眼形成1:1匹配,实质上是未匹配网眼之间形成了9:2的匹配关系。至此完成了不同比例尺道路网眼数据中所有网眼之间的匹配。
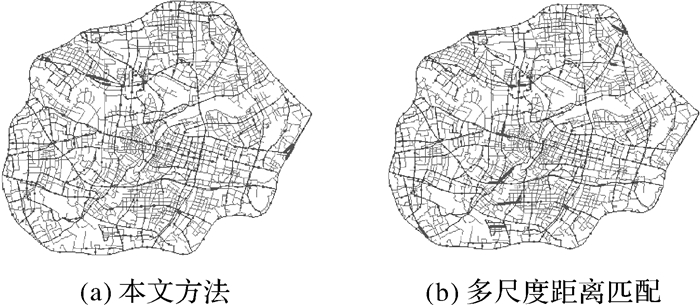
依据网眼匹配识别提取得到的大比例尺复合道路网眼,构成大比例尺道路网的骨架网眼。对提取的匹配网眼的边界道路和内部道路进行按照stroke一致性原则进行合并,并建立道路网眼与道路的拓扑映射关系。经过处理后,原来匹配网眼边界道路之间存在的N:1或M:N匹配关系变为“1:1”匹配关系,减少了待匹配对象的数量,大大简化了匹配的难度,提高了匹配的准确度。对同一数据利用陈玉敏的多尺度道路网的距离匹配算法[17],试验数据的匹配结果如图 12所示,试验统计结果如表 3所示。
|
| 图 12 两种不同方法的多尺度道路匹配结果 Fig. 12 Results of multi-scale match of road in two different methods |
3.3 对比分析
根据试验结果,当数据中出现小短线时,多尺度距离匹配算法在匹配过程中会出现小短线附近的道路与其形成错误匹配,出现这种现象的原因在于算法本身的缺陷,当线要素较短小时,其本身作为点集的数量很少,造成大部分甚至所有点都落入与其相邻的较长道路线要素的缓冲区内,造成错误匹配。而在本文方法中,由于较短小的线要素也是作为网眼的边界要素,在匹配时只需考虑与之所在网眼对应的网眼的边界要素即可,能够出现有效避免这些较短小道路线要素的错误匹配,如图 13所示。
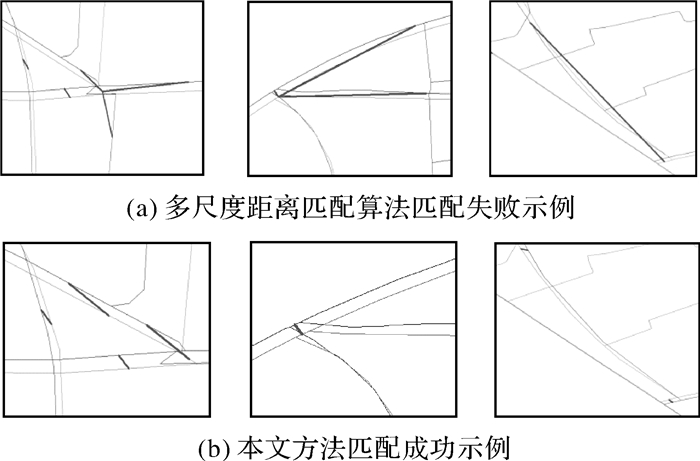
|
| 图 13 两种匹配方法实例对比 Fig. 13 The contrast experiment of the two matching methods |
对于同名道路线要素差异度较大的情况,多尺度距离匹配算法也存在不足,存在无法完成匹配的情况,而本文方法,对形态相似性并没有很高的依赖性,因此在匹配时具有一定的优势。如图 14,形态具有一定差异的同名道路,利用多尺度距离匹配方法未能实现匹配,而本文方法则利用同名要素所在网眼的对应关系较容易地实现了二者的匹配。
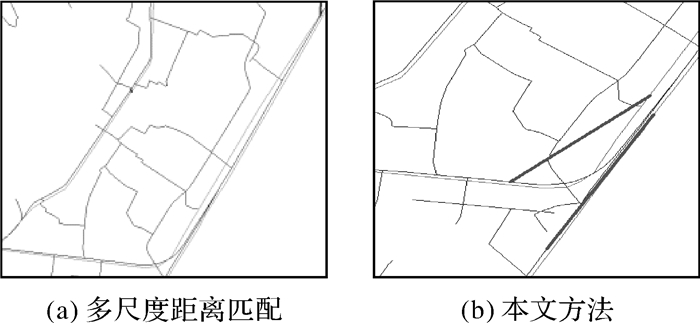
|
| 图 14 匹配方法实例对比 Fig. 14 The contrast experiment of the two matching methods |
通过试验的对比结果可以得出,本文所提算法在匹配率和准确率上相比多尺度距离匹配算法都具有一定优势,原因主要在于以下两点:第一,本文方法利用网眼约束道路,通过对网眼的匹配,使道路的模糊对应关系转变匹配网眼的道路清晰的对应关系,缩小了匹配道路的搜索范围,同时降低了道路本身对位置和形态相似的依赖性,在多尺度匹配中具有较好的现实意义;第二,分类匹配的思想,将道路分为网眼边界道路和内部道路,使匹配被限制在同类别的道路中进行,减少了干扰,提高了匹配对应的准确性。
4 结论道路网的匹配往往采用几何匹配的方式处理,而在多尺度道路网的匹配中,如果不经过提取而直接利用几何特征进行匹配,匹配的效果往往很不理想,原因是道路在不同尺度下的几何形态、拓扑关系和属性信息存在差异,无法保证数据具有稳定的匹配基础,同时大比例尺数据中众多其他的道路数据会对匹配过程产生较大干扰,导致匹配的不确定性增加。本文方法通过网眼匹配提取出主要的道路匹配候选集,排除了不相关道路要素参与到匹配过程中,同时降低了匹配时对道路几何形态的依赖,相比于传统的匹配方法,提高了匹配准确率。
网眼匹配关系的提取是本算法的一个关键,如果位置偏差较大,会对匹配结果产生负面影响。针对这一情况,可以考虑首先选取小比例尺数据中少量高等级骨架道路,构成更大的道路网眼,大网眼抗位置误差的能力更强,首先对这些大网眼进行匹配关系提取,匹配完成后,利用匹配结果进行位置纠正,可以大大减少数据的位置误差,可以有利于提高后续更小道路网眼匹配关系提取的精度。
| [1] | 陈俊杰. 不同尺度下地理实体的一体化组织与表达方法研究[D]. 杭州: 浙江大学, 2011. CHEN Junjie. Study on the Integrative Organization and Representation Method for Geographical Entity in Different Scales[D]. Hangzhou: Zhejiang University, 2011. |
| [2] | 王艳慧, 李小娟, 宫辉力. 地理要素多尺度表达的基本问题[J]. 中国科学E辑:技术科学, 2006, 49(S2): 39–47. WANG Yanhui, LI Xiaojuan, GONG Huili. On Multi-scale Representations of Geographic Features[J]. Science in China Series E: Technological Sciences, 2006, 49(S2): 39–47. |
| [3] | BALLEY S, PARENT C, SPACCAPIETRA S. Modelling Geographic Data with Multiple Representations[J]. International Journal of Geographical Information Science, 2004, 18(4): 327–352. DOI:10.1080/13658810410001672881 |
| [4] | 艾廷华, 成建国. 对空间数据多尺度表达有关问题的思考[J]. 武汉大学学报(信息科学版), 2005, 30(5): 377–382. AI Tinghua, CHENG Jianguo. Key Issues of Multi-scale Representation of Spatial Data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 377–382. |
| [5] | 张强, 武芳, 钱海忠, 等. 基于关键比例尺的空间数据多尺度表达[J]. 测绘科学技术学报, 2011, 28(5): 383–386. ZHANG Qiang, WU Fang, QIAN Haizhong, et al. Milestone Scales Oriented Spatial Data Multi-representation Techniques[J]. Journal of Geomatics Science and Technology, 2011, 28(5): 383–386. |
| [6] | 魏海平. GIS中多尺度地理数据库的研究与应用[J]. 测绘学院学报, 2000, 17(2): 134–137. WEI Haiping. The Research and Application of Multi-scale Geographic Database in GIS[J]. Journal of Institute of Surveying and Mapping, 2000, 17(2): 134–137. |
| [7] | 武芳, 张强, 巩现勇, 等. 一种匹配分类的空间数据多尺度表达与变换模型[J]. 测绘科学技术学报, 2014, 31(4): 331–335. WU Fang, ZHANG Qiang, GONG Xianyong, et al. Matching and Classification Model for Multi-scale Transformation and Representation of Spatial Data[J]. Journal of Geomatics Science and Technology, 2014, 31(4): 331–335. |
| [8] | 徐枫, 邓敏, 赵彬彬, 等. 空间目标匹配方法的应用分析[J]. 地球信息科学学报, 2009, 11(5): 657–663. XU Feng, DENG Min, ZHAO Binbin, et al. A Detailed Investigation on the Methods of Object Matching[J]. Journal of Geo-Information Science, 2009, 11(5): 657–663. |
| [9] | 陈竞男, 钱海忠, 王骁, 等. 提高线要素匹配率的动态化简方法[J]. 测绘学报, 2016, 45(4): 486–493. CHEN Jingnan, QIAN Haizhong, WANG Xiao, et al. Improving the Matching Rate of Line Feature by Using Dynamic Simplification[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 486–493. DOI:10.11947/j.AGCS.2016.20150074 |
| [10] | WALTER V, FRITSCH D. Matching Spatial Data Sets: A Statistical Approach[J]. International Journal of Geographical Information Science, 1999, 13(5): 445–473. DOI:10.1080/136588199241157 |
| [11] | 翟仁健. 基于全局一致性评价的多尺度矢量空间数据匹配方法研究[D]. 郑州: 信息工程大学, 2011. ZHAI Renjian. Research on Automated Matching Methods for Multi-scale Vector Spatial Data Based on Global Consistency Evaluation[D]. Zhengzhou: Information Engineering University, 2011. |
| [12] | SAALFELD A. Conflation Automated Map Compilation[J]. International Journal of Geographical Information Systems, 1988, 2(3): 217–218. DOI:10.1080/02693798808927897 |
| [13] | ZHANG Meng, SHI Wei, MENG Liqiu. A Generic Matching Algorithm for Line Networks of Different Resolutions[C]//Proceedings of the 8th ICA Workshop on Generalisation and Multiple Representation.A Coruña, Spain: [s.n.], 2005. |
| [14] | VOLZ S. An Iterative Approach for Matching Multiple Representations of Street Data[C]//Proceedings of ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data. Hanover, Germany: [s.n.], 2006. |
| [15] | VON GÖSSELN G. A Matching Approach for the Integration, Change Detection and Adaptation of Heterogeneous Vector Data Sets[C]. XXII International Cartography Conference. A Coruña, Spain: The International Cartographic Association, 2005. |
| [16] | 刘海龙, 钱海忠, 王骁, 等. 采用层次分析法的道路网整体匹配方法[J]. 武汉大学学报(信息科学版), 2015, 40(5): 644–651. LIU Hailong, QIAN Haizhong, WANG Xiao, et al. Road Networks Global Matching Method Using Analytical Hierarchy Process[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 644–651. |
| [17] | 陈玉敏, 龚健雅, 史文中. 多尺度道路网的距离匹配算法研究[J]. 测绘学报, 2007, 36(1): 84–90. CHEN Yumin, GONG Jianya, SHI Wenzhong. A Distance-based Matching Algorithm for Multi-scale Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 84–90. DOI:10.3321/j.issn:1001-1595.2007.01.015 |
| [18] | 赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4): 416–421. ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 416–421. |
| [19] | 栾学晨, 杨必胜, 李秋萍. 基于结构模式的道路网节点匹配方法[J]. 测绘学报, 2013, 42(4): 608–614. LUAN Xuechen, YANG Bisheng, LI Qiuping. Pattern-based Node Matching Approach for Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 608–614. |
| [20] | 赵浩. 城市道路分级分类网眼树的提取及其应用[D]. 北京: 北京建筑大学, 2014. ZHAO Hao. Extracting and Application on the Classification of Urban Roads Mesh Tree[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2014. |
| [21] | 翟仁健, 武芳, 黄博华, 等. 城市道路网面域层次结构特征的识别与表达[J]. 测绘科学技术学报, 2014, 31(4): 413–418. ZHAI Renjian, WU Fang, HUANG Bohua, et al. A Method for Recognition and Representation of Areal Hierarchy of Urban Road Networks[J]. Journal of Geomatics Science and Technology, 2014, 31(4): 413–418. |
| [22] | 徐柱, 刘彩凤, 张红, 等. 基于路划网络功能评价的道路选取方法[J]. 测绘学报, 2012, 41(5): 769–776. XU Zhu, LIU Caifeng, ZHANG Hong, et al. Road Selection Based on Evaluation of Stroke Network Functionality[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 769–776. |
| [23] | THOMSON R C, RICHARDSON D E. The 'Good Continuation' Principle of Perceptual Organization Applied to the Generalization of Road Networks[C]//Proceedings of the 19th International Cartographic Conference. Ottawa, Canada: ICA, 1999. |
| [24] | THOMSON R C, BROOKS R. Efficient Generalisation and Abstraction of Network Data Using Perceptual Grouping[C]//Proceedings of the 5th International Conference on GeoComputation. United Kingdom: University of Greenwich, 2000. |
| [25] | HUTTENLOCHER D P, KLANDERMAN G A, RUCKLIDGE W J. Comparing Images Using the Hausdorff Distance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(9): 850–863. DOI:10.1109/34.232073 |