2. 天津市测绘院, 天津 300381;
3. 国土资源部城市土地资源监测与仿真重点实验室, 广东 深圳 518034
2. Tianjin Institute of Surveying and Mapping, Tianjin 300381, China;
3. Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Land and Presources, Shenzheng 518034, China
在大数据时代,越来越多的领域如金融、电商、医疗等开始有意识地收集和积累数据,数据量增速越来越快,在这些数据中,57%的信息与空间相关[1]。大数据所蕴含的时空特征、分布规律等空间知识可以通过抽象概括用数字、自然语言表达,也可以采用基于视觉语言的可视化表达方式。而基于视觉语言的可视化表达方式更为直接,具有形象、易感受等特点。可视化在数据挖掘中发挥了重要的作用,已产生了许多有效的可视化挖掘工具并得到了广泛的应用,如平行坐标轴[2]、Treemap[3]等。在空间数据挖掘中,地图常作为知识表达工具将空间信息和挖掘分析得到的结果形象化展现,或是与其他的可视化数据挖掘工具(如平行坐标轴)相结合来表现空间数据[4]。而有关地图作为知识挖掘工具探索和挖掘空间知识的研究较少[5]。
空间关联规则是空间数据挖掘的重要组成部分,同位模式是空间关联规则的重要类型,同位模式表示布尔空间要素子集,这些子集的实例频繁地同时出现于地理邻近区域[6]。同位模式挖掘应用领域广泛,涉及生态和环境管理、公共安全、城市规划、商业和旅游等多领域,如对犯罪事件的依赖关系进行分析以服务于公共安全[7],移动商务服务商根据邻近用户的服务请求模式提供基于位置的广告和推荐服务[8],对苏果超市与其他零食连锁超市的竞争关系进行分析以指导新超市选址[9]。
同位模式挖掘可以分为针对欧氏空间以及针对网络空间(人为现象和事件通常邻近、沿着或发生于网络,如交通事故、街头犯罪、城市基础设施的分布等,这些现象被称为网络空间现象,可抽象表达为位于网络上或邻近网络的点[10-11])两类。对于欧氏空间,空间同位模式的挖掘主要采用两类方法[6]:空间统计方法和数据挖掘方法。空间统计方法使用空间相关性指标描述不同类型空间要素的关系,包括交叉k函数[12],平均最近邻距离,空间回归模型[13],同位系数[14]以及改进的地理加权同位系数[15]。数据挖掘方法可分为基于聚类的叠置方法[7]以及基于关联规则的方法[16-17]。基于关联规则的方法主要通过将事务的概念泛化,选择同位模型定义事务,然后设计类似的Apriori算法以挖掘同位模式。由于空间异质性的存在,同一空间不同区域内可能存在特殊的局部同位模式,有少量文献对区域同位模式进行了探索,将空间同位模式挖掘方法应用于用户事先指定的空间区域集[18],或使用k-mediods算法划分聚类的方式搜索区域同位模式[19],或基于k最近邻图挖掘区域同位模式[20]。对于网络空间,同位模式挖掘方法的研究较少,这也是本研究所关注的问题。由于网络空间与欧氏空间性质不同,网络空间是离散的而欧氏空间是连续的,网络空间是异质的而欧氏空间是同质的,网络空间采用最短路径距离作为距离测度而欧氏空间采用欧氏距离,网络空间分析不能直接运用平面欧式空间的方法[21-22]。目前,网络空间同位模式挖掘的方法主要有网络交叉k函数,网络交叉最近邻距离[23],以及对网络进行划分定义同位模型进行统计推断的方法[24]。
以上同位模式挖掘方法均是采用统计或是数据挖掘的方式,属于抽象思维的范畴,要求对复杂的数学公式、算法和相关参数等有深刻的理解。本文提出一种基于色彩加色法的网络空间同位模式可视化挖掘方法,可顾及空间异质性,探索局部同位模式,属于形象思维范畴,具有直观、形象和易感受等特点。
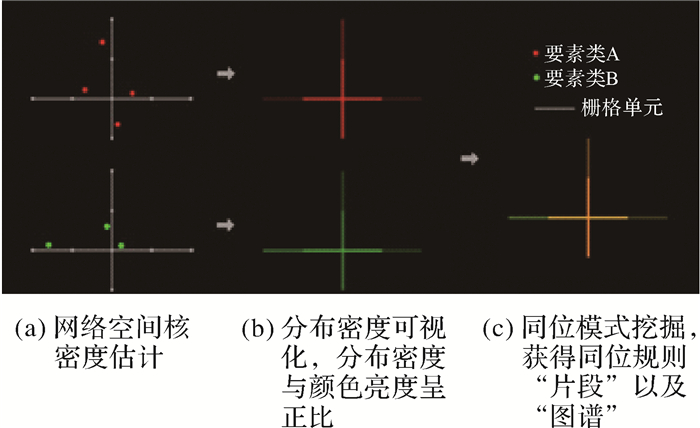
1 方法本方法利用视觉语言表达网络空间现象之间的影响和交互作用,建立视觉与网络空间现象之间影响和交互作用的认知之间的联系,挖掘网络空间同位模式。首先,建立单个地理现象分布情况与颜色之间的映射,然后进行颜色混合获得两地理现象相互影响的认知。具体来说,对于两个要素类,首先采用网络空间核密度估计方法表征单个要素类的网络空间影响域,根据计算得到的核密度属性对两个要素类的分布密度进行可视化;然后基于色光加色混合原理,对两个不同要素类的可视化结果进行色彩混合,获得同位规则“片段”以及同位规则“图谱”,如图 1所示。
|
| 图 1 网络空间同位模式可视化挖掘主要流程 Fig. 1 The main process of a visualization method for network co-location mining |
1.1 网络空间核密度估计
空间现象的交互效应遵循地理学第一定律,受距离衰减效应的影响。网络空间核密度估计顾及了地理学第一定律,是一种网络空间中点密度的计算方法,可用于表达网络空间现象的分布情况和影响范围,为网络空间同位模式的挖掘提供支持。目前已有多种网络空间核密度估计算法提出[11, 25-26],计算结果表现出距离核心越近的区域所受中心辐射值越大的特征。
核密度的公式定义为
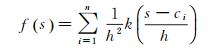 (1)
(1)
式中,f(s)是位置s处的核密度计算函数;h为距离衰减阈值;n为与位置s的距离小于或等于h的要素点数;k函数表示权重函数。不同的权重函数对最后的结果影响不大。本文以4次空间权重函数为例
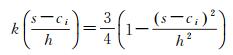 (2)
(2)
对网络空间进行离散化,建立栅格空间,即将网络在交叉点打断后再按一定长度l打断,得到栅格单元集,设栅格单元为Li,其中i=1, 2, …,n, n为网络空间所包含的栅格单元个数。计算单个要素类的分布密度。本文采用文献[27]的算法得到单个要素类的分布密度,每个栅格单元都获得一个密度属性值Ki。对于两个要素类A和B,设要素类A对应的栅格单元密度属性值为K_Ai,要素类B对应的栅格单元密度属性值为K_Bi。
1.2 同位规则“片段”及“图谱”的构建根据网络空间核密度估计的结果,建立颜色与单个地理现象分布情况之间的映射,然后基于颜色混合的原理,获得两地理现象相互影响和交互作用的认知,挖掘同位模式。
加色混合又称色光混合,是指不同的色光或色料的反射光同时或在极短的时间内刺激了视网膜,从而产生另一种新色调的混合形式[27]。
色光三原色为红(R)、绿(G)、蓝(B)。
加色混合的基本规律:
(1) 将三原色光等量混合,可得到白光(W),R+G+B=W。
(2) 将三原色光中任意两色光等量混合,可分别得出青(C)、品红(M)、黄(Y)。
G+B=C,R+G=Y,B+R=M。
(3) 两原色光非等量混合,颜色偏向比例大的一方。
(4) 原色光混合后的亮度高于原有色光的亮度。
(5) 相混合的各色光的能量值相加,等于被混合色光能量的值。
本文使用RGB颜色空间表示颜色。颜色空间由颜色的3个参数组成的颜色三维空间,3个参数在对应的三维空间用色量的均匀变化相交织起来,构成一个理想的颜色空间。颜色空间中的任何一点都代表某一特定颜色。RGB颜色空间是用色光三原色来描述物体颜色特征,其取值范围为0~255,数值越大,颜色能量越大、越明亮。
根据要素类栅格单元密度属性值K_Ai,K_Bi设置栅格单元的颜色,不同要素类所设置的栅格单元的颜色分别为C_Ai,C_Bi,由RGB 3个参数(R, G, B)描述,然后对两不同颜色的栅格单元进行颜色混合,混合后栅格单元颜色为C_A & Bi,其中i=1, 2, …n, n为网络空间所包含的栅格单元个数。采用RGB颜色空间描述颜色。
单个要素类颜色设置的公式如下所示
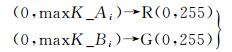 (3)
(3)
式中,→为颜色映射算子,将单个要素类栅格单元密度属性值映射到某一颜色参数。对于要素类A,C_Ai(R, 0, 0),K_Ai与R参数值呈正比。对于要素类B,C_Bi(0, G, 0),K_Bi与G参数值呈正比。栅格单元密度属性值越大,其颜色能量越大、越明亮。
不同要素的栅格单元完成分布情况的色彩渲染后,进行栅格单元的颜色混合。不同颜色的栅格单元进行颜色混合公式如下
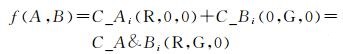 (4)
(4)
式中,f(A, B)为颜色混合公式,基于加色混合原理,将两类要素对应的栅格单元进行颜色混合,颜色的各参数分别相加,得到由新颜色渲染的栅格单元,每个栅格单元可看作一个同位规则“片段”。对于完成颜色混合后的栅格单元Li,当R=G,即两原色光等量混合时,得到黄色(Y);当R≠G,即两原色光非等量混合时,颜色偏向比例大的一方。图 2显示了不同分布密度的两个要素类的颜色混合情况,短线表示栅格单元。如第一列以及第一行所示,要素类A的分布密度使用红光表示,要素类B的分布密度使用绿光表示,密度值越高颜色能量越大越亮,当密度值为0时,颜色为(0, 0, 0)。表格中主对角线上栅格单元为能量不同的黄光,从表格左上角到右下角颜色能量逐渐增大,颜色变亮。在栅格单元的尺度下,右下角栅格单元同位模式最强;由副对角线中点向左下角和右上角两顶点同位模式减弱,栅格单元颜色偏红,表明要素类A占优,栅格单元颜色偏绿,表明要素类B占优。

|
| 图 2 同位规则“片段” Fig. 2 Co-location rule "segment" |
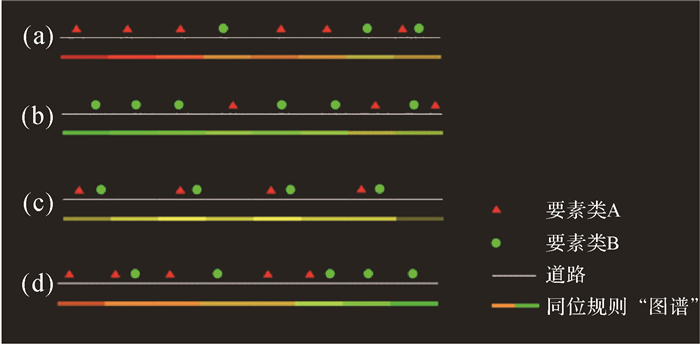
道路由栅格单元组成,同位规则“片段”组合形成同位规则“图谱”。如图 3所示,在同位规则“图谱”的尺度上,即某一路段的尺度上,同位规则“图谱”可分为3类。某一要素占优型,如图 3(a)的同位规则“图谱”由色相偏红的同位规则“片段”组成,表明要素类A占优,图 3(b)的同位规则“图谱”由色相偏绿的同位规则“片段”组成,表明要素类B占优。同位模式强,如图 3(c)的同位规则“图谱”由色相偏黄的同位规则“片段”组成,表明要素类A和要素类B在这条路段上同位规则强。同位模式较强,如图 3(d)的同位规则“图谱”包含色相偏黄的同位规则“片段”以及数量大体一致的色相偏红以及偏绿的同位规则“片段”。
|
| 图 3 同位规则“图谱” Fig. 3 Co-location rule "map" |
1.3 基于加色混合同位模式挖掘方法的分析
同位模式的数据挖掘方法中,同位规则定义为:A⇒B(CS, CC%),A∩B=Ø,CS表示支持度,CC%表示置信度。本文可视化方法所得结果与数据挖掘方法所计算所得结果间有一定的联系。设进行色彩混色前,要素类A对应的道路颜色的R参数不为0,G参数和B参数为0,要素类B对应的道路颜色的G参数不为0,R参数和B参数为0,完成道路色彩混合得到同位规则“图谱”。观察同位规则“图谱”,粗略来看,同位规则A⇒B的支持度与呈图 3(c)和图 3(d)模式的道路占总道路的百分比相关,且百分比越高、色光能量越高,支持度越高,同位规则A⇒B和同位规则B⇒A的支持度相等。同位规则A⇒B的置信度与呈图 3(c)和图 3(d)模式的道路色光能量占颜色R值不为0的道路色光能量的百分比相关。同位规则A⇒B和同位规则B⇒A的置信度不相等。
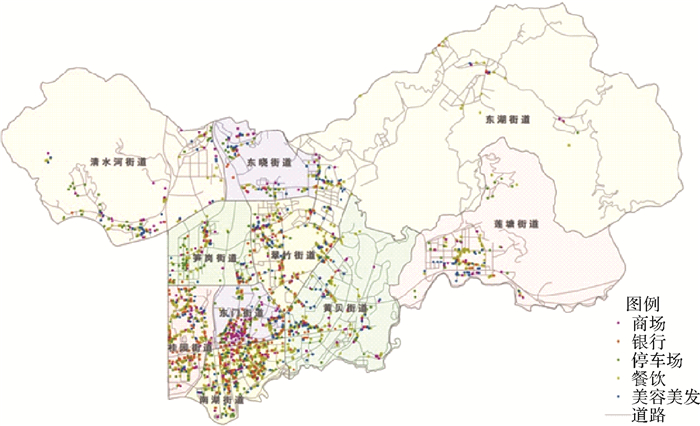
2 试验 2.1 数据基于上述思想,本文基于C#语言,采用ArcGIS Add-in开发了试验工具。以深圳市罗湖区为研究区域,采用1:1000比例尺的路网数据,以城市商业服务设施POI(point of interest)为分析对象,具体包括商场(339个POI点)、银行(315个POI点)、停车场(339个POI点)、餐饮(1345个POI点)、美容美发(373个POI点)。试验目的是挖掘商场与其他商业服务设施间的同位规则(商场⇒其他商业服务设施)。
2.2 结果与分析首先,采用网络空间核密度估计方法表征单个商业服务设施的网络空间影响域。将网络空间离散化,本文采用25 m的栅格单元。确定式(1) 中网络空间核密度估计距离衰减阈值,本文选择公共服务设施布局中为基本步行圈层范围(500 m)[28]作为距离衰减阈值。根据式(1)、式(2) 计算不同商业服务设施在网络空间中的密度,每个栅格单元获得各商业服务设施的密度属性值。
然后,对不同要素在网络空间中的分布情况进行可视化。依据式(3) 对单个商业服务设施的颜色设置,其中商场所对应路网颜色的G参数和B参数为0,其他商业服务设施所对应路网颜色的R参数和B参数为0,得到不同商业服务设施的分布热力图,如图 5所示。商场、餐饮、银行停车场的分布热点位于罗湖火车站——国贸——东门一带(图中白色圈所示),并沿着深南东路发展(带双箭头白线所示),符合罗湖区将罗湖火车站——国贸——东门一带建设成市级的商业核心区以及将深南路建设成市级商贸发展轴的规划(1998—2010年)。笋岗片区也出现停车场的分布热点(图 5(c)橙黄色圈所示),这一现象可能与落户区将笋岗片区建设成为市级以消费性物流为主的物流中心的规划有关。而美容美发热点分布较为分散。
|
| 图 4 研究区域 Fig. 4 Study area |

|
| 图 5 深圳罗湖区部分商业服务设施分布可视化结果 Fig. 5 Visualization of the distribution of some of the commercial service facilities in Luohu district |
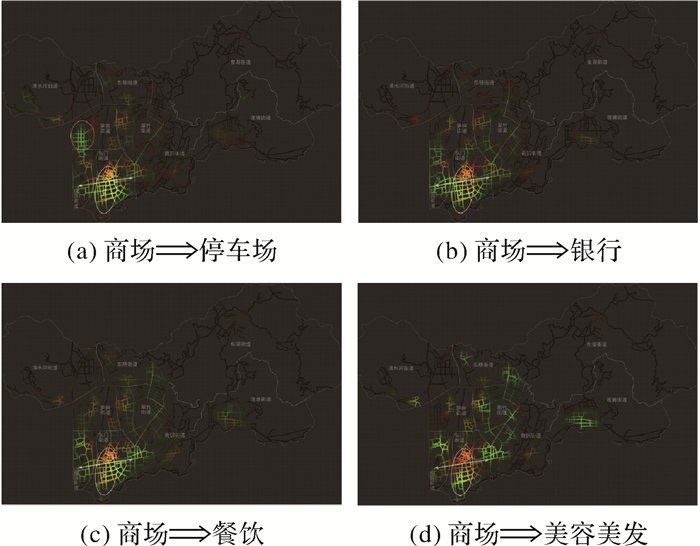
最后,基于加色混合原理获得商业服务设施间的同位规则图谱。根据式(4),将商场对应的栅格单元分别与其他商业服务设施对应的栅格单元进行颜色混合,得到图 6的结果。
|
| 图 6 深圳罗湖区部分商业服务设施同位规则“图谱” Fig. 6 Co-location rule "map" of some of the commercial service facilities in Luohu district |
在整个区域尺度上,商场⇒停车场同位规则“图谱”中(图 6(a)),道路多呈现偏黄(与图 3(c)相近)或是由红到绿渐变(与图 3(d)相近)的模式,说明商场和停车场总是频繁出现在地理邻近的区域,商场⇒停车场的同位模式最强。商场⇒餐饮同位规则“图谱”中(图 6(c)),多呈现偏绿(与图 3(b)相近)以及部分偏黄(与图 3(c)相近)的模式,说明餐饮占占优,商场⇒餐饮的同位模式较强。商场⇒银行同位规则“图谱”中(图 6(b)),部分道路呈现偏黄(与图 3(c)相近)或是由红到绿渐变(与图 3(d)相近)的模式,说明商场⇒银行的同位模式较强。商场⇒美容美发同位规则“图谱”中(图 6(d)),多呈现偏绿(与图 3(b)相近)以及部分偏红(与图 3(a)相近)的模式,说明商场⇒美容美发的同位模式很弱。
局部来看,如图 6(a)、(b)、(c)所示,商业核心区罗湖火车站——国贸——东门一带(图中白色圈所示),商场和银行,商场和停车场,商场和餐饮总是频繁出现在邻近的区域,特别是在南湖社区与东门社区交界一带同位模式最强。如图 6(a)所示,由于笋岗片区是物流中心(图中橙黄色圈所示),该地区呈现亮绿色,停车场的分布“占优”。
3 结论可视化在知识发现、数据挖掘中扮演了重要角色。本文提出了一种基于色彩加色法的可视化挖掘网络空间同位模式的方法。与已有同位模式挖掘方法不同,该方法属于可视化挖掘方法,也是首次将可视化用于同位模式挖掘。该方法具有以下优点:可同时挖掘空间同位模式以及由于空间异质性的存在造成的局部同位模式;顾及地理学第一定律,考虑地理现象受到距离衰减效应的影响;具有直观,形象、易感受和易理解等特点。
下一步研究将集中在两个方面:① 单个要素类颜色设置的颜色映射方法,式(3) 未对→为颜色映射算子进行明确规定,采用何种变换需根据实际情况,考虑多种因素,如分布密度的统计分布特征,人对色彩的感受等; ② 同位模式的量化表达方法,有些情况下,仅有视觉感受可能还不够。
| [1] | HAHMANN S, BURGHARDT D. How Much Information is Geospatially Referenced? Networks and Cognition[J]. International Journal of Geographical Information Science, 2013, 27(6): 1171–1189. DOI:10.1080/13658816.2012.743664 |
| [2] | INSELBERG A. The Plane with Parallel Coordinates[J]. The Visual Computer, 1985, 1(2): 69–91. DOI:10.1007/BF01898350 |
| [3] | JOHNSON B, SHNEIDERMAN B. Tree-maps: A Space-filling Approach to the Visualization of Hierarchical Information Structures[C]//Proceedings of IEEE Conference on Visualization, 1991. San Diego, CA: IEEE, 1991: 284-291. |
| [4] | OPACH T, RØD J K. Do Choropleth Maps Linked with Parallel Coordinates Facilitate An Understanding of Multivariate Spatial Characteristics?[J]. Cartography and Geographic Information Science, 2014, 41(5): 413–429. DOI:10.1080/15230406.2014.953585 |
| [5] | 艾廷华. 大数据驱动下的地图学发展[J]. 测绘地理信息, 2016, 41(2): 1–7. AI Tinghua. Development of Cartography Driven by Big Data[J]. Journal of Geomatics, 2016, 41(2): 1–7. |
| [6] | HUANG Y, SHEKHAR S, XIONG H. Discovering Colocation Patterns from Spatial Data Sets: A General Approach[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(12): 1472–1485. DOI:10.1109/TKDE.2004.90 |
| [7] | ESTIVILL-CASTRO V, LEE I. Data Mining Techniques for Autonomous Exploration of Large Volumes of Geo-referenced Crime Data[C]//Proceedings of the 6th International Conference on GeoComputation. Brisbane: University of Queensland, 2001: 24-26. |
| [8] | YOO J S, SHEKHAR S. A Joinless Approach for Mining Spatial Colocation Patterns[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(10): 1323–1337. DOI:10.1109/TKDE.2006.150 |
| [9] | RUI Yikang, YANG Zaigui, QIAN Tianlu, et al. Network-constrained and Category-based Point Pattern Analysis for Suguo Retail Stores in Nanjing, China[J]. International Journal of Geographical Information Science, 2016, 30(2): 186–199. DOI:10.1080/13658816.2015.1080829 |
| [10] | YAMADA I, THILL J C. Local Indicators of Network-constrained Clusters in Spatial Point Patterns[J]. Geographical Analysis, 2007, 39(3): 268–292. DOI:10.1111/gean.2007.39.issue-3 |
| [11] | BORRUSO G. Network Density Estimation: A GIS Approach for Analysing Point Patterns in A Network Space[J]. Transactions in GIS, 2008, 12(3): 377–402. DOI:10.1111/tgis.2008.12.issue-3 |
| [12] | CRESSIE N. Statistics for Spatial Data[M].2nd ed. New York: John Wiley & Sons, 2015. |
| [13] | CHOU Y H. Exploring Spatial Analysis in Geographic Information Systems[M].Santa Fe, NM: OnWord Press, 1997. |
| [14] | LESLIE T F, KRONENFELD B J. The Colocation Quotient: A New Measure of Spatial Association between Categorical Subsets of Points[J]. Geographical Analysis, 2011, 43(3): 306–326. DOI:10.1111/j.1538-4632.2011.00821.x |
| [15] | CROMLEY R G, HANINK D M, BENTLEY G C. Geographically Weighted Colocation Quotients: Specification and Application[J]. The Professional Geographer, 2014, 66(1): 138–148. DOI:10.1080/00330124.2013.768130 |
| [16] | SHEKHAR S, HUANG Yan. Discovering Spatial Co-location Patterns: A Summary of Results[M]//JENSEN C S, SCHNEIDER M, SEEGER B, et al. Advances in Spatial and Temporal Databases. Berlin Heidelberg: Springer, 2001: 236-256. |
| [17] | 边馥苓, 万幼. k-邻近空间关系下的空间同位模式挖掘算法[J]. 武汉大学学报(信息科学版), 2009, 34(3): 331–334. BIAN Fuling, WAN You. A Novel Spatial Co-location Pattern Mining Algorithm Based on k-nearest Feature Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 331–334. |
| [18] | CELIK M, KANG J M, SHEKHAR S. Zonal Co-location Pattern Discovery with Dynamic Parameters[C]//Proceedings of the 7th IEEE International Conference on Data Mining. Omaha: IEEE, 2007: 433-438. |
| [19] | EICK C F, PARMAR R, DING Wei, et al. Finding Regional Co-location Patterns for Sets of Continuous Variables in Spatial Datasets[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Irvine, CA: ACM, 2008: 30. |
| [20] | QIAN Feng, CHIEW K, HE Qinming, et al. Mining Regional Co-location Patterns with kNNG[J]. Journal of Intelligent Information Systems, 2014, 42(3): 485–505. DOI:10.1007/s10844-013-0280-5 |
| [21] | BORRUSO G. Network Density Estimation: A GIS Approach for Analysing Point Patterns in A Network Space[J]. Transactions in GIS, 2008, 12(3): 377–402. DOI:10.1111/tgis.2008.12.issue-3 |
| [22] | OKABE A, SUGIHARA K. Spatial Analysis along Networks: Statistical and Computational Methods[M].Chichester, West Sussex: John Wiley & Sons, 2012. |
| [23] | OKABE A, YAMADA I. The K-function Method on A Network and Its Computational Implementation[J]. Geographical Analysis, 2001, 33(3): 271–290. |
| [24] | 田晶, 王一恒, 颜芬, 等. 一种网络空间现象同位模式挖掘的新方法[J]. 武汉大学学报(信息科学版), 2015, 40(5): 652–660. TIAN Jing, WANG Yiheng, YAN Fen, et al. A New Method for Mining Co-location Patterns Between Network Spatial Phenomena[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 652–660. |
| [25] | OKABE A, SATOH T, SUGIHARA K. A Kernel Density Estimation Method for Networks, its Computational Method and a GIS-based Tool[J]. International Journal of Geographical Information Science, 2009, 23(1): 7–32. DOI:10.1080/13658810802475491 |
| [26] | 禹文豪, 艾廷华, 刘鹏程, 等. 设施POI分布热点分析的网络核密度估计方法[J]. 测绘学报, 2015, 44(2): 1378–1383. YU Wenhao, AI Tinghua, LIU Pengcheng, et al. Network Kernel Density Estimation for the Analysis of Facility POI Hotspots[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 1378–1383. DOI:10.11947/j.AGCS.2015.20140538 |
| [27] | 程杰铭, 陈夏洁, 顾凯. 色彩学[M].2版. 北京: 科学出版社, 2006. CHENG Jieming, CHEN Xiajie, GU Kai. Chromatology[M].2nd ed. Beijing: Science Press, 2006. |
| [28] | 郭迁一. 深圳市基本生活单元公共服务设施配置研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. GUO Qianyi. Research on the Public Service Facilities' Allocation of Basic Living Unit in Shenzhen[D]. Harbin: Harbin Institute of Technology, 2012. |


