2. 地球空间信息协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
随着对地观测卫星技术的发展,高分辨率的遥感影像已经应用到城市规划、作物分类、灾害检测等领域[1]。影像分割作为高分辨率遥感影像信息提取与目标识别的前提和基础,是实现从数据到信息的对象化提取的过渡环节和关键步骤,具有十分重要的地位[2]。相对于中低分辨率遥感影像高分辨率遥感影像拥有更加丰富的地物信息,如清晰的地物轮廓形状信息、明显的纹理信息等,但也增加了影像噪声对影像分割的影响[3-4]。传统的基于像素的影像分割方法如mean-shift算法[5]、分水岭算法[6]等易受高分辨率影像中“椒盐”噪声的影响,难以得到理想的分割结果。面向对象的影像分割方法可以克服影像中“椒盐”噪声的影响[7],并利用对象的结构、光谱信息等特征提高影像分割的精度,如文献[1]结合对象结构和光谱特征实现影像分割,文献[8]利用对象光谱、结构和纹理信息分割影像,文献[9]结合对象形状和光谱特征进行影像分割,文献[10]利用对象光谱和纹理实现影像分割,eCognition软件中的FNEA算法根据对象形状与光谱实现影像分割[11],但面向对象的影像分割方法需要调整分割尺度来获得合适的影像分割结果,而合适的分割尺度又难以确定。
针对影像分割方法易受噪声影响,且难以确定合适影像分割尺度的问题,本文提出一种融合超像素与最小生成树的高分辨率遥感影像分割方法。用简单线性迭代聚类(simple linear iterative clustering,SLIC)算法对影像过分割生成超像素,克服影像噪声对影像分割的影响。用基于最小生成树分割思想的区域动态约束聚类(regionalization with dynamically constrained agglomerative clustering and partitioning,REDCAP)算法对超像素初次合并获得分割数-方差和、分割数-局部方差、分割数-局部方差变化率指标图,根据3个指标图获得合适的影像分割数,再次用REDCAP算法对超像素重新聚类合并得到最终的影像分割结果。通过定性对比试验和定量评价验证本文方法的有效性。
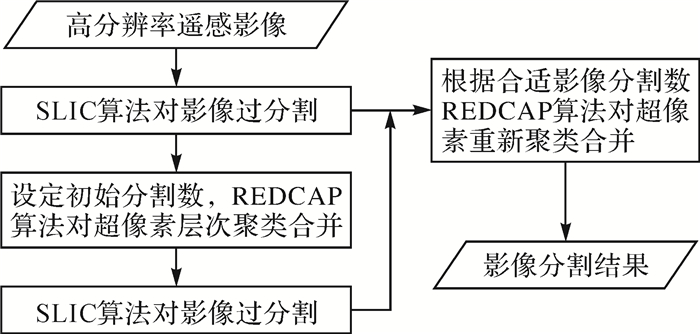
1 方法本文方法主要分为4个步骤:① SLIC算法对影像过分割生成超像素;② 设定初始影像分割数,用REDCAP算法对超像素层次聚类合并;③ 得到每次合并的分割数对应的方差和(sum of squared deviations,SSD)、局部方差(local variance,LV)、局部方差变化率(rate of LV change,ROC-LV)指标图,确定合适的影像分割数;④ 根据合适影像分割数用REDCAP算法对超像素重新聚类合并。总体流程图如图 1所示。
|
| 图 1 分割流程图 Fig. 1 The flow chart of the proposed approach |
1.1 超像素的生成
文献[12]提出了超像素这一概念,所谓超像素是指具有相似纹理、颜色、亮度等特征的相邻像素构成的图像块。文献[13]提出SLIC算法生成超像素。该算法将彩色图像转换为CIELAB颜色空间和XY坐标下的5维特征向量,然后对5维特征向量构造度量标准,对图像像素进行局部聚类生成超像素[14]。相对于分水岭算法、区域增长算法、基于图的图像分割算法[15]等传统的影像过分割算法生成的超像素,SLIC算法生成的超像素具有更好的地物边界依附性、更加规则紧凑的形状,并且SLIC算法可以人为控制生成超像素的个数和具有良好的抗噪性[16]。SLIC算法的具体步骤为:
(1) 初始化种子点。假设影像中有N个像素点,预设将影像分为K个大小均匀超像素,则每个超像素的大小为N/K。将初始划分矩形格网中心处的像素作为超像素的种子点,且每个种子点间的距离近似为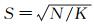
(2) 相似性度量。计算影像中像素与种子点间的相似程度,将最相似种子点的标签赋给该像素。通过不断迭代相似性判断过程,直到收敛,则相似性的度量关系如下
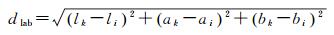 (1)
(1)
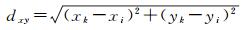 (2)
(2)
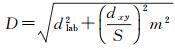 (3)
(3)
式中,[lk ak bk xk yk]为种子点的5维特征向量;[li ai bi xi yi]为待判断像素点的5维特征向量;dlab为像素点间的颜色差异;dxy为像素点间的空间距离;D为两个像素的相似度;S为种子点的间距;m为平衡参数,用来衡量颜色值与空间信息在相似度衡量中的比重。D取值越小,说明两个像素越相似。
对于影像中像素与种子点相似性判断时,只在以种子点为中心的2S×2S区域内搜索相似像素点,而不是在整张图像中寻找,如图 2所示。

|
| 图 2 像素搜索范围示意图 Fig. 2 Pixel search scope |
(3) 后续处理。SLIC算法有时会使属于同一标签的超像素内的像素不连通,会产生一些孤立的像素。对于这种现象在聚类分割结束后进行后续处理,使孤立像素被重新分配到距离它空间距离最近的超像素中,从而生成紧凑且连通的超像素。
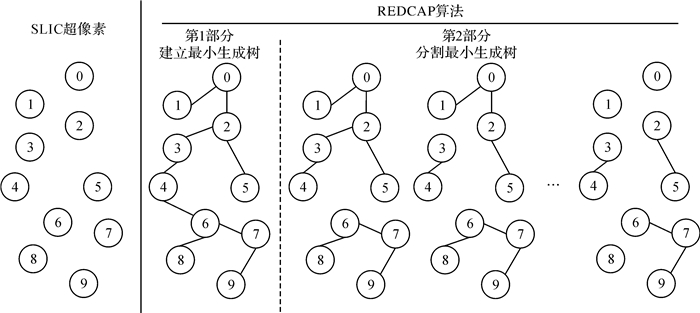
1.2 超像素的合并REDCAP算法[17]是一种动态的区域聚类算法,该算法可以充分利用各区域间的属性差异与邻接关系进行区域合并,使最终合并在同一簇中的区域具有最大的同质性。该算法首先根据区域间的邻接关系与属性差异建立连接各区域的最小生成树,在生成最小生成树的过程中根据Full-Older-CLK规则实时调整属于不同簇的相邻区域间的相似性差异,在最小生成树生成后,根据切割树得到的子树中包含的区域同质性最大原则切割树,最终切割生成一系列子树,这些子树中所包含的区域即被合并在一起。本文中把超像素作为区域单元,用REDCAP算法对超像素进行聚类合并,REDCAP算法合并超像素的流程示意图如图 3所示。
|
| 图 3 超像素合并流程示意图 Fig. 3 Diagram of merging superpixles |
统计每个超像素所包含的像素点的光谱均值作为超像素的光谱属性值,本文的试验数据为经融合后的包含3个波段的遥感影像,3个波段分别作为R、G、B波段,则超像素的光谱属性为Si(Ri、Gi、Bi),则光谱属性计算公式如式(4)-(6) 所示
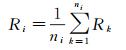 (4)
(4)
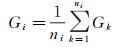 (5)
(5)
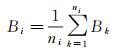 (6)
(6)
相邻超像素之间的属性差异Ci, j计算公式如式(7) 所示
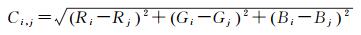 (7)
(7)
式中,ni为第i个超像素所包含的像素点的个数;Rk、Gk、Bk为第i个超像素中包含的第k个像素点的R、G、B属性值;Ci, j为超像素i与超像素j之间的光谱差异。
1.3 分割数的确定和超像素的重新合并REDCAP算法唯一的参数设置是输入最终生成子树的个数即最终影像的分割数,当切割生成多少子树时能够得到合适的影像分割结果,这里涉及到尺度问题。关于研究空间格局的最佳尺度,文献[18]认为在某一空间分辨率水平下,若空间格局得以体现并且模型运行的结果能获得有重要意义的转变,那么这个空间分辨水平就是合适的,或者说对于研究该问题来说是最佳的。文献[19]提出用量测不同分辨率景观地物之间的相互关系,通过利用一个n×n像素的移动窗口,来计算窗口内像素光谱属性标准差的均值,即局部方差,最后形成局部方差曲线图得到最佳影像分辨率。其中包含的逻辑思想是“如果影像的空间分辨率优于场景中物体的大小,n×n窗口内像素相似性较高,求得的局部方差值较低。如果影像的空间分辨率与场景中物体大小相近,n×n窗口内像素相似性较低,求得的局部方差值较高。通过局部方差探索影像中像素间的自相关性”[20]。
文献[21]对局部方差法进行改进提出尺度参数评价(estimation of scale parameter,ESP)理论,用多尺度分割代替n×n窗口,求得不同分割尺度对应的LV值。根据不同尺度对应的LV值得到分割尺度-LV曲线图,在曲线图趋于平稳时对应的尺度能有效反应影像的空间结构,则影像有意义的分割尺度处于该尺度范围内。在有意义的尺度范围内求得不同尺度对应的ROC-LV值,画出分割尺度-ROC-LV曲线图,分割尺度-ROC-LV曲线图反映LV值从一种物体到另一种物体的改变,在曲线图中当ROC-LV值剧烈变化时对应的尺度是有意义的,根据得到的有意义尺度获得影像的多尺度分割结果。
目前通过局部方差思想求影像有意义的分割结果,均是自下而上获得分割尺度-LV曲线图,需要设定影像的分割尺度阈值[22-23]。本文结合ESP理论与REDCAP算法合并超像素的过程提出自上而下求得影像合适尺度,用REDCAP算法对超像素不同层次的合并情况表示不同尺度下影像的分割结果。REDCAP算法对超像素合并,首先生成连接所有超像素的最小生成树,根据设定分初始分割数对最小生成树进行分割,在分割过程中以每次分割生成子树中包含的超像素区域作为每次分割情况下求LV值、SSD值的计算窗口,获得不同分割数对应的LV值、SSD值,画出分割数-LV值、分割数-SSD值、分割数-ROC-LV曲线图。观察分割数-SSD值与分割数-LV值曲线图,确定曲线图平稳时分割数所在区间范围,则合适的影像分割数处于该区间范围内。在分割数-ROC-LV值曲线图中,在确定的合适影像分割数所在区间范围内,当ROC-LV值剧烈变化时对应的分割数即为合适的影像分割数。
根据得到的合适影像分割数用REDCAP算法对超像素重新聚类合并,得到最终的影像的分割结果。
对超像素进行聚类合并,每次合并的影像分割数对应的SSD、LV、ROC-LV的计算公式如下
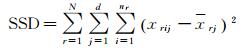 (8)
(8)
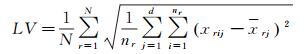 (9)
(9)
式中,N为设定的分割数即分割得到的子树的个数;r为设定的N棵子树中第r棵子树的标签;i为标签为r的子树中第i个超像素的标签;j为标签为i的超像素属性j的标签;nr为标签为r的子树中所包含的超像素的个数;d为超像素的属性个数;xrij为子树r中i超像素的j属性值;xrj为子树r中所有超像素的j属性均值
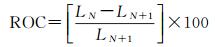 (10)
(10)
式中,LN为分割数为N的LV值;LN+1为分割数为N+1的LV值;所求的ROC值即为分割数为N所对应的ROC-LV指标。
1.4 分割结果评价分割结果评价是影像分割研究中必不可少的一步,虽然已经提出了多种分割评价方法,但目前仍没有统一的标准评价流程[1]。本文采用目视判别与定量评价相结合的方法对本文方法的有效性进行评价。
目视判别是一种最基本、最常用的评价方法。通过目视判别可以直观地观察分割结果中区域的几何形态、过分割、欠分割等情况。而且,只有分割结果和目视评价的效果吻合时,定量评价指标才能使人信服[24]。因此,在目视判别的基础上采用Kappa系数[25]和对象一致性误差(object-level consistency error,OCE)[26]对本文方法进行定量评价。其中Kappa系数表述了分割方法对地物分类结果与真实的地物分类结果的一致性程度,Kappa系数的取值范围为[0,1],当Kappa系数越大时说明分割方法对地物的分类结果与真实地物的分类结果越一致。OCE来描述分割方法的分割结果与真实的分割结果一致性程度,OCE评价方法可以有效地评价图像的过分割与欠分割现象,OCE满足0≤OCE(Ig, Is)≤1,其中,Ig为地面参考对象,Is为实际分割对象;当OCE=0时,表示分割完全符合地面参照对象。相比较而言,OCE越小,表示分割效果越好。
为了更加全面的评价本文方法的性能,将本文方法的分割结果与EDSION软件中mean-shift分割算法和eCognition软件中FNEA算法进行了对比评价。
2 试验结果与分析所使用的试验平台CPU为Inter(R) Pentium(R)双核,2 GB内存,Windows7操作系统。本文方法用VC++6.0软件进行编程实现。采用两幅QuickBird高分辨率影像来验证本文方法的有效性。用mean-shift算法和FNEA算法调整参数进行多次分割试验,并采用目视解译的方式选择整体效果最佳的分割结果与本文方法分割结果进行对比。
2.1 试验1 2.1.1 试验数据试验1使用的数据为美国佛罗里达州城区的QuickBird全色及红、绿、蓝多波段经PANSHARPEN融合后的影像,影像大小为512×512像素,各波段分辨率为0.61 m。该影像主要包括房屋、道路、湖泊、树林等地物如图 4(a),影像过分割生成超像素的结果如图 4(b)。

|
| 图 4 试验1影像数据 Fig. 4 Remote sensing image of test 1 |
2.1.2 影像分割数选择
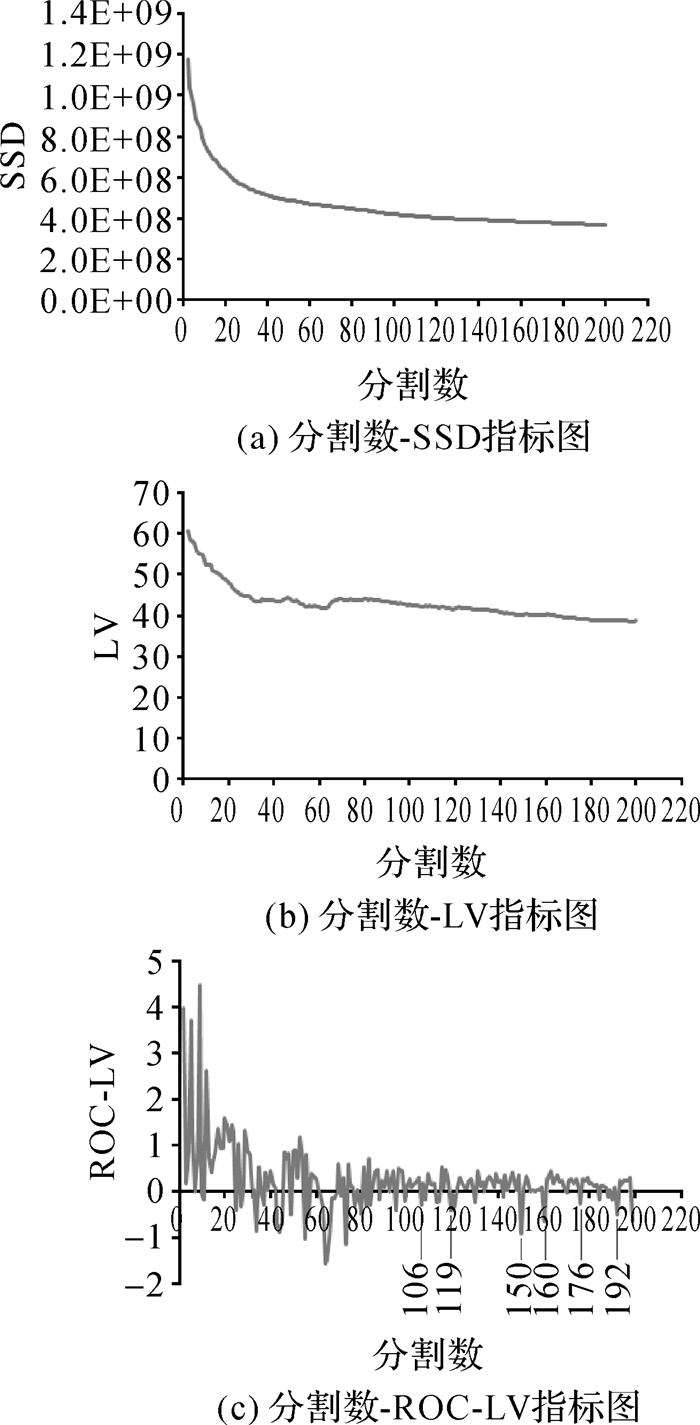
用REDCAP算法对超像素进行聚类合并,初始设定把超像素合并为200个区域,根据每次合并的分割数对应的SSD值、LV值、ROC-LV值,画出分割数-SSD值、分割数-LV、分割数-ROC-LV指标图如图 5(a)、(b)、(c)。在图 5(a)、图 5(b)中当分割数大于100时走势图趋于平稳,则影像合适的分割数处于分割数大于100的范围内。在图 5(c)中,当分割数为106、119、150、160、176、192时ROC-LC值剧烈变化,则将超像素合并为106、119、150、160、176、192个区域时对应的分割结果是有意义的,经过目视判别当超像素合并为106个区域时整体分割效果最好,则将超像素合并为106个区域时作为影像的分割结果。
|
| 图 5 试验1指标图 Fig. 5 The index chart of test 1 |
2.1.3 目视评价
图 6(a)为影像的目视解译结果;图 6(b)为mean-shift算法的影像分割结果,其参数设置为:minimum region=200,spatial=5,color=6.5;图 6(c)为FNEA算法的影像分割结果,其参数设置为:shape=0.1, compactness=0.7,scale=100;图 6(d)为本文方法把影像分割为106个区域的分割结果。在矩形框标定的区域内,FNEA算法难以区分出光谱相似的建筑物与道路对象,出现欠分割现象,而mean-shift算法与本文方法可以较好地区分建筑物与道路。两个箭头所指的湖泊区域,在内部光谱特征变化较大的湖泊区域内mean-shift算法产生了大量的过分割现象,而FNEA算法和本文方法的分割结果与目视解译结果基本一致。总的来说,FNEA算法难以区分出光谱相似的不同地物,mean-shift算法在内部光谱特征变化较大的同种地物区域内易产生过分割现象,而本文方法可以较好地平衡影像分割的过分割与欠分割现象。

|
| 图 6 试验1结果 Fig. 6 The experimental results of test 1 |
2.1.4 定量评价
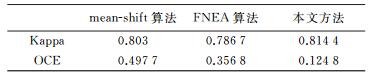
表 1列出了3种不同算法对影像分割结果的Kappa系数和OCE系数的评价情况。在表 1中本文方法的Kappa系数大于mean-shift算法与FNEA算法,说明本文方法对地物分类结果优于mean-shift算法和FNEA算法,此外本文方法的Kappa系数为0.814 4,说明本文方法对地物的分类结果与实际地物的分类结果基本一致。本文方法的OCE指标为0.124 8,低于mean-shift算法的0.497 7和FNEA算法的0.356 8,说明本文方法与目视解译分割结果更一致。
2.2 试验2 2.2.1 试验数据
试验2使用的数据为美国佛罗里达州郊区的QuickBird全色及红、绿、蓝多波段经PANSHARPEN融合后的影像,影像大小为512×512像素,分辨率为0.61 m。影像中主要包括道路、河流、森林、草地、耕地等地物如图 7(a)。对影像过分割处理生成超像素结果如图 7(b)。

|
| 图 7 试验2影像数据 Fig. 7 Remote sensing image of test 2 |
2.2.2 影像分割数选择
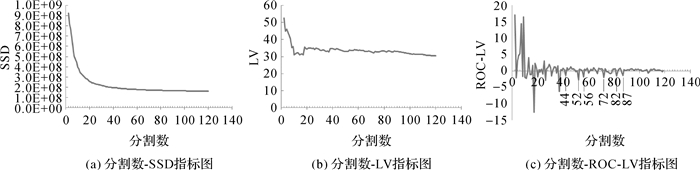
初始设定REDCAP算法把超像素合并为120个区域,得到每次合并的分割数对应的SSD值、LV值、ROC-LV值,根据得到的分割数对应的SSD值、LV值、ROC-LV值画出分割数-SSD、分割数-LV、分割数-ROC-LV指标图如图 8(a)、(b)、(c)。在分割数-SSD指标图、分割数-LV指标图中当分割数大于40时走势图基本趋于平稳,则影像合适的分割数处于分割数大于40的范围内。在分割数-ROC-LV指标图中,当分割数为44、52、56、72、82、87时ROC-LV值发生剧烈变化,则分割数为44、52、56、72、82、87时的分割结果是有意义的,经过目视对比观察当分割数为44时影像的整体分割结果最好,则影像合适的分割数为44。
|
| 图 8 试验2指标图 Fig. 8 The index chart of test 2 |
2.2.3 目视评价
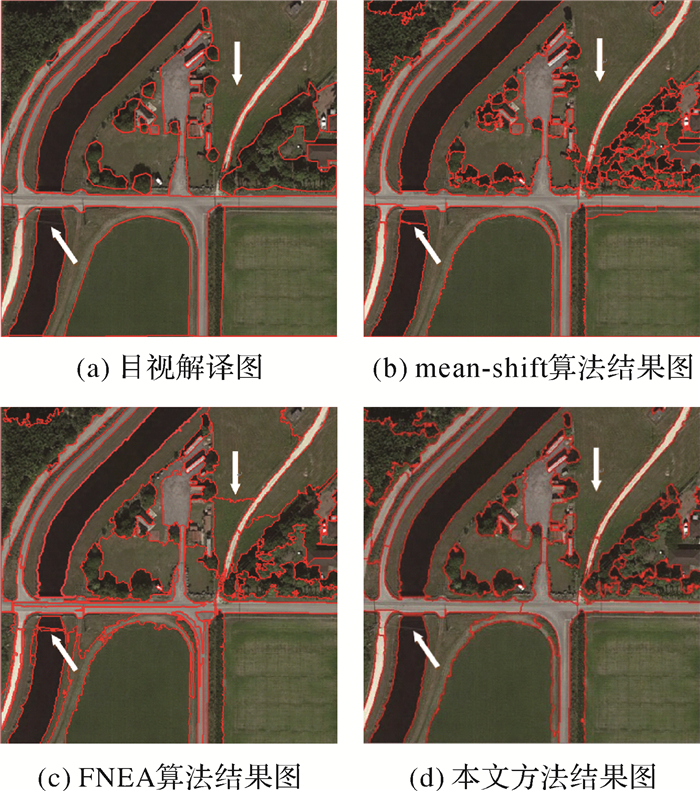
图 9(a)为影像的目视解译图;图 9(b)为影像的mean-shift算法结果图,算法参数设置为:minimum region=200,spatial=7,color=6.5;图 9(c)为影像的FNEA算法结果图,其参数设置为:shape=0.1, compactness=0.9,scale=100;图 9(d)为本文方法把影像分割为44个区域的试验结果。在箭头所指的草地区域FNEA算法产生过分割现象,而本文算法与目视解译基本一致,说明本文方法在内部光谱特征变化较大的草地区域可以得到更好的分割结果。在箭头所指的河流区域mean-shift算法与FNEA算法把明显的一条河流分为两段,出现过分割现象,而本文方法可以正确地分割这段河流。从整体上对比观察3种算法的分图与目视解译图,本文方法分割结果图与目视解译图更接近,说明本文方法可以得到良好的影像分割结果。
|
| 图 9 试验2结果 Fig. 9 The experimental results of test 2 |
2.2.4 定量评价
表 2列出了在mean-shift算法、FNEA算法与本文方法对影像分割结果Kappa系数和OCE系数的评价。本文方法的Kappa系数为0.841 7大于mean-shift算法的0.747 4与FNEA算法的0.794 8,本文方法可以更好的区分各地物类型,对各地物的分类结果与实际地物的分类结果基本上一致。本文方法的OCE指标为0.369低于mean-shift算法的0.502 5与FNEA算法的0.688 4,说明本文方法对影像有更好的分割结果。
3 结论
针对影像分割易受噪声影响、难以确定合适影像分割数的问题,本文提出一种融合超像素与最小生成树的高分辨率遥感影像分割方法,该方法首先用SLIC算法对影像进行过分割生成SLIC超像素克服影像噪声对分割结果的影响。用REDCAP算法对SLIC超像素进行两次区域划分,首次划分得到分割数对应的SSD值、LV值、ROC-LV值指标图确定合适的影像分割数,再次划分是根据合适影像分割数用REDCAP算法对SLIC超像素重新进行区域划分从而得到影像分割结果。通过两组试验对本文方法与mean-shift算法、FNEA算法进行定性与定量对比评价,本文方法可以良好地平衡影像分割中的过分割与欠分割现象,获得整体分割效果良好的影像分割结果。下一步将对本文方法进行算法优化提高运行效率。
| [1] | 刘婧, 李培军. 结合结构和光谱特征的高分辨率影像分割方法[J]. 测绘学报, 2014, 43(5): 466–473. LIU Jing, LI Peijun. A High Resolution Image Segmentation Method by Combined Structural and Spectral Characteristics[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 466–473. DOI:10.13485/j.cnki.11-2089.2014.0087 |
| [2] | 周成虎, 骆剑承. 高分辨率卫星遥感影像地学计算[M].北京: 科学出版社, 2009. ZHOU Chenghu, LUO Jiancheng. Geo-computing of High Resolution Satellite Remote Sensing Image[M].Beijing: Science Press, 2009. |
| [3] | YI Lina, ZHANG Guifeng, WU Zhaocong. A Scale-synthesis Method for High Spatial Resolution Remote Sensing Image Segmentation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 4062–4070. DOI:10.1109/TGRS.2012.2187789 |
| [4] | LI Deren, ZHANG Guifeng, WU Zhaocong, et al. An Edge Embedded Marker-based Watershed Algorithm for High Spatial Resolution Remote Sensing Image Segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(10): 2781–2787. DOI:10.1109/TIP.2010.2049528 |
| [5] | COMANICIU D, MEER P. Mean Shift: A Robust Approach toward Feature Space Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603–619. DOI:10.1109/34.1000236 |
| [6] | VINCENT L, SOILLE P. Watersheds in Digital Spaces: An Efficient Algorithm Based on Immersion Simulations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(6): 583–598. DOI:10.1109/34.87344 |
| [7] | ZHANG Xueliang, XIAO Pengfeng, FENG Xuezhi, et al. Toward Evaluating Multiscale Segmentations of High Spatial Resolution Remote Sensing Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3694–3706. DOI:10.1109/TGRS.2014.2381632 |
| [8] | 巫兆聪, 胡忠文, 张谦, 等. 结合光谱、纹理与形状结构信息的遥感影像分割方法[J]. 测绘学报, 2013, 42(1): 44–50. WU Zhaocong, HU Zhongwen, ZHANG Qian, et al. On Combining Spectral, Textural and Shape Features for Remote Sensing Image Segmentation[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 44–50. |
| [9] | 李慧, 唐韵玮, 刘庆杰, 等. 一种改进的基于最小生成树的遥感影像多尺度分割方法[J]. 测绘学报, 2015, 44(7): 791–796. LI Hui, TANG Yunwei, LIU Qingjie, et al. An Improved Algorithm Based on Minimum Spanning Tree for Multi-scale Segmentation of Remote Sensing Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 791–796. DOI:10.11947/j.AGCS.2015.20140060 |
| [10] | YUAN Jiangye, WANG Deliang, LI Rongxing. Remote Sensing Image Segmentation by Combining Spectral and Texture Features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 16–24. DOI:10.1109/TGRS.2012.2234755 |
| [11] | BAATZ M, SCHÄPE A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-scale Image Segmentation[J]. Journal of Photogrammetry and Remote Sensing, 2000, 58(3-4): 12–23. |
| [12] | REN Xiaofeng, MALIK J. Learning a Classification Model for Segmentation[C]//Proceedings of 9th IEEE International Conference on Computer Vision. France: IEEE, 2003: 10-17. |
| [13] | ACHANTA R, SHAJI A, SMITH K, et al. SLIC Superpixels Compared to State-of-the-art Superpixel Methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274–2282. DOI:10.1109/TPAMI.2012.120 |
| [14] | 王春瑶, 陈俊周, 李炜. 超像素分割算法研究综述[J]. 计算机应用研究, 2014, 31(1): 6–12. WANG Chunyao, CHEN Junzhou, LI Wei. Review on Superpixel Segmentation Algorithms[J]. Application Research of Computers, 2014, 31(1): 6–12. |
| [15] | FELZENSZWALB P F, HUTTENLOCHER D P. Efficient Graph-based Image Segmentation[J]. International Journal of Computer Vision, 2004, 59(2): 167–181. DOI:10.1023/B:VISI.0000022288.19776.77 |
| [16] | 董志鹏, 梅小明, 陈杰, 等. 简单线性迭代聚类的高分辨率遥感影像分割[J]. 遥感信息, 2016, 31(6): 83–88. DONG Zhipeng, MEI Xiaoming, CHEN Jie, et al. Image Segmentation of High Resolution Remote Sensing Imagery Based on Simple Linear Iterative Clustering[J]. Remote Sensing Information, 2016, 31(6): 83–88. |
| [17] | GUO D. Regionalization with Dynamically Constrained Agglomerative Clustering and Partitioning (REDCAP)[J]. International Journal of Geographical Information Science, 2008, 22(7): 801–823. DOI:10.1080/13658810701674970 |
| [18] | 明冬萍, 王群, 杨建宇. 遥感影像空间尺度特性与最佳空间分辨率选择[J]. 遥感学报, 2008, 12(4): 529–537. MING Dongping, WANG Qun, YANG Jianyu. Spatial Scale of Remote Sensing Image and Selection of Optimal Spatial Resolution[J]. Journal of Remote Sensing, 2008, 12(4): 529–537. |
| [19] | WOODCOCK C E, STRAHLER A H. The Factor of Scale in Remote Sensing[J]. Remote Sensing of Environment, 1987, 21(3): 311–332. DOI:10.1016/0034-4257(87)90015-0 |
| [20] | LEES B. The Spatial Analysis of Spectral Data: Extracting the Neglected Data[J]. Applied GIS, 2006, 2(2): 14.1–14.13. |
| [21] | DRĂGUŢ L, TIEDE D, LEVICK S R. ESP: A Tool to Estimate Scale Parameter for Multiresolution Image Segmentation of Remotely Sensed Data[J]. International Journal of Geographical Information Science, 2010, 24(6): 859–871. DOI:10.1080/13658810903174803 |
| [22] | MING Dongping, LI J, WANG Junyi, et al. Scale Parameter Selection by Spatial Statistics for GeOBIA: Using Mean-shift Based Multi-scale Segmentation as an Example[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 106: 28–41. DOI:10.1016/j.isprsjprs.2015.04.010 |
| [23] | MING Dongping, CI Tianyu, CAI Hongyue, et al. Semivariogram-based Spatial Bandwidth Selection for Remote Sensing Image Segmentation with Mean-Shift Algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 813–817. DOI:10.1109/LGRS.2011.2182604 |
| [24] | LI Peijun, GUO Jiancong, SONG Benqin, et al. A Multilevel Hierarchical Image Segmentation Method for Urban Impervious Surface Mapping Using very High Resolution Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2011, 4(1): 103–116. DOI:10.1109/JSTARS.2010.2074186 |
| [25] | 许妙忠, 丛铭, 万丽娟, 等. 视觉感受与Markov随机场相结合的高分辨率遥感影像分割法[J]. 测绘学报, 2015, 44(2): 198–205, 213. XU Miaozhong, CONG Ming, WAN Lijuan, et al. A Methodology of Image Segmentation for High Resolution Remote Sensing Image Based on Visual System and Markov Random Field[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 198–205, 213. DOI:10.11947/j.AGCS.2015.20130453 |
| [26] | POLAK M, ZHANG Hong, PI Minghong. An Evaluation Metric for Image Segmentation of Multiple Objects[J]. Image and Vision Computing, 2009, 27(8): 1223–1227. DOI:10.1016/j.imavis.2008.09.008 |