2. 辽宁工程技术大学测绘与地理科学学院, 辽宁 阜新 123000;
3. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
2. School of Surveying, Mapping and Geoinformation Science, Liaoning Technology University, Fuxin 123000, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
几何精度是衡量国产测绘遥感卫星性能的重要指标之一。在光学立体测绘应用中,相比于平面精度,高程精度由于受基高比、平台稳定性等因素影响难以保证。激光雷达(light detection and ranging,LiDAR)作为一种高精度测距仪器,因具有方向性好、测距精度高等特点,被广泛用于航天航空摄影测量领域获取高精度高程信息[1-3]。在星载激光测高方面,美国、欧空局等开展的地球、月球和火星等天体探测中都含有LiDAR传感器,如对地观测GLAS系统[4]、对火星观测的MOLA系统[5]、对空间小行星观测的NLR系统、对月球观测的CLEMENTINE系统[6]以及我国对月观测的嫦娥一号LiDAR系统[7]等,大多主要用于制作天体表面的三维地形。
2016年5月30日,我国在太原卫星发射中心成功发射了资源三号02星,它是继资源三号01星[8-9]后的一颗立体测绘业务卫星。该星在国内首次搭载了一台用于对地观测的试验性载荷--激光测高仪,用于开展地表高程测量试验,其基本参数如表 1所示。
在星载激光测高仪地面研制与测试过程中,由于激光光束能量集中且受到外界影响较小,在实验室标定后,一般具有很高的指向和测距精度。然而随卫星发射升空,由于火箭推力产生的力矩变化、平台振动、外界环境变化等因素影响,星上有效载荷与平台的相对安装关系等可能会发生变化[10-12],从而引起激光平面及高程误差。此外,卫星在500 km左右轨道高度发射激光脉冲至地面,经过大气层时将产生大气延迟等,这些都会带来测距误差。
美国ICESat上搭载的GLAS系统是当前世界上主要的对地观测激光测高仪。针对GLAS存在的系统误差,国内外研究学者开展了很多检校方法研究。文献[13-15]采用海平面作为参考,通过卫星姿态机动,环绕观测固定目标来获取GLAS测距观测值,从而改正指向误差。文献[16-17]通过在检校场内布设可捕获卫星过顶时激光光斑红外信号的探测器来消除系统误差。文献[18-19]通过机载红外相机获取地面布设的一系列红外发射器基准点,实现激光指向和测距检校。文献[20-21]通过角锥棱镜(CCR)在反射波中产生的独特信号,获取其在GLA01数字波形中的时间信息,从而标定时间同步误差。文献[22-24]在选取加州和南极两个地区,利用仿真的波形与已知参考地形对比来检校激光的指向和测距误差。
由于资源三号02星只具备整星横滚侧摆能力,无法满足卫星机动检校需求。作为试验性载荷,搭载的激光测距仪仅仅提供测距信息而不下传波形数据,基于波形仿真与地形参考匹配等几何检校方法并不适用。本文针对资源三号02星激光测高仪特点,提出基于地面探测器的激光测高仪在轨几何检校方法,该方法在分析了激光测高仪、卫星平台、地球椭球面等几何关系的基础上,构建了以指向和测距为系统误差的严密几何检校模型,以激光测距值残差最小为原则,利用地面探测器捕获的激光光斑位置作为参考,实现系统误差参数高精度在轨几何检校。利用卫星在轨测试期间多个试验场数据进行检校后,并利用ALOS DSM等数据和外业控制点作为参考,对检校后激光测高精度进行全面分析与验证,试验结果表明了该方法的有效性和正确性。
1 激光几何检校与高程精度分析 1.1 激光测距原理如图 1所示,激光测距是根据激光脉冲渡越的时间来获取距离值。根据波形确定激光脉冲的时间差

|
| 图 1 激光渡越时间示意图 Fig. 1 Shematic diagram of laser transit time |
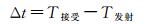 (1)
(1)
激光到观测表面的距离可表示为
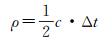 (2)
(2)
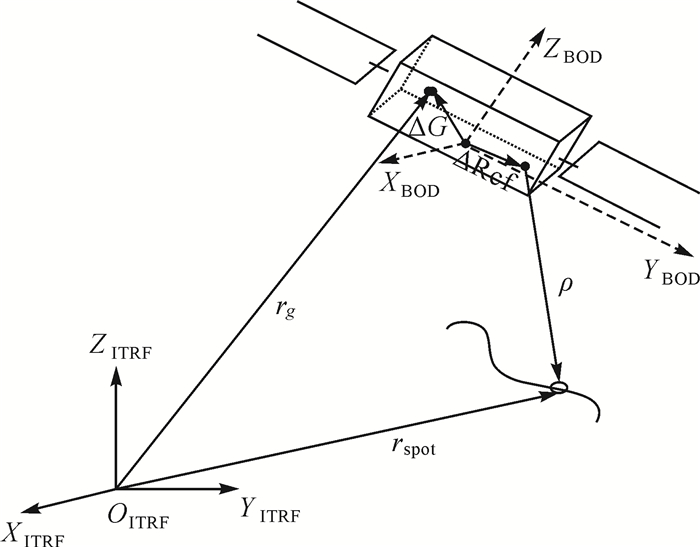
激光测高几何模型示意图如图 2所示,星载激光测高仪通过发射和接受激光脉冲的时间差来推算目标到卫星的距离,再根据卫星的姿态轨道参数解算出卫星到该目标处参考椭球的距离,从而得到目标距离参考椭球的相对高程信息。
|
| 图 2 激光测高仪几何模型 Fig. 2 The geometric model of laser altimeter |
综合考虑卫星平台质心、激光器发射位置、GPS天线以及地球椭球面的相对位置偏移和旋转几何关系,构建严密的星载激光测高仪几何检校模型,矩阵形式如式(3) 所示
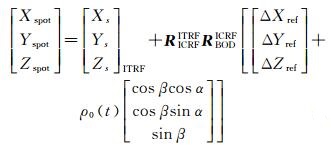 (3)
(3)
式中, 


将式(3) 转换为测距值的表达式
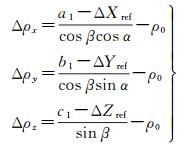 (4)
(4)
式中,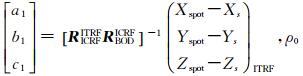
激光出光参考点到地面光斑的距离误差可以表示为
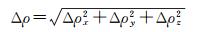 (5)
(5)
以激光到地面光斑质心的测距残差最小为原则,根据测距和指向角的关系,可将式(5) 列误差方程为
 (6)
(6)
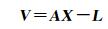 (7)
(7)
式中,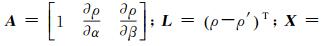
将检校的指向角、测距参数代入式(3) 中,利用对应时刻的姿态和轨道信息,计算激光点在WGS-84地心直角坐标系下三维坐标[Xspot Yspot Zspot]T,将其转化到大地坐标,从而得到激光光斑在WGS-84椭球下大地坐标[B L H]T。
转换公式为
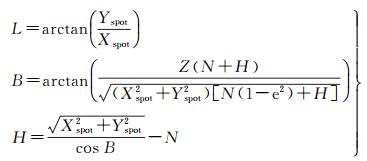 (8)
(8)
式中,N为椭球面卯酉圈的曲率半径;e为椭球的第一偏心率;H为计算出的激光点椭球高,如果参考DEM或者实测外业点高程为海拔高,进行重力高程异常改正即可。
利用平面坐标(B,L)在公开的参考DEM数据中内插椭球高程值H′,或者在该平面位置外业实测控制点椭球高程值H′。此时以内插或实测得到的高程值H′为参考真值来评价激光几何模型解算的H,计算二者的差值,即
 (9)
(9)
依次对整轨所有激光点进行计算,并进行高程残差统计,若整轨有n个激光点,统计高程残差的均值及中误差为
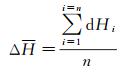 (10)
(10)
 (11)
(11)
将以上高程残差的均值ΔH及中误差σH作为激光高程精度的评价指标。
2 检校试验分析与验证 2.1 在轨几何检校试验与分析 2.1.1 检校试验数据获取2016年8月9日至8月29日,在内蒙古苏尼特右旗开展了资源三号02星激光测高仪外业在轨几何检校试验,试验场地如图 3所示,该区域地形平坦,多为草场。试验期间天气晴朗,云量较少。根据激光几何定位预报位置信息进行激光探测器布设。探测器按照沿轨和垂轨方向布设成矩形阵列,两探测器之间设定等间距。矩形阵列的长度取决于激光足印位置在沿轨和垂轨方向上的预报精度。8月9日过境,探测器之间间隔设置为20 m,8月14日过境探测器间隔为25 m,8月29日过境探测器间隔为10 m。激光探测器布设现场如图 4所示,其中,图 4(a)为卫星过境时布设的激光探测器阵列,图 4(b)为用于捕获激光足印的能量探测器。

|
| 图 3 激光地面几何检校场 Fig. 3 Laser altimeter calibration site |

|
| 图 4 激光探测器阵列布设 Fig. 4 Laser detector array |
利用高精度地面足印位置预报,提前在外业布设激光探测器,成功捕获到了激光足印,探测器响应的激光足印能量阵列经预处理后,其分布如图 5所示。从图 5可以看出,激光足印的能量峰值和分布并不完全一致,这主要是由于卫星三次过境的大气条件不尽相同。激光光束经过大气折射和散射后,地面足印中所呈现的能量峰值和分布也会有所差异。此外,尽管地面探测器试验前进行响应一致性定标,在试验中仍然会出现一些偏差,可能也是导致激光足印的能量峰值和分布并不完全一致的原因之一。

|
| 图 5 试验捕获的激光光斑能量分布三维视图 Fig. 5 3D view of energy distribution in captured laser footprints |
2.1.2 大气校正
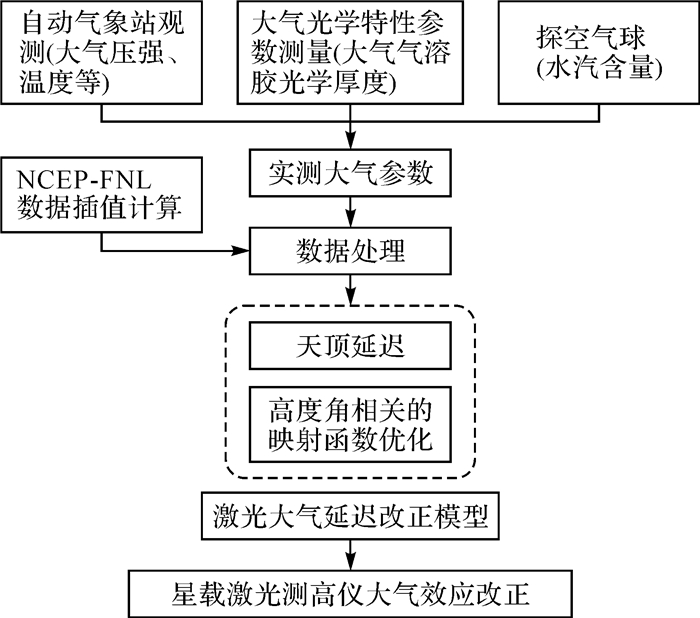
星载激光测高仪发射的激光束穿过大气层时受大气折射影响,引起激光脉冲传输延迟。结合资源三号02星激光测距仪参数,试验选择映射函数模型,利用附近气象观测站探空气球获取的大气数据,计算星载激光测高仪大气折射延迟改正量。技术流程如图 6所示,计算的大气延迟改正结果如表 2所示。
|
| 图 6 基于同步观测的星载激光测高仪大气效应改正技术流程 Fig. 6 Atmospheric effect correction based on synchronous observation |
2.1.3 在轨几何检校分析
试验采用2016年8月9日、8月14日和8月29日3个检校场获取的激光足印中心坐标作为地面控制,先采用单检校场独立以及多检校场联合等不同组合方式对资源三号02星激光测高仪系统参数进行标定,再利用3个检校场数据对检校结果进行外推验证,从而反映各参数的检校精度。发射前实验室指向测定值为激光光轴与卫星平台的X、Y和Z三轴的夹角。为了便于比较,统一将本方法标定的指向参数α、β转换为三轴夹角,然后给出了与设计指向的偏差。联合检校时可以检校指向和测距值。由于单场控制少,仅能检校指向误差,因此,测距偏差主要为硬件系统误差。不同检校场数据下的检校结果与地面设计值的偏差以及该参数外推到其他检校场的验证结果如表 3所示。
将表 3中3个检校场分别独立检校出的激光指向参数,转换到激光视轴指向矢量后,计算矢量夹角,发现夹角变化量为5~8个角秒。这部分误差主要是由于指向标定过程中,姿态、轨道、测距以及地面探测器中心位置等误差引入。在精密定轨和大气校正后,轨道和测距误差影响较小,而星敏和陀螺联合处理确定的姿态随机误差大约在3个角秒左右。另外为了保证试验成功率,其中两次试验布设的地面探测器间隔较大,分别为20和25 m。激光足印中心位置提取精度在10 m左右,引起指向误差在4个角秒。从总体上看,3个时段的指向无系统趋势变化,说明这段时间指向检校结果相对比较稳定。此外对比多场联合检校的测距误差与单场的测距误差,变化量在0.02 m以内,非常稳定。
从表 3可以看出,基于单一检校场检校后,利用其他检校场参考数据进行验证,平面精度优于20 m,高程精度优于0.9 m。利用3个检校场数据进行联合检校后进行验证,可以看出,平面精度优于10 m,高程精度优于0.7 m,平面和高程精度较单场检校均有明显提升,说明单个检校场观测数据少,且无法兼顾系统误差参数随时间变化部分,因此检校精度相对较低,因此试验将联合检校参数作为最终检校结果。
2.2 检校前后激光高程精度对比与分析为了分析检校前后激光测高精度变化情况,本文采用两种不同的地面参考数据进行验证和评价,一是利用公开的全球DEM数据评价其相对精度;二是利用激光足印内外业实测的控制点评价其绝对精度。其中,由于全球DEM数据精度有限,本文仅仅利用其评价得出的相对精度来说明检校是否消除了激光测高仪高程测量的系统误差。而利用激光足印内外业实测的控制点对比得出的绝对精度,则为激光测高仪的高程精度评价指标。
2.2.1 基于全球DEM的相对高程精度分析当前公开的参考DEM数据主要有ALOS-DSM、ASTRE-GDEM和SRTM[25-26]。根据发布高程精度来看,30 m格网的ALOS-DSM(简称AW3D30) 精度相对较高,标称精度为5 m(1σ)[27-28]。以AW3D30数据为参考,随机挑选8轨资源三号02星激光数据,对比分析在不同地形坡度下激光高程精度在检校前后的变化情况。试验结果如表 5所示。为了更加直观,抽取其中第944和1081两轨检校前后结果对比如图 7-10所示。

|
| 图 7 第944轨ZY3激光测高与AW3D30高程对比(检校前) Fig. 7 The elevation comparison between laser altimeter data and AW3D30 on 944th path (before calibration) |

|
| 图 8 第944轨ZY3激光测高与AW3D30高程对比(检校后) Fig. 8 The elevation comparison between laser altimeter data and AW3D30 on 944th path (after calibration) |

|
| 图 9 第1081轨ZY3激光测高与AW3D30高程对比(检校前) Fig. 9 The elevation comparison between laser altimeter data and AW3D30 on 1081th path (before calibration) |
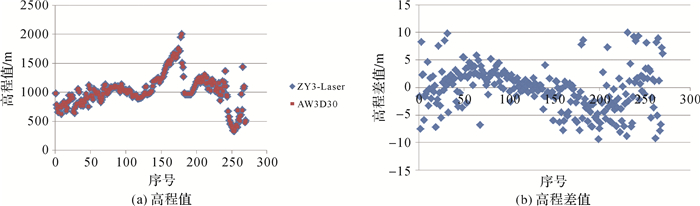
|
| 图 10 第1081轨ZY3激光测高与AW3D30高程对比(检校后) Fig. 10 The elevation comparison between laser altimeter data and AW3D30 on 1081th path (after calibration) |
表 4统计了0~2°,2°~5°,5°~10°,10~15° 4种不同坡度范围内,资源三号02星激光测高在检校前后与AW3D30的高程对比情况。很明显可以看出,在激光测高仪检校前,利用激光测量的高程值与参考AW3D30高程的差值较大,在坡度分别为0~2°,2°~5°,5°~10°,10~15°时,差值均值在70-100米,这说明存在明显的系统误差,差值的中误差分别为100~140 m、100~150 m、100~160 m、160~210 m,这主要是因为真实指向与设计值偏差较大,引起平面和高程误差较大。随着坡度增加,误差有逐渐增加的趋势。

|
经过在轨几何检校之后,对激光测量的高程值与AW3D30高程差值分析,在坡度分别为0~2°,2°~5°,5°~10°,10~15°时,差值的均值降低到-2~2米。随着坡度增加,基本在0上下浮动,这一点同样从图 8(b)和图 10(b)中也可以看出,说明系统误差已基本消除,差值的中误差分为2~3 m,3~4 m,4~5 m,5~6 m。相比于检校前均值和中误差,检校后精度有明显提升。同样随着坡度增加,二者的高程差值有逐步增大趋势,这主要是因为在坡度增加的情况下,相同的平面误差会引起更大的高程误差。
2.2.2 基于地面控制点的绝对高程精度分析为了精确评价资源三号02星激光测高仪高程测量精度,试验采用外业实测的方式,利用RTK测量平坦地区激光足印范围内的地面高程信息,用于激光测高数据的绝对精度验证。这些控制点平面和高程精度在5 cm以内,能够更精确地评价检校后的激光测高精度。本试验测量了第1081轨9个激光光斑内的控制点数据,分析和对比检校前后高程精度变化。
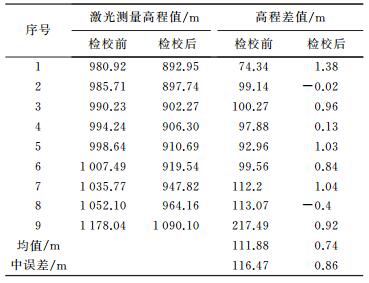
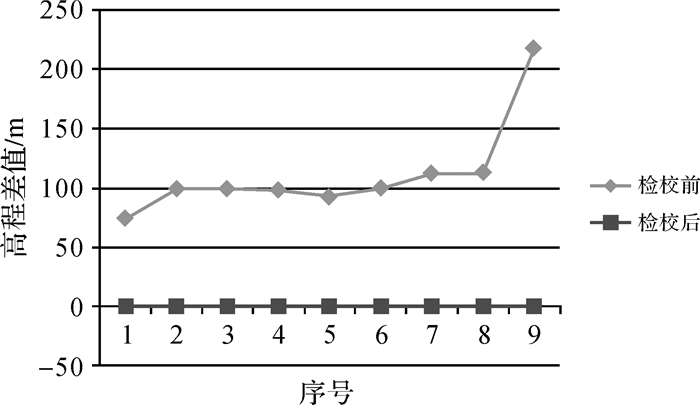
由于检校前后平面位置变化较大,检校前激光测量高程精度由AW3D30参考评价,检校后以实测的控制点作为参考评价。检校前后激光高程数据与各自参考数据的高程差值如图 11所示,统计结果如表 5所示。
|
| 图 11 检校前后激光高程及其差值变化 Fig. 11 The difference between laser elevation data and GCPs |
从图 11可以很明显看出,检校后激光高程测量值精度有大幅提升。表6给出了9个激光测量高程值与控制点相比较情况,激光高程均值和中误差由检校前的111.88±116.47 m降低到检校后0.74±0.86 m,精度提升了2个数量级。结果表明,检校后在平坦地区激光绝对高程精度优于1 m。
3 结论激光测高仪在轨几何检校是其高精度测绘应用的重要保证。本文针对资源三号02星激光测高仪的系统几何误差,提出了一种基于地面探测器的在轨几何检校方法,构建了以指向和测距为系统误差的几何检校模型,利用多个地面检校场数据和地面参考数据进行检校与验证分析,结论如下:
(1) 经过多检校场联合在轨几何检校后,利用ALOS-DEM进行高程精度验证,检校后激光高程精度由检校前100~140 m提高到了2~3 m。
(2) 经过平坦地区少量外业控制点数据验证,高程绝对精度达到1 m左右,可为资源三号和其他卫星进行全球无控测图提供高精度的高程控制数据。
本文提出了资源三号02星激光测高仪在轨几何检校模型,并对资源三号02星激光测高仪进行了系统检校,总体上方法可行。但由于外业作业难度较大,加上首台激光测高仪的试验性质,使得实际可供检校的数据不多。我们将在后续的工作中继续完善相关工作,并为后续其他国产激光测高仪提供有力的技术支撑。
| [1] | 李松. 星载激光测高仪发展现状综述[J]. 光学与光电技术, 2004, 2(6): 4–6. LI Song. Recent Progress of Spaceborne Laser Altimeter System[J]. Optics & Optoelectronic Technology, 2004, 2(6): 4–6. |
| [2] | 李然, 王成, 苏国中, 等. 星载激光雷达的发展与应用[J]. 科技导报, 2007, 25(14): 58–63. LI Ran, WANG Cheng, SUN Guozhong, et al. Development and Applications of Spaceborne LiDAR[J]. Science & Technology Review, 2007, 25(14): 58–63. DOI:10.3321/j.issn:1000-7857.2007.14.010 |
| [3] | 张翼飞, 杨辉. 激光高度计技术及其应用[J]. 中国航天, 2007(12): 19–23. ZHANG Yifei, YANG Hui. Laser Altimeter Technology and its Applications[J]. Aerospace China, 2007(12): 19–23. DOI:10.3969/j.issn.1672-9463.2007.12.006 |
| [4] | GLAS Instrument Team.Geoscience laser altimeter system preliminary design review[Z]. NASA Goddard Space Flight Center, 1998(2): 12-14. |
| [5] | 许春晓, 周峰. 星载激光遥感技术的发展及应用[J]. 航天返回与遥感, 2009, 30(4): 26–31. XU Chunxiao, ZHOU Feng. Development and Applications of Space-borne Laser Remote Sensing Technology[J]. Spacecraft Recovery & Remote Sensing, 2009, 30(4): 26–31. |
| [6] | 徐代升, 黄庚华, 舒嵘, 等. 星载激光高度计综合性能分析[J]. 红外, 2005(1): 1–8. XU Daisheng, HUANG Genghua, SHU Rong, et al. Comprehensive Aerformance Analysis of Space-borne Laser Altimeter[J]. Infrared, 2005(1): 1–8. |
| [7] | 王建宇, 舒嵘, 陈卫标, 等. 嫦娥一号卫星载激光高度计[J]. 中国科学:物理学力学天文学, 2010, 53(10): 1914–1920. WANG Jianyu, SHU Rong, CHEN Weibiao, et al. Laser altimeter of CE-1 payloads system[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(10): 1914–1920. |
| [8] | 李德仁. 我国第一颗民用三线阵立体测图卫星——资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317–322. LI Deren. China's First Civilian Three-line-array Stereo Mapping Satellite: ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317–322. |
| [9] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191–198. TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of ZiYuan-3 Surveying Satellite and its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191–198. |
| [10] | 蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523–529, 553. JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-Line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523–529, 553. |
| [11] | 李奇峻, 范大昭, 雷蓉, 等. 资源三号多光谱影像谱段间相对内参关系标定及高精度配准[J]. 测绘学报, 2016, 45(6): 685–690. LI Qijun, FAN Dazhao, LEI Rong, et al. Calibration for Relative Interior Orientation Relationship and Band-to-band Registration with High Accuracy of ZY-3 Multi-spectral Image[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 685–690. DOI:10.11947/j.AGCS.2016.20150363 |
| [12] | 曹金山, 袁修孝, 龚健雅, 等. 资源三号卫星成像在轨几何定标的探元指向角法[J]. 测绘学报, 2014, 43(10): 1039–1045. CAO Jinshan, YUAN Xiuxiao, GONG Jianya, et al. The Look-angle Calibration Method for On-orbit Geometric Calibration of ZY-3 Satellite Imaging Sensors[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1039–1045. DOI:10.13485/j.cnki.11-2089.2014.0147 |
| [13] | LUTHCKE S B, ROWLANDS D D, MCCARTHY J J, et al. Spaceborne Laser-Altimeter-Pointing Bias Calibration from Range Residual Analysis[J]. Journal of Spacecraft and Rockets, 2000, 37(3): 374–384. DOI:10.2514/2.3571 |
| [14] | LUTHCKE S B, ROWLANDS D D, WILLIAMS T A, et al. Reduction of ICESat systematic geolocation errors and the impact on ice sheet elevation change detection[J]. Geophysical Research Letters, 2005, 32(21): L21S05. |
| [15] | SCHUTZ B E, ZWALLY H J, SHUMAN C A, et al. Overview of the ICESat Mission[J]. Geophysical Research Letters, 2005, 32(21): L21S01. |
| [16] | MAGRUDER L, SILVERBERG E, WEBB C, et al. In Situ Timing and Pointing Verification of the ICESat Altimeter Using a Ground-Based System[J]. Geophysical Research Letters, 2005, 32(21): L21S04. |
| [17] | MAGRUDER L A, SULEMAN M A, SCHUTZ B E. ICESat Laser Altimeter Measurement Time Validation System[J]. Measurement Science and Technology, 2003, 14(11): 1978–1985. DOI:10.1088/0957-0233/14/11/016 |
| [18] | MAGRUDER L A, RICKLEFS R L, SILVERBERG E C, et al. ICESat Geolocation Validation Using Airborne Photography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2758–2766. DOI:10.1109/TGRS.2010.2040831 |
| [19] | SCHUTZ B E. GLAS Altimeter Post-Launch Calibration/Validation Plan, Version 1.0[M].Austin, TX: Center for Space Research, The University of Texas at Austin, 2001. |
| [20] | MAGRUDER L A, WEBB C E, URBAN T J, et al. ICESat Altimetry Data Product Verification at White Sands Space Harbor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(1): 147–155. DOI:10.1109/TGRS.2006.885070 |
| [21] | MAGRUDER L A, SCHUTZ B E, Silverberg E C. Laser Pointing Angle and Time of Measurement Verification of the ICESat Laser Altimeter using a Ground-based Electro-optical Detection System[J]. Journal of Geodesy, 2003, 77(3-4): 148–154. DOI:10.1007/s00190-003-0319-4 |
| [22] | MARTIN C F, THOMAS R H, KRABILL W B, et al. ICESat Range and Mounting Bias Estimation Over Precisely-Surveyed Terrain[J]. Geophysical Research Letters, 2005, 32(21): L21S07. |
| [23] | 马跃, 阳凡林, 易洪, 等. 对地观测星载激光测高仪在轨姿态系统误差检校方法[J]. 红外与激光工程, 2015, 44(8): 2401–2405. MA Yue, YANG Fanlin, YI Hong, et al. Calibration Method of On-orbit Attitude Systematic Error for Space-Borne Laser Altimeter of Earth Observation[J]. Infrared and Laser Engineering, 2015, 44(8): 2401–2405. |
| [24] | HARDING D J, CARABAJAL C C. ICESat waveform measurements of within-footprint topographic relief and vegetation vertical structure[J]. Geophysical Research Letters, 2005, 32(21): L21S10. |
| [25] | 杜小平, 郭华东, 范湘涛, 等. 基于ICESat/GLAS数据的中国典型区域SRTM与ASTER GDEM高程精度评价[J]. 地球科学—中国地质大学学报, 2013, 38(4): 887–897. DU Xiaoping, GUO Huadong, FAN Xiangtao, et al. Vertical Accuracy Assessment of SRTM and ASTER GDEM over Typical Regions of China Using ICESat/GLAS[J]. Earth Science—Journal of China University of Geosciences, 2013, 38(4): 887–897. |
| [26] | 陈俊勇. 对SRTM3和GTOPO30地形数据质量的评估[J]. 武汉大学学报(信息科学版), 2005, 30(11): 941–944. CHEN Junyong. Quality Evaluation of Topographic Data from SRTM3 and GTOPO30[J]. Geomatics and Information Science of Wuhan University, 2005, 30(11): 941–944. |
| [27] | TAKAKU J, TADONO T, TSUTSUI K. Generation of High Resolution Global DSM from ALOS PRISM[J]. International Society for Photogrammetry and Remote Sensing, 2014, XL-4: 243–248. |
| [28] | TADONO T, ISHIDA H, ODA F, et al. Precise Global DEM Generation by ALOS PRISM[C]//ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Suzhou, China: ISPRS, 2014, Ⅱ-4: 71-76. |