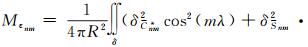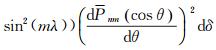2. 北京空间飞行器总体设计部, 北京 100094;
3. 航天东方红卫星有限公司, 北京 100094
2. Beijing Institute of Spacecraft System Engineering, Beijing 100094, China;
3. DFH Satellite Co.Ltd., Beijing 100094, China
海洋测高卫星作为空间大地测量一个重要的观测平台,可提供高精度和高分辨率的海洋重力异常、垂线偏差数据[1-4]。以上数据对于军事(如导航)和经济(如资源勘探)等均具有十分重要的作用。为此,国外发展了大量的测高卫星,数量超过10颗[5]。我国也成功发射了HY-2A卫星[6],但有关的海洋重力场产品暂未发布。为了弥补在此领域数据的不足,我国后续还将发展HY-2B和HY-2C卫星,以及基于SAR或干涉SAR技术的新型测高卫星[7]。而如何利用这些卫星数据来得到我们所需要的重力异常产品,在卫星设计之初就需要进行细致深入的分析。特别是重力异常产品不是海洋测高卫星的直接产品,因此如何由测高精度导出重力异常的精度以及如何由重力异常的目标精度导出测高的精度要求无疑是十分重要的课题。对于如何由测高数据得到重力异常,当前常用的方法之一是垂线偏差法[8-11],即首先由测高数据计算得到垂线偏差,然后再进一步计算得到重力异常。由于从测高数据到垂线偏差的计算公式相对简单,所对应的误差传播公式十分明确,因此本文将重点讨论垂线偏差和重力异常的误差匹配关系。
关于此问题,当前已有一些结论。文献[12]基于扰动重力和垂线偏差的傅立叶变换关系,得出1 μrad的垂线偏差误差等价于1 mGal的重力异常误差。文献[7]基于此结论给出了精度为1 mGal,分辨率为1′的重力异常精度所对应的基于传统高度计、SAR高度计和干涉SAR高度计的测高精度要求。然而,文献[10]在讨论测高数据偶然误差对海洋重力异常反演的影响时,所得出的结论随着计算方法的不同有较大不同。文献[11]根据Vening-Meinesz公式的离散解析公式,通过数值计算得出的结论显示大约4 μrad的垂线偏差误差对应于1 mGal的重力异常误差;文献[13]基于如下的重力误差δg和垂线偏差误差δθ估式讨论了高程异常的推估及精度
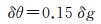 (1)
(1)
式中,δg以mGal为单位;δθ以秒(″)为单位。此式与上述文献中的结论均不一致。
以上文献中结论不太一致的原因主要可能有以下几个方面:
(1) 文献[12]在讨论垂线偏差与重力异常的精度匹配关系时,仅考虑了一个方向的垂线偏差,而文献[10]和文献[11]考虑了两个分量的共同影响,显然考虑两个方向更为全面。
(2) 在考虑垂线偏差两个分量的共同影响时,需要考虑不同分量间的相关性[14]以及观测误差之间的相关性,这也会对最终的结论带来影响。
(3) 在直接利用垂线偏差与重力异常之间的积分公式来讨论误差传播关系时,会引入计算误差的影响,同时积分中的误差传播如何通过离散化来讨论需要作进一步研究[15]。因此,尽管上述文献中的结论不完全一致,但在其特定的前提下都有其合理性,有关的结论需要在相同的前提下才能进行比较。
为了从不同的角度来研究垂线偏差和重力异常的精度匹配关系,本文利用已有的超高阶重力场模型来讨论1 μrad的垂线偏差误差所对应的重力异常误差。首先从重力异常和垂线偏差的球谐函数计算公式入手,从理论上推导二者受引力位系数误差影响所产生的误差,并讨论二者的匹配关系,然后通过已有的重力场模型来验证有关结论。
1 理论分析本节利用球谐函数来对重力异常和垂线偏差的误差匹配关系进行理论分析,然后给出有关公式。
1.1 重力异常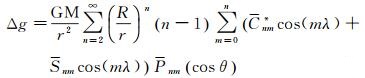 (2)
(2)
式中,GM为引力常数;(r, θ, λ)为计算点球坐标;R为地球平均半径;Pnm(cos θ)为完全正规化的n阶m次勒让德函数;Cnm*、Snm为完全正规化的地球扰动引力位系数[19]。若引力位系数的误差为独立的高斯白噪声,令为: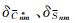
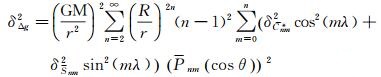 (3)
(3)
则其在地球表面(地球平均半径所在的球面,此时r=R)的均值为
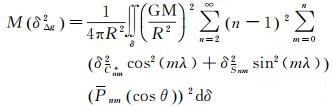 (4)
(4)
式中,dδ=R2sin θdθdλ。根据球谐函数的正交性以及文献[14]中所给出的重力异常方差-协方差的计算公式,可得
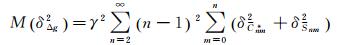 (5)
(5)
其中,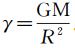
垂线偏差北向分量(ε)和东向分量(η)的计算公式如下
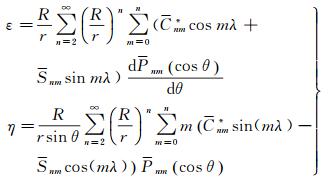 (6)
(6)
令垂线偏差误差为δε、δη,则有
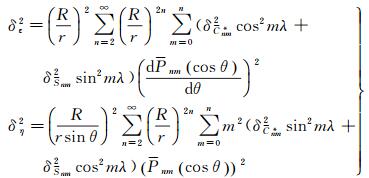 (7)
(7)
和重力异常类似,垂线偏差误差在地球表面的均值分别为
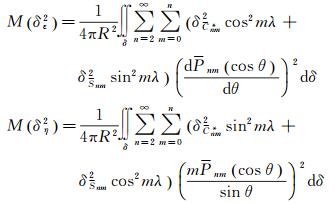 (8)
(8)
下面依次对式(8) 积分的最终计算公式进行推导。
1.2.1 北向分量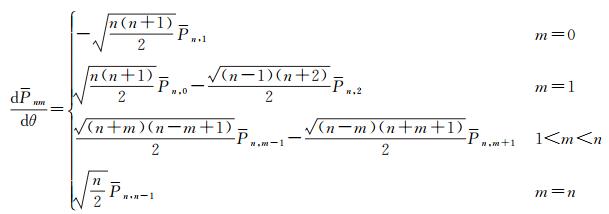 (9)
(9)
根据文献[24],可得
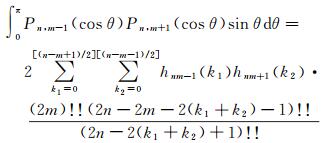 (10)
(10)
式中,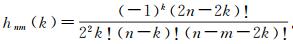
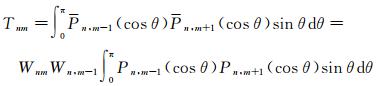 (11)
(11)
式中,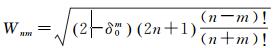
当m=0时
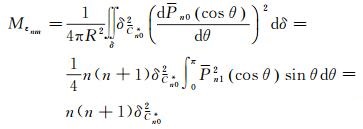 (12)
(12)
当m=1时
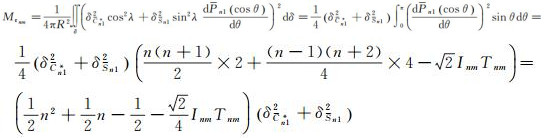 (13)
(13)
式中,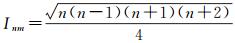
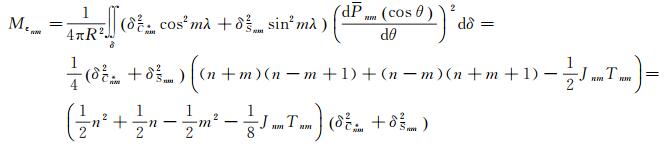 (14)
(14)
式中,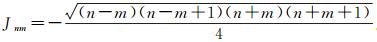
当m=n时
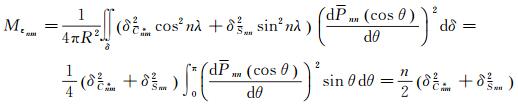 (15)
(15)
综合得
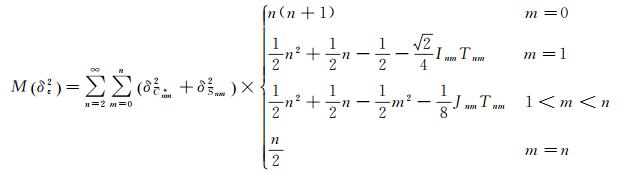 (16)
(16)
同理,令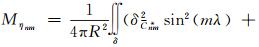
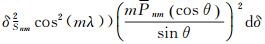
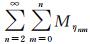
当m=0时,M(δη2)=0。
当m≠0时,
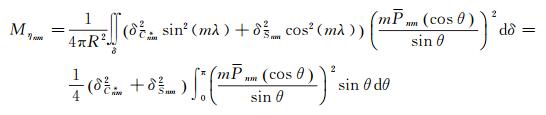 (17)
(17)
因为勒让德函数满足
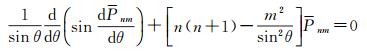 (18)
(18)
所以
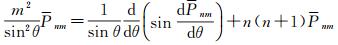
等式两边同时乘以Pnmsin θ可得
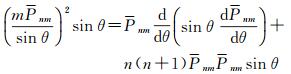
对上式两边同时积分可得
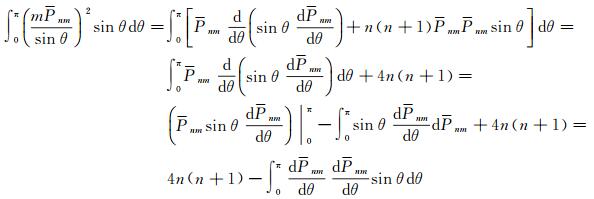 (19)
(19)
由北向分量的推导可得
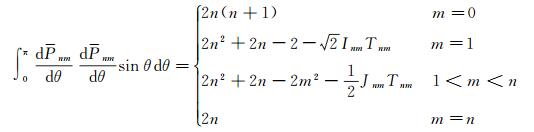 (20)
(20)
所以有(m≠0)
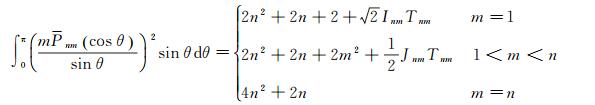 (21)
(21)
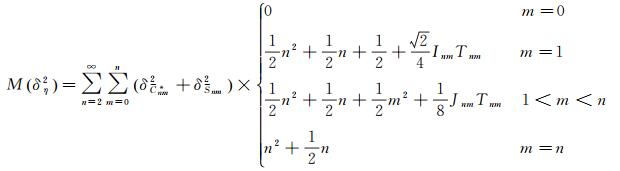 (22)
(22)
最终得
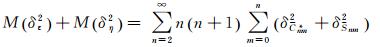 (23)
(23)
当n较小时,引力位模型系数精度一般较高,同时低阶项项数少,因此低阶项位系数引起的误差不会成为重力异常误差和垂线偏差误差中的主量;当n较大时,位系数误差往往较大,且中高阶项数多,因此中高阶项位系数引起的误差会成为重力异常误差和垂线偏差误差的主量。由于n较大时,(n-1)2≈n(n+1),对比重力异常和垂线偏差的误差公式,可得
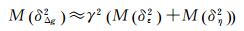 (24)
(24)
根据此式,若垂线偏差各方位向等精度测量,且假定两个分量垂线偏差精度均为1 μrad,由此对应的重力异常精度约为1.4 mGal; 反之,若重力异常的精度为1 mGal,则所对应的垂线偏差的精度约为0.7 μrad。该结论和式(1) 一致,但和文献[12]所给出的结论略有不符,原因是文献[12]仅考虑了一个方向的垂线偏差观测误差,而在计算重力异常的过程中,垂线偏差的两个分量都需要。
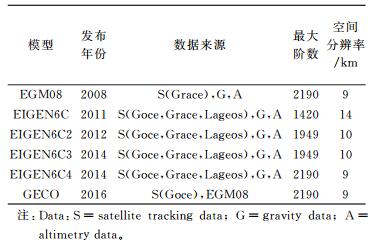
2 数值试验传统卫星测高(如HY2高度计)的输出采样间隔大约为7 km[7],根据采样定律[26],其可恢复的地球重力场信号的最小尺度为14 km,所对应的重力场模型的最大阶数为1429。如果对原始高度计数据进行重采样,并融合多颗测高卫星数据,则可解算的重力场模型的阶次将高于1429。当前公开发布的重力场模型的最高阶数已超过2000阶。为了检核式(24) 的正确性,同时也为了使该公式适合于测高卫星的指标设计,现选用GFZ(German Research Centre for Geosciences)所发布的所有阶数大于1000阶的重力场模型进行计算分析。所采用的模型的基本信息见表 1,误差阶方差RMS(root mean square)[27]如图 1所示。
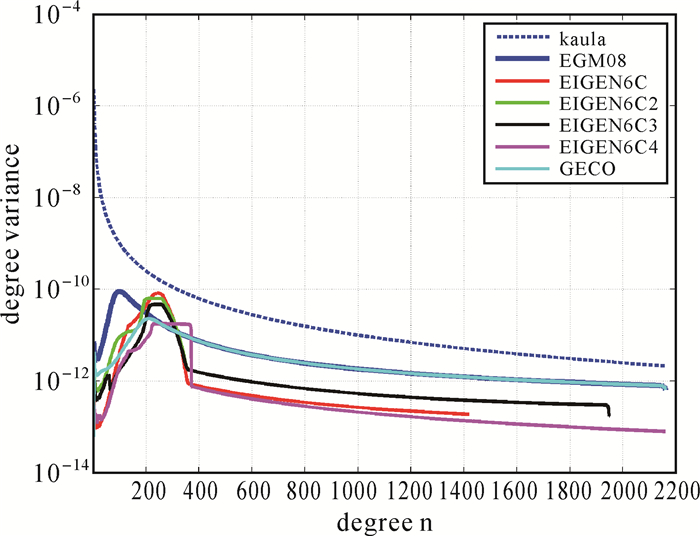
|
| 图 1 误差阶方差RMS Fig. 1 Error degree variance RMS |
由表 1可知,以上模型均使用了测高卫星数据。同时从空间分辨率来看,以上模型能满足测高卫星的设计要求,因此适合用于讨论测高卫星所得垂线偏差和重力异常的精度匹配关系。从图 1可看出,以上模型的误差分布互不相同,若以上结果均满足式(24),则可证明上节所得结论的正确性。为此利用上述模型进行如下计算:
(1) 选用以上模型所有阶位系数误差值按式(3) 计算全球1°×1°格网点的重力异常误差,其均值令为δΔg;
(2) 选用以上模型所有阶位系数误差值按式(7) 计算全球1°×1°格网点的垂线偏差误差,然后根据式(24) 推算出重力异常误差,令为δ′Δg,计算公式如下
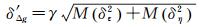 (25)
(25)
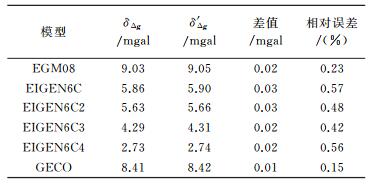
这里的M(δε2)、M(δη2)为所有格网点垂线偏差误差的均值。最终的统计结果见表 2,其中差值为直接计算得到的重力异常误差与推算出的重力异常误差差值的绝对值,即∣δΔg-δ′Δg∣,相对误差为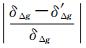
由表 2可知:由式(24) 利用垂线偏差误差推算出的重力异常误差与利用式(3) 计算得到的重力异常误差近似相等,差值小于0.05 mgal,相对误差小于1%。因此验证了本文所推导的垂线偏差和重力异常误差匹配关系的正确性。
3 结论从重力异常和垂线偏差的球谐函数计算公式入手,本文首先从理论上推导了引力位系数误差所引起的重力异常误差和垂线偏差误差满足的近似比例关系,同时也得到了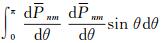
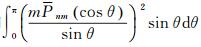
值得说明的是,在利用实际测高数据计算重力异常的过程中,无法避免会受到计算误差的影响,例如在使用Vening-Meinesz公式时,积分中的离散化网格大小、奇异因子的处理方法等均会导致最终所计算的重力异常误差有所不同。这正是文献[10-11]所得出的结论与本文所得结论不一致的原因。
综上所述,笔者建议若要根据重力异常产品的指标来确定卫星载荷的设计精度时,可考虑采用本文的结论,而若利用实际的卫星测高数据,来计算最终的重力异常产品时,可参考文献[10-11]有关的工作来选择精度较高的计算方法。
| [1] | 许厚泽, 王海瑛, 陆洋, 等. 利用卫星测高数据推求中国近海及邻域大地水准面起伏和重力异常研究[J]. 地球物理学报, 1999, 42(4): 465–471. XU Houze, WANG Haiying, LU Yang, et al. Geoid Undulations and Gravity Anomalies from T/P and ERS-1 Altimeter Data in the China Sea and Vicinity[J]. Chinese Journal of Geophysics, 1999, 42(4): 465–471. |
| [2] | 翟国君, 黄谟涛, 谢锡君, 等. 卫星测高数据处理的理论与方法[M].北京: 测绘出版社, 2000. ZHAI Guojun, HUANG Motao, XIE Xijun, et al. The Theory and Method of Satellite Altimeter Data Processing[M].Beijing: Surveying and Mapping Press, 2000. |
| [3] | 黄谟涛, 翟国君, 管铮, 等. 海洋重力场测定及其应用[M].北京: 测绘出版社, 2005. HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. Marine Gravity Field Measurement and Its Application[M].Beijing: Surveying and Mapping Press, 2005. |
| [4] | 王海瑛, 许厚泽, 王广运. 中国近海海域Geosat卫星测高海平面和海面地形研究[J]. 科学通报, 1997, 42(8): 852–855. WANG Haiying, XU Houze, WANG Guangyun. Research of Mean Sea Surface and Sea Surface Topography of the Seas Adjacent to China from Geosat Mission[J]. Chinese Science Bulletin, 1997, 42(8): 852–855. |
| [5] | 李建成, 金涛勇. 卫星测高技术及应用若干进展[J]. 测绘地理信息, 2013, 38(4): 1–8. LI Jiancheng, JIN Taoyong. On the Main Progress of Satellite Altimetry and Its Applications[J]. Journal of Geomatics, 2013, 38(4): 1–8. |
| [6] | BAO Lifeng, GAO Peng, PENG Hailong, et al. First Accuracy Assessment of the HY-2A Altimeter Sea Surface Height Observations: Cross-calibration Results[J]. Advances in Space Research, 2015, 55(1): 90–105. DOI:10.1016/j.asr.2014.09.034 |
| [7] | BAO Lifeng, XU Houze, LI Zhicai. Towards A 1 mGal Accuracy and 1 Min Resolution Altimetry Gravity Field[J]. Journal of Geodesy, 2013, 87(10-12): 961–969. DOI:10.1007/s00190-013-0660-1 |
| [8] | SOLTANPOUR A, NAHAVANDCHI H, GHAZAVI K. Recovery of Marine Gravity Anomalies from ERS1, ERS2 and ENVISAT Satellite Altimetry Data for Geoid Computations over Norway[J]. Studia Geophysica et Geodaetica, 2007, 51(3): 369–389. DOI:10.1007/s11200-007-0021-8 |
| [9] | HWANG C. Inverse Vening Meinesz Formula and Deflection-Geoid Formula: Applications to the Predictions of Gravity and Geoid over the South China Sea[J]. Journal of Geodesy, 1998, 72(5): 304–312. DOI:10.1007/s001900050169 |
| [10] | 黄谟涛, 翟国君, 管铮, 等. 利用卫星测高数据反演海洋重力异常研究[J]. 测绘学报, 2001, 30(2): 179–184. HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. On the Recovery of Gravity Anomalies from Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2): 179–184. |
| [11] | 彭富清, 陈双军, 金群峰. 卫星测高误差对海洋重力场反演的影响[J]. 测绘学报, 2014, 43(4): 337–340. PENG Fuqing, CHEN Shuangjun, JIN Qunfeng. Influence of Altimetry Errors on Marine Geopotential Recovery[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 337–340. DOI:10.13485/j.cnki.11-2089.2014.0050 |
| [12] | SANDWELL D T, SMITH W H, SARAH G, et al. Bathymetry from Space: White Paper in Support of A High-resolution, Ocean Altimeter Mission[C]//Proceedings of High-resolution Ocean Topography Science Working Group Meeting. Version 1.5. [S.l.]: CEOAS, 2001. |
| [13] | 陈俊勇. 高程异常的推估及精度[J]. 测绘通报, 1993(4): 3–8, 22. CHEN Junyong. Estimation and Its Precision of Height Anomaly[J]. Bulletin of Surveying and Mapping, 1993(4): 3–8, 22. |
| [14] | TSCHERNING C C, RAPP R H. Closed Covariance Expressions for Gravity Anomalies, Geoid Undulations and Deflections of the Vertical Implied By Anomaly Degree Variance Models[R]. Reports of the Department of Geodetic Science. No. 208. Columbus, OH: The Ohio State University, 1974. |
| [15] | XU Peiliang. Error Estimates of Velocities and Displacements from Accelerographs[J]. Geophysical Journal International, 2012, 188(3): 1061–1064. DOI:10.1111/gji.2012.188.issue-3 |
| [16] | 海斯卡涅W A, 莫里兹H. 物理大地测量学[M]. 卢福康, 胡国理, 译. 北京: 测绘出版社, 1979. HEISKANEN W, MORITZ H. Physical Geodesy[M]. LU Fukang, HU Guoli, trans. Beijing: Surveying and Mapping Press, 1979. |
| [17] | 赫尔默特·莫里兹. 高等物理大地测量学[M]. 宁津生, 管泽霖, 译. 北京: 测绘出版社, 1984. MORITZ H. Advanced Physical Geodesy[M]. NING Jinsheng, GUAN Zelin, trans. Beijing: Chinese Surveying Mapping Press, 1984. |
| [18] | FANTINO E, CASOTTO S. Methods of Harmonic Synthesis for Global Geopotential Models and Their First-, Second-and Third-order Gradients[J]. Journal of Geodesy, 2009, 83(7): 595–619. DOI:10.1007/s00190-008-0275-0 |
| [19] | 万晓云, 于锦海. 极地空白对GOCE引力场恢复的影响[J]. 测绘学报, 2013, 42(3): 317–322. WAN Xiaoyun, YU Jinhai. Influence of Polar Gaps on Gravity Field Recovery Using GOCE Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 317–322. |
| [20] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M].3版. 武汉: 武汉大学出版社, 2014. Survey Adjustment Department of SGG WHU. Error Theory and Foundation of Surveying Adjustment[M].3rd ed. Wuhan: Wuhan University Press, 2014. |
| [21] | 万晓云. 引力场梯度张量的非奇异公式推导[J]. 武汉大学学报(信息科学版), 2011, 36(12): 1486–1489. WAN Xiaoyun. New Derivation of Nonsingular Expression for Gravitational Gradients Calculation[J]. Geomatics and Information Science of Wuhan University, 2011, 36(12): 1486–1489. |
| [22] | 于锦海, 万晓云. 计算Legendre函数导数的非奇异方法[J]. 测绘科学技术学报, 2010, 27(1): 1–3, 8. YU Jinhai, WAN Xiaoyun. Non-singular Formula for Computing Derivatives of Legendre Functions[J]. Journal of Geomatics Science and Technology, 2010, 27(1): 1–3, 8. |
| [23] | 刘晓刚, 吴晓平, 赵东明, 等. 扰动重力梯度的非奇异表示[J]. 测绘学报, 2010, 39(5): 450–457. LIU Xiaogang, WU Xiaoping, ZHAO Dongming, et al. Non-singular Expression of the Disturbing Gravity Gradients[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 450–457. |
| [24] | 党诵诗. 物理大地测量的数学基础[M].北京: 测绘出版社, 1988. DANG Songshi. Mathematical Foundation of Physical Geodesy[M].Beijing: Surveying and Mapping Press, 1988. |
| [25] | 魏子卿. 完全正常化缔合勒让德函数及其导数与积分的递推关系[J]. 武汉大学学报(信息科学版), 2016, 41(1): 27–36. WEI Ziqing. Recurrence Relations for Fully Normalized Associated Legendre Functions and Their Derivatives and Integrals[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 27–36. |
| [26] | 维纳·K英格尔, 约翰·G·普罗克斯. 数字信号处理(MATLAB版)[M]. 刘树棠, 译. 西安: 西安交通大学出版社, 2009. INGLE V K, PROAKIS J G. Digital Signal Processing Using MATLAB[M]. Liu Shutang, trans. Xi'an: Xi'an Jiaotong University Press, 2009. |
| [27] | 宁津生, 邱卫根, 陶本藻. 地球重力场模型理论[M].武汉: 武汉测绘科技大学出版社, 1990. NING Jinsheng, QIU Weigen, TAO Benzao. Theory of Earth Gravity Field Model[M].Wuhan: Wuhan Surveying and Mapping Science and Technology University Press, 1990. |