2. 信息工程大学理学院, 河南 郑州 450001
2. Institute of Science, Information Engineering University, Zhengzhou 450001, China
随着多个卫星导航系统的发展,可见星数大大增加,使得多颗卫星同时发生故障的概率增大。为此,很多学者对多星故障监测问题进行了研究。目前,处理多故障的RAIM算法有很多种类,总的来说可分为4类:一是基于粗差探测和剔除理论的多故障处理算法[1-4];二是基于稳健估计理论的多故障处理算法[5-7];三是RANCO(range consensus)方法,RANCO处理卫星多故障的方法从根本上来说也是粗差探测,但并不是传统意义上的粗差探测方法,而是从图像处理中引进的一种新型的多粗差处理方法[8-10];另外还有GLR(generalized likelihood ratio)方法[11]等。
文献[1]指出当多个故障出现时,传统w-检验法的检验统计量之间呈现相关性,这种相关性导致了虚警率和误判率升高,因此该文基于可靠性原理提出了克服相关性的准则并设计了基于扩展w-检验法的卫星多故障处理方法。文献[3]提出了探测两个粗差的算法,其核心思想也是对w-检验法进行改进。文献[2]将以前存在的用以探测单个卫星故障的算法,包括χ2检验法和w-检验法,推广到了探测两个卫星故障的场合。文献[4]通过向量相关时间序列区分单个粗差和多个粗差的粗差集,提出精密单点定位的RAIM算法。文献[5]将抗差M估计引入RAIM算法中,证明了M估计能够消除卫星多故障对导航解的负面影响,但是当故障个数增加到4个以上时,导航解算结果仍然会出现偏差。文献[6]通过降低粗差观测值对应的权进行粗差探测,这基本上是稳健估计的思想;但是,该文对粗差采取逐个剔除的方式,其可行性并未得到严格的证明。文献[7]讨论了一种改进的M估计在卫星多故障探测中的应用。文献[8]提出了处理多故障的RANCO算法,该方法首先利用4颗基准卫星计算导航解,然后利用该导航解计算所有未参加定位解算的卫星对应的观测残差,作为伪距一致性检验的统计量。
卫星多故障的探测和识别是研究新型RAIM算法的基础,也是拓展RAIM应用领域的必要条件,但是通过对该类算法发展现状的分析可知,还存在许多需要解决的问题。首先,目前的多故障处理算法对故障个数和故障偏差大小的处理存在局限性,对两个以上的故障无法处理,即使有些算法对两个以上的故障进行了处理,但是小故障偏差的误判率太高,不能满足导航用户的要求;其次,有的故障处理模型未明确给出,有的未考虑观测量之间的时间相关性。不精确的故障检测模型会影响RAIM算法的故障探测率,限制RAIM的适用范围。鉴于此,本文提出了基于独立分量分析(ICA)的伪距多变量时间序列异常值探测方法,以期能够较好地解决卫星故障的探测和识别问题。
1 基于独立分量分析的伪距多变量时间序列的异常值探测方法ICA是一种信号处理和数据分析的新方法[12-13],最初是为了解决盲源信号分离问题而提出来的,目前已经被广泛地应用于人脸识别、远程通信、神经科学计算和时间序列分析等多个领域。独立分量分析的目的是将多维随机向量转换为统计上尽可能独立的成分。
1.1 伪距多变量时间序列的独立分量分析假设Lt=[L1t L2t…Lht]T代表历元t的伪距观测值,h为可见星数,GNSS线性化观测方程为
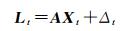 (1)
(1)
式中,A为h×k维观测矩阵并且假设A列满秩;Xt=[x1t x2t…xkt]T为k×1维状态参数向量,由定位参数和接收机钟差所组成;Δt=[Δ1t Δ2t…Δht]T为h×1维随机误差向量,包含电离层残差、对流层残差、多路径误差以及接收机噪声,假设Δt~Nh(0, ΣΔ),ΣΔ=diag(σ12, σ22, …, σh2)。
与式(1) 相对应的卫星多故障探测模型[14-15]可构建为
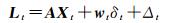 (2)
(2)
式中,wt=[w1t w2t…wht]T代表异常扰动大小;当δt=1时,表示当前时刻存在故障卫星;当δt=0时,表示当前时刻的观测值正常。
由于受到观测噪声等因素的影响,卫星故障对观测值的影响不易被察觉;直接基于式(2) 进行异常值探测,对微小慢变的故障、多故障和小故障的探测效果往往不是很理想。事实上,式(2) 并未考虑不同历元的观测值之间的时间相关性,这是目前多故障探测算法普遍存在的问题[16-23]。而且,假设误差服从正态分布往往不符合实际情况。注意到可通过ICA将原始观测值分解为独立分量的线性组合,并把异常值对多变量时间序列的影响集中在一个或多个独立分量上[24],而且与原始多变量时间序列观测值相比较,独立分量对异常值具有更强的敏感性。鉴于此,本文引入独立分量分析的方法对卫星多故障进行探测。
为此需对伪距观测序列{Lt}实施独立分量分析,即将Lt=[L1t L2t…Lht]T写成独立分量的线性组合。由假设矩阵A列满秩可知,A的列向量a1, a2, …, ak是线性无关的,由线性代数扩充定理[25]可知,扩充向量集合{a1, a2, …, ak},可得到线性空间Rh的一组基向量;进而基于该基向量集就可以得出混合矩阵,从而把Lt=[L1t L2t…Lht]T写成独立分量的形式。
事实上,由wt∈Rh,根据投影定理[25]可知,存在唯一的向量w1t∈μ(A)和w2t∈μ⊥(A),使得
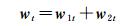 (3)
(3)
式中,μ(A)为由A的列向量所生成的线性空间,μ⊥(A)为μ(A)的关于线性子空间Rh的正交补空间。不妨设w1t=b1a1+…+bkak∈μ(A)和
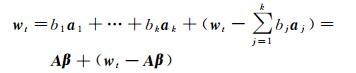 (4)
(4)
式中,β=[b1 b2…bk]T为实系数向量。
由于w2t∈μ⊥(A),所以w2t与向量集合{a1, a2, …, ak}正交。对w2t进行单位化,令c1=(w2t-Aβ)/‖w2t-Aβ‖,则可得到线性无关的向量组a1, …, ak, c1,对该向量组继续扩充,即可得到Rh的一组基向量a1, a2, …, ak, c1, c2…, ch-k,并记[A C]=[a1 a2…ak c1 c2…ch-k]。令εt=[A C]ηt,则Lt=[L1t L2t…Lht]T可写成如下独立分量的线性组合
 (5)
(5)
式中,x1t+b1δt+η1t, …, xkt+bkδt+ηkt;‖w-Aβ‖δt+ηk+1, t, ηk+2, t, …, ηht为h个独立分量;[A C]为混合矩阵。
令
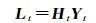 (6)
(6)
式中,Ht为混合矩阵;Yt为独立分量向量。
从Yt的组成可以看出,独立分量可以分为3类:一是‖w-Aβ‖δt+ηk+1, t,它由卫星故障引起的扰动和噪声所组成;二是{x1t+b1δt+η1t, …, xkt+bkδt+ηkt},它由状态分量、卫星故障引起的扰动和噪声所组成;三是{ηk+2, t, …, ηht},它仅仅由噪声所组成。显然,第一类、第二类独立分量中均含有异常扰动,并且后者比前者更显著。进一步,如果原始伪距观测值Lt在历元t受到卫星故障影响,则至少有一个独立分量会在历元t显著地出现异常。由此可见,ICA将异常值对多变量时间序列观测值的影响集中在了一个或多个独立分量上。
1.2 伪距多变量时间序列的异常值探测根据以上分析,笔者可以基于独立分量序列构造异常值的探测方法,其基本思想是:只要有一个独立分量不符合判别规则就可以断定该时刻的多变量时间序列观测值出现异常。这里,提出一种基于cσ准则的异常值判别方法:如果在历元t至少有一个独立分量值超出式(7) 所限定的范围
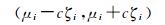 (7)
(7)
则判定在历元t多变量时间序列观测值含有异常值。
式(7) 中的μi和ζi为第i个独立分量序列的均值和标准差,应该由第i个独立分量在历元t以前的序列值估计得到。由此可见,上述异常值探测算法为批处理的。这无法满足在线监测卫星故障的要求,为此,将在下文对算法进行改进,以满足实时性的要求。另外,从形式上看,已经构建了基于独立分量分析的异常值探测方法。但是,在实际应用中,混合矩阵和独立分量都是未知的,需要借助于一定的算法将其估计出来。目前,关于独立分量分析的估计方法已经很成熟,其中信息极大化算法、Fast ICA算法和扩展的信息极大化算法在国际上的应用非常广泛。本文将采用Fast ICA算法完成有关估计。关于Fast ICA算法的具体内容,这里不再详述,可参见文献[24]。
式(7) 中的c值不能取为正态分布的分位点,这是由独立分量的非高斯性所决定的。为此,本文借助于契比雪夫不等式[25]给出c值的一种确定方法。考虑契比雪夫不等式
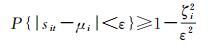 (8)
(8)
式中,sit代表第i个独立分量序列,ε为任意正数。这个不等式给出了在随机变量sit的分布未知的情况下,事件{|sit-μi| < ε}的概率的下限估计值。例如,在式(8) 中取ε=4ζi则可得到
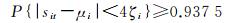 (9)
(9)
这说明取c=4时,独立分量sit的值以93.75%的概率落在区间(μi-4ζi, μi+4ζi)内;又如在式(8) 中取ε=4.47ζi,则可得到
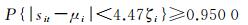 (10)
(10)
这说明取c=4.47时,独立分量sit的值以95.00%的概率落在区间(μi-4.47ζi, μi+4.47ζi)内。
2 基于干扰模型的异常扰动大小的估值方法在进行异常值探测后,需要给出异常扰动大小的估值方法,这是RAIM故障识别的基础。为此,对每颗卫星的观测值从时间方向上建立所谓的时间序列干预模型[27-31]。即,如果第j颗卫星从历元1至历元n的观测值{Lj1,Lj2, …, Ljn}经探测在某个历元含有异常值,则该观测值序列可用如下的干预模型表示
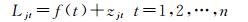 (11)
(11)
式中,zjt符合如下的AR(p)模型
 (12)
(12)
式中,Φ(B)=I-ϕ1B-…-ϕpBp;{at}为相互独立同分布的高斯白噪声序列,均值为0,标准差为Ωj;zjt代表未受异常扰动的干净数据;f(t)代表异常扰动的大小。依据卫星故障探测的实际情况,根据时间序列中异常值探测理论可知,f(t)的表达式取为wj, dξt(d),wj, d为第j颗卫星在历元d的异常扰动大小,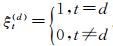
假设已由上述方法探测出了异常值所发生的历元,即d已知,那么为了估计异常扰动的大小,对式(11) 的两边同时左乘于Φ(B),得到
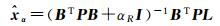 (13)
(13)
令Φ(B)Ljt=ljt,Φ(B)ξt(d)=mt,则式(13) 可写为
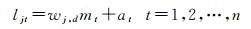 (14)
(14)
对式(14) 运用最小二乘法,可得到异常扰动大小的估值为
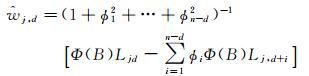 (15)
(15)
为满足卫星多故障探测的实时性[32-37]要求,本节采用滑动窗口的思想,将多故障探测批处理算法改造为逐历元实时的多故障探测算法,其主要思想为:根据独立分量分析模型的估计算法,选取适当的滑动窗口长度m,当有新数据读入时,采用L1=L2, L3, …, Lm=Lm+1的形式对数据进行更新,利用更新后的数据探测第m+1个历元的观测值是否含有故障。
将上述思想与异常扰动大小的估值方法相结合,设计和提出一种多故障在线探测和识别的新算法,其具体实施步骤为:
步骤1:初始化。读取前m个历元的观测值{L1, L2, …, Lm},m一般取为30即可,采用Fast ICA算法对观测值序列进行独立分量分析,得到独立分量序列sit, i=1, …, r,r为t时刻独立分量的个数,求出每个独立分量序列的均值和标准差μi0, σi0,i=1, …, r。利用公式(7) 对这些观测值进行故障探测。
步骤2:数据更新。读取第m+1历元的伪距观测值Lm+1=[L1(m+1) L2(m+1)…Lh(m+1)]T,对数据进行更新L1=L2, L3, …, Lm=Lm+1。
步骤3:故障探测。采用Fast ICA算法进行独立分量分析,得到独立分量序列及其均值和标准差μi1, σi1;利用式(7) 对第m+1个历元的观测值进行故障探测。
步骤4:故障识别。如果探测到第m+1个历元的观测值含有故障,则利用观测值Lj2, Lj3,…, Ljm, Lj(m+1)估计wj, m+1的大小,估值公式可根据式(15) 获得
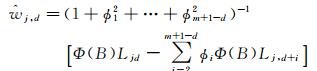 (16)
(16)
同理可以获得异常扰动估值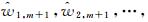
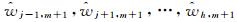
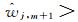
步骤5:故障剔除。剔除故障后,如果可见星数仍大于或等于4,则重新计算定位误差。如果定位误差在正常范围内,则继续处理下一个历元的观测值;如果定位误差仍然异常,则向用户告警。
4 试验与分析 4.1 故障探测和识别效果的验证取北京iGMAS站2013年9月5日14时至23时10 h的北斗民用观测数据,采样间隔为30 s,利用I支路B1频点的伪距观测值进行单频伪距单点定位。为了验证新算法探测和识别多故障的效果,在第31个历元的BD5和BD9星上分别加入5 m和6 m的伪距偏差,在第600个历元的BD3和BD7星上分别加入7 m和4 m的伪距偏差。
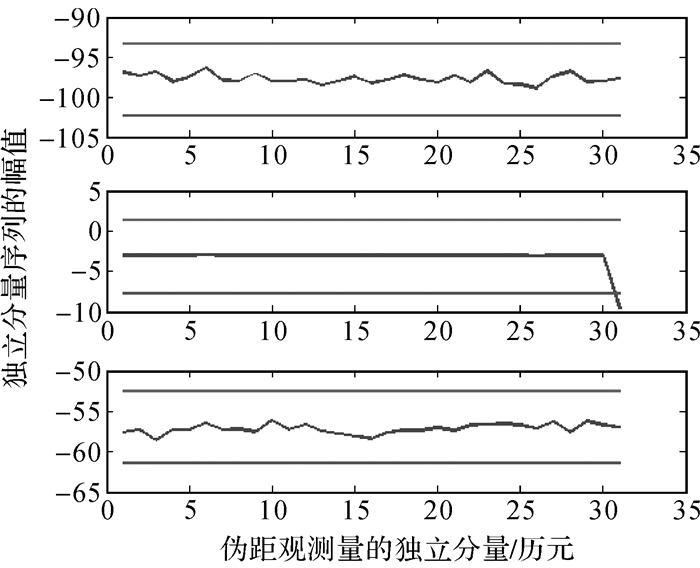
采用新算法对上述数据进行处理。首先,按照2012年12月发布的北斗卫星导航系统空间信号接口控制文件中的算法计算卫星位置、进行卫星钟差改正和地球自转效应改正、利用八参数Klobuchar模型进行电离层改正、利用Saastamoinen模型进行对流层改正。其次,对经过改正后的伪距观测值进行故障探测和识别,取滑动窗口的长度m=30。即每次采用Fast ICA算法对30个历元的伪距观测值进行独立分量模型估计,独立分量序列的个数取为3。c的取值根据虚警率PFA来确定,这里虚警率取为0.05,因此由P{|sit-μi| < ε}≥1-PFA计算可得c的值为4.47。遍历第31个历元和第600个历元的伪距观测值时,所得到的独立分量序列分别如图 1和图 2所示。
|
| 图 1 监测第31个历元的观测数据时的独立分量序列 Fig. 1 Independent component series of the 31st epoch when monitoring the observations |
|
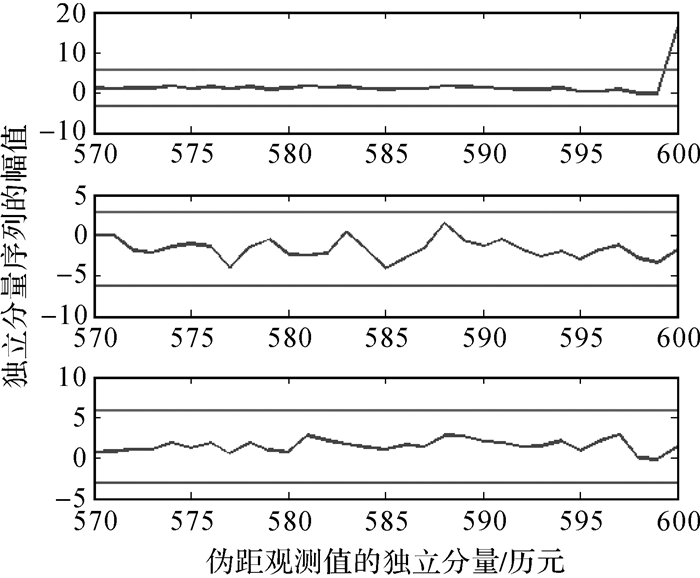
| 图 2 监测第600个历元的观测数据时的独立分量序列 Fig. 2 Independent component series of the 600th epoch when monitoring the observations |
从图 1可以看出,在监测第31个历元的观测数据时,第2个独立分量序列的第31个分量超出了正常范围,从图 2可以看出,在监测第600个历元的观测数据时,第1个独立分量序列的第600个分量超出了正常范围。由前述规则可知,在第31个历元和第600个历元,存在卫星故障。
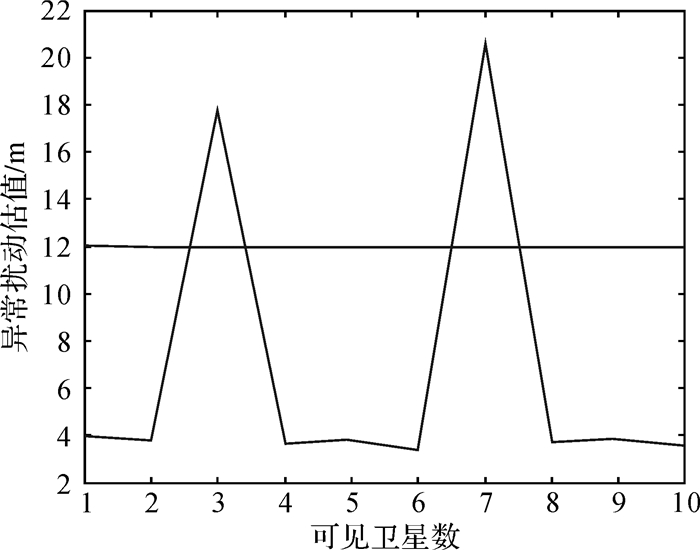
下面进一步确定故障发生在哪几颗卫星上。为此,对伪距观测值进行模型拟合,构建时间序列干预模型,根据估值式(16) 得到异常扰动大小的估值,如图 3和图 4所示。从图 3可知,第5个(BD5) 和第8个(BD9) 观测值含有的异常扰动估值远远大于噪声水平,而其他的观测值含有的异常扰动估值仅在1倍的噪声水平上下浮动,由此可确定在第31个历元,BD5和BD9均为故障星。同理,从图 4可确定在第600个历元,BD3和BD7均为故障星。

|
| 图 3 第31个历元的观测值的异常扰动估值 Fig. 3 The estimates of the abnormal magnitudes of the observations at the 31 epoch |
|
| 图 4 第600个历元的观测值的异常扰动估值 Fig. 4 The estimates of the abnormal magnitudes of the observations at the 600 epoch |
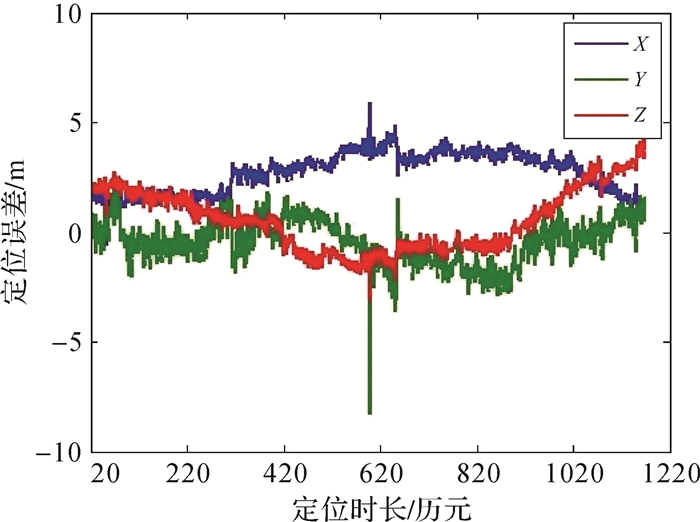
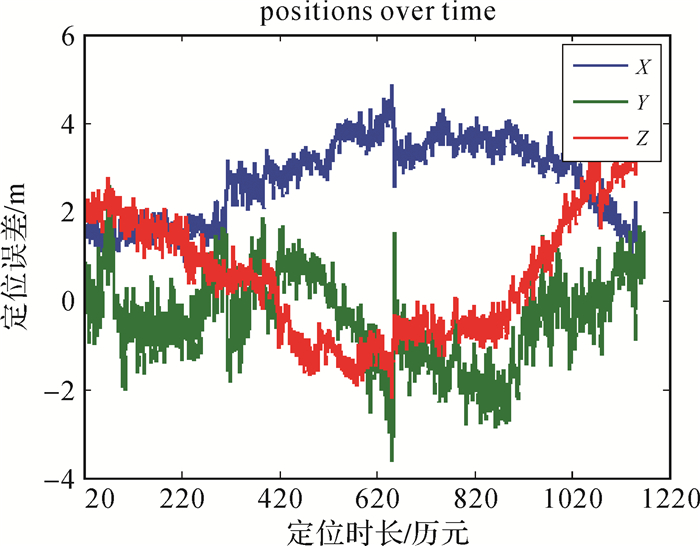
图 5和图 6分别给出了故障剔除前后,在CGCS2000坐标系下的定位误差。比较结果可知,故障剔除后定位精度得到了提高。从图中可以看出,故障识别后,定位误差在正常范围内,可以向用户提供定位服务。这说明利用本文提出的故障识别算法可以正确地识别故障,提高了导航系统的连续性。
|
| 图 5 故障剔除前的定位误差 Fig. 5 The positioning errors before faults removal |
|
| 图 6 故障剔除后的定位误差 Fig. 6 The positioning errors after faults removal |
4.2 故障正确探测率的统计
为了统计新算法的故障正确检测率,笔者取中国境内5个iGMAS监测站的I支路北斗民用观测数据,观测时间为72 h(2013年9月7日至10日),采样间隔为30 s,共有43 200个历元的伪距观测值。验证方案设计为:在每个站的可见星中随机选出2~3颗星,在其伪距观测值中人为引入故障偏差,偏差大小从5~150 m,步长为5 m;然后扣除伪距观测量中的各项误差,包括卫星钟差改正、电离层延迟改正、对流层延迟改正、地球自转改正和相对论效应改正;最后,用新算法进行故障探测并进行故障探测率的统计。
为了查看本文提出的新算法较以往的多故障探测算法的效果,笔者对上述数据采取Stanford大学提出的RANCO多故障探测算法进行故障探测并进行故障正确探测率的统计。总的结果如图 7所示。

|
| 图 7 卫星故障探测正确率 Fig. 7 The correct detection probability of satellite faults |
从图 7可知,当故障偏差为5 m时,新算法的故障正确探测率就已经达到了85%,并且随着故障偏差的增大,故障正确探测率逐渐稳定在100%上。即新算法对于小故障具有较好的探测效果;然而,RANCO方法对于40 m以下的故障,其探测效果都不是很理想,另外该方法涉及复杂的初始子集选取问题,并且探测阈值的变动对其探测效果也有较大的影响。
5 结论(1) 鉴于ICA将异常值对多变量时间序列的影响集中在一个或多个独立分量上,与原始的多变量时间序列相比较,独立分量对异常值具有更强的敏感性,提出了基于ICA的多变量时间序列异常值探测方法,并且利用契比雪夫不等式给出了异常值探测的阈值。
(2) 根据RAIM的实时性要求,采用滑动窗口的思想将上述批处理探测算法改造为实时的多变量时间序列异常值探测算法,据此设计了一种多故障在线探测和识别的新算法,并给出了新RAIM算法的实施流程;新算法对于每个历元的数据处理平均时间为300 ms,最短单历元处理时间为120 ms,最长单历元处理时间为400 ms,由此可知算法符合实时性要求。
(3) 引入时间序列干预模型进行多星故障识别,即利用一元时间序列干预模型估计出每颗卫星的故障大小,然后根据3σ准则确定出故障星的位置,以达到故障识别的目的。
(4) 基于独立分量分析的多卫星故障探测和识别算法的优势在于放宽了观测值误差需服从正态分布这个传统的假设,适合于处理那些观测噪声较大的数据。
| [1] | HEWITSON S, WANG J L. GNSS Receiver Autonomous Integrity Monitoring (RAIM) for Multiple Outliers[J]. Journal of Navigation, 2006, 4(4): 47–54. |
| [2] | KNIGHT N L, WANG Jinling, RIZOS C, et al. GNSS Integrity Monitoring for Two Satellite Faults[C]//Proceedings of the IGNSS Symposium. Qld: IGNSS, 2009. |
| [3] | NI Junjie, ZHU Yongxin, GUO Wei. An Improved RAIM Scheme for Processing Multiple Outliers in GNSS[C]//Proceedings of the 21st International Conference on Advanced Information Networking and Applications Workshops (AINAW'07). Niagara Falls: IEEE, 2007: 840-845. |
| [4] | 秘金钟, 李玮, 谷守周. 精密单点定位用户自主式完备性监测算法[J]. 测绘学报, 2011, 40(S1): 63–67. BI Jinzhong, LI Wei, GU Shouzhou. Precise Point Positioning RAIM Method[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 63–67. |
| [5] | WANG Jinling, WANG Jian. Mitigating the Effect of Multiple Outliers on GNSS Navigation with M-estimation Schemes[C]//Proceedings of the International Global Navigation Satellite Systems Society (IGNSS) Symposiumm. Sydney: IGNSS, 2007: 1-9. |
| [6] | ZHANG Yun, WU Falin, ISSHIKI H. A New Cascade Method for Detecting GPS Multiple Outliers Based on Total Residuals of Observation Equations[C]//Proceedings of the 2012 IEEE/ION Position Location and Navigation Symposium. Myrtle Beach: IEEE, 2012: 208-215. |
| [7] | 仝海波, 张国柱. 改进M估计的抗多个粗差定位解算方法[J]. 测绘学报, 2014, 43(4): 366–371. TONG Haibo, ZHANG Guozhu. Robust Positioning Algorithm with Modified M-estimation for Multiple Outliers[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 366–371. |
| [8] | SCHROTH G, ENE A, BLANCH J, et al. Failure Detection and Exclusion via Range Consensus[C]//Proceedings of the ENC GNSS Conference. Toulouse: Institute of Communication and Navigation, 2008. |
| [9] | SCHROTH G, RIPPL M, ENE A, et al. Enhancements of the Range Consensus Algorithm (RANCO)[C]//Proceedings of the 21st ION GNSS Conference. Savannah: ION, 2008. |
| [10] | RIPPL M, SCHROTH G, BELABBAS B, et al. A Probabilistic Assessment on the Range Consensus(RANCO) RAIM Algorithm[C]//Proceedings of the ION ITM. Anaheim: ION, 2009: 248-255. |
| [11] | NIKIFOROV I. Advanced RAIM Algorithms for Safe Navigation Based on the Constrained GLR Test[C]//Proceedings of the American Control Conference. New York: IEEE, 2007: 1840-1845. |
| [12] | ABED-MERAIM K, LOUBATON P, MOULINES E. A Subspace Algorithm for Certain Blind Identification Problems[J]. IEEE Transactions on Information Theory, 1997, 43(2): 499–511. DOI:10.1109/18.556108 |
| [13] | AMARI S I. Natural Gradient Works Efficiently in Learning[J]. Neural Computation, 1998, 10(2): 251–276. DOI:10.1162/089976698300017746 |
| [14] | DE LACY M C, REGUZZONI M, SANSÒ F, et al. The Bayesian Detection of Discontinuities in a Polynomial Regression and Its Application to the Cycle-slip Problem[J]. Journal of Geodesy, 2008, 82(9): 527–542. DOI:10.1007/s00190-007-0203-8 |
| [15] | ZHANG Qianqian, GUI Qingming. A New Bayesian RAIM for Multiple Faults Detection and Exclusion in GNSS[J]. Journal of Navigation, 2015, 68(3): 465–479. DOI:10.1017/S0373463314000721 |
| [16] | YUN H, YUN Y, KEE C. Carrier Phase-based RAIM Algorithm Using a Gaussian Sum Filter[J]. The Journal of Navigation, 2011, 64(1): 75–90. DOI:10.1017/S0373463310000330 |
| [17] | NIKOLAIDIS R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002. |
| [18] | GALEANO P, PEÑA D, TSAY R S. Outlier Detection in Multivariate Time Series by Projection Pursuit[J]. Journal of the American Statistical Association, 2006, 101(474): 654–669. DOI:10.1198/016214505000001131 |
| [19] | YANG Yuanxi, GAO Weiguang. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177–183. DOI:10.1007/s00190-006-0041-0 |
| [20] | CANNAVO F, MATTIA M, ROSSI M, et al. A New Algorithm for Automatic Outlier Detection in GPS Time Series[C]//EGU General Assembly. Vienna: EGU, 2010, 12: 2010-5027. |
| [21] | KLEIJER F. Time Series Analysis of the Daily Solutions of the AGRS[M].Heidelberg: Springer, 2002. |
| [22] | PERFETTI N. Detection of Station Coordinate Discontinuities within the Italian GPS Fiducial Network[J]. Journal of Geodesy, 2006, 80(7): 381–396. DOI:10.1007/s00190-006-0080-6 |
| [23] | KHODABANDEH A, AMIRI-SIMKOOEI A R, SHARIFI M A. GPS Position Time-series Analysis Based on Asymptotic Normality of M-estimation[J]. Journal of Geodesy, 2012, 86(1): 15–33. DOI:10.1007/s00190-011-0489-4 |
| [24] | BARAGONA R, BATTAGLIA F. Outliers Detection in Multivariate Time Series by Independent Component Analysis[J]. Neural Computation, 2007, 19(7): 1962–1984. DOI:10.1162/neco.2007.19.7.1962 |
| [25] | 黄益生. 高等代数[M].北京: 清华大学出版社, 2004. HUANG Yisheng. Advanced Algebra[M].Beijing: Tsinghua University Press, 2004. |
| [26] | HYVARINEN A. Fast and Robust Fixed-point Algorithms for Independent Component Analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626–634. DOI:10.1109/72.761722 |
| [27] | CHEN C, TIAO G C. Random Level-shift Time Series Models, ARIMA Approximations, and Level-shift Detection[J]. Journal of Business & Economic Statistics, 1990, 8(1): 83–97. |
| [28] | TSAY R S. Outliers, Level Shifts, and Variance Changes in Time Series[J]. Journal of Forecasting, 1988, 7(1): 1–20. DOI:10.1002/(ISSN)1099-131X |
| [29] | MCCULLOCH R E, TSAY R S. Bayesian Analysis of Autoregressive Time Series via the Gibbs Sampler[J]. Journal of Time Series Analysis, 1994, 15(2): 235–250. DOI:10.1111/j.1467-9892.1994.tb00188.x |
| [30] | TSAY R S, PENA D, PANKRATZ A E. Outliers in Multivariate Time Series[J]. Biometrika, 2000, 87(4): 789–804. DOI:10.1093/biomet/87.4.789 |
| [31] | SÁNCHEZ M J, PEÑA D. The Identification of Multiple Outliers in ARIMA Models[J]. Communications in Statistics: Theory and Methods, 2003, 32(6): 1265–1287. DOI:10.1081/STA-120021331 |
| [32] | ZHANG Qianqian, GUI Qingming. Carrier-phase RAIM Algorithm Based on a Vector Autoregressive Model[M].Heidelberg: Springer, 2015: 125-142. |
| [33] | 陈金平. GPS完善性增强研究[D]. 郑州: 信息工程大学, 2001. CHEN Jinping. Research of GPS Integrity Augmentation[D]. Zhengzhou: Information Engineering University, 2001. |
| [34] | 牛飞. GNSS完好性增强理论与方法研究[D]. 郑州: 信息工程大学, 2008. NIU Fei. Theory and Technique on GNSS Integrity Augment[D]. Zhengzhou: Information Engineering University, 2008. |
| [35] | 秘金钟. GNSS完备性监测方法、技术与应用[D]. 武汉: 武汉大学, 2010. BI Jinzhong. GNSS Integrity Monitoring Method, Technology and Application[D]. Wuhan: Wuhan University, 2010. |
| [36] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [37] | 吴有龙, 王晓鸣, 杨玲, 等. GNSS/INS紧组合导航系统自主完好性监测分析[J]. 测绘学报, 2014, 43(8): 786–795. WU Youlong, WANG Xiaoming, YANG Ling, et al. Autonomous Integrity Monitoring of Tightly Coupled GNSS/INS Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 786–795. DOI:10.13485/j.cnki.11-2089.2014.0136 |


