2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 江西省数字国土重点实验室, 江西 南昌 330013
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, Nanchang 330013, China
近年来,在海底地形测量技术中多波束测深系统成为海洋测量的主要设备,给研究区域的海底地形构建带来了丰富的数据资料[1]。高精度的海底地形地貌信息是保障海上船只航行及舰艇作战训练安全的必备资料,也是海洋工程、资源开发和海洋科学研究等多个应用领域的重要基础信息[2]。为了提高海底地形构建的精度,必须采用合适的算法对多波束测深数据进行处理,众多学者作了大量的研究工作[3]。文献[3]提出了抗差Kriging拟合方法,该方法在精确估计的同时能够检测测深数据的异常点,但是该方法需要测深数据满足平稳假设或内蕴假设,只能对平坦的海底数据进行处理。
最小二乘配置最初是由Trarup提出,是用来研究地球形状和重力场的一种数学方法[4],随后Moritz和Wolf对最小二乘配置作了进一步研究[5-6]。如今,最小二乘配置已被广泛应用于地壳形变分析[7-9]、高程异常[10]、重力异常[11]、坐标转换[12]等领域。文献[13]将最小二乘配置应用于海道测量非定位点的估计中,利用区域深度场信息解算出非定位点的水深值,该方法方便精度评估,取得了不错的效果。最小二乘配置能够顾及多波束测深数据具有趋势性和随机性的影响,但无法探测出多波束测深数据中的粗差或异常点,针对于此问题,文献[14]提出了一种抗差最小二乘配置方法进行处理,取得了良好的效果。文献[15]对多波束测深数据处理的传统抗差最小二乘配置方法和抗差Kriging拟合方法进行了比较分析,通过试验验证了在多波束测深数据处理中,最小二乘配置在模型上优于Kriging拟合方法。但现有的多波束测深数据处理的配置法均基于二次多项式拟合趋势项,一般情况下,特别是在海底地形起伏较大时,二次多项式难以表征海底地形的整体变化趋势,甚至拟合的地形可能会出现“龙格现象”[16],从而导致后续的经验协方差函数估计存在偏差;另一方面,由于海况环境、测量仪器以及人为等因素的影响,多波束测深数据不可避免的存在粗差点或异常点的情况,迫切需要一种有效的抗差方法进行处理。
为了解决以上两个问题,提高多波束测深数据处理的精度,本文提出一种抗差最小二乘配置迭代解法,该方法以多面函数代替传统的二次多项式拟合海底地形的趋势项,应用Huber权函数并通过迭代的方式求出经验协方差函数参数估计和最小二乘配置解。最后利用本文方法、传统的抗差最小二乘配置方法及最小二乘配置方法进行实际的多波束测深数据处理,验证了本文方法的有效性与可行性。
1 多波束测深数据处理的最小二乘配置方法最小二乘配置方法能够同时顾及到海底地形的趋势项及随机项,根据海底地形生成的特点,建立多波束测深观测模型[17-18]
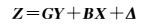 (1)
(1)
式中, Z为测深值;GY为海底地形连续的整体变化趋势;G为趋势项的系数矩阵;Y为非随机参数;BX表示海底地形不规则波动的随机部分;B=[I, 0];I表示单位矩阵;X=[S S′]T;S为多波束测深数据已测点的信号向量;S′为多波束测深数据未测点的信号向量;Δ为多波束测深值的随机误差。对应的随机模型为
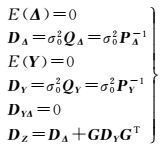 (2)
(2)
式中,DΔ为测深值方差阵,PΔ为测深值权阵。将式(1) 改写成误差方程形式
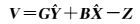 (3)
(3)
根据广义最小二乘原则,构造目标函数
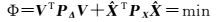 (4)
(4)
式中,PX为多波束测深已测点与未测点的权阵,由式(4) 求自由极值,并通过整理,得
 (5)
(5)
将式(3) 代入式(5),通过法方程解算,得到多波束测深数据处理的最小二乘配置解[17]
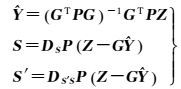 (6)
(6)
式中,P=(DΔ+DS)-1;DS为测深值已测点信号协方差;DS′S为测深值未测点信号与已测点信号的协方差。其中,DS和DS′S由经验协方差函数给出,常选定高斯函数进行拟合[8-9, 14]
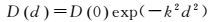 (7)
(7)
式中,D(0) 表示距离为0的方差, k为待定系数,根据下面公式计算D(0)、D(d)和k
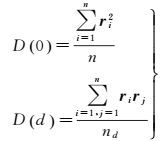 (8)
(8)
式中,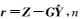
 (9)
(9)
式中,(xi, yi)为i点测深值的坐标,Y=[a b c d e f]T为二次多项式模型待估参数。但一般情况下,特别是在海底地形起伏较大的区域,利用二次多项式拟合海底的整体连续变化趋势可能会出现“龙格现象”[16],不能够精确地表征海底地形的整体连续变化情况。本文针对此问题,提出利用多面函数代替传统的二次多项式进行海底地形整体变化趋势的拟合。
文献[19—20]提出了多面函数模型来逼近不规则表面的思想,即任何的一个数学表面均可由一系列的数学表面的总和,以任意的精度进行逼近。文献[21]提出了基于多面函数的最小二乘配置改进方法,该方法利用多面函数拟合地壳形变的趋势项,并得到了较好的效果。假设海底地形的整体趋势是一个连续不规则变化的表面,基于多面函数的优良特性,利用多面函数对海底地形的整体趋势项进行逼近[20]
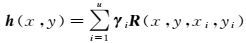 (10)
(10)
式中,γi为待定系数, R为核函数,(xi, yi)为核函数的选定点坐标。其中,核函数R的表达形式为
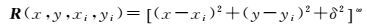 (11)
(11)
式中,δ为平滑因子,具有调整核函数性状的作用,ω为可选择的非零实数,不同的ω值,有不同形式的核函数,一般选取0.5、-0.5和2/3。根据研究区域的地形及试验情况,本文多面函数3要素取值为:δ=0.1,ω=0.5,选定点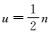
 (12)
(12)
以多面函数拟合海底地形的整体连续变化趋势,在最小二乘配置的框架下,把多面函数融入最小二乘配置中,此时基于多面函数的最小二乘配置函数模型为
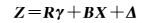 (13)
(13)
式中,Rγ表示海底地形的整体连续变化部分;R为n×m维的核函数矩阵;γ为m×1维的待定系数向量;BX为海底地形不规则变化的随机部分。同理,根据广义最小二乘原理,解得基于多面函数的最小二乘配置解[21]
 (14)
(14)
多波束测深系统是现今海洋测深的主要数据采集设备,它获取的数据覆盖范围广,采样密度高等特点而被广泛应用。但由于海洋测量相比于陆地测量存在较多的不稳定因素,导致多波束测深数据存在粗差或异常点的情况较多,当多波束测深数据含有粗差或异常点时,给出的最小二乘配置解并非是一个最优解。针对多波束测深数据含有粗差或异常点的问题,在文献[21—24]的基础上,本文提出了抗差最小二乘配置方法处理含有粗差或异常点的多波束测深数据。该方法首先进行观测值权阵的初始化,具体权阵初始化步骤如下:
(1) 对多波束测深数据消除整体连续变化趋势,求取初始残差值
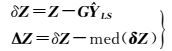 (15)
(15)
式中,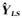
(2) 根据给出的残差初始值,计算初始方差因子,利用该式去计算参数的抗差解具有50%的高崩溃污染率
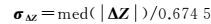 (16)
(16)
(3) 选取Huber权函数计算权因子[14]
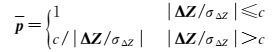 (17)
(17)
式中, c一般取值1.5~2.5。值得注意的是,由于需要进行权阵与协方差阵之间的转换,为了转换的需要,避免权阵为0,从而导致无法解算的问题,本文选取Huber权函数[14]。假设多波束测深数据独立等精度观测,则式(17) 给出的权因子可直接作为观测值的初始权阵p0,即有p0=p。
2.2 协方差函数的抗差拟合方法经验协方差函数拟合的准确性是求解最小二乘配置问题的关键。经验协方差函数的拟合主要为求解协方差函数(式(7))的两个参数解D(0) 和k。由上述得到的更新后的观测值权阵,代入式(8),得到抗差后的D(0) 解
 (18)
(18)
设ρ+1个等间距dΞ=Ξ×η,式中η=0, 1, 2, …, ρ,表示等间距个数,Ξ为各分段的距离。由于多波束测深数据点分布不规则,在计算过程中选取一个常量Δd,且为了满足在计算过程中能够利用到所有的观测数据,一般取值Δd=Ξ/2。利用满足|dij-dΞ<Δd的点对的r求取对应的协方差函数值σ(dΞ),为了抵抗粗差或异常点对求解协方差函数参数k的影响,同样的,根据更新后的观测值方差阵代入式(8),得到D(dΞ)
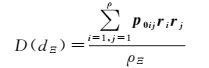 (19)
(19)
式中,ρΞ为满足|dij-dΞ|<Δd的点对总个数。根据式(18) 和式(19) 给出的结果代入式(7),得出一组k值[24]
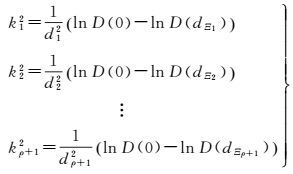 (20)
(20)
式(20) 的D(0) 和D(dΞ)虽然均由抗差方法给出,但是在计算D(dΞ)的过程中,把满足|dij-dΞ|<Δd条件的所有点对近似看作距离为dΞ的点对,需要进一步对ρ+1个k进一步进行抗差处理。具体步骤如下:
(1) 首先对式(20) 左边的k2开根号处理,并取其中位数,计算其残差值,即
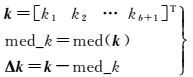 (21)
(21)
(2) 根据给出的残差初始值,计算初始方差因子
 (22)
(22)
(3) 选取Huber权函数计算权因子
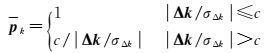 (23)
(23)
最后通过迭代计算,给出稳健的协方差函数参数k的值。抗差最小二乘配置迭代解法的计算步骤如下:
(1) 初始化协方差函数,给出协方差函数的初始值D(0)(0)=1,k(0)=0。利用观测值中位数,初始观测值方差阵,以多面函数拟合趋势项,计算得到最小二乘配置的初始解;
(2) 由步骤(1) 得到的初始最小二乘配置解,去除趋势项,根据Huber权函数更新观测值方差阵,随后进行信号协方差统计,根据3.2节的方法得到协方差函数的参数解D(0) 和k;
(3) 由步骤(2) 得到的新的协方差函数以及更新后的观测值方差阵,计算信号协方差Ds,把Ds和更新后的观测值方差阵代入式(14),计算得到新的最小二乘配置解。
(4) 上述3步给出该算法的一个循环计算,通过重复步骤(2)~(3),直至满足迭代条件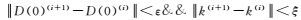
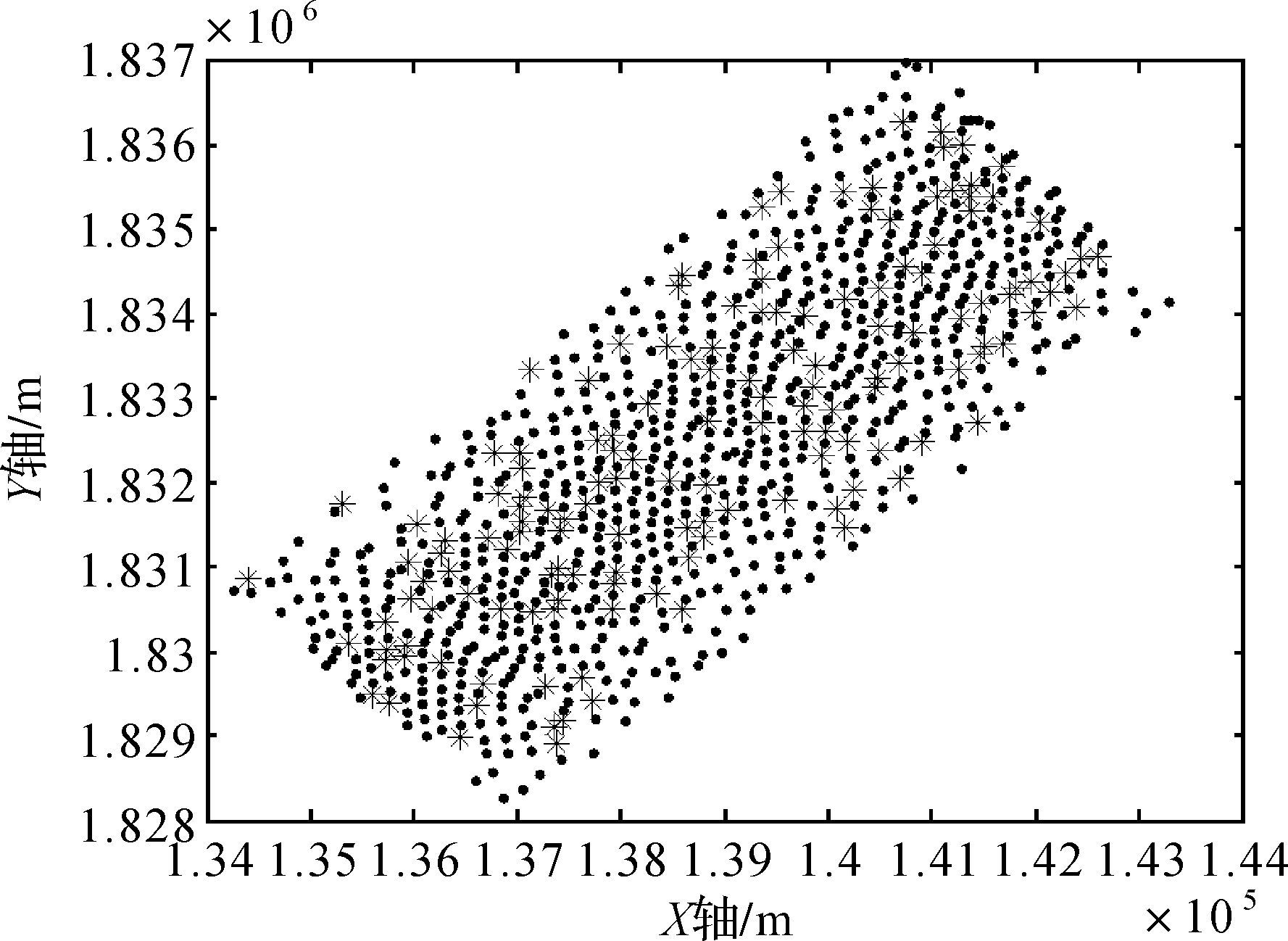
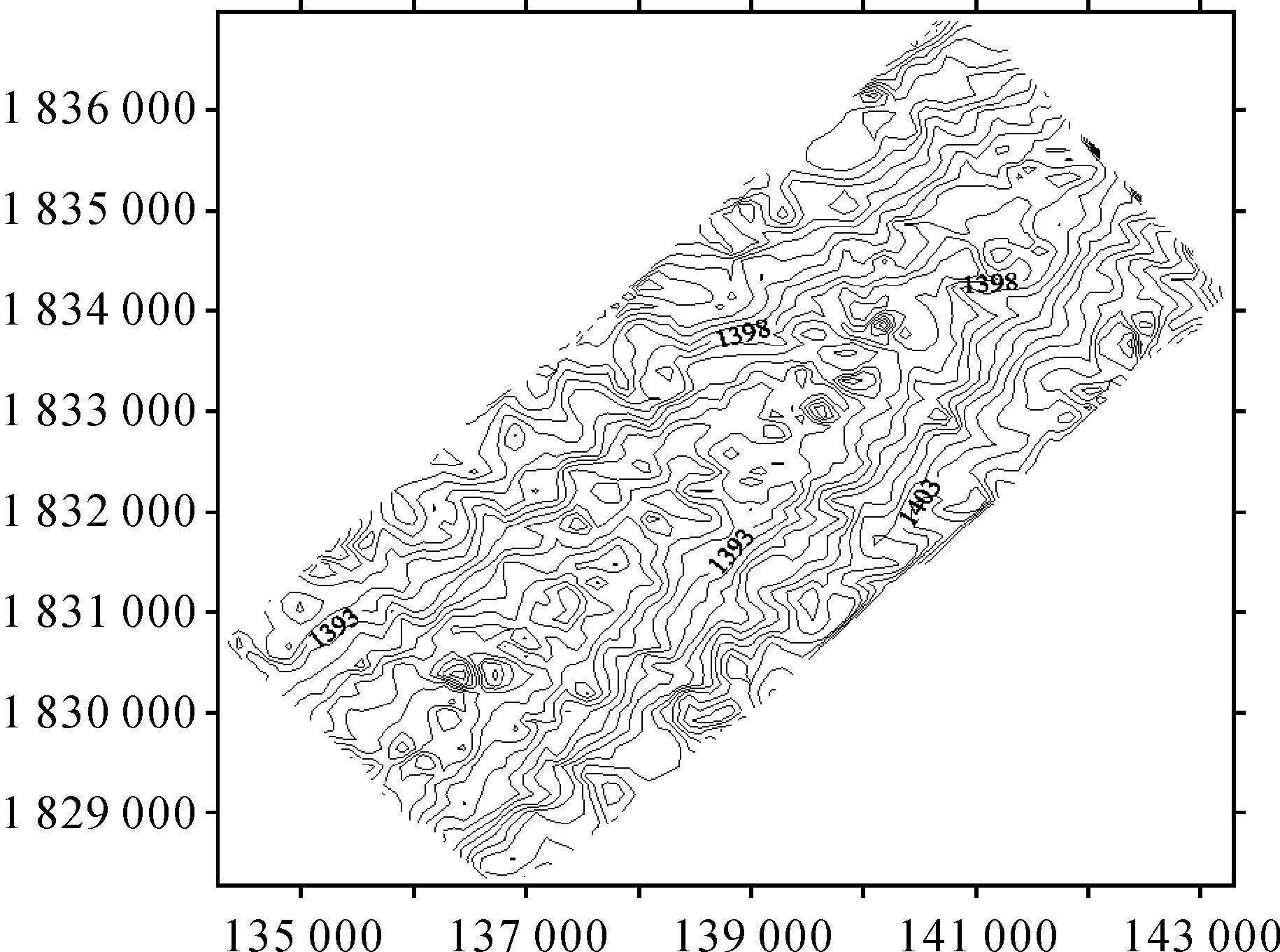
本文数据来自于中国某海域,水深范围为1100~1400 m,海底地形起伏变化较大。本文选取其中一个条带作为试验数据,由于数据量较大,冗余点较多,首先进行了数据抽稀处理,共选取886个多波束测深数据点,其中随机抽取不含粗差的150个点作为检核点,所有数据如图 1所示,星点为检核点,其余为已测点。测深值等高线图如图 2所示。
|
| 图 1 多波束测深数据分布图 Fig. 1 Multi-beam data distribution map |
|
| 图 2 原始数据测深等高线图 Fig. 2 Contour map of raw data |
为了验证本文算法的有效性,分别利用本文算法、传统抗差最小二乘配置方法、基于多面函数的最小二乘配置方法和基于二次多项式的最小二乘配置方法进行多波束测深数据处理,设计的4种方案如下所示:
方案1:基于二次多项式的最小二乘配置法,该法以二次多项式拟合趋势项,计算检核点的水深值和外符精度;
方案2:基于二次多项式的传统抗差最小二乘配置法,计算检核点的水深值和外符精度;
方案3:基于多面函数的最小二乘配置法,该法以多面函数拟合趋势项,计算检核点的水深值和外符精度;
方案4:基于多面函数的抗差最小二乘配置迭代解法,该法以多面的函数拟合趋势面,结合抗差的方法进行协方差函数拟合,计算检核点的水深值和外符精度。
通过以上4种方案对实际多波束测深数据进行处理,4种方案的外符精度如表 1所示,残差统计如图 3所示。
| m | |||
| 算法 | 最大值 | 最小值 | 外符精度 |
| 方案1 | 2.694 25 | -3.463 94 | 1.205 97 |
| 方案2 | 2.713 93 | -3.447 57 | 1.215 78 |
| 方案3 | 2.736 75 | -1.791 88 | 0.935 86 |
| 方案4 | 1.738 86 | -1.753 55 | 0.897 84 |

|
| 图 3 4种方案检核点残差统计图 Fig. 3 Residual statistics chart of external check points using four schemes |
通过表 1可以看出,基于多面函数的最小二乘配置方法的各项指标均比传统的基于二次多项式的最小二乘配置要优。在外符精度上,基于多面函数的最小二乘配置(方案3) 和基于二次多项式的最小二乘配置方法(方案1) 的外符精度分别为0.935 86 m和1.205 97 m,相比于传统的方法,基于多面函数的最小二乘配置方法在外符精度上提高了0.270 11 m,说明了以多面函数拟合海底地形的趋势项更能反映研究区域海底地形的整体连续变化的趋势,去除趋势项后得到的随机变化部分也更为平稳,因此可以利用该方法得到更为正确的信号值。通过比较两种方法的残差统计图(图 3),可以看出基于多面函数的最小二乘配置方法给出的残差小于传统的基于二次多项式的最小二乘配置方法的残差,进一步验证多面函数拟合趋势项的有效性。另一方面,通过比较分析传统的抗差最小二乘配置方法(方案2) 与基于多面函数的最小二乘配置方法(方案3) 可以发现,虽然传统的抗差方法进行了抗差处理,但是由于二次多项式不能较好地表征海底地形的整个连续变化趋势,使得后续由扣除趋势项后得到的残差进行拟合得到的协方差函数发生了偏差,导致推估的效果比没有考虑到抗差的基于多面函数的最小二乘配置方法要差。最后,本文抗差最小二乘配置方法的推估效果最好,在外符精度上,比基于二次多项式的最小二乘配置方法提高了0.308 13 m,比传统的抗差最小二乘配置方法提高了0.317 94 m,比基于多面函数的最小二乘配置方法提高了0.038 02 m,说明了本文抗差方法能在一定程度上克服多波束测深数据中粗差或异常点对最小二乘配置结果的影响;同时,相比传统的抗差方法,本文方法推估精度更高。同样的,为了进一步验证本文抗差方法的有效性的,给出四种方案的经验协方差函数的参数解,具体如表 2所示。本文抗差最小二乘配置能够在一定程度上抵抗多波束测深数据中粗差或异常点的影响,给出协方差函数更符合实际情况,更为客观的反映点位之间的相关性。
| 参数 | 方案1 | 方案2 | 方案3 | 方案4 |
| D(0) | 13.921 78 | 13.006 26 | 2.440 06 | 0.931 10 |
| k2 | 6.952 40×10-8 | 6.870 77×10-8 | 5.970 79×10-8 | 3.357 09×10-7 |
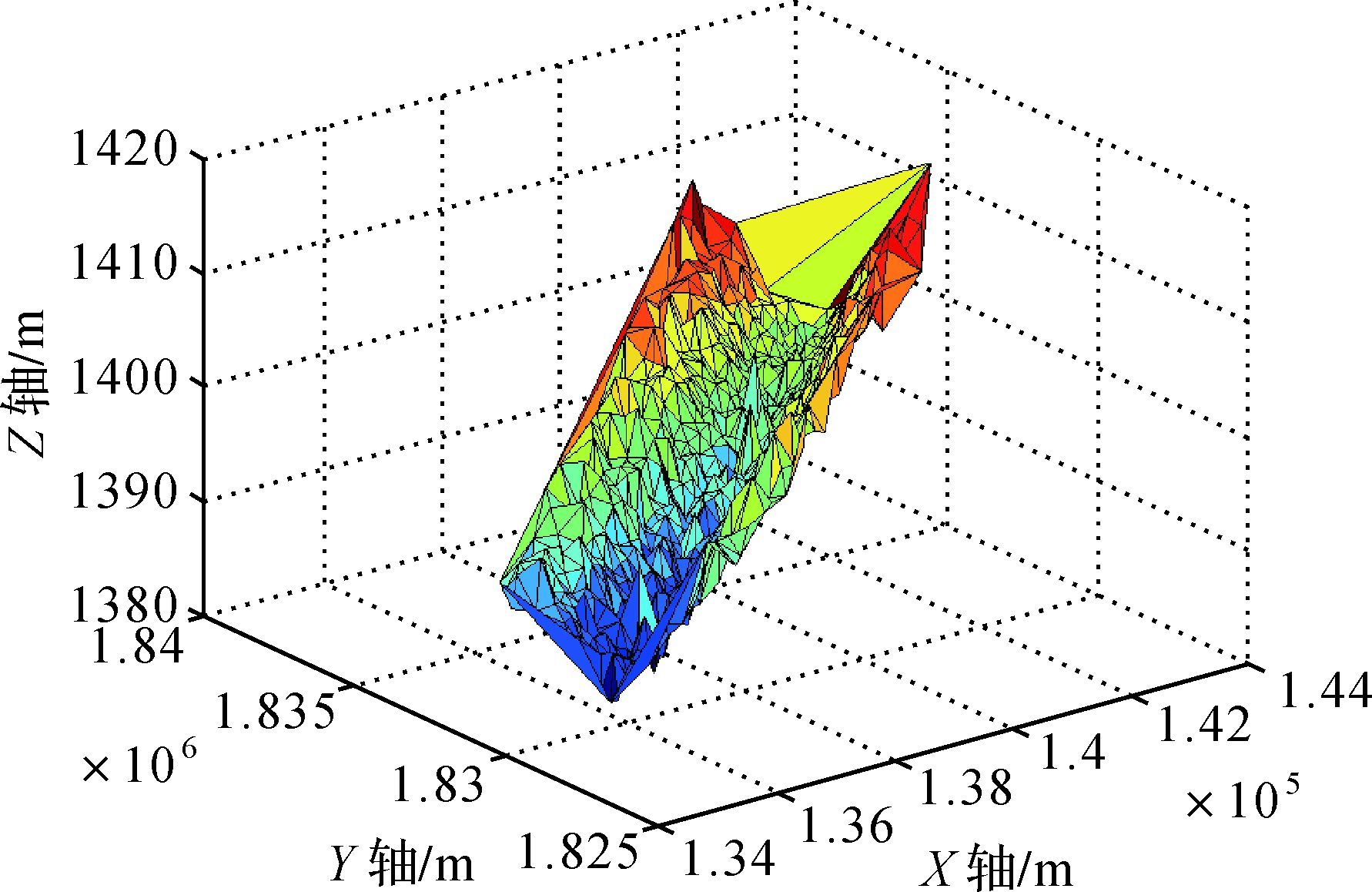
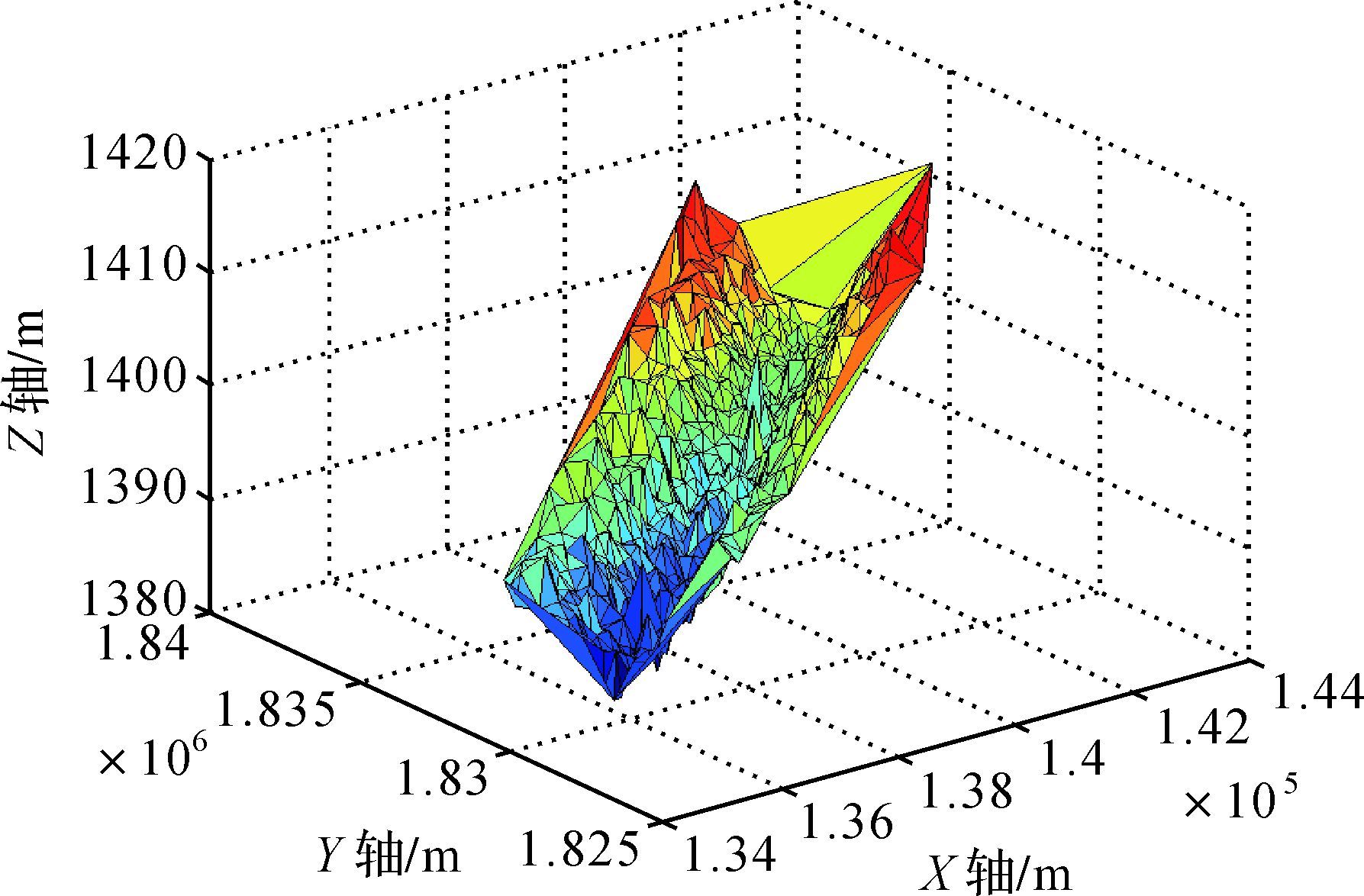
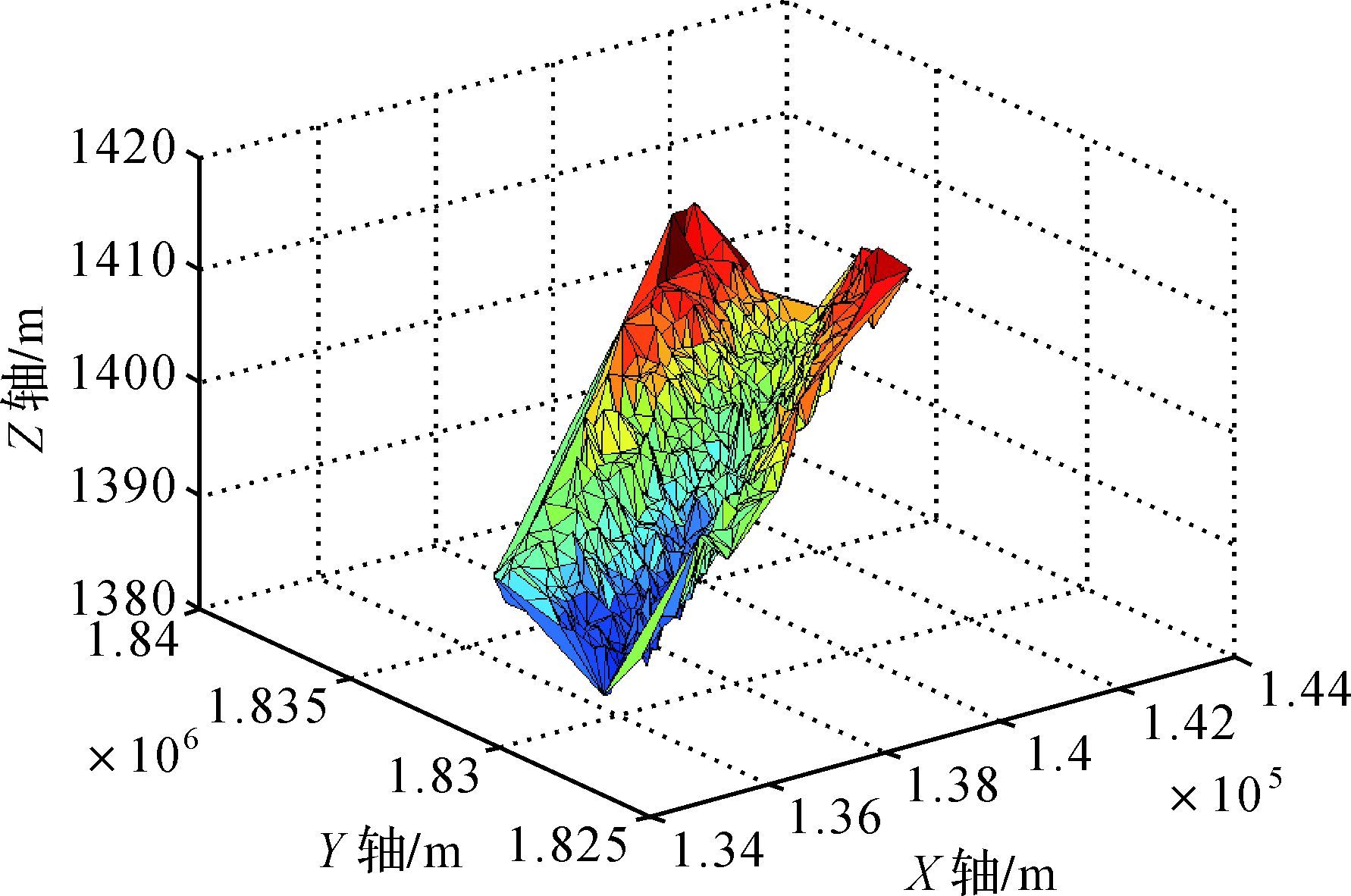
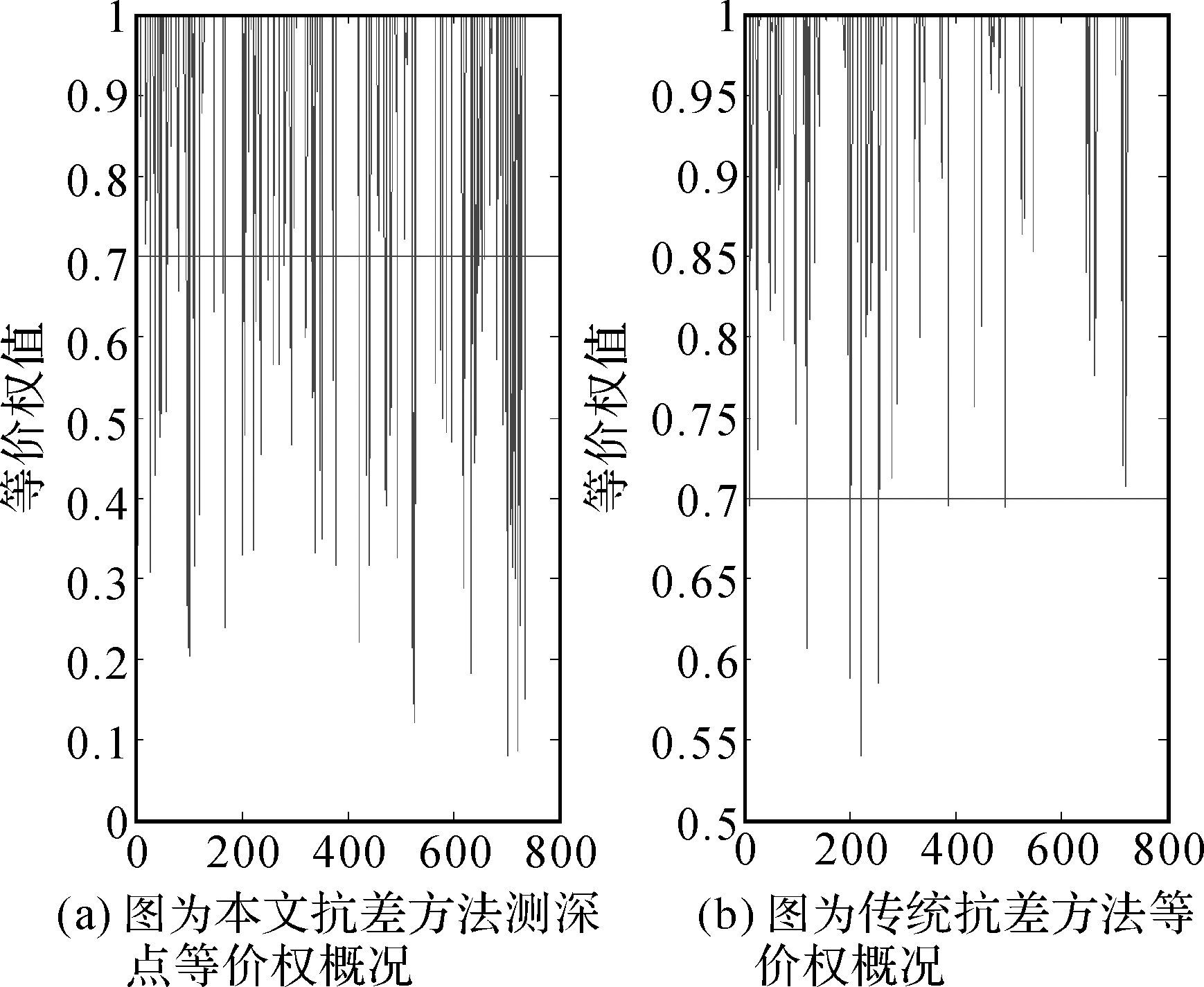
针对TIN中Delaunay三角形网有利于数据更新以及地形特征分析等特点[25],分别利用原始多波束测深数据、传统抗差最小二乘配置以及本文抗差最小二乘配置处理后的多波束测深数据生成Delaunay三角形网图,具体如图 4、图 5和图 6所示。其中,在试验过程中,把等价权p<0.7对应的测深数据标定为异常点。值得注意的是,本文抗差方法共探测出67个测深异常点,而传统的抗差方法仅能探测出7个测深异常点,具体如图 7所示,说明本文抗差方法更能有效地识别出测深数据中异常点。分析比较图 4、图 5和图 6可以发现,本文抗差最小二乘配置在剔除测深数据中的异常点后的TIN图更能体现出测区的地形特征,基于此转化为等值线或规则格网的精度将得到一定程度上的提高[14]。
|
| 图 4 原始多波束测深数据TIN图 Fig. 4 TIN chart of original multi-beam data |
|
| 图 5 传统抗差方法处理后的多波束测深数据TIN图 Fig. 5 TIN chart of multi-beam data using traditional robust least squares collocation |
|
| 图 6 经本文抗差方法处理后的TIN图 Fig. 6 TIN chart of multi-beam data using robust least squares collocation was proposed in this paper |
|
| 图 7 两种抗差方法测深点等价权值概况 Fig. 7 Equivalent weight of sounding points for two robust methods |
4 结论
为了进一步提高多波束测深数据处理的精度,本文提出了一种抗差最小二乘配置迭代解法,给出了具体的求解公式以及迭代算法,通过算例验证了本文方法的有效性,得出了以下的结论:
(1) 针对现有配置法的趋势项的二次曲面数学模型通常无法精确表征海底地形的整体连续变化趋势的问题,本文提出以多面函数代替传统的方法拟合海底地形的趋势项,通过算例验证了该方法的有效性,进一步提高了配置法在多波束测深数据处理中的推估精度。
(2) 针对多波束测深数据存在粗差或异常点时,常规最小二乘配置方法给出的协方差函数不能精确表征其统计特性的问题,提出了一种抗差最小二乘配置迭代解法,以迭代计算的方式给出了经验协方差函数的参数估计和最小二乘配置解,通过算例验证了本文方法在一定程度上能够克服多波束测深数据中粗差或异常点的影响,提高了推估的精度,相比于传统的抗差方法,本文抗差方法能够更为有效地识别出测深数据中的异常点。
最小二乘配置问题的关键是确定合理的协方差函数,接下来还需进一步研究协方差函数的确定方法,从而进一步提高最小二乘配置推估的精度。
致谢: 感谢东华理工大学王胜平博士提供多波束测深数据。
| [1] | 朱庆, 李德仁. 多波束测深数据的误差分析与处理[J]. 武汉测绘科技大学学报, 1998, 23(1): 1–4. ZHU Qing, LI Deren. Error Analysis and Processing of Multibeam Soundings[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(1): 1–4. |
| [2] | 陆秀平, 黄谟涛, 翟国君, 等. 多波束测深数据处理关键技术研究进展与展望[J]. 海洋测绘, 2016, 36(4): 1–6. LU Xiuping, HUANG Motao, ZHAI Guojun, et al. Development and Prospect of Key Technologies for Multibeam Echosounding Data Processing[J]. Hydrographic Surveying and Charting, 2016, 36(4): 1–6. |
| [3] | 王海栋, 柴洪洲, 王敏. 多波束测深数据的抗差Kriging拟合[J]. 测绘学报, 2011, 40(2): 238–242. WANG Haidong, CHAI Hongzhou, WANG Min. Multibeam Bathymetry Fitting Based on Robust Kriging[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 238–242. |
| [4] | BORRE K. Mathematical Foundation of Geodesy:Selected Papers of Torben Krarup[M]. Berlin Heidelberg: Springer, 2006. |
| [5] | MORITZ H. Advanced Physical Geodesy[M]. Karlsruhe: Wichmann, Abacus Press, 1980. |
| [6] | WOLF H. Über Verallgemeinerte Kollokation[J]. Zeitschrift für Vermessungswesen, 1974, 99(11): 475–478. |
| [7] | EL-FIKY G S, KATO T. Continuous Distribution of the Horizontal Strain in the Tohoku District, Japan, Predicted by Least-squares Collocation[J]. Journal of Geodynamics, 1998, 27(2): 213–236. DOI:10.1016/S0264-3707(98)00006-4 |
| [8] | 柴洪洲, 崔岳, 明锋. 最小二乘配置方法确定中国大陆主要块体运动模型[J]. 测绘学报, 2009, 38(1): 61–65. CHAI Hongzhou, CUI Yue, MING Feng. The Determination of Chinese Mainland Crustal Movement Model Using Least-squares Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 61–65. DOI:10.3321/j.issn:1001-1595.2009.01.011 |
| [9] | 江在森, 刘经南. 应用最小二乘配置建立地壳运动速度场与应变场的方法[J]. 地球物理学报, 2010, 53(5): 1109–1117. JIANG Zaisen, LIU Jingnan. The Method in Establishing Strain Field and Velocity Field of Crustal Movement Using Least Squares Collocation[J]. Chinese Journal of Geophysics, 2010, 53(5): 1109–1117. |
| [10] | YANG Y X, ZENG A M, ZHANG J. Adaptive Collocation with Application in Height System Transformation[J]. Journal of Geodesy, 2009, 83(5): 403–410. DOI:10.1007/s00190-008-0226-9 |
| [11] | JARMOLOWSKI W. Least Squares Collocation with Uncorrelated Heterogeneous Noise Estimated by Restricted Maximum Likelihood[J]. Journal of Geodesy, 2015, 89(6): 577–589. DOI:10.1007/s00190-015-0800-x |
| [12] | YOU R J, HWANG H W. Coordinate Transformation between Two Geodetic Datums of Taiwan by Least-Squares Collocation[J]. Journal of Surveying Engineering, 2006, 132(2): 64–70. DOI:10.1061/(ASCE)0733-9453(2006)132:2(64) |
| [13] | 徐卫明, 刘雁春. 海道测量中非定位点的精密确定方法[J]. 系统仿真学报, 2007, 19(20): 4612–4615. XU Weiming, LIU Yanchun. Methods of Determining Non-Position Points in Hydrographic Survey[J]. Journal of System Simulation, 2007, 19(20): 4612–4615. DOI:10.3969/j.issn.1004-731X.2007.20.002 |
| [14] | 王海栋, 柴洪洲, 赵东明. 基于抗差最小二乘配置的海底地形生成研究[J]. 系统仿真学报, 2010, 22(9): 2091–2094. WANG Haidong, CHAI Hongzhou, ZHAO Dongming. Research on Seabed Terrain Generation Based on Robust Least-squares Collocation[J]. Journal of System Simulation, 2010, 22(9): 2091–2094. |
| [15] | 王海栋. 多波束系统测深异常处理理论与方法研究[D]. 郑州: 信息工程大学, 2010. WANG Haidong.Research on the Theories and Algorithms of Processing the Bathymetry Outlier in Multibeam Echosounder System[D]. Zhengzhou:Information Engineering University, 2010. |
| [16] | 薛树强, 杨元喜. 广义反距离加权空间推估法[J]. 武汉大学学报(信息科学版), 2013, 38(12): 1435–1439. XUE Shuqiang, YANG Yuanxi. Generalized Inverse Distance Weighting Method for Spatial Interpolation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1435–1439. |
| [17] | 黄维彬. 近代平差理论及其应用[M]. 北京: 解放军出版社, 1992: 92-118. HUANG Weibin. Theory of Adjustment and Its Applications in Geodesy[M]. Beijing: The PLA Press, 1992: 92-118. |
| [18] | YANG Yuanxi. Robustfying Collocation[J]. Manuscripta Geodaetica, 1992, 17(1): 21–28. |
| [19] | HARDY R L. Multiquadric Equations of Topography and Other Irregular Surfaces[J]. Journal of Geophysical Research, 1971, 76(8): 1905–1915. DOI:10.1029/JB076i008p01905 |
| [20] | HARDY R L. The Application of Multiquadric Equations and Point Mass Anomaly Models to Crustal Movement Studies[R]. NOAA Technical Report NOS 76 NGS 11. Rockville, Maryland:US Department of Commerce, National Oceanic and Atmospheric Administration, National Ocean Survey, National Geodetic Survey, 1978. |
| [21] | 谢曦霖, 许才军, 温扬茂, 等. 一种基于多面函数的改进最小二乘配置方法[J]. 武汉大学学报(信息科学版), . XIE Xilin, XU Caijun, WEN Yangmao, et al. A Refined Least Squares Collocation Method Based on Multiquadric Function[J]. Geomatics and Information Science of Wuhan University, . DOI:10.13203/j.whugis20150664 |
| [22] | 杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993. YANG Yuanxi. Robust Estimation Theory and Its Applications[M]. Beijing: Bayi Publishing House, 1993. |
| [23] | SCHAFFRIN B, BOCK Y. Geodetic Deformation Analysis Based on Robust Inverse Theory[J]. Manuscripta Geodaetica, 1994, 19(1): 31–44. |
| [24] | 刘念. 协方差函数的抗差拟合[J]. 测绘科学, 2001, 26(3): 25–28. LIU Nian. Robust Fitting of Covariance Function[J]. Science of Surveying and Mapping, 2001, 26(3): 25–28. |
| [25] | BROUNS G, DE WULF A, CONSTALES D. Multibeam Data Processing:Adding and Deleting Vertices in a Delaunay Triangulation[J]. Hydrographic Journal, 2001(101): 3–9. |


