2. 昆明理工大学国土资源工程学院, 云南 昆明 650093;
3. 国家基础地理信息中心, 北京 100830
2. Faculty of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093, China;
3. National Geomatics Center of China, Beijing 100830, China
具有空间格局特征的居民地、丛集岛屿群、湖泊群、水体污染源与流行病等均可抽象为点状特征的地理对象或事件。依据地理对象或事件的位置研究空间分布是完全随机模式(complete spatial randomness,CSR)、集聚模式(clustering pattern,CP),还是规则模式(regular pattern,RP)是空间点模式分析的重要内容[1]。当两个空间分布之间存在空间相关性,或前期分布与后期分布存在时间相关性,此二元点模式时空效应研究对空间决策具有重要指导意义,如居民点时空分布与教育、医疗、交通因素的相关性分析;犯罪热点地点的空间异质性与空间依赖性[2];前期商业网点分布是否影响后期餐饮网点分布等。
点模式趋同假说可追溯至1956年以经济学家Solow和Swan为代表创建的新古典经济增长模型[3-4]。相关研究证实,经济增长趋同研究往往重视时间因素而忽视了空间因素。诸多分布现象通常以点事件作为基本单元,在细节表达上抽象为点过程。空间趋同表达了地理事件空间分布与演化的时空变化性质。空间区域特征、空间关系和空间过程所产生的空间效应对趋同的形成与演化有重要影响[5],如地震发生、疾病分布、犯罪热点、极端气温点过程和矿化点过程[6]等。一元点模式的分析方法与假设检验具有相似的逻辑计算过程,假设参照为某一概率分布,如泊松过程。以全局莫兰指数(Global Moran’s Ⅰ)为代表的量度方法用单一值描述点状对象或事件与空间分布距离(密集度)的总体相关性较难适用空间差异度量。用于二元点模式研究的Moran闪点图、局部莫兰指数(Anselin Local Moran’s Ⅰ)、吉尔里C数(Geary’s C)与高低聚类(Getis’G)局部统计量[7]的邻近性以距离计量得出,往往导致空间信息失衡[8],一方面,高低聚集(HL)、低高聚集(LH)、高高聚集(HH)、低低聚集(LL)无法体现出空间非邻近对象或事件之间的相关关系;另一方面,单观测值标准差的标准化并未顾及多观测值条件的整体评价。此外,点模式的结构信息与空间聚类、制图综合、空间分析的具体应用密切关系[9]。综合线面特征分布的点目标多尺度聚类方法[10]、加权Voronoi图模糊C-均值集聚法[11]、基于邻近图、k阶空间邻近的点群层次聚类方法[12-13],以及基于k-means+DBI(Davies bouldin index)聚类的点群层次Voronoi图综合方法[14],在点群集聚过程中,由于未顾及空间相关性,使得分簇结构在空间分布上往往表现出很强的随机性,构建出的不同结构形态点模式势必得出不同的时空分布与演变论断,曲解空间现象发生机理。
空间即存在依赖性分布,又存在随机性分布,空间独立性假设是否真的不予成立?为什么研究空间依赖性的同时又探究空间随机性?科学实践表明,消除空间依赖性影响的关键在于观测与抽样[15]。根据地理学第一定律,地理事物或属性在空间分布上互相关,距离越近,相关性越大[16]。针对上述问题,提出了一种利用Voronoi邻近关系提取点群中潜在的空间Voronoi邻近与空间非Voronoi邻近的强趋同性点模式方法。首先,在空间聚类过程中引入空间相关性,设计Voronoi邻近相关表(voronoi adjacency correlation table,VACT)聚类算法,将满足Voronoi邻近关系的对象标记为该拓扑尺度下的独立性样本空间;其次,通过Voronoi邻近指数(voronoi adjacency index,VAI)算法快速测度空间点过程,结合统计分布假设检验,使用拉普拉斯平滑算子实现点模式多观测值的总体空间趋同计算;最后,利用λ截距阵提取出强趋同度性点模式。
1 点模式Voronoi邻近剖分 1.1 Voronoi邻近点对提取定义1 普通Voronoi图
在二维欧几里得空间中,存在空间点集P={p1,p2,…,pn},如图 1(a)所示。若pi,pj∈P满足式(1) 关系,则称由满足条件p构成的空间域为点pi的Voronoi图,记为Vor(pi),如图 1(b)所示

|
| 图 1 Voronoi最邻近点查找 Fig. 1 The nearest point search by Voronoi adjacency relation |
 (1)
(1)
式中,dom(pi,pj)=dis(p-pi)≤dis(p-pj)(0<i,j≤n,i≠j,i,j∈N*);dis(·)算子为两点之间的欧氏距离算子。
定义2 Voronoi最邻近点对
若pi的Voronoi图Vor(pi)满足式(2) 关系
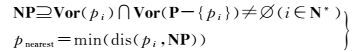 (2)
(2)
式中,NP为点pi的Voronoi邻近点集;min(·)为集合最小距离值算子。
则pnearest为与pi构成的最邻近点对。如图 1(c)所示的最邻近点对p与np。
1.2 Voronoi邻近对象聚类依据适应性抽样原则,空间集聚样本的邻近对象具有较高同一性,不宜在同一样本空间内抽取,此时邻近对象间存在的相互作用力可视为一种放松相互独立假设[17],则邻近关系尺度下剖分而构成的各单元集可视作独立假设的样本空间。邻近对象的邻近测度并非对象本身的空间邻近关系,确切地说是对象的Voronoi邻近[18]。
依据Voronoi邻近关系、点群Voronoi面积分布与空间相关性,Voronoi面积越小,空间表现越集聚,相关性也越强。设计了一种依据Voronoi邻近性集聚样本空间的算法,该算法意义在于:① 针对K-means初始聚类中心的敏感性,依据Voronoi面积与Voronoi邻近关系实现数据的自适性分类;② K-means聚类根据距离对空间数据从全局上进行聚类,未顾及空间分布、空间局部相关性,分类器会呈现如图 2中虚线所示。在地理空间分布中,由于空间边界共享的局部依赖性,最优集群性结构表达应如图 2所示的点模式1、点模式2。由此可见,K-means方法割裂了空间邻近性分布结构。据此,本文点群集聚算法将空间局部相关性引入聚类过程,确保点模式集聚的空间结构形态合理性。
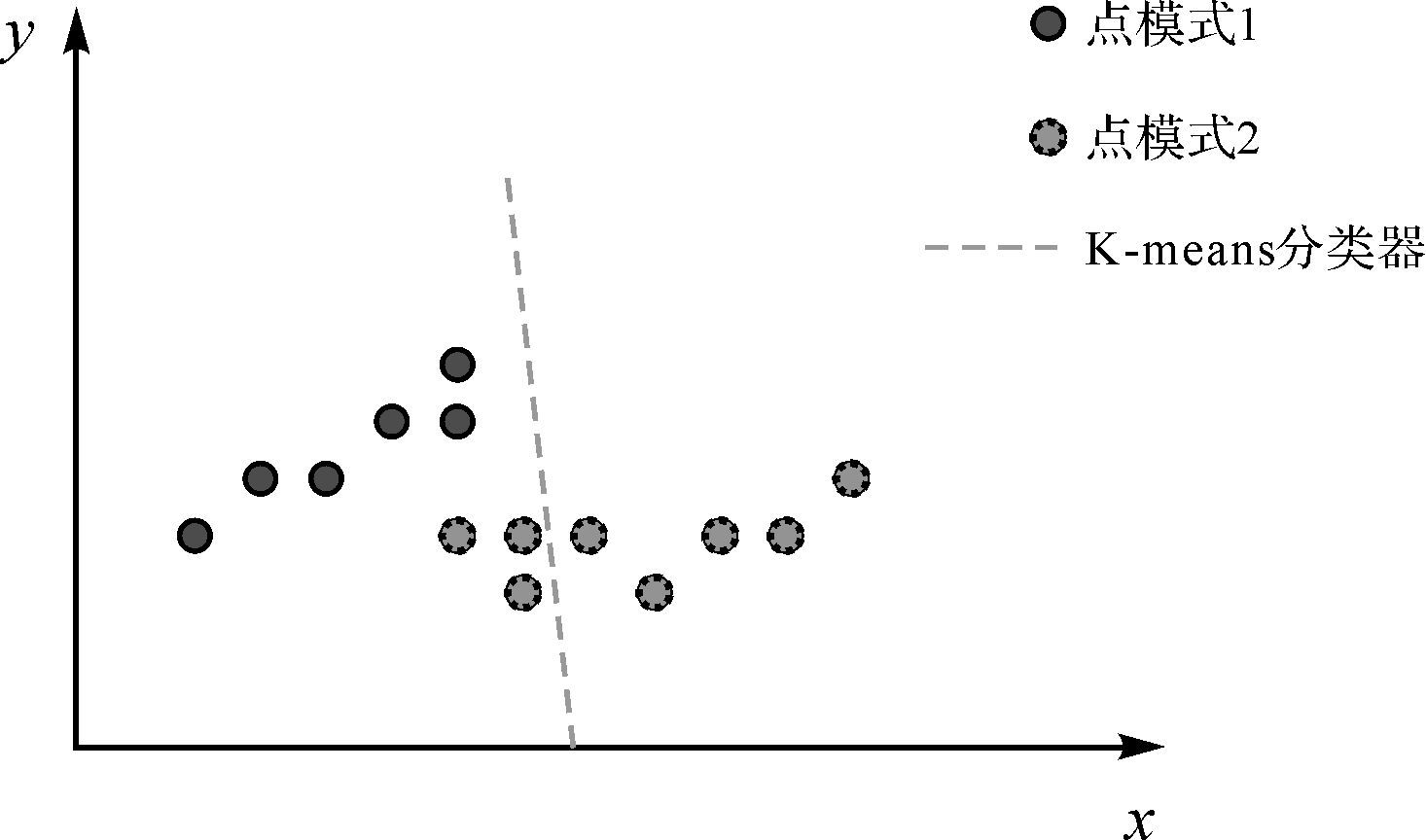
|
| 图 2 K-means算法割裂点模式结构形态 Fig. 2 Point pattern configuration partitioned by K-means algorithm |
算法1:Voronoi邻近相关表(VACT)聚类
输入:空间点集P={p1,p2,…,pn}。
输出:空间聚类样本SC={SC1,SC2,…,SCm}。
(1) 根据空间点集P,构建其Voronoi区域Vor(pi)←createVor(P)。
(2) 按照Voronoi面积由小到大的顺序对Vor(pi)排序,并置pi的类别属性为ck(k=1,2,…,n),构成数组RR←sort(Vor(pi))。
(3) 构建邻近相关表NN←null。
(4) 遍历点集Vor(pi)中的点pi,查找在NN中是否存在与pi邻近的点pj←findNP(pi,NN)。
① 如果pj≡∅,最邻近相关表NN中加入pj,SCk=NN←add(pj)(k=1,…,n)。
② 如果pj≠∅,则cpj←cpi,最邻近相关表NN中加入pj,SCk=NN←add(pj),在RR中删除RR←delete(pj)。
(5) 算法结束。
2 点模式趋同度量地理空间中的集群对象由于受多种因素影响,其空间分布的发生、发展在形态表达上会出现某种扩散或排列性趋同,不仅近距离的邻近对象存在关联,而且远距离非邻近对象也存在一定相关性。鉴于吉尔里C数、莫兰指数空间相关性分析方法的空间关系权重定义差异对空间相关性的分析和认识的影响[19],从空间分布模式、描述性统计(样本平均数、方差)、解释描述结果的推论性统计(样本假设检验)3个方面度量点模式趋同。
2.1 分布模式度量点模式分布的测度方法主要有K函数、最邻近指数(nearest neighbor index,NNI)、核函数等[20],由于K函数的计算结果难以直观地判读出分布性质[21];核函数又表现为主观性带宽τ问题[22],所以,常用最邻近指数,但随着数据点的增多,其计算量呈几何性增大。为此,利用VAI算法快速测度点模式,确定点模式是空间随机分布、集聚分布,还是规则分布。
算法2:Voronoi邻近指数(VAI)计算
输入:空间点集P={p1,p2,…,pn}。
输出:最邻近指数NI。
(1) 构建空间点集P的Voronoi图,Vor(P)←createVor(P)。
(2) 利用Vor(P)确定与点pi邻近的候选点集points←findAdjVor(pi,Vor(P)),从候选点集points中计算出与点pi最邻近点的距离dk←nearestDist(pi,points)(k=1,…,n)。
(3) 计算各点与其最邻近点的平均距离,avg_d←∑dk/n;area(·)计算点集P的Voronoi面积总和SA,SA←∑area(Vor(P))。
(4) 计算最邻近指数,NI←2×avg_d×(n/SA)-1/2。
(5) 算法结束。
图 3所示NNI的Voronoi表达是一个渐进过程,度量值1至0,偏离随机分布,集聚性分布逐渐增强;1至2.15规则性分布逐渐增强。同时界定3种空间分布的标准是一个在统计上仍需进一步探究的问题,文献[23—25]给出了对空间分布界定不一致的情况,见表 1所示的最邻近指数空间分布界定。
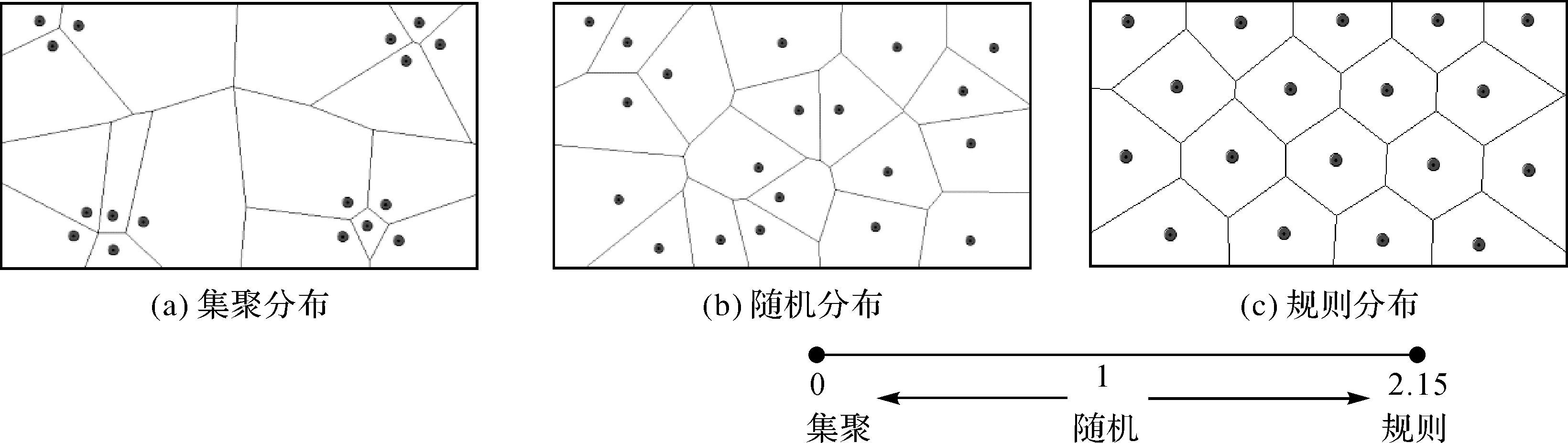
|
| 图 3 点模式的Voronoi图表达 Fig. 3 Point pattern represented by Voronoi |
| 空间分布/界定标准 | I1(林炳耀,1985) | I2(郭仁忠,1997) | I3(梁会民,2001) | 本文界定域 |
| CP | 接近0.0 | 小于1.0 | 小于或等于0.5 | 小于或等于2/3 |
| CSR | 1.0 | 1.0 | 大于0.5且小于1.5 | 大于2/3且小于7/6 |
| RP | 2.15 | 大于1.0 | 大于或等于1.5 | 大于或等于7/6 |
由于最邻近点指数分类的界定标准不同,本文利用已有研究采用加权的方式界定空间离散、集聚与规则分布的区间。针对I1与I2的CSR均为1.0,取其权值相等,建立式(3)
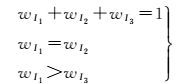 (3)
(3)
解算式(3),得
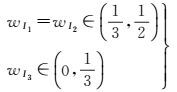 (4)
(4)
根据表 1中CSR的界定值1.0、1.0、0.5,代入式(4),得CSR的界定区间,结果见式(5)
 (5)
(5)
统计学中p值检验的真实程度反映了样本变量与总体变量相关联的可靠程度。假设满足某参数的两个p元正态样本:U={U1,U2,…,Ui}、V={ V1,V2,…,Vj}~N(μ,∑),构建F统计量表达如式(6) 所示
 (6)
(6)
式中,μU、μV代表样本U、V均值;m、n代表U、V样本个数。在显著性水平α下,其零假设H0和备择假设H1如式(7)
 (7)
(7)
在计算出样本U、V的样本均值及样本方差u,SU*2;v,SV*2基础上,根据F统计量临界值表,如果满足式(8)
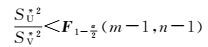 (8)
(8)
则接受零假设H0,表明两样本在数值波动方面没有明显差异,即两样本相容,可视为源于同一样本空间,反之亦然。
2.3 分布均值度量当方差检验无明显差异时,表明样本源于同一总体。此时,在显著性水平α下,相应的均值零假设H0、备择假设H1如式(9)
 (9)
(9)
构建检验t分数,如式(10)
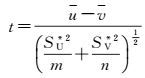 (10)
(10)
式中,u,SU*2;v,SV*2为对应样本U、V的均值、方差;m、n为样本个数。
若在t检验临界值表中查得,t>t1-α(m+n-2),表明二者存在均值上的显著性差异,则拒绝零假设,选择备择假设。当方差相容、检验均值不相容时,该样本为同一总体中的差别抽样;当检验方差、均值检验均相容时,说明为同一总体下的无差别抽样[26]。
2.4 综合提取度量利用p值的反向推导对事件作出恰当估计需更多信息,如效应客观存在的概率就是不可或缺的重要一面[27],但这样的信息有时并不容易得到。针对单项指标检验的弊端,通过多项指标,即统计量纲为分布模式(随机、聚类或规则)、分布距离均值、距离方差检验的综合评价来度量点模式趋同度。由于假设检验论证结果为非零假设即备择假设的逻辑结构,体现出相容性与非相容性二者必居其一,因此,依据多项指标检验结果逻辑值的均值描述对事件作出反向判断。经对多个独立性指标的相容性检验,综合性指标(Overall Index,OI)的拉普拉斯平滑计算表达如式(11) 所示
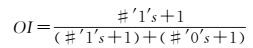 (11)
(11)
式中,#′1′s:相容性指标基数;#′0′s:非相容性指标基数。
根据此平滑计算的鲁棒性,从式(11) 不难看出:当检验指标均相容或均非相容时,由于存在其他未知的指标因素(时空因素),点模式的趋同由初始确定性的逻辑真值1或逻辑假0判断转变为一种不确定性度量。为了从不确定性度量中提取出强趋同点模式,定义λ值为趋同一致强度的度量标准。对上述Laplace平滑结果构成的矩阵A,采用λ截矩阵法对矩阵元素值x与度量标准λ进行比较运算,从而提取出所要表达的强趋同点模式,形式化表达如式(12) 所示
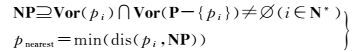 (12)
(12)
腾冲位于中国西南边陲的滇西南,村镇多集中在中北部地区,聚落规模大小不一,小聚落多坐落于偏远山区;大聚落多分布在中部经济发达地区[28]。以图 4所示的1:50 000比例尺、云南省腾冲市某区域当地坐标系下的177个居民点试验数据为研究案例,利用C#+ArcGIS Engine9.3实现VACT、VAI,以及点模式趋同度计算、强趋同性点模式提取的试验研究。

|
| 图 4 云南腾冲居民点 Fig. 4 Residential points of Tengchong Yunnan |
3.1 VACT与K-means+DBI对比
利用VACT集聚算法,经图 5居民点Voronoi图,剖分出图 6所示的最邻近拓扑尺度下点模式的Voronoi邻近单元集,图 7为文献[14]的整体最优自适应聚类算法K-means+DBI的计算结果。从表 2所示的集聚要素对比可知:① 在初始聚类中心计算上,K-means+DBI的计算复杂度为O(n2),而VACT算法的计算复杂度为O(n);② 在自适应控制上,DBI每次聚类的迭代过程均需计算与各聚类中心的最远距离点、类内距与类间距相似度,以确定最优聚类个数,而VACT在候选集中查找最邻近的空间对象,涉猎空间分布的局部性邻近依赖。由此,K-means+DBI方法产生了图 7所示类别1与类别2的分割线破坏了图 6中点模式15、点模式19的地理空间结构形态完整性。③ 在空间结构特征上,K-means+DBI的欧氏距离未顾及原空间分布特征,而VACT集聚结果则保持了原空间分布结构;④ 在聚类精细化程度上,K-means+DBI方法划分出图 7所示的4类点模式空间分布格局与本文方法得出的22类结果相比,其对空间结构的表达程度更多体现为宏观性,掩盖了在小面积单元下所具有的有意义的地理变化单元,如图 7中的类簇4可细化为图 6中的点簇12与点簇22。因此,VACT聚类产生的点模式空间结构形态对空间分析更为稳健。

|
| 图 5 居民点Voronoi图 Fig. 5 Residential Voronoi diagrams |

|
| 图 6 居民点VACT聚类 Fig. 6 VACT clustering on residential points |

|
| 图 7 居民点K-means+DBI聚类 Fig. 7 K-means+DBI clustering on residential points |
| 方法\参量 | 初始聚类中心 | 自适应控制 | 结构特征 | 类别 |
| K-means+DBI | 欧氏距离极大值点 | DBI | 未顾及 | 4 |
| VACT | Voronoi面积最小值点 | Voronoi邻近相关表 | 顾及 | 22 |
3.2 趋同度计算
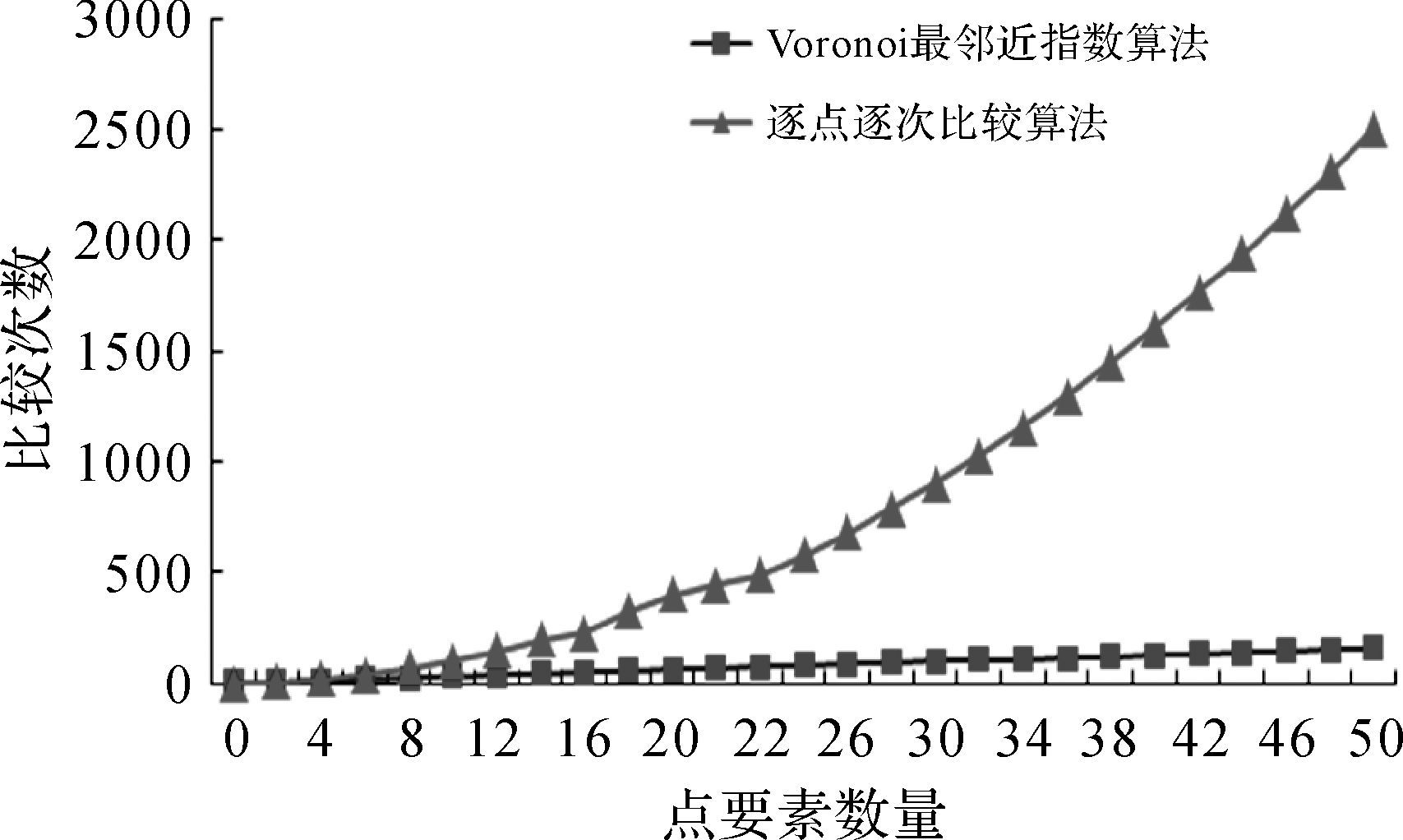
根据VAI,图 6试验区点模式空间分布的计算结果见表 3。VAI在精确过滤模式下,从特定范围的拓扑邻近候选集中查找与之的距离最近点,其复杂度O(n)与逐点逐次计算复杂度O(n2)的比较如图 8所示。作为趋同度量中的一个重要指标,在多个点模式NNI的重复计算过程中,VAI可提高计算效率。点模式分布的距离方差、距离均值度量见表 4和表 5。
| 点模式 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 分布模式 | 0.484 | 0.542 | 0.442 | 0.406 | 0.551 | 0. 415 | 0.513 | 0.563 | 0.504 | 1.015 | 1.087 |
| 点模式 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 分布模式 | 0.765 | 1. 122 | 0.623 | 0.766 | 0.972 | 0.938 | 1.018 | 1.002 | 0.956 | 0.621 | 0.598 |
|
| 图 8 邻近指数计算复杂度比较 Fig. 8 Comparison of nearest indices computational complexity |
| 点模式 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 距离方差 | 0.040 9 | 0.230 3 | 0.094 2 | 0.023 3 | 1.594 4 | 0.024 7 | 0.095 2 | 0.298 9 | 0.041 7 | 0.233 8 | 0.439 8 |
| 点模式 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 距离方差 | 0.338 9 | 1.606 4 | 0.588 7 | 0.742 5 | 0.654 6 | 0.769 1 | 0.935 | 0.678 2 | 0.777 | 0.054 2 | 0.011 2 |
| km | |||||||||||
| 点模式 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 距离均值 | 0.000 894 | 0.002 402 | 0.001 242 | 0.009 063 | 0.015 015 | 0.009 452 | 0.001 251 | 0.006 763 | 0.000 904 | 0.006 159 | 0.008 576 |
| 点模式 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 距离均值 | 0.006 573 | 0.015 221 | 0.006 263 | 0.009 669 | 0.012 202 | 0.013 875 | 0.018 299 | 0.012 264 | 0.013 566 | 0.001 011 | 0.000 421 |
3.3 强趋同提取
结合表 3、表 4、表 5,在选取显著性p值为0.1条件下,利用假设检验方法及临界值表检验各点模式在分布模式、距离方差、距离均值指标下的相容性,并将检验结果通过Laplace平滑算子及λ截矩阵(λ=3/5>50%)计算提取出14个强趋同点模式,检验结果见表 6、示意图如图 9所示,其中点模式2(图 6中点模式16、17、19与20)、点模式6(图 6中点模式2、8与10)、点模式7(图 6中点模式3与7)、点模式8(图 6中点模式4与6) 在点过程、平均距离、紧凑性上表现出非Voronoi邻近条件下样本空间强趋同的独立同分布;点模式1(图 6中点模式5与13) 则表现为Voronoi邻近条件下的空间强趋同分布。

|
| 图 9 强趋同模式提取 Fig. 9 Strong convergent pattern extraction |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |
| 1 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . |
| 2 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | ||
| 3 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | |
| 4 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . |
| 5 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . |
| 6 | 0 | 0 | 0 | 3/5 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | |
| 7 | 0 | 0 | 3/5 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . |
| 8 | 0 | 3/5 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . | . |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . | . |
| 10 | 0 | 3/5 | 0 | 0 | 0 | 0 | 0 | 3/5 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . | . |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . | . |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . | . |
| 13 | 0 | 0 | 0 | 0 | 3/5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . | . |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | . | . |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . | |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . | . | . |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/5 | 4/5 | . | . | . | . | . |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | . | . | . | . |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/5 | 3/5 | 0 | 4/5 | . | . | . |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/5 | 3/5 | 0 | 3/5 | 4/5 | . | . |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 | |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/5 |
从试验数据直观发现居民点与道路、水系交通条件呈现出一定的空间相关性,相对于图 7的大尺度聚元点模式2,均沿河流与道路分布,难以确定主导因素,而图 6的小尺度聚元点模式5和13,根据p值置信趋同检验,点模式5与点模式13的空间强趋同分布,表明在地理空间布局上存在相同的因素共同制约两者的空间布局,结合试验数据与邻近性,此微观尺度的空间连续性分布与道路的相关性要大于与水系要素的相关性。此外,根据二两者的空间Voronoi邻近性也可合并归类,作为探寻局部区域多尺度下的空间分析对象,为面元计算的尺度可变性研究提供参考。图 9中的点模式8对应图 6中的点模式4和点模式6,表现为CP空间分布,在此微观尺度下,单独的点模式分布表现为空间分布的不确定性,难以断定其相关性,经两者趋同综合度量,结合两者周边地理实体数据,其间的强趋同表明二者分布共同受到道路约束,此空间非Voronoi邻近的强趋同点模式可为探索地理隔离条件下的趋同关系研究提供一种视角。
综上,在空间宏观条件下,点模式的分布多表现为空间连续的集聚性分布,易于发现集聚成因;在空间微观条件下,点模式即存在空间连续分布的依赖性,也存在空间离散分布的随机性,其与环境相关性的主导要素难以确定,而趋同关系则可从内部细节上把握点模式空间分布的综合影响、确定相关性及局部邻近性的空间多尺度分析。在农村居民点城镇化发展动态格局上,空间聚落体系发展与交通运输方式、自然资源空间布局紧密相关,基于Voronoi邻近关系的点模式趋同提取可揭示出聚落空间的结构形态及其局部性相关关系,发现影响空间趋同的制约因素。
4 结论针对传统一元点模式趋同分析单一全局观测值规则检验的局限性,最邻近指数、Moran’s Ⅰ、空间拓扑邻近与非邻近关系在二元点模式相关性研究中的不足,提出了Voronoi邻近关系支持下的点模式趋同提取方法,其中Voronoi邻近相关表集聚算法(VACT)验证了空间相关性保持点模式形态结构完整的重要性;Laplace平滑的局部多项指标(VAI,方差、均值检验)综合评价可对趋同事件做出合理性估计;Voronoi邻近与非Voronoi邻近的强趋同点模式λ提取可为发现空间格局及其相关性、探究趋同关系约束因子,为揭示城镇居民点的地理空间布局、疾病分布、公共安全、实践社会学等空间点过程的研究提供有力工具。针对趋同度度量方式、影响因素多元化,综合生态、经济、人文等多种驱动因素探究空间依赖的多层次性之间存在的空间趋同关系理解空间格局演化与预测,以及多种趋同因素中主导因素的提取是后续研究中需要进一步探讨和解决的问题。
| [1] | 周成虎. 点模式分析[J]. 地理科学进展, 1989, 8(2): 8–11. ZHOU Chenghu. Point Pattern Analysis[J]. Progress in Geography, 1989, 8(2): 8–11. DOI:10.11820/dlkxjz.1989.02.003 |
| [2] | 陆娟, 汤国安, 张宏, 等. 犯罪热点时空分布研究方法综述[J]. 地理科学进展, 2012, 31(4): 419–425. LU Juan, TANG Guo'an, ZHANG Hong, et al. A Review of Research Methods for Spatiotemporal Distribution of the Crime Hot Spots[J]. Progress in Geography, 2012, 31(4): 419–425. DOI:10.11820/dlkxjz.2012.04.004 |
| [3] | SOLOW R M. A Contribution to the Theory of Economic Growth[J]. The Quarterly Journal of Economics, 1956, 70(1): 65–94. DOI:10.2307/1884513 |
| [4] | SWAN T W. Economic Growth and Capital Accumulation[J]. Economic Record, 1956, 32(2): 334–361. DOI:10.1111/ecor.1956.32.issue-2 |
| [5] | LE GALLO J, ERTUR C. Exploratory Spatial Data Analysis of the Distribution of Regional per Capita GDP in Europe, 1980-1995[J]. Papers in Regional Science, 2003, 82(2): 175–201. DOI:10.1007/s101100300145 |
| [6] | 裴韬, 李婷, 周成虎. 时空点过程:一种新的地学数据模型、分析方法和观察视角[J]. 地球信息科学学报, 2013, 15(6): 793–800. PEI Tao, LI Ting, ZHOU Chenghu. Spatiotemporal Point Process:A New Data Model, Analysis Methodology and Viewpoint for Geoscientific Problem[J]. Journal of Geo-Information Science, 2013, 15(6): 793–800. |
| [7] | ORD J K, GETIS A. Local Spatial Autocorrelation Statistics:Distributional Issues and an Application[J]. Geographical Analysis, 1995, 27(4): 286–306. |
| [8] | 陈军, 闫超德, 赵仁亮, 等. 基于Voronoi邻近的移动地图自适应裁剪模型[J]. 测绘学报, 2009, 38(2): 152–155. CHEN Jun, YAN Chaode, ZHAO Renliang, et al. Voronoi Neighbor-based Self-adaptive Clipping Model for Mobile Maps[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 152–155. DOI:10.3321/j.issn:1001-1595.2009.02.010 |
| [9] | 毛政元. 集聚型空间点模式结构信息提取研究[J]. 测绘学报, 2007, 36(2): 181–186. MAO Zhengyuan. The Study of Extracting Structure Information of a Clustered Spatial Point Pattern[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 181–186. DOI:10.3321/j.issn:1001-1595.2007.02.012 |
| [10] | 余莉, 甘淑, 袁希平, 等. 综合线面特征分布的点目标多尺度聚类方法[J]. 测绘学报, 2015, 44(10): 1152–1159. YU Li, GAN Shu, YUAN Xiping, et al. Multi-Scale Clustering of Points Synthetically Considering Lines and Polygons Distribution[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1152–1159. DOI:10.11947/j.AGCS.2015.20150136 |
| [11] | 唐亮, 黄培之, 谢维信. 顾及数据空间分布特性的模糊C-均值聚类算法研究[J]. 武汉大学学报(信息科学版), 2003, 28(4): 476–479. TANG Liang, HUANG Peizhi, XIE Weixin. A New Method of FCM Considering the Distribution of Spatial Data[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 476–479. |
| [12] | 郭庆胜, 郑春燕, 胡华科. 基于邻近图的点群层次聚类方法的研究[J]. 测绘学报, 2008, 37(2): 256–261. GUO Qingsheng, ZHENG Chunyan, HU Huake. Hierarchical Clustering Method of Group of Points Based on the Neighborhood Graph[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 256–261. DOI:10.3321/j.issn:1001-1595.2008.02.022 |
| [13] | 宋晓眉, 程昌秀, 周成虎, 等. 利用k阶空间邻近图的空间层次聚类方法[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1496–1499. SONG Xiaomei, CHENG Changxiu, ZHOU Chenghu, et al. Spatial Hierarchical Clustering Method Based on k-order Spatial Neighboring Map[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1496–1499. |
| [14] | 李佳田, 康顺, 罗富丽. 利用层次Voronoi图进行点群综合[J]. 测绘学报, 2014, 43(9): 1300–1306. LI Jiatian, KANG Shun, LUO Fuli. Point Group Generalization Method Based on Hierarchical Voronoi Diagram[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 1300–1306. DOI:10.13485/j.cnki.11-2089.2014.0166 |
| [15] | GOTWAY C A, YOUNG L J. Combining Incompatible Spatial Data[J]. Journal of the American Statistical Association, 2002, 97(458): 632–648. DOI:10.1198/016214502760047140 |
| [16] | MILLER H J. Tobler's First Law and Spatial Analysis[J]. Annals of the Association of American Geographers, 2004, 94(2): 284–289. DOI:10.1111/j.1467-8306.2004.09402005.x |
| [17] | 姜成晟, 王劲峰, 曹志冬. 地理空间抽样理论研究综述[J]. 地理学报, 2009, 64(3): 368–380. JIANG Chengsheng, WANG Jinfeng, CAO Zhidong. A Review of Geo-Spatial Sampling Theory[J]. Acta Geographica Sinica, 2009, 64(3): 368–380. DOI:10.11821/xb200903012 |
| [18] | 陈军. Voronoi动态空间数据模型[M]. 北京: 测绘出版社, 2002. CHEN Jun. Voronoi-based Dynamic Spatial Data Model[M]. Beijing: Publishing House of Surveying and Mapping, 2002. |
| [19] | 徐彬. 空间权重矩阵对Moran's I指数影响的模拟分析[D]. 南京: 南京师范大学, 2007. XU Bin. Simulation Analysis of the Influence of Spatial Weight Matrix on Moran's I Index[D]. Nanjing:Nanjing Normal University, 2007. |
| [20] | DIGGLE P J. Statistical Analysis of Spatial Point Patterns[M]. London: Academic Press, 1983. |
| [21] | 沈陈华. 丹阳市农村居民点空间分布尺度特征及影响因素分析[J]. 农业工程学报, 2012, 28(22): 261–268. SHEN Chenhua. Spatial Distribution Scale Characteristics of Rural Settlements and Analysis on Influencing Factors in Danyang City[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(22): 261–268. DOI:10.3969/j.issn.1002-6819.2012.22.036 |
| [22] | GATRELL A C, BAILEY T C, DIGGLE P J, et al. Spatial Point Pattern Analysis and Its Application in Geograp-hical Epidemiology[J]. Transactions of the Institute of British Geographers, 1996, 21(1): 256–274. DOI:10.2307/622936 |
| [23] | 林炳耀. 计量地理学概论[M]. 北京: 高等教育出版社, 1986. LIN Bingyao. Introduction to Quantitative Geography[M]. Beijing: Higher Education Press, 1986. |
| [24] | 郭仁忠. 空间分析[M]. 武汉: 武汉测绘科技大学出版社, 1997. GUO Renzhong. Spatial Analysis[M]. Wuhan: Wuhan Technical University of Surveying and Mapping Press, 1997. |
| [25] | 梁会民, 赵军. 基于GIS的黄土塬区居民点空间分布研究[J]. 人文地理, 2001, 16(6): 81–83. LIANG Huimin, ZHAO Jun. Study on the Spatial Distribution Characteristics of Settlement in Loess Plateau by GIS[J]. Human Geography, 2001, 16(6): 81–83. |
| [26] | JOHNSON R A, WICHERN D W. Applied Multivariate Statistical Analysis[M]. Upper Saddle River, NJ: Prentice Hall, 2002. |
| [27] | NUZZO R. Scientific Method:Statistical Errors[N]. Nature, 2014-02-12. |
| [28] | 左明星. 腾冲边陲移民聚落空间形态探析[D]. 昆明: 昆明理工大学, 2006. ZUO Mingxing. The Grope and Analysis of Migrant Settlement Spatial Form in Tengchong[D]. Kunming:Kunming University of Science and Technology, 2006. |


