2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 中国测绘科学研究院, 北京 100830
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Chinese Academy of Surveying and Mapping, Beijing 100830, China
地图综合在保证读者能清晰阅读地图图形的同时,需表达出地理要素或现象的特性和空间分布。建筑物群空间分布模式是社会政治、经济、文化与自然因素综合作用在地域上的空间反映,在邻近地理空间中建筑物群会呈现出一定的组织规律[1]。因此,建筑物群综合过程中需要对建筑物群空间分布模式进行探测。
建筑物群空间分布模式探测的研究成果比较多,文献[2]提出了一种基于邻近关系的无参数建筑物群聚类方法;文献[3]在最小生成树(minimum spanning tree, MST)基础上考虑大小、方向等空间特征能探测出用于典型化的建筑物子群;文献[4]应用城市形态学方法和格式塔原则对建筑物群进行聚类;文献[5-7]对影响聚类的建筑物空间特征指标进行了选择和改进。同时,伴随计算机技术的发展,神经网络和能量最小化等智能化方法也被用于建筑物群聚类[8-10]。在建筑物群聚类基础上,往往还需要找到子群中特殊的空间排列,文献[11]通过模板识别了简单直线排列;文献[12]则利用建筑物间空间关系和建筑物空间特征指标严格定义了H型、T型、E型、L型、Z型、阶梯型和格网型模板;文献[13]提出了用于建筑物群典型化的格网排列识别方法;文献[14]通过对MST进行修剪,实现了直线型排列和曲线型排列的识别;文献[1, 15]基于邻近图剪枝,识别了多连通直线型排列和格网型排列;文献[16]从空间推理出发,提出了识别建筑物空间排列的层次方法。另外,建筑物自身空间特征指标的研究成果主要包括:欧洲的Agent计划详细分析了建筑物图形特征的指标体系,并详细研究了其中几个主要指标[17];文献[18]研究了建筑物方位的计算方法;文献[19]研究了建筑物空间特征的主成份;文献[20]重点研究了城市建筑物群的区划。
综上所述,不论是从建筑物自身图形特征的相似性,还是从建筑物间的邻近关系,都可以从不同侧面划分建筑物子群。但是,针对建筑物群综合的需要,我们必须同时知道建筑物子群这两方面的信息,并尽可能快速找到有特殊排列方式的子群。因此,本文试图找到有代表性的用于建筑物群分类的特征指标;将建筑物群的分类和空间聚类结合起来,并用多种邻近图探测建筑物群中的特殊空间排列,而不只是用MST。
1 建筑物群分类的代表性指标地图上的建筑物图形目标往往有相应的空间特征,可以用不同指标进行描述,有时同一个空间特征可以用不同指标描述,例如,地图上一个建筑物图形目标的大小、形状和方位,其中形状可以从图形的形态特征、形状矩阵特征、力矩特征、光谱特征等方面进行指标描述[21]。分类时往往需要找到这些指标中更有代表性的指标,笔者从有关建筑物空间特征指标的文献中归纳了描述建筑物图形空间特征的指标共计24个,见表 1。
| 项目 | 特征指标 |
| 大小 | 周长(Perimeter)、面积(Area)、最小面积外接矩形面积(SArea)、凸包面积(CArea)、最长弦(LChord)平均半径(MeanR) |
| 形状 | 形状指数(ShapeIndex)、凹度(Concavity)、紧密度(IPQ指标(IPQCom)、Ritter’s measure(RCom)、Richardson’s measure(RicCom)、Gibbs’s measure(GibCom)、DCM(DCMCom)、Bottema compactness(BotCom)、Boyce-Clark index(BoyClaCom))、延展度(Elongation)、圆度(Ballard and Brown eccentricity(BBEccentricity)、Davis circularity(DCircularity))、椭圆度(Ellipticity)、复杂度(分维数(Fd)、边数(EdgeCount)) |
| 方位 | 最长边方位(MWO)、基于墙的均值方位(SWWO)、最小面积外接矩形方位(SMBRO) |
建筑物群分类常用统计学中的聚类方法,这些方法要求指标之间尽量相互独立,但是表 1所列的指标有些是相互关联的,例如:ShapeIndex与紧密度中的IPQCom指标互为倒数;延展度描述建筑物延伸程度,椭圆度描述建筑物扁度,扁的建筑物延伸程度大,且两者数学原理相似;一个建筑物椭圆度越大,它往往越圆,圆是椭圆的一个特例。因此,利用主成份分析方法对这些指标进行分析。主成份分析通过正交变换将一组可能存在相关性的变量转换为一组新的线性不相关变量,能有效对建筑物空间特征指标进行降维,并分析其中指标的代表性。为防止小样本造成偶然性,随机选择OSM地图上北京市海淀区某区域1390个建筑物进行了指标计算,并对计算得到的24个参数进行了主成份分析。主成分分析前,由于各指标量纲不一样,需进行标准化处理,标准化方法见参考文献[19],主成分贡献率与主成分系数矩阵分别见表 2和表 3。
| 成分 | 特征值 | 百分数/(%) | 累积贡献率/(%) |
| 1 | 11.871 | 49.464 | 49.464 |
| 2 | 5.204 | 21.682 | 71.146 |
| 3 | 2.592 | 10.800 | 81.946 |
| 4 | 1.643 | 6.845 | 88.791 |
| 5 | 0.928 | 3.865 | 92.656 |
| | | | |
| 指标 | 主成分 | |||
| 1 | 2 | 3 | 4 | |
| Perimeter | -0.185 | 0.326 | -0.008 | 0.018 |
| Area | -0.055 | 0.390 | -0.053 | 0.201 |
| SArea | -0.079 | 0.395 | -0.033 | 0.076 |
| CArea | -0.075 | 0.397 | -0.039 | 0.114 |
| LChord | -0.208 | 0.264 | -0.022 | 0.151 |
| MeanR | -0.205 | 0.259 | -0.025 | 0.168 |
| ShapeIndex | 0.263 | 0.012 | 0.057 | -0.194 |
| Concavity | 0.145 | -0.087 | -0.108 | 0.580 |
| IPQCom | 0.279 | 0.090 | -0.040 | 0.044 |
| RCom | -0.055 | -0.290 | 0.035 | -0.090 |
| RicCom | 0.281 | 0.075 | -0.044 | 0.078 |
| GibCom | 0.264 | 0.148 | -0.014 | -0.153 |
| DCMCom | 0.265 | 0.145 | -0.017 | -0.142 |
| BotCom | -0.271 | -0.128 | 0.023 | 0.110 |
| BoyClaCom | 0.232 | 0.046 | -0.057 | 0.183 |
| Elongation | 0.206 | 0.179 | 0.030 | -0.392 |
| Ellipticity | 0.253 | 0.134 | -0.014 | -0.171 |
| BBEccentricity | 0.275 | 0.122 | -0.026 | -0.064 |
| DCircularity | -0.263 | -0.012 | 0.057 | -0.193 |
| Fd | 0.280 | -0.064 | -0.036 | 0.081 |
| EdgeCount | -0.099 | 0.225 | 0.055 | -0.394 |
| MWO | 0.055 | 0.030 | 0.572 | 0.010 |
| SWWO | 0.062 | 0.050 | 0.580 | 0.087 |
| SMBRO | 0.059 | 0.041 | 0.545 | 0.083 |
从表 2的主成分贡献率来看,前4个特征值大于1的主成分已占所有指标信息量的88%以上,能有效描述建筑物的图形特征。表 3是主成分系数矩阵,反映了主成分与指标间的相关程度,这些相关程度的值可以为选择代表性指标提供依据。从表 3看出,主成分1主要由ShapeIndex、IPQCom、RicCom、GibCom、DCMCom、BotCom、Ellipticity、BBEccentricity、DCircularity和Fd等指标决定(见表 3下划线部分,下文相同),是反映形状的主成分。主成分2主要由Area、SArea、CArea等指标决定,是反映大小的主成分。主成分3主要由MWO、SWWO、SMBRO等指标决定,是反映方位的主成分。主成分4主要由EdgeCount和Concavity指标决定,也是反映形状的主成分。因此,建筑物图形空间特征只需从大小、形状和方位3个方面描述。建筑物大小通常用面积进行描述,但是主成分分析发现,指标SArea和指标CArea对于大小描述更有代表性,因而这里选择CArea作为代表性指标。在形状特征描述中,代表性的指标有很多,在关联度最大的3个指标中,考虑到IPQCom指标计算相对简单,且较为常用,因而选择IPQCom描述建筑物形状的紧密度,当然,也可以直接选择RicCom或Fd;另外,虽然在统计规律上凹度(Concavity)和边数(EdgeCount)在主成份4中都比较重要,但是,建筑物是人工物体,通常形状趋于方正,边数越多就说明越复杂,因此这里选择边数(EdgeCount)作为描述建筑物图形复杂度的一个代表性指标,当然,也可以直接选择凹度(Concavity)。在方位描述方面,可以直接选择基于墙的均值方位(SWWO)这个指标,但是,从视觉认知角度考虑,这里选择了最小面积外接矩形方位作为直观体现一个建筑物整体方位的指标。因此,从统计规律和认知规律来看,可以把凸包面积(CArea)、IPQ指标(IPQCom)、边数(EdgeCount)和最小面积外接矩形方位(SMBRO)4个指标作为建筑物图形特征的代表性指标,见表 4。
| 建筑物空间特征 | 指标 | 公式或说明 |
| 大小 | 凸包面积(CArea) | 图形凸包面积 |
| 形状 | IPQ指标(IPQCom) | IPQCom=4πA/P2 |
| 边数(EdgeCount) | 图形的边数或节点个数 | |
| 方位 | 最小面积外接矩形方位(SMBRO) | 图形最小面积外接矩形的长轴方位 |
2 基于邻近关系的特定建筑物子群提取
通常利用MST表达建筑物间的空间邻近关系,但是MST对建筑物间的空间邻近关系描述只限制在最邻近的连通图关系上,而描述空间邻近关系的图还有最邻近图(nearest neghborhood graph, NNG)、相对邻近图(relative neighborhood graph, RNG)和Gabriel图(Gabriel graph, GG)等[26],本文试图同时利用NNG、MST、RNG和GG 4种邻近图探测特定空间排列的建筑物子群,并进行比较分析。
建筑物成群与其所处地理环境有关,道路往往对建筑物群形成天然分区,因而对建筑物群进行空间聚类时需优先考虑道路对建筑物群的划分。当利用建筑物重心建立三角网描述建筑物间邻近关系时,由于道路和建筑物的阻隔,很多三角网边连接的建筑物实际上并不相邻,因而需要删除穿过道路或建筑物的三角网边,在得到的新三角网中,利用建筑物间最短距离建立MST,通过判断MST中边属性的连续性,实现对建筑物群的空间聚类[14]。建筑物群空间聚类结果如图 1所示,图 1(a)中粗线表示应删除的边,图 1(b)是删除后形成的空间聚类结果。
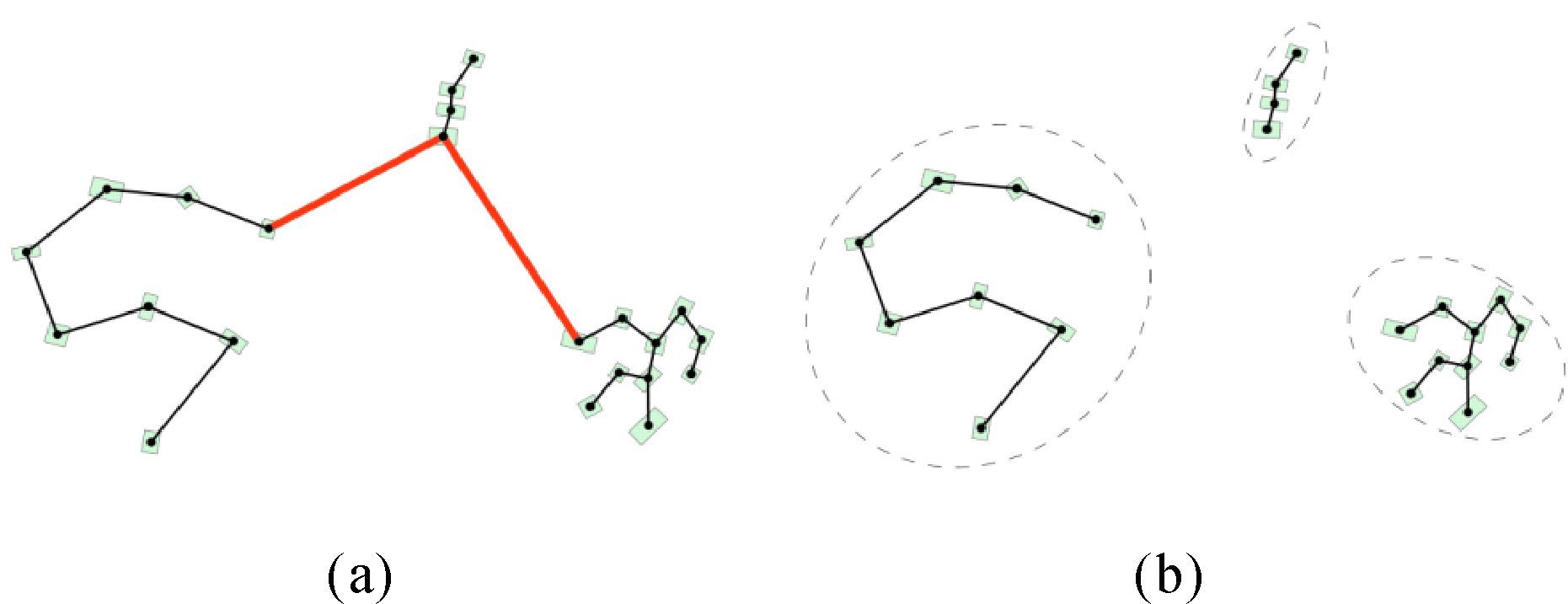
|
| 图 1 基于MST的空间聚类 Fig. 1 Spatial clustering of buildings based on MST |
基于邻近图也可以识别出特定排列方式的建筑物子群,例如直线型空间排列。若只考虑建筑物间的邻近关系,可以直接利用邻近图中邻近边的方向差异和长度差异来提取直线型空间排列。方向差异(DO)用邻近图中邻近边的夹角表示;长度差异(DL)用邻近图中邻近边长度的倍数表示。设它们的阈值分别为δO和δL,若DO≥δO,同时DL≤δL,则认为这两条邻近边所关联的建筑物形成了直线排列。设置δO=165°,δL=3,图 2(a)至图 2(d)分别为利用NNG、MST、RNG和GG提取的直线型空间排列结果,提取结果用粗线标出。可以看出,从图 2(c)和图 2(d)中发现的排列更有利于作为一个完整的地图综合对象,这说明用多个邻近图进行建筑物子群排列特征挖掘是必要的。
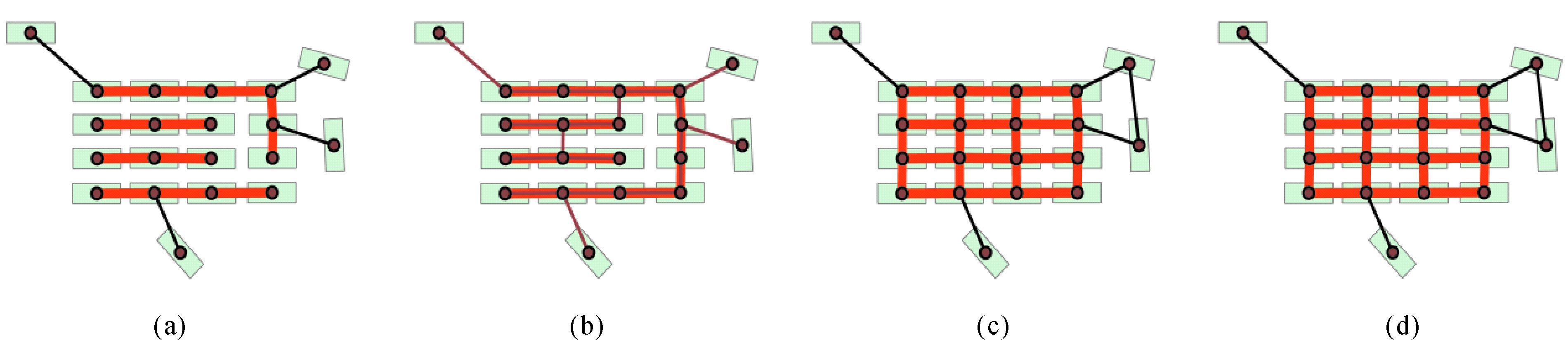
|
| 图 2 基于4种邻近图的直线型空间排列 Fig. 2 Linear patterns recognition based on four kinds of proximity graphs |
3 试验与分析 3.1 建筑物群分类与空间聚类
采用OSM地图上北京海淀区局部1:8000居民地作为试验数据,对建筑物群进行系统聚类,聚类终止条件为当类间距离大于2时,聚类终止。直接使用凸包面积(CArea)、IPQ指标(IPQCom)、边数(EdgeCount)和最小面积外接矩形方位(SMBRO)4个指标的分类结果见图 3,将原始192个建筑物分成了16类。这里需要说明的是:建筑物方位采用建筑物最小面积外接矩形方位指标进行计算,系统聚类时方位差异为两建筑物方位的数值差异,但是实际上当建筑物方位差异大于90°时,其差异应该为该差异角度的补角,所以导致当两个建筑物方位指标差异过大时,往往会被分为两类,如类2和类3,尽管两类形状和大小相近,但是方位指标数值差异过大,因而被分成两类。利用参考文献[14]所描述的方法所得空间聚类结果见图 3。
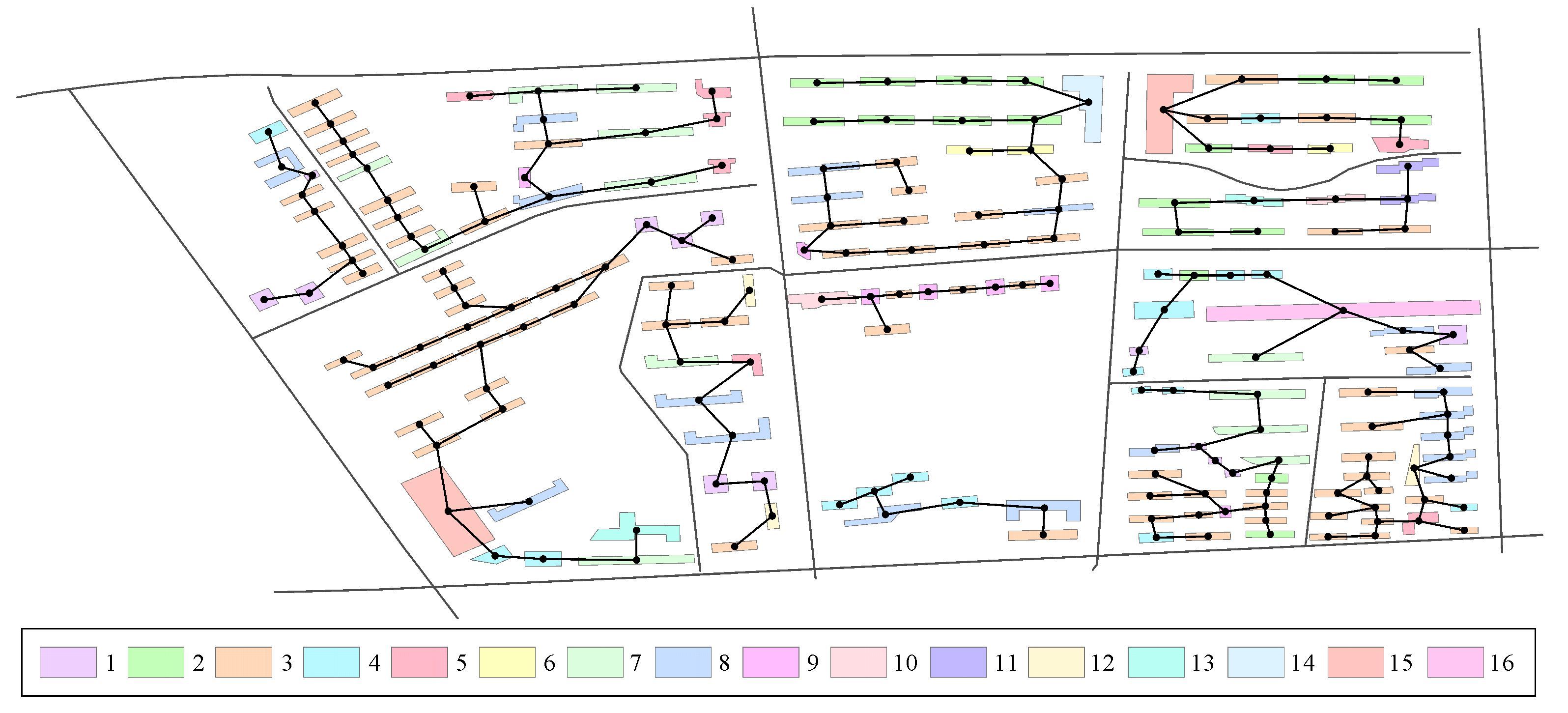
|
| 图 3 建筑物群分类与空间聚类 Fig. 3 Classification and spatial clustering of buildings |
3.2 直线型空间排列提取
在建筑物群空间聚类基础上可以进一步提取特定的空间排列,先对聚类形成的子群分别建立4种邻近图,然后,利用与前文相同的约束条件,提取子群中的直线型空间排列,结果见图 4。图 4(a)为NNG上提取的结果,图 4(b)为MST上提取的结果,图 4(c)为RNG上提取的结果,图 4(d)为GG上提取的结果。从图 4可以看出,RNG较MST更有利于提取直线型空间排列。另外,GG虽然能识别更多隐藏的直线型空间排列,但是这些隐藏的直线型空间排列在视觉上并不明显,且会造成提取的排列之间相互交叉,易产生误导。图 4(c)的部分排列中建筑物为同类建筑物,另外,还有些排列中存在两类建筑物,甚至个别排列中存在多类建筑物,这些分布特征在建筑物群综合过程中通常需要考虑。
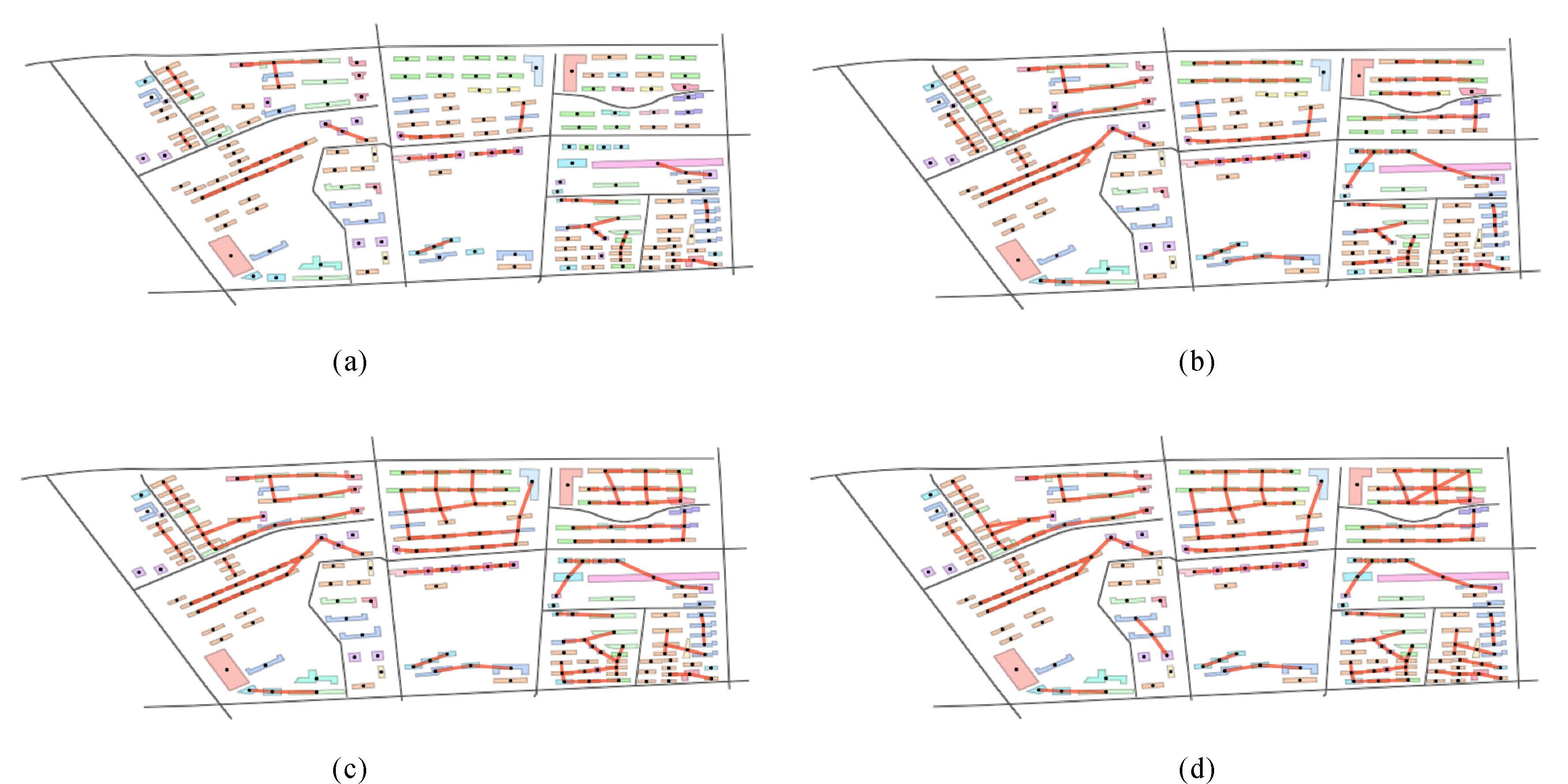
|
| 图 4 空间聚类基础上基于4种邻近图的直线型空间排列 Fig. 4 Linear patterns recognition based on four kinds of proximity graphs and spatial clustering |
另外,在建筑物群分类基础上也需要提取类似的空间排列,笔者针对某一个类别的建筑物子群建立RNG,并利用RNG提取直线型空间排列,结果见图 5。对比图 5和图 4(c)可以看出,在空间特征相似的建筑物子群中能发现新的直线型空间排列,如图 5中椭圆圈出的标号分别为1、2、3、4、5的子群,其中4号子群是不相邻的离散直线型空间排列。
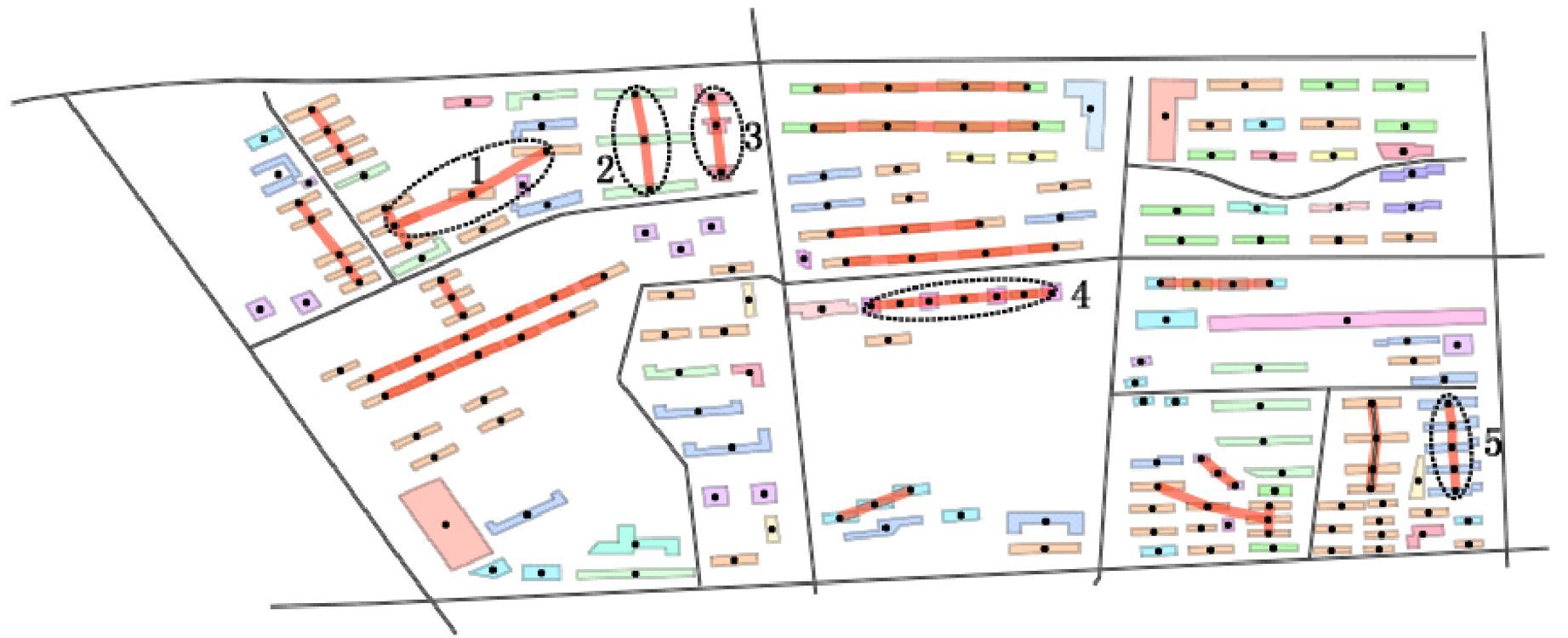
|
| 图 5 在分类基础上基于RNG图的直线型空间排列 Fig. 5 Linear patterns recognition based on RNG and building classification |
3.3 影响因素分析
在邻近图中,建筑物之间的邻近距离可以用建筑物间的重心距离表示,也可以用建筑物间的最短距离表示。用不同的邻近距离计算方法,提取的直线型空间排列会不一致。图 6(a)为在重心距离生成的RNG中提取的直线型空间排列,对比图 4(c)可以看出结果不一致,如图 6(a)中椭圆圈出部分,这能作为最终直线型空间排列提取结果的一个有效补充。
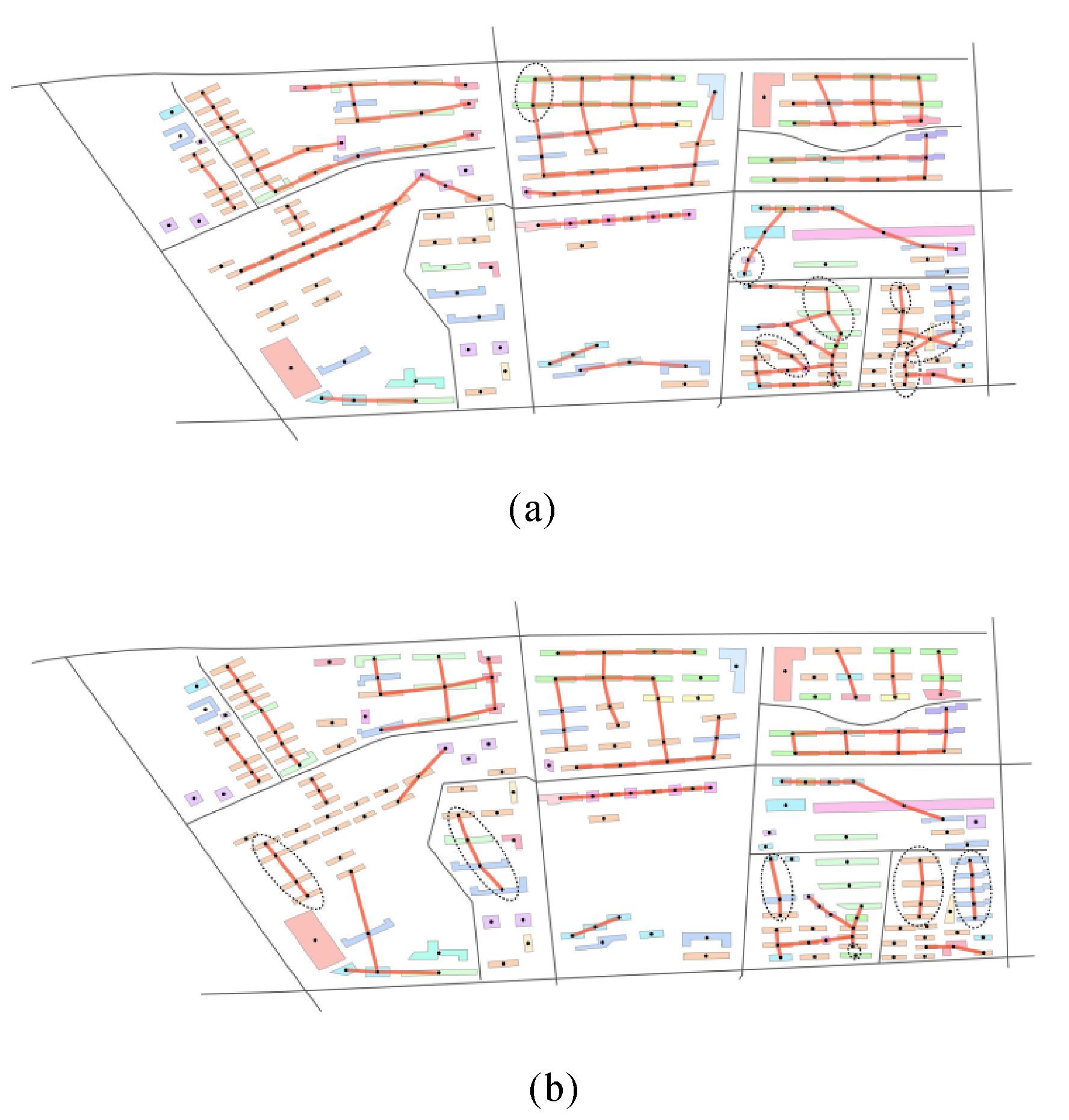
|
| 图 6 基于RNG图的直线型空间排列 Fig. 6 Linear patterns recognition based on RNG |
建筑物群分类采用的聚类终止条件取决于对建筑物相似程度的定义。若需要对建筑物群进行精细分类,可以设置相对苛刻的聚类终止条件。另外,提取建筑物群中直线型空间排列时,可以调整相关参数,但是必须符合视觉特征约束。如图 6(b)为在RNG上提取的直线型空间排列,其中,调整δO=155°,对比图 4(c)可以看出,由于适当放宽了方向阈值约束,图 6(b)中椭圆圈出部分也被认为属于直线排列。
除了距离计算方法和排列约束条件外,4种邻近图(NNG、MST、RNG、GG)对直线型空间排列的提取也有非常大的影响,这可以依据图 4中的提取结果进行客观评价,目前尚无定量的方法来评价基于视觉认知的直线型空间排列提取结果[1]。图 4(a)是从NNG上提取的结果,可以看出有明显的直线型空间排列没有识别出;图 4(b)是从MST上提取的结果,这也是目前常用的方法,但是与图 4(c)中从RNG上提取的结果相比较,明显有多条直线型空间排列没有识别;图 4(d)是从GG上提取的结果,有多处直线型空间排列是建筑物群综合过程中不需要考虑的空间分布特征。
从整个试验结果来看,在基于4种邻近图提取的直线型空间排列中,基于RNG提取的直线型空间排列结果最为理想,如图 4所示,符合地图综合中建筑物群结构维护的需要,也为提取建筑物群“矩阵式排列”提供了基础;基于建筑物属性分类结果,从RNG上提取的直线型排列结果(图 5)能在空间特征相似的子群中寻找到新的直线排列;分别在分类和空间聚类基础上提取的直线型空间排列结果可以互相补充,它们的并集能更完备地表达区域内建筑物群空间分布特征。
4 结论为了有效解决特定建筑物子群的提取问题,本文既考虑了建筑物自身的空间特征,也将建筑物所处的空间环境纳入到了建筑物子群的划分中,更全面地研究了不同邻近图在发现空间排列中的作用。试验证明了RNG图更有利于建筑物群空间排列的提取,利用本文所提出的方法能更有效地找到建筑物群综合中较单纯的综合对象,有助于建筑物群自动综合中地理特征的保持和表达。此外,该方法也可用于建筑物其他类型的空间排列特征识别,并以此为基础实施建筑物群的综合。当然,该方法同样可用于任意点群的空间排列方式识别。但是该方法所考虑的建筑物是2维的,用建筑物中心点代表了建筑物,因此算法上有一定的局限性。需要进一步研究的内容主要是:随着建筑物地理信息内容的逐渐丰富,例如建筑物的高度、用途等,建筑物群分类和空间聚类所考虑的因素应该更多;在直线型空间排列的提取过程中,约束条件中的阈值应该依据地理区域的不同而有所变化,不同的直线型空间排列也应该有不同的重要程度;建筑物群的邻近图也不只这4种,利用多种邻近图识别更多更复杂的空间排列也是后续研究的重点。
| [1] | 巩现勇, 武芳. 城市建筑群网格模式的图论识别方法[J]. 测绘学报, 2014, 43(9): 960–968. GONG Xianyong, WU Fang. The Graph Theory Approach to Grid Pattern Recognition in Urban Building Groups[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 960–968. DOI:10.13485/j.cnki.11-2089.2014.0125 |
| [2] | ANDERS K H. A Hierarchical Graph-clustering Approach to Find Groups of Objects[C]//The 5th Workshop on Progress in Automated Map Generalization. Paris:[s.n.], 2003. |
| [3] | REGNAULD N. Contextual Building Typification in Automated Map Generalization[J]. Algorithmica, 2001, 30(2): 312–333. DOI:10.1007/s00453-001-0008-8 |
| [4] | LI Z, YAN H, AI T, et al. Automated Building Generalization Based on Urban Morphology and Gestalt Theory[J]. International Journal of Geographical Information Science, 2004, 18(5): 513–534. DOI:10.1080/13658810410001702021 |
| [5] | 艾廷华, 郭仁忠. 基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报, 2007, 36(3): 302–308. AI Tinghua, GUO Renzhong. Polygon Cluster Pattern Mining Based on Gestalt Principles[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 302–308. DOI:10.3321/j.issn:1001-1595.2007.03.011 |
| [6] | YAN Haowen, WEIBEL R, YANG Bisheng. A Multi-parameter Approach to Automated Building Grouping and Generalization[J]. Geoinformatica, 2008, 12(1): 73–89. DOI:10.1007/s10707-007-0020-5 |
| [7] | ZHANG Liqiang, DENG Hao, CHEN Dong, et al. A Spatial Cognition-based Urban Building Clustering Approach and Its Applications[J]. International Journal of Geographical Information Science, 2013, 27(4): 721–740. DOI:10.1080/13658816.2012.700518 |
| [8] | ALLOUCHE M K, MOULIN B. Amalgamation in Cartographic Generalization Using Kohonen's Feature Nets[J]. International Journal of Geographical Information Science, 2005, 19(8-9): 899–914. DOI:10.1080/13658810500161211 |
| [9] | WANG Yuebin, ZHANG Liqiang, MATHIOPOULOS P T, et al. A Gestalt Rules and Graph-cut-based Simplification Framework for Urban Building Models[J]. International Journal of Applied Earth Observation and Geoinformation, 2015, 35: 247–258. DOI:10.1016/j.jag.2014.09.012 |
| [10] | 程博艳, 刘强, 李小文. 一种建筑物群智能聚类法[J]. 测绘学报, 2013, 42(2): 290–294. CHENG Boyan, LIU Qiang, LI Xiaowen. Intelligent Building Grouping Using a Self-organizing Map[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 290–294. |
| [11] | RAINSFORD D, MACKNESS W. Template Matching in Support of Generalisation of Rural Buildings[C]//The 10th International Symposium on Spatial Data Handling. Berlin Heidelberg:Springer, 2002:137-151. |
| [12] | YANG Weiping. Identify Building Patterns[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing:ISPRS, 2008:391-398. |
| [13] | ANDERS K H. Grid Typification[C]//Proceedings of the 12th International Symposium on Spatial Data Handling. Berlin Heidelberg:Springer, 2006:633-642. |
| [14] | ZHANG Xiang, AI Tinghua, STOTER J, et al. Building Pattern Recognition in Topographic Data:Examples on Collinear and Curvilinear Alignments[J]. Geoinformatica, 2013, 17(1): 1–33. DOI:10.1007/s10707-011-0146-3 |
| [15] | 巩现勇, 武芳, 钱海忠, 等. 建筑群多连通直线模式的参数识别方法[J]. 武汉大学学报(信息科学版), 2014, 39(3): 335–339. GONG Xianyong, WU Fang, QIAN Haizhong, et al. The Parameter Discrimination Approach to Multi-connected Linear Pattern Recognition in Building Groups[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3): 335–339. |
| [16] | DU Shihong, SHU Mi, FENG C C. Representation and Discovery of Building Patterns:A Three-level Relational Approach[J]. International Journal of Geographical Information Science, 2016, 30(6): 1161–1186. DOI:10.1080/13658816.2015.1108421 |
| [17] | Department of Geography, University of Zurich. Selection of Basic Measures[EB/OL]. http://agent.ign.fr/deliverable/DC1.html, 1999. |
| [18] | DUCHÊNE C, BARD S, BARILLOT X, et al. Quantitative and Qualitative Description of Building Orientation[C]//5th Workshop on Progress in Automated Map Generalization. Paris:[s.n.], 2003. |
| [19] | BURGHARDT D, STEINIGER S. Usage of Principal Component Analysis in the Process of Automated Generalisation[C]//Proceedings of the 22nd International Cartographic Conference. A Coruna, Spain, 2005. |
| [20] | STEINIGER S, LANGE T, BURGHARDT D, et al. An Approach for the Classification of Urban Building Structures Based on Discriminant Analysis Techniques[J]. Transactions in GIS, 2008, 12(1): 31–59. DOI:10.1111/tgis.2008.12.issue-1 |
| [21] | PEURA M, ⅡVARINEN J. Efficiency of Simple Shape Descriptors[M]//ARCELLI C, CORDELLA L P, SANNITI DI BAJA G. Aspects of Visual form Processing. Singapore:World Scientific, 1997:443-451. |
| [22] | LI Wenwen, GOODCHILD M F, CHURCH R. An Efficient Measure of Compactness for Two-dimensional Shapes and Its Application in Regionalization Problems[J]. International Journal of Geographical Information Science, 2013, 27(6): 1227–1250. DOI:10.1080/13658816.2012.752093 |
| [23] | MACEACHREN A M. Compactness of Geographic Shape:Comparison and Evaluation of Measures[J]. Geografiska Annaler, 1985, 67(1): 53–67. DOI:10.2307/490799 |
| [24] | ZHANG Dengsheng, LU Guojun. Review of Shape Representation and Description Techniques[J]. Pattern Recognition, 2004, 37(1): 1–19. DOI:10.1016/j.patcog.2003.07.008 |
| [25] | ŽUNIC' J, HIROTA K, ROSIN P L. A Hu Moment Invariant as a Shape Circularity Measure[J]. Pattern Recognition, 2010, 43(1): 47–57. DOI:10.1016/j.patcog.2009.06.017 |
| [26] | 郭庆胜, 郑春燕, 胡华科. 基于邻近图的点群层次聚类方法的研究[J]. 测绘学报, 2008, 37(2): 256–261. GUO Qingsheng, ZHENG Chunyan, HU Huake. Hierarchical Clustering Method of Group of Points Based on the Neighborhood Graph[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 256–261. DOI:10.3321/j.issn:1001-1595.2008.02.022 |


