2. 中国测绘科学研究院, 北京 100830;
3. 国家测绘工程技术研究中心, 北京 100039
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. National Engineering Research Center of Surveying and Mapping, Beijing 100039, China
2012年1月9日,我国成功发射第一颗自主的民用高分辨率光学传输型立体测绘卫星—资源三号(ZY-3) 卫星。2016年5月30日11时17分,我国成功发射资源三号02星,它是资源三号系列卫星的第2颗,实现两颗资源三号测绘卫星组网运行。资源三号系列卫星影像在空间分辨率、定位精度与时效性等方面代表了我国自主民用遥感卫星的领先水平,可以服务于基础测绘、国土、农业、环境、减灾、规划等各行业影像数据需求,具有广阔的应用前景。
然而对于绝大多数基于光学传感器的遥感影像来说,最大的问题是易受恶劣天气的影响,当云、雾或者水汽等在信号传播路线上形成一定规模,会导致图像的不准确甚至被遮盖,导致地物信息缺失,阻碍遥感影像发挥应有的作用价值,造成巨大的经济损失。例如2006、2007年北京全城有云覆盖的天气约占总量的46%,我国地处亚热带的南方地区云覆盖频率更高。通常,云雾覆盖率超过10~15%的影像不能应用于测绘研究中,然而根据1991年至1998年的卫星资料显示,由于云雾天气的影响,我国南方地区获取的NOAA/AVHRR气象卫星数据的平均有效利用率不足7%[1]。由此可见,去云不仅是遥感影像进行准确解译的基础,也是增强遥感数据有效性的重要途径,故遥感影像去云具有十分重要的实际意义。
目前,遥感影像去云主要分为薄云去除和厚云去除,薄云去除的方法主要有基于直方图匹配去云法[2-3]、基于多光谱图像去云法[4-5]和基于单幅图像去云法等,厚云去除的方法主要有基于支持向量机法[6-7]、基于光谱及几何法[8]、基于数据融合去云法[9-10]等。在遥感影像去云方法中,去除厚云的处理较去除薄云的方法更为棘手,引起了不少学者的关注。近几年,在压缩感知理论发展的基础上,利用过完备字典进行稀疏表示的方法在图像处理邻域得到了广泛的应用,也为遥感影像云去除处理提供了新思路。文献[11]提出的K-SVD字典训练算法,依据误差最小原则,对误差项进行SVD分解,选择使误差最小的分解项作为更新的字典原子和对应的原子系数,经过不断的迭代从而得到优化的解,实现输入信号字典自适应的稀疏表示。
本文应用多时域资源三号遥感影像,以K-SVD字典学习算法为基础,为其字典训练过程添加排序准则,使得不同图像的字典原子排列顺序尽可能相似,减少同区不同时的遥感影像间的差异,达到较好的去除云与阴影的效果。此方法对于薄云、厚云均适用,但针对厚云效果较为明显,故以下将以厚云情况为例。
1 K-SVD理论基础 1.1 压缩感知压缩感知(compressed sensing, CS)也称为稀疏采样,是一个全新的采样理论,它通过开发信号的稀疏特性,在远小于Nyquist采样率的条件下,用随机采样获取信号的离散样本,然后通过非线性重建算法完美地重建信号[12]。压缩感知理论已在信息论、图像处理、地球科学、光学、微波成像、模式识别、地质等领域得到广泛应用。
压缩感知理论的实质是利用多个观测值无失真地恢复出长度为M的原始信号,主要内容涉及信号的稀疏表示、测量矩阵的设计和信号恢复算法,其数学表达为:在已知长度M的一维测量值y和测量矩阵H(M×N)的基础上,求解欠定方程组y=Hx,得到长度N、稀疏度K(即含有K个非零值)的一维原信号x。但是一般的自然信号x本身并不稀疏,需要某种转换进行稀疏表示,故令x=Sα,S(N×L,L≫N)为稀疏基矩阵,α为稀疏系数(α只有K个是非零值(K≪N)),原理表示如图 1所示。
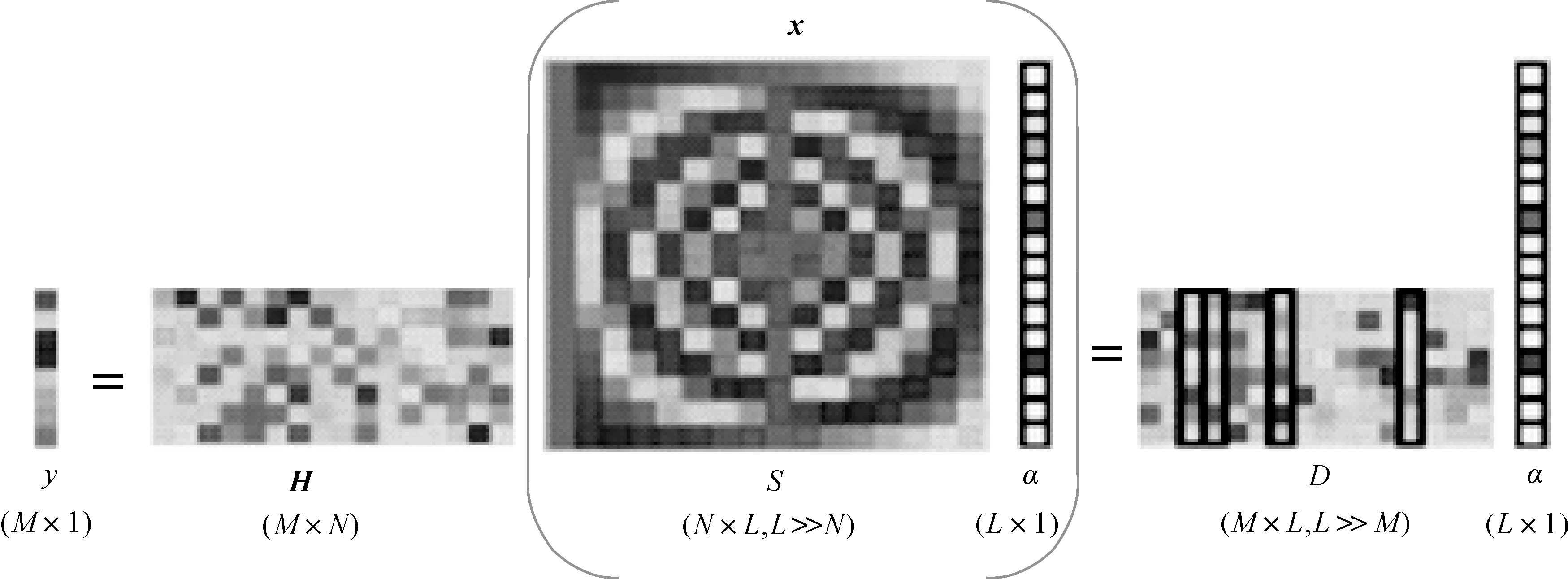
|
| 图 1 压缩感知原理 Fig. 1 Compressive sensing schematic |
1.2 K-SVD字典训练
字典训练以压缩感知理论为基础,是数据稀疏表示的最优表示,能够训练出性能优良、规模更加紧凑的新字典,使字典的原子特性更加符合需要表示的图像信号。原来的关注点一直聚集在给定一个字典条件下分解信号的追踪算法,这个字典要根据一个适应一系列训练信号的特定的线性变换得来。而文献[11]证明了用于稀疏表示的过完备字典不仅可以根据给定的函数集选择得到,还可以依据输入的信号自适应的表示,此外,K-SVD具有很强的适应性,可以与任意一种常见的稀疏编码追踪算法结合,例如,基追踪(basic pursuit,BP)算法[13]、匹配追踪(matching pursuit,MP)算法[14]、正交匹配追踪(orthogonal matching pursuit,OMP)算法[15-16]和焦点欠定系统求解[17-18](the focal underdetermined system solver,FOCUSS)等。K-SVD的本质是使用包含原信号原子的超完备字典,由原子的稀疏线性组合恢复信号。它是由K-means聚类过程产生,可以基于现有字典进行稀疏编码,然后通过循环迭代逐个更新字典的原子和稀疏系数,字典列的更新与稀疏表示的更新能使最终输出的字典更好地适应数据,并且聚合更快。由此可见,K-SVD算法的目的是寻找最佳过完备字典表示W个样本信号{yi}i=1W,它是稀疏表示的重要成分,求解满足式
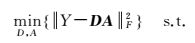
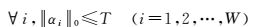 (1)
(1)
式中,D=[d1,d2,…,dL]∈RM×L、A=[α1,α2,…,αW]∈RL×W分别代表所求的过完备字典和信号的稀疏矩阵;Y=[y1,y2,y3,…,yW]∈RM×W为已知的数据集;T为给定的稀疏系数中非零元素个数的上限值。
对于尺寸为V×V的图像,可以被滑动重叠的分为若干尺寸为b2,b≪V的小块。每一个小块都可以表示为b2维向量y∈RM×1,该向量就是原始图像的一个块向量。字典D是一个M×L的矩阵,D∈RM×L,由L个原子组成,每个原子同样也为M维向量di∈RM×1,由于字典D是过完备的基的集合,所以M≪L。字典学习和稀疏表示都是对于这些小块进行的,决定了字典的尺寸,使得字典的行数为M=b2,以及字典的列数(训练的原子个数)由冗余因子r和b共同决定为L=rb2。按照K-SVD通常设定,本文试验参数取r=4,b=8,得到块大小b2=64,字典行数M=64,原子个数L=256,K-SVD迭代次数取10,最大训练块的个数设置大于(V-b+1)2,并且根据测试取稀疏表示全局误差参数为25×1.15,基于块恢复的流程图如图 2所示。
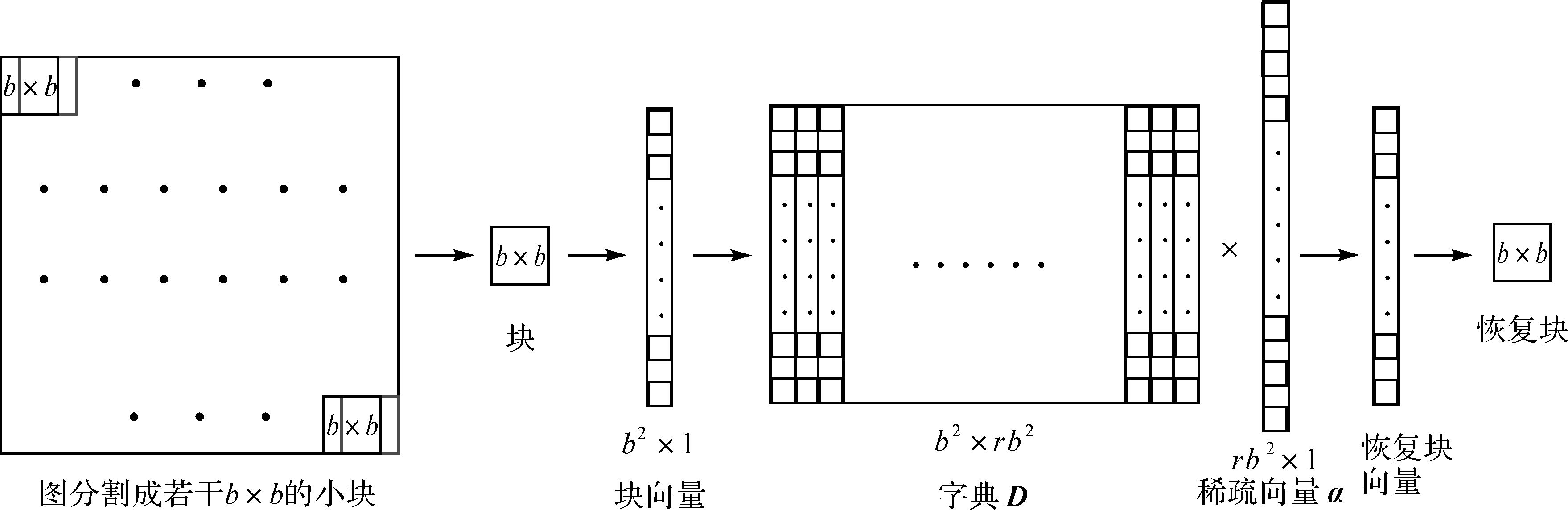
|
| 图 2 基于块恢复的流程 Fig. 2 Flowchart of block-based reconstruction |
该算法运行的主要步骤是:① 初始字典:设置以标准正交基为列的初始字典D0(多为DCT矩阵);② 稀疏编码:选用任意一个追踪算法计算每一个样本信号yi对应的稀疏向量αi,其求解满足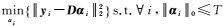
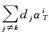
近年来,K-SVD算法已在图像的压缩、识别、修饰、去噪和重建等领域取得了突出效果,并被不断优化改进,但在遥感影像去云方面刚开始起步,为遥感影像去云提供了新的思路。文献[19]应用压缩感知理论重建云区域,分别试验比较了不同尺寸的云覆盖和不同类型地区的云区域恢复效果;文献[20]首次提出将定量遥感影像与字典学习结合;文献[21]将多光谱遥感影像结合多时域字典学习重建云污染区域。本文在改进K-SVD字典学习的原子训练过程的基础上结合正交匹配追踪算法,重建遥感影像云区域,丰富地物信息。
2 本文算法 2.1 AO-DL算法将字典学习算法应用于遥感影像云去除,用字典稀疏表示同区不同时的遥感影像时,由于不同的拍摄条件和部分不同的图像内容(地物的变化、云的遮盖),得到的字典原子的排序绝对不同,因此用有云影像的字典和无云影像的稀疏系数矩阵直接恢复有云图像难以实现。但是若对两个字典的原子按照特定的规则重新排序,使其顺序尽可能相同时,则可以减少影像间的差异,能很大程度地改善影像去云的效果。
本文改进了字典学习算法,在基于以上块训练所得字典的基础上,再将字典原子按照某种特定的准则进行重排序,得到基于块的字典训练原子重排序,称为变序字典学习(atoms-reordered dictionary learning,AO-DL)。目前,字典学习算法有Sparsenet字典学习算法[22]、MOD(method of optimal directions)字典学习算法[23]、K-SVD字典学习算法、在线字典学习(online dictionary learning,ODL)算法[24]和结构字典学习算法[25]等。本文选用K-SVD算法和以最大相关系数为重排序准则实现AO-DL,其中K-SVD算法已在1.2节中简单介绍,以下将重点说明字典原子重排序的方法。
应用最大相关系数进行字典原子重排序:
(1) 数据准备。寻找一张灰度均匀的图像作为标准图,记为image0;输入图,记为image(i)。
(2) K-SVD计算,得到图像对应的字典。image0对应的K-SVD图像字典记为D0M×L,image(i)对应的K-SVD图像字典记为D(i)M×L。
(3) 关联矩阵计算。依次计算字典D0的L个原子对应字典D(i)的每个原子的相关系数(correlation coefficient),形成系数矩阵,记为CML×L。即字典D0的第n列原子与字典D(i)的所有原子的L个相关系数对应为CM第n列的L个元素。
(4) 计算排列顺序,记为order。根据CM每列中最大相关系数所在的位置,形成一个排列顺序。也就是说,order是一个1×L的数组,它的第n个元素即为CM第n列的最大相关系数所在的那个行数f,即order[n]=f。这就意味着字典D(i)的第f列原子与D0的第n列原子是最相关的。
(5) 得到原子重新排序后的字典D(i)M×L*。按照order元素顺序对字典D(i)的原子进行重新排序,得到新字典D(i)M×L*。
由此,输入图像的字典基于标准图像的字典按照一种的有规则的排列顺序(本文所指的规则就是最大相关法)生成了新字典,具体AO-DL算法实现流程图如图 3所示。

|
| 图 3 AO-DL算法流程 Fig. 3 Flowchart of AO-DL algorithm |
2.2 AO-DL云去除
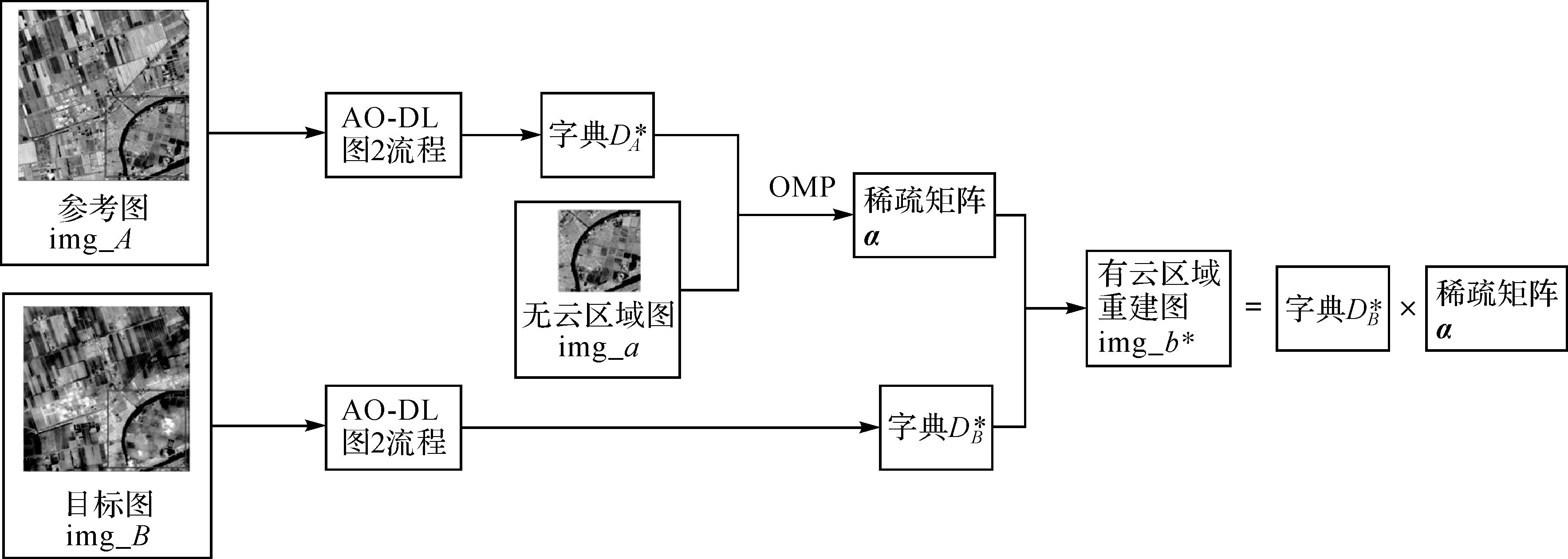
AO-DL算法完成后,可以令输出的字典按照一定的规则进行原子重排序。将此算法应用于遥感影像云去除中,输入一张无云影像作为参考图像img_A和一张有云影像作为目标图像img_B,两张图像经过AO-DL算法后对应产生两个带有各自影像属性以及相同的原子排序规则的字典,分别为字典DA*和字典DB*。然后,运用正交匹配追踪(OMP)算法令img_A中的部分无云区域图用字典DA*原子的线性组合稀疏表示出来,得到稀疏矩阵α。最后,将带有目标图像属性的字典DB*与稀疏矩阵α相乘,得到目标图img_B中对应有云区域的去云重建图img_b*,算法流程如图 4所示。应用该方法得到的去云图可以在拥有原影像属性的同时有效地去除云和阴影的遮盖。
|
| 图 4 AO-DL云去除流程 Fig. 4 Cloud removal flowchart of AO-DL |
3 试验与结果 3.1 数据准备
论文试验数据列举两组资源三号(ZY-3) 卫星影像,第1组为分别于2015年2月9日与2015年8月15日拍摄的天津市宁河区以农田区域为主的影像,取4763×3576像素,1个像素长2.1 m;第2组为分别于2015年8月15日与2016年2月8日拍摄的天津市滨海新区影像,取3046×2500像素,1个像素长2.1 m。试验数据集如图 5所示,详细信息见表 1。

|
| 图 5 试验数据集 Fig. 5 Test data set |
| 影像类型 | 组数 | 标记 | 尺寸 | 云量 | 日期 | 地点 | 区域类型 |
| ZY-3 | V | img_A | 4763×3576 | 无云 | 2015-02-09 | 天津市 宁河区 |
农田 |
| img_B | 4763×3576 | 有云 | 2015-08-15 | ||||
| W | lmg_A | 3046×2500 | 无云 | 2016-02-08 | 天津市 滨海新区 |
城市 | |
| lmg_B | 3046×2500 | 有云 | 2015-08-15 |
3.2 试验
论文主要讨论遥感影像云去除处理,对于云区域的选取采用手工框选实现的,因此本文不涉及云覆盖区域的自动监测内容。在算法试验之前,应用ENVI先对同区域不同时域的两幅原始图像进行影像配准,满足RMS不超过1.0,然后对两幅图像的重叠区域进行矩形剪裁。由于本文算法只需要保证框选出的试验矩形图中包含云即可,而不用像一般检测算法一样精确地检测出云的具体轮廓。本文试验矩形区域的选取采用以相同的经纬度坐标矩形角点为参照标准,固定长宽,框选出试验矩形范围,即有云图像与无云图像的试验矩形的角点经纬度坐标是同一的,从而保证试验矩形区域像素的对应性。试验从原始有云污染的遥感影像中截取云覆盖区域以及无云影像的对应区域,并按照图 4所示流程进行试验, V组数据K-SVD算法的重建效果如图 6所示,两组数据云覆盖区域本文改进算法AO-DL的重建效果如图 7和图 8所示。由试验结果可见,变序字典学习AO-DL算法对于资源三号遥感影像去云有着较好的效果。

|
| 图 6 未改进算法的重建结果 Fig. 6 The reconstruction result of unimproved algorithm |

|
| 图 7 V组数据AO-DL的重建效果 Fig. 7 AO-DL reconstruction result from data V |

|
| 图 8 W组数据AO-DL的重建结果 Fig. 8 AO-DL reconstruction result from data W |
采用均方根误差(root mean square error,RMSE)定量描述重建图像的恢复效果,计算有云影像的局部无云区域与重建图像的对应区域的误差,例如图 7效果与图 6效果比较,AO-DL方法重建图像局部区域与对应原清晰影像的均方根误差为2.286,而未改进的字典学习法直接参与去云的均方根误差为4.524,可见将字典原子按照特定的规则重新排序后,重建图像的质量得到了显著的提升。改进后的方法与现有的绝大多数去云方法相比,其优点为:降低了云检测要求、操作简单、字典中含有原图像的属性等,其缺点为:算法处理时间较长,并且精度有待提高。
4 总结与展望变序字典学习AO-DL算法应用多时域遥感影像,可以利用含有原图像属性的字典进行遥感影像的云污染区域重建,得到较好的恢复效果,并适用于不同类型区域。论文方法与现有绝大多数去云方法相比,有着降低了云检测要求、操作简单、字典中含有原图像的属性等优点,但是该方法在大面积成片云区域的情况下处理时间较长,且精度有待提高,主要因为该算法是在K-SVD算法的基础上进行的改进,应用K-SVD字典学习算法重建影像存在较原始清晰影像稍有模糊的问题,但对于有严重信息丢失的影像而言,此算法可以成功的补充大部分丢失的信息,因此相信字典学习算法将会更加广而应用。
后续主要有以下两点改进方向:一是进一步改善算法,减缓边缘模糊,提高精度;二是将尝试结合不同源的遥感影像加入到字典学习算法中,补充影像信息,从而提高云去除重建图像的精度。
| [1] | 喻昕玥. 基于小波变换的遥感影像薄云去除研究[D]. 南昌: 东华理工大学, 2015. YU Xinyue. Study on Removing Thin Cloud of Remote Sensing Image Based on Wavelet Transform[D]. Nanchang:East China Institute of Technology, 2015. |
| [2] | RICHTER R. A Spatially Adaptive Fast Atmospheric Correction Algorithm[J]. International Journal of Remote Sensing, 1996, 17(6): 1201–1214. DOI:10.1080/01431169608949077 |
| [3] | ARTAMONOV E S, PROTASOV K T. Restoration of Fragments of Satellite Images of the Earth's Underlying Surface Shadowed by Haze and Clouds[C]//Proceedings of SPIE 3983, Sixth International Symposium on Atmospheric and Ocean Optics. Tomsk, Russia:IEEE, 1999, 3983:170. |
| [4] | EL-ARABY E, EL-GHAZAWI T, LE MOIGNE J, et al. Reconfigurable Processing for Satellite on-Board Automatic Cloud Cover Assessment[J]. Journal of Real-Time Image Processing, 2009, 4(3): 245–259. DOI:10.1007/s11554-008-0107-8 |
| [5] | JEDLOVEC G J, HAINES S L, LAFONTAINE F J. Spatial and Temporal Varying Thresholds for Cloud Detection in GOES Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(6): 1705–1717. DOI:10.1109/TGRS.2008.916208 |
| [6] | 梁栋, 孔颉, 胡根生, 等. 基于支持向量机的遥感影像厚云及云阴影去除[J]. 测绘学报, 2012, 41(2): 225–231. LIANG Dong, KONG Jie, HU Gensheng, et al. The Removal of Thick Cloud and Cloud Shadow of Remote Sensing Image Based on Support Vector Machine[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 225–231. |
| [7] | 唐王琴, 梁栋, 胡根生, 等. 基于支持向量机的遥感图像厚云去除算法[J]. 遥感技术与应用, 2011, 26(1): 111–116. TANG Wangqin, LIANG Dong, HU Gensheng, et al. The Algorithm for Removing Thick Clouds in Remote Sensing Image Based on Support Vector Machine[J]. Remote Sensing Technology and Application, 2011, 26(1): 111–116. DOI:10.11873/j.issn.1004-0323.2011.1.111 |
| [8] | 秦雁, 邓孺孺, 何颖清, 等. 基于光谱及几何信息的TM图像厚云去除算法[J]. 国土资源遥感, 2012, 24(4): 55–61. QIN Yan, DENG Ruru, HE Yingqing, et al. Algorithm for Removing Thick Clouds in TM Image Based on Spectral and Geometric Information[J]. Remote Sensing for Land & Resources, 2012, 24(4): 55–61. DOI:10.6046/gtzyyg.2012.04.10 |
| [9] | 牛凌宇. 多源遥感图像数据融合技术综述[J]. 空间电子技术, 2005, 2(1): 1–5. NIU Lingyu. Multi-source Remote Sensing Image Data Fusion Technology Review[J]. Space Electronic Technology, 2005, 2(1): 1–5. |
| [10] | 郑永安, 陈玉春, 宋建社, 等. 基于提升机制小波变换的SAR与多光谱图像融合算法[J]. 计算机工程, 2006, 32(6): 195–197. ZHENG Yong'an, CHEN Yuchun, SONG Jianshe, et al. Fusion Algorithm of SAR and Multi-spectral Images Based on Lifting Scheme Wavelet Transform[J]. Computer Engineering, 2006, 32(6): 195–197. |
| [11] | AHARON M, ELAD M, BRUCKSTEIN A. rmK-SVD:An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311–4322. DOI:10.1109/TSP.2006.881199 |
| [12] | CANDES E J, WAKIN M B. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21–30. DOI:10.1109/MSP.2007.914731 |
| [13] | CHEN S S, DONOHO D L, SAUNDERS M A. Atomic Decomposition by Basis Pursuit[J]. SIAM Review, 2001, 43(1): 129–159. DOI:10.1137/S003614450037906X |
| [14] | MALLAT S G, ZHANG Zhifeng. Matching Pursuits with Time-frequency Dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. DOI:10.1109/78.258082 |
| [15] | PATI Y C, REZAⅡFAR R, KRISHNAPRASAD P S. Orthogonal Matching Pursuit:Recursive Function Approximation with Applications to Wavelet Decomposition[C]//Proceedings of the Conference Record of the Twenty-Seventh Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA:IEEE, 1993, 1:40-44. |
| [16] | CHEN S, BILLINGS S A, LUO W. Orthogonal Least Squares Methods and Their Application to Non-linear System Identification[J]. International Journal of Control, 1989, 50(5): 1873–1896. DOI:10.1080/00207178908953472 |
| [17] | TROPP J A. Greed is Good:Algorithmic Results for Sparse Approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231–2242. DOI:10.1109/TIT.2004.834793 |
| [18] | GORODNITSKY I F, RAO B D. Sparse Signal Reconstruction from Limited Data Using FOCUSS:A Re-weighted Minimum Norm Algorithm[J]. IEEE Transactions on Signal Processing, 1997, 45(3): 600–616. DOI:10.1109/78.558475 |
| [19] | LORENZI L, MELGANI F, MERCIER G. Missing-area Reconstruction in Multispectral Images under a Compressive Sensing Perspective[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(7): 3998–4008. DOI:10.1109/TGRS.2012.2227329 |
| [20] | LI Xinghua, SHEN Huanfeng, ZHANG Liangpei, et al. Recovering Quantitative Remote Sensing Products Contaminated by Thick Clouds and Shadows Using Multitemporal Dictionary Learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 7086–7098. DOI:10.1109/TGRS.2014.2307354 |
| [21] | XU Meng, JIA Xiuping, PICKERING M, et al. Cloud Removal Based on Sparse Representation via Multitemporal Dictionary Learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(5): 2998–3006. DOI:10.1109/TGRS.2015.2509860 |
| [22] | OLSHAUSEN B A, FIELD D J. Emergence of Simple-cell Receptive Field Properties by Learning a Sparse Code for Natural Images[J]. Nature, 1996, 381(6583): 607–609. DOI:10.1038/381607a0 |
| [23] | SADEGHI M, BABAIE-ZADEH M, JUTTEN C.Learning Overcomplete Dictionaries Based on Parallel Atom-Updating[C]//Proceedings of 2013 IEEE International Workshop on Machine Learning for Signal Processing (MLSP). Southampton, UK:IEEE, 2013:1-5. |
| [24] | MAIRAL J, BACH F, PONCE J, et al. Online Learning for Matrix Factorization and Sparse Coding[J]. The Journal of Machine Learning Research, 2010(11): 19–60. |
| [25] | SZABO Z, POCZOS B, LÖRINCZ A. Online Group-structured Dictionary Learning[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI:IEEE, 2011:2865-2872. |


