2. 中国科学院地理科学与资源研究所, 北京 100101;
3. 中国科学院遥感与数字地球研究所, 北京 100101
2. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China;
3. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
高光谱图像是由二维空间信息和一维光谱信息组成的三维数据,具有图谱合一且波段连续的特点,在军事监测、农业、林业、地质勘探和大气监控等多个领域都得到了广泛的应用[1]。高光谱图像质量受多种复杂因素影响,高光谱图像在获取和传输过程中引入了大量噪声[2],如热噪声、光子噪声[3]等。这些噪声不仅影响图像视觉效果还影响其后续处理和应用(如高光谱图像分类[4]、混合像元分解[5]、目标检测[6]等),因此有效的高光谱图像去噪方法对高光谱数据的处理、分析和应用非常重要。
高光谱图像去噪方法是当前的研究热点问题,目前针对高光谱图像去噪问题提出了多种方法。这些方法主要分为3类:逐波段处理、联合光谱-空间域变换方法和基于张量分解方法。
(1) 逐波段处理方法,该方法将高光谱图像每个波段的二维图像分别进行处理,但这类方法忽略了光谱相关性。采用2D图像去噪方法,如非局部矩阵[7]、K-SVD[8]和BM3D[9]方法对高光谱图像每个波段去噪。
(2) 联合光谱-空间域变换方法,对高光谱图像的空间域和光谱域进行特定变换来进行去噪。如文献[10]提出的混合空间-光谱小波收缩去噪(HSSNR)方法。文献[11]提出使用小波收缩和PCA方法对高光谱图像进行降维,以达到图像去噪目的。文献[12]提出了一种光谱-空间自适应总变分(SSAHTV)模型进行高光谱图像去噪方法。非局部光谱-空间结构稀疏表示的高光谱图像去噪方法等在文献[13]中进行描述。
(3) 基于张量分解方法,高光谱图像被认为是一个3D张量,可采用张量分解技术对高光谱图像张量进行处理。多维维纳滤波(MWF)方法[14],通过对高光谱数据进行TUCKER3分解后,执行维纳滤波实现去噪。文献[15]提出低秩张量近似(LRTA)方法,该方法的特点是通过Tucker分解[16]获得高光谱图像低秩近似进行去噪。文献[17]基于张量CP分解提出PARAFAC方法进行高光谱去噪取得不错效果,但在重构过程会产生伪影。文献[18]非局部方法引入张量进行多光谱图像去噪方法。文献[19]采用张量子空间的高光谱影像多维滤波算法进行高光谱图像去噪。基于张量方法将高光谱图像作为一个整体进行处理充分考虑高光谱图像各波段的相关性,但忽略了高光谱图像的空间非局部相似性,没有反映图像结构信息。
充分考虑高光谱图像非局部相似性和光谱相关性,本文提出了一种基于张量组稀疏表示的高光谱图像去噪方法。采用张量组稀疏表示模型对高光谱图像进行稀疏表示,对获得的稀释系数进行重构得到去噪后的高光谱图像。
1 张量组稀疏表示高光谱图像去噪稀疏表示作为一种新的信号表示方法广泛用于各种图像处理任务。稀疏表示是通过字典中少量元素的线性组合来表示信号,图像稀疏表示是用少量的原子来逼近图像。稀疏表示中字典的发展从最开始的正交基到冗余的正交基,再到过完备字典。过完备字典中的原子能更好地解析图像的结构信息,且更符合人眼视觉特性。
图像稀疏表示是计算图像在字典D下的稀疏表示系数Z,字典D为一系列原子di的组合,且m>d表示字典是过完备字典。稀疏表示模型如式(1) 所示
 (1)
(1)
式中,||·||0表示系数中非零元素数目。
基于稀疏表示图像去噪方法原理是采用冗余字典对图像进行稀疏分解。因为随机噪声不存在结构性,不能被字典原子稀疏表示,因而通过稀疏分解可以保留原始图像的有用信息而去除和信息无关的噪声。将图像有用信息看作是稀疏分量,而将噪声看作图像稀疏表示后的残差。基于稀疏表示去噪先提取图像的稀疏分量,然后利用获得的稀疏分量重建图像,即得去噪声后的图像。一般步骤是先将图像分块,然后对每个图像块进行稀疏表示,利用获得的稀疏表示,对图像块进行重建,最后,组合图像分块获得去噪图像。
从稀疏表示的观点看,无噪声图像能在字典基上稀疏表示,即通过少量的字典原子及对应的表示系数表示图像,且这些系数值往往较大;而噪声在相应字典下表示不是稀疏的,且表示系数较小。稀疏编码图像去噪过程中,较大的系数值在稀疏编码步骤中被保留下来,噪声对应的小的系数则被去除,对保留的稀疏编码系数重构获得去噪后的图像。
1.1 张量稀疏表示传统图像稀疏表示主要针对二维图像,而高光谱图像是同时具有光谱和空间特性,因此对高光谱图像的表示应同时考虑光谱和空间特性。高光谱图像可用一个3阶张量完整保存光谱和空间信息,使用3D高光谱图像分块替代二维图像中的图像分块将图像稀疏表示方法扩展到高光谱图像稀疏表示。首先,将高光谱图像分为重叠的小的3D高光谱全波段分块{Xi}i=1n,分块数目为n=(dW-dw+1)(dH-dh+1),其中dW和dH表示图像大小,dW和dH表示分块大小。每个高光谱分块包含局部空间结构和光谱信息。
高光谱图像分块稀疏表示描述如下
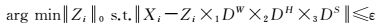 (2)
(2)
式中,Xi为高光谱图像块分组;{DW∈Rdw×mW}和{DH∈Rdh×mH}分别为水平和垂直方向的空间字典;{DS∈Rds×mW}为光谱字典,满足mW>dw,mH>dh,mS>ds表示字典是过完备字典;Zi为用空间字典DW、DH和光谱字典DS表示Xi的系数张量。
1.2 高光谱图像张量组稀疏表示除了稀疏性,非局部自相似性是图像的另一个重要性质。非局部自相似性是指图像的纹理和结构存在重复,即图像中不同位置的图像块具有很强的相似性。结合图像稀疏性和非局部自相似性的非局部稀疏表示已成功应用于不同图像处理任务。
非局部自相似性可扩展到高光谱图像,如图 1所示。首先,高光谱图像划分为多个小的全波段分块。然后,按一定准则将相似分块通过聚类形成分组。如图 1(b)中黄色的分块表示河流,黑色的分块表示建筑区域。通过分块和聚类操作后,获得的所有聚类分组表示为{xjk}j=1nk(k=1, 2, …,K),其中k表示第k个聚类分组, K为所有聚类数目,nk为第k个聚类中分块数目,xjk表示第k个聚类分组中的第j个高光谱图像分块。最后,对每个高光谱图像聚类分组进行稀疏表示,由于每组高光谱图像分块相似,进行高光谱图像分块组进行稀疏表示时,则分组中每个分块稀疏表示系数具有相似的结构。在对高光谱图像分块聚类稀疏表示过程中,每个分块聚类有共同的空间字典DW、DH和光谱字典DS。

|
| 图 1 高光谱图像的非局部自相似性 Fig. 1 The nonlocal similarity of hyperspectral image |
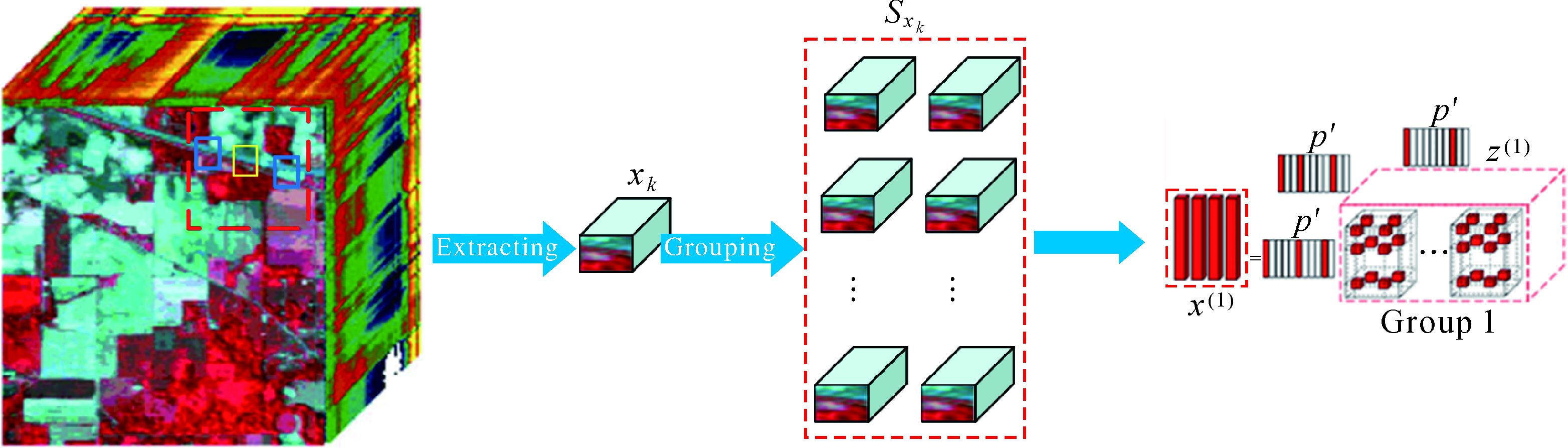
高光谱图像非局部张量稀疏表示模型为
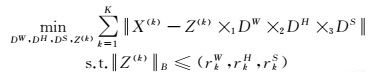 (3)
(3)
式中,||Z(k)||B≤(rkW, rkH, rkS)表示张量分块组稀疏度正则,用来保证表示系数的稀疏性。组稀疏正则如图 2所示,可看作是二维图像组稀疏在高光谱图像上的扩展。每个聚类分组由相似的高光谱图像分块组成,则聚类分组中的每个分块有相似的稀疏表示结构。
|
| 图 2 非局部张量组稀疏表示 Fig. 2 The nonlocal tensor group sparse representation |
对高光谱图像张量分块采用K-means++方法[20]进行聚类形成张量聚类分组,然后对张量聚类分组中高光谱图像分块进行稀释表示。
1.3 问题求解假设字典DW、DH、DS是足够冗余的,使得不同的聚类在进行张量稀疏表示时,使用的字典原子没有重复,则张量组稀疏表示问题能进一步简化。设稀疏表示的空间和光谱字典分别表示为DW=[D1W,D2W,…,DkW], DH=[D1H,D2H,…,DkH]和DS=[D1S,D2S, …, DkS],其中对每个聚类使用的子字典分别为DkW∈Rdw×rkW,DkH∈Rdh×rkH和DkS∈Rds×rkS。空间字典和光谱字典原子数目分别为∑k=1KrkW=mW, ∑k=1KrkH=mH和∑k=1KrkS=mS,则高光谱图像的每个分块聚类X(k)稀疏表示仅与子字典DkW、DkH和DkS相关。在这种假设下,则式(3) 中每个子问题等价表示为张量Tucker分解问题
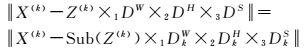 (4)
(4)
式中,Sub(Z(k))∈RrkW×rkS×rkS×nk表示Z(k)的核心子张量,则张量组稀疏表示问题分解为一系列聚类X(k)(k=1, 2,…, K)在对应字典DkW、DkH和DkS上的稀疏表示
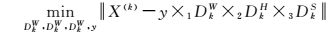 (5)
(5)
通过这种变换,原始问题(3) 能转化为一系列小问题,使得问题更容易求解。
高光谱图像的分块聚类X(k)的每个分块在空间是相关的,且高光谱图像本身的光谱是相关的,意味着每个聚类X(k)中存在大量的信息冗余能由低秩张量近似表示
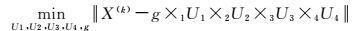 (6)
(6)
式中,U1∈RdkW×rkW、U2∈RdkH×rkH、U3∈RdkS×rkS、U4∈RdkN×rkN分别为聚类X(k)对应的张量数据在4个维度上的基向量,且满足dkW≥rkW, dkH≥rkH,dkS≥rkS和dkN≥rkN,其中g∈RrkW×rkH×rkS×rkN叫作核心张量。张量组稀疏表示式(6) 通过Tucker分解进行求解字典基Ui (i=1, 2, 3, 4) 和核心张量g。通过组合所有的字典基和核心张量来重构张量以实现高光谱图像去噪。
为了求解式(6),需要确定组稀疏正则参数rkW、rkH、rkS和rkN,其对应张量Tucker分解中的每个维度的秩参数。对每个分块聚类X(k)张量数据进行张量矩阵化,对矩阵化后的不同维度i(i=1, 2, 3, 4) 的矩阵X(i)(k)采用AIC/MDL方法[21]确定参数rkW、rkH、rkS和rkN。
高光谱图像张量组稀疏表示去噪算法总结如下:
输入:有噪声的高光谱图像H∈RdW×dH×dS
输出:空间字典DW=[D1W, D2W, …,DkW],DH=[D1H, D2H, …,DkH]和光谱字典DS=[D1S, D2S, …, DkS],核心张量Z(k)和去噪后的高光谱图像H′。
(1) 将高光谱图像进行分块操作获得小的全波段分块。
(2) 对所有的分块通过聚类形成不同分组X(k)∈Rdw×dh×ds×nk,k=1,2,…, K, nk表示每个聚类中分块数目。
(3) 对聚类X(k)按4个不同维度进行矩阵获得X(1)(k)、X(2)(k)、X(3)(k)和X(4)(k),并对这些矩阵采用AIC/MDL方法进行秩参数rkW、rkH、rkS和rkN的估计。
(4) 对X(k)执行张量分解获得Ui(i=1, 2, 3, 4) 和核心张量g,并设DkW=U1, DkH=U2,DkS=U3和Sub(Z(k))=g×4U4,并用子张量Sub(Z(k))来表示张量Z(k)。
(5) 利用Z(k)、DW、DH、DS重构高光谱图像分块,并对重叠分块进行平均获得去噪高光谱图像H′。
2 试验结果及分析为了验证提出算法的性能,在模拟数据和真实高光谱图像上进行试验,并与典型高光谱图像去噪方法进行比较,从主观视觉效果和客观图像质量方面进行评价。试验中相关参数设置如下:高光谱图像分块的空间大小为8×8,每个分块聚类中包含块的个数为40,相邻图像块之间的间隔为4,构造相似块聚类的相似块搜索窗口大小设置为40×40。试验仿真的硬件平台为主频为3.00 GB的酷睿E8400计算机,软件平台为64位Windows7操作系统和Matlab R2010b仿真软件。
2.1 模拟试验在高光谱图像数据库[22]上进行模拟试验。该数据库包含50幅室内和室外场景的高光谱图像。图像的尺寸为1392×1040像素,光谱波段数为31,波段范围为420~720 nm,每个波段范围是10 nm。在模拟试验中,对高光谱图像添加固定强度的泊松噪声和不同强度的高斯噪声及添加固定强度的高斯噪声和不同强度的泊松噪声模拟有噪声的高光谱图像进行试验。
为了处理泊松-高斯混合噪声,引入VST(variance-stabilizing transformation)[23]变换处理混合噪声。VST将泊松噪声或者泊松-高斯噪声转化到高斯噪声。试验中,去噪前对噪声图像执行VST变换,去噪后使用相应的逆变换获得高光谱图像去噪结果。
为了验证提出算法的有效性,将提出算法和几种方法进行比较。比较方法包括BwK-SVD[24]、NLM3D方法[25]、BM4D方法[26]、LRTA[27]和PARAFA方法[28]。采用信噪比(PSNR)、结构相似度(SSIM)[29]和特征相似度(FSIM)[30]进行算法性能评价。其中,PSNR和SSIM分别从最小均方误差和结构一致性角度描述目标图像和参考图像的相似性,FSIM用来描述目标图像和参考图像的感知一致性。
图 3显示模拟情况1下不同方法在波段1的去噪结果。图 5显示了在模拟情况2下不同方法波段5的去噪结果。图 4和图 6描述不同的去噪方法在不同模拟情况下各个波段上的PSNR、SSIM和FSIM的平均结果。表 1和表 2分别给出了两种模拟情况下不同方法的图像质量评价指标值,反映了去噪算法的综合性能。

|
| 图 3 方式1第1波段去噪结果 Fig. 3 Noise reduce result at band 1 in case 1 |
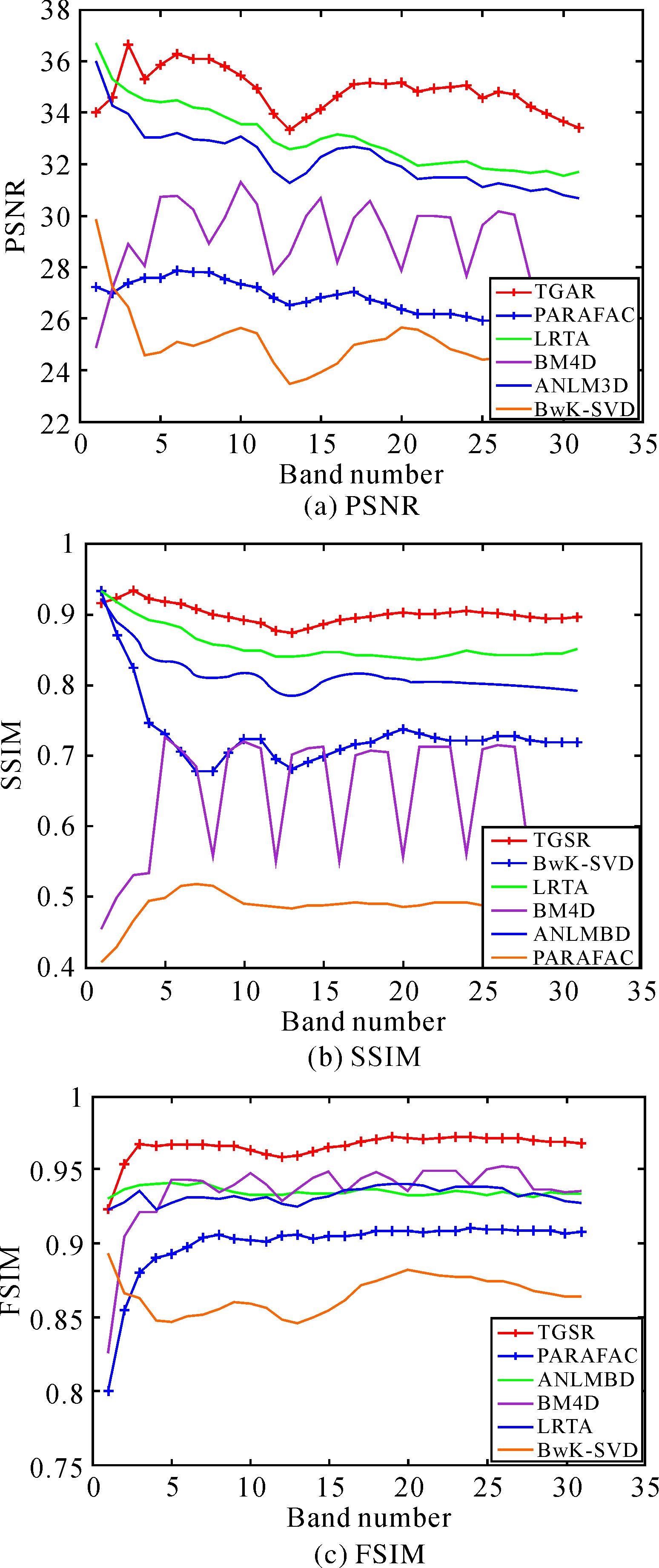
|
| 图 4 不同去噪方法对方式1每个波段的PSNR、SSIM和FSIM值 Fig. 4 The PSNR、SSIM and FSIM by different methods in case 1 |

|
| 图 5 方式2第5波段去噪结果 Fig. 5 Noise reduce result at band 5 in case 2 |
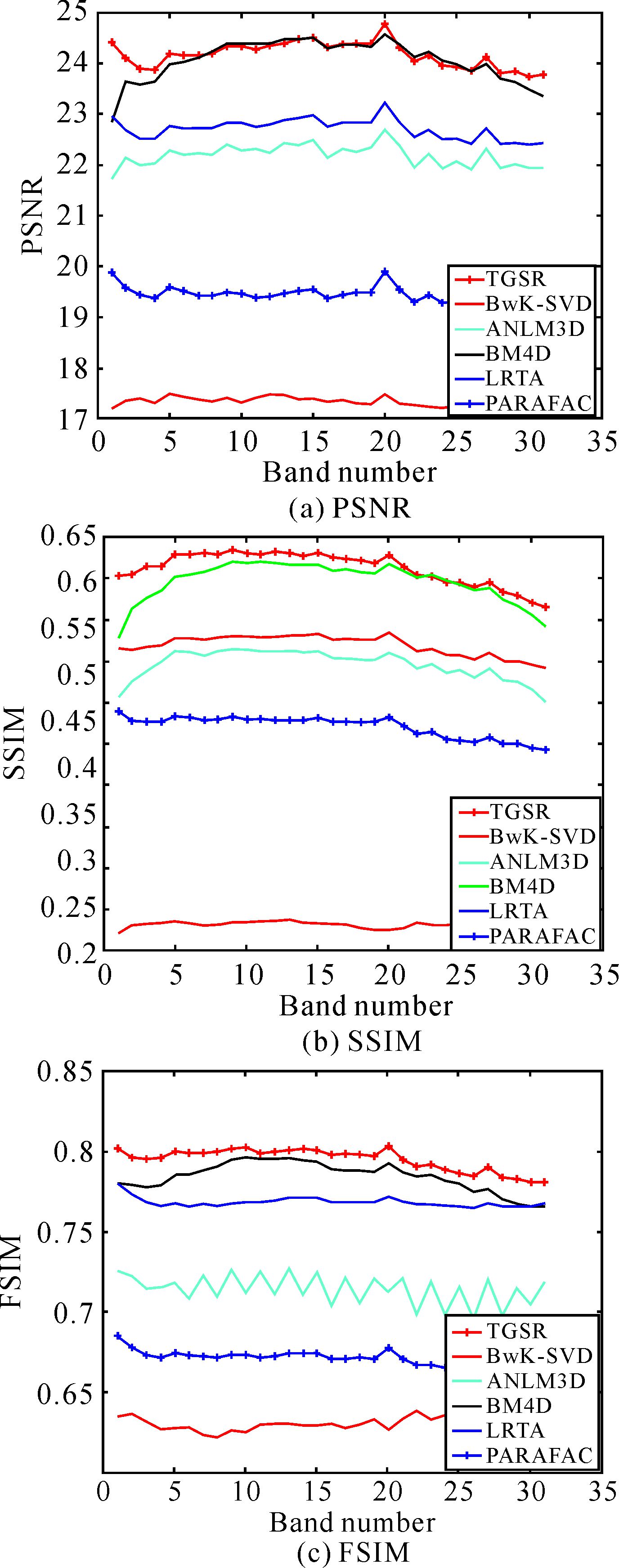
|
| 图 6 不同去噪方法对方式2每个波段的PSNR、SSIM和FSIM值 Fig. 6 The PSNR, SSIM and FSIM by different methods in case 2 |
| 方法 | PSNR/dB | SSIM | FSIM |
| 噪声图像 | 14.52±0.04 | 0.160±0.032 | 0.846±0.081 |
| BwK-SVD | 24.69±1.08 | 0.506±0.042 | 0.788±0.045 |
| NLM3D | 33.41±2.21 | 0.836±0.036 | 0.926±0.020 |
| BM4D | 31.07±2.14 | 0.688±0.023 | 0.927±0.018 |
| LRTA | 34.26±2.74 | 0.850±0.064 | 0.925±0.017 |
| PARAFAC | 29.37±2.43 | 0.788±0.113 | 0.886±0.027 |
| 提出方法 | 36.34±2.14 | 0.908±0.034 | 0.963±0.013 |
比较图 3和图 5中分部对应的在不同方式模拟噪声情况下不同去噪方法的去噪结果,提出的张量组稀疏表示高光谱图像去噪方法与其他方法相比具有较好的结果。从图中可以看出,本文提出的方法不仅能有效抑制噪声且能很好保留边界等细节信息。NLM3D和BM4D方法能较好地去除混合噪声,但图像的边界和纹理细节也遭到了很大破坏。将NLM3D和BM4D方法去噪结果与原始图像相比,图像中的墙面和窗户的边界和纹理细节有部分信息丢失。LRTA和PARARAFAC去噪结果中图像会产生部分痕迹,且边界信息不能很好地保留。特别是图 5(g)中PARARAFAC方法恢复的结果,有明显的重构伪影。逐波段去噪方法BwK-SVD方法尽管去噪后图像的边界和纹理纹理等细节得到一定的保护, 但图像中仍残留着部分的椒盐噪声, 在一定程度上影响了视觉效果。本文提出方法能较好地去除混合噪声, 且去噪后图像能很好地保持图像的边界和纹理等细节信息。
图 4和图 6是不同高光谱图像去噪方法在不同情况下的混合噪声去噪的PSNR、SSIM和FSIM在每个波段上的结果。从图 4和图 6中可以看出,使用张量组稀疏表示方法获得去噪后高光谱图像各波段的PSNR、SSIM和FSIM明显高于其他方法。表 1和表 2描述的总体评价结果中,提出方法的PSNR、SSIM和FSIM平均值高于其他方法。图 4和图 6及表 1和表 2表明提出算法的客观效果均优于其他高光谱图像去噪算法的去噪效果。
| 方法 | PSNR/dB | SSIM | FSIM |
| 噪声图像 | 10.78±1.22 | 0.131±0.034 | 0.521±0.074 |
| BwK-SVD | 17.53±1.76 | 0.189±0.018 | 0.637±0.031 |
| NLM3D | 22.42±1.18 | 0.491±0.031 | 0.723±0.051 |
| BM4D | 24.31±1.43 | 0.584±0.028 | 0.786±0.018 |
| LRTA | 22.86±1.18 | 0.527±0.062 | 0.769±0.038 |
| PARAFAC | 19.61±1.06 | 0.436±0.078 | 0.678±0.043 |
| 提出方法 | 24.46±1.03 | 0.613±0.026 | 0.795±0.013 |
2.2 真实数据试验
对AVIRIS获得的Indian Pines高光谱遥感图像进行试验验证算法性能。获得的高光谱图像的空间大小为145×145像素,具有220个波段,光谱范围为0.4~2.5 μm。在高光谱图像去噪前将第150~163波段对应的大气和水吸收波段从原始高光谱数据中去掉。
真实高光谱图像有较多波段,仅选择第3、110和204 3个波段来说明不同方法的去噪性能。这3个波段具有不同特点,第3个波段图像中存在条带噪声,第110个波段的图像的灰度值较小,使得图像偏暗,而第204波段图像灰度值较大,使得图像偏亮。3个波段的去噪结果分别如图 7—图 9所示。从视觉效果上来看,本文提出的方法比其他去噪方法具有更好的去噪效果,试验结果表明提出算法不仅能有效去除图像噪声,且能很好地保存图像边界和结构信息。使用NLM3D和BM4D方法进行去噪使得去噪后的图像过平滑且大部分边界信息丢失。使用LRTA和PARAFAX去噪,虽然将整个高光谱图像当作一个张量考虑了高光谱图像各波段的相关性,但忽略空间信息的非局部自相似性,导致部分细节信息丢失且去噪结果过平滑。逐波段的BwK-SVD方法,没有考虑每个波段的噪声强度和不同像素空间信息的差异,去噪后的图像过平滑,且在平滑区域仍有部分噪声,特别在第3波段有垂直条带噪声和高斯-泊松混合噪声。图 7表明存在条带噪声的情况下,本文提出的算法在去噪同时也能有效抑制条带噪声。图 7—图 9表明提出算法能对有条带噪声、亮度偏暗和亮度偏亮的各波段混合噪声去噪去的较好的效果,说明了提出算法的稳健性。

|
| 图 7 真实高光谱图像第3波段(具有条带噪声)去噪结果 Fig. 7 Denoising results in the real data experiment band 3 |

|
| 图 8 真实高光谱图像第110波段(图像亮度偏暗)去噪结果 Fig. 8 Denoising results in the real data experiment band 10 |

|
| 图 9 真实高光谱图像第204波段(图像亮度偏亮)去噪结果 Fig. 9 Denoising results in the real data experiment band 1 |
3 结论
本文提出了一种基于张量组稀疏表示的高光谱图像去噪方法。该方法将高光谱图像看作张量考虑高光谱图像各波段的相关性,同时考虑图像的局部稀疏性和非局部自相似性。首先将高光谱图像划分为小的分块,并对相似块进行聚类,然后对聚类采用张量组稀疏表示进行图像去噪。结果表明:与经典的高光谱图像去噪方法相比,本文提出的方法能更有效除去高光谱图像中的噪声,并能更好地保留图像的边缘和纹理等细节信息。该算法虽然能有效对高光谱图像去噪,但运算时间较长,减少时间复杂度是需要解决的问题。
| [1] | 童庆禧, 张兵, 郑兰芬. 高光谱遥感-原理、技术与应用[M]. 北京: 高等教育出版社, 2006. TONG Qingxi, ZHANG Bing, ZHENG Lanfen. Hyperspectral Remote Sensing-principle, Technology and Application[M]. Beijing: Higher Education Press, 2006. |
| [2] | KEREKES J P, BAUM J E. Full-spectrum Spectral Imaging System Analytical Model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 571–580. DOI:10.1109/TGRS.2004.841428 |
| [3] | USS M L, VOZEL B, LUKIN V V, et al. Local Signal-dependent Noise Variance Estimation from Hyperspectral Textural Images[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 469–486. DOI:10.1109/JSTSP.2010.2104312 |
| [4] | 陈昭, 王斌, 张立明. 基于低秩张量分析的高光谱图像降维与分类[J]. 红外与毫米波学报, 2013, 32(6): 569–575. CHEN Zhao, WANG Bin, ZHANG Liming. Dimensionality Reduction and Classification Based on Lower Rank Tensor Analysis for Hyperspectral Imagery[J]. Journal of Infrared and Millimeter Waves, 2013, 32(6): 569–575. |
| [5] | 崔宾阁, 张杰, 马毅, 等. 高分辨率图像辅助提取高光谱图像端元[J]. 遥感学报, 2014, 18(1): 192–205. CUI Bin'ge, ZHANG Jie, MA Yi, et al. High-resolution Image-assisted Endmember Extraction of Hyperspectral Image[J]. Journal of Remote Sensing, 2014, 18(1): 192–205. |
| [6] | 杨可明, 薛朝辉, 贾涛涛, 等. 高光谱影像小目标谐波分析探测模型[J]. 测绘学报, 2013, 42(1): 34–43. YANG Keming, XUE Zhaohui, JIA Taotao, et al. A Harmonic Analysis Model of Small Target Detection of Hyperspectral Imager[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 34–43. |
| [7] | 黄芝娟, 唐超影, 陈跃庭, 等. 基于非局部相似性和低秩矩阵的遥感图像重构方法[J]. 光学学报, 2016, 36(6): 0611002. HUANG Zhijuan, TANG Chaoying, CHEN Yueting, et al. Remote Sensing Image Reconstruction Method Based on Non-local Similarity and Low Rank Matrix[J]. Acta Optica Sinica, 2016, 36(6): 0611002. |
| [8] | 秦振涛, 杨武年, 潘佩芬. 基于稀疏表示和自适应字典学习的"高分一号"遥感图像去噪[J]. 光电工程, 2013, 40(9): 16–21. QIN Zhentao, YANG Wunian, PAN Peifen. The Remote Sensing Image Denoising of "The First Satellite of High Resolution" Based on Sparse Representation and Dictionary Learning[J]. Opto-Electronic Engineering, 2013, 40(9): 16–21. |
| [9] | DABOV K, FOI A, KATKOVNIK V, et al. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080–2095. DOI:10.1109/TIP.2007.901238 |
| [10] | OTHMAN H, QIAN Shen'en. Noise Reduction of Hyperspectral Imagery Using Hybrid Spatial-spectral Derivative-domain Wavelet Shrinkage[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(2): 397–408. DOI:10.1109/TGRS.2005.860982 |
| [11] | CHEN Guangyi, QIAN Shenen. Simultaneous Dimensionality Reduction and Denoising of Hyperspectral Imagery Using Bivariate Wavelet Shrinking and Principal Component Analysis[J]. Canadian Journal of Remote Sensing, 2008, 34(5): 447–454. DOI:10.5589/m08-058 |
| [12] | YUAN Qiangqiang, ZHANG Liangpei, SHEN Huanfeng. Hyperspectral Image Denoising Employing A Spectral-Spatial Adaptive Total Variation Model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3660–3677. DOI:10.1109/TGRS.2012.2185054 |
| [13] | QIAN Yuntao, YE Minchao. Hyperspectral Imagery Restoration Using Nonlocal Spectral-spatial Structured Sparse Representation with Noise Estimation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2): 499–515. DOI:10.1109/JSTARS.2012.2232904 |
| [14] | MUTI D, BOURENNANE S, MAROT J. Lower-rank Tensor Approximation and Multiway Filtering[J]. SIAM Journal on Matrix Analysis and Applications, 2008, 30(3): 1172–1204. DOI:10.1137/060653263 |
| [15] | RENARD N, BOURENNANE S, BLANC-TALON J. Denoising and Dimensionality Reduction Using Multilinear Tools for Hyperspectral Images[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(2): 138–142. DOI:10.1109/LGRS.2008.915736 |
| [16] | TUCKER L. Some Mathematical Notes on Three-mode Factor Analysis[J]. Psychometrika, 1966, 31(3): 279–311. DOI:10.1007/BF02289464 |
| [17] | LIU Xuefeng, BOURENNANE S, FOSSATI C. Denoising of Hyperspectral Images Using the PARAFAC Model and Statistical Performance Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3717–3724. DOI:10.1109/TGRS.2012.2187063 |
| [18] | PENG Yi, MENG Deyu, XU Zongben, et al.Decomposable Nonlocal Tensor Dictionary Learning for Multispectral Image Denoising[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Columbus, OH:IEEE, 2014:2949-2956. |
| [19] | 郭贤, 黄昕, 张乐飞, 等. 采用张量子空间的高光谱影像多维滤波算法[J]. 测绘学报, 2013, 42(2): 253–259. GUO Xian, HUANG Xin, ZHANG Lefei, et al. Tensor Subspace Based Multiway Filtering Algorithm for Hyperspec-tral Images[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 253–259. |
| [20] | ARTHUR D, VASSILVITSKⅡ S. K-Means++:The Advantages of Careful Seeding[C]//Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms. New Orleans, Louisiana:ACM, 2007:1027-1035. |
| [21] | WAX M, KAILATH T. Detection of Signals by Information Theoretic Criteria[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(2): 387–392. DOI:10.1109/TASSP.1985.1164557 |
| [22] | CHAKRABARTI A, ZICKLER T.Statistics of Real-world Hyperspectral Images[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI:IEEE, 2011:193-200. |
| [23] | MAKITALO M, FOI A. Optimal Inversion of the Generalized Anscombe Transformation for Poisson-Gaussian Noise[J]. IEEE Transactions on Image Processing, 2013, 22(1): 91–103. DOI:10.1109/TIP.2012.2202675 |
| [24] | AHARON M, ELAD M, BRUCKSTEIN A. rmK-SVD:An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311–4322. DOI:10.1109/TSP.2006.881199 |
| [25] | MANJÓN J V, COUPÉ P, MARTíBONMATí L, et al. Adaptive Non-local Means Denoising of Mr Images with Spatially Varying Noise Levels[J]. Journal of Magnetic Resonance Imaging, 2010, 31(1): 192–203. DOI:10.1002/jmri.22003 |
| [26] | MAGGIONI M, KATKOVNIK V, EGIAZARIAN K, et al. Nonlocal Transform-Domain Filter for Volumetric Data Denoising and Reconstruction[J]. IEEE Transactions on Image Processing, 2013, 22(1): 119–133. DOI:10.1109/TIP.2012.2210725 |
| [27] | RENARD N, BOURENNANE S, BLANC-TALON J. Denoising and Dimensionality Reduction Using Multilinear Tools for Hyperspectral Images[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(2): 138–142. DOI:10.1109/LGRS.2008.915736 |
| [28] | LIU Xuefeng, BOURENNANE S, FOSSATI C. Denoising of Hyperspectral Images Using the PARAFAC Model and Statistical Performance Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3717–3724. DOI:10.1109/TGRS.2012.2187063 |
| [29] | WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image Quality Assessment:from Error Visibility to Structural Similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. DOI:10.1109/TIP.2003.819861 |
| [30] | ZHANG Lin, ZHANG Lei, MOU Xuanqin, et al. FSIM:A Feature Similarity Index for Image Quality Assessment[J]. IEEE Transactions on Image Processing, 2011, 20(8): 2378–2386. DOI:10.1109/TIP.2011.2109730 |



