2. 海军工程大学理学院, 湖北 武汉 430033
2. College of Science, Naval University of Engineering, Wuhan 430033, China
摄影测量有着悠久的历史,目前已广泛用于不同比例尺的地形测量及工业、建筑等非地形测量[1-3]。尽管其对象与任务千差万别,但主要方法都是从二维影像重建三维模型[4-5],在重建的三维模型上提取所需的各种信息,其中重建三维模型的基础就是根据影像确定目标点的空间位置。作为一种常用定位方法,立体像对的空间前方交会是根据立体像对左右两影像的内、外方位元素和同名像点的影像坐标量测值来确定该点的物方空间坐标[6]。这种方法易于理解,运算简便,却无法充分利用更多像片的观测数据。一旦立体像对中的某张影像量测数据包含较大误差,则必然导致错误的解算结果,即其抗差性能较差。随着近景、航空、航天等摄影测量技术的发展[7-10],包含同一目标点的影像在数量上已经相当可观,充分利用这些像片信息,并尽可能降低误差对解算结果的影响,最终实现地面点定位,具有重要意义。文献[11]曾提出基于多张像片前方交会的人工标志点匹配方法,并取得较好的匹配效果,然而该方法仍是通过依次实现双片空间前方交会的方法进行物方点筛选。在地面点定位过程中,若能直接利用所有的观测信息,不仅可以减少依次筛选与逐个剔除而引起的时间耗费,也能有效避免因个别像片观测条件差而引起的定位偏差,最终解算出更精确的地面点位置。总体最小二乘方法[12-18]顾及了所有的观测信息,被广泛用于解决测量学中观测数据含有误差的问题,均取得较好成效。考虑到空间前方交会的主要思路是“同名射线必在物方空间交于一点”,而实际作业中通常会有测量误差的存在,同名射线不会严格相交,因此,可利用总体最小二乘方法,根据“目标点到多条同名射线的距离平方和最短”这一原则构建目标函数来实现地面点定位[19-21]。最后,通过引入稳健估计理论和借助选权迭代法以规避粗差干扰,并为精度高的观测信息赋予较高的权重[22-27],给出可直接用于多张像片的空间前方交会公式。
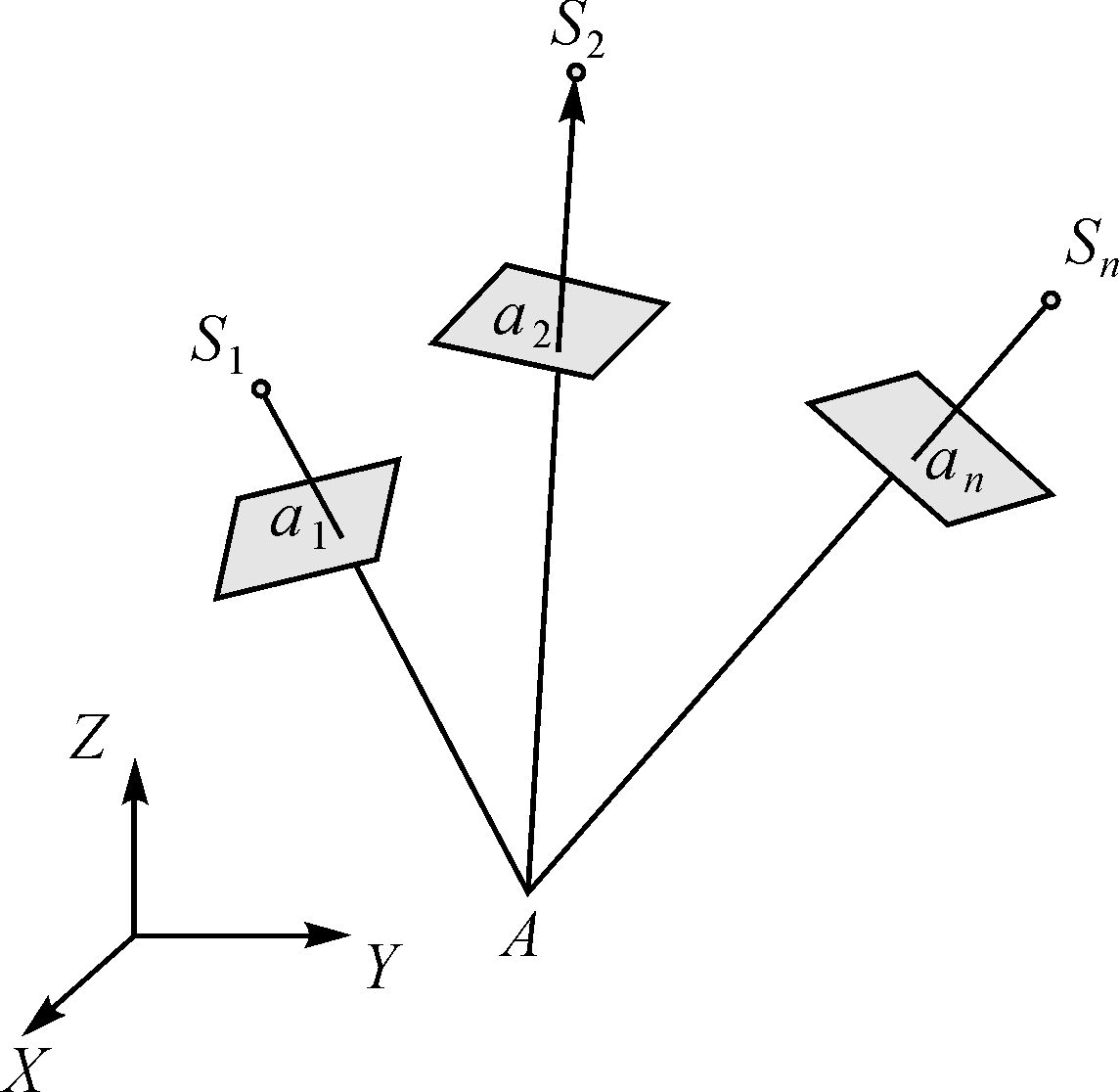
1 多像片前方交会定义如图 1所示,在多个摄影站点S1、S2、…、Sn对地面进行摄影,可获取n张像片。地面点A在这n张像片的构象分别为a1、a2、…、an。已知n张像片的内、外方位元素,将像片按内、外方位元素置于摄影时的位置,在理想情况下,同名射线S1a1、S2a2、…、Snan必将交于一点,即地面点A。这种利用多张像片的内、外方位元素及同名像点的像空间坐标,通过交会解算相应模型点坐标的过程,称为多张像片的空间前方交会。
|
| 图 1 多像空间前方交会示意图 Fig. 1 Sketch of space intersection appropriate for multi-images |
2 多像片前方交会过程 2.1 构建目标函数
考虑到像点的量测误差等因素,这些同名射线并不一定交于同一点甚至不一定相交,在综合考虑所有观测信息的条件下,可通过构建目标函数,求到同名射线距离的平方和最小的点作为A点
 (1)
(1)
式中,pi为权重;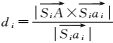
 (2)
(2)
考虑到矢量叉乘与点乘之间的关系,则式(2) 可等价变换为
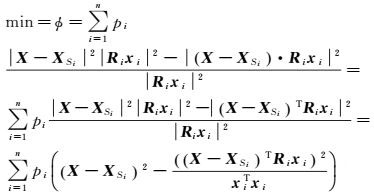 (3)
(3)
式中,各像片权重pi,旋转矩阵Ri,摄影中心XSi,像点坐标xi均为已知,仅地面点A的坐标X为未知。通过解算“到同名射线距离的平方和最小”这一条件而得出的X,即为考虑了所有观测点信息的地面点坐标。
2.2 总体最小二乘估计为使得地面点A的坐标X满足目标函数φ=min这一条件,即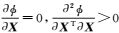
 (4)
(4)
由于式(4) 中XTRixi是一个标量,满足其转置等于自身,有XTRixi=(XTRixi)T=xiTRiTX,将式(4) 进一步化简,可得
 (5)
(5)
式中, I为单位阵,当n=1时,I-RixixiTRiT/|xi|2的行列式为0,即系数矩阵不可逆,无法进一步求出地面点A的坐标,这是因为单个像点及其投影中心只能确定地面点的空间方向,而无法确定其位置。当n≥2,若n条射线Siai相互平行时,此时每张像片上I-RixixiTRiT/|xi|2项相同,系数矩阵可合并为(I-R1x1x1TR1T/|x1|2)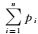
由于式(5) 系数矩阵的每一项中I-RixixiTRiT/|xi|2具有特征值0、1、1,故对应二次型χT(I-RixixiTRiT/|xi|2)χ(χ≠0) 非负。在其他情况下,即存在n≥2条不平行的同名射线时,χT(I-RixixiTRiT/|xi|2)χ不可能同时为0。因此,可得式(5) 系数矩阵的二次型
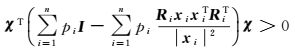 (6)
(6)
故式(5) 系数矩阵正定,可逆。因此,必然可确定满足目标函数最小的地面点A,为
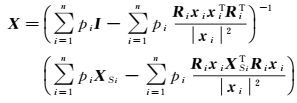 (7)
(7)
由于目标函数对X的一阶导数为0的点有且仅有一个,且其二阶导数即为式(5) 的系数矩阵,根据上述判定,可知其正定,说明该驻点确实是极小值点,故式(7) 即为地面点A的加权总体最小二乘估计。
2.3 选权迭代法由于在实际测量工作中客观条件的限制,很难完全避免粗差的存在或做到完全同等精度量测。在平差过程中,通常引入权作为比较观测值之间相对精度高低的指标,并为精度较高的观测数据赋予较高的权重。但是,在各像片量测误差分布未知的情况下,难以对各像片进行定权。随着解算地面点坐标时可利用像片数目的增多,为使参数的估值尽可能充分利用观测数据中的有效信息,规避有害信息的干扰,经常会引入稳健估计的方法。本文选用IGG选权迭代法来为观测像片赋权。主要步骤如下:
(1) 令目标函数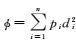
(2) 分别求地面点A到各射线Siai的距离di,及标准差,如下
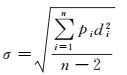 (8)
(8)
(3) 根据IGG方案[27],定义等价权因子wi,如下
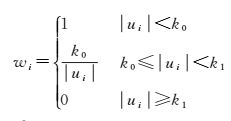 (9)
(9)
式中,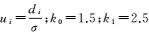
(4) 令
(5) 重复(2)~(4) 步,进行迭代运算,直至两次估值结果差异小于限差为止。
3 算例分析为验证本文方法的可靠性,并分析误差对于该方法的影响,以及其对粗差的探测效果,假定地面点A的地面摄影测量坐标真值X0=[200 100 50]T,单位为m以及3组已知内、外方位元素的像片(见表 1—表 3),其中f为焦距;XS=(XS YS ZS)T为摄影中心的地面摄影测量坐标;φ、ω、κ为像片旋转角。
| 方位元素 | 像片1 | 像片2 | 像片3 | 像片4 | 像片5 | 像片6 |
| f/mm | 80 | 80 | 100 | 100 | 200 | 200 |
| XS/m | -600 | -200 | 0 | 400 | 600 | 800 |
| YS/m | -500 | -300 | -100 | 300 | 500 | 700 |
| ZS/m | 600 | 600 | 700 | 700 | 800 | 800 |
| φ/° | 10 | 20 | 15 | 10 | 15 | 10 |
| ω/° | 10 | 20 | 20 | 5 | 20 | 15 |
| κ/° | 10 | -10 | 5 | -5 | -10 | 5 |
| 方位元素 | 像片1 | 像片2 | 像片3 | 像片4 | 像片5 | 像片6 |
| f/mm | 80 | 80 | 100 | 100 | 200 | 200 |
| XS/m | -600 | -200 | 0 | 400 | 600 | 800 |
| YS/m | -500 | -300 | -100 | 300 | 500 | 700 |
| ZS/m | 20 000 | 20 000 | 22 000 | 22 000 | 25 000 | 25 000 |
| φ | -20° | -5° | -100′ | 15′ | 5° | 20° |
| ω | 10° | -5° | -20′ | 20′ | 5° | 0 |
| κ | -10° | 1 | -30′ | 1′ | 3 | 5° |
| 方位元素 | 像片1 | 像片2 | 像片3 | 像片4 | 像片5 | 像片6 |
| f/mm | 80 | 100 | 200 | 80 | 100 | 200 |
| XS/m | -600 | 0 | 600 | -200 | 400 | 800 |
| YS/m | -500 | -100 | 500 | -300 | 300 | 700 |
| ZS/m | 600 | 700 | 800 | 20 000 | 22 000 | 25 000 |
| φ | 10° | 15° | 15° | -5° | 15′ | 20° |
| ω | 10° | 20° | 20° | -5° | 20′ | 0 |
| κ | 10° | 5° | -10° | 1 | 1′ | 5° |
3.1 算法可靠性验证 3.1.1 算法正确性验证
为验证算法的正确性,利用严格共线方程可以推算出该地面点在不同像片上对应像点的像空间坐标xi。之后,将这3组像片分别进行空间前方交会,可得出地面点A的新坐标X,最后将其与真值进行比较。
该算例中已知每组6张像片的内、外方位元素,地面点坐标真值按照严格共线方程模拟出每张像片上对应的像点坐标,此时可认为各像片具有同等精度条件,即各像片的权重均为1,利用本文方法解算出的地面点坐标为X=[200 100 50]T,单位为m与真值相同,该算例验证了本文算法的正确性。
3.1.2 算法稳健性验证为验证本文方法的稳健性,以第1组数据为例,在各像片像点坐标上加入0.5个像素(像素大小为4 μm)的高斯噪声,并在像片1中的像点横坐标加入2 mm的粗差,再利用本文方法进行多张像片的空间前方交会,ds为交会结果与真值的位移偏差。初次运算时为每张像片赋予权重为1,每次运算的权和地面点估计结果,列于表 4。
| 迭代次数 | 权重像1 | 权重像2 | 权重像3 | 权重像4 | 权重像5 | 权重像6 | X/m | Y/m | Z/m | ds/m |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 201.982 | 99.859 | 53.978 | 4.447 |
| 1 | 0.883 | 1 | 1 | 1 | 1 | 1 | 201.812 | 99.899 | 53.672 | 4.096 |
| 2 | 0.818 | 1 | 1 | 1 | 1 | 1 | 201.557 | 99.949 | 53.203 | 3.561 |
| 3 | 0.723 | 1 | 1 | 1 | 1 | 1 | 201.203 | 99.998 | 52.526 | 2.798 |
| 4 | 0 | 1 | 1 | 1 | 1 | 1 | 199.997 | 100.006 | 49.997 | 0.007 |
| 5 | 0 | 1 | 1 | 1 | 1 | 1 | 199.997 | 100.006 | 49.997 | 0.007 |
而若采用传统立体像对空间前方交会方法,由于它仅考虑两张像片的信息且无法剔除粗差,故将产生C62=15种计算结果,具体数值见表 5。为对比不同方法的解算结果,将地面点真值及不同方法解算值的空间分布情况绘于图 2。
| 交会结果 | X/m | Y/m | Z/m | ds/m |
| 1 | 176.906 | 74.735 | 81.727 | 46.672 |
| 2 | 193.689 | 89.31 | 70.531 | 23.993 |
| 3 | 204.157 | 98.41 | 63.548 | 14.261 |
| 4 | 206.422 | 100.362 | 62.037 | 13.648 |
| 5 | 208.513 | 102.18 | 60.642 | 13.802 |
| 6 | 200.027 | 100.038 | 49.935 | 0.08 |
| 7 | 199.986 | 100.006 | 49.992 | 0.017 |
| 8 | 199.993 | 99.997 | 49.982 | 0.02 |
| 9 | 199.989 | 99.995 | 49.987 | 0.018 |
| 10 | 199.998 | 100.016 | 50.03 | 0.034 |
| 11 | 200.005 | 100.008 | 50.005 | 0.011 |
| 12 | 200.005 | 100.01 | 50.007 | 0.013 |
| 13 | 199.969 | 99.981 | 49.937 | 0.073 |
| 14 | 199.981 | 99.995 | 49.977 | 0.03 |
| 15 | 200.009 | 100.007 | 50.011 | 0.016 |
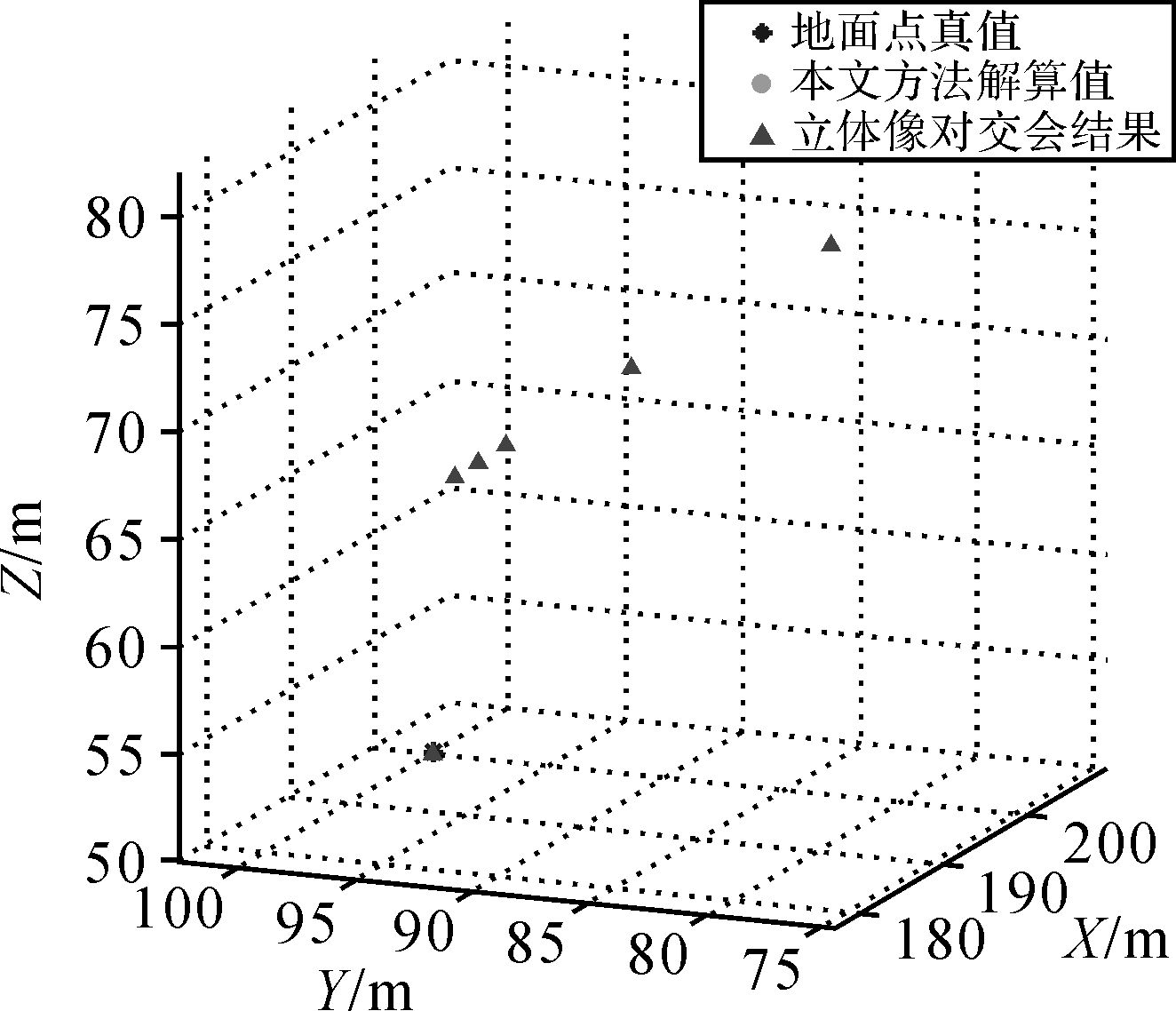
|
| 图 2 不同方法解算结果的空间分布 Fig. 2 Distributions of calculated ground point by different methods |
由表 4可以看出,经过多次迭代,含有粗差的像片权重逐渐减小到0,使其在平差中不起作用。本文方法可通过在平差过程中为观测值重新赋权来规避粗差,具有较好的抗差性。而传统立体像对空间前方交会方法,由于难以利用多余的观测信息,受单张像片观测精度的影响较大,抗差性能较差。从图 2、表 5中可以看出,由于粗差的存在,立体像对空间前方交会结果中至少有5个估值与地面点真值相比具有较大偏差。
此外,本文方法除了可剔除粗差的影响外,对于随机误差也有较好的平衡作用。由图 2、表 4、表 5可以看出,采用加权总体最小二乘的多像空间前方交会结果精度优于立体像对的解算精度,能取得更稳定的交会结果,该算例验证了本文方法的稳健性。
3.2 不同误差对算法的影响分析为系统分析该算法的特点,需分别研究像点观测值误差及外方位线元素、角元素误差对解算结果的影响,以及它们的综合影响。以下将从误差对于交会精度的影响以及目标点交会偏差两方面进行分析。
3.2.1 误差对交会精度的影响分析经试验,3种误差分别对本文算法交会精度的影响具有类似的特性。因此,为节省篇幅,文中将重点针对像点坐标误差对于交会精度的影响进行分析,同时直接给出外方位线元素、角元素分别对于算法交会精度的影响结果,而对其过程不再赘述。
为分析本文方法交会精度受像点坐标误差的影响情况,重复进行10 000次试验后,将99.9%置信度对应的精度值作为其交会精度。图 3(a)—图 3(f)分别为不同误差水平下(像点观测误差由0.5~3个像素(像素大小为4 μm)递增),10 000次试验中小航高像片的定位精度频数直方图。

|
| 图 3 小航高像片在不同噪声水平下的交会精度 Fig. 3 Intersection accuracy of images at small heights under different noises in image coordinates |
由图 3可以看出,当像点坐标的误差水平不同,本文方法具有不同的交会精度。像点坐标含有的误差越小,交会精度越高;像点坐标误差越大,交会结果的精度越低。其中,在像点坐标含有1.5个像素误差水平下,可实现1 dm的交会精度。考虑到本文交会方法可以综合考虑多张像片的信息,具有更好的稳健性,因此它对于观测误差的敏感程度较低。为说明这一特性,并与传统立体像对空间前方交会方法进行对比,在置信度为99.9%的情况下,可绘制其交会精度随着像点坐标误差(0~100像素误差,间隔0.5像素进行试验)的变化曲线,如图 4(a)所示。

|
| 图 4 不同航高像片交会精度随像点坐标误差的变化趋势 Fig. 4 Intersection accuracy of images at different heights with image coordinates errors |
同理,可绘制出另两组像片组合(大航高像片组合(0~0.5像素误差,间隔0.01像素进行试验)及混合航高像片组合(0~15像素误差,间隔0.5像素进行试验))的交会精度随着像点坐标误差的变化曲线,分别如图 4(b)、图 4(c)所示。
由图 4可以看出,传统立体像对与本文多像空间前方交会方法的交会精度均随着像点坐标误差的增大而近似线性下降。且同等误差水平条件下,各组像片采用本文方法具有明显较高的交会精度。
为给出本文算法交会精度随着像点坐标误差的变化率,可利用Origin的Linear Fit功能拟合出直线的斜率。类似地,由于交会精度随着外方位线元素(试验数据:小航高像片组合外方位线元素误差0~5 m,间隔0.1 m进行试验;大航高像片组合外方位线元素误差0~0.5 m,间隔0.01 m进行试验;混合航高像片组合0~5 m外方位线元素误差,间隔0.1 m进行试验)、角元素(试验数据:小航高像片组合外方位角元素误差0~600″,间隔10″进行试验;大航高像片组合外方位角元素误差0~5″,间隔0.01″进行试验;混合航高像片组合0~90″外方位角元素误差,间隔1″进行试验)误差也呈线性递减趋势,可同样给出直线斜率,列于表 6,其中像点坐标、线元素、角元素误差的横坐标单位分别为像素、米及角秒。
| 像片 | 像点坐标 | 线元素 | 角元素 |
| 小航高 | 0.065 86 | 2.321 11 | 0.010 87 |
| 大航高 | 35.625 52 | 46.178 3 | 5.064 03 |
| 混合航高 | 1.012 99 | 3.043 39 | 0.141 13 |
由表 6可以得出,采用本文多像空间前方交会方法,当小航高像片上像点坐标在1个像素误差水平时,可实现约7 cm的交会精度,而当误差为100个像素时,仍可实现7 m的交会精度;大航高像片上像点坐标在0.5个像素误差水平条件下,具有约18 m的交会精度,而混合航高像片的像点坐标在1个像素误差水平时,具有1 m左右的交会精度。小航高像片外方位线元素在1 m误差水平条件下,可实现约2.3 m的交会精度;大航高像片外方位线元素在0.5 m误差水平条件下,具有约23 m的交会精度,而混合航高像片外方位线元素在1 m误差水平条件下,具有约3 m的交会精度。小航高像片外方位角元素在1″误差水平条件下,具有约1 cm的交会精度;大航高像片外方位角元素在1″误差水平下,具有5 m左右的交会精度,而混合航高像片外方位线元素在1″误差水平条件下,具有1.5 dm左右的交会精度。
结合图 4及表 6可以得出,同等误差水平条件下,本文方法前方交会精度远远优于传统立体像对方法。利用本文方法进行空间前方交会的过程中,小航高像片的交会精度受误差影响最小,具有最高的交会精度,混合航高像片次之,而大航高像片对误差最为敏感。因此,在处理大航高像片数据时,可适当增加小航高像片信息,可有效降低其对误差的敏感性,进而提高交会精度。
3.2.2 误差对交会点位置偏差的影响分析为充分分析本文算法受误差的影响特点,需研究地面点交会结果随着误差的偏移情况。参考文献[28],设计以下仿真试验。
(1) 地面点坐标真值:在一定区域范围内选取均匀分布的100个地面点,其坐标已知。
(2) 误差大小:分别在像点坐标、外方位线元素、角元素上引入10像素、100 m、30″的误差。
(3) 地面点坐标解算值:引入步骤(2) 中的误差,利用本文方法进行多像空间前方交会,获得地面点位置的解算值。
(4) 交会结果分析:将地面点解算值与真值进行比较,绘制地面点解算值各分量的偏差示意图,如图 5—图 7所示。最后,分析不同误差对于交会结果的影响及它们的综合影响。
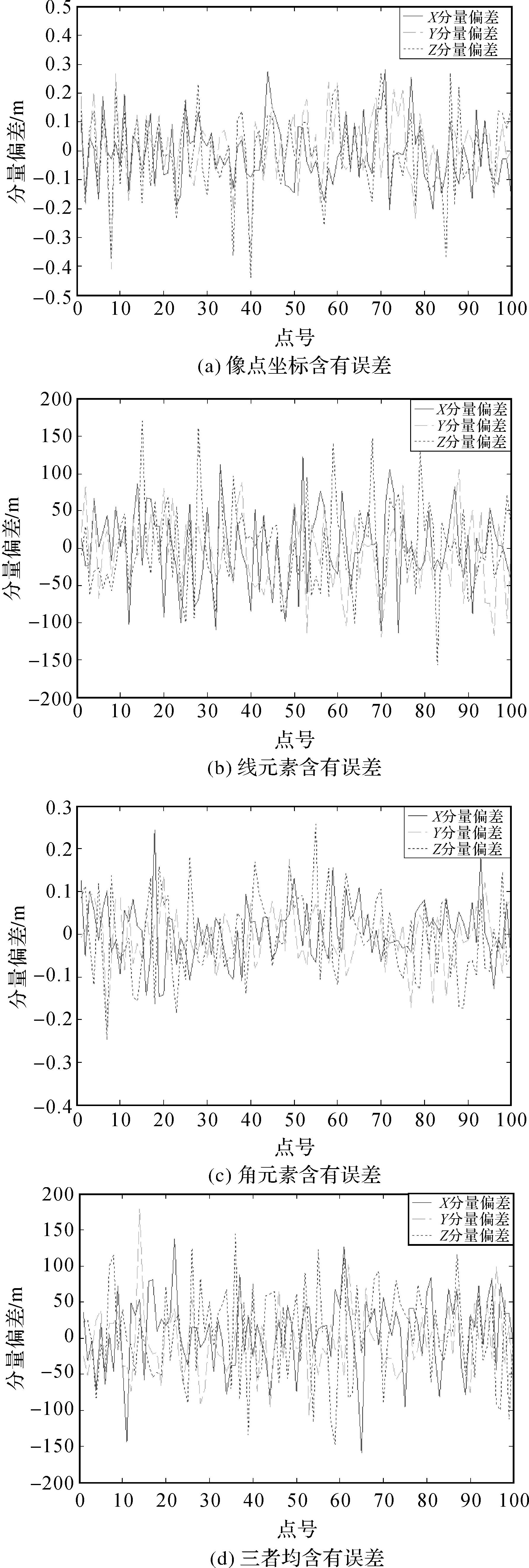
|
| 图 5 小航高像片上不同误差引起的地面点位置偏差分布图 Fig. 5 Deviation distribution of ground points brought by different errors on images at small heights |
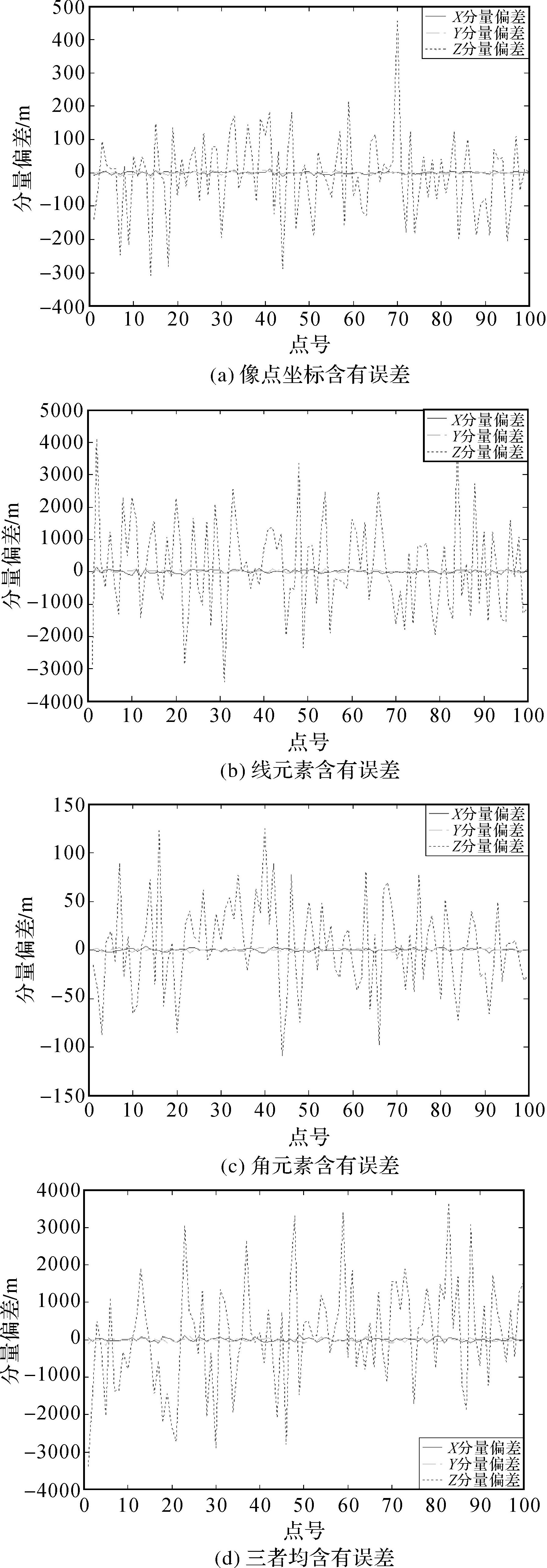
|
| 图 6 大航高像片上不同误差引起的地面点位置偏差示意图 Fig. 6 Deviation of ground points brought by different errors on images at large heights |

|
| 图 7 小航高像片上不同误差引起的地面点位置偏差分布图 Fig. 7 Deviation distribution of ground points brought by different errors on images at mixed heights |
由图 5可以看出,小航高像片在单独加载像点坐标、外方位线元素、角元素误差时,其X、Y、Z 3分量之间的偏差曲线幅度较为相似,没有明显差别,但整体来说,线元素上的100 m误差将使得交会结果与真值之间产生最大的偏差。在3种噪声的综合影响下,X、Y、Z 3分量之间的偏差幅度相近,整体幅度水平接近于单独加载100 m线元素误差的情形。
由图 6可以看出,大航高像片在单独加载像点坐标、外方位线元素、角元素误差时,其X、Y分量的偏差幅度相近,明显较Z分量更为稳定,受误差的影响较小。整体来说,线元素上的100 m误差将使得交会结果与真值之间产生最大的偏差。在3种噪声的综合影响下,整体偏差幅度与单独加载100 m线元素误差的情形相近。
由图 7可以看出,相对于大航高像片组合,在混合航高像片中, Z分量对于各种误差的敏感程度大大降低,甚至在单独加载像点坐标和角元素误差的情况下,较X及Y分量偏差幅度更小。而在单独加载线元素误差时, Z分量表现的稍为敏感,偏差幅度较X及Y分量略大。
综合图 5—图 7可得,同等噪声水平分别加载到不同航高的像片组合中,会引起交会结果的偏差程度不同,其中小航高像片交会偏差最小,混合航高像片次之,大航高像片交会结果最差。在利用大航高进行多像空间前方交会时,目标点的Z分量对于误差较为敏感,以致交会结果产生较大偏差。此时,可以适当利用小航高像片信息,有效降低Z分量对误差的敏感程度,进而实现更高的交会精度。
3.3 对粗差的剔除效果分析为系统分析本文算法的特性,需研究该方法对于粗差的剔除能力。经验证,当粗差分别存在于像点坐标或外方位元素中时,本文算法对于粗差的探测能力具有一些通性,此部分仅以粗差存在像点坐标中予以说明。同时,考虑到粗差出现的概率低且文中各组像片的数目较少,因此文中仅考虑每组像片数据中仅有一个粗差的情况。
首先,分别在小航高、大航高像片组合中第1张像片的横坐标上加入不同大小的粗差,同时使像点坐标误差逐渐增加,可绘制不同粗差的剔除率随着像点坐标误差变化的曲线,如图 8、图 9所示。

|
| 图 8 小航高像片粗差剔除率随像点坐标误差的变化曲线 Fig. 8 Gross error elimination of images at small height with noises in image coordinates |

|
| 图 9 大航高像片粗差剔除率随像点坐标误差的变化曲线 Fig. 9 Gross error elimination of images at large height with noises in image coordinates |
由图 8—图 9可以看出,同等粗差情况下,粗差剔除率随着像点坐标误差的增大而逐渐减小,即噪声越小,更容易发现粗差。在同等像点坐标误差水平时,大粗差更容易被剔除。小航高的像片在具有小于17个像素像点坐标误差时,可以完全剔除大于1 mm的粗差。在像点坐标误差小于100个像素时,小航高的像片可以不小于98%的概率剔除大于4 mm的粗差。大航高的像片在含有0.1个像素的像点坐标误差时,可以以95%的概率剔除1像素的粗差,在像点坐标0.5个像素以内的误差时,可以99%的概率剔除6个像素的粗差。
为了分析混合航高像片组合的粗差剔除能力,本文在混合航高像片组合中的低航高与高航高像片上分别加以同等大小粗差,并绘制粗差剔除率随着噪声的变化曲线,如图 10(a)—图 10(b)所示。

|
| 图 10 混合航高像片粗差剔除率随像点坐标误差的变化曲线 Fig. 10 Gross error elimination of images at mixed height with noises in image coordinates |
对比图 10(a)、图 10(b)可以看出,在混合航高像片组合中,当像点坐标误差为5个像素时,可以98%的概率剔除大航高像片上包含的0.1 mm的粗差;当像点坐标误差为15个像素时,可以接近100%的概率剔除大航高像片上包含的0.4 mm以上的粗差。而在同等像点坐标误差水平条件下,包含在小航高像片中的同等大小的粗差则难以被剔除。即混合航高像片组合对于大航高像片上的粗差更敏感,同等误差水平条件下,出现在大航高像片上的粗差更容易被发现。这是因为在同等大小粗差存在时,大航高像片上的粗差会引起它所决定的同名射线产生较大偏差,因此在选权迭代过程中会被赋予较小的权重。若小航高像片上的粗差继续增大超过一定数值时,即由它决定的同名射线发生更大偏差时,可使其很快被剔除。
4 结语参考传统立体像对的空间前方交会原理,根据“目标点到同名射线距离的加权平方和最小”这一原则建立目标函数,实现多像空间前方交会,可得出如下结论:
(1) 根据总体最小二乘方法建立目标函数,对待求参数求一阶和二阶导数,当至少存在两条不平行的同名光线时,即可利用本文方法进行空间前方交会来确定地面点坐标。
(2) 采用选权迭代的方法,可以有效剔除观测数据中包含的粗差,规避粗差对于解算结果的干扰,同时为精度较高的观测数据赋予更高的权重,更利于得到精确的交会结果。
(3) 相对于立体像对,多张像片的空间前方交会能利用更多的观测信息,提高观测数据的利用率,可有效降低物点估计值Z分量对于大航高像片所含误差的敏感性,使估计结果具有更好的稳健性,一定程度上丰富了摄影测量理论。
| [1] | 冯其强, 李广云, 李宗春. 数字工业摄影测量技术及应用[M]. 北京: 测绘出版社, 2013. FENG Qiqiang, LI Guangyun, LI Zongchun. Digital Industrial Photogrammetry Technology and Applications[M]. Beijing: Surveying and Mapping Press, 2013. |
| [2] | 张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2009. ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry[M]. Wuhan: Wuhan University Press, 2009. |
| [3] | 王佩军, 徐亚明. 摄影测量学[M]. 武汉: 武汉大学出版社, 2005. WANG Peijun, XU Yaming. Photogrammetry[M]. Wuhan: Wuhan University Press, 2005. |
| [4] | 郑顺义, 郭宝云, 李彩林. 基于模型和广义点摄影测量的圆柱体自动三维重建与检测[J]. 测绘学报, 2011, 40(4): 477–482. ZHENG Shunyi, GUO Baoyun, LI Cailin. 3D Reconstruction and Inspection of Cylinder Based on Geometric Model and Generalized Point Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 477–482. |
| [5] | 张春森, 张卫龙, 郭丙轩, 等. 倾斜影像的三维纹理快速重建[J]. 测绘学报, 2015, 44(7): 782–790. ZHANG Chunsen, ZHANG Weilong, GUO Bingxuan, et al. Rapidly 3D Texture Reconstruction Based on Oblique Photography[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 782–790. DOI:10.11947/j.AGCS.2015.20140341 |
| [6] | 盛庆红, 肖晖. 卫星遥感与摄影测量[M]. 北京: 科学出版社, 2015. SHENG Qinghong, XIAO Hui. Satellite Remote Sensing and Photogrammetry[M]. Beijing: Science Press, 2015. |
| [7] | 曾凡洋, 钟若飞, 宋杨, 等. 车载全景影像核线匹配和空间前方交会[J]. 遥感学报, 2014, 18(6): 1230–1236. ZENG Fanyang, ZHONG Ruofei, SONG Yang, et al. Vehicle Panoramic Image Matching Based on Epipolar Geometry and Space Forward Intersection[J]. Journal of Remote Sensing, 2014, 18(6): 1230–1236. |
| [8] | 张祖勋, 郭大海, 柯涛, 等. 抗震救灾中航空摄影测量的应急响应[J]. 遥感学报, 2008, 12(6): 852–857. ZHANG Zuxun, GUO Dahai, KE Tao, et al. The Use of Aerial Photogrammetry in the Fast Response for China Earthquake Rescue[J]. Journal of Remote Sensing, 2008, 12(6): 852–857. |
| [9] | 王任享, 胡莘, 王新义, 等. "天绘一号"卫星工程建设与应用[J]. 遥感学报, 2012, 16(S): 2–5. WANG Renxiang, HU Xin, WANG Xinyi, et al. The Construction and Application of Mapping Satellite-1 Engineering[J]. Journal of Remote Sensing, 2012, 16(S): 2–5. |
| [10] | 王任享, 胡莘, 王建荣. 天绘一号无地面控制点摄影测量[J]. 测绘学报, 2013, 42(1): 1–5. WANG Renxiang, HU Xin, WANG Jianrong. Photogrammetry of Mapping Satellite-1 without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 1–5. |
| [11] | 冯其强, 黄桂平, 李广云. 基于多片前方交会的工业摄影测量自动匹配[J]. 中国图像图形学报, 2009, 14(6): 1194–1198. FENG Qiqiang, HUANG Guiping, LI Guangyun. Auto-matching of Artificial Target Points in Industrial Photogrammetry Based on Space Intersection[J]. Journal of Image and Graphics, 2009, 14(6): 1194–1198. |
| [12] | 张晓东, 杨元喜, 胡庆武, 等. 可量测序列影像的加权整体最小二乘导航[J]. 应用科学学报, 2013, 31(2): 147–153. ZHANG Xiaodong, YANG Yuanxi, HU Qingwu, et al. Weighted Global Least Square Navigation Based on Measurable Image Sequence[J]. Journal of Applied Sciences-Electronics and Information Engineering, 2013, 31(2): 147–153. |
| [13] | 龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888–894. GONG Xunqiang, LI Zhilin. A Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 888–894. DOI:10.13485/j.cnki.11-2089.2014.0140 |
| [14] | 王彬, 李建成, 高井祥, 等. 抗差加权整体最小二乘模型的牛顿-高斯算法[J]. 测绘学报, 2015, 44(6): 602–608. WANG Bin, LI Jiancheng, GAO Jingxiang, et al. Newton-Gauss Algorithm of Robust Weighted Total Least Squares Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 602–608. DOI:10.11947/j.AGCS.2015.20130704 |
| [15] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883–893. DOI:10.1137/0717073 |
| [16] | VAN HUFFEL S, VANDEWALLE J. The Total Least Squares Problem:Computational Aspects and Analysis[M]. Philadelphia: SIAM, 1991. |
| [17] | MARKOVSKY I, VAN HUFFEL S. Overview of Total Least-squares Methods[J]. Signal Processing, 2007, 87(10): 2283–2302. DOI:10.1016/j.sigpro.2007.04.004 |
| [18] | 张贤达. 矩阵分析与应用[M]. 2版. 北京: 清华大学出版社, 2013. ZHANG Xianda. Matrix Analysis and Applications[M]. Beijing: Tsinghua University Press, 2013. |
| [19] | 胡川, 陈义, 朱卫东, 等. 整体最小二乘和最小二乘拟合空间直线的比较[J]. 大地测量与地球动力学, 2015, 35(4): 689–692. HU Chuan, CHEN Yi, ZHU Weidong, et al. Comparisons of Total Least Squares and Least Squares for Fitting Spatial Lines[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 689–692. |
| [20] | DING Ye, ZHU Limin, DING Han. Semidefinite Programming for Chebyshev Fitting of Spatial Straight Line with Applications to Cutter Location Planning and Tolerance Evaluation[J]. Precision Engineering, 2007, 31(4): 364–368. DOI:10.1016/j.precisioneng.2007.04.001 |
| [21] | 潘国荣, 唐杭. 特征分解与选权迭代在空间直线拟合中的应用[J]. 东南大学学报(自然科学版), 2013, 43(S2): 250–255. PAN Guorong, TANG Hang. Application of Eigen Decomposition and Selecting Weight Iteration in Spatial Line Fitting[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(S2): 250–255. |
| [22] | 姚宜斌, 刘经南, 施闯. 相关稳健估计及其在测量数据处理中的应用[J]. 测绘信息与工程, 2001, 2001(3): 5–8. YAO Yibin, LIU Jingnan, SHI Chuang. Dependent Robust Estimation and Its Applications in Survey Data Processing[J]. Journal of Geomatics, 2001, 2001(3): 5–8. |
| [23] | 杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. 测绘学报, 2002, 31(2): 95–99. YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95–99. |
| [24] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2012. LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2012. |
| [25] | 王新洲, 陶本藻, 邱卫宁, 等. 高等测量平差[M]. 北京: 测绘出版社, 2013. WANG Xinzhou, TAO Benzao, QIU Weining, et al. Advanced Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 2013. |
| [26] | 费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社, 2015. FEI Yetai. Errors Theory and Data Processing[M]. Beijing: China Machine Press, 2015. |
| [27] | 周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115–120. ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115–120. |
| [28] | 袁修孝, 曹金山. 高分辨率卫星遥感精确对地目标定位理论与方法[M]. 北京: 科学出版社, 2012. YUAN Xiuxiao, CAO Jinshan. Theories and Methods of Precise Object Positioning for High Resolution Satellite Imagery[M]. Beijing: Science Press, 2012. |



