2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 解放军 95899 部队, 北京 100085
2. State Key Laboratory of Information Engineering in Surveying Mapping and Remote Sensing, Wuhan 430079, China;
3. 95899 Troops, People's Liberation Army, Beijing 100085, China
线阵CCD航空相机根据扫描方式的不同可以分为推扫式成像和摆扫式成像[1]。目前,对于推扫式成像方式的理论、方法和应用的研究较多,业已形成一套较为成熟的处理方法和流程,而对于摆扫式成像方式的研究则相对较少[2-3]。近年来,随着“高分辨率、大视场”技术指标的提出[4],通过摆扫式成像获取地面宽覆盖区域影像的这种方式逐渐引起研究人员的关注。几何校正是线阵影像应用必需的处理环节[5],与面阵框幅式成像方式不同,线阵CCD传感器是行中心投影,原始影像上每一行对应不同的外方位元素,导致线阵影像几何校正比面阵影像更复杂。线阵影像基于严格模型间接法几何校正的关键是坐标反投影计算,即根据物方坐标计算其对应的像方坐标。在这个过程中,首先需要确定物方点的最佳曝光时刻,即确定成像时刻对应的最佳扫描行,进而根据最佳扫描行对应的外方位元素计算物方点对应的像方坐标。现有的最佳扫描行搜索算法主要可分为基于像方的方法和基于物方的方法。传统的基于像方的方法是在影像上进行顺序或迭代搜索[6-10],其效率较为低下,且受到扫描行数量的影响,扫描行数越多,所需的时间越长。文献[11-12]提出了一种基于物方的最佳扫描行搜索方法,文献[13]对其进行了改进。基于物方的方法利用线阵CCD与其投影中心构建扫描行中心投影面,通过估算物点与任意扫描行中心投影面之间的扫描行数目,定位与物点最邻近的扫描行中心投影面。这种方法利用简单的几何计算即可快速搜索最佳扫描行,但其只适用于线阵推扫式影像。当相机为摆扫式成像时,构建的扫描行中心投影面之间不满足近似平行的关系,此时物点到起始扫描行中心投影面的距离并不能作为其位于哪一个投影面的判断依据,导致基于物方的最佳扫描行搜索算法失效。
利用传统的基于像方的顺序搜索[7]或迭代搜索[8-9]方法进行线阵摆扫式影像坐标反投影计算,其低下的效率已成为制约大数据量快速处理的瓶颈。针对这一问题,本文在分析现有线阵影像坐标反投影计算方法的基础上,根据影像上地物间关系约束的规则,提出将校正影像中相邻地物点的最佳扫描行作为当前点最佳扫描行的先验值,利用该先验值进行最佳扫描行搜索。经试验验证了该方法的正确性与高效性,可同时用于线阵摆扫式影像和线阵推扫式影像坐标反投影计算中。
1 线阵摆扫式影像坐标反投影计算线阵摆扫式成像,即相机沿垂直飞行方向进行扫描,通过平台向前飞行,获取垂直飞行方向的地面序列条带影像。与推扫式成像相比,在地面像元分辨率和有效像元数相同的情况下,摆扫式成像系统的视场可以随着摆镜转角的增加而增大,而推扫式成像系统的视场则为固定值[4]。利用摆扫式成像方式的这一优势,目前高性能的航空侦察相机,大多是以远距离倾斜成像(long range oblique photography,LOROP)为特点的长焦距斜视相机,如Goodrich公司的DB-110相机,Raytheon公司的全球鹰相机和ROI公司的CA-295相机等[14-15]。与中、短焦推扫式相机以垂直或小角度倾斜的成像方式相比,长焦距斜视相机的优点是可以在我方上空飞行,避免在敌防空区侦察飞行而受到打击,其侦察半径和侦察效率大幅提升,弥补了垂直成像方式的不足[16]。而另一方面,长焦距、远距离、斜视摆扫的成像方式,导致了长焦距斜视相机获取的影像畸变较大,且距离相机的近端和远端的分辨率不一致,给目视判读和影像拼接造成了很大困难。因此,需要对其原始影像进行几何校正,以改正其畸变和投影变形;若以数字高程模型为基准进行校正,则可获得具备地理编码的影像。下面,首先以长焦距斜视线阵摆扫式相机为例,分析其成像原理和特点,进而论述利用二分法进行坐标反投影计算的具体步骤。
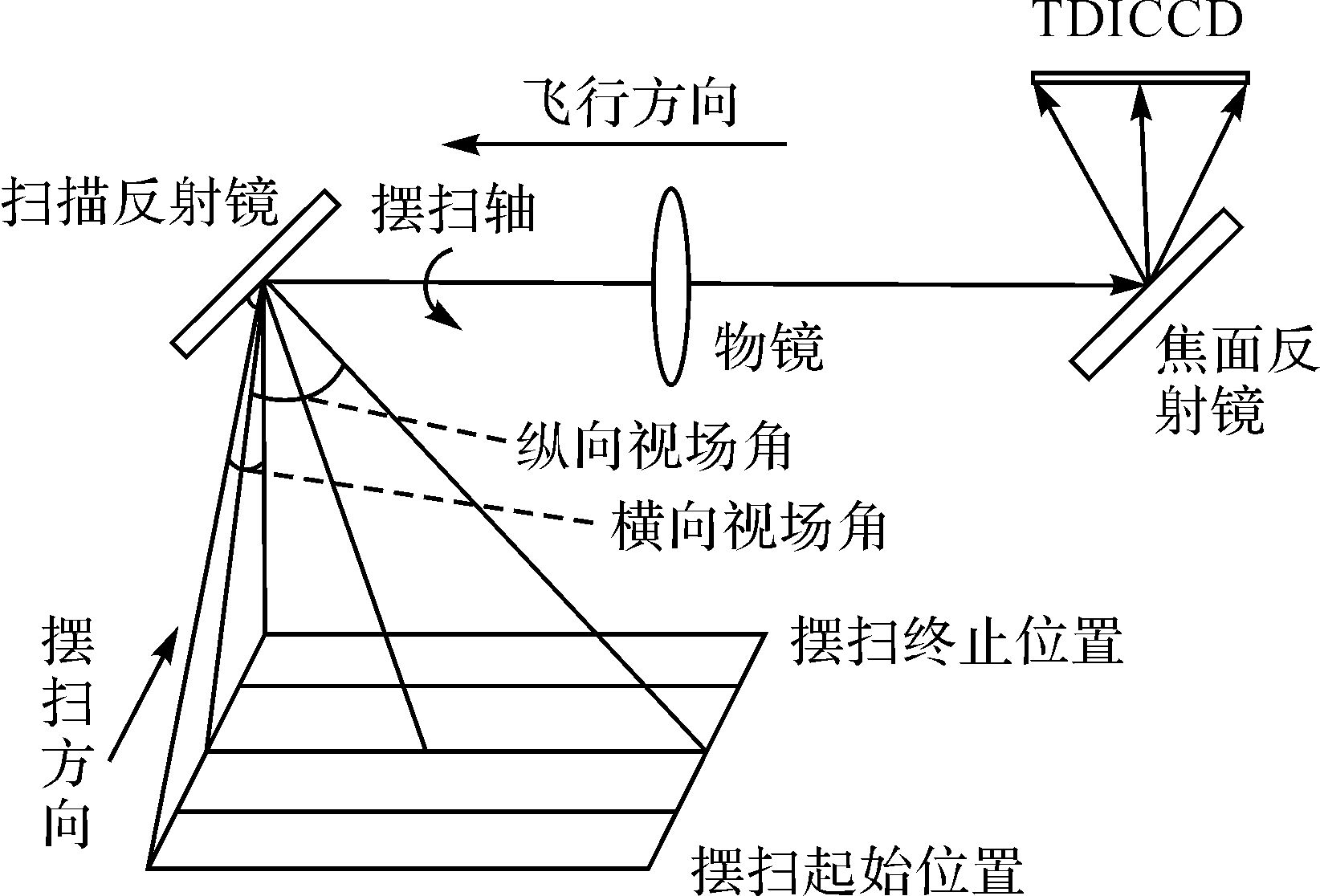
1.1 线阵摆扫式影像严格成像模型线阵摆扫式相机成像原理如图 1所示。
|
| 图 1 线阵摆扫式相机物像相对运动光路示意 Fig. 1 Illustration about whiskbroom camera object-to-image relative motion optical path |
线阵摆扫式相机的光学系统由4部分组成[16],分别为扫描反射镜、光学镜头、调焦反射镜和TDICCD。摆扫轴与飞机飞行方向平行,随着飞机的向前运动,相机的纵向(飞行方向)视场不断平移,纵向视场角内的地物信息不断更新;随着相机沿摆扫轴的转动,横向(摆扫方向)视场不断累加,横向视场角内的地物信息不断更新。纵向视场的推进与横向视场的延展,使得一次扫描获取的影像地面覆盖宽度大大增加。由于长焦线阵摆扫式相机焦距较长,无法如短焦推扫式相机一样垂直安装在飞机上,考虑到平台装机空间的限制,常采用卧式结构设计,利用扫描反射镜与调焦反射镜折转光路,将地面景物光线折转至探测器上[17]。
线阵推扫式成像方式的扫描角(相机视轴与竖直方向的夹角)的是固定的,与之不同,摆扫式成像方式的扫描角在一个扫描周期内(相机从摆扫起始位置到摆扫终止位置的过程)是连续变化的。因此,摆扫式成像方式的旋转矩阵应包括姿态角和扫描角,如式(1) 所示
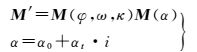 (1)
(1)
式中,M′为总体旋转矩阵;M(φ, ω, κ)、M(α)分别为姿态角和扫描角对应的旋转矩阵;α为扫描角;α0为起始摆扫角度;αt为扫描角变化率(在一次飞行任务中为固定值);i为扫描行的编号。
线阵摆扫式影像像点坐标计算公式为式(2) 所示的共线条件方程
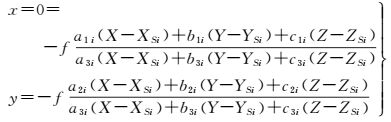 (2)
(2)
式中,(x, y)为像点的像平面坐标;f为相机焦距;XSi、YSi、ZSi为第i条扫描行对应的外方位线元素,a1i, b1i,…,c3i为旋转矩阵M′的元素;(X, Y, Z)是物方点坐标。
1.2 二分法坐标反投影计算当影像为下视推扫成像时,二分法最佳扫描行搜索[8]原理如图 2所示。AB为扫描线的两个端点,若地面点P在T时刻成像,则P点与该时刻的摄影中心S的连线与焦平面的焦点p必然位于AB上,即p与直线AB的距离dx为0。

|
| 图 2 二分法最佳扫描行搜索原理示意 Fig. 2 Illustration about searching of best imaging scan line |
与线阵推扫式成像相同,线阵摆扫式成像也是行中心投影。线阵摆扫成像的摆扫方向相当于推扫式成像的推扫方向,区别在于:推扫式影像是通过平台的向前运动进行成像,而摆扫式影像则是通过相机的摆动进行成像。因此,可将二分法用于线阵摆扫式影像最佳扫描行搜索中。将图 2中点P(X, Y, Z)往右移(右摆成像)或左移(左摆成像)即可得到线阵摆扫成像的二分法搜索原理示意图,其基本步骤为:① 若影像的扫描行数为M,设定初始窗口为[1, M],令TS(0)=1, TE(0)=M, T(0)=(TS(0)+TE(0))/2;② 分别将TS(0)、TE(0)、T(0)对应的外方位元素代入共线条件方程中计算dx,并记为dxS(0)、dxE(0)、dx(0);③ 若dxS(0)·dx(0)≤0,令TS(1)=TS(0), TE(1)=T(0);反之若dxE(0)·dx(0)≤0,则令TS(1)=T(0), TE(1)=TE(0);迭代进行搜索直至搜索窗口宽度小于一定的阈值;④ 遍历最终窗口中的扫描行,dx绝对值最小的扫描行为P点的最佳扫描行。
在上述传统的二分法最佳扫描行搜索过程中,实际上是对整景影像进行全局搜索,利用dx的正负来判断最佳扫描行位于哪个窗口内,通过不断缩小窗口定位最佳扫描行。该方法没有顾及地物之间的相邻约束关系,未能充分利用这一先验知识,导致每个物方点坐标反投影都需要经过多次共线方程迭代计算,使得其效率较为低下。因此,本文提出将这种相对不变的地物关系约束作为先验知识,引导最佳扫描行的搜索。通过快速定位当前点的初始最佳扫描行,将二分法的全局搜索转化为在小范围内的邻近搜索,从而减少共线方程的迭代计算次数,大大提高算法的效率。
2 利用地物关系约束的最佳扫描行搜索方法 2.1 算法原理由于平台运动、振动等原因,导致相机光轴指向发生偏移,表现在原始影像上就是影像的扭曲和变形。但地物相邻两点之间成像时间差较小,飞机的姿态变化不大,使得两个点的成像位置相距不会太远。此时地物间的关系是相对不变的,与推扫或摆扫的成像方式无关,投影到像方平面上其相对关系也是固定的。然而,由于飞机速度、姿态变化,地面非平坦等原因,在较大范围内,dx只能作为一个定性判断指标,无法作为一个定量判断指标。而在确定了当前物方相邻点的最佳扫描行后,由于这两个点之间曝光时刻相距极近(或同一时刻曝光),可以认为飞机速度、姿态是相对平稳的。此时,dx可以作为一个定量估算指标,即可以根据dx来估算当前点的最佳扫描行与相邻点的最佳扫描行之间的扫描行数目,快速定位最佳扫描行的初始位置。在确定了当前点的最佳扫描行的初始位置后,通过构建以其为中心的搜索窗口,利用像点坐标值理论上应与成像CCD探元的焦平面坐标一致这一最佳扫描行判断准则,进行最佳扫描行的精确搜索。
2.2 算法流程当采用间接法进行逐点几何校正时,利用地物关系约束的坐标反投影计算主要可分为3个阶段:地物关系约束界定、定位最佳扫描行初始位置和最佳扫描行精确搜索,如图 3所示。

|
| 图 3 基于地物关系约束的坐标反投影计算算法流程 Fig. 3 Flow chart of coordinate back projection algorithm based on object relation constraint |
2.2.1 地物关系约束界定
间接法几何校正时,在求得校正影像的大小后,通常是对校正影像逐行或逐列进行坐标反投影计算。本文以逐行校正为例进行论述,逐列校正的情形与此类似。
要利用地物关系约束来引导最佳扫描行的搜索,首先要对这种关系约束进行界定。因校正影像表达的是地物间正确的几何关系,其行列方向与原始影像的行列方向可能不一致,如原始影像是沿东西方向进行摆扫或推扫,而校正影像是按南北方向记录(即原始影像的行方向为南北方向,校正影像的行方向为东西方向)。这种情况下,校正影像的某一行的终点与其下一行的起始点之间在原始影像上相距较远,此时无法将dx作为一个定量估算指标。因此,若当前点为某行起始点,将其前一行的起始点作为相邻点;若当前点不为某行起始点时,将当前行的前一点作为相邻点。在进行这样的地物关系约束界定后,能保证当前点与相邻点在物方几何关系上是正确的,因而他们在原始影像上相距不远。校正影像的起始行起始点因无先验值,故利用二分法进行最佳扫描行搜索。在得到了起始行起始点的最佳扫描行后,其余各点均可利用相邻点的最佳扫描行作为先验值。
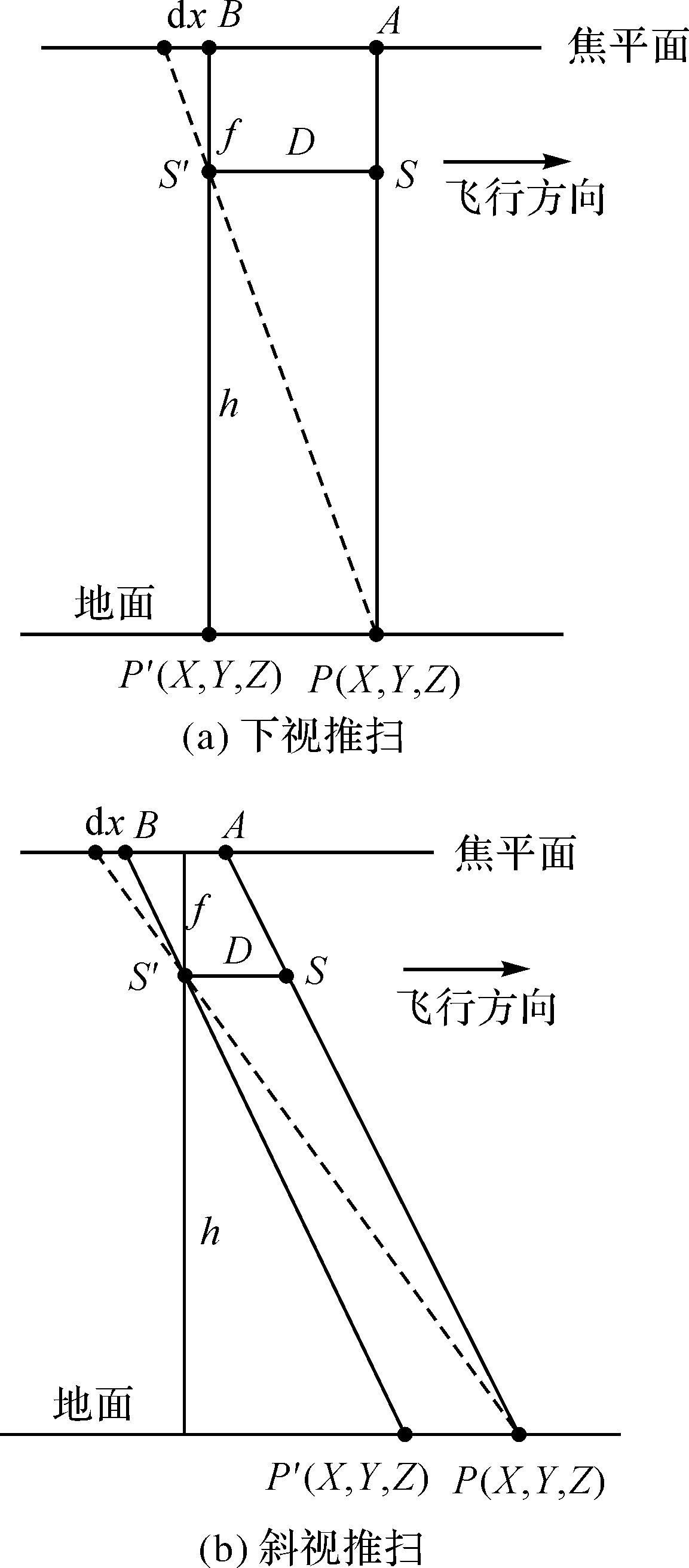
2.2.2 定位最佳扫描行初始位置下面首先分析线阵推扫式成像的情形,再扩展到线阵摆扫式成像的情形。如图 4(a)所示,在下视推扫式成像时,假设P点对应的最佳扫描行的摄影中心为S,其在焦平面上的位置为A;与P点相邻一点P′的最佳扫描行的摄影中心为S′,其在焦平面上的位置为B。
|
| 图 4 推扫式成像时定位最佳扫描行初始位置原理 Fig. 4 Schematic of positioning initial best scan line of pushbroom image |
要估算A与B之间的扫描行数目,可通过S与S′之间的距离D来进行。S与S′之间的距离D可根据P点以S′为中心的反投影坐标dx进行计算,如式(3) 所示
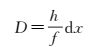 (3)
(3)
式中, h为飞机的相对航高;f为相机的焦距。
若相邻两个扫描行之间摄影中心的平均距离为d,则A与B之间的扫描行数目n如式(4) 所示
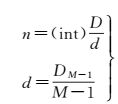 (4)
(4)
式中,DM-1表示原始影像首末扫描行对应的摄影中心之间的距离, M为原始影像上扫描行的数目。
若相邻点的最佳扫描行为N,则当前点的最佳扫描行初始位置N′为
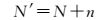 (5)
(5)
斜视(前视或后视)推扫时的情形如图 4(b)所示,其计算方法与下视推扫时相同。
相机为线阵摆扫式成像时的情形如图 5所示。假设飞机垂直向内飞行,相机沿垂直飞行方向向右摆扫,不同的扫描行对应的扫描角度各不相同,在一个成像周期内其扫描角是连续变化的[14]。线阵摆扫式成像相机通常都安装有稳像装置[18-21],使得相机的姿态在较短时间内保持相对平稳,因此,可将一定范围内的线阵扫描成像看成是类似面阵成像的形式。
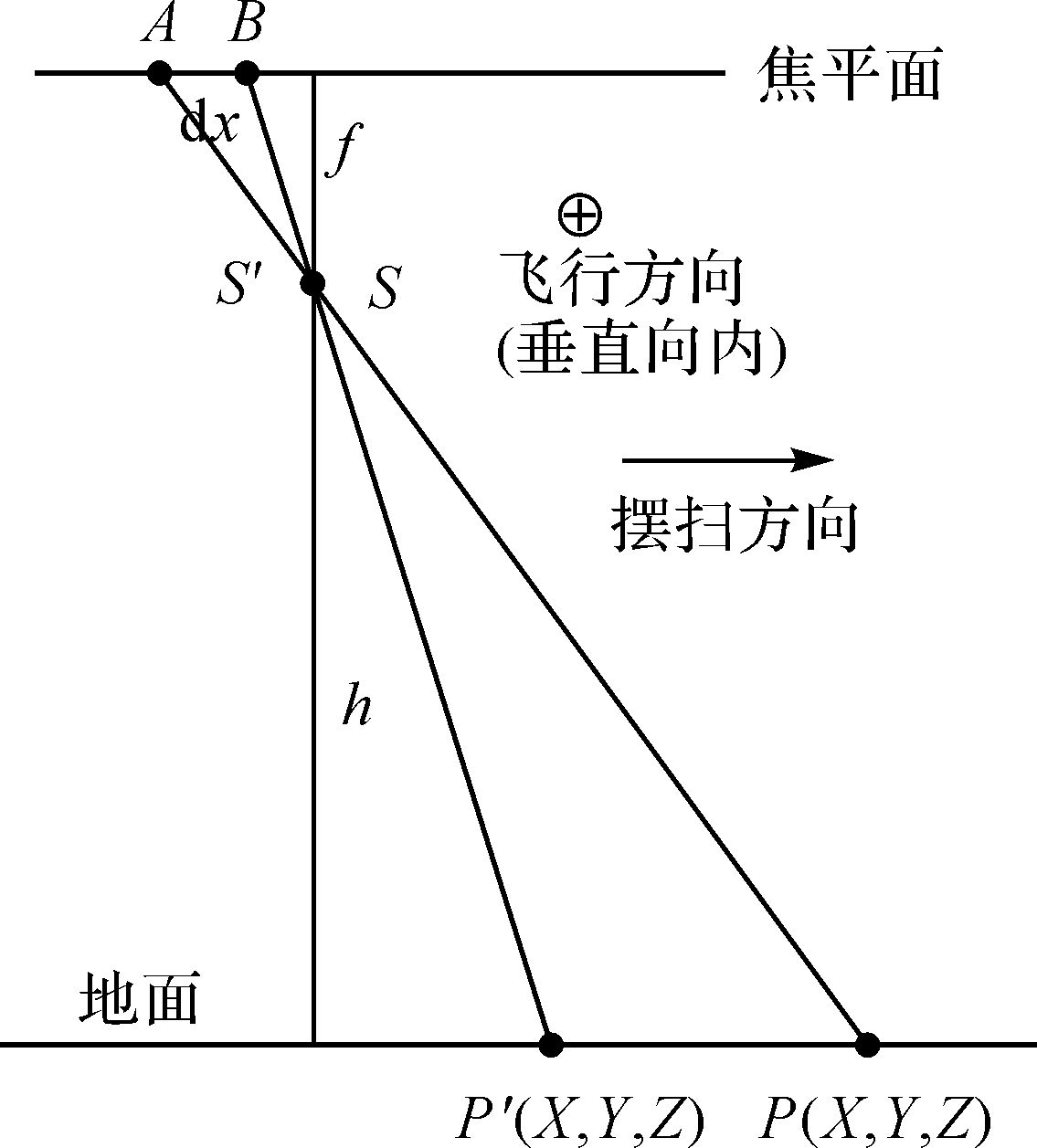
|
| 图 5 侧视摆扫时定位最佳扫描行初始位置原理 Fig. 5 Schematic of positioning initial best scan line of whiskbroom image |
如图 5所示, P点的前一点P′对应的扫描行位于焦平面的B处,以B点为主点,构建一个小面阵,将P点坐标和焦平面上B点对应的外方位元素代入共线条件方程(如式(2) 所示)中,得到P点在焦平面上的位置A, A点与主点B的距离为dx,则A点对应的扫描行即为P点的最佳扫描行初始位置。此时A与B之间的扫描行数目n如式(6) 所示
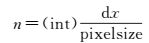 (6)
(6)
式中,pixelsize为CCD在扫描方向的像元尺寸大小。
2.2.3 最佳扫描行精确搜索由于平台向前飞行、姿态变化、地面高度变化等原因,上述计算得到的最佳扫描行初始位置并不一定是当前点实际的最佳扫描行,需要进行进一步的判断。由于已经定位了最佳扫描行的初始位置,因此可以构建一个小窗口,利用dx=0这一判断准则来搜索最佳扫描行。其具体步骤如下:① 以最佳扫描行初始位置为中心,构建一个宽度为L的窗口,窗口的起始行为TS=N′-L,结束行为TE=N′+L;② 分别利用TS、TE计算dxS和dxE;③ 若dxS·dxE>0,说明最佳扫描行不在搜索窗口内,则加大窗口宽度L,重新计算dxS和dxE,直至dxS·dxE≤0;此时,最佳扫描行位于搜索窗口内,且必然位于窗口的两端或两端往窗口内侧的一行,即此时的TS、TE或TS+1、TE-1四者中的其中一行;④ 比较上述4个扫描行对应的dx绝对值大小,绝对值最小的扫描行则为当前点的最佳扫描行N,利用dx计算出最佳扫描行的子像素精确值N=N-dx/pixelsize。
2.3 算法实现利用地物关系约束的线阵影像坐标反投影计算的具体步骤如下:
(1) 对起始行起始点执行二分法搜索最佳扫描行,并记录该点的最佳扫描行,进入步骤(7);
(2) 判断当前点是否为某一非起始行的起始点;若是,则将前一行的起始点作为相邻点,进入步骤(3),若否,则将当前行的前一个点作为相邻点,进入步骤(3);
(3) 将相邻点的最佳扫描行作为当前点最佳扫描行的先验值,进入步骤(4);
(4) 根据当前点的物方坐标以及最佳扫描行先验值,按式(4)(推扫式成像时)或式(6)(摆扫式成像时)计算扫描行增量值,确定最佳扫描行初始位置,进入步骤(5);
(5) 根据最佳扫描行初始位置,设置窗口宽度L=1,判断最佳扫描行是否在搜索窗口内,若是,则进入步骤(6);若否,则加大窗口宽度,设置步进值为1,直至搜索窗口包含最佳扫描线,进入步骤(6);
(6) 比较窗口两端的dx绝对值大小,进行最佳扫描行精确搜索,进入步骤(7);
(7) 根据最佳扫描行,进行物方坐标反投影计算。
3 试验结果与分析为验证本文算法的有效性和适用性,利用线阵摆扫式模拟影像数据(数据1) 和ADS40影像数据(数据2) 进行试验。试验环境为Microsoft Win7 64位操作系统,CPU为Inter(R) Core(TM) 1.70 GHz,内存容量为8 GB,程序在VC++开发环境下编写实现。
3.1 试验数据数据1为利用ISPRS-Commission Ⅲ提供的Vaihingen地区正射影像和对应的数字表面模型所生成的模拟影像,正射影像和数字表面模型的大小均为20 250×21 300,分辨率均为0.09 m。根据某线阵摆扫式相机的成像模型,利用共线条件方程由像点坐标计算物点坐标的公式,将正射影像上物点坐标处的内插灰度值赋予像点坐标处,生成线阵摆扫式模拟影像,影像的列数为12 000,行数为20 250。分别设置飞行高度为6000、8000和10 000 m,起始摆扫角度设置为60°,从左向右摆扫,生成3景不同飞行高度的模拟影像。设置模拟相机的焦距为1600 mm,其CCD大小为9 μm,当飞行高度为8000 m时,模拟影像起始摆扫位置的分辨率为0.09 m。设置飞行方向为正北方向匀速飞行,利用飞机实际飞行过程中连续记录的相机摆扫成像时的30组姿态数据(图 6),利用拉格朗日二阶内插得到每一扫描行对应的姿态数据。图 7(a)和(b)所示分别为正射影像R波段影像和飞行高度为8000 m时生成的模拟影像局部区域。由图 7(b)可见,模拟影像上具备明显的大倾角斜视成像特点,影像畸变较大。
|
| 图 6 模拟影像姿态变化 Fig. 6 Orientation change of the simulated image |

|
| 图 7 试验区域正射影像和生成的模拟影像局部区域 Fig. 7 Experimental local area of the ortho-image and simulated image |
数据2为ADS40影像数据,2009年8月12日于河南省登封市拍摄,其航高为3200 m,试验中使用ADS40相机前视和后视全色波段以及下视红色波段的3景影像,其信息如表 1所示。
| 影像 | 传感器 | 通道 | 影像大小 (行×列) |
数据量/ MB |
| ADS40前视 | PANF28A | 全色 | 45 984×12 000 | 526 |
| ADS40下视 | REDN00A | 红色 | 42 016×12 000 | 480 |
| ADS40后视 | PANB14A | 全色 | 43 024×12 000 | 492 |
图 8所示分别为ADS40下视传感器原始影像及采用二分法和本文方法将其纠正到平均高程面后的影像局部区域。从图 8(a)中可见,ADS40原始影像存在较大程度的扭曲和变形,如图中的公路扭曲变形明显;将其进行纠正后可以改正这种扭曲和变形畸变,得到几何关系正确的影像。

|
| 图 8 ADS40原始影像及校正影像局部区域 Fig. 8 Local area of the ADS40 original image and correction image |
3.2 试验结果分析
在数据1的模拟影像和数据2的原始影像中间选取格网分布的100万个像点,给定地面平均高程,利用共线条件方程计算出对应的模拟地面点。将这些地面点按其平面坐标及校正影像分辨率进行分行排列(每行的地面点个数可能不一致),坐标反投影计算时逐行进行。分别利用二分法和本文方法对这些模拟地面点进行坐标反投影计算,得到对应的像点坐标,并与原始像点坐标进行对比,统计坐标反投影计算的最大误差和中误差,得到的结果如表 2和表 3所示。
| 飞行高度/m | 二分法 | 本文方法 | ||||||
| 计算时间/ms | 最大误差/像素 | 中误差/像素 | 计算时间/ms | 最大误差/像素 | 中误差/像素 | 加速比 | ||
| 6000 | 665 | 0.001 412 | 0.000 877 | 220 | 0.000 942 | 0.000 457 | 3.02 | |
| 8000 | 683 | 0.001 432 | 0.000 901 | 227 | 0.000 478 | 0.000 466 | 3.01 | |
| 10 000 | 678 | 0.000 558 | 0.000 349 | 223 | 0.000 372 | 0.000 184 | 3.04 | |
| 影像 | 二分法 | 本文方法 | ||||||
| 计算时间/ms | 最大误差/像素 | 中误差/像素 | 计算时间/ms | 最大误差/像素 | 中误差/像素 | 加速比 | ||
| 前视 | 584 | 0.003 075 | 0.000 558 | 175 | 0.003 010 | 0.000 326 | 3.35 | |
| 下视 | 569 | 0.001 682 | 0.000 403 | 172 | 0.001 682 | 0.000 252 | 3.31 | |
| 后视 | 572 | 0.001 804 | 0.000 410 | 173 | 0.001 800 | 0.000 250 | 3.31 | |
为了验证算法的高效性,分别利用二分法和本文方法对数据一的模拟影像和数据二的原始影像进行逐点几何校正,统计所需的时间,结果如表 4所示。由于一景线阵影像的数据量较大,为了进一步提高效率,采用多线程并行处理的方法进行几何纠正。表 4中T1为二分法逐点几何校正所需时间,T2为本文方法逐点几何校正所需时间,T3为本文方法采用多线程并行处理所需时间,试验中并行线程数设置为4。
| 影像 | 二分法 | 本文方法 | ||||
| 计算时间 T1/ms |
计算时间 T2/ms |
计算时间 T3/ms |
加速比 T1/T2 |
加速比 T1/T3 | ||
| 6000 | 306 025 | 95 928 | 42 837 | 3.19 | 7.14 | |
| 8000 | 302 791 | 97 158 | 43 195 | 3.12 | 7.01 | |
| 10000 | 298 520 | 97 877 | 42 529 | 3.05 | 7.02 | |
| 前视 | 361 313 | 103 191 | 45 446 | 3.50 | 7.95 | |
| 下视 | 323 695 | 105 676 | 45 306 | 3.06 | 7.14 | |
| 后视 | 327 178 | 104 587 | 45 649 | 3.13 | 7.17 | |
分析以上试验结果,可以得出以下几点结论:
(1) 二分法和本文方法均可用在线阵摆扫式影像几何校正中,得到消除了几何畸变的影像。从表 2和表 3可以看出,在坐标反投影计算精度方面,本文方法与二分法结果精度相当,处于同一个数量级,均小于0.01像素,完全满足实际使用时的需要。分析本文的算法原理,所使用的最佳扫描行判断准则与二分法其实是相同的,从这个意义上讲,本文方法也属于基于像方的方法。在表 2中,3种不同高度的模拟影像其分辨率各不相同,其结果精度基本一致,说明坐标反投影计算的精度与影像分辨率无关;在表 3中,线阵推扫式成像的前视、下视、和后视影像的结果精度基本一致,说明坐标反投影计算的精度与推扫式成像的成像角度无关。
(2) 在效率方面,本文方法与二分法相比具有较大优势,加速比在3倍以上。基于像方的坐标反投影计算过程,其运算量主要集中于共线条件方程的迭代计算上。二分法对整个影像进行折半窗口搜索,对于4万多行的影像,每个点需要14~18次迭代计算,耗时较长;而本文方法利用地物的相邻关系约束作为先验知识,将二分法对整张影像的全局搜索转化为小范围的邻近精确搜索,采用相邻点的最佳扫描行作为先验值,能快速定位当前点最佳扫描行的初始位置,省去了二分法进行迭代的繁琐过程。在整个计算过程中,仅需对起始行起始点进行一次二分法最佳扫描行搜索,其余各点均可根据地物关系约束界定规则获取其相邻点,进行4~6次共线条件方程计算便可定位到最佳扫描行,因此效率大大提高。
(3) 从表 4可看出,本文算法进行并行处理后其效率能进一步提高,与二分法单核处理相比达到7倍的加速。对一景500兆数据量的影像,其运算时间不到一分钟。本文还对ADS40下视推扫的7张影像进行了逐点几何纠正试验,总共数据量为2.84 GB,在单机4核并行环境下仅需7 min即可完成。因此,对于大数据量线阵影像几何纠正问题,本文算法具备一定的实际应用价值。若要进一步提升效率,可在纠正影像上设一格网(例如31×31像素),然后利用本文算法计算出每个格网点的反投影坐标,对于格网内的每个点,其反投影坐标则通过双线性内插获得。但这种方法是不严密的,当格网间的点所对应的姿态发生跳变时,因其姿态变化是非线性的,双线性内插出来的结果可能与其实际的位置有一定的误差,然而这样的误差一般在可接受的范围内。
4 结束语本文在分析线阵摆扫式影像的成像特点及现有线阵影像坐标反投影算法的基础上,根据影像上地物关系与实际地物相一致的特点,提出一种利用地物关系约束的线阵影像坐标反投影计算方法。根据地物关系的先验性,将校正影像上相邻点的最佳扫描行作为当前点最佳扫描行的先验值,通过估算与先验值之间的扫描行数目,定位最佳扫描线的初始位置,然后进行最佳扫描行的精确搜索。试验结果表明,提出的方法能快速有效地进行最佳扫描行的搜索,解决了传统二分法窗口迭代搜索方法效率较低、耗时较长的问题,可用于线阵影像几何校正过程中。此外,该方法不受扫描行数增加的影响,也与成像方式无关,可同时用于线阵摆扫式影像和线阵推扫式影像几何校正中,因此具有较好的适用性。线阵摆扫式成像方式具有宽视场、高效率、灵活机动等优点,逐渐被应用于航空侦察、敏捷卫星机动成像等场合中。从这个方面看,本文的研究具有较为重要的现实意义。进一步的研究包括针对线阵摆扫式成像的物像几何关系特点,如何将基于物方几何约束的方法应用于线阵摆扫式影像几何校正中,以进一步提高其效率。
| [1] | 范秀英, 鲍金河, 张勇. 摆扫式TDI-CCD航空相机传感器MTF分析[J]. 光学技术, 2012, 38(5): 634–637. FAN Xiuying, BAO Jinhe, ZHANG Yong. Analysis on Image Sensor MTF of Whiskbroom Scan TDI-CCD Aerial Camera[J]. Optical Technique, 2012, 38(5): 634–637. |
| [2] | 张艳, 王涛, 徐青, 等. 无人机载线阵摆扫CCD影像几何校正[J]. 测绘科学技术学报, 2006, 23(3): 168–170. ZHANG Yan, WANG Tao, XU Qing, et al. Rectification for Linear Whiskbroom CCD Imagery Acquired on Pilotless Aircraft[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(3): 168–170. |
| [3] | 王俊华, 庞怡杰, 王晶, 等. CCD相机中高空摆扫航摄数字图像的系统校正[J]. 地球信息科学, 2007, 9(5): 105–109. WANG Junhua, PANG Yijie, WANG Jing, et al. The System Correction of Digital Image by CCD Camera of Whisk Broom Model in Middle-High Space[J]. Geo-Information Science, 2007, 9(5): 105–109. |
| [4] | 苗壮, 何斌, 王俊琦, 等. 空间相机摆扫成像建模及摆镜角速度残差分析[J]. 航天返回与遥感, 2015, 36(6): 39–47. MIAO Zhuang, HE Bin, WANG Junqi, et al. Modeling of Space Camera for Whiskbroom Imaging and Analysis of Pendulum Mirror Angular Velocity Residual[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(6): 39–47. |
| [5] | CRAMER M. The ADS40 Vaihingen/Enz Geometric Performance Test[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(6): 363–374. DOI:10.1016/j.isprsjprs.2006.05.004 |
| [6] | 赵双明, 李德仁. ADS40机载数字传感器平差数学模型及其试验[J]. 测绘学报, 2006, 35(4): 342–346. ZHAO Shuangming, LI Deren. Experimentation of Adjustment Math Model for ADS40 Sensor[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 342–346. DOI:10.3321/j.issn:1001-1595.2006.04.009 |
| [7] | 赵双明, 李德仁. ADS40影像几何预处理[J]. 武汉大学学报(信息科学版), 2006, 31(4): 308–311. ZHAO Shuangming, LI Deren. Geometric Pre-Process of ADS40 Image[J]. Geomatics and Information Science of Wuhan University, 2006, 31(4): 308–311. |
| [8] | 刘军, 王冬红. 基于Level 0产品的ADS40正射影像快速生成[J]. 遥感学报, 2007, 11(2): 247–251. LIU Jun, WANG Donghong. Efficient Orthoimage Generation from ADS40 Level 0 Products[J]. Journal of Remote Sensing, 2007, 11(2): 247–251. DOI:10.11834/jrs.20070234 |
| [9] | 刘军, 张永生, 王冬红, 等. INS/DGPS支持的机载线阵推扫影像几何校正[J]. 遥感学报, 2006, 10(1): 21–26. LIU Jun, ZHANG Yongsheng, WANG Donghong, et al. Geometric Rectification of Airborne Linear Array Pushbroom Imagery Supported by INS/DGPS System[J]. Journal of Remote Sensing, 2006, 10(1): 21–26. DOI:10.11834/jrs.20060104 |
| [10] | 刘军. GPS/IMU辅助机载线阵CCD影像定位技术研究[D]. 郑州: 信息工程大学, 2007: 95-99. LIU Jun. A Study on the Positioning Theory of Airborne Line CCD Imagery Supported by GPS/IMU[D]. Zhengzhou:Information Engineering University, 2007:95-99. |
| [11] | 王密, 胡芬, 王海涛. 一种基于物方几何约束的线阵推扫式影像坐标反投影计算的快速算法[J]. 测绘学报, 2008, 37(3): 384–390. WAND Mi, HU Fen, WAND Haitao. A Fast Algorithm for Back Project Calculation of Linear Array Pushbroom Imageries Based on Object-Space Geometric Constraint[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 384–390. DOI:10.3321/j.issn:1001-1595.2008.03.020 |
| [12] | WANG Mi, HU Fen, LI Jonathan, et al. A Fast Approach to Best Scanline Search of Airborne Linear Pushbroom Images[J]. Photogrammetric Engineering and Remote Sensing, 2009, 75(9): 1059–1067. DOI:10.14358/PERS.75.9.1059 |
| [13] | 耿迅, 徐青, 邢帅, 等. 基于最佳扫描行快速搜索策略的线阵推扫式影像微分纠正算法[J]. 测绘学报, 2013, 42(6): 861–868. GENG Xun, XU Qing, XING Shuai, et al. Differential Rectification of Linear Pushbroom Imagery Based on the Fast Algorithm for Best Scan Line Searching[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 861–868. |
| [14] | 刘波, 贾继强, 丁亚林, 等. 斜视航空相机的斜距离焦补偿[J]. 光学精密工程, 2014, 22(5): 1274–1279. LIU Bo, JIA Jiqiang, DING Yalin, et al. Oblique Distance Defocus Compensation for Oblique Photographic Airborne Camera[J]. Optics and Precision Engineering, 2014, 22(5): 1274–1279. |
| [15] | LANGE D, IYENGAR M, MAVER L, et al. The Goodrich 3rd Generation DB-110 System:Successful Flight Test on the F-16 Aircraft[C]//Proceedings of SPIE 6546, Airborne Intelligence, Surveillance, Reconnaissance (ISR) Systems and Applications Ⅳ. Orlando, Florida:SPIE, 2007(6546):654607. |
| [16] | 刘志明. 长焦距斜视航空相机图像拖影与扭曲补偿技术研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2014: 13-14. LIU Zhiming. Research on Image Smear and Distortion Compensation in Long Focus Slope Aerial Camera[D]. Changchun:Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics), 2014. |
| [17] | 田海英, 刘明. 基于扫描反射镜的航空相机前向像移补偿[J]. 光电工程, 2014, 41(9): 20–24. TIAN Haiying, LIU Ming. The Forward Image Motion Compensating Scheme of Aerial Camera Based on Scanning Mirror[J]. Opto-Electronic Engineering, 2014, 41(9): 20–24. |
| [18] | 周前飞, 刘晶红, 居波, 等. 面阵CCD航空相机斜视图像的几何校正[J]. 液晶与显示, 2015, 30(3): 505–513. ZHOU Qianfei, LIU Jinghong, JU Bo, et al. Geometric Correction of Oblique Images for Array CCD Aerial Cameras[J]. Chinese Journal of Liquid Crystals and Displays, 2015, 30(3): 505–513. |
| [19] | 杨飞, 金光, 曲宏松, 等. 航天时间延迟积分CCD相机摆扫成像快速几何校正设计与分析[J]. 光学学报, 2014, 34(1): 75–81. YANG Fei, JIN Guang, QU Hongsong, et al. Design and Analysis about Rapid Geometric Correction of Space Whiskbroom Time Delayed and Integration CCD Camera[J]. Acta Optica Sinica, 2014, 34(1): 75–81. |
| [20] | PETRUSHEVSKY V, TSUR D. Condor TAC:EO/IR Tactical Aerial Reconnaissance Photography System[C]//Proceedings of SPIE 8360, Airborne Intelligence, Surveillance, Reconnaissance (ISR) Systems and Applications Ⅸ. Baltimore, Maryland:SPIE, 2012(8360):836003. |
| [21] | HE Yulan, XIAO Xiangguo, LI Yuan, et al. Optical System Design for the Aerial Camera with Dual Band, Common Optical Path, Long Focal, Oblique View and Focusing[C]//Proceedings of SPIE 9677, AOPC 2015:Optical Test, Measurement, and Equipment. Beijing, China:SPIE, 2015(9677):96771O. |
| [22] | 苗壮, 何斌. 基于摆扫反射镜的大视场成像像移模型[J]. 计算机测量与控制, 2016, 24(2): 242–246. MIAO Zhuang, HE Bin. Image Motion Model of Large Field of View Imaging Based on Swing Mirror[J]. Computer Measurement & Control, 2016, 24(2): 242–246. |
| [23] | 李福东. 航空远距离倾斜摄影相机扫描稳像及像移补偿技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. LI Fudong.Research on Scanning & Motion Compensation of Airborne Camera for Long Range Oblique Photography[D]. Harbin:Harbin Institute of Technology, 2015. |
| [24] | HAN J Y, MARCHUK S, KIM H, et al. Imaging EO/IR Optical System for Long Range Oblique Photography[C]//Proceedings of SPIE 8020, Airborne Intelligence, Surveillance, Reconnaissance (ISR) Systems and Applications Ⅷ. Orlando, Florida:SPIE, 2011, 8020:802009. |
| [25] | HENRY D J. ISR Systems:Past, Present, and Future[C]//Proceedings of SPIE 9828, Airborne Intelligence, Surveillance, Reconnaissance (ISR) Systems and Applications ⅩⅡ. Baltimore, Maryland:SPIE, 2016(9828):982802. |


