2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 武汉讯图科技有限公司, 湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping & Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Wuhan Xuntu Technology Co. Ltd., Wuhan 430079, China
伴随着低空航空摄影测量的兴起,利用低空无人机(unmanned aerial vehicle,UAV)进行航空摄影测量作业越来越方便快捷[1-2]。无人机具有灵活、操作简单方便、安全可靠、低成本、无需机场起降、对气候条件约束较小和能在阴云天气条件下进行航空摄影作业等优点[2-4]。由于无人机影像纹理信息丰富,能够快速灵活地获取到小面积区域的高分辨率数字航空影像,如小城镇、局部地区以及重大建设工程等。运用获取的这些高分辨率无人机影像,可以方便快捷地进行正射影像生成,环境测量,交通监测,城市真三维模型的重建研究和应用工作[4-6],特别是在应对灾害的应急反应领域中更加方便有效。低空航空摄影测量作为传统航空摄影测量的有益补充,在地形图测绘、资源生态环境调查、城乡规划与建设、重大工程建设、灾害应急反应领域等领域应用的越来越广[5]。目前,现有的航摄仪大多数采用多镜头集成的小型数码非量测相机[7-8],所获取影像的像幅面较小,单幅影像的地面覆盖范围有限。如果采用这种小像幅非量测相机进行拍摄作业,将会受到低空摄影平台载荷量小、飞行高度低、受气流影响大和航线保持困难,所拍摄的航摄影像相对于常规航空摄影像片旋偏角大、航线弯曲度大和由于影像倾斜度大且没有规律造成重叠度不规则等问题。这些问题将会直接影响到后续空三加密解算的精度。与传统的航空摄影测量比较,为了保证精度就需要布设更多的控制点,这样大大增加了野外布控的测量工作量。GPS辅助空中三角测量技术的出现[9-10],有效解决了低空摄影测量对地面控制点的依赖问题,可使摄影测量需要的野外作业大量减少[11]。
GPS辅助光束法平差方法是利用高精度GPS载波相位测量差分技术,通过获取摄影机曝光瞬间投影中心的三维坐标,然后将其视为附加观测值纳入区域网联台平差中,经采用统一的数学模型和算法整体确定目标点位的一种联合平差方法[12-16]。但是一般来说,GPS接收机与摄影机的操作往往相互独立,GPS信号的历元ti与摄影机曝光时刻tj之间存在时间偏移Δt,即曝光延迟[17]。一些文献中阐述时间偏移量可通过硬件设施解决,但是采用无人机进行摄影测量作业时受限于无人机体积小、载荷小和使用成本低的特点,一般而言都只配备导航型GPS,而没有搭载时间同步设备。即使搭载价格昂贵的同步设备,也仍然不能完全消除曝光延迟的影响。因此,利用缺少曝光同步装置的无人机进行航空摄影时,会导致记录的相机曝光时刻与实际相机曝光时刻之间存在一个延迟[18]。这种延迟会导致GPS记录位置与相机曝光时刻位置存在差异,而GPS辅助光束法平差所需要的正是某个曝光点瞬间航空摄影时刻相机的位置。因此,解决无人机曝光延迟问题具有一定的理论意义与实用价值。
使用无人机作业时,若保持匀速飞行,针对单航带可通过采用近似消除GPS相位中心和相机曝光中心的几何偏移的传统方法,在平差模型中添加一固定偏移参数补偿曝光延迟影响。但由于无人机受自身条件限制,作业时受气流影响较大,难以保持匀速直线飞行状态,即曝光瞬间无人机的瞬时速度与瞬时方向各不相同,实际曝光时刻GPS记录位置与记录曝光时刻GPS位置之间的位置偏移量也各不相同,即各个曝光点的误差影响不一致。针对这个问题,本文以传统的光束法平差模型为基础,构建一个适用于无人机GPS辅助光束法平差的平差模型对各个曝光点的曝光延迟误差进行补偿处理。该模型引入每一曝光瞬间的速度矢量以及曝光延迟时间Δt,构建曝光延迟模型,并以扩展模型方式在光束法平差模型中融入曝光延迟,将未知的曝光延迟作为待定参数与其他系统误差代入方程组统一求解。
总之,传统的GPS辅助光束法平差方法虽然一定程度上能够解决低空摄影测量对地面控制点的依赖问题,但是采用无人机摄影测量作业时由于无人机无法保持匀速飞行会造成曝光瞬间无人机的瞬时速度与瞬时方向各不相同,即各个曝光点的曝光延迟误差影响不一致,如果依旧采用传统方法来补偿曝光延迟误差显然是不合理的。本文从曝光延迟造成的无人机曝光未同步问题出发,阐述曝光延迟的机理,分析曝光延迟对无人机GPS辅助光束法平差的影响,并以扩展模型方式在光束法平差模型中融入曝光延迟模型,提出了一种顾及曝光延迟的无人机GPS辅助光束法平差方法,是对GPS辅助光束法平差应用范围的进一步拓展。
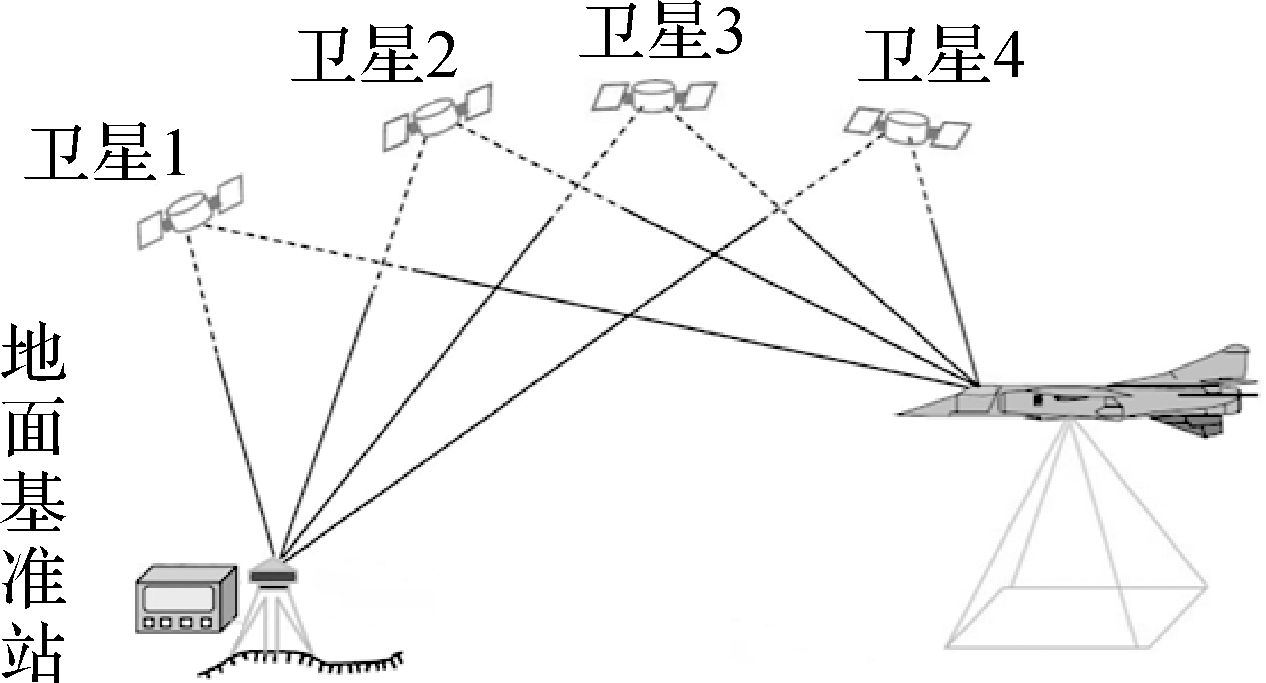
1 传统GPS辅助光束法平差基本原理 1.1 传统GPS辅助光束法区域网平差如图 1所示,GPS辅助光束法区域网平差是利用装在飞机上的一台GPS接收机和固定在某个地面参考点上的另一台或几台GPS接收机同时、快速连续地记录相同的GPS卫星信号,通过载波相位差分动态GPS相对定位技术的离线数据后处理获取摄影机曝光时刻GPS天线相位中心的三维坐标——GPS摄站坐标,然后将其视为附加观测值引入进摄影测量区域网中,采用统一的数学模型和算法,整体确定点位并对其质量进行评定的理论、技术和方法[13-19]。由于GPS辅助空中三角测量技术的应用广泛,只需要利用少量的像控点就可以进行空三平差解算,解决了传统空中三角测量需要大量地面控制点参与平差解算来保证空三精度要求的难点问题,很大程度上节省了航空摄影测量的外业工作量。
|
| 图 1 GPS辅助空中三角测量示意图 Fig. 1 GPS-supported Aerial Triangulation |
1.2 传统的GPS辅助光束法平差模型
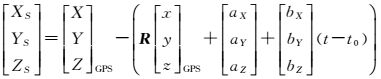
传统的GPS辅助光束法区域网平差模型为
 (1)
(1)
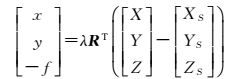 (2)
(2)
式中,[XS YS ZS]T表示实际曝光时刻投影中心的坐标;R表示影像外方位元素的3个角元素φ、w、κ所构成的正交变换矩阵

RT表示其转置矩阵;[x y -f]T表示像点在像空间坐标系下的坐标值;λ是投影系数在解算过程中会相互抵消;[X Y Z]T表示像点在像空间辅助坐标下的坐标值;[X Y Z]GPST表示相机曝光时刻记录的摄站点GPS位置;[x y z]GPST表示GPS天线相位中心在像空间坐标系下的坐标值;[aX aY aZ]T和[bX bY bZ]T分别代表GPS线性偏移系统误差改正参数中的中固定部分和随时间变化的部分;t表示该曝光点的曝光时刻;t0为参考时刻。
2 顾及曝光延迟的无人机GPS辅助光束法平差 2.1 曝光延迟机理使用无人机进行摄影测量作业时,由于相机从接收信号到曝光需要一定的反应时间导致曝光延迟,而GPS差分模块和相机接收信号的操作是相互独立的,GPS差分模块记录位置的时刻要早于相机曝光时记录位置的时刻,导致两者不同步[18, 20]。机载GPS动态定位所提供的是GPS记录观测历元动态接收天线的三维位置,而GPS辅助光束法平差所需要的是某一个曝光瞬间航空摄影的瞬间相机的位置[12-13],两种位置数据由于曝光延迟的影响存在误差。
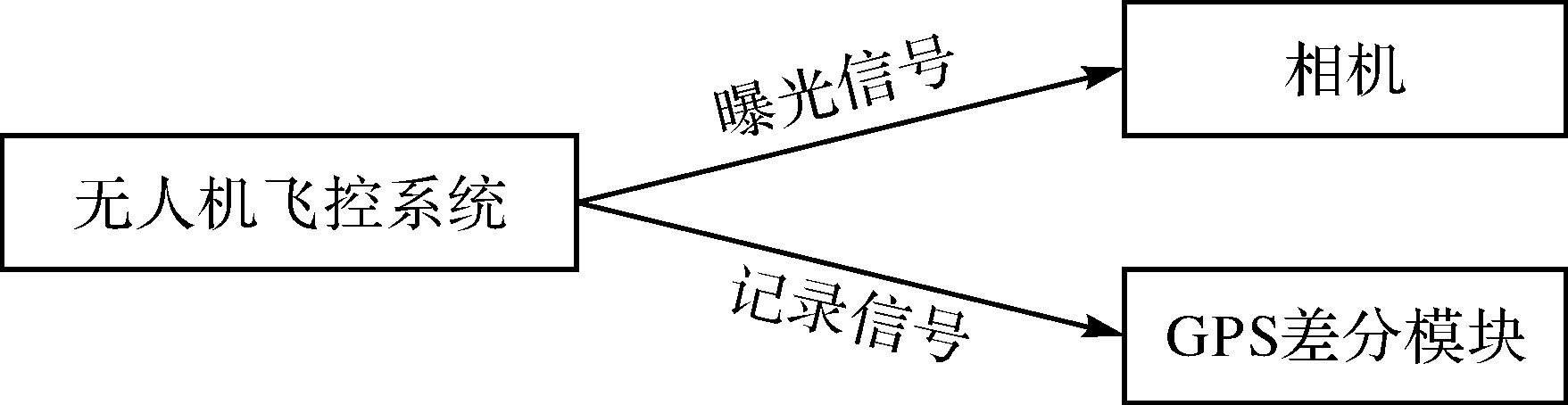
图 2所示为目前在无人机航摄领域内能够看到的比较常见的一种GPS记录方式,这种GPS记录方式无法避免会存在曝光延迟的影响。当飞控系统同时将信号发送给相机和GPS差分模块时,由于相机从接收信号到曝光需要一定的反应时间导致曝光延迟,从而造成GPS差分模块和相机接收信号两者不同步。GPS差分模块记录时的位置要早于相机曝光时位置,这样就会导致两者不同步产生较大误差,并且由于相机每次从接收信号到曝光所需时间不相同导致同步误差波动较大。针对这种曝光延迟带来的误差影响,本文考虑将曝光延迟参数引入到GPS辅助光束法平差模型中进行解算。图 3所示即为无人机作业时相机的曝光延迟误差在各航带、各个曝光点大致示意图。
|
| 图 2 GPS记录方式 Fig. 2 GPS recording mode |

|
| 图 3 相机各个曝光点的曝光延迟误差 Fig. 3 Exposure delay error for each exposure point of the camera |
无人机作业时,可依据其POS信息以及影像信息判定其飞行方向。由图 3可知,航带strip 1、strip 3、strip 5、strip 7的飞行方向朝上,航带strip 2、strip 4、strip 6飞行方向朝下。结合各个曝光点的误差影响,本文针对各个曝光点的误差影响不一致的问题,引入曝光延迟参数模型,在传统GPS光束法平差模型的基础上扩展和延伸,构建了一种更加适用于无人机GPS辅助空三的GPS辅助光束法平差平差模型。
2.2 顾及曝光延迟的无人机GPS辅助光束法平差模型传统的GPS辅助光束法平差方法解决了低空摄影测量需要大量地面控制点参与平差解算来保证空三精度要求的难点问题,很大程度上节省了航空摄影测量的外业工作量[5, 11]。针对无人机摄影测量作业时,无法保持匀速飞行的状态会造成曝光瞬间无人机的瞬时速度与瞬时方向各不相同,即各个曝光点的曝光延迟误差影响不一致的问题,如果仍然采用近似消除GPS相位中心和相机曝光中心的几何偏移的传统方法,在平差模型中添加一固定偏移参数补偿曝光延迟影响,显然是不合理的。因此,本文充分考虑到曝光瞬间各个曝光点的误差影响不一致的问题,以传统光束法平差模型为基础建立了顾及曝光延迟的GPS系统误差模型和曝光延迟模型,并且将其融入光束法平差模型中,建立了一种顾及曝光延迟的无人机GPS辅助光束法平差模型。
2.2.1 顾及曝光延迟的GPS系统误差模型由于受到相机曝光延迟的影响,导致GPS记录与航摄相机拍摄操作不同步,GPS记录操作要早于航摄相机拍摄操作。相机曝光时刻GPS记录的瞬时坐标与GPS接收到飞控系统的信号开始记录的坐标之间存在如下的关系
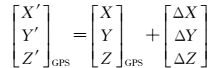 (3)
(3)
式(3) 中,[X′ Y′ Z′]GPST表示相机实际曝光时刻GPS的坐标;[X Y Z]GPST表示GPS接收到飞控系统的信号开始记录时的GPS坐标;[ΔX ΔY ΔZ]T表示记录曝光时刻与实际曝光时刻的GPS坐标间的位置偏移矢量。
由于无人机自身质量小,惯性小,在进行飞行作业过程中很容易受到气流的影响,飞行时很难保持以匀速的状态飞行。因此,在各个相机曝光时刻的位移矢量[ΔX ΔY ΔZ]T是不相同的。但是相机每次从接收信号到曝光这个过程中,其曝光延迟时间相对都比较短,可以把飞行器在曝光延迟时间内看作是匀速飞行的状态,因此式(3) 可变化为如下形式
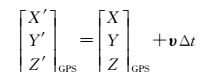 (4)
(4)
式(4) 中,[X′ Y′ Z′]GPST表示实际曝光时刻GPS坐标;[X Y Z]GPST表示记录曝光时刻GPS坐标;υ为记录曝光时刻的飞行器速度矢量,速度矢量的获取是由差分GPS软件输出连续时刻的速度矢量,然后由GPS记录的瞬时曝光时刻,通过拉格朗日多项式内插方法内插出实际曝光时刻的瞬时速度矢量;Δt为曝光延迟时间。
2.2.2 建立曝光延迟模型如图 4所示,由于摄影中心S的位置与GPS天线相位中心的位置存在如下几何关系

|
| 图 4 GPS接收机与相机的关系 Fig. 4 The relationship between GPS receiver and camera |
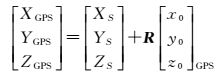 (5)
(5)
将式(5) 做一个变形可以得到如下公式
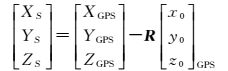 (6)
(6)
式中,[XS YS ZS]T表示真实曝光时刻摄影中心的位置;[XGPS YGPS ZGPS]T表示真实曝光时刻GPS天线相位中心的位置;[x0 y0 z0]GPST表示GPS天线相位中心在像空间坐标系下的坐标值;R和RT分别表示利用影像外方位元素的角元素φ、ω、κ所构成的正交变换矩阵及其转置矩阵。
综合分析式(3)—(6),以及结合GPS本身系统误差影响以及曝光延迟带来的误差影响,结合真实曝光时刻摄影像中心与真实曝光时刻的GPS位置的几何关系可建立摄站点的曝光延迟模型如下
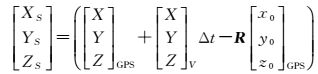 (7)
(7)
式中,[X Y Z]VT表示当前时刻的无人机平台在3个方向上的速度矢量;Δt表示曝光延迟时间。
2.2.3 在平差模型中加入含有曝光延迟的GPS附加参数式(3)—(7) 所示模型可以得到记录曝光时刻与实际曝光时刻的摄站点坐标间的关系。以记录曝光时刻的摄站点坐标为GPS观测值,来建立误差方程式,将误差方程式加入到平差数学模型误差方程组中,可得到如下平差数学模型
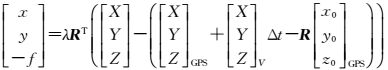 (8)
(8)
式(8) 中,[x y -f]T表示像点(x, y)在像空间坐标系下的坐标值;λ表示投影系数在求解过程中相互抵消;R=RφRwRk是一个3×3阶的正交变换矩阵,由影像外方位元素的3个姿态角元素φ、ω、κ所对应的9个方向余弦构成;RT为转置矩阵;[X Y Z]GPST表示记录曝光时刻的摄站点GPS位置;[x0 y0 z0]T表示GPS天线相位中心在像空间坐标系下的坐标值;[X Y Z]VT表示当前时刻的无人机平台在3个方向上的速度矢量;[X Y Z]T表示像点所对应的像空辅助坐标;Δt表示相机曝光延迟时间。
式(8) 所示的平差数学模型与传统的光束法平差模型相比较,其中一个重要特点是结合无人机摄影测量作业的特点,考虑相机的曝光延迟时间Δt以及各个曝光瞬间的位置偏移,针对各个曝光点的曝光延迟误差进行逐点曝光补偿。相较于传统的方法,本文方法更加侧重于对各个曝光点的曝光延迟误差进行逐点曝光补偿,更加适合于无人机的GPS辅助光束法平差方法。在模型解算过程中,将曝光延迟作为求解未知量与其他系统误差代入方程组内进行统一求解,消除由于曝光不同步所带来的误差影响,从而提高GPS辅助空三平差精度。
本文所提出的一种顾及曝光延迟的无人机GPS辅助光束法平差模型是在传统GPS辅助光束法平差模型的理论基础上进行扩展和延伸,而构建的一种更加适用于无人机GPS辅助光束法平差的平差模型。该模型针对各个曝光点的曝光延迟误差影响不一致,分别对各个曝光点的曝光延迟误差进行补偿,从而提高无人机影像空三加密的精度。
3 试验结果与分析 3.1 试验数据试验影像通过飞思非量测相机获取,拍摄区域为浙江宁波北仑柴桥地区,共7条航线,142幅影像,影像覆盖实地面积近9 km2(影像信息如表 1所示),测区范围内地形较为平坦。影像曝光瞬间GPS数据通过差分GPS数据获得。
| 区域名称 | 浙江宁波柴桥地区 |
| 摄影相机 | 飞思相机 |
| 检校焦距 | 51.230 84 mm |
| 影像大小 | 10 328×7760 pix |
| 拍摄面积 | 9 km2 |
| 平均航高 | 400 m |
| 航线数 | 7条 |
| 像片总数 | 142张 |
| 像素大小 | 5.2 μm |
3.2 试验方案设计
为了验证本文所提出的顾及曝光延迟的GPS辅助光束法平差方法的可行性,以及分析控制点的个数对平差结果的影响,试验采取6种试验方案进行试验分析比较。这六种试验方案的控制点布点原则,参考无人机航测布设控制点的一些基本原则[21-22],具体方案如下:
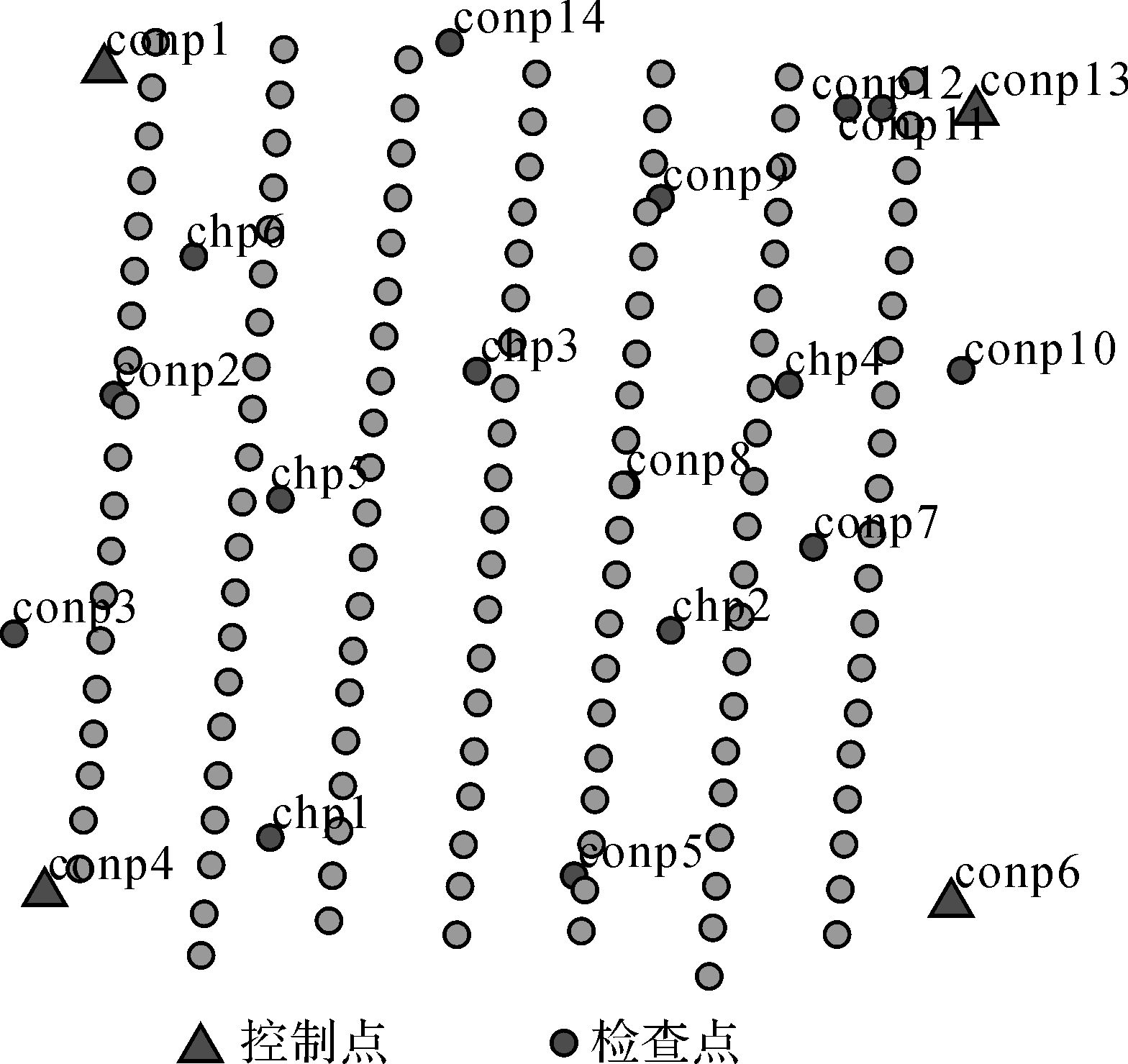
(1) 方案1。采用常规的光束法平差方法,测区四角布设像控点,其余点做检查点(如图 5所示)。
|
| 图 5 方案1 Fig. 5 Scheme 1 |
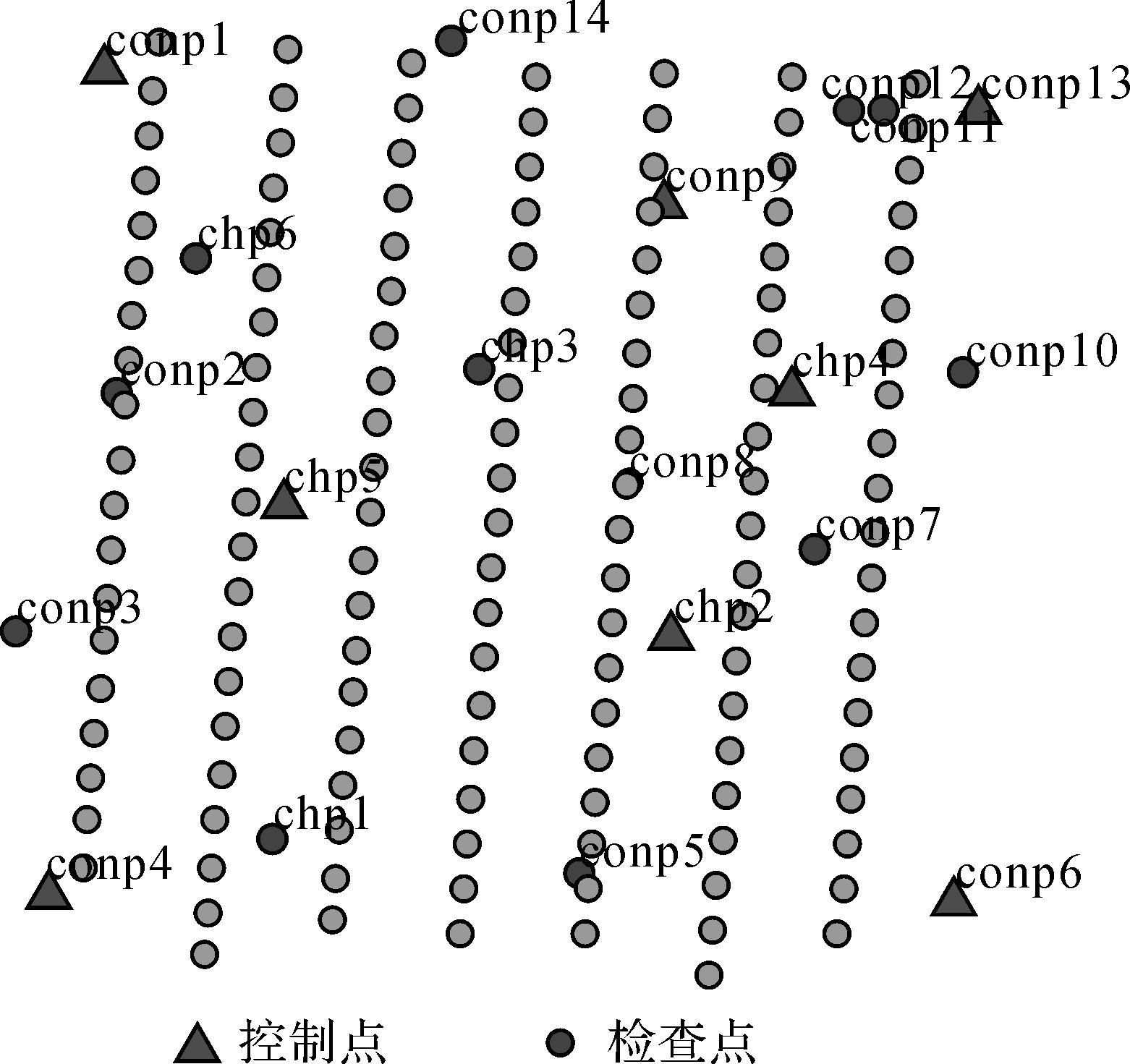
(2) 方案2。采用常规的光束法平差方法,测区四角布点,以及内部布设4个像控点,其余点作为检查点参与平差解算(如图 6所示)。
|
| 图 6 方案2 Fig. 6 Scheme 2 |
(3) 方案3。采用常规的光束法平差方法,测区四角布点,外加内部均匀布设8个像控点,其余点作为检查点参与平差解算(如图 7所示)。

|
| 图 7 方案3 Fig. 7 Scheme 3 |
(4) 方案4。采用传统的GPS辅助光束法平差,像控点布设方式与方案1相同,其余点作为检查点参与平差解算。
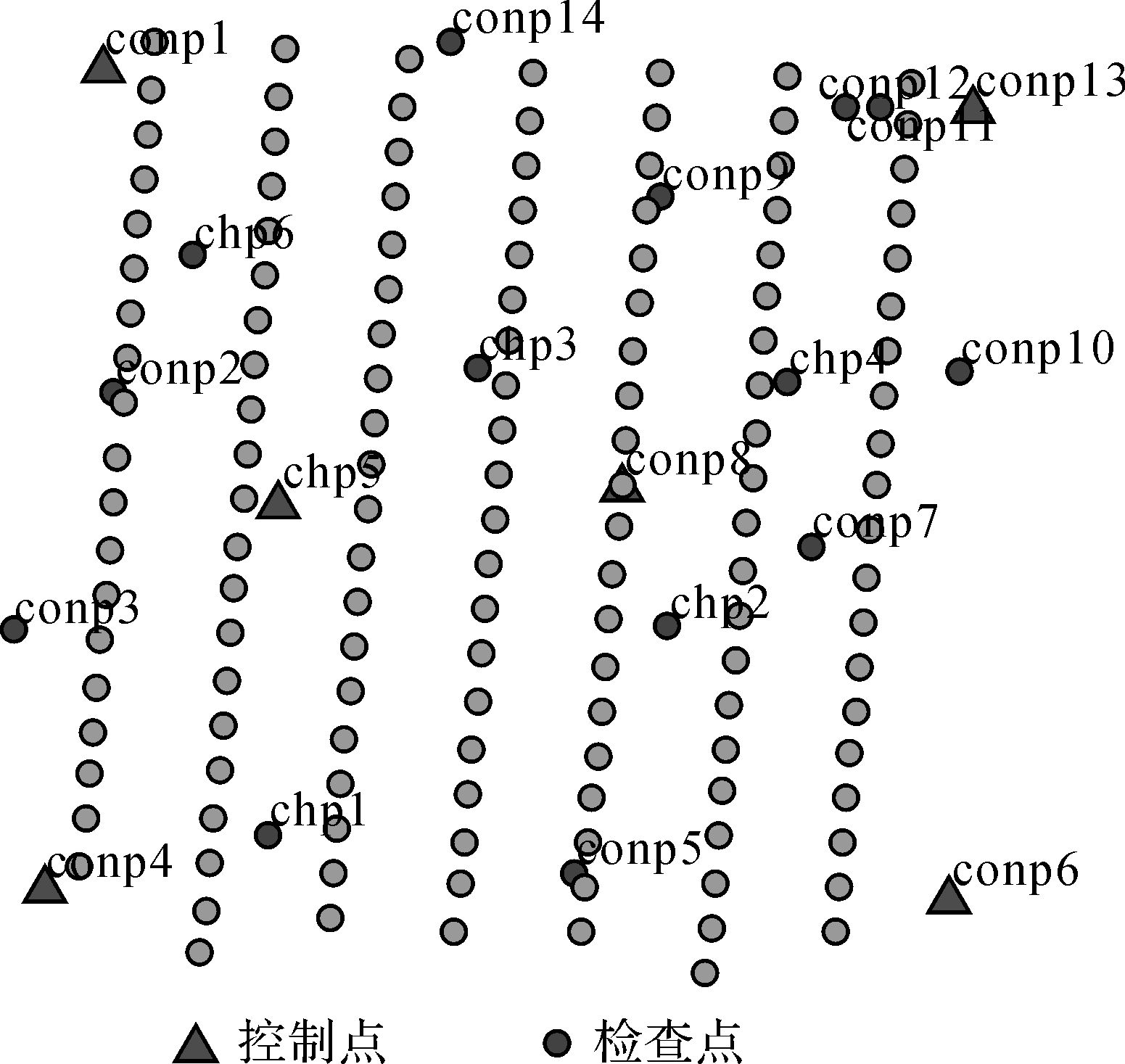
(5) 方案5。采用传统的GPS辅助光束法平差,测区四角布设像控点以及测区内增加2个像控点方式,其余点作为检查点参与平差解算(如图 8所示)。
|
| 图 8 方案5 Fig. 8 Scheme 5 |
(6) 方案6。采用本文提出的顾及曝光延迟的GPS辅助光束法平差方法,像控点布设方式与方案4相同,其他点作为检查点参与平差解算。
3.3 试验结果分析本次试验采用常规光束法平差、GPS辅助光束法平差以及本文提出的顾及曝光延迟的GPS辅助光束法平差方法进行空三加密。方案1、方案2、方案3采用常规光束法平差方法;方案4、方案5采用传统的GPS辅助光束法平差方法;方案6采用本文提出的顾及曝光延迟的无人机GPS辅助光束法平差方法。控制点的精度为:方案1平面最大误差0.070 634 m,高程最大误差1.403 557 m;方案2平面最大误差0.094 918 m,高程最大误差-0.226 24 m;方案3平面最大误差0.069 859 m,高程最大误差0.141 116 m;方案4平面最大误差0.094 21 m,高程最大误差0.129 653 m;方案5平面最大误差0.069 386 m,高程最大误差0.090 127 m;方案6平面最大误差0.070 276 m,高程最大误差0.093 772 m。如图 9所示,除了方案1的高程精度无法满足规范要求,其他方案的平面、高程精度均小于0.4 m能够满足规范要求[23]。检查点的精度比较如表 2所示。

|
| 图 9 不同控制点布设方案控制点精度分析比较 Fig. 9 The comparison of the precision of control points among different control point layout methods |
| 不同方案不同平差方式的检查点精度比较 | |||||||
| 平差方式 | 试验方案 | 控制点数 | 检查点数 | 平面中误差/m | 高程中误差/m | 平面最大误差/m | 高程最大误差/m |
| 常规光束平差 | 方案1 | 4 | 16 | 0.084 18 | 1.325 04 | 0.139 51 | 1.966 74 |
| 方案2 | 8 | 12 | 0.060 14 | 0.100 55 | 0.102 19 | 0.191 40 | |
| 方案3 | 12 | 8 | 0.044 42 | 0.063 03 | 0.067 68 | -0.130 8 | |
| 传统GPS辅助 光束法平差 |
方案4 | 4 | 16 | 0.076 33 | 0.116 14 | 0.136 01 | 0.193 67 |
| 方案5 | 6 | 14 | 0.051 24 | 0.071 13 | 0.129 87 | 0.158 63 | |
| 本文平差方法 | 方案6 | 4 | 16 | 0.053 91 | 0.079 04 | 0.130 94 | 0.162 10 |
(1) 采用常规的光束法平差方法,在测区四角布点可以对平面精度进行控制,但是要控制高程精度,仅仅是在4个边角上布设控制点是远远不够的。
(2) 分析比较采用常规的光束法平差方法、传统的GPS辅助光束法平差方法以及本文提出的顾及曝光延迟的无人机GPS辅助光束法平差方法的平差结果,可以发现随着控制点数量的递增,平面、高程精度都进行了提高。同时可以看出使用4个控制点进行传统的GPS辅助光束法平差以及本文提出的顾及曝光延迟的无人机GPS辅助光束法平差时,其平面、高程精度已经达到了使用8个控制点进行常规光束法平差的精度。由此可以看出GPS辅助光束法平差方法能够在使用少量控制点的情况下就能够达到实际作业生产要求。
(3) 方案4、5采用的是传统的GPS辅助光束法平差方法,而方案6是本文提出的平差方法,是在传统的GPS辅助光束法平差模型中考虑到曝光延迟产生的影响,以及应用顾及曝光延迟的GPS辅助光束法平差模型进行光束法平差解算。对比方案4、方案5和方案6的平差结果,相同控制点个数情况下,在使用本文提出的GPS辅助光束法平差进行试验的方案6,其平面、高程精度相比使用传统GPS辅助光束法平差进行试验的方案4都有了明显提高。同时在方案5中增加2个控制点的情况下其平面、高程精度与也只与方案6的平面、高程精度相当。
控制点的多少关系到空中三角测量的精度,适当增加控制点数量,可提高空中三角测量的精度,但是并不是控制点密度越大越好——控制点数量达到一定程度后对空三的精度影响不会太大,反而会加大外业的工作量[21-22]。GPS辅助光束法平差方法在使用少量控制点情况下就能满足实际作业生产要求,而本文提出的顾及曝光延迟的无人机GPS辅助光束法平差方法充分考虑了各个曝光点曝光误差影响不一致的问题进行了逐点误差补偿,其空三精度在传统GPS辅助光束法平差方法的基础上有了进一步的提高。
4 结束语传统GPS辅助光束法平差方法解决了常规光束法平差方法依赖控制点数量的问题,但没有充分考虑到无人机摄影测量作业时相机各个曝光点的曝光延迟影响不一致的问题。本文针对无人机摄影测量相机曝光延迟未知的情况,提出了一种顾及曝光延迟的无人机GPS辅助光束法平差方法。该方法充分考虑了相机曝光延迟的影响,并将其引入到空三平差模型中进行解算,解算精度在传统GPS辅助光束法平差方法的基础上有了进一步的提高,其应用对无人机摄影测量数据生产具有一定的现实意义。
| [1] | ADAM C, VINCENT G, EVERETT A. Unmanned Aircraft Systems in Remote Sensing and Scientific Research:Classification and Considerations of Use[J]. Remote Sensing, 2012(4): 1671–1692. |
| [2] | 李德仁, 李明. 无人机遥感系统的研究进展与应用前景[J]. 武汉大学学报(信息科学版), 2014, 39(5): 505–513. LI Deren, LI Ming. Research Advance and Application Prospect of Unmanned Aerial Vehicle Remote Sensing System[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 505–513. |
| [3] | 毕凯, 李英成, 丁晓波, 等. 轻小型无人机航摄技术现状及发展趋势[J]. 测绘通报, 2015(3): 27–31. BI Kai, LI Yingcheng, DING Xiaobo, et al. Aerial Photogrammetric Technology of Light Small UAV:Status and Trend of Development[J]. Bulletin of Surveying and Mapping, 2015(3): 27–31. |
| [4] | 李德仁, 肖雄武, 郭丙轩, 等. 倾斜影像自动空三及其在城市真三维模型重建中的应用[J]. 武汉大学学报(信息科学版), 2016, 41(6): 711–721. LI Deren, XIAO Xiongwu, GUO Bingxuan, et al. Oblique Image Based Automatic Aerotriangulation and Its Application in 3D City Model Reconstruction[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 711–721. |
| [5] | 袁修孝, 高宇, 邹小容. GPS辅助空中三角测量在低空航测大比例尺地形测图中的应用[J]. 武汉大学学报(信息科学版), 2012, 37(11): 1289–1293. YUAN Xiuxiao, GAO Yu, ZOU Xiaorong. Application of GPS-supported Aerotriangulation in Large Scale[J]. Topographic Mapping Based on Low-altitude Photogrammetry,, 2012, 37(11): 1289–1293. |
| [6] | 姬渊, 秦志远, 王秉杰, 等. 小型无人机遥感平台在摄影测量中的应用研究[J]. 测绘技术装备, 2008, 10(1): 46–48. JI Yuan, QIN Zhiyuan, WANG Bingjie, et al. Research on the Application of Small Unmanned Aerial Vehicle (UAV) Remote Sensing Platform in Photogrammetry[J]. Geomatics Technology and Equipment, 2008, 10(1): 46–48. |
| [7] | 林宗坚. UAV低空航测技术研究[J]. 测绘科学, 2011, 36(1): 5–9. LIN Zongjian. UAV Borne Low Altitude Photogrammetry System[J]. Science of Surveying and Mapping, 2011, 36(1): 5–9. |
| [8] | 林宗坚, 苏国中, 支晓栋. 无人机双拼相机低空航测系统[J]. 地理空间信息, 2010, 8(4): 1–3. LIN Zongjian, SU Guozhong, ZHI Xiaodong. UAV Borne Double Camera Low Altitude Photogrammetry System[J]. Geospatial Information, 2010, 8(4): 1–3. |
| [9] | ACKERMANN F. Practical Experience with GPS Supported Aerial Triangulation[J]. Photogrammetric Record, 1994, 16(84): 861–874. |
| [10] | 袁修孝, 付建红, 楼益栋. 基于精密单点定位技术的GPS辅助空中三角测量[J]. 测绘学报, 2007, 36(3): 251–255. YUAN Xiuxiao, FU Jianhong, LOU Yidong. GPS-supported Aerotriangulation Based on GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 251–255. |
| [11] | 李峰, 杨海东, 张建刚, 等. 利用GPS辅助空三的高原大比例尺航摄测图研究[J]. 测绘通报, 2012(8): 21–23. LI Feng, YANG Haidong, ZHANG Jiangang, et al. The Study of Large-scale Mapping in Plateau Based on GPS-supported Aerotriangulation[J]. Bulletin of Surveying and Mapping, 2012(8): 21–23. |
| [12] | 李德仁, 袁修孝. GPS辅助光束法区域网平差-太原试验GPS航摄飞行试验结果[J]. 测绘学报, 1995, 24(2): 1–7. LI Deren, YUAN Xiuxiao. GPS-supported Bundle Block Adjustment:The Test Results of GPS Aerial Flight in Taiyuan[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(2): 1–7. |
| [13] | 袁修孝. GPS辅助空中三角测量原理及应用[M]. 北京: 测绘出版社, 2001. YUAN Xiuxiao. The Principle and Application of GPS-supported Aerial Triangulation[M]. Beijing: Publishing House of Surveying and Mapping, 2001. |
| [14] | 蔡文惠, 梁国华. IMU/DGPS辅助航空摄影测量应用探讨[J]. 测绘通报, 2009, 4: 41–43. CAI Wenhui, LIANG Guohua. Discussion on Application of IMU/DGPS Aerial Photogrammetry[J]. Bulletin of Surveying and Mapping, 2009, 4: 41–43. |
| [15] | 李学友. IMU/DGPS辅助航空摄影测量综述[J]. 测绘科学, 2005, 30(5): 110–113. LI Xueyou. Principle and Application of IMU/DGPS-based Photogrammetry[J]. Science of Surveying and Mapping, 2005, 30(5): 110–113. |
| [16] | 严海英, 石洁, 孙艳新. GPS辅助空中三角测量在新疆基础测绘中的应用[J]. 测绘通报, 2005(5). YAN Haiying, SHI Jie, SUN Yanxin. Use of GPS-supported Aerial Triangulation in Fundamental Surveying and Mapping of Xinjiang[J]. Bulletin of Surveying and Mapping, 2005(5). |
| [17] | 袁修孝. GPS辅助光束法平差中系统偏移的处理[J]. 武汉测绘科技大学学报, 1995, 3(20): 198–201. YUAN Xiuxiao. The Systematic Offset Psoussing in GPS-supported Bundle Block Adjustment[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1995, 3(20): 198–201. |
| [18] | 李军正, 李建文, 郝金明, 等. GPS接收机动态检定场中的时间同步问题[J]. 测绘科学与技术, 2006, 6: 429–431. LI Junzheng, LI Jianwen, HAO Jinming, et al. The Time Synchronization in the Kinematic Verification Network for GPS Receivers[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 6: 429–431. |
| [19] | 李德仁, 袁修孝. 误差处理与可靠性理论(第2版)[M]. 武汉: 武汉大学出版社, 2012. LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. 2nd ed. Wuhan: Wuhan University Press, 2012. |
| [20] | 江振治, 韩挺瑞, 王新义. GPS辅助空中三角测量中时间偏移的处理[J]. 解放军测绘研究所学报, 2002, 22(1): 6–8. JIANG Zhenzhi, HANG Tingrui, WANG Xinyi. Processing of Time Offset in GPS Assisted Aerial Triangulation[J]. Journal of PLA Institute of Surveying and Mapping, 2002, 22(1): 6–8. |
| [21] | 朱进, 丁亚洲, 陈攀杰, 等. 控制点布设对无人机影像空三精度的影响[J]. 测绘科学, 2016, 41(5): 116–120. ZHU Jin, DING Yazhou, CHEN Panjie, et al. Influence of Control Points' Layout on Aero-triangulation Accuracy for UAV Images[J]. Science of Surveying and Mapping, 2016, 41(5): 116–120. |
| [22] | 买小争, 杨波, 冯晓敏. 无人机航摄像控点布设方法探究[J]. 测绘通报, 2012: 268–271. MAI Xiaozheng, YANG Bo, FENG Xiaoming. Research on the Method of Layout of Unmanned Aerial Vehicle[J]. Bulletin of Surveying and Mapping, 2012: 268–271. |
| [23] | GB7930-87, 1: 5001: 10001: 2000地形图航空摄影测量内业规范[S]. B7930-87, 1:5001:10001:2000 Topographic Maps Specifications for Aerophotogrammetric Office Operation[S]. |


