2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 中国矿业大学(北京)地球科学与测绘工程学院, 北京 100083
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. College of Geoscience and Surveying Engineering, China University of Mining and Technology, Beijing 100083, China
倾斜航空摄影技术是国际测绘领域近些年发展起来的一项新技术,极大地扩展了遥感影像的应用领域[1-4]。使用倾斜航空影像进行高精度测绘、三维信息提取和三维城市模型构建等应用首先要解决如何精确计算倾斜航空影像的外方位元素的问题,这通常是经过摄影测量区域网平差,即空三加密过程解决的。而如何利用影像匹配算法,可靠而又精确地获取具有足够“光线束”且在影像中尽量均匀分布的连接点用于平差解算,是涉及自动空三加密过程的一个关键问题。与传统的近似垂直航空影像相比,倾斜航空影像之间存在地物几何变形、分辨率差异、影像旋转、地物相互遮挡等问题,传统基于灰度和多数基于特征的影像匹配算法在应用于倾斜航空影像时成功率和可靠性大大降低,甚至失败。
目前,国内外针对倾斜航空影像中连接点的自动提取已经开展了大量研究[5-10]。其中常用的一类方法是在影像中提取具有仿射不变性的区域,建立描述子然后再进行匹配,包括基于SIFT、MSER、Harris-Affine & Hessian-Affine等仿射不变特征算子的类似算法[7, 11-15],这类方法的缺点是一般基于影像间的两两匹配,且对大倾角倾斜影像的匹配效果不好。另一类方法则是利用基于SIFT或MSER算子的匹配算法对原始影像像对A、B先进行粗匹配得到一定数量的同名点对,再计算出两幅影像之间的一个关系矩阵H。然后以影像B为参考影像,利用H矩阵对影像A进行纠正得到校正影像A′,对校正影像A′和影像B进行SIFT匹配,再将校正影像A′上匹配出的特征点反算到原始影像A上。该类方法及其改进版本[11, 16-17]被广泛采用,但其结果严重依赖于初始匹配点的分布和匹配正确率,尚难以保证匹配效果。目前,ASIFT算法因具备完全的仿射不变性且对大倾角倾斜影像的匹配效果较好得到较大关注,与SIFT、MSER等相比较,ASIFT算法在对图像旋转、尺度缩放、光照变化上具有更强的稳健性[18]。然而,由于该算法采用近似于穷举法来模拟两个相机轴定向参数,对两幅图像通过一系列的仿射变换得到两组图像序列,再利用SIFT算法对两组图像序列进行特征匹配,计算复杂度极高而效率很低,对于海量的航空倾斜影像,且每个影像像素都达千万级的影像此算法难以满足实际的应用需求。
针对现有方法存在的问题,本文提出了一种实用化的倾斜航空影像全自动连接点匹配和联合区域网平差方法。首先,充分利用POS数据和平均飞行高度数据,避免了现有大多数算法所采用的类似于“盲搜索”和“穷举法”、预先纠正倾斜视影像等耗时且稳健度低的缺陷;其次,针对倾斜航空影像因遮挡严重,尺度和光照变化大而引起的同名点匹配困难,在充分利用POS系统提供的初始外方位元素的基础上,顾及其误差,组合使用改进的ASIFT算法和基于窗口的多角度多视影像匹配算法,并采用由粗到细的多分辨率分层匹配策略得到最终的自动转点结果;最后,利用典型试验区域的倾斜航空影像数据针对算法的性能进行了试验,试验结果验证了所研发的算法的可靠性、精度和实际性能。
1 倾斜航空影像几何成像模型分析及区域网平差当前几乎所有的倾斜航摄系统都是多相机系统,且配备一个POS系统获取姿态,对于这类多相机系统,区域网平差可以采用以下3种方式[6]:
方法1——无约束的联合定向方式,即每景影像都使用独立的外方位元素,对于相同相机拍摄的影像使用共同的内方位元素。这种方式没有加入诸如影像之间的相对姿态等的约束
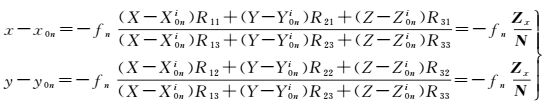 (1)
(1)
式中
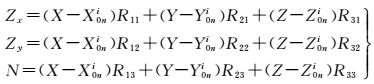
x0n、y0n、fn是n个相机的内方位元素;(X0ni, Y0ni, Z0ni)是第n个相机在第i个摄站的投影中心;R为旋转矩阵。
方法2——附加相对约束的定向方式,即将每个摄站的多个相机整体作为一个刚体单位进行平差,相机之间的相互关系(相对位置/姿态角)则作为约束信息加入到光束法平差之中,此时倾斜影像的共线方程可理解为下视相机与倾斜相机两个影像坐标系之间经过分别平移和旋转后的一个函数(式(2))。该方式的优势在于不仅降低了未知数的个数,也使网型更加稳定
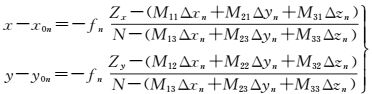 (2)
(2)
式中, M是倾斜相机相对于下视相机的旋转矩阵;Δxn、Δyn、Δzn是相机投影中心之间的距离;x0n、y0n、fn是n个相机的内方位元素; Zx、Zy、N同式(1)。
方法3——直接定向方式。该方式首先将下视影像进行传统的空三解算获得精确的方位元素,然后利用已经检校过的倾斜相机与下视相机之间的旋转平移参数解算出倾斜影像的方位元素。
以上所述3种平差方式各有利弊,方法3最简单精度也最差,多传感器的潜力没有得到充分的发挥。即使检校参数是已知的,但是随着时间的推移,检校参数的稳定性是值得怀疑的。方法1平差模型较为独立,方法2模型相对严格,理论上可以得到的精度将更高。然而必须注意的是,方法2和方法3都有一个前提,即多个相机必须同时曝光,而目前并非所有的倾斜摄影测量系统都遵循这一规则。因此方法1是相对较为通用的一种方法,但平差计算量极大。根据这些平差模型的利弊,实际平差过程中采用了一种组合方法,即在剔除较大粗差(大于
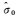
在使用方法1进行倾斜航空影像的区域网平差时,首先需要应对待估计的未知数成倍增长所带来的计算量增大,和因连接点的“光线束”比传统的近似垂直航空摄影要大而引起的改化法方程带宽很大的问题。另外,也要考虑由于各个镜头的视角不同而带来的影像分辨率不一致的情况(相当于像点观测的精度实际是有差异的),这间接地加大了粗差探测的难度。因此,在传统的最小二乘光束法平差的基础上,研发了基于稳健估值原理的粗差自动探测与剔除关键算法,算法适用于摄影测量网平差中可能存在的大粗差(>3b)、中等粗差
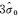
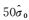
在使用倾斜航空影像进行区域网平差时,由于待估计的未知数和观测数量巨大,通过解算每个观测的多余观测分量,再由验后方差分量估计原理导出的选权迭代法[21]进行粗差探测,势必导致平差解算效率显著下降,难以满足实际的应用需求。本文以稳健估值和验后方差分量估计原理作为基本的理论指导,根据倾斜航空影像数据的实际特点,设计相应的权函数和策略以达到粗差自动探测与剔除的目的。本文使用的权函数基本形式为
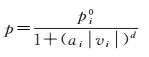 (3)
(3)
式中
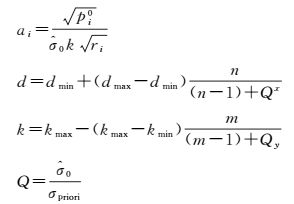
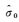
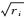
(1) 由于计算多余观测分量ri太耗时,因此,假定ri恒等于1。
(2) Q值的大小决定权函数的形状,由于受初始参数精度、粗差数量和大小的影响,平差开始时Q值势必较大,此时权函数曲线较为平缓。随着参数精度的不断提高和粗差的不断发现和剔除, Q值越来越小,直至趋近于1,此时权函数曲线较为陡峭。这样的一种策略,使得迭代初期不会因粗差和参数精度的影响而放弃原本正确的观测,优先剔除大中等粗差(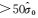
(3) 区域网初始定向时,即最顶层金字塔影像匹配结果进行第1次区域网平差时,此时初始参数精度和像点匹配精度较差,因此选用较大的系数k和较小的系数d,保证初始网的稳定求解。本文实际处理过程中,系数k和d联合选取的原则是保证平差系统不剔除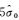

(4) 初始定向完成后,逐级金字塔影像定向时,定向参数精度逐渐提高,平差网中粗差主要表现为小粗差,而且比例较低(通常小于5%),因此,系数k和d联合选取的原则是随着金字塔影像级数的下降而下降(保证剔除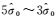

为了计算参考影像上给定点的匹配点,本文提出了基于窗口的多角度多视影像匹配模型WMVM(该匹配模型可以看作文献[19-20]中GC3方法的扩充,因此在此省略了算法及其优缺点的详细描述)。根据这种方法,一个影像被选作参考影像,其他影像视作搜索影像,文中选择归一化影像相关(NCC)用于参考影像与搜索影像窗口间相似性测度。
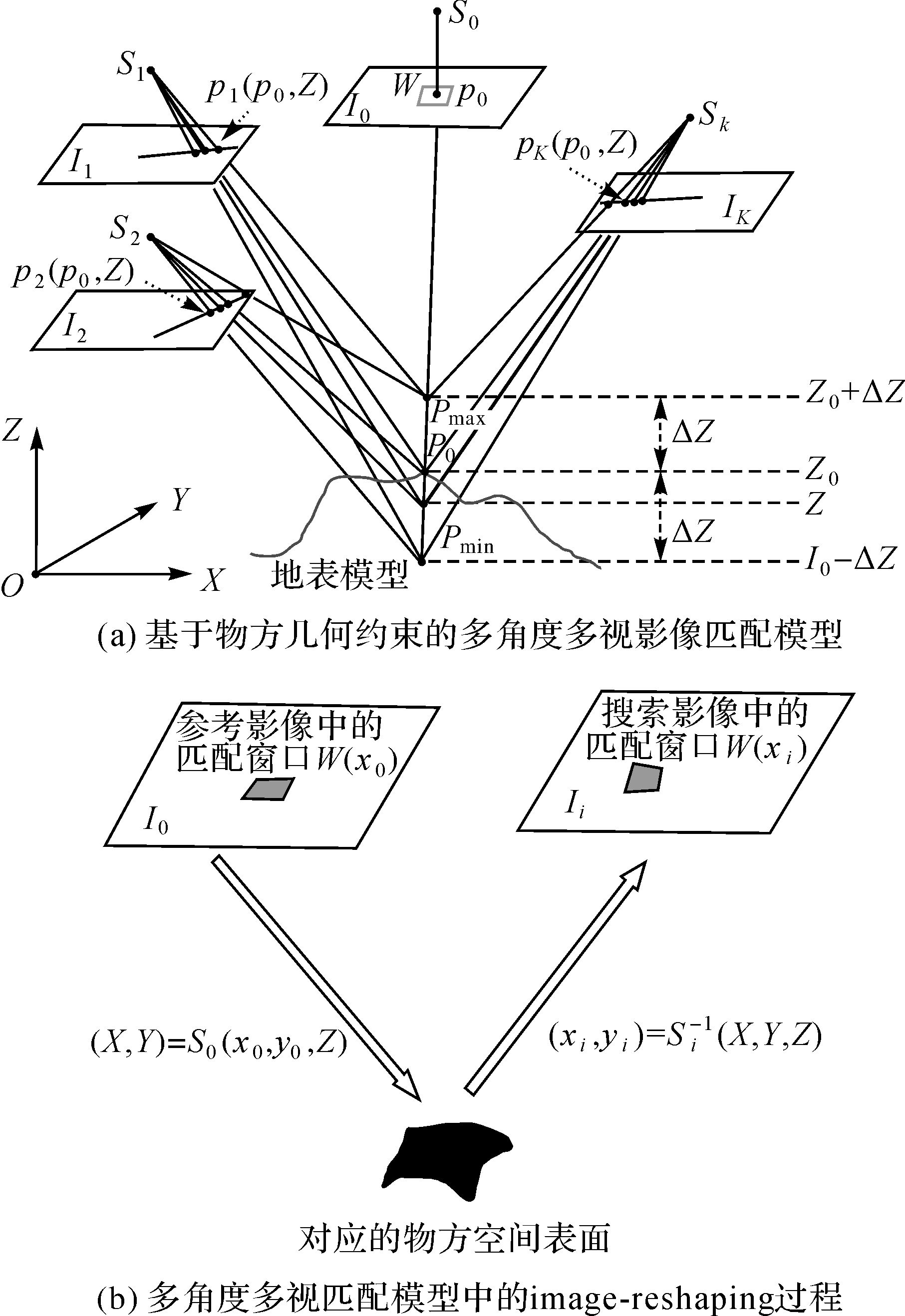
如图 1(a),假设有K+1景航空遥感影像{I0,Ii, i=1, …, K},现选取中间的一景影像作为参考影像I0,其他的至少一景影像为搜索影像Ii, i=1, …, K。它们组成了K个立体像对,即像对I0-I1、I0-I2、…、I0-IK。对于参考影像上的一个给定特征点p0,其物方空间的对应点一定位于通过点p0的摄影光线S0P0上。首先,假设Z0为点p0的概略高程值,就可以通过共线方程式(相当于摄影光线S0P0与高程平面Z0相交)获得点的三维坐标P0(X0, Y0, Z0),再假设给定概略高程值Z0的容差为ΔZ,即可以得到对应于高程Z0-ΔZ和Z0+ΔZ的两个物方点Pmin和Pmax,而点p0在物方空间的对应点则一定位于摄影光线段PminPmax之上。然后,利用影像的精确定向元素,将摄影光线段PminPmax分别投影到搜索影像Ii上以得到给定点p0在影像Ii上的同名核线(段),而点p0的匹配点也一定位于搜索影像的Ii上的核线上。因此,WMVM算法隐含地利用了影像及影像之间的核线约束条件。
|
| 图 1 多角度多视影像匹配模型过程示意图 Fig. 1 Illustration of the window-based multiple-viewing image matching procedure |
定义I0(p)和Ii(p)为影像的灰度值矩阵。在参考影像上,以给定点p0为中心定义一个匹配窗口W。假设已经获得成像区域的近似高程。利用参考影像的定向元素将窗口投影到概略DEM上,在物方空间即可以获得对应于匹配窗口W的小面元。同样的,也可以将该小面元投影到搜索影像上,从而获得给定点p0在搜索影像上的相应匹配窗口。在本文中称该过程为image-reshaping(图 1(b))。
定义点p0(对于某一高程值Z)在参考影像I0和搜索影像Ii上相应的匹配窗口之间的相似性测度为SCi, i=1, …, K。其中, W和s分别为参考影像上的匹配窗口和位于该窗口内的一个像点;n为匹配窗口W的大小;pi(p0, Z)为搜索影像上对应于s的像点,它可以通过image-reshaping过程获得,为加快计算速度其灰度值可以通过对搜索影像Ii进行双线性内插获得。为有效消除成像时因光照条件变化引起的影像灰度值差异,在本文中选择归一化相关系数NCCi(p0, Z)作为相似测度(式(4))
 (4)
(4)
由式(4) 可以看出,与传统的归一化相关系数的定义不同,这里NCCi(p0, Z)是像点p0(其中,
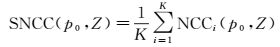 (5)
(5)
由式(5) 可以看出,SNCC(p0, Z)也是像点p0和Z:Z∈[Z0-ΔZ, Z0+ΔZ]的函数,使SNCC达到最大值时的高程Z正是给定点p0的正确高程值,其中,点p0在搜索影像上的搜索范围由初始高程的容差ΔZ确定。简单地说,该算法利用了这样一个事实:正确的匹配在所有像对的NCC曲线中都呈现峰值,且都对应于给定点的真实高程值,而伪匹配虽然在单个像对的NCC曲线中可能也呈现峰值,但由于各像对成像几何关系的不同,峰值在不同像对NCC曲线中的位置是不同的。因此,通过对各像对的NCC曲线进行加和平均,正确的匹配在SNCC曲线中得到进一步增强,而对应于伪匹配的峰值则互相抵消而在SNCC曲线中被抑制。由此,通过定义SNCC就可以同时匹配多景影像,并且直接获得给定特征点p0的三维坐标。
在WMVM的在实际应用中,匹配窗口可采用矩形窗口,考虑到在地物表面断裂附近隐含在基于窗口的影像匹配中的光滑约束并不成立,也可以采用非矩形匹配窗口或根据匹配窗口中的影像纹理信息对影像灰度进行加权处理。由图 1(b)可知,通过image-reshaping过程,在参考影像上的一个矩形匹配窗口可以同搜索影像上的非矩形窗口进行相关,这样,由地形起伏、影像成像几何及成像比例尺所引起的变形就可以在影像相关过程中自动得到补偿。由此可见,WMVM算法可同时匹配多幅重叠影像,能够很好地减小信息盲区,具有解决立体匹配系统中的遮挡、几何变形(包括缩放和旋转)、地物表面断裂、特征相似等瓶颈问题的能力。
3 基于窗口的多角度多视匹配模型WMVM的影像同名像点自动匹配方法针对倾斜航空影像的特点,在设计稳健和实用化的影像连接点自动匹配方法时应该考虑如下3个方面:首先,目前的倾斜航空摄影系统都可以提供POS数据,这些数据可被利用来进行诸如影像间重叠范围的确定、影像间的几何变形的事先校正、影像匹配初值的确定以及匹配搜索范围的限定等步骤,从而避免采用类似于“盲搜索”和“穷举法”等耗时且稳健度低的算法;其次,考虑到POS数据存在误差,所以影像间的自动转点必须使用由粗到精的金字塔匹配策略,而且在每一级金字塔影像上完成所有影像间的自动转点后进行POS辅助的区域网平差,逐级提高影像外方位元素值的精度,进而在金字塔影像匹配过程中逐步缩小影像匹配时的搜索空间,有效抑制误匹配发生的概率;最后,基于窗口的多视影像匹配算法WMVM需要事先知道精确的影像定向参数,从而保证正确的匹配是符合影像核线几何约束的。试验证明,WMVM方法在正确匹配点偏离核线1.0个像素以上时其性能会大幅下降,这样即使采用由粗到精的金字塔匹配策略也要求影像的外方位元素所造成的像方误差不大于数十个像素。因此,在最低分辨率金字塔影像中采用一种改进后的ASIFT算法,获取可靠的连接点数据并进行区域网平差来精化由机载POS系统提供的初始影像外方位元素,然后再利用WMVM算法完成连接点的匹配。
综合以上考虑,本文在基于窗口的多角度多视匹配算法WMVM的基础上,研发了可靠的倾斜航空影像同名点自动匹配技术,该算法主要包括如下基本步骤:
(1) 匹配过程中使用从由粗到细的多分辨率分层匹配策略。在这种策略中,影像表达为不同分辨率的层次,称之为影像金字塔(影像PL0-PLK,其中K为金字塔影像级数,一般设为4,且相邻金字塔影像之间的分辨率比率为2.0,PL0为原始分辨率影像,则PL4的分辨率为PL0的1/16)。另外,为减少影像噪声和其他的影像瑕疵并增强影像重要的纹理信息,Wallis滤波将被用来对参加匹配的影像进行自适应增强,为其后的特征提取和影像匹配阶段提供良好的影像数据。
(2) 在金字塔影像的最高层PLK,利用测区中每张影像的近似外方位元素和已知的成像区域概略最小/最大高程值确定一个最大高程面Zmax和一个最低高程面Zmin,分别计算影像四角的地理范围。以其中一张影像例如I0为基准匹配影像,计算它与其他影像在这两个高程面上的重叠比例,在最高高程面上重叠10%,最低高程面重叠30%,则认为他们具有重叠度而作为待匹配影像Ii=1-n,其中n为符合重叠度条件得待匹配影像数。找出基准影像I0和待匹配影像Ii后,利用SIFT特征进行I0与Ii初始相对几何关系(关系矩阵H)的确定。为保证相对几何关系矩阵H的稳健估计,使用了ASIFT算法并进行了改进,即首先利用影像的近似外方位元素将影像I0与Ii纠正到Zmean=(Zmax+Zmax)/2水平面上得到校正后影像I0′与Ii′,然后利用SIFT算法在校正后影像I0′与Ii′重叠范围内进行同名特征点的匹配,得到一定数量的同名特征点并分别反算到纠正前的影像上。
影像I0与Ii间的几何关系矩阵H可以表示为相似变换、仿射变换或透视变换。在这里采用二维透视变换H。为了剔除粗差点,采用RANSAC算法加二维透视变换,获取可靠的几何关系矩阵H,利用这组几何关系,在分辨率更低一级影像上进行灰度匹配以获取数量更多,分布更为均匀的同名点,然后再利用相同的粗差剔除方法,获取新的几何关系矩阵H′。最后,利用求出的影像I0与Ii,i=1-n间的关系矩阵HI, i=1-n′,在本级影像I0中提取Harris-Affine特征点并利用最小二乘匹配方法将特征点匹配到相应影像Ii,i=1-n中,获取子像素级精度的同名连接点。整个测区匹配完毕后,进行区域网平差以获取较为准确的外方位元素。同时利用平差后连接点的加密坐标,计算每张影像的新的平均高程Zmean和测区的最高Zmax以及最低高程Zmin信息。
该步骤实质上是一种改进的ASIFT算法,由于仅仅在最低分辨率影像金字塔中采用该算法,且利用影像的初始外方位元素对影像进行预纠正,然后再利用SIFT特征进行初始相对关系的确定,从而避免了原始ASIFT算法的缺陷,提高了算法的效率。另外,这里的影像纠正过程等价于存在一个虚拟的水平相机在垂直视角进行摄影获得虚拟的水平影像的过程。这种虚拟的水平影像消除了倾斜影像尺度不一的影响,使得匹配的问题转换为只需要使用一种尺度不变的特征点检测算子及其描述,即可获得稳健的匹配点,由于文中采取了SIFT特征点和描述,以此克服因POS数据不准确而生成的虚拟水平相片中仍然可能存在的尺度和旋转问题,因此大大提高了匹配过程的可靠性。使用改进后ASIFT算法进行的大量测试表明了算法的有效性,在图 2(a)中显示了一组在1:16金字塔影像中获得的特征点匹配结果。这组影像由于使用短焦镜头成像因而存在较大的几何变形,使用基于SIFT算子的匹配方法无法获得正确的结果,而使用改进后的ASIFT算法则成功获取了很可靠的匹配结果。在图 2(b)中显示了另外两组使用改进后算法得到的匹配结果。

|
| 图 2 ASIFT算法在最低分辨率金字塔影像中的匹配效果 Fig. 2 Matching results of lowest resolution images by using the proposed modified ASIFT algorithm |
(3) 在金字塔影像上往下一级PLK-1,由于在上一级金字塔影像上完成所有影像间的自动转点后进行了区域网平差,获得了较高精度的影像外方位元素值(精化后的外方位元素),此时开始进行基于WMVM算法的多视影像匹配来获得连接点。首先,选择一张影像为基准影像I0,将影像进行分块并在每一影像块内利用Harris-Affine算子提取至少一个特征点,这样尽可能地保证了特征点分布的均匀性。
然后,对于影像I0的每一个特征点,利用上一级金字塔匹配时获得的平均高程Zmean和精化后的影像外方位元素预测其在其他影像中的初始位置,同时也确定了该连接点的同名点所在的影像集合Ii,其中i=1-n, n为特征点的“光线束”。利用基准影像I0在高程范围内(Zmean-(Zmax-Zmin)/3, Zmean+(Zmax-Zmin)/3) 内进行WMVM多视影像匹配,从而获得每个特征点在多景影像中的像坐标。由于WMVM本质上仍然是一种基于区域的灰度匹配ABM(area-based matching)方法,而ABM在匹配窗口尺寸的确定上是一个难题,通常大窗口可靠性高但是精度低,小窗口的精度高但是可靠性又差。为抑制误匹配发生的概率,本文将使用如下判据确定“正确可靠”的匹配:
a.对于特定尺寸的匹配窗口(例如7×7 pixel),计算次大与最大相关系数的比值ρ=σsec/σmax,如果该比值大于0.75则为该匹配结果是可靠的。
b.在满足a的条件下,如果最大与次大相关系数所对应的匹配点之间的距离大于3.0像素,则为该匹配结果是可靠的。
c.利用不同的窗口大小(从7×7、11×11到15×15 pixel)进行多次匹配,如果针对所有窗口大小情况下同时满足以上两个条件,则认为该匹配结果是正确而且可靠的。
按照上面的准则,以每一景影像为基准影像处理完所有的影像,获得在本级金字塔影像上的连接点。最后,调用区域网平差软件进行平差,自动剔除粗差点(观测值)和获取更新后的外方位元素。利用平差后连接点的加密坐标,更新每张影像的平均高程Zmean和测区的最高Zmax以及最低高程Zmin信息。
(4) 将剔去错误匹配后的所有连接点换算到分辨率更高一级PLK-2的影像上,然后使用最小二乘匹配在PLK-2级的影像上进行匹配。检查每张影像上像点分布是否均匀,如果不均匀,则在PLK-2级影像上分块提取更为密集的Harris特征,利用步骤(3) 中的方法进行匹配获取连接点,然后调用平差解算程序剔除粗差并获取更为精确的影像外方位元素。依此类推,向更高分辨率影像上进行同样的方法处理,直到原始分辨率级别PL0为止。为提高自动提取的连接点的几何精度,在原始分辨率影像中利用最小二乘匹配方法获取最终的连接点数据。
需要注意的是,基于WMVM算法的多视影像匹配在仅仅匹配两景影像时很容易引入误匹配且这类误匹配因其“光线束”为2,在随后的区域网平差过程中也无法自动剔除,因此所有“光线束”为2的连接点将被删除。另外,为保证连接点自动提取的效率,基于OMP并行的方式实现了以点特征提取和连接点WMVM匹配为“并行粒度”的多进程并行化,因为从上面的描述可以很容易地看出,对于每个特征点,其特征提取和WMVM匹配都是相互独立的,而且WMVM因算法复杂度高在连接点匹配过程中是最耗时的。
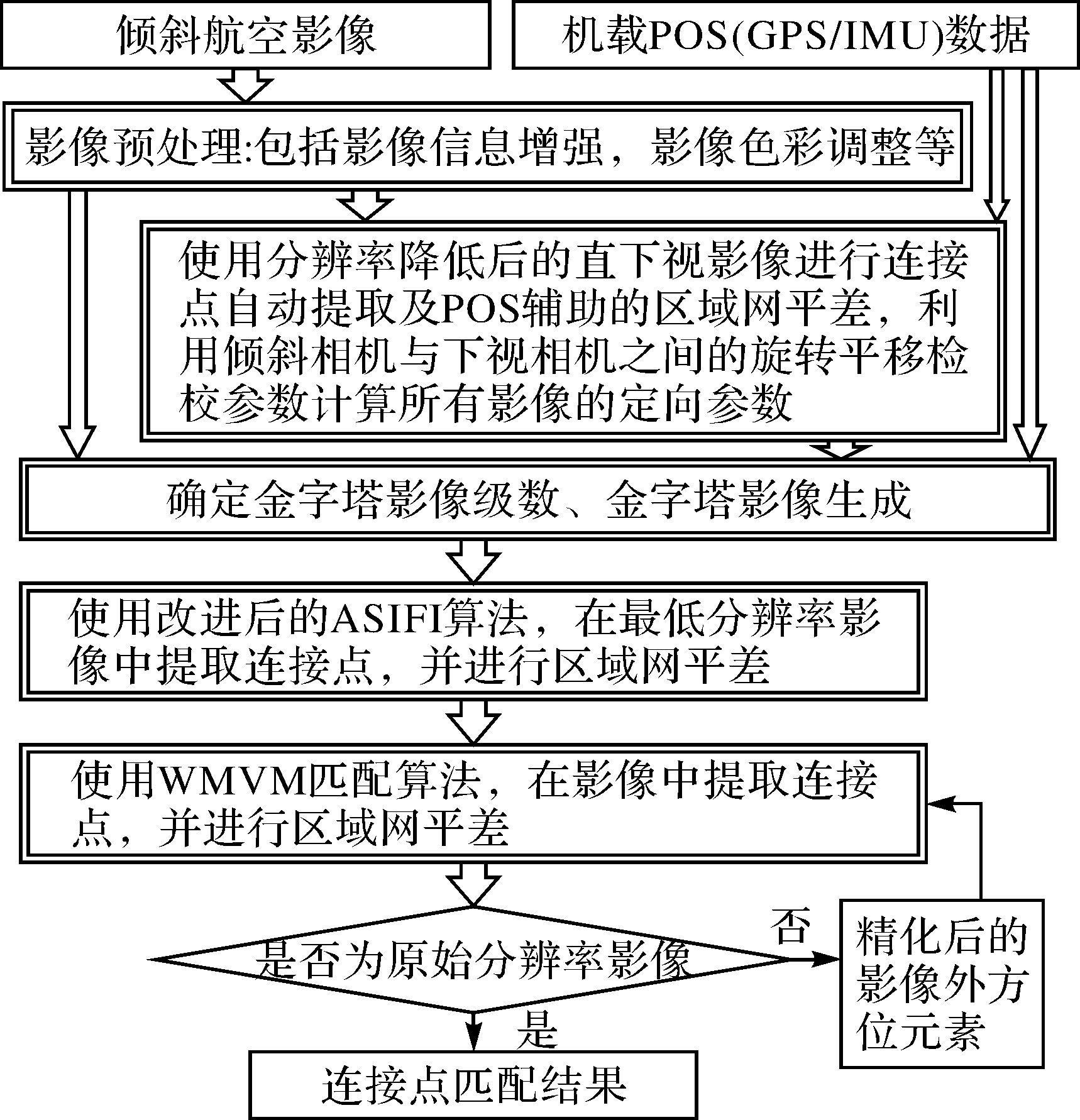
综上所述,本文提出的连接点自动提取步骤如图 3所示。
|
| 图 3 本文倾斜航空影像自动空三基本流程 Fig. 3 Flow-chart of the proposed tie-point matching procedure |
4 试验验证与分析
为验证本文所提出的算法的可靠性、精度和实际性能,收集了多款类型倾斜相机在不同成像区域的不同地面分辨率的倾斜航空影像数据(见表 1),利用一台双核CPU(2.5 GHz主频,16进程)、16GB内存的图形工作站,使用自主开发的软件PixelGrid-3DImage(基于VC++2015开发,64位OS),针对算法的可靠性、提取的连接点的分布、精度、算法的性能等问题展开了大量试验并获得了可与商业化软件系统(如Smart3DTM)相近的结果。
| 试验数据 | 基本参数 | 数据描述 |
| 数据集-1 | IGI Penta DigiCam数据,5镜头;影像大小8956×6708 pixel,倾斜像机倾斜角为45°,焦距50.0 mm/80.0 mm(下视/倾斜) | 4条航带,218景影像;飞行高度为810 m,地面平均高60 m,下视影像的GSD为10 cm |
| 数据集-2 | UltraCam UCO数据,7镜头;影像大小11674×7514/6870×4520 pixel,倾斜像机倾斜角为45°,焦距51.0 mm/70.5 mm(下视/倾斜) | 13条航带,2002景影像,飞行高度为1740 m,地面平均高1050 m,下视影像的GSD为8 cm |
| 数据集-3 | SWDC-5数据,5镜头;影像为8176×6132 pixel,倾斜像机倾斜角为40°,焦距80.0 mm/100.0 mm(下视/倾斜) | 5条航带,1925景影像;飞行高度为830 m,地面平均高30 m,下视影像的GSD为5 cm |
| 数据集-4 | 无人机倾斜航空影像数据,5镜头;影像大小7360×4912像素,倾斜像机倾斜角为38°,焦距35.0 mm/50.0 mm(下视/倾斜) | 9条航带,1390景影像,飞行高度为680 m,地面平均高400 m,下视影像的GSD为8 cm |
| 数据集-5 | TOPDC-5数据,5镜头;影像大小10 320×7750 pixel,倾斜像机倾斜角为45°,焦距47.0 mm/80.0 mm(下视/倾斜) | 24条航带,3720景影像;飞行高度为880 m,地面平均高60 m,下视影像的GSD为10 cm |
首先,使用POS辅助的自由网平差方法,针对数据处理所用的时间、成功提取连接点的数量、分布和内符合精度进行试验。由表 2可以看出,上述几组试验基本验证了本文所提算法的性能。首先,全自动提取的连接点经区域网平差并自动剔除粗差后,其单位权中误差都达到了子像素,连接点在影像中的分布也比较均匀(见图 4)。其次,由于采用了多视影像匹配方法,所获得的连接点的“光线束”可有效保证区域网的连接强度,对于试验数据集-2、数据集-3等常规60%/30%航向/旁向重叠度的影像,自动提取连接点的“光线束”平均为24左右,对于数据集-1和数据集-4这样的大重叠度影像(85%/60%航向/旁向重叠度),连接点的“光线束”平均为75以上,最大“光线数”甚至超过了100,这些冗余信息非常利于平差过程中粗差的剔除。第三,由图 5所示的自动提取连接点的例子可以看出,基于WMVM算法的连接点自动提取方法很好地解决影像中因地物遮挡、缩放和旋转等几何变形、地物表面断裂、特征相似等困难匹配问题,也能够同时顾及倾斜航空影像之间辐射响应和摄影分辨率不一致的实际情况,甚至是人工都十分难以量测的情况都可以获得正确的匹配结果。
| 试验数据 | 处理时间(连接点提取) | 连接点点数 | 自由网平差精度(单位权中误差) |
| 数据集-1 | 近50 min | 46 332 | 2.2 μm(0.4 pixel) |
| 数据集-2 | 8.5 h | 296 296 | 2.9 μm(0.6 pixel) |
| 数据集-3 | 7 h 20 min | 370 370 | 2.5 μm(0.4 pixel) |
| 数据集-4 | 6.5 h | 236 578 | 2.8 μm(0.6 pixel) |
| 数据集-5 | 近11 h | 605 616 | 2.5 μm(0.4 pixel) |

|
| 图 4 利用试验数据集-1自动提取的连接点在影像中的分布 Fig. 4 Distribution of the tie-points extracted from experimental dataset-1 |

|
| 图 5 一个自动匹配的连接点示例 Fig. 5 An example of tie-point which automatic extracted from the oblique aerial images |
在对比试验中,分别采用市场上较为普遍的商业化软件,即Acute3D的Smart3DTM(V4.3.0.506)、AGISOFT的PhotoScanTM(V1.2.0,64位)软件系统对数据集-5在相同型号配置的机器上进行了自动空三数据处理,处理结果见表 3。需要说明的是,由于数据量过大(3720景影像,单景影像大小为10 320×7750 pixel),在使用PhotoScan软件时降低了影像的分辨率(原影像大小的1/2)。由表 3可以看出,文章所提出的算法在数据处理时间,连接点数量及分布、连接点提取精度等方面达到了可与这些商业化软件相比较的结果。
| 软件名称 | 处理时间 | 连接点点数 | 自由网平差精度(单位权中误差) |
| Smart3DTM | 10.6 h | 591 422 | 3.5 μm(0.6 pixel) |
| PhotoScanTM | 32 h 8 min | 1 256 065 | 2.5 μm(0.4 pixel) |
| 本文算法 | 近11 h | 605 616 | 2.5 μm(0.4 pixel) |
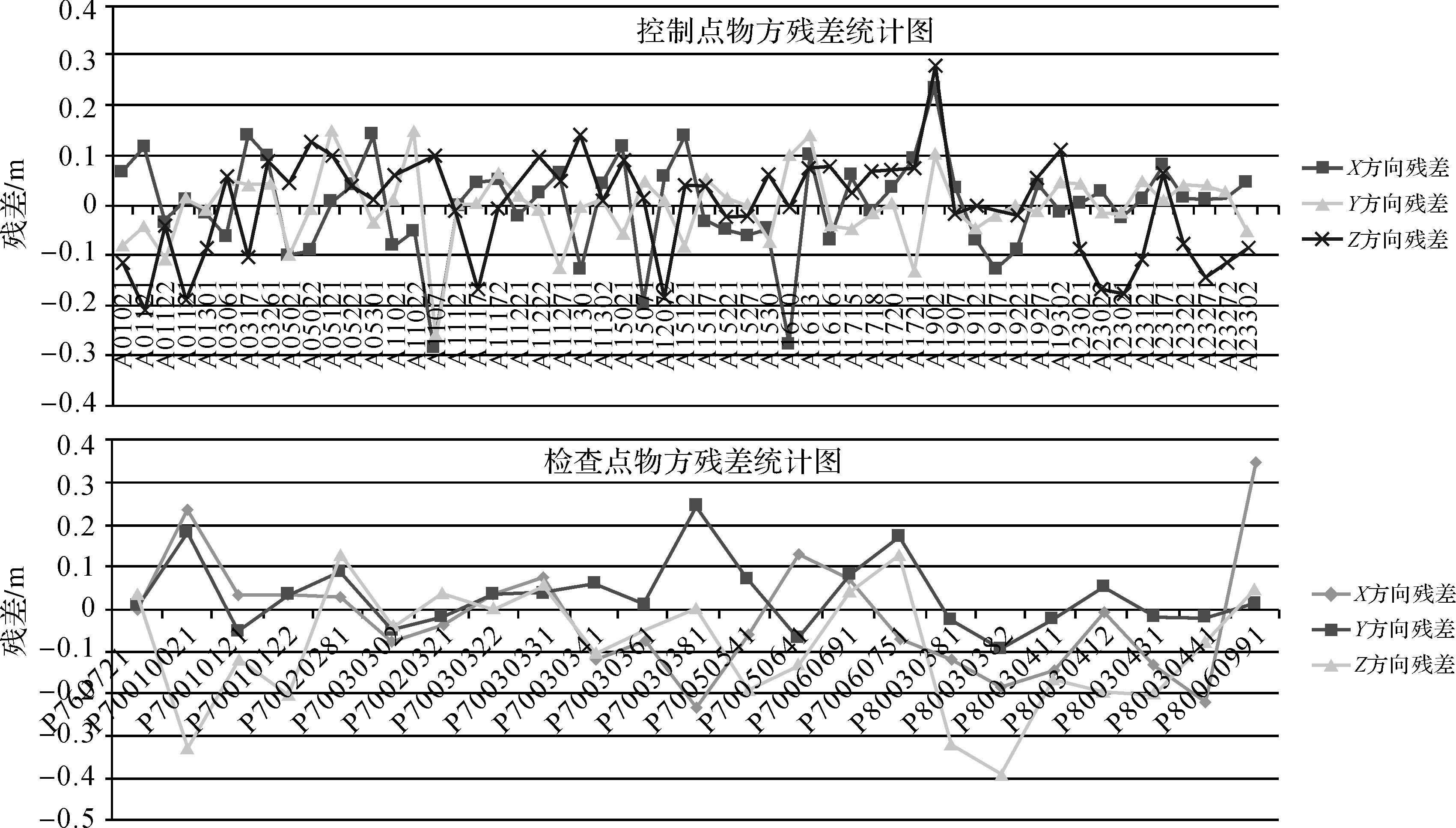
在试验数据集-5中,全区均匀分布有55个GPS平高控制点,其中23个GPS点可作为检查点,且所有的点都为明显地物点。在精确量测出所有控制点和检查点后进行联合区域网平差(残差分布见图 6)。其中,平差后像点单位权中误差为σ0=2.7 μm;控制点残差X方向中误差为0.096 m, Y方向为0.070 m, Z方向为0.100 m;检查点残差X方向中误差为0.137 m, Y方向为0.230 m, Z方向为0.167 m。该精度应该可以满足1:1000比例尺的地形图测绘。从利用该组数据进行的平差试验可以看出:利用所有影像(包括下视影像和所有方向的倾斜影像)进行联合区域网平差后高程中误差与平面中误差基本相同,显示使用所有影像进行联合平差在高程精度方面得到了提高,部分原因是引入倾斜方向的影像后像点的空间交会条件增强。
|
| 图 6 试验数据集-5区域网平差控制点及检查点残差示意图 Fig. 6 Illustration of residuals of GCPs and check points for the experimental dataset-5 |
为进一步验证该结论,选取另外一组更高分辨率的小数据集(包含4条航带,429景UltraCam UCO影像,GSD为5 cm,7个地面控制点),分别针对所有影像和仅下视影像使用文中所提的算法进行了平差试验。由表 4中控制点的残差数据可以看出,利用所有影像联合区域网平差的精度相对于仅仅利用下视影像得到了较明显的提高。但同时由于倾斜视影像的分辨率相较直下视影像一般要低一些,所以在高程方向上精度的提高并不如预想的显著。随后的试验中需要利用更多的数据进行详尽验证。
| cm | |||||||
| 点号 | 所有影像 | 仅下视影像 | |||||
| X残差 | Y残差 | Z残差 | X残差 | Y残差 | Z残差 | ||
| G357 | 2.1 | 0.4 | 2.6 | -0.8 | 1.7 | -11.2 | |
| G358 | 0.5 | -1.3 | -2.9 | 1.0 | 3.5 | -5.9 | |
| G359 | -2.7 | 0.2 | -11.2 | 1.3 | -1.0 | 8.4 | |
| G382 | -0.7 | 0.8 | 10.3 | 1.8 | 2.4 | -17.8 | |
| G0031 | -0.8 | -0.6 | -30.2 | -0.5 | -4.4 | 53.5 | |
| G0182 | -0.2 | 1.1 | 10.7 | -0.6 | -1.3 | -19.1 | |
| G0184 | 1.6 | -0.4 | 7.5 | -3.7 | -2.5 | -11.5 | |
5 结论
本文在分析国内外针对倾斜摄影影像数据自动空三处理算法的基础上,提出了一种实用化的倾斜航空影像全自动连接点匹配和联合区域网平差方法。一方面,针对倾斜航空影像因遮挡严重,尺度变化大和几何变形严重而引起的同名点匹配困难问题,充分利用POS数据等初始数据,同时顾及这些数据的误差,通过有效组合一种改进的ASIFT算法和基于窗口的多角度多视影像匹配模型WMVM,使用由粗到细的多分辨率分层匹配策略完成连接点的全自动提取;另一方面,本文在传统的最小二乘光束法平差的基础上,根据倾斜航空影像数据的特点,提出了基于稳健估值原理的粗差自动探测与剔除关键算法。本文提出的组合方法避免了现有大多数算法所采用的类似于“盲搜索”和“穷举法”、预先纠正倾斜视影像等耗时且稳健度低的缺陷,是一种实用化的解决倾斜影像自动空三的方法。
最后,利用多组传感器(如UltraCam UCO、SWDC-5等)和城市中心区、居民区和城乡结合部等典型试验区域的倾斜航空影像数据针对算法的性能进行了大量试验,试验结果验证了所研发的算法的可靠性、精度和实际性能,结果见图 5、图 6。
| [1] | 王伟, 黄雯雯, 镇姣. Pictometry倾斜摄影技术及其在3维城市建模中的应用[J]. 测绘与空间地理信息, 2011, 34(3): 181–183. WANG Wei, HUANG Wenwen, ZHEN Jiao. Pictometry Oblique Photography Technique and Its Application in 3D City Modeling[J]. Geomatics & Spatial Information Technology, 2011, 34(3): 181–183. |
| [2] | 杨久勇, 高峰, 向宇. 倾斜航空摄影的原理与特点[C]//中国测绘学会2010年学术年会论文集. 南京: 中国测绘学会, 2010: 341-344. YANG Jiuyong, GAO Feng, XIANG Yu. Principle & Characteristics of the Oblique Aerial Photogrammetry[C]//Proceedings of the Society of Geodesy、Photogrammetry and Cartography. Nanjing:China Surveying and Mapping Society, 2010:341-344. |
| [3] | 田野, 向宇, 高峰, 等. 利用Pictometry倾斜摄影技术进行全自动快速三维实景城市生产——以常州市三维实景城市生产为例[J]. 测绘通报, 2013(2): 59–62. TIAN Ye, XIANG Yu, GAO Feng, et al. Automatic and Fast 3D True City Production Based on Pictometry Oblique Photogrammetry Technology[J]. Bulletin of Surveying and Mapping, 2013(2): 59–62. |
| [4] | 桂德竹, 林宗坚, 张成成. 倾斜航空影像的城市建筑物三维模型构建研究[J]. 测绘科学, 2012, 37(4): 140–142. GUI Dezhu, LIN Zongjian, ZHANG Chengcheng. Research on Construction of 3D Building Based on Oblique Images from UAV[J]. Science of Surveying and Mapping, 2012, 37(4): 140–142. |
| [5] | WEITH-GLUSHKO S, SALVAGGIO C. Automatic Tie-point Generation for Oblique Aerial Imagery:An Algorithm[EB/OL].[2012-03-10]. http://testcis.cis.rit.edu/cnspci/references/theses/senior/weith-glushko2004.pdf. |
| [6] | RUPNIK E, NEX F, REMONDINO F. Automatic Orientation of Large Blocks of Oblique Images[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences:XL-1/W1. Hannover:ISPRS, 2013:299-304. |
| [7] | 姚国标, 邓喀中, 张力, 等. 融合互补仿射不变特征的倾斜立体影像高精度自动配准方法[J]. 测绘学报, 2013, 42(6): 869–876. YAO Guobiao, DENG Kazhong, ZHANG Li, et al. An Automated Registration Method with High Accuracy for Oblique Stereo Images Based on Complementary Affine Invariant Features[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 869–876. |
| [8] | WIEDEMANN A, MORé J. Orientation Strategies for Aerial Oblique Images[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences:XXXIX-B1. Melbourne:ISPRS, 2012:185-189. |
| [9] | 闫利, 费亮, 叶志云, 等. 大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–317. YAN Li, FEI Liang, YE Zhiyun, et al. Automatic Tie-points Extraction for Triangulation of Large-scale Oblique Multi-view Images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 310–317. DOI:10.11947/j.AGCS.2016.20140673 |
| [10] | 戴激光, 王新亮, 郭一洋. 一种稳健的倾斜航空影像粗差探测方法[J]. 测绘通报, 2014(5): 28–31. DAI Jiguang, WANG Xinliang, GUO Yiyang. A Robust Method of Gross Error Detection for Oblique Aerial Image[J]. Bulletin of Surveying and Mapping, 2014(5): 28–31. DOI:10.13474/j.cnki.11-2246.2014.0151 |
| [11] | NISTÉR D. An Efficient Solution to the Five-point Relative Pose Problem[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(6): 756–770. DOI:10.1109/TPAMI.2004.17 |
| [12] | LÄBE T, FÖRSTNER W. Automatic Relative Orientation of Images[C]//Proceedings of the 5th Turkish-German Joint Geodetic Days. Berlin:[s.n.], 2006. |
| [13] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [14] | MATAS J, CHUM O, URBAN M, et al. Robust Wide-baseline Stereo from Maximally Stable Extremal Regions[J]. Image and Vision Computing, 2004, 22(10): 761–767. DOI:10.1016/j.imavis.2004.02.006 |
| [15] | MIKOLAJCZYK K, SCHMID C. Scale & Affine Invariant Interest Point Detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63–86. DOI:10.1023/B:VISI.0000027790.02288.f2 |
| [16] | YANG Huachao, ZHANG Shubi, WANG Yangbo. Robust and Precise Registration of Oblique Images Based on Scale-invariant Feature Transformation Algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 783–787. DOI:10.1109/LGRS.2011.2181485 |
| [17] | YU Yinan, HUANG Kaiqi, CHEN Wei, et al. A Novel Algorithm for View and Illumination Invariant Image Matching[J]. IEEE Transactions on Image Processing, 2012, 21(1): 229–240. DOI:10.1109/TIP.2011.2160271 |
| [18] | MOREL J M, YU Guoshen. ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 438–469. DOI:10.1137/080732730 |
| [19] | ZHANG Li. Automatic Digital Surface Model (DSM) Generation from Linear Array Images[D]. Zurich:Institute of Geodesy and Photogrammetry, ETH Zurich, 2005. |
| [20] | ZHANG Li, GRUEN A. Multi-image Matching for DSM Generation from IKONOS Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 195–211. DOI:10.1016/j.isprsjprs.2006.01.001 |
| [21] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002. LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002. |


