2. 西安测绘研究所, 陕西 西安 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
我国全球卫星导航系统试验卫星已搭载新型星间链路载荷。星间链路载荷提供的高精度星间/星地观测量可以弥补我国北斗卫星导航系统监测站区域布设缺陷,提高系统综合服务性能[1-2]。同时,星间测量技术的引入也为导航卫星弱化地面系统支持,实现自主导航提供了可能。
利用星间测量改善导航卫星定轨精度不是一个新话题。早在20世纪90年代GPS正式运行阶段,美国就开展了基于UHF测量体制的星间链路增强定轨研究工作[3]。文献[4-10]等研究结果表明,当由UHF星间测距导出距离测量噪声为2.92 m,钟差测量噪声为0.23 m,且星间测量系统偏差包含常数项和周期项条件下,当全球布设地面监测站数量为12个时,相对于独立使用地面站伪距相位数据,增加星间链路数据后轨道和钟差确定精度可提高10%;当全球布设地面监测站数量为18个时,星间链路数据对钟差确定精度的改善同样超过10%。考虑到数据仿真采用的UHF星间测距精度相比伪距测量精度低一个数量级,且美国地面监测站可全球优化布设,因此,上述结果并不能完全体现星间链路技术的优势。文献[11-13]系统分析了Ka星间测量体制下星间测量对精密定轨的贡献,其仿真结果表明,在假设Ka星间测距噪声为10 cm的条件下,1个地面监测站与星间链路数据组合,定轨精度优于26 cm,钟差确定精度优于0.2 ns,已能够满足常规导航星历更新精度需求。俄罗斯GLONASS系统面临与中国北斗类似的地面监测站区域布设问题,因此在星间链路应用研究方面给予了更多的重视。早期GLONASS卫星搭载S波段星间测距载荷,其测量噪声在0.4 m左右。最新GLONASS卫星搭载激光星间链路,星间测量噪声优于10 cm,能够达到的星地联合定轨精度为轨道三维位置误差小于0.5 m,径向误差小于1 cm,时间同步精度优于2 ns,预报12 h优于6 ns。自主定轨误差轨道径向可小于50 cm,沿迹方向小于110 cm[14]。上述结果表明,星间测量对导航卫星定轨及时间同步精度有显著改善。
目前,我国北斗导航系统在轨试验卫星已经有5颗装备星间链路载荷,同时有若干个地面站具备Ka星地测量功能,已经能够提供连续稳定的星间、星地观测数据。我国星间链路载荷精度水平如何,星间测量能在多大程度上改进导航卫星轨道是需要评估的问题,本文给出了实测数据用于定轨的初步试验结果。
1 星间测量观测方程及数据预处理北斗星间链路采用Ka星间体制[15, 17],按照预定路由规划表,每颗卫星采用时分方式与可建链卫星或地面站构建星间、星地测量链路。每次建链,每对卫星分时产生双向星间测距观测量。采用双向测量的主要原因是利用双向测量可解耦得到星间测距观测量和星间时间同步观测量。由于Ka星间双向测量并非严格意义上的双向同步观测,因此,需要对Ka星间观测量进行预处理[15-21]。双向星间测距观测方程为
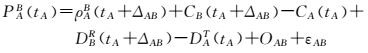 (1)
(1)
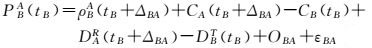 (2)
(2)
式中,PAB、PBA分别星间双向观测量;tA、tB分别为卫星A、B信号名义发射时刻,由星间链路路由规划确定;ρAB、ρBA分别为A、B卫星相互收发时刻的星间距;ΔAB、ΔBA分别为信号传播时延;CA、CB分别为A、B卫星钟差;DAT、DAR为卫星A接收及发射时延;DBT、DBR为卫星B接收及发射时延,考虑到设备收发时延的相对稳定性,可认为该项时延在3 d内为常数;OAB、OBA为天线相位中心改正、相对论等其他观测修正量;εAB、εBA为测量噪声。地面Ka观测站可作为伪卫星处理,同时需要在测量模型上增加对流层时延修正。电离层对Ka星间测量影响在亚厘米级,可不考虑。
星间双向数据预处理目标是将一对互测卫星之间观测时刻不同的双向观测量归化到同一观测时刻,以便分离钟差和距离观测量。本文预处理采用两步预处理方式,第1步,将不同发射时刻的一对观测量归化到同一观测时刻,同时修正相对论、天线相位改正和星地对流层等测量误差。第2步则利用时间归化后的观测量组合形成特定时刻瞬间星间伪距观测量。
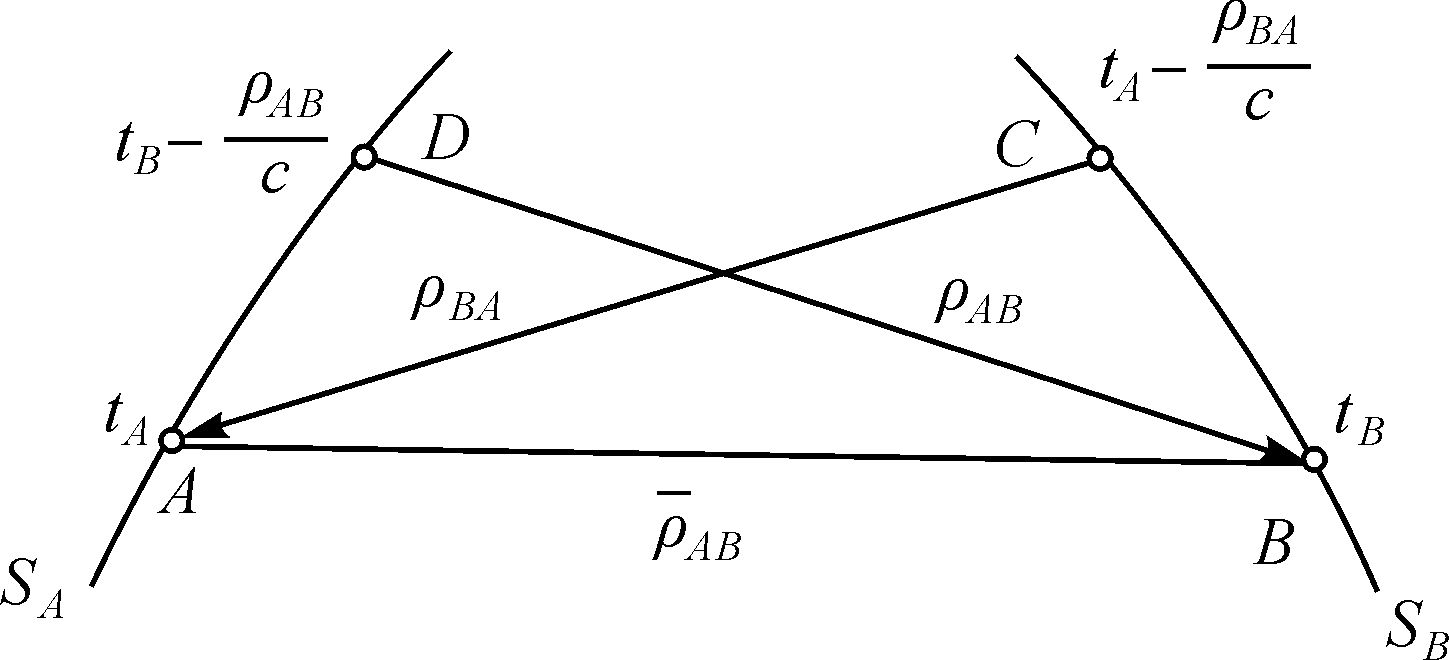
利用星间同一发射时刻星间双向测距观测量计算瞬间星间距原理如图 1所示。
|
| 图 1 星间双向测距预处理原理 Fig. 1 The preprocessing method for the dual ISL observation |
假设经过历元归化后的接收时刻tA、tB为同一时刻t0,ρAB为瞬间距离值,ρAB、ρBA为时刻t0对应的包含传播时延的距离,则有
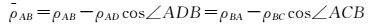 (3)
(3)
式中,ρAD、ρBC可利用卫星先验轨道确定,其精度主要取决于卫星速度精度,目前卫星速度误差在毫米/秒量级,由此可估计出ρAD、ρBC计算误差在毫米级。如果卫星先验速度误差大于毫米/秒,则需要通过其他观测量改进轨道或采用迭代计算法减小预处理误差。
利用预处理后的瞬间星间伪距观测量组合可形成星间距观测方程和星间时间同步观测方程如下
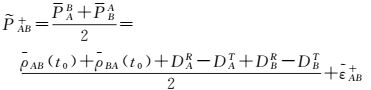 (4)
(4)
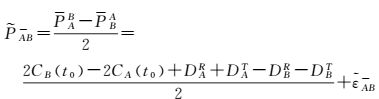 (5)
(5)
式中,PAB、PBA为经过预处理后t0时刻瞬间伪距观测量;ρAB(t0)=ρBA(t0)为t0时刻星间距理论值;CA、CB分别为卫星瞬间钟差;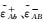
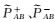
由上式看出,对于星间测距观测量而言,系统误差为每颗卫星收发时延之差相加,而对于时间同步观测量而言,系统误差则表现为每颗卫星收发时延之和相减。
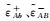
星间双向测距经过预处理可得到特定测量时刻的瞬间星间距观测量,借助卫星运动动力学方程,可构建瞬间星间测距观测量与卫星初始动力学参数之间的关系方程,采用最小二乘或滤波等最优参数估计方法解算该方程可得到改进的卫星动力学参数。
卫星动力学方程为
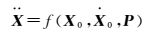 (6)
(6)
利用先验轨道及动力学参数,采用数值积分法对上述方程及其对应的变分方程积分可得到特定历元的参考轨道和状态转移矩阵。利用参考轨道对星间链路观测方程线性化,可得到线性化观测方程如下
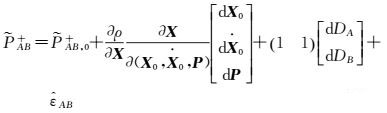 (7)
(7)
式中,
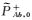
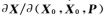
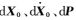
上述方程建立了预处理后的星间测距观测量与卫星先验轨道参数之间的关联,组合多天观测量,采用最小二乘估计可得到改进的卫星状态参数改正值。经过迭代计算可得到最终修正后的轨道和星间测量系统偏差参数。
上述动力学定轨过程涉及卫星轨道动力学模型的选择,本次定轨采用与地面L波段定轨类似的动力学模型,即地球引力场模型考虑到30阶次。考虑日月引力,日月位置利用JPL星历计算;考虑太阳光压力,太阳光压先验模型采用ROCK模型。同时利用Bernese ECOM模型估计经验力,考虑相对论和固体潮引力位影响。地球自转参数采用IERS B公报值。
定轨精度的评价可采用轨道重叠弧段法[17, 22]、激光测量或与其他地面L波段载波相位数据与Ka数据联合定轨软件结果互比法[25]。本文主要采用轨道重叠弧段法以及激光评估法。
3 试验结果分析利用2015年11月26日—11月30日北斗试验卫星实测Ka星间/星地数据进行精密定轨试验。试验卫星编号Sat31、Sat33、Sat34,地面Ka站编号A1,同时采集了地面6个站L波段观测数据。
定轨采用两种方式,第1种是完全采用星间和星地Ka数据定轨,评价自主定轨精度;第2种则是采用地面L波段数据与Ka数据联合定轨,评价Ka数据对L波段定轨结果的贡献。
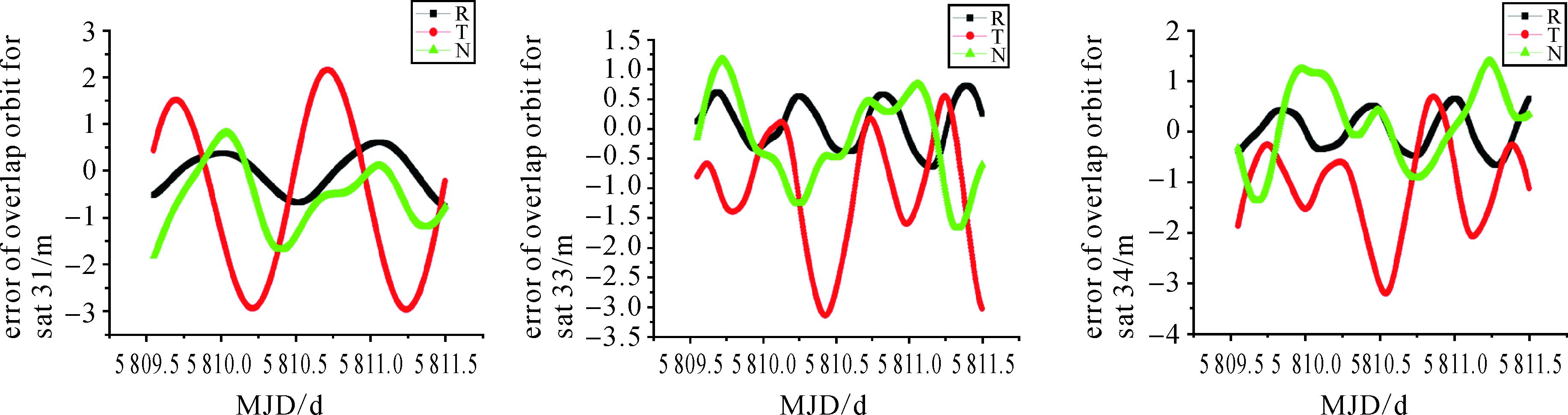
3.1 Ka独立定轨结果分别利用11月27日—29日以及11月28日—30日3颗卫星一个地面站3 d星间链路数据,采用动力学方法定轨,解算参数包括:每颗卫星6个初始轨道状态参数和5个太阳光压参数,每颗卫星解算1个收发时延参数。地面站估计1个收发时延参数,其坐标固定采用ITRF2005实测值。卫星和地面站收发时延参数对应于式(5) 中的距离偏差,相当于每颗卫星收发时延之和。用轨道重叠弧段精度评价定轨精度,结果见图 2,其中R、T、N分别代表轨道面径向、沿迹和法向3方向。
|
| 图 2 卫星轨道重叠弧段统计 Fig. 2 The statistic of the overlap orbit error for Ka only data |
分别对上述3颗卫星轨道重叠弧段进行统计。Sat31轨道3个方向误差分别为径向0.403 m、沿迹1.814 m、法向0.858 m;Sat33轨道3方向误差分别为径向0.405 m、沿迹1.421 m、法向0.773 m;Sat34轨道3方向误差分别为径向0.372 m、沿迹1.409 m、法向0.795 m。
为检核上述定轨结果,搜集了同期激光观测数据进行精度评估。全球激光数据非常有限,上述时段内针对试验卫星仅有编号为7941的站对Sat33卫星有3个激光标准点测量。该3个激光测量点激光评估误差分别为-0.244 m、-0.188 m、-0.170 m,与重叠弧短评估的轨道径向误差统计值精度相当。
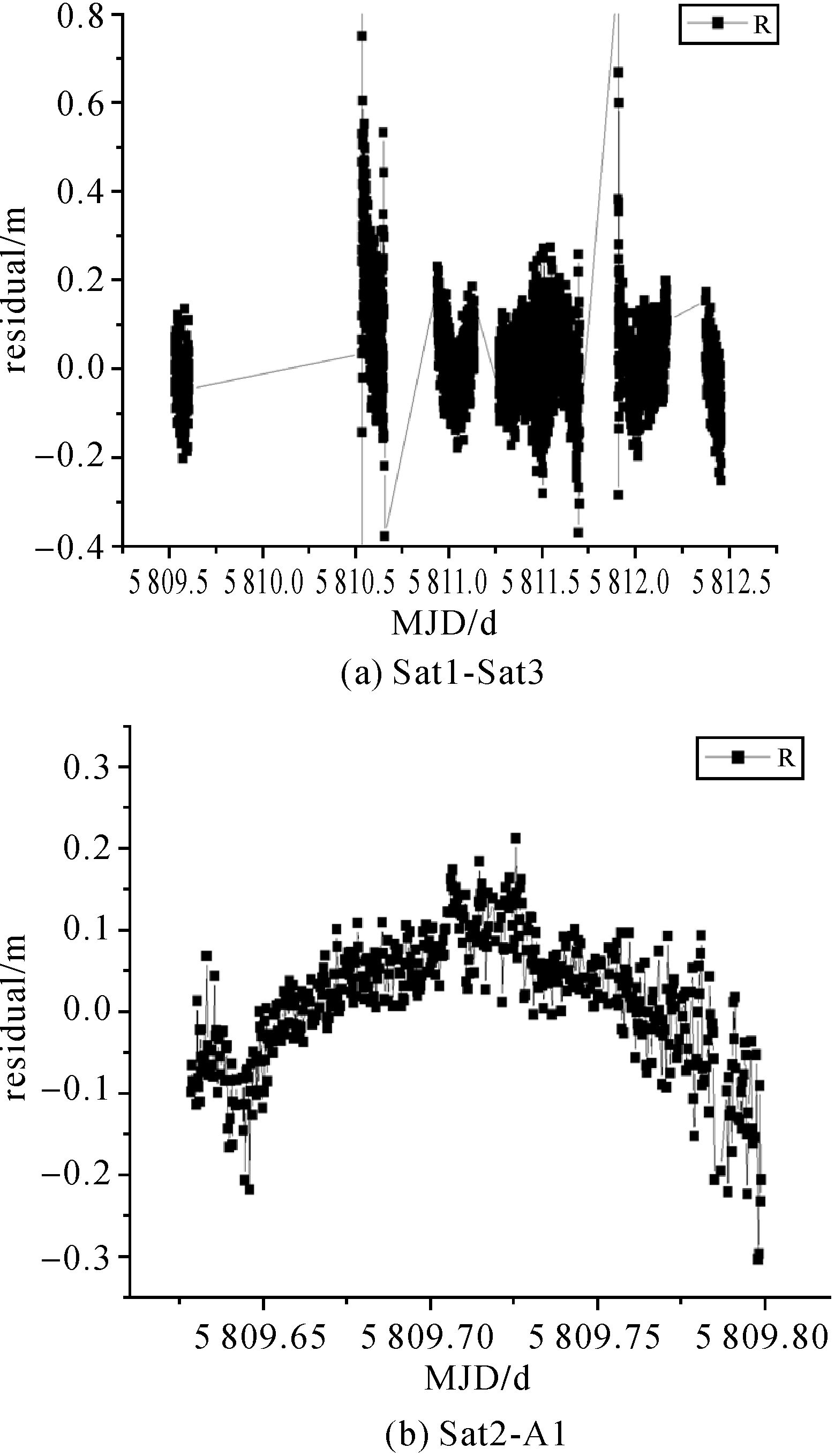
上述结果表明,独立采用星间链路定轨,轨道三维位置误差小于3 m, R方向误差小于0.5 m(见图 3)。星间链路测量残差小于0.2 m;通过对残差进行短期(1 h内)一阶多项式拟合看出测量高频噪声小于0.1 m。上述结论也在笔者与同期其他软件定轨结果的互比中得到验证。需要指出的是,由于激光数据有限,上述结果主要采用轨道重叠弧段统计结果。
|
| 图 3 定轨残差统计图 Fig. 3 The statistic of the residual error |
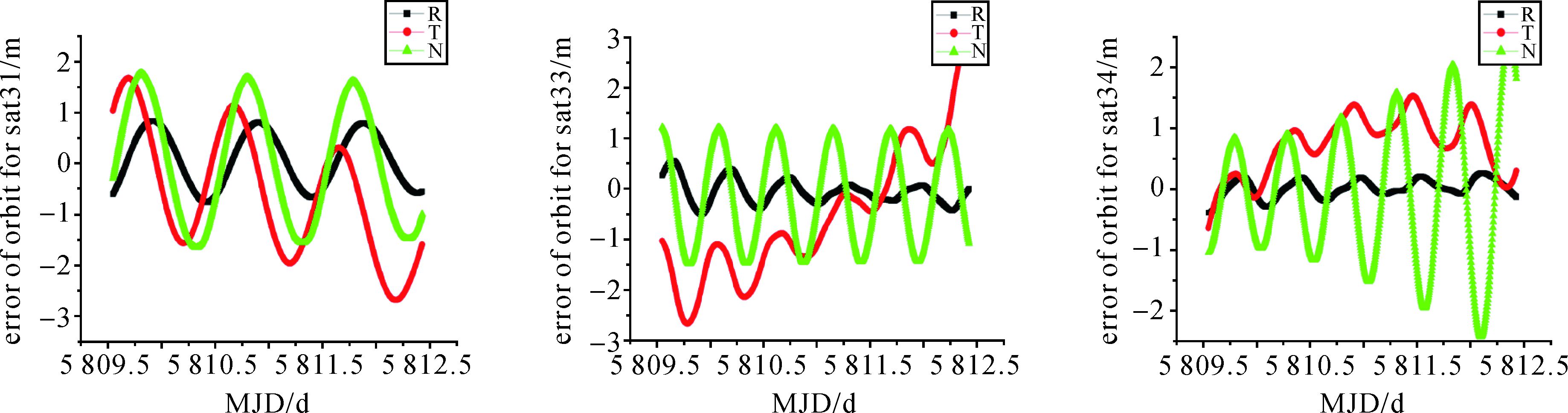
将Ka定轨结果与国内6个监测站L波段载波相位定轨结果比较,结果见图 4。
|
| 图 4 国内站L波段定轨结果与Ka独立定轨结果互比 Fig. 4 The orbit error between L-Band and Ka observation |
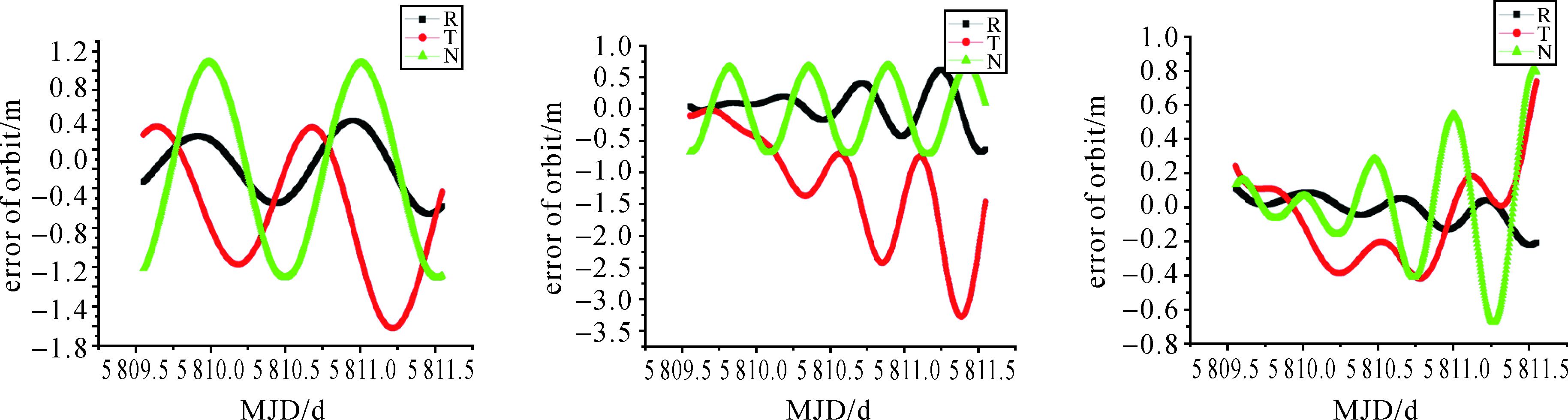
由图 4看出,除了卫星Sat31轨道径向方向误差稍大外,其余两颗卫星国内6个地面站定轨结果与独立采用Ka数据定轨结果误差最大值小于3 m。6个地面站L波段载波相位定轨结果为地面运控系统结果,其轨道径向定轨误差小于0.3 m[23](见图 5)。
|
| 图 5 试验卫星L波段定轨误差(Sat1、Sat2、Sat3) Fig. 5 The orbit error for the orbit determination with L-band observation |
| m | |||
| 链路编号 | 残差标准差 | 残差最大值 | 残差最小值 |
| Sat1-Sat2 | 0.104 | 0.971 | -0.753 |
| Sat1-Sat3 | 0.142 | 0.994 | -0.540 |
| Sat2-Sat3 | 0.072 | 0.244 | -0.175 |
| Sat1-A1 | 0.116 | 0.128 | -0.297 |
| Sat2-A1 | 0.067 | 0.143 | -0.141 |
| Sat3-A1 | 0.080 | 0.212 | -0.304 |
利用上述方法定轨同时可解算得到每颗卫星和地面Ka站的设备时延参数。结果表明两个弧段解算的卫星和地面设备时延整数部分相同,小数部分差异见表 2。
| m | |||||
| 卫星编号 | 11月27日—29日 | 11月28日—30日 | |||
| 时延小数部分 | 解算中误差 | 时延小数部分 | 解算中误差 | ||
| Sat1 | .833 5 | 0.006 0 | .877 8 | 0.022 4 | |
| Sat2 | .696 3 | 0.004 8 | .640 0 | 0.018 6 | |
| Sat3 | .655 7 | 0.007 8 | .582 7 | 0.020 0 | |
| A1 | .455 2 | 0.008 2 | .734 1 | 0.068 6 | |
由表 2可以看出,除了锚固站外,解算的设备时延参数短期稳定性较好。为评估设备时延参数长期稳定性,采用上述同样处理策略处理了2016年3月31日—4月1日3 d Ka星间、星地数据,将解算的时延参数与上述结果比较,最大误差小于0.55 m。说明设备时延参数短期变化相对稳定,短期内将时延参数作为常数解算是合理的。
上述结论与全球系统星间链路仿真数据定轨结果精度有差距,分析原因,可能由于目前试验卫星仅有3颗,定轨几何结果相对较弱,链路拓扑不稳定,随着卫星数量的增加以及链路路由规划策略的合理化,定轨精度可进一步改善。
3.2 Ka与L波段联合定轨结果为评估Ka星间测距观测量对星地联合定轨的影响,利用11月27日—30日Ka星间数据与同期地面6个测站L波段伪距相位观测数据进行联合定轨试验。联合定轨估计的参数包括:每颗卫星估计6个初始状态参数和5个光压参数, L波段监测站坐标固定,同时估计卫星和L波段地面监测站钟差参数以及载波相位模糊度参数和对流层参数[17, 23-25],对于Ka观测量,每颗卫星估计1个设备时延参数。利用轨道重叠弧段评估定轨精度。
独立采用地面L波段数据定轨,轨道重叠弧段误差见图 5。
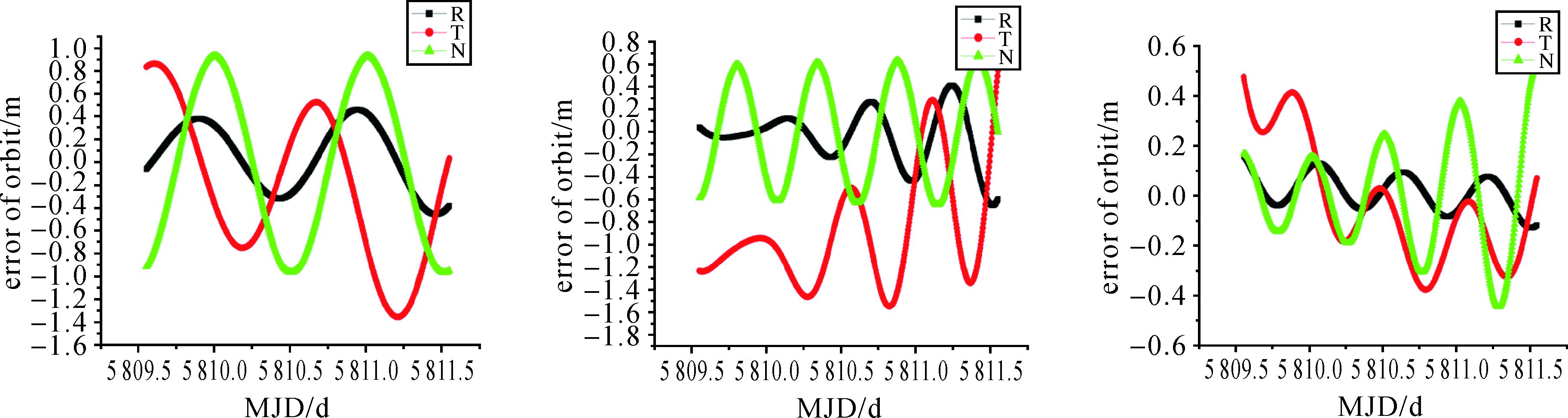
增加Ka观测数据后, L波段数据与Ka数据组合定轨,轨道重叠弧段误差见图 6。
|
| 图 6 试验卫星L波段与Ka组合定轨误差(S1、S2、S3) Fig. 6 The orbit error for the orbit determination with Ka observation and L-band observation |
定轨结果统计比较见表 3。
| m | |||||||
| 卫星编号 | L波段独立定轨 | L波段数据与Ka数据联合定轨 | |||||
| R | T | N | R | T | N | ||
| S1 | 0.291 | 0.794 | 0.771 | 0.288 | 0.691 | 0.668 | |
| S2 | 0.281 | 1.515 | 0.491 | 0.240 | 1.023 | 0.441 | |
| S3 | 0.081 | 0.257 | 0.313 | 0.071 | 0.239 | 0.217 | |
利用同期7941号激光站对Sat33卫星联合定轨结果进行评估,3个测量点评估结果分别为-0.192 m、-0.168 m、-0.156 m。对比独立Ka定轨结果,精度有改善。
从表 3可以看出,增加Ka星间链路数据后,卫星定轨精度有所改善,其中R和T方向改善较为突出。考虑到试验卫星Ka星间链路在上述定轨弧段有一半以上时间仅有1条或两条链路,可以设想,如果链路数量完整,星地联合定轨结果改善将会更加显著。
4 结论高精度星间链路数据如何处理以及其对导航卫星定轨精度能有何种程度的改善是我国全球卫星导航系统需要解决的问题。本文从我国北斗试验卫星实测高精度星间链路数据出发,研究了星间链路数据预处理方法,给出了独立利用星间链路数据定轨的初步结果,分析了Ka星间链路数据对L波段定轨结果的贡献。分析结果表明,试验卫星星间链路测量具有较高的精度和稳定性,测量噪声优于10 cm。一个地面锚固站星地链路与星间链路数据定轨,除了轨道面沿迹方向精度稍差外,轨道径向和法向于地面6个L波段监测站定轨精度相当。Ka星间链路数据与L波段数据联合定轨能够改善L波段定轨精度。
高精度星间链路数据处理对于我国卫星导航系统而言是相对较新的技术,本文的结果并没有对星间测量系统差变化特性等进行深入分析,星间链路定轨结果仍有许多改进余地,本文主要结论仅体现了初步结果,星间链路数据处理方向后续仍需要更加深入的工作。
致谢: 特别感谢上海天文台胡小工研究员、唐成盼博士给予的帮助。
| [1] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 57(1): 144–152. YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 57(1): 144–152. |
| [2] | 杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 40(5): 505–510. YANG Yuanxi. Concepts of Comprehensive PNT and Related Key Technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 40(5): 505–510. DOI:10.11947/j.AGCS.2016.20160127 |
| [3] | PARKINSON B W, SPILKER J J Jr, AXELRAD P, et al. Global Positioning System:Theory & Applications[M]. Washington D C: American Institute of Aeronautics and Astronautics, 1996. |
| [4] | MERRIGAN M J, SWIFT E R. Expected Improvement in NIMA Precise Orbit and Clock Estimates Due to Adding Crosslink Ranging Data[R]. NSWCDD/TR-99/98. Dahlgren, Virginia:[s.n.], 1999. |
| [5] | ABUSALI P A M, TAPLEY B D, SCHUTZ B E. Autonomous Navigation of Global Positioning System Satellites Using Cross-link Measurements[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 321–327. DOI:10.2514/2.4238 |
| [6] | RAJAN J A. Highlights of GPS Ⅱ-R Autonomous Navigation[C]//Proceedings of the ION 58th Annual Meeting of the Institute of Navigation and CIGTF 21st Guidance Test Symposium. Albuquerque, NM:[s.n.], 2002. |
| [7] | RAJAN J A, ORR M, WANG P. On-Orbit Validation of GPS ⅡR Autonomous Navigation[C]//Proceedings of the ION 59th Annual Meeting of the Institute of Navigation and CIGTF 22nd Guidance Test Symposium. Albuquerque, NM:[s.n.], 2002. |
| [8] | RAJAN J A, BRODIE P, RAWICZ H. Modernizing GPS Autonomous Navigation with Anchor Capability[C]//Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS/GNSS 2003). Portland, OR:ION. 2003:1534-1542. |
| [9] | EBERHARD G. Precise GNSS-2 Satellite Orbit Determination Based on Inter-satellite-links[C]//Proceedings of the 14th International Symposium on Space Flight Mechanics. Iguassu, Brazil:William Park & Associates Ltd., 1999. |
| [10] | WU A. Estimate of the GPS Block ⅡR AutoNav Clock Behavior[C]//Proceeding of the 1999 Joint Meeting of the European Frequency and Time Forum, 1999 and the IEEE International Frequency control Symposium. Besancon, France:IEEE, 1999:279-282. |
| [11] | WOLF R. Satellite Orbit and Ephemeris Determination Using Inter Satellite Links[D]. Munchen:University of Munchen, 2000. |
| [12] | FERNÁNDEZ F A. Inter-satellite Ranging and Inter-satellite Communication Links for Enhancing GNSS Satellite Broadcast Navigation Data[J]. Advances in Space Research, 2011, 47(5): 786–801. DOI:10.1016/j.asr.2010.10.002 |
| [13] | HAMMESFAHR J, HORNBOSTEL A, HAHN J, et al. Usage of Two-directional Link Techniques for Determination of the Satellite State for GNSS-2[C]//Proceedings of 1999 National Technical Meeting of the Institute of Navigation. San Diego, CA:[s.n.], 1999:531-540. |
| [14] | IGNATOVICH E I, SCHEKUTJE A F. Results of Imitating Tests of Some Versions of Onboard Algorithms for SC Glonass Intersatellite Measurement Processing[C]//15th Saint Petersburg International Conference on Integrated Navigation Systems. Saint Petersburg, Russia, 2008:348-355. |
| [15] | 毛悦, 宋小勇, 贾小林, 等. 星间链路观测数据归化方法研究[J]. 武汉大学学报(信息科学版), 2013, 38(29): 1201–1206. MAO Yue, SONG Xiaoyong, JIA Xiaolin. Naturalisation Method Research on Inter-satellite Link Observation Data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(29): 1201–1206. |
| [16] | KIM J. Simulation Study of a Low-low Satellite-to-satellite Tracking Mission[D]. Austin:University of Texas at Austin, 2000. |
| [17] | 宋小勇. 北斗导航卫星精密定轨技术研究[D]. 西安: 长安大学, 2009. SONG Xiaoyong. Study on the Orbit Determination of Compass Navigation Satellite[D]. Xi'an:Chang'an University, 2009. |
| [18] | 牛飞, 韩春好, 张义生, 等. 基于星间链路支持的导航卫星自主完好性监测设计仿真[J]. 测绘学报, 2011, 40(S1): 73–79. NIU Fei, HAN Chunhao, ZHANG Yisheng, et al. Design and Simulation for Satellite Autonomous Integrity Monitoring Based on Inter-satellite-links[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 73–79. |
| [19] | 阮仁桂, 冯来平, 贾小林. 导航卫星星地/星间链路联合定轨中设备时延估计方法[J]. 测绘学报, 2014, 43(2): 137–142. RU AN Rengui, FENG Laiping, JIA Xiaolin. Equipment Delay Estimation for GNSS Satellite Combined Orbit Determination with Satellite-ground Link and Inter-satellite Link Observations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 137–142. DOI:10.13485/j.cnki.11-2089.2014.0020 |
| [20] | 耿涛, 刘经南, 赵齐乐, 等. 星地监测网下的北斗导航卫星轨道确定[J]. 测绘学报, 2011, 40(S): 46–51. GENG Tao, LIU Jingnan, ZHAO Qile, et al. Compass Precise Orbit Determination Based on Space Ground Monitoring Network[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 46–51. |
| [21] | 曹月玲, 胡小工, 周善石, 等. 基于星间链路的BDS导航系统实时星历和钟差分离修正[J]. 天文学进展, 2015, 33(1): 122–133. CAO Yueling, HU Xiaogong, ZHOU Shanshi, et al. The Method for Real-time Wide Area Differential Corrections of BDS with Inter Satellite Links[J]. Progress in Astronomy, 2015, 33(1): 122–133. |
| [22] | 杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646–650. YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646–650. |
| [23] | 周善石. 基于区域监测网的卫星导航系统精密定轨方法研究[D]. 上海: 中国科学院研究生院, 2011. ZHOU Shanshi. Studies on Precise Orbit Determination Theory and Application for Satellite Navigation System with Regional Tracking Network[D]. Shanghai:University of Chinese Academy of Sciences, 2011. |
| [24] | SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China Earth Sciences, 2015, 55(7): 1079–1086. |
| [25] | 郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014. GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan:Wuhan University, 2014. |



