2. 中国科学院大学, 北京 100049;
3. 北京卫星导航中心, 北京 100094;
4. 同济大学测量与国土信息工程系, 上海 200092;
5. 德国地学研究中心, 波茨坦 14473
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Satellite Navigation Center, Beijing 100094, China;
4. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China;
5. German Research Center for Geosciences, Potsdam 14473, Germany
中国自主发展和建立的北斗卫星导航系统(BDS)于2012年底向亚太部分地区提供服务。北斗卫星导航系统采用了不同于GPS等系统的独特系统设计,采用更适用于区域卫星导航服务的地球静止轨道(geostationary earth orbit,GEO)卫星和倾斜地球同步轨道(inclined geostationary earth orbit,IGSO)卫星,联合中高轨(medium earth orbit,MEO)卫星的星座设计[1-4]。受限于监测站分布的约束,主控站数据处理对于MEO卫星的可视弧段较短,IGSO卫星也存在出入境情况,GEO卫星几何位置相对于地球静止,使得卫星轨道[5-10]和卫星钟差[11]解算高度相关。以上情况对北斗系统数据处理及高精度服务提出了很高的挑战。
北斗卫星导航系统在系统设计时就融合考虑了基本服务与广域差分的一体化,给用户提供开放以及授权服务。其中,开放服务为用户免费提供基本导航信息,而授权服务为授权用户提供差分和完好性等信息以提高其服务性能[3, 13-14]。北斗广域差分系统在基本导航参数的基础上,利用服务区域内均匀分布的地面监测站数据,计算差分改正数并通过GEO卫星向用户进行广播[15]。
目前北斗广域差分系统播发的参数包括等效钟差改正数以及服务单频授权用户的电离层格网模型[15-17]。其中,等效钟差的处理利用了CNMC(code noise and multipath correction)[18-19]平滑后的伪距观测数据,其包含了卫星轨道的径向误差的改正以及卫星钟差的改正。等效钟差的精度受到伪距残余噪声的限制,并且无法包含卫星轨道误差切向和法向分量的影响。为尽量降低伪距观测值噪声的影响,需要采用相位观测数据。而相位观测数据的引入涉及复杂的模糊度参数计算。相位历元间差分能够消除模糊度参数[20-22],文献[20-21]采用该方法进行低轨卫星的后处理精密定轨;文献[22]采用相位历元间差分实时估计卫星钟差历元间变化及其累加值,同时利用伪距估计钟差的初始偏差,并将该初始偏差加到历元间差分累加值上获取卫星钟差。基于非差伪距数据和相位历元间差分综合的基本思想,本文建立了钟差改正和轨道改正统一处理的广域差分新模型。该模型利用了高精度相位观测值,并新增了轨道改正数。
考虑到现有的用户接收机在不进行协议改造的情况下,只能使用钟差改正数,无法使用轨道改正数。为不影响现有用户的使用,在利用新模型进行广域差分数据处理时,对轨道改正数径向分量进行约束为0,从而得到的轨道改正数包含了轨道误差在轨道切向和法向的改正,其表示在地固坐标系下为包含三维分量的改正数。同时,钟差改正数仍然包含了轨道改正数的径向分量,与现有等效钟差一致。
1 现有广域差分卫星钟差模型任意测站对一颗卫星sat的无电离层组合伪距、相位观测方程为[23-25]
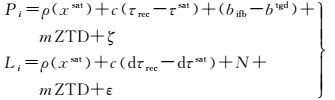 (1)
(1)
式中,Pi、Li分别伪距、相位观测值;ρ为星地理论距离,受卫星轨道xsat误差的影响;i为频点标识;τrec、τsat分别为测站和卫星钟差;bifb、btgd分别为测站和卫星伪距的硬件延迟;N为模糊度参数;m和ZTD为对流层投影函数以及天顶对流层延迟;ζ、ε为包含多路径误差等的噪声。
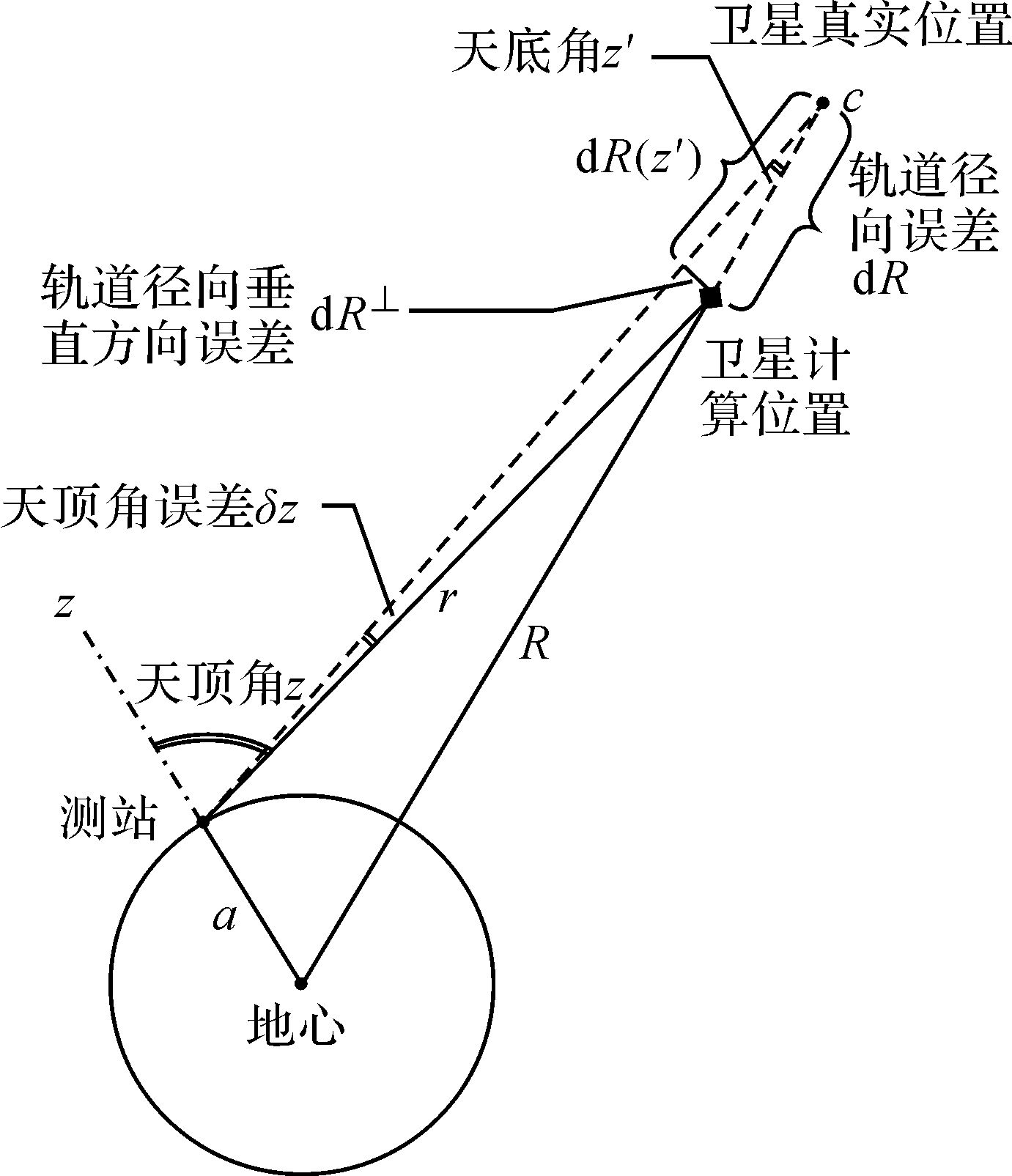
在式(1) 中,卫星伪距硬件延迟频间偏差参数btgd的残余误差会被吸收到卫星钟差中,而测站伪距硬件延迟频间偏差参数bifb的残余误差会被吸收到测站钟差参数中。距离测量中的卫星钟差误差与方向无关,而卫星星历误差对不同用户视线方向投影的影响主要为卫星轨道径向方向,如图 1所示。图中R为卫星距离地心的距离,dR为轨道径向误差,dR⊥为径向垂直方向的轨道误差。从图中可以得出:忽略dR⊥的影响,如果卫星轨道在径向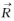
|
| 图 1 卫星轨道误差对测站测距影响示意图 Fig. 1 The satellite orbit errors impact on the ranging of a station |
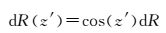 (2)
(2)
超过95%以上轨道径向误差dR会被钟差参数吸收[27],因此轨道误差对用户定位的影响主要是由于不同视向上观测改正的差值ΔdR(z′)[28]
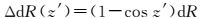 (3)
(3)
根据卫星星座参数,GPS卫星最大天底角约为14°,GLONASS卫星最大天底角约为14.3°,北斗GEO/IGSO卫星最大天底角约为8.7°,而北斗MEO卫星最大天底角约为13.5°。从而以上卫星轨道径向误差在不同天底角引起的测距误差占轨道径向误差的比例为1.2%~3.1%。考虑到目前米级的轨道精度,轨道径向误差在不同方向造成的测距误差在厘米量级。
基于以上讨论,轨道径向误差不同方向造成的测距误差为厘米量级。因此,目前北斗系统采用的广域差分模型忽略了卫星星历在不同方向投影误差的影响,也即式(1) 待求参数只为测站钟差以及卫星钟差。由于卫星钟差参数包含了卫星轨道误差在各站视线方向的平均误差,因此被称为等效钟差。
目前北斗系统采用的广域差分处理中只用到了伪距观测值,首先采用CNMC算法,进行伪距数据多路径误差的实时处理。在此基础上利用导航电文中提供的卫星轨道、钟差以及卫星硬件延迟频间偏差参数对相关误差进行修正;对流层的修正采用监测站实测气象参数,结合经验的大气模型进行修正。计算采用双频无电离层组合观测值,固定测站精确坐标以及一个参考站钟,实时获取其他站钟及卫星等效钟差。
2 伪距相位综合的广域差分新模型 2.1 基本模型等效钟差所采用的计算数据为监测站的伪距观测值,其计算精度受到伪距噪声的影响。虽然CNMC能够减小多路径的误差,但是该算法的有效性较大程度上依赖于相位数据的连续性。在相位观测存在新模糊度时,CNMC需要重新收敛。并且等效钟差模型忽略了轨道在垂直于径向方向的误差影响。图 2表示了轨道各个方向误差引起的用户测距误差,图中,轨道径向方向对用户测距的影响由式(3) 计算。而轨道法向和切向综合方向的误差为dR⊥,其对用户测距的影响dR⊥(z′)为

|
| 图 2 轨道各分量误差对测站测距影响示意图 Fig. 2 Each component of the orbit errors impact on the ranging of a station |
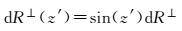 (4)
(4)
测站若位于卫星对地径向方向则测距不受轨道误差dR⊥的影响,而在卫星高度角为0°的时候dR⊥的影响达到最大。根据北斗卫星星座参数,卫星轨道径向垂直方向的误差在不同天底角引起的测距误差占轨道误差dR⊥的比例,GEO/IGSO卫星最大可达15%,MEO卫星最大可达23%。目前北斗GEO卫星轨道切向误差在8~10 m,轨道法向误差约为1~2 m,IGSO/MEO卫星轨道切向和法向误差均为1~2 m[29]。从而轨道法向以及切向的误差在不同视线方向影响较大,全球范围内GEO卫星法向以及切向轨道误差投影差异最大可达到米级,IGSO/MEO卫星法向以及切向轨道误差投影差异最大可达到分米级。对于更高精度的广域差分定位需求,需要在广域差分中考虑轨道在除径向外其他方向上的误差。
基于几何法定轨的原理,定义式(1) 待求参数为dp=(dxsat, dysat, dzsat, dτrec, dτsat)。以伪距观测值为例,将式(1) 展开为
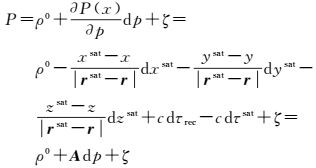 (5)
(5)
式中,ρ0为修正了公共误差的星地几何距离;(xsat, ysat, zsat)为基于广播星历获取的该历元卫星轨道,而risat为其矢量;(dxsat, dysat, dzsat)为待求的轨道改正数;(x, y, z)为测站的坐标;r为其矢量;dτrec、dτsat分别为测站、卫星钟差改正数;A为系数阵。
2.2 相位历元间差分模型为提高广域差分参数求取的精度,需要在伪距观测值处理的基础上增加相位观测值。式(1) 中的相位观测值处理包含了模糊度参数。在实时逐历元处理模式下,模糊度参数的存在将造成实时差分参数存在较长时间的收敛过程;此外在出现数据中断或者周跳的情况下,模糊度参数需要重新收敛。
对式(1) 相邻历元ti、ti-1的相位观测值作差分
 (6)
(6)
式中,Δ为差分算子。可以看到历元间差分后,在没有周跳的情况下,模糊度得到了消除;历元间对流层延迟的差异体现在投影函数的差异上,在轨道改正数更新的周期内(一般为6 min)该项影响可忽略。式(6) 中的待求参数包括卫星轨道、钟差改正数以及测站钟差改正数,由于没有模糊度参数,因此以上方程解算不存在收敛性的问题。并且在相位数据丢失或者发生周跳的情况下,只影响当前历元相位历元间差分数据的处理,不影响后续连续历元。
定义p=(pi, pi-1)为式(6) 的待求参数,应用最小二乘,在p0处将式(6) 写成误差方程的形式
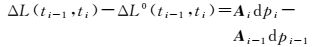 (7)
(7)
式中,Ai、Ai-1为ti、ti-1的系数矩阵。定义dΔpi=dpi-dpi-1为轨道和钟差参数在历元间的变化,同时定义l=ΔL(ti-1, ti)-ΔL0(ti-1, ti),则式(7) 可以重新写为
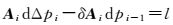 (8)
(8)
式中,δAi=Ai-Ai-1,-δAi中钟差改正数的对应系数为0。轨道改正数对应系数与历元间隔以及卫星运动速度有关,根据文献[21]的分析,忽略δAidpi-1引起的最大误差约为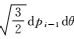
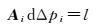 (9)
(9)
以上即为基于相位历元间差分的广域差分改正数模型。模型采用了高精度的相位观测值,消除了模糊度参数,简化了相位观测数据处理的复杂度,提高了广域差分改正数解算的精度。
2.3 伪距相位综合的广域差分改正数利用式(9) 计算的是历元间轨道、钟差改正数的变化量。基于伪距观测值利用式(5) 解算的是卫星轨道、钟差改正数的绝对值。在卫星轨道、钟差历元间变化结果中,只要已知其中任意一个历元的绝对值,所有与该历元一起形成连续观测的卫星轨道、卫星钟差也被确定,这在测量平差领域就归结为基准问题。
将历元ti基于伪距的卫星轨道、钟差为xc, i作为实际参数的虚拟观测值
 (10)
(10)
式中,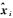
定义历元ti基于相位的卫星轨道、钟差变化为xφ, i-xφ, i-1,将其也作为虚拟观测值,可写为
 (11)
(11)
式中,
以每个历元的方差阵Pi作为权阵,伪距相位权重比取1:2000。对处理弧段的所有n个历元叠加,式(10) 写为法方程的形式为
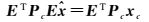 (12)
(12)
式中, E为单位阵。式(11) 写为法方程的形式
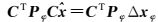 (13)
(13)
式中, C为式(11) 对应的系数阵
 (14)
(14)
式中,Pc和Pφ为伪距和相位的分块权矩阵,且有
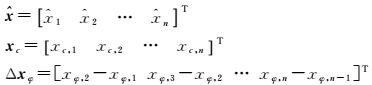 (15)
(15)
联合式(12)、(13) 就可以得到基于伪距相位综合的卫星轨道、钟差改正数,并且实现轨道改正、钟差改正的分离。在实时系统连续处理时,可采用实时滑动窗口的处理模式,即每次处理采用固定弧长的数据,每来一个新数据原弧段内最早的一个数据将被剔除。
以上钟差改正数的使用方式与现有等效钟差一致,而用户对于新增轨道改正数的使用需要更新其接收协议,并且轨道改正数需与钟差改正数叠加使用。现有的用户接收机在不进行协议改造的情况下,无法使用轨道改正数,只能使用钟差改正数,在此情况下,为不影响现有用户的改正效果,钟差改正数仍然需要包含轨道改正数中径向分量。因此以上数据处理中,对轨道改正数径向分量增加值为0的约束。在此基础上,计算得到的钟差改正数包含了轨道改正径向分量,与现有等效钟差一致;而表示在地固坐标系下包含三维分量的轨道改正数,则仅包含轨道误差的轨道切向和法向的改正。
3 模型分析选用2016-04-08—2016-04-17 10 d的北斗观测数据,对以上广域差分新模型进行分析验证。按照北斗广域差分信息播发协议,轨道改正数的计算频度为6 min,钟差改正数的计算频度为18 s[30]。以下分别从观测数据采样率、监测站个数等方面对新模型进行分析。参与计算验证的测站分布如图 3所示,其中不同颜色的测站用于3.3节验证测站个数对模型参数的影响。所选测站坐标已精密测定,位置精度优于5 cm,可以作为准确值用于评估区域卫星导航系统的定位误差。

|
| 图 3 选取的北斗观测站分布 Fig. 3 Distribution of the selected BeiDou observation stations |
3.1 改正数结果
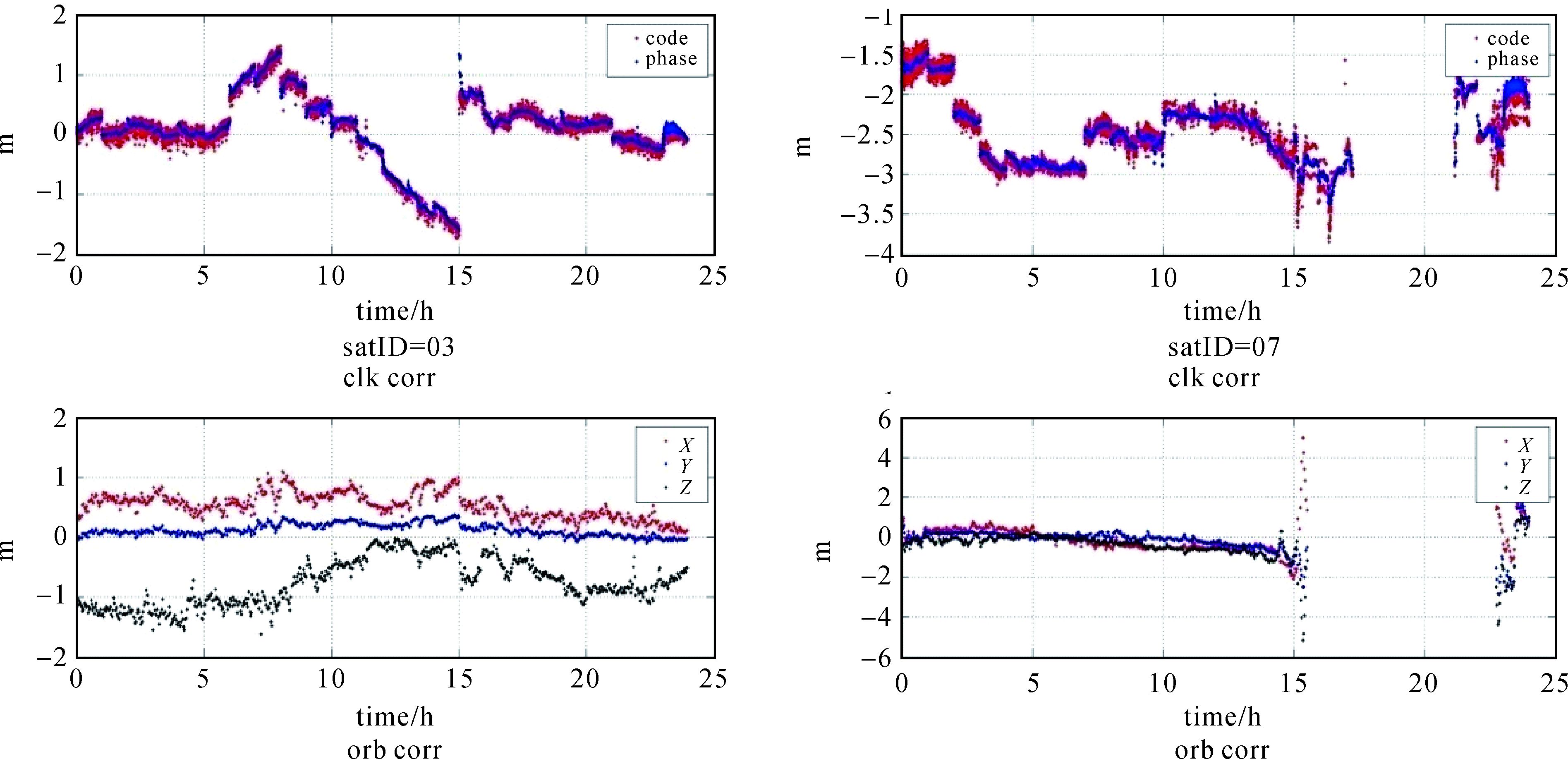
图 4表示了2016-04-08采用图 3红色7个测站数据计算的3号、7号卫星差分改正数结果时间序列。上部子图中红色曲线为伪距数据解算的等效卫星钟差结果,蓝色曲线为综合伪距相位数据解算的卫星钟差结果,下部子图为新模型中解算的卫星轨道改正数。可看到伪距解算的等效钟差结果包含了伪距噪声,而伪距相位综合解算的等效钟差更为平滑,减少了伪距噪声的影响。图 4也可以看到,在广播星历更新的时候,卫星钟差会发生分米级甚至米级的跳变,这是由于相邻的两条卫星广播星历轨道、钟差预报误差跳变引起的;而卫星的轨道误差改正数变化较为平稳,在广播星历更新后变化较小。同时,IGSO、MEO移动卫星在出入境时,受到观测几何条件的影响,轨道误差改正数会出现较大的噪声。
|
| 图 4 3号、7号卫星差分改正数时间序列图 Fig. 4 Differential corrections of C03 and C07 |
3.2 采样率对改正数精度的影响分析
北斗广域差分系统采用的观测数据为1 Hz的高频数据,每秒计算一组等效钟差改正数,在此基础上按照北斗卫星导航系统空间信号接口控制文件ICD(interface control document)的规定每18 s播发一次。基于论文提出的广域差分新模型,数据处理增加了相位观测数据的处理以及伪距相位结果的综合,因此大大增加了数据处理的计算量。为保证数据处理实时性的冗余,需要将处理的频度降低为每3 s处理一次。测站采样率的不同将造成数据量的差异,从而可能对改正数的改正效果产生影响,因而需要评估不同采样率数据对广域差分改正数解算精度的影响。
采用用户差分距离误差UDRE(user differential ranging error)对星基增强系统空间信号的精度进行评估。UDRE计算公式[25]为
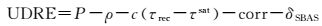 (16)
(16)
式中, P为伪距观测值;ρ为几何距离;τrec、τsat分别为测站和卫星钟差、corr为公共误差,包含对流层延迟、电离层延迟及卫星和接收机硬件延迟等,对流层延迟使用测站实测气象数据和经验模型进行估计,电离层延迟利用双频数据组合消除,卫星和接收机硬件延迟利用北斗给出的DCB参数进行消除;δSBAS为星基改正数信息。通常对不同历元的UDRE进行RMS统计,反映系统空间信号的精度,其值越小则表示系统精度越高。
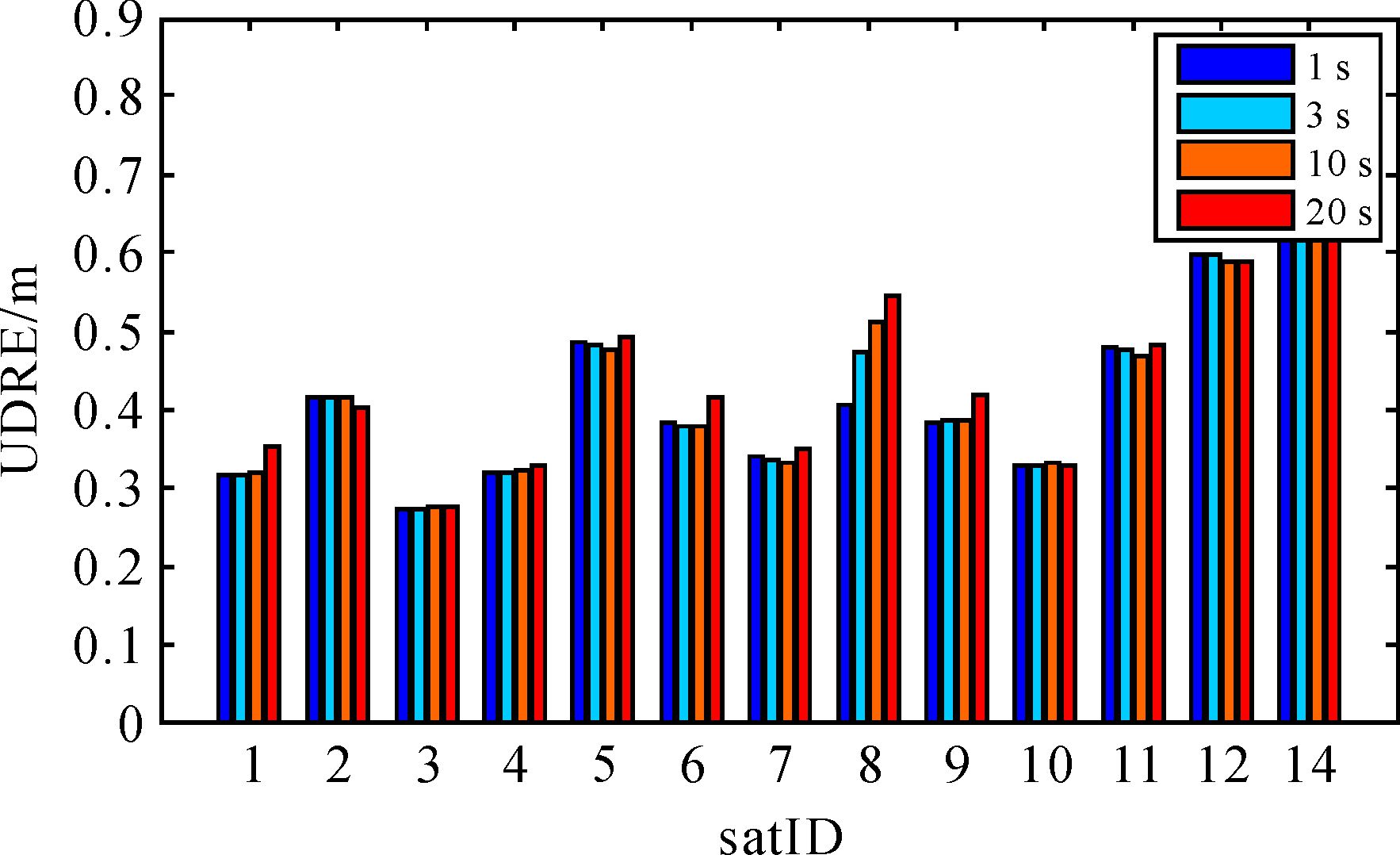
采用图 3红色7个测站数据分析采样率对改正数解算精度的影响。测站数据采样率分别设为1 s、3 s、10 s和20 s。图 5为采用CNMC的伪距观测值在不同采样率情况下新广域差分模型下卫星差分距离误差UDRE的RMS统计结果。
|
| 图 5 不同数据采样率北斗卫星UDRE的RMS统计图 Fig. 5 BeiDou satellite UDRE results with different data sample rate |
通过图 5的比较分析,可以看到卫星UDRE的RMS随采样率的变大而增大。当采样率在1 s、3 s、10 s和20 s时的卫星UDRE的RMS统计值分别是0.420 m、0.422 m、0.422 m、0.447 m。可看到当采样率在10 s以内时,与采样率为1 s时的UDRE相比变化不大;从而将采样率调整为3 s既满足了系统处理时效的要求,同时基本上不影响参数求取的精度。图 5中,当数据采样率在20 s时,解算的差分改正数的改正精度增大了约2.5 cm,这主要是受到采样数据量减少的影响。
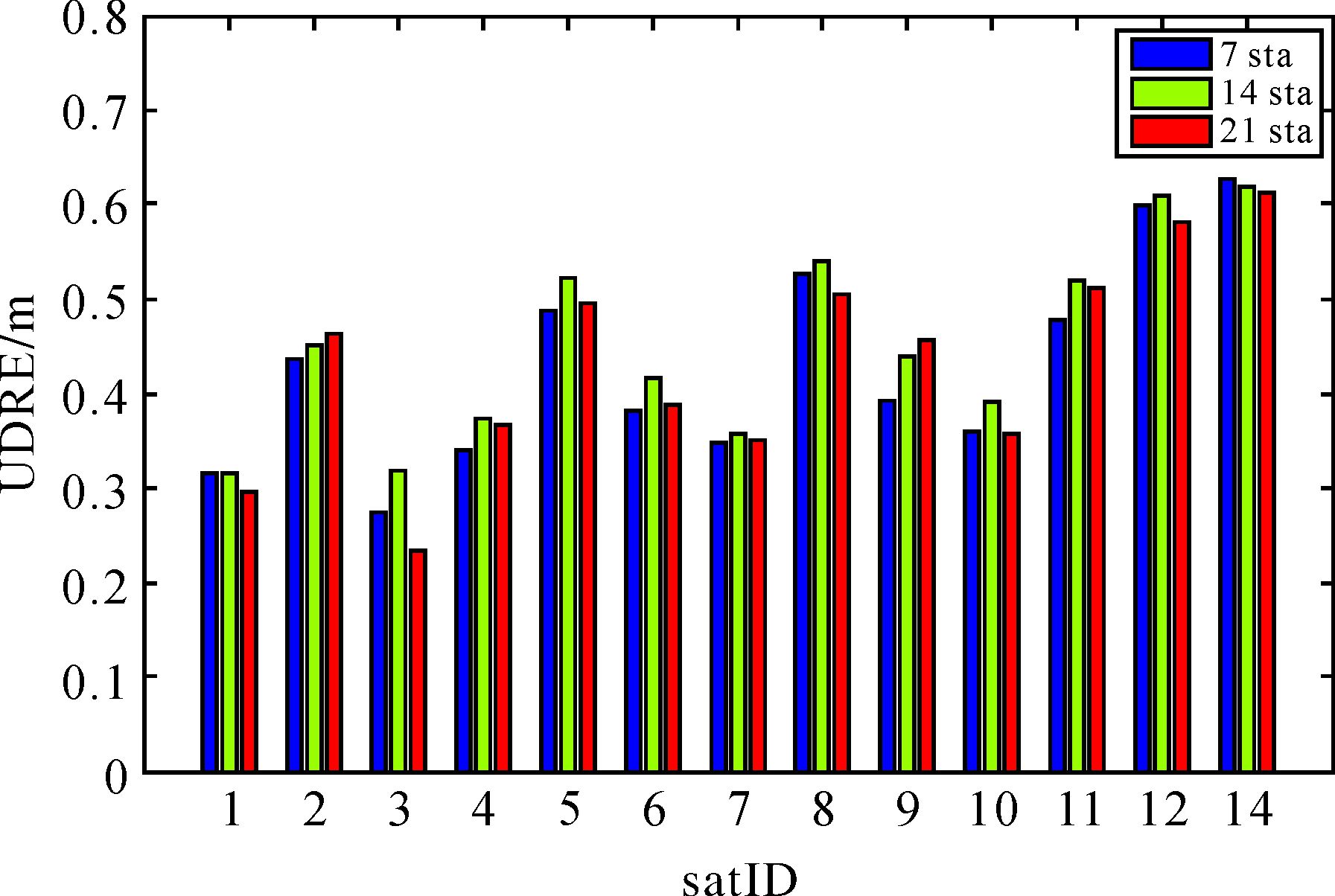
3.3 监测站个数对改正数精度的影响分析广域差分改正数的计算中,测站分布也是影响参数计算精度的一个因素。以下分别采用7个、14个、21个测站计算广域差分改正数。测站分布如图 3所示:其中7个测站为红色测站,基本上实现了的中国服务区域的整体覆盖;14个测站的情况采用了红色和蓝色测站,在7个站的基础上主要在西南以及北部方向进行了补充;21个测站则包含了图中所有测站,主要在中部以及南海进行了补充。以上测站网络中,随着测站个数增加以及观测网络的扩大,移动卫星的跟踪弧段也相应得到了延长,从而广域差分系统中相应卫星的可用差分服务时间也得到了增加。
图 6统计了使用不同测站网络进行广域差分各颗卫星UDRE的RMS统计。在以上观测网络下,北斗卫星UDRE的RMS平均值基本一致,分别为0.449 m、0.485 m、0.442 m。文中的7个站是目前系统观测数据最好的测站(Ⅰ类),其他测站为Ⅱ类测站。不同类别的测站设备的要求不同,目前Ⅱ类站的数据质量普遍低于Ⅰ类站。14个站的统计结果比7个站略差的原因是有3个Ⅱ类站的数据质量较差,从而导致了卫星的UDRE稍微偏大。在采用21个站的情况下也有个别星的结果变差,这也是由于测站数据质量的原因。以上结果表明:在相同覆盖范围的情况下,测站个数的增加对于广域差分服务精度影响不大。不过从系统服务来说,测站网络的增加对于广域差分系统的作用在于扩展差分服务的时间,增加了观测数据,从而能够提高服务的可靠性以及稳健性。
|
| 图 6 不同测站个数分布北斗卫星UDRE统计图 Fig. 6 BeiDou satellite UDRE results with different station numbers |
4 综合伪距相位观测的广域差分服务精度分析 4.1 系统空间信号精度
为分析伪距相位观测综合的广域差分新模型的精度,首先比较现有基于伪距等效钟差模型以及新模型广域差分系统的卫星UDRE的结果,如图 7所示。

|
| 图 7 2016-04-08—2016-04-17各颗卫星UDRE结果统计 Fig. 7 BeiDou satellite UDRE results during 2016-04-08—2016-04-17 |
图 7中,卫星编号1—5为GEO卫星,6—10为IGSO卫星,11—14为MEO卫星;模型1代表等效钟差模型,模型2代表综合伪距相位的新模型。对于GEO卫星,模型1平均UDRE为0.48 m,模型2平均UDRE为0.35 m,提高百分比为27%;对于IGSO卫星,模型1平均UDRE为0.56 m,模型2平均UDRE为0.36 m,提高百分比为35%;对于MEO卫星,模型1平均UDRE为0.69 m,模型2平均UDRE为0.52 m,提高百分比为24%。
MEO移动卫星的UDRE结果较大,原因是MEO卫星入境弧度过短,入境过程中CNMC伪距中残余的多路径误差以及出入境时几何构型差影响了差分改正数的精度。以上结果表明综合伪距相位的广域差分模型能显著改善卫星UDRE。
4.2 用户实时动态定位基于以上分析的结果,利用2016-04-08—2016-04-17 10 d的实测数据进行伪距相位综合的广域差分新模型下系统的服务精度的评估。比较了基于伪距等效钟差模型以及新模型的广域差分服务系统,测站伪距双频动态定位的结果。在定位计算中,观测数据使用了CNMC平滑的双频伪距无电离层组合值,对流层、固体潮、相对论、卫星和接收机天线相位中心改正等采用模型计算扣除,采用逐历元实时动态的策略进行用户最小二乘定位解算。
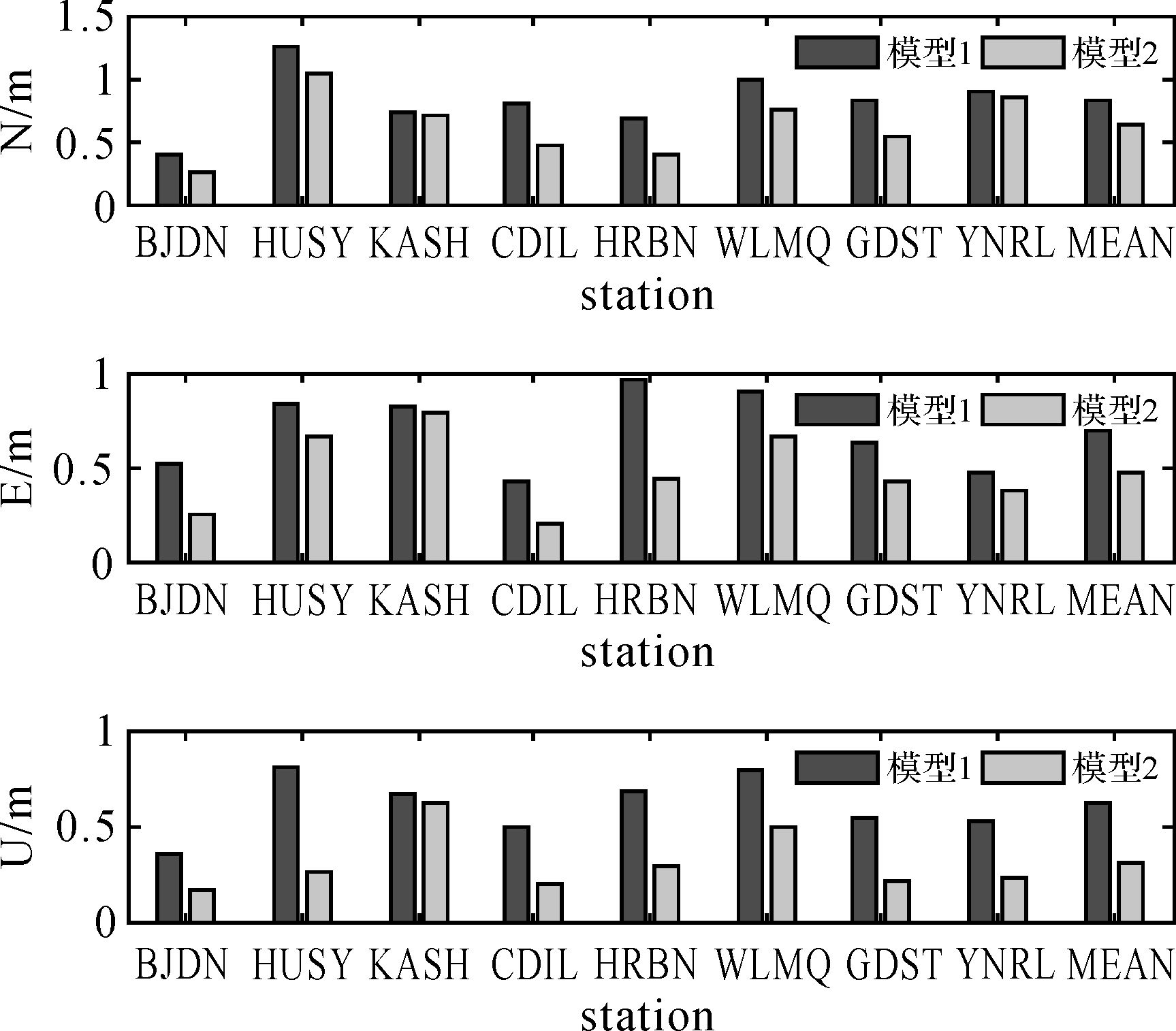
统计动态坐标与精确坐标的差异,图 8表示了中国国土范围内8个测站在测站站心地平坐标系中东西、南北及高程方向的定位精度(RMS)。模型1代表等效钟差模型,模型2代表综合伪距相位的广域差分新模型。
|
| 图 8 2016-04-08—2016-04-17用户站差分服务下定位结果统计 Fig. 8 SPP results of two differential models for user stations during 2016-04-08—2016-04-17 |
图 8中,3个子图分别显示了不同测站在南北、东西、高程方向10 d定位结果的统计情况。两种差分服务下用户定位三维精度分别达到了1.17 m和0.85 m。对于不同测站,增强服务下模型2相对于模型1,用户定位精度在南北、东西,特别是高程方向都得到了显著提高。根据表 1中不同测站的定位统计结果,基于本文提出的新广域差分模型,双频用户伪距定位在南北、东西、高程方向的定位精度分别提升了23%、32%和52%。测站三维定位精度由1.17 m提升到0.85 m,提高27%。
| m | ||||
| 模型 | N | E | U | 3D |
| 模型1 | 0.82 | 0.69 | 0.65 | 1.17 |
| 模型2 | 0.63 | 0.47 | 0.31 | 0.85 |
| 提升比率/(%) | 23 | 32 | 52 | 27 |
5 结论
本文首先介绍了等效钟差的计算模型,并从采用的观测数据精度以及改正数参数形式两方面对其进行提升。首先,数据处理引入了更高精度相位观测数据。考虑到相位观测数据的模糊度参数处理复杂,直接使用将大大增加实时处理系统设计的复杂性;本文利用相位历元间差分数据,通过历元间差分消除了模糊度参数,简化了处理处理的复杂性。其次,新模型还增加了轨道改正数的计算,用于改正目前等效模型中没有考虑的轨道切向和法向分量上的误差。
论文阐述了广域差分新模型的详细模型,并从数据采样率、监测站个数分布等角度对模型进行了分析。最后利用北斗的实测数据对该模型进行了精度测试,得到以下结论:
(1) 当数据采样率在1 s、3 s、10 s和20 s的时候,随着数据采样率的增加,卫星UDRE基本上随采样率的变大而增大,当采样率小于10 s时,UDRE基本没影响;选取分布较为均匀的测站,用少量的测站就可以实现星基增强的效果。
(2) 利用相位历元间差分数据和伪距数据,综合解算差分改正数,提高了差分信息的解算精度。对于GEO卫星,卫星UDRE提高百分比为27%,对于IGSO卫星,提高百分比为35%,对于MEO卫星,提高百分比为24%。
(3) 采用新模型得到的广域差分改正数显著改善了用户定位精度。南北、东西、高程方向的定位精度分别提升了23%、32%和52%。测站三维定位精度提高了27%。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 57(1): 144–152. YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 57(1): 144–152. |
| [3] | 胡志刚. 北斗卫星导航系统性能评估理论与试验验证[D]. 武汉: 武汉大学, 2013. HU Zhigang. BeiDou Navigation Satellite System Performance Assessment Theory and Experimental Verification[D]. Wuhan:Wuhan University, 2013. |
| [4] | 北斗卫星导航系统简介[EB/OL]. http://www.beidou.gov.cn/xtjs.html. BeiDou Satellite Navigation System[EB/OL]. http://www.beidou.gov.cn/xtjs.html. |
| [5] | ZHOU Shanshi, HU Xiaogong, WU Bin, et al. Orbit Determination and Time Synchronization for a GEO/IGSO Satellite Navigation Constellation with Regional Tracking Network[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1089–1097. DOI:10.1007/s11433-011-4342-9 |
| [6] | 施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 55(7): 1079–1086. SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China Earth Sciences, 2012, 55(7): 1079–1086. |
| [7] | 刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132–1138. LI U Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132–1138. DOI:10.13485/j.cnki.11-2089.2014.0186 |
| [8] | 雷辉, 李志刚, 杨旭海, 等. 基于转发式的北斗卫星导航系统地球静止轨道卫星精密定轨试验[J]. 测绘学报, 2011, 40(S): 31–33. LEI Hui, LI Zhigang, YANG Xuhai, et al. Precise Orbit Determination Experiment of Compass-GEO Based on Transponder Ranging[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 31–33. |
| [9] | 耿涛, 刘经南, 赵齐乐, 等. 星地监测网下的北斗导航卫星轨道确定[J]. 测绘学报, 2011, 40(S): 46–51. GENG Tao, LIU Jingnan, ZHAO Qile, et al. Compass Precise Orbit Determination Based on Space-ground Monitoring Network[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 46–51. |
| [10] | 刘伟平, 郝金明, 田英国, 等. 北斗卫星导航系统双差动力法精密定轨及其精度分析[J]. 测绘学报, 2016, 45(2): 131–139. LIU Weiping, HAO Jinming, TIAN Yingguo, et al. Solution Method and Precise Analysis of Double-difference Dynamic Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 131–139. DOI:10.11947/j.AGCS.2016.20150190 |
| [11] | 陈良, 耿长江, 周泉. 北斗/GPS实时精密卫星钟差融合解算模型及精度分析[J]. 测绘学报, 2016, 45(9): 1028–1034. CHEN Liang, GENG Changjiang, ZHOU Quan. Estimation Model and Accuracy Analysis of BeiDou/GPS Real-time Precise Satellite Clock Error Integrated Resolving[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1028–1034. DOI:10.11947/j.AGCS.2016.20150296 |
| [12] | 陈俊勇, 刘经南, 张燕平, 等. 分布式广域差分GPS实时定位系统[J]. 测绘学报, 1998, 27(1): 1–8. CHEN Junyong, LIU Jingnan, ZHANG Yanping, et al. On Distributed Wide Area Differential GPS Real Time Kinematic Positioning System[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(1): 1–8. |
| [13] | 邢楠. 广域差分技术在COMPASS系统定位服务中的应用[D]. 北京: 中国科学院大学, 2013. XING Nan. Research on the Application of Wide Area Differential Technique to Compass System[D]. Beijing:University of Chinese Academy of Sciences, 2013. |
| [14] | CAO Yueling, HU Xiaogong, ZHOU Jianhua, et al. Kinematic Wide Area Differential Corrections for Beidou Regional System Basing on Two-way Time Synchronization[C]//SUN J, JIAO W, WU H, et al. Proceedings of China Satellite Navigation Conference (CSNC). Berlin:Springer, 2014:277-288. |
| [15] | CAO Yueling, HU Xiaogong, WU Bin, et al. The Wide-area Difference System for the Regional Satellite Navigation System of Compass[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1307–1315. DOI:10.1007/s11433-012-4746-1 |
| [16] | WU Xiaoli, ZHOU Jianhua, TANG Bo, et al. Evaluation of Compass Ionospheric Grid[J]. GPS Solutions, 2014, 18(4): 639–649. DOI:10.1007/s10291-014-0394-4 |
| [17] | WU Xiaoli, HU Xiaogong, WANG Gang, et al. Evaluation of Compass Ionospheric Model in GNSS Positioning[J]. Advances in Space Research, 2013, 51(6): 959–968. DOI:10.1016/j.asr.2012.09.039 |
| [18] | WU Xiaoli, ZHOU Jianhua, GANG Wang, et al. Multipath Error Detection and Correction for GEO/IGSO Satellites[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1297–1306. DOI:10.1007/s11433-012-4741-6 |
| [19] | 常志巧, 胡小工, 郭睿, 等. CNMC与Hatch滤波方法比较及其在北斗相对定位中的精度分析[J]. 中国科学:物理学力学天文学, 2015, 45(7): 079508. CHANG Zhiqiao, HU Xiaogong, GUO Rui, et al. Comparison between CNMC and Hatch Filter & Its Precision Analysis for BDS Precise Relative Positioning[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2015, 45(7): 079508. |
| [20] | BOCK H.Efficient Methods for Determining Precise Orbits of Low Earth Orbiters Using the Global Positioning System[D]. Berne:Astronomical Institute, University of Berne, 2003. |
| [21] | 陈俊平. 低轨卫星精密定轨研究[D]. 上海: 同济大学, 2007. CHEN Junping. On Precise Orbit Determination of Low Earth Orbiters[D]. Shanghai:Tongji University, 2007. |
| [22] | GE Maorong, CHEN Junping, DOUŠA J, et al. A Computationally Efficient Approach for Estimating High-rate Satellite Clock Corrections in Realtime[J]. GPS Solutions, 2012, 16(1): 9–17. DOI:10.1007/s10291-011-0206-z |
| [23] | TSAI Y J. Wide Area Differential Operation of the Global Positioning System:Ephemeris and Clock Algorithms[D]. Palo Alto, CA:Stanford University, 1999. |
| [24] | 陈刘成, 胡小工, 封欣, 等. 区域导航系统实时广域差分修正模型与方法[J]. 中国科学院上海天文台年刊, 2010(1): 45–53. CHEN Liucheng, HU Xiaogong, FENG Xin, et al. The Models and Arithmetic for WADS Real-time Corrections of Regional Satellite Navigation System[J]. Annals of Shanghai Observatory Academia Sinica, 2010(1): 45–53. |
| [25] | 曹月玲. BeiDou区域导航系统广域差分及完好性监测研究[D]. 北京: 中国科学院大学, 2014. CAO Yueling. Studies on The Wide-Area Differential Correction and Integrity Monitoring for the Regional Satellite Navigation System of BeiDou[D]. Beijing:University of Chinese Academy of Sciences, 2014. |
| [26] | ZHU S Y, MASSMANN F H, YU Y, et al. Satellite Antenna Phase Center Offsets and Scale Errors in GPS Solutions[J]. Journal of Geodesy, 2003, 76(11-12): 668–672. DOI:10.1007/s00190-002-0294-1 |
| [27] | GE M, GENDT G, DICK G, et al. Impact of GPS Satellite Antenna Offsets on Scale Changes in Global Network Solutions[J]. Geophysical Research Letters, 2005, 32(6). DOI:10.1029/2004GL022224 |
| [28] | SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a Consistent Absolute Phase-center Correction Model for GPS Receiver and Satellite Antennas[J]. Journal of Geodesy, 2007, 81(12): 781–798. DOI:10.1007/s00190-007-0148-y |
| [29] | MONTENBRUCK O, STEIGENBERGER P, HAUSCHILD A. Broadcast Versus Precise Ephemerides:A Multi-GNSS Perspective[J]. GPS Solutions, 2015, 19(2): 321–333. DOI:10.1007/s10291-014-0390-8 |
| [30] | 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号(2. 0版)[R]. 北京: 中国卫星导航系统管理办公室, 2013. China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal (Version 2.0)[R]. Beijing:China Satellite Navigation Office, 2013. |



