2. 中国测绘科学研究院, 北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
建立有效的变形预报模型是分析变形监测资料、理解变形机理和检验工程设计理论的重要手段[1],同时,变形预报成果为灾害预警和工程安全性评估提供了重要的决策依据。20世纪70年代初,国内外学者相继提出了变形预报的统计模型、确定性模型和混合模型[2]。为考虑变形体在不同观测时刻的空间状态,并建立各个状态之间的联系,一些学者提出了变形的时间序列分析模型[3]、卡尔曼滤波模型[4]、贝叶斯动态模型[5]等预报理论与方法。将变形体作为一个整体,综合考虑变形体多个监测点的空间相关性,提出了多点变形预测模型[6-7]。此外,由于变形过程受一些非线性、不确定性因素的影响,变形预报的灰色系统理论、突变理论、神经网络、小波分析等方法[8]也得到广泛的应用。
变形预报结果存在一定程度的不确定性。这种不确定性的产生,一方面是由于自然环境因素、地质条件及各种荷载 (力) 等综合影响并且在动态变化之中,从而导致变形过程的不确定性;另一方面,由于监测数据存在误差,岩土体本构关系复杂,难以建立精确的数学模型。用不精确的模型来描述、模拟复杂的动态变形过程,这种不确定性也是显而易见的[9-11]。然而,已有的变形预报方法只给出一个确定的预报值,并不能较完整地定量化表征变形预报的不确定性;同时,单值的变形预报结果在一定程度上制约着灾害预警和工程安全性评估的可靠性。因此,变形预报的不确定性研究是一个亟待解决的问题。
目前,变形预报的不确定性研究相当有限[12-15]。概率作为表征水文预报、气象预报不确定性的一种方式已得到广泛的应用[16-18]。因此,本文针对变形预报的不确定性,拟采用MCMC (Markov Chain Monte Carlo,MCMC) 算法[19]和贝叶斯预测理论[20],综合考虑监测数据误差和反演模型参数不确定性的影响,提出了变形概率预报方法。该方法以概率分布的形式描述变形预报的不确定性,通过概率规则来实现预报的学习和推理过程,最大限度地利用了预报当前时刻的所有信息。对概率预测分布的Gibbs抽样计算,可求得预报量的均值、方差及置信区间等信息,定量地分析了变形预报的不确定性,同时,该方法提供了预报值的可靠性区间,对灾害预警和工程安全性评估具有重要的参考价值。
1 变形概率预报方法 1.1 不确定性反演分析不确定性反演分析是指运用随机过程、模糊数学、分形几何等不确定性数学工具来分析量测信息的不确定性及反演模型的非确定性。在工程领域,不确定性反演分析主要有极大似然估计、贝叶斯方法、卡尔曼滤波法等[21], 贝叶斯反演分析是在贝叶斯理论的基础上,将参数的先验信息、量测信息的不确定性,按贝叶斯法则考虑在目标函数中,由似然函数递推待求参数的后验概率密度函数[22]。
对变形监测分析而言,若Y=(y1, y2, …, yn) 为n期变形监测数据,φ(θ) 是以θ=(θ1, θ2, …, θk) 为参数的变形分析模型,则变形监测数据Y与变形分析模型φ(θ) 之间的关系为[23-24]
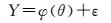 (1)
(1)
式中,ε为随机变量,且ε~N (0, τ-1);τ为未知的待定参数,表示监测数据误差和模型结构的不确定性。
若监测数据Y=(y1, y2, …, yn) 服从正态分布
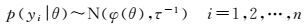 (2)
(2)
则变形观测值的似然函数为
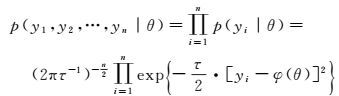 (3)
(3)
根据贝叶斯理论,并顾及参数的先验分布π(θ),变形模型参数的后验概率分布为
 (4)
(4)
从式 (4) 可以看出,监测数据误差和模型结构的不确定性通过贝叶斯反演分析传递到参数的后验概率分布中来, 参数的后验概率分布π(θ|y1, y2, …, yn) 描述了参数的不确定性。
1.2 概率预报递推算法根据文献[25]的研究,利用贝叶斯预测理论来推断未来时刻的观测值必须依靠预测分布。若将预测值 (ypre) 作为一个附加的未知参数,并与模型参数 (θ) 一起进行估计,利用联合后验概率分布p(ypre, θ|yobs) 来推断未来观测值的边缘后验分布p(ypre|yobs)
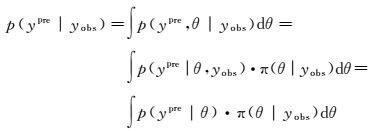 (5)
(5)
式 (5) 的概率预测分布p(ypre|yobs) 涵盖了参数后验分布π(θ|yobs) 和预测值的函数分布p(ypre|θ),以概率分布的形式描述了变形预报的不确定性。
在完全没有获得变形观测数据的情况下,利用参数的先验分布π(θ) 可求得未知且可观测的数据分布为
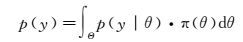 (6)
(6)
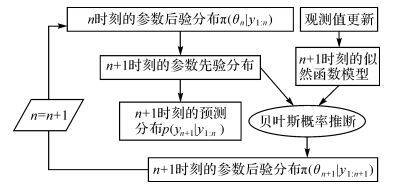
在实际变形分析中,预测通常是在获得一定的观测数据之后进行。在不同的时间间隔获取的变形监测数据,利用贝叶斯递推算法推断出某一时刻变形的一步概率预测分布 (图 1),过程如下:
|
| 图 1 变形概率预报的贝叶斯递推算法 Fig. 1 Deformation probability forecasting of Bayesian recursive algorithm |
(1) 当t1时刻变形监测数据y1获取以后,根据式 (4) 可推断出t1时刻参数的后验分布为
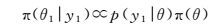 (7)
(7)
根据式 (5),t1时刻的一步预测分布为
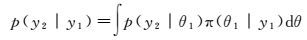 (8)
(8)
(2) 随着t2时刻监测数据y2获取,将t1时刻参数的后验分布 (π(θ1|y1) 作为t2时刻参数的先验分布,结合新的监测数据y2来推断t2时刻参数的后验分布
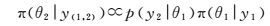 (9)
(9)
同理,t2时刻的一步预测分布为
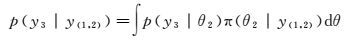 (10)
(10)
(3) 依次递推,当tn时刻监测数据y1、y2、…、yn获取后,逐次递推的模型参数后验分布为
 (11)
(11)
同理,tn时刻的一步预测分布为
 (12)
(12)
随着观测数据的不断更新,并不断地对参数的先验信息进行更新与修正,使得参数的估计越来越准确,相应的预测分布也随之更新与修正, 实现了利用概率规则的学习和推理过程。
1.3 概率预测分布的数值计算Gibbs抽样算法是应用最为广泛的MCMC算法之一[26]。文献[27]将Gibbs抽样应用到复杂、高维的后验概率分布计算,不仅求得未知参数的估计值,还获得参数的方差、置信区间及MC误差等信息。由于变形模型的参数后验概率分布 (式 (4)) 和变形的概率预测分布 (式 (5)) 的计算都涉及高维、非标准的分布,很难用传统的数值方法来计算。因此,本文采用Gibbs抽样算法进行概率分布的数值计算,具体的过程如下:
设θ0=(θ10, θ20, …, θk0) 为变形分析模型参数θ=(θ1, θ2, …, θk) 的任一初值,然后逐一从下述满条件分布进行抽样:从参数满条件分布π(θ1|θ20, θ30,…, θk0, y1, y2, …, yn) 中抽取θ11;然后依次从参数满条件分布π(θk|θ11, θ21,…, θk-11, y1, y2, …, yn) 中抽取θk1;从预测满条件分布p(yn+1|θ11, θ21,…, θk1, y1, y2, …, yn) 中抽取yn+11。
从这样一个完整的抽样过程称之为一次迭代,并用η(1)=(θ1(1), θ2(1), …, θk(1), yn+1(1)) 来表示生成的向量。第二次迭代是以η(1)=(θ1(1), θ2(1), …, θk(1), yn+1(1)) 作为初值,重复上述迭代抽样过程。在足够的退火期 (burn-in period) 后,经过t次迭代产生Gibbs抽样序列η=η(1), η(2), …, η(t)可形成了一个Markov链,收敛到独立于初始值的平稳分布π(θ|y1, y2, …, yn) 和p(yn+1|y1, y2, …, yn)。此时,就可以利用采样数据的统计计算结果进行未来时刻的变形预测及不确定性分析。
2 工程实例分析为了验证本文提出的变形概率预报方法的可行性及其精度,利用宁杭高速公路k95+520段地基沉降观测数据[28]进行地基沉降泊松曲线模型拟合与预测,利用WinBUGS软件编程来实现本文的方法。
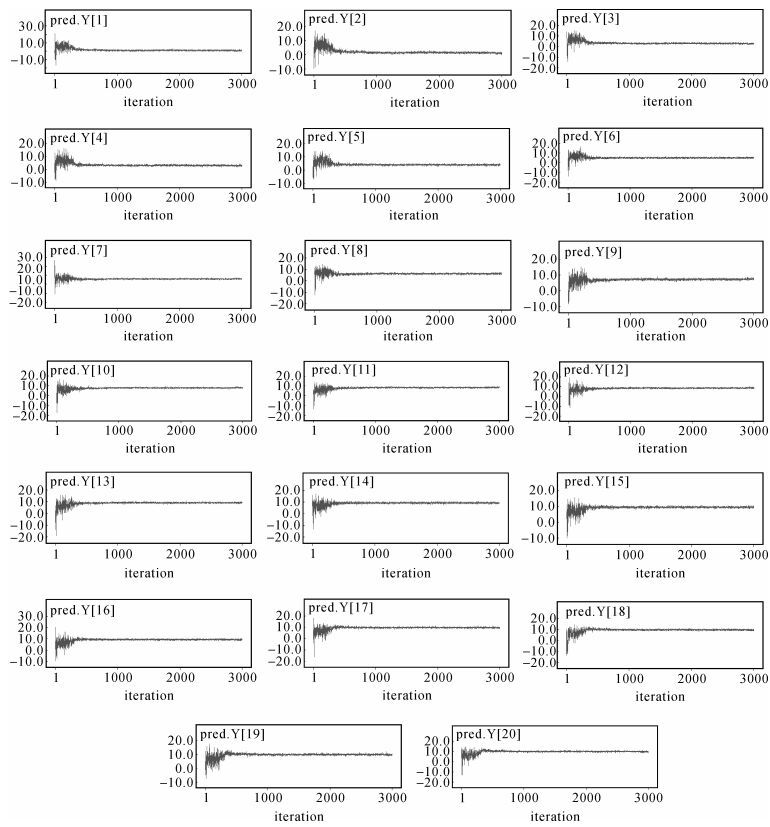
2.1 MCMC计算收敛性判断采用MCMC方法构造的Markov链,再经过足够长的预热过程后达到稳定,即满足遍历性、归一性和平稳性条件的Markov过程,之后的各个状态采样值可视为来自目标分布。利用Gelman收敛准则可直观、准确地判断Markov链的收敛性,即后验分布的Gibbs采样轨迹图趋于一条直线,说明迭代采样过程是收敛的[29]。通过对20期的一步预测分布的Gibbs采样轨迹图判断 (图 1),Markov链在大约经过500次采样预热之后,采样轨迹图趋于一条直线,说明沉降变形预测分布的采样值收敛较快,且本次Gibbs抽样迭代计算是收敛的。
|
| 图 2 变形预测分布的采样轨迹 Fig. 2 The sampling trajectory of deformation prediction distribution 注:横坐标表示采样迭代次数;纵坐标表示预测分布的采样值,单位为cm。 |
2.2 概率分布曲线及不确定性分析
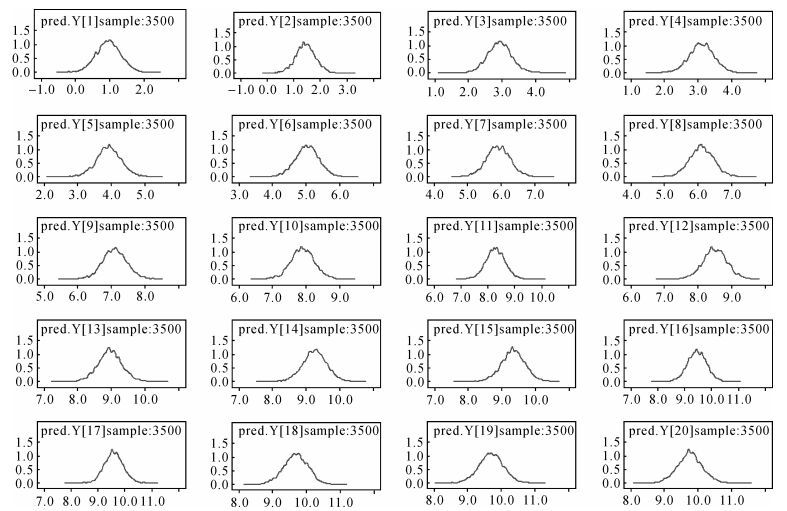
考虑到监测数据误差及模型参数反演等不确定性因素影响,以变形概率预测分布来代替传统的变形预报值 (一个常数)。Markov链收敛以后的采样值可视为来自变形概率预测分布的独立样本,利用采样值绘制变形的概率预报分布曲线 (图 3)。当预测量概率分布曲线比较陡且拖尾较小时,相应的置信区间宽度变小,即预报的不确性小;当预测的概率分布曲线比较缓且拖尾较大时,相应的置信区间宽度变大,即预报的不确定性较大。
|
| 图 3 沉降量的概率预测分布曲线 Fig. 3 The probability prediction distribution curve of settlement 注:横坐标表示变形预测采样值,单位为cm;纵坐标表示概率密度。 |
2.3 预报值及可靠性区间计算
Markov链收敛以后的采样值可视为来自变形概率预测分布的独立样本,用于预测量的统计计算及可靠性分析。表 1列出了20期地基沉降一步概率预测分布采样值的统计结果,预报量的均值、标准差、95%置信区间及MC误差等信息,较好地表征了变形预报的不确定性。
| 时间/d | 沉降观测值 /cm |
Bayes概率方法 | 免疫算法 /cm |
最小二乘 拟合方法/cm |
|||
| 均值/cm | 标准差/cm | 95%置信区间/cm | MC误差 | ||||
| 5 | 0.51 | 0.961 | 0.364 8 | [0.248,1.665] | 0.011 3 | 1.06 | 0.94 |
| 10 | 1.44 | 1.445 | 0.384 8 | [0.673,2.206] | 0.013 5 | 1.54 | 1.41 |
| 20 | 2.71 | 2.931 | 0.374 3 | [2.210,3.690] | 0.010 9 | 3.01 | 2.90 |
| 21 | 3.21 | 3.104 | 0.384 7 | [2.318,3.846] | 0.011 6 | 3.20 | 3.09 |
| 25 | 3.57 | 3.924 | 0.383 6 | [3.159,4.690] | 0.007 5 | 3.99 | 3.91 |
| 30 | 5.35 | 5.027 | 0.360 9 | [4.302,5.722] | 0.005 4 | 5.06 | 5.01 |
| 34 | 5.88 | 5.909 | 0.367 2 | [5.171,6.658] | 0.008 9 | 5.92 | 5.90 |
| 35 | 6.56 | 6.110 | 0.374 3 | [5.391,6.869] | 0.007 9 | 6.13 | 6.12 |
| 40 | 7.48 | 7.099 | 0.374 2 | [6.355,7.844] | 0.010 2 | 7.10 | 7.10 |
| 45 | 7.82 | 7.897 | 0.364 2 | [7.135,8.632] | 0.009 9 | 7.92 | 7.91 |
| 48 | 8.05 | 8.284 | 0.364 9 | [7.565,9.002] | 0.009 4 | 8.32 | 8.30 |
| 50 | 8.38 | 8.501 | 0.369 1 | [7.755,9.226] | 0.008 4 | 8.56 | 8.52 |
| 55 | 8.59 | 8.961 | 0.368 1 | [8.224,9.708] | 0.007 1 | 9.03 | 8.96 |
| 60 | 8.84 | 9.252 | 0.363 8 | [8.514,9.965] | 0.006 0 | 9.37 | 9.27 |
| 62 | 9.01 | 9.339 | 0.361 1 | [8.617,10.07] | 0.006 8 | 9.48 | 9.36 |
| 65 | 9.18 | 9.464 | 0.361 3 | [8.744,10.17] | 0.007 1 | 9.61 | 9.47 |
| 70 | 9.81 | 9.590 | 0.367 0 | [8.888,10.33] | 0.007 6 | 9.76 | 9.60 |
| 75 | 10.04 | 9.683 | 0.370 5 | [8.927,10.40] | 0.009 6 | 9.87 | 9.69 |
| 76 | 10.06 | 9.702 | 0.379 3 | [8.953,10.44] | 0.008 9 | 9.89 | 9.71 |
| 80 | 10.11 | 9.760 | 0.378 1 | [9.016,10.52] | 0.008 6 | 9.94 | 9.74 |
| RMS拟合残差 | 1.839 8 | 2.078 8 | 1.850 5 | ||||
2.4 不同方法预报结果比较
为了验证本文的变形概率预测分布方法的有效性,与相同数据、同一模型的免疫算法、最小二乘算法的拟合预测结果进行比较 (表 1),通过拟合残差对比,变形的概率预报方法不仅预测精度优于免疫算法和最小二乘方法,而且给了预测值的可靠性区间,从而突出了该方法的有效性及优势。
此外,从3种方法的预测误差序列图来看,预测误差的正负性均呈现出明显的一致,但概率预报方法的预测误差略小于其他两种方法 (图 4)。在20期预测中,有12期免疫算法预测的预测误差大于其他两种方法,而最小二乘的预测误差虽与概率预报方法相当,但残差略大 (表 1)。

|
| 图 4 3种方法的预测误差序列图 Fig. 4 Three methods of prediction error sequence diagram |
3 结论
针对变形过程的不确定性,本文提出了变形概率预报方法,通过概率规则实现预报的递推过程。主要结论如下:① 将参数的先验信息、监测信息的不确定性,按贝叶斯法则考虑在目标函数中,并利用其预测理论推断出下一时刻变形的一步概率预测分布;② 通过对一步概率预测分布的抽样计算,得出了预报量的均值、标准差、95%置信区间等信息,较好地表征了变形预报的不确定性;③ 结合工程实例,通过对比不同预测方法的结果表明,变形概率预报方法预测精度较高,表明了该方法的有效性,同时,本文方法给出了预测值的可靠性区间,对于工程灾害预警及安全性评估具有一定的实用性。
| [1] | 黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 2版. 武汉: 武汉大学出版社, 2010. HUANG Shengxiang, YIN Hui, JIANG Zheng. Deformation Monitoring Data Processing[M]. 2nd ed. Wuhan: Wuhan University Press, 2010. |
| [2] | 徐伟, 何金平. 基于多尺度小波分析的大坝变形自回归预测模型[J]. 武汉大学学报 (工学版), 2012, 45(3): 285–289. XU Wei, HE Jinping. Forecast Model of Dam Deformation Based on Multi-scale Wavelet Analysis and Autoregressive Method[J]. Engineering Journal of Wuhan University, 2012, 45(3): 285–289. |
| [3] | 潘国荣. 基于时间序列分析的动态变形预测模型研究[J]. 武汉大学学报 (信息科学版), 2005, 30(6): 483–487. PAN Guorong. Forecast Model of Dynamic Deformation Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2005, 30(6): 483–487. |
| [4] | 马攀, 孟令奎, 文鸿雁. 基于小波分析的Kalman滤波动态变形模型研究[J]. 武汉大学学报 (信息科学版), 2004, 29(4): 349–353. MA Pan, MENG Lingkui, WEN Hongyan. Kalman Filtering Model of Dynamic Deformation Based on Wavelet Analysis[J]. Geomatics and Information Science of Wuhan University, 2004, 29(4): 349–353. |
| [5] | 魏冠军, 党亚民, 章传银. 应用贝叶斯动态模型的地基沉降概率分析与预测[J]. 测绘科学, 2012, 37(2): 52–53. WEI Guanjun, DANG Yamin, ZHANG Chuanyin. Foundation Settlement Probability Analysis and Prediction Based on Bayes Dynamic Linear Model[J]. Science of Surveying and Mapping, 2012, 37(2): 52–53. |
| [6] | 李广春, 戴吾蛟, 杨国祥, 等. 时空自回归模型在大坝变形分析中的应用[J]. 武汉大学学报 (信息科学版), 2015, 40(7): 877–881. LI Guangchun, DAI Wujiao, YANG Guoxiang, et al. Application of Space-Time Auto-Regressive Model in Dam Deformation Analysis[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 877–881. |
| [7] | 尹晖, 周晓庆, 张晓鸣. 非等间距多点变形预测模型及其应用[J]. 测绘学报, 2016, 45(10): 1140–1147. YIN Hui, ZHOU Xiaoqing, ZHANG Xiaoming. Non-equidistant Multi-Point Deformation Prediction Model and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1140–1147. DOI:10.11947/j.AGCS.2016.20160005 |
| [8] | 张正禄, 黄全义, 文鸿雁, 等. 工程的变形监测分析与预报[M]. 北京: 测绘出版社, 2007. ZHANG Zhenglu, HUANG Quanyi, WEN Hongyan, et al. Deformation Monitoring Analysis and Prediction for Engineering Constructions[M]. Beijing: Surveying and Mapping Press, 2007. |
| [9] | 刘维宁. 岩土工程反分析方法的信息论研究[J]. 岩石力学与工程学报, 1993, 12(3): 193–205. LIU Weining. Study of Back Analysis Methods in Rock and Soil Engineering by the Information Theory[J]. Chinese Journal of Rock Mechanics and Engineering, 1993, 12(3): 193–205. |
| [10] | NEUMANN I, KUTTERER H. Congruence Tests and Outlier Detection in Deformation Analysis with Respect to Observation Imprecision[J]. Journal of Applied Geodesy, 2007(1): 1–7. DOI:10.1515/jag.2007.001 |
| [11] | EICHHORN A. Tasks and Newest Trends in Geodetic Deformation Analysis: A Tutorial[C]//Proceedings of the 15th European Signal Processing Conference. Poznan: IEEE, 2007: 1156-1160. |
| [12] | 刘宁, 郭志川, 罗伯明. 地基沉降的概率分析方法和可靠度计算[J]. 岩土工程学报, 2000, 22(2): 143–150. LIU Ning, GUO Zhichuan, LUO Boming. Probabilistic Analysis and Reliability Assessment for Foundation Settlement[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(2): 143–150. |
| [13] | 贺钢, 蒋楚生. 边坡岩土工程不确定性及对策分析[J]. 铁道工程学报, 2010, 27(4): 19–22. HE Gang, JIANG Chusheng. Analysis of Uncertainty of Slope Rock-Soil Engineering and Countermeasure[J]. Journal of Railway Engineering Society, 2010, 27(4): 19–22. |
| [14] | 杨杰, 胡德秀, 吴中如. 大坝安全监控模型因子相关性及不确定性研究[J]. 水利学报, 2004, 35(12): 99–105. YANG Jie, HU Dexiu, WU Zhongru. Multiple Co-linearity and Uncertainty of Factors in Dam Safety Monitoring Model[J]. Journal of Hydraulic Engineering, 2004, 35(12): 99–105. DOI:10.3321/j.issn:0559-9350.2004.12.016 |
| [15] | NEUMANN I, KUTTERER H. Geodetic Deformation Analysis with Respect to Observation Imprecision[C]//XXⅢ FIG Congress. Munich, Germany: [s.n.], 2006. |
| [16] | 杜钧, 邓国. 单一值预报向概率预报转变的价值:谈谈概率预报的检验和应用[J]. 气象, 2010, 36(12): 10–18. DU Jun, DENG Guo. The Utility of the Transition from Deterministic to Probabilistic Weather Forecasts-Verification and Application of Probabilistic Forecasts[J]. Meteorological Monthly, 2010, 36(12): 10–18. DOI:10.7519/j.issn.1000-0526.2010.12.002 |
| [17] | KRZYSZTOFOWICZ R. Bayesian Theory of Probabilistic Forecasting via Deterministic Hydrologic Model[J]. Water Resources Research, 1999, 35(9): 2739–2750. DOI:10.1029/1999WR900099 |
| [18] | 邢贞相, 芮孝芳, 崔海燕, 等. 基于AM-MCMC算法的贝叶斯概率洪水预报[J]. 水利学报, 2007, 38(12): 1500–1506. XING Zhenxiang, RUI Xiaofang, CUI Haiyan, et al. Bayesian Probabilistic Flood Forecasting Model Based on Adaptive Metropolis-MCMC Algorithm[J]. Journal of Hydraulic Engineering, 2007, 38(12): 1500–1506. DOI:10.3321/j.issn:0559-9350.2007.12.014 |
| [19] | PAPAIOANNOU I, BETZ W, ZWIRGLMAIER K, et al. MCMC Algorithms for Subset Simulation[J]. Probabilistic Engineering Mechanics, 2015, 41: 89–103. DOI:10.1016/j.probengmech.2015.06.006 |
| [20] | WEST M, HARRISON J. Bayesian Forecasting and Dynamic Models[M]. New York: Springer-Verlag, 1997. |
| [21] | 杨杰, 胡德秀, 吴中如. 基于最大熵原理的贝叶斯不确定性反分析方法[J]. 浙江大学学报 (工学版), 2006, 40(5): 810–815. YANG Jie, HU Dexiu, WU Zhongru. Bayesian Uncertainty Inverse Analysis Method Based on POME[J]. Journal of Zhejiang University (Engineering Science), 2006, 40(5): 810–815. |
| [22] | 陈斌, 刘宁, 卓家寿. 岩土工程反分析的扩展贝叶斯法[J]. 岩石力学与工程学报, 2004, 23(4): 555–560. CHEN Bin, LIU Ning, ZHUO Jiashou. Extended Bayesian Method of Inverse Analysis in Geoengineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(4): 555–560. |
| [23] | YALÇINKAYA M, TANIR E.A Study on Using Bayesian Statistics in Geodetic Deformation Analysis[C]//Proceedings of the 11th FIG Symposium on Deformation Measurements. Santorini, Greece: [s.n.], 2003. |
| [24] | KOCH K R. Bayesian Inference with Geodetic Applications[M]. Berlin Heidelberg, Germany: Springer-Verlag, 1990. |
| [25] | NTZOUFRAS I. Bayesian Modeling Using WinBUGS[M]. New York: Wiley, 2009. |
| [26] | GEMAN S, GEMAN D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, PAMI-6(6): 721–741. DOI:10.1109/TPAMI.1984.4767596 |
| [27] | GELFAND A E, SMITH A F M, LEE T M. Bayesian Analysis of Constrained Parameter and Truncated Data Problems Using Gibbs Sampling[J]. Journal of the American Statistical Association, 1992, 87(418): 523–532. DOI:10.1080/01621459.1992.10475235 |
| [28] | GUO Jia, ZHENG Junjie, LIU Yong. Application of an Immune Algorithm to Settlement Prediction[J]. Journal of Zhejiang University-SCIENCE A, 2009, 10(1): 93–100. DOI:10.1631/jzus.A0820289 |
| [29] | SMITH A F M, ROBERTS G O. Bayesian Computation via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods[J]. Journal of the Royal Statistical Society Series B: Methodological, 1993, 55(1): 3–23. |



