位置签到是基于位置的社交网络 (LBSN) 中一个重要的功能,指的是利用具有位置服务 (LBS) 的设备记录用户当前位置等信息并发布到社交网络上的行为[1-3]。签到的位置在形态上表现为点要素,在城市总体空间中具有分块聚集的特征,一定程度上反映了城市居民的空间活动情况。分析和研究位置签到所形成的热点热区是面向地理空间的居民移动性研究的重要组成[4],可以帮助更好地把握城市空间结构、探索城市的商圈及变化[5]进而能够协助解决城市公共交通、资源配置、规划决策等问题。
现有的位置签到热区研究方式主要包括标准差椭圆法[6]与核密度分析法[1, 7-8]。标准差椭圆法仅能够大略表示热区所在的空间范围与扩张方向;对于核密度分析法来说,由于要素的密度是由核密度函数计算而来,密度区外形往往过于平滑并趋于球状,无法较为准确地反映签到热区的真实空间形态。空间聚类是空间数据挖掘与空间分析的重要手段之一[9]。基于密度的聚类能够自动剔除空间分布较稀疏的对象,将局部空间密度较高的对象聚集为一类,发现任意形状的簇[10-11],可以较好地发现位置签到数据所形成的活动热区,并能体现其真实形态特征[12-13]。基于密度的聚类法如DBSCAN[14-15]、ADBSC[16]、LDBSC[9]以及格网密度法[17]都把密度簇内部看成是密度均匀的,并且直接以对象间的空间距离作为相似性度量指标来进行聚类,没有考虑空间位置上的重复性问题。然而,现有的LBSN位置签到普遍带有位置候选功能,列出了当前可能处于的候选位置让用户自行选择。当不同的签到行为 (不同用户或不同时间的签到) 选择同一候选位置进行签到时就会产生签到位置重复现象。这样以来很可能将重复位置上的全部对象聚成一类,且错误地获取密度峰值等重要信息,由此得到的聚类热区很难反映其变化趋势,在表达上难以到达较好的效果。
文献[18]提出了快速搜索和查找密度峰值聚类算法 (clustering by fast search and find of density peaks,CFSFDP)。该聚类方法先快速寻找密度峰值,然后进行密度聚类,具有效率高、结果稳定的优点,且在低维数据上表现效果良好[19]。本文在CFSFDP算法思想的基础上,选择新浪微博位置签到数据为数据源,针对签到位置的重复特性,围绕密度峰值点搜索和基于密度峰值的聚类两个方面提出了签到位置数据的密度峰值快速搜索与聚类方法,一方面可以帮助更好地寻找城市活动热区及热区中心,另一方面也为LBSN位置签到的聚类研究提供了一种方法。
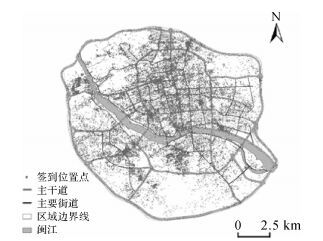
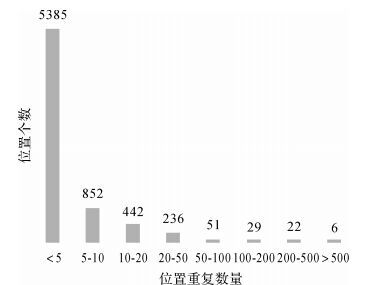
1 研究区签到位置数据分析本研究选择了福州市主城区作为研究区,其范围覆盖了福州市三环路内部区域。数据来自于新浪微博API采集2015年8月1日至10月31日的新浪微博位置签到原始文本,签到总量115 191条,选取其中的签到ID、签到经纬度信息来构建签到位置点对象。带有位置的签到72 354,重复率37.2%,最大重复数721条。数据位置分布如图 1所示,位置重复数量统计情况如图 2所示。在构建空间点对象之前需要将经纬度坐标转换成平面坐标以方便计算对象间的空间距离,单位为米。
|
| 图 1 签到对象的位置分布 Fig. 1 Location distribution of check-in points |
|
| 图 2 福州市主城区签到位置重复数量统计图 Fig. 2 Statistic of reduplication of check-in locations about Fuzhou |
2 签到位置数据的密度峰值快速搜索与聚类方法 2.1 CFSFDP算法分析
CFSFDP算法基于对象的局部密度来搜索密度峰值并聚类,兼有密度聚类和谱聚类的特性。密度峰值点的最主要特征是其局部密度比包围它的临近点的局部密度都要大,并且距离其他密度峰值点都较远[20-21]。在搜索密度峰值前首先需要计算每个对象pi的两个量值:ρi和δi。
其中, ρi表示pi的局部密度,含义是数据集中到pi的距离小于或等于dc的对象个数。dc称为截断距离,为用户给出的参数。ρi的具体表达如下
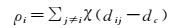 (1)
(1)
式中,dij表示第i与第j对象之间的空间距离;χ(x) 计算方法为:若x<0,χ(x)=1;若x>=0,χ(x)=0。为避免不同的点对象具有相同局部密度而且能够识别异形簇,一般采用指数核的形式来定义局部密度[21],表达如下
 (2)
(2)
δi的具体表达如下
 (3)
(3)
式中,δi表示密度大于ρi的对象中与pi最近距离。若ρi为最大值,δi为距离pi最远对象与pi间距离。
计算出全部ρi和δi后,根据CFSFDP对峰值点的定义,从决策图上选择横纵坐标都比较大的点作为密度峰值点。密度峰值搜索完成之后,根据参数dc来确定边界区密度阈值,对余下对象按照阈值进行密度划分从而实现去噪目的。最终所获得的密度簇成员包含了密度峰值点和密度核心点两大部分,靠近每个密度簇周围的噪声点称之为簇的光晕 (halo) [18]。
CFSFDP算法直接基于点对象的空间距离来搜索峰值点并聚类。对于存在位置重复的签到对象,直接运用可能会产生如下效果:① 位置重复数量较多的点及其临近对象的局部密度较大,更容易被判断成密度峰值点。理想的峰值点应当是被众多低于其局部密度的点所包围;但实际中,位置重复数量较多的对象有可能位于簇的边缘,甚至其位置在空间上是离群的,从而降低了聚类簇的表达效果;② 由于同一重复位置上对象的局部密度和δ值都是相同的,很有可能获得一系列位置相同的峰值点。因此,在峰值点的搜索过程中必须考虑位置重复情况。作为密度峰值发现的第一步,首先需要对局部密度的概念进行修改。
2.2 考虑签到位置重复的密度峰值点快速搜索 2.2.1 局部密度改进方案为了保留位置重复信息,需要对原始对象的数据结构进行修改。将重复的空间位置进行合并,并为之添加一个属性:位置重复频率dFreq,dFreq∈N+,用以表达该位置上原始对象的实际数量。经过位置合并后,一种新型的空间点要素FPoint的数据结构如下:
Class FPoint{
int PID, //点要素编号
double X, //墨卡托横坐标
double Y, //墨卡托纵坐标
int dFreq, //位置重复频率 (默认值1)
double density, //局部密度 (ρ)
double delta, //高密度点最邻近值 (δ值)
int ptype, //要素种类 (0--未分配;1--峰值;2--核心点;3--边界点;-1--噪声点)
int clusterid //所属簇的ID
}
FPoint对象间的空间密度关系由空间位置和位置重复频率dFreq共同决定,其中dFreq作为要素密度关系表达的第三维,属于纵向的量值,反映了该位置上签到数量规模。为更准确表达签到位置在城市空间中的密度分布情况,FPoint对象的局部密度必须要考虑位置重复频率的影响。本文将重复频率作为一种影响因子,在局部密度的定义中以权重的形式单独考虑,FPoint对象FPi的局部密度ρi表达如下
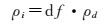 (4)
(4)
式中,ρd是按照式 (1) 所算出的局部密度,仅与对象位置有关;df表示的是重复频率dFreq在局部密度中占的权重。对于df,一种是直接将位置重复频率作为权重值,由此计算出的局部密度记为ρdf。由于FPoint对象集合的dFreq极差一般很大,会导致ρdf之间的极差过大,容易将局部密度过大的边缘点或离群点作为密度峰值,起不到预期效果。另一种是对dFreq+1取对数作为df,由此算出的局部密度记为ρdlnf,能够很好地降低dFreq所造成的极差。具体表达如下
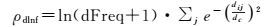 (5)
(5)
式中,dFreq表示当前对象的位置重复频率;dij表示第i与第j对象之间的空间距离;dc为截断距离。
以上3种形式局部密度值的极差情况如表 1所示。
| 局部密度 | 最大值 | 最小值 | 极差 |
| ρd | 1 264.347 2 | 1.641 | 1 262.706 2 |
| ρdf | 621 054.079 6 | 1.641 | 621 052.438 6 |
| ρflnf | 6 660.614 4 | 1.137 8 | 6 659.476 6 |
由表可知,ρdf的极差是ρd的100倍以上,而ρflnf与ρd两者间的极差没有数量级的差别,因此采用式 (5) 来计算局部密度既能符合要求效果又相对理想。
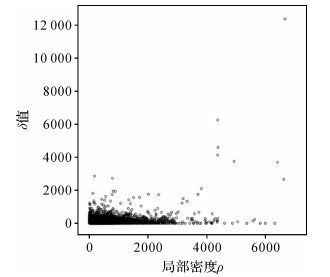
2.2.2 ρ0和δ0的确定根据FPoint对象集,计算每个对象的ρi和δi,绘制如图 3所示的决策图。决策图可大致分为左右两个部分,左半部分对象较集中分布较密,右半部分较稀疏。
|
| 图 3 FPoint对象集决策图 Fig. 3 Decision graph of FPoint collection |
密度峰值搜索本质上就是从对象集中筛选出ρi和δi都很大的对象。现有的部分研究[18, 22-23]采用人为观察的方式从决策图上确定ρi和δi阈值来筛选出密度峰值点,选择标准很大程度上会受到使用者主观因素的影响,容易将干扰对象误判为峰值点。另一部分学者[24-27]则通过定义一个新的量值γi=ρi*δi,尝试分析γ值的异常变化特征来自动提取出密度峰值。但是,γ值异常部分与正常部分的分界ε难以自动确定,如图 4所示。因此对于FPoint对象集,必须从ρi和δ本身的概率分布特征出发寻找各自潜在的规律,确定各自的阈值ρ0和δ0来实现密度峰值的准确提取。

|
| 图 4 γ值散点图及异常分界ε位置 Fig. 4 Scatter diagram of γ values and its ε position |
根据式 (4) 中对局部密度的定义,FPoint对象的局部密度ρi由ρd和df两个部分共同决定,只有ρd和df都较大时,FPoint对象才能拥有较高的局部密度。在FPoint对象集决策图中,核心点必然位于决策图的右半部分,即密度较高但数量较为有限的区域。为了提取密度峰值应当首先求解ρ0,确定疏密两部分的交界。
2.2.2.1 ρ0的确定对FPoint对象的局部密度特征进行量化处理。以标准正态函数为核对局部密度值进行核密度估计,核密度曲线如图 5所示。曲线以ρb处为界分成左右两部分,其中右侧区域拥有较大的局部密度但频率普遍很小,与决策图上所表现出的特征一致。由此得知,ρb即为ρ0,峰值点必然位于ρb右侧区域。图 5中核密度分布曲线在形态上均不符合任何已知分布,但是经观察发现,ρb所在的区域曲线形态呈现两大特征:① 总体呈下降趋势;② ρb左侧下降趋势较陡,右侧总体平缓,ρb处于陡和缓的分界点上。ρ0确定过程如下:

|
| 图 5 局部密度的核密度曲线图 Fig. 5 Kernel density diagram for local densities |
(1) 设置斜率绝对值的阈值为kt,并对核密度曲线的横纵坐标进行归一化处理;
(2) 计算核密度曲线中每个自变量处的斜率,记为ki,计算如下
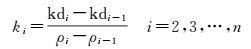 (6)
(6)
式中,ρi表示第i个FPoint对象FPi经过归一化后的局部密度,kdi表示ρi经过归一化后的核密度值。
(3) 从右向左寻找第一个绝对值接近于kt的ki,其对应的局部密度即为ρ0。
经试验发现,对文所采用的数据集,kt取0.5左右可取得较理想的结果,可根据实际效果适当调整。
2.2.2.2 δ0的确定局部密度大于ρ0且δi较大的对象即为密度峰值点,从密度大于ρ0的对象中确定δ0即可获取峰值目标,记为{FPoint}ρ。从δ值的角度,{FPoint}ρ中包含了两种类型的FPoint对象:密度簇的核心点,该类对象占{FPoint}ρ的绝大部分,其临近对象为同一簇内部的其他核心点或是密度峰值点,δ值很小;密度峰值点,根据峰值点的定义,其δ值较周围对象明显大得多,而且数量十分有限。综上,通过δ的数量特征方可从{FPoint}ρ中确定峰值点。
根据以上结论,若在{FPoint}ρ中将密度峰值点视为δ值异常对象,通过异常检查的方式可确定阈值δ0。本文中{FPoint}ρ中对象的δ值分布直方图如图 6所示。

|
| 图 6 δ值分布直方图及指数分布拟合曲线 Fig. 6 Histogram of δ values and its fitting curve |
直方图呈现出从高到低的阶梯状分布,并且在形态上可大略呈现指数分布的特征,可以采用极大似然估计的方式来获取该指数分布的参数θ,即
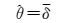 (7)
(7)
式中,δ为对象集δ值的均值。
设{FPoint}ρ中δ值小于δ0的对象为正常部分,其发生概率为pt。根据指数分布的分布函数计算出δ0,表达如下
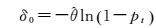 (8)
(8)
经试验发现,pt取99.5%左右可取得较理想的效果。
2.2.3 密度峰值搜索总体流程(1) 构建FPoint对象集合。对原始的签到点对象,统计每个位置上的重复频率dFreq。然后按照FPoint的数据结构以各项属性值构建Fpoint对象集合{FPoint}n,其中第i个对象记为FPi。
(2) 逐个计算{FPoint}n中两两对象之间的欧氏距离dij构造距离矩阵Dn×n。
(3) 根据dFreq属性和Dn×n采用式 (6) 计算每个FPi的局部密度ρi并赋值给该对象density属性。
(4) 根据density属性和Dn×n采用式 (3) 计算出每个FPi的δi并赋值给该对象的delta属性。
(5) 对{FPoint}n中所有对象以ρ为横轴,δ为纵轴绘决策图。根据2.2.2中的思路确定ρ0和δ0筛选出density大于ρ0且delta大于δ0的对象作为密度峰值点。
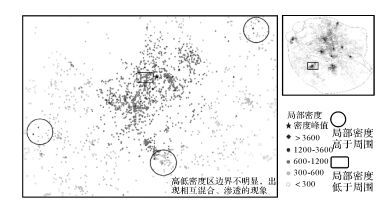
2.3 峰值点密度簇聚类算法由于位置重复频率dFreq的影响,FPoint对象的局部密度分布在地图空间中会产生如图 7效果:一部分紧靠密度峰值的对象由于dFreq值过低而使局部密度低于其周围的对象,而那些处于簇边缘甚至明显偏离簇的点对象由于dFreq值过高而使局部密度高于其周围的对象。从总体上看,对象密度区之间的密度边界不明显,出现相互混合、渗透现象。
|
| 图 7 简单分类后的不同局部密度FPoint对象的空间分布 Fig. 7 Spatial distribution for FPoints with different local density by simple classification |
这种情形下无法再使用CFSFDP中基于密度阈值的划分方法来对FPoint对象进行聚类。因此,在获取密度集群时必须考虑对象的密度连通性来保证簇的连续与边界的完整,将远离密度簇的位置离群点剔除。
针对不同局部密度FPoint对象的空间分布特征,对密度簇中的核心点、边界点等概念进行定义。
点集T:表示已提取的全部密度峰值对象构成的点集。
点集D:表示不含密度峰值点的所有FPoint对象所构成的点集。
核心点:对于数据对象p∈D,如果p的局部密度ρp大于等于密度阈值ρt,则称p为核心点。
边界点:对于数据对象p∈D,如果p的局部密度ρp小于密度阈值ρt,但p位于某个核心点或峰值点的Eps邻域内,则称p为边界点
密度直达:对于对象p和q,若p在q的Eps邻域内,且p为核心点, q也为核心点或峰值点,则称对象p是从对象q出发直接密度可达的,简称密度直达。
密度可达:对于点集D,当存在一个对象链p1、p2、p3、…、pn,其中p1=q,pn=p。对于pi∈D,如果在条件 (Eps,ρt) 下pi + 1从pi密度直达,则称对象p从对象q在条件 (Eps,ρt) 下密度可达。
密度相连:如果数据集D中存在一个对象o,使得对象p和q是从o在 (Eps,ρt) 条件下密度可达的,那么称对象p和q在 (Eps,ρt) 条件下密度相连。
簇和噪声:由某一个密度峰值点开始,由该点及其密度可达的所有对象构成一个簇。点簇的成员包括峰值点、核心点和边界点。不属于任何簇的对象称为噪声。
基于以上概念,峰值点密度簇的聚类算法流程如下:
(1) 任取点集T中的某一峰值点Pi,遍历点集D,寻找在 (Eps,ρt) 条件下所有与Pi密度直达的核心点构成初级核心点簇{C}1并从D中去除。
(2) 在点集D中,以 (Eps,ρt) 条件扩展核心簇{C}1,构成核心点簇{C}2并从D中去除。即寻找与{C}1中每个核心点密度直达、密度可达和密度相连的所有核心点连同{C}1构成Pi的最终核心点簇。
(3) 寻找Pi和核心点周围所有的边界点连同Pi构成最终的峰值点密度簇{P}i
(4) 重复 (1)~(3) 直到对T中所有峰值点找完全部密度簇为止。
3 试验分析本文试验环境为CPU 2.5 GHz、内存8 GB。对本文数据集统计位置重复频率所构建对象集记为{FPoint}。
3.1 参数选取 3.1.1 截断距离dc的选取dc为本方法中唯一需要用户给出的参数。最佳的dc应当使得所有对象在dc邻域内邻居数的均值占样本总数n的t比例, t取1%~2%[18, 26-27]。由于数据样本总量较大,这种方式实现起来比较困难。一个可行的代替方案是:计算{FPoint}中两两对象之间的距离并升序排序,以排序后的样本的第t·N个距离作为dc, N为排序后距离的总个数。经多次试验发现, t取1%时所获得的dc可实现较好的效果。本文中,{FPoint}的dc设置为421.2 m。
3.1.2 聚类参数ρt与Eps的选取为了保证每个峰值点周围都有足够的核心点,在聚类之前可以将所有的点要素按照density字段采用Jenks自然断裂点法进行分类。对聚类后的结果进行观察,如果某个类别可以保证每个峰值点周围都有足够多的该类成员,就以该类别的下界作为密度阈值ρt。在确定ρt后,对于每个峰值点pi,记pi周围局部密度大于ρt且距离pi最远的对象与峰值点之间的距离为Epsi,取Epsi中的最小值作为参数Eps。
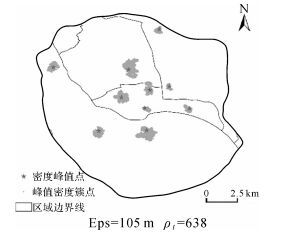
3.2 结果分析与讨论 3.2.1 密度峰值搜索与聚类结果以2.1中的思路对{FPoint}锁定阈值ρ0和δ0来提取密度峰值,然后按照3.1中的方法设置聚类参数ρt与Eps,对象集的聚类结果如图 8所示。聚类结果显示,从数据集内搜索出了10个密度峰值点,以此确定了10个峰值密度簇,簇的外形完整连续,边界清晰,可有效地表达城市热区的形态及变化特征;从图上还可以发现,由于考虑了位置重复情况,密度峰值点不一定位于簇的几何密度中心,由此所表示的居民活动中心不仅更加真实而且一定程度上反映出热区的空间集中趋势。
|
| 图 8 密度峰值点和聚类簇分布图 Fig. 8 Distribution of density peaks and clusters by our approach |
3.2.2 聚类结果的比较
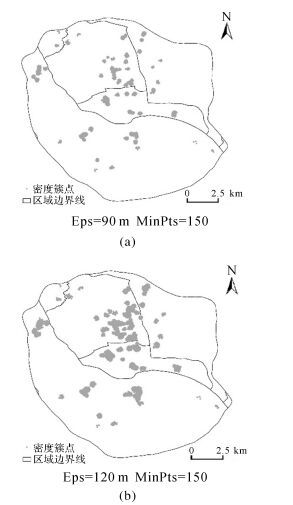
为了进一步体现本文方法在签到位置聚类中相比现有方法的有效性,分别给出了CFSFDP的密度峰值提取和聚类结果以及不同参数的DBSCAN算法和ADBSC算法的聚类结果。其中图 9为相同截断距离下的CFSFDP聚类结果;图 10为MinPts取150,Eps分别取90 m和120 m的DBSCAN聚类结果;图 11为k取5[16],ε分别取10%和25%的ADBSC聚类结果。

|
| 图 9 CFSFDP峰值点和聚类簇分布图 Fig. 9 Distribution of density peaks and clusters by CFSFDP |
|
| 图 10 不同参数下的DBSCAN聚类结果图 Fig. 10 Clusters by DBSCAN with different parameters |
对比图 8和图 9发现,CFSFDP算法所提取的密度峰值大多处于簇的几何中心。在簇形表现上,大多数的簇外形近似于球状,并且存在离群位置对象聚成一类的情况 (图 9中的A、B处)。进一步观察发现,这类离群位置上的签到重复度很高,在CFSFDP中拥有极高的局部密度,由于位置离群造成δ也相对较大,满足了密度峰值点的构成条件,但峰值点周围的签到位置过于稀疏,点位过少,很难汇聚成边界清晰外形完整的峰值密度簇,无法有效地表达活动热区。此外,CFSFDP聚类出的某些密度簇还包含了离群点 (图 9中的C处) 或游离的子簇 (图 9中的框选区域,其中D处在图 8中是一个完整的峰值密度簇)。
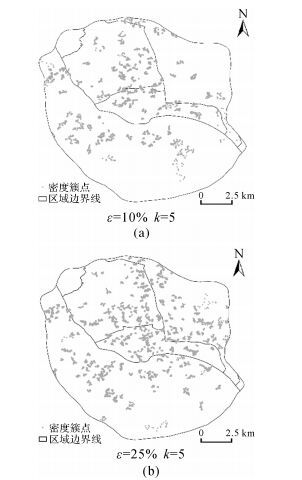
对比图 8和图 10,可看出DBSCAN算法所得密度簇的总数较多但绝大多数空间规模较小,在Eps参数较小时存在将一个完整的簇割裂的情况。结果中包含了大量由重复度较高的离群位置构成的细碎密度簇,在热区的表达上不具有代表性;ADBSC算法善于发现聚集程度不同的密度簇,但是对比图 8和图 11发现,不同参数条件下ADBSC算法所得到的密度簇空间规模都很小且不完整,显得支离破碎,且存在一些密度簇的点位数量过少的情况。
|
| 图 11 不同参数下的ADBSC聚类结果图 Fig. 11 Clusters by ADBSC with different parameters |
3.2.3 分析与讨论
聚类结果的比较表明,CFSFDP、DBSCAN以及ADBSC都存在将位置重复度较高的离群位置点集合聚成一类的情况。根本原因在于,以上方法中密度峰值点或核心点的选择标准直接由落入邻域内的目标数量来决定,没有单独考虑当前要素与目标之间的位置重复性。本文聚类法引入位置重复频率的概念,将位置重复造成的影响与自身空间位置属性分隔开来,从而可以较好地避免以上情况。通过对签到文本内容的进一步观察发现,位置离群数据中有相当大的一部分为广告类信息,这显然不足以说明该位置拥有较高的居民活动量。综合以上两点可知,在带有位置重复的签到对象的聚类上,本文方法较以上三者更为合适,在不依赖于任何模型和先验知识的前提下能够探索出相对准确、合理的居民活动特征,在基于位置签到的城市居民活动研究上更为实用。
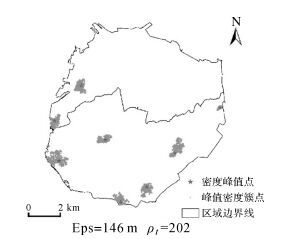
同样采用本文聚类方法,以厦门岛为例,选择相同时间段内的新浪微博签到记录共计71 811条,位置重复率67.9%,签到对象的位置分布如图 12所示,聚类结果如图 13所示。聚类结果显示,所提取的8个峰值密度簇都具有连续和完整的外形,并且不存在离群位置选为峰值的情况;密度峰值点的空间分布能较好地体现出该地区从西南向东北方向延伸并沿四周边界分布的城市空间结构。结果表明,本文的聚类方法在不同空间结构的城市区域上都能取得较为准确可靠的效果,具有良好的空间适应性。

|
| 图 12 厦门岛签到对象的位置分布图 Fig. 12 Location distribution of check-in points in Xiamen island |
|
| 图 13 厦门岛密度峰值点和聚类簇分布图 Fig. 13 Distribution of density peaks and clusters by our approach for Xiamen island |
本文聚类方法的不足之处主要体现在计算效率上。其中时间开销主要集中在ρi和δi的计算上,复杂度达到O(n2) 级别,相比于CFSFDP没有明显提升,一定程度上影响了海量签到数据的处理能力。对于这一问题,可通过对{FPoint}建立合适的空间索引来提升邻近对象的检索效率,结合云计算方案来使整体计算效率大幅提高。此外,本方法仅考虑签到记录的空间位置属性,没有利用签到文本或其他属性信息来实现指定条件约束下的聚类研究,有待进一步研究。
4 结论基于密度的聚类算法,如DBSCAN、ADBSC、CFSFDP,以点对象间的空间距离作为相似性度指标,对存在位置重复的LBSN签到数据聚类时会将位置重复度较高的离群位置对象集合聚成一类,造成聚类错误。论文以CFSFDP为基础,针对以上问题提出了签到位置数据的密度峰值快速搜索与聚类方法,并以福州市新浪微博签到数据为例进行了聚类试验和分析,为位置签到的聚类研究提供了新的方法。论文总结如下:
(1) 在CFSFDP “先找峰值后聚类”算法思想的基础上,提出位置重复频率的概念,借此对CFSFDP的局部密度重新定义,实现位置重复影响与自身空间位置属性的分离;为保证搜索到的密度峰值相比传统的观察法和γ值法更加准确,论文通过研究概率分布特征的方式来确定局部密度和δ的合理阈值;针对局部密度的空间分布特性,论文提出的聚类方法考虑对象的密度连通性,保证峰值密度簇的连续与边界的完整。
(2) 以新浪微博签到数据为例,进行了试验对比和分析,研究结果表明:论文提出的聚类方法所提取的密度峰值位置准确,簇形完整、连续,形状任意,具有较好的空间适用性;密度峰值点可以反映热区的集中趋势,因此所发现的规律相比采用DBSCAN、ADBSC更加细致、丰富。
(3) 论文所提的聚类方法能够从位置签到数据中获取更为准确、合理的城市活动热区及热区中心,且不依赖任何模型和先验知识,在基于位置签到的城市居民活动规律研究上更为实用。
对于论文聚类方法存在的不足之处,进一步的工作主要集中在两个方面:① 选择合适的空间索引来提高邻近对象的检索效率;将算法迁移到云平台来提高整体计算效率;② 在提高计算效率的前提下考虑签到文本内容的约束,实现包含指定关键词信息的签到密度峰值及聚类簇的提取。
| [1] | 张子昂, 黄震方, 靳诚, 等. 基于微博签到数据的景区旅游活动时空行为特征研究——以南京钟山风景名胜区为例[J]. 地理与地理信息科学, 2015, 31(4): 121–126. ZHANG Ziang, HUANG Zhenfang, JIN Cheng, et al. Research on Spatial-Temporal Characteristics of Scenic Tourist Activity Based on Sina Microblog: a Case Study of Nanjing Zhongshan Mountain National Park[J]. Geography and Geo-Information Science, 2015, 31(4): 121–126. |
| [2] | LIU Yu, SUI Zhengwei, KANG Chaogui, et al. Uncovering Patterns of Inter-urban Trip and Spatial Interaction from Social Media Check-in Data[J]. PLoS One, 2014, 9(1): e86026. DOI:10.1371/journal.pone.0086026 |
| [3] | LONG Xuelian, JIN Lei, JOSHI J. Exploring Trajectory-Driven Local Geographic Topics in Foursquare[C]//Proceedings of the 2012 ACM Conference on Ubiquitous Computing. New York, NY: ACM, 2012: 927-934. |
| [4] | 陆锋, 刘康, 陈洁. 大数据时代的人类移动性研究[J]. 地球信息科学学报, 2014, 16(5): 665–672. LU Feng, LIU Kang, CHEN Jie. Research on Human Mobility in Big Data Era[J]. Journal of Geo-Information Science, 2014, 16(5): 665–672. |
| [5] | 胡庆武, 王明, 李清泉. 利用位置签到数据探索城市热点与商圈[J]. 测绘学报, 2014, 43(3): 314–321. HU Qingwu, WANG Ming, LI Qingquan. Urban Hotspot and Commercial Area Exploration with Check-in Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 314–321. DOI:10.13485/j.cnki.11-2089.2014.0045 |
| [6] | 申悦, 柴彦威. 基于GPS数据的北京市郊区巨型社区居民日常活动空间[J]. 地理学报, 2013, 68(4): 506–516. SHEN Yue, CHAI Yanwei. Daily Activity Space of Suburban Mega-community Residents in Beijing Based on GPS Data[J]. Acta Geographica Sinica, 2013, 68(4): 506–516. DOI:10.11821/xb201304006 |
| [7] | 禹文豪, 艾廷华, 刘鹏程, 等. 设施POI分布热点分析的网络核密度估计方法[J]. 测绘学报, 2015, 44(12): 1378–1383. YU Wenhao, AI Tinghua, LIU Pengcheng, et al. Network Kernel Density Estimation for the Analysis of Facility POI Hotspots[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1378–1383. DOI:10.11947/j.AGCS.2015.20140538 |
| [8] | 王波, 甄峰, 张浩. 基于签到数据的城市活动时空间动态变化及区划研究[J]. 地理科学, 2015, 35(2): 151–160. WANG Bo, ZHEN Feng, ZHANG Hao. The Dynamic Changes of Urban Space-time Activity and Activity Zoning Based on Check-in Data in Sina Web[J]. Scientia Geographica Sinica, 2015, 35(2): 151–160. DOI:10.11820/dlkxjz.2015.02.004 |
| [9] | 刘启亮, 李光强, 邓敏. 一种基于局部分布的空间聚类算法[J]. 武汉大学学报 (信息科学版), 2010, 35(3): 373–377. LIU Qiliang, LI Guangqiang, DENG Min. A Local Distribution Based Spatial Clustering Algorithm[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 373–377. |
| [10] | 曾绍琴, 李光强, 廖志强. 空间聚类方法的分类[J]. 测绘科学, 2012, 37(5): 103–106. ZENG Shaoqin, LI Guangqiang, LIAO Zhiqiang. A New Category of Spatial Clustering Methods[J]. Science of Surveying and Mapping, 2012, 37(5): 103–106. |
| [11] | 柳盛, 吉根林. 空间聚类技术研究综述[J]. 南京师范大学学报 (工程技术版), 2010, 10(2): 57–62. LIU Sheng, JI Genlin. A Review of Researches on Spatial Clustering[J]. Journal of Nanjing Normal University (Engineering and Technology Edition), 2010, 10(2): 57–62. |
| [12] | NASIBOV E N, ULUTAGAY G. Robustness of Density-based Clustering Methods with Various Neighborhood Relations[J]. Fuzzy Sets and Systems, 2009, 160(24): 3601–3615. DOI:10.1016/j.fss.2009.06.012 |
| [13] | BIRANT D, KUT A. ST-DBSCAN: an Algorithm for Clustering Spatial-temporal Data[J]. Data & Knowledge Engineering, 2007, 60(1): 208–221. |
| [14] | LU Min, WANG Zuchao, LIANG Jie, et al. OD-Wheel: Visual Design to Explore OD Patterns of a Central Region[C]//Proceedings of 2015 IEEE Pacific Visualization Symposium. Hangzhou: IEEE, 2015: 87-91. |
| [15] | PAN Gang, QI Guande, WU Zhaohui, et al. Land-use Classification Using Taxi GPS Traces[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 113–123. DOI:10.1109/TITS.2012.2209201 |
| [16] | 李光强, 邓敏, 刘启亮, 等. 一种适应局部密度变化的空间聚类方法[J]. 测绘学报, 2009, 38(3): 255–263. LI Guangqiang, DENG Min, LIU Qiliang, et al. A Spatial Clustering Method Adaptive to Local Density Change[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 255–263. DOI:10.3321/j.issn:1001-1595.2009.03.011 |
| [17] | 周素红, 郝新华, 柳林. 多中心化下的城市商业中心空间吸引衰减率验证——深圳市浮动车GPS时空数据挖掘[J]. 地理学报, 2014, 69(12): 1810–1820. ZHOU Suhong, HAO Xinhua, LIU Lin. Validation of Spatial Decay Law Caused by Urban Commercial Center's Mutual Attraction in Polycentric City: Spatio-temporal Data Mining of Floating Cars' GPS Data in Shenzhen[J]. Acta Geographica Sinica, 2014, 69(12): 1810–1820. DOI:10.11821/dlxb201412007 |
| [18] | RODRIGUEZ A, LAIO A. Clustering by Fast Search and Find of Density Peaks[J]. Science, 2014, 344(6191): 1492–1496. DOI:10.1126/science.1242072 |
| [19] | 马春来, 单洪, 马涛, 等. 一种基于CFSFDP改进算法的重要地点识别方法研究[J]. 计算机应用研究, 2017, 34(1): 136–140. MA Chunlai, SHAN Hong, MA Tao, et al. Research on Important Places Identification Method Based on Improved CFSFDP Algorithm[J]. Application Research of Computers, 2017, 34(1): 136–140. |
| [20] | LIU Peiyu, LIU Yingying, HOU Xiuyan, et al. A Text Clustering Algorithm Based on Find of Density Peaks[C]//Proceedings of the 7th International Conference on Information Technology in Medicine and Education. Huangshan: IEEE, 2015: 348-352. |
| [21] | XIE Juanying, GAO Hongchao, XIE Weixin, et al. Robust Clustering by Detecting Density Peaks and Assigning Points Based on Fuzzy Weighted K-nearest Neighbors[J]. Information Sciences, 2016, 354: 19–40. DOI:10.1016/j.ins.2016.03.011 |
| [22] | DU Mingjing, DING Shifei, JIA Hongjie. Study on Density Peaks Clustering Based on k-Nearest Neighbors and Principal Component Analysis[J]. Knowledge-Based Systems, 2016, 99: 135–145. DOI:10.1016/j.knosys.2016.02.001 |
| [23] | 谢娟英, 屈亚楠. 密度峰值优化初始中心的K-medoids聚类算法[J]. 计算机科学与探索, 2016, 10(2): 230–247. XIE Juanying, QU Yanan. K-medoids Clustering Algorithms with Optimized Initial Seeds by Density Peaks[J]. Journal of Frontiers of Computer Science and Technology, 2016, 10(2): 230–247. |
| [24] | LIU Dongchang, CHENG Shifeng, YANG Yiping. Density Peaks Clustering Approach for Discovering Demand Hot Spots in City-scale Taxi Fleet Dataset[C]//Proceedings of the 18th International Conference on Intelligent Transportation Systems. Las Palmas: IEEE, 2015. |
| [25] | 马春来, 单洪, 马涛. 一种基于簇中心点自动选择策略的密度峰值聚类算法[J]. 计算机科学, 2016, 43(7): 255–258. MA Chunlai, SHAN Hong, MA Tao. Improved Density Peaks Based Clustering Algorithm with Strategy Choosing Cluster Center Automatically[J]. Computer Science, 2016, 43(7): 255–258. DOI:10.11896/j.issn.1002-137X.2016.07.046 |
| [26] | 沈忱, 祁昆仑, 刘文轩, 等. 基于FSFDP-BoV模型的遥感影像检索[J]. 地理与地理信息科学, 2016, 32(1): 55–59. SHEN Chen, QI Kunlun, LIU Wenxuan, et al. Remote Sensing Image Retrieval Research Based on FSFDP-BoV Model[J]. Geography and Geo-Information Science, 2016, 32(1): 55–59. |
| [27] | 蒋礼青, 张明新, 郑金龙, 等. 快速搜索与发现密度峰值聚类算法的优化研究[J]. 计算机应用研究, 2016, 33(11): 3251–3254. JIANG Liqing, ZHANG Mingxin, ZHENG Jinlong, et al. Optimization of Clustering by Fast Search and Find of Density Peaks[J]. Application Research of Computers, 2016, 33(11): 3251–3254. |



