2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
道路网络作为一个城市的骨架,是整个城市的“生命线”,是城市社会经济活动、交通运输赖以进行的物质载体。准确的路网信息不但是城市建设、交通规划管理、紧急事件响应等基础建设的根基,而且为人们日常出行或行程规划提供了必要的辅助。我国的城镇化进程推进了道路的建设与完善,使路网结构处于快速变化之中,导致了城市路网数据现势性相对滞后[1]。常见的路网信息提取和更新方法,或基于专业GPS设备的地表测量[2],需要专业的道路测量车辆与数据采集人员,信息获取周期长,后期提取工作量大,且维护费用昂贵;或基于高清遥感影像的图像处理[3-4],受限于图像处理技术,难以进行自动化作业,提取效率不高。近年来,伴随着移动端定位技术的日趋成熟,国内外研究者逐渐开始研究基于日常民用低成本GPS设备轨迹数据的路网信息提取方法,追踪装载GPS设备的大众交通工具可以方便快捷地收集到覆盖整个道路网络的大众出行轨迹数据,加以处理计算可以快速提取路网信息。
现有的轨迹数据路网信息提取方法大致分为基于轨迹数据的路网信息重建与基于轨迹数据的路网信息改进两类。前者直接从轨迹数据集提取整个路网的几何特征。比如文献[5]基于AI聚类技术结合“划窗”算法,将原始轨迹采样点逐个连接构成轨迹线,通过连接多条轨迹线增量绘制整个未知区域的路网结构;文献[6-7]对轨迹进行聚类提取道路中心线,并以行进路径和交叉点最终确定路网结构;文献[8]提出了基于Delaunay三角网的时空轨迹融合与路网生成方法。后者通过计算轨迹数据来改进已有地图中的道路信息,比如文献[9-11]基于初始地图与轨迹数据来改进路网中指定道路的中心线。然而,前文中提到的众多从轨迹数据中提取路网信息的方法存在一定的局限性。首先,直接从浮动车轨迹数据中提取信息重建整个路网需要处理海量轨迹数据,导致巨大的计算资源消耗,尤其是当路网中存在较大的交叉区域或者重叠区域时,计算复杂度更高。其次,目前对于已有路网信息的改进,或通过整体重建路网后进行比对确定更新,计算成本太高;或依赖人工识别后选定区域更新,无法实现自动化批量处理。
由此,本文提出了一种新的螺旋式路网数据更新方法,在“检查-分析-提取-更新”这一过程中,检查路网中潜在的问题路段,将参与计算的轨迹数据限定在问题路段所属的局部区域内,从而避免对整个轨迹数据集的计算。文章首次将轨迹地图匹配技术引入路网数据更新中,设计了基于轨迹-地图匹配的路网更新框架。结合路网数据和轨迹行为的特点,设计基于HMM模型的路网检查方法,以轨迹-路网匹配过程中的断点来发现并锁定路网中潜在问题路段的位置,并对问题路段进行分类分析。在此基础上,建立问题路段邻域,针对邻域内问题路段的不同类型,设计相应的路段信息纠正方案,并根据邻域局部范围内获取的相关轨迹数据子集,采用不同的路段信息提取方法,进而探讨了局部范围内路网更新标准,最终结合原有路网基线完成对现有路段信息的改进和更新。该方法不再直接将算法施加于海量的轨迹数据集,只针对原有路网中问题路段所属小范围邻域内的部分轨迹数据子集进行计算,减少了计算量的同时,也减轻了整个路网数据更新过程对人工干预的依赖,大大提高了效率。
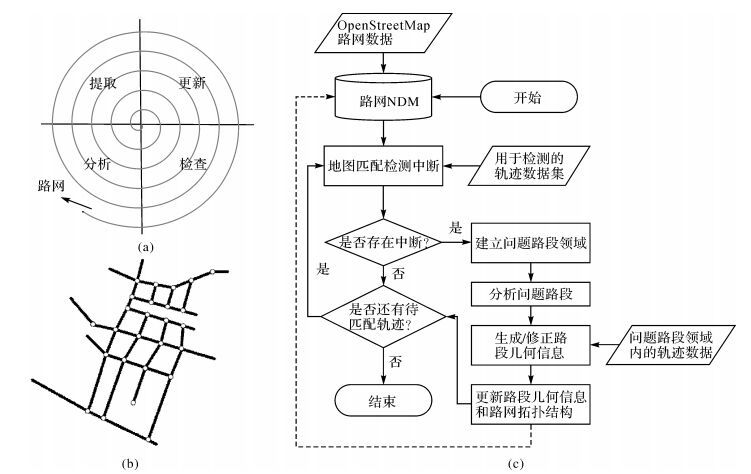
1 基于轨迹地图匹配的路网更新策略在轨迹地图匹配过程中,由于路网数据本身存在问题 (比如路段缺失) 将导致匹配发生中断,即轨迹地图匹配的中断能够直接反映路网数据中存在的问题。基于这一认识,本文设计了一种螺旋向前推进的路网更新策略,采用“检查→分析→提取→更新”过程进行螺旋式迭代 (如图 1(a)所示)。该螺旋式过程使得系统可以把问题分散到各个轨迹所经过的局部范围内,沿着螺线进行若干次迭代完成路网更新,避免将大量计算资源消耗在处理整个轨迹数据集上。螺旋式更新框架的另一个优势在于其执行上的灵活性,既可以对轨迹数据集所覆盖的路网区域进行多次螺旋式迭代检测更新,也可以指定某一条轨迹对特定路线进行检测更新。在详细介绍路网更新框架之前,首先给出相关的基本概念。
|
| 图 1 路网更新框架流程 Fig. 1 Flowchart of road network renewal |
定义1:路网,G=(N, L),是由边 (L) 和节点 (N) 两类NDM基本元素的集合组织表达的道路网络 (如图 1(b)所示)。其中,N=(ni|i=1, 2, …, K) 是路网中路段节点的集合,L=(lj|j=1, 2, …, H) 是路段在路网中所对应弧段的集合。
定义2:轨迹,T=(Pi|i=1, 2, …, M),为多个GPS采样点Pi组成的序列。其中,Pi包含移动对象在该采样点的位置和时间信息。
路网表现在二维空间上是由多个路段相互连接、交叉或者并行所组成的一个整体 (图 1(b)),轨迹数据是移动对象运动过程的空间位置采样点序列。轨迹地图匹配则是将轨迹采样点序列转换为具有空间语义信息的路段序列。当路网G中的某位置缺少路段的信息,或路段的信息有错误时,则认为该路网的这一位置存在问题路段。例如,实际路网中的路段a和b之间有连通关系 (即存在节点),如果相关路网数据中没有记录a或者b(缺少路段的信息),或者没有记录a与b之间的连通关系 (路段的信息有错误),则a(或者b) 被视为问题路段,轨迹地图匹配在a与b之间发生中断。
整个更新框架始于从OSM获取基于“节点-边”通用网络模型NDM[9](network data model) 组织的原始路网数据G,随后进入螺旋式更新过程 (如图 1(c)所示) 螺旋中每轮迭代,读入单条轨迹数据T检查地图匹配中断,如未发生中断则结束本轮操作,从轨迹数据集中读入下一条轨迹开始新一轮迭代;否则,针对各中断所在位置分别建立问题路段邻域,分析问题路段类型,进而从轨迹数据中提取路段几何信息等对路网进行更新,然后等待进入下轮迭代。如果后续未有待匹配轨迹读入,则视为整个螺旋过程结束。
2 基于轨迹-地图匹配的路网检测 2.1 基于HMM模型的地图匹配本节重点讨论基于HMM模型的轨迹-地图匹配技术的路网检查方法。轨迹-地图匹配方法大致可分为4种类型[12]:基于几何特征的地图匹配[13]、基于拓扑的地图匹配[14]、基于概率的地图匹配[15]以及基于高阶技术的地图匹配 (基于高阶技术的地图匹配,泛指那些使用更精致概念 (more refined concepts) 的地图匹配方法,例如卡尔曼滤波[16]、隐马尔科模型[17-22]等)。
本文选取一阶HMM (隐马尔科夫模型) 模拟轨迹在路网中的移动,将轨迹在路网中的移动定义为在路段两个节点之间移动的马尔科夫过程,以采样点到节点的大圆距离 (great circle distance) 为判定依据,提取与采样点最邻近的n个节点为潜在匹配候选路段节点。基于HMM的地图匹配过程中,问题路段会导致单次匹配的马尔科夫过程不连续,进而造成匹配路径中的断点,最终引发的匹配中断。
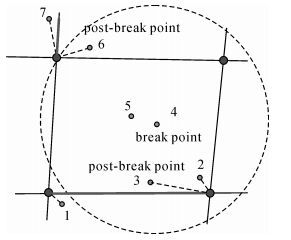
如图 2所示,沿观测值序列方向,取轨迹采样点各自最邻近的n个节点建立HMM模型进行地图匹配。整个匹配过程分别有两个断点导致中断:第一次在采样点为P4到P7,轨迹经过了一条未被路网数据记录的道路,导致P5和P6这两点到候选路段节点的观测概率极低;第二次在采样点P9到P10,轨迹路径所对应道路在路网数据中间存在拓扑错误,导致P9对应路段对其后可能路段的转移概率为0或非常小。通常这种中断会影响地图匹配输出结果的质量,因此会在匹配过程中被当成噪声或者异常值通过算法处理后选择性跳过 (这些也是造成地图匹配结果误差的原因),然而本文则反向关注到了匹配中断与问题路段的相关性,即这些匹配中断的背后所反映出来的问题很大程度上就是路网数据的问题。由此,本文接下来将利用这一点,以匹配过程中断来定位路网中问题路段所在的位置。

|
| 图 2 基于HMM地图匹配的中断 Fig. 2 Breaks of map-matching based on HMM |
2.2 问题路段分析与检查
基于HMM的地图匹配过程使得对路网数据的检查变成了可能,本节将对可能探测到的问题路段进行分析,以便在后续处理中能针对不同特点的问题路段采用相应的处理方法。结合路网数据自身特点,可将问题路段划分为两大类:
2.2.1 路段信息错误通过大众采集数据在线协同绘制的路网数据 (如本文中所使用的OpenStreeMap数据) 往往会因为上传用户采集数据的质量而造成种种问题,常见的是路段间的拓扑错误,即本应相互连接的路段没有闭合等。
2.2.2 路段信息缺失新道路信息的采集相对于城市建设的滞后往往会造成路网数据中道路或部分路段的缺失。例如,移动对象经过了一条新建的路段或者城市中某一区块 (如小区或者公园),而现有路网数据没有及时更新该路段的信息。
给定一条轨迹T与路网G,当且仅当轨迹T上单个或者连续多个采样点位置与路网匹配过程的中断满足以下任一条件时,则称该中断所在位置存在问题路段:
(1) 轨迹采样点到所有道路的观测概率都非常小或为0(即采样点到最近路段的距离远大于某一距离阈值)。
(2) 轨迹上连续两个采样点对应的匹配路段间转移概率都非常小或为0。
(3) 轨迹上连续采样的所匹配路段距离与采样间隔时间的比值 (即轨迹匹配后的平均移动速度) 超过路段本身实际速度限制 (或预设的某一速度阈值)。
如果问题路段邻近区域内轨迹采样点与路网信息同时满足以下条件时,判定为路段信息错误 (其余判定为路段信息缺失):
(1) 最大观测概率的节点之间状态转移概率非常小。
(2) 最大观测概率的节点间的大圆距离远小于其路径距离。
(3) 观测点间的实际均速度远低于完成对应节点间转移所需要的平均速度。
基于以上概念,本文设计的问题路段检测算法,关键步骤如图 3所示。从轨迹起点开始检查初始概率 (initial probability),如果满足阈值设定的条件则继续向后检查;否则将其标记为中断点,然后以下一采样点为起点,重新计算初始概率,继续检查过程。如果检查未到轨迹终点,发生上述任意一种情况都会视为当前匹配检查的一个中断,即主动终止对当前采样点位置的检查,以下一个采样点为起点,开始新一轮检查。需要注意的是,轨迹本身存在较大噪声时也可能造成匹配中断,因此需要预先对轨迹数据本身进行筛选去噪。

|
| 图 3 问题路段检查算法 Fig. 3 The algorithm of find breaks |
3 基于轨迹数据的局部-地图匹配的路网检测
本节首先基于问题路段建立路段邻域,进而判定问题路段类型,然后依据所发现问题路段的类型特点有针对性地设计处理方法,最终完成对路网信息的更新。针对路段信息错误,依据邻域内轨迹数据与非问题路段进行修正;针对路段信息缺失,依据问题路段邻域内轨迹数据分布情况的不同,文中采用PAM聚类的道路特征点提取或基于缓冲区的道路骨架线提取两种方法从GPS轨迹数据中提取路段几何信息。
3.1 问题路段分析处理如图 4所示,本文设定以发生匹配中断的轨迹采样点 (称之为分裂点,break point) 为中心,以其沿轨迹上前后两个最邻近的有效匹配采样点 (pre-break point与post-break point) 之间的最大距离为半径建立的圆形区域,设为问题路段邻域。
|
| 图 4 问题路段邻域 Fig. 4 The neighborhood of a condemned road segment |
依照先易后难的原则,优先对路段信息错误进行处理,检查问题路段邻域内原有路段之间的连通关系,判定break point前后有效匹配的采样点所对应的最大观测概率节点间的最短距离,拉伸合并已有路段使之符合最短距离,最后更新交叠信息。针对路段信息缺失,设计从问题路段邻域内的多条子轨迹中提取缺失路段的几何信息进行修补,从而避免单条轨迹稀疏可能导致的信息丢失。显然,道路提取的方法受制于轨迹数据本身的采样情况,根据问题路段邻域内轨迹数据分布情况的不同分别采用相应的提取方法。从数据库中提取落入问题路段邻域内的子轨迹数据,以之前用于路网检查的轨迹采样点为中心,以平均道路宽度为半径,计算其周边范围内所包含的轨迹点数量,即子轨迹采样点密度。如果采样点密度不满足密度阈值minPts,则采取缓冲区骨架提取方法,否则默认使用PAM聚类方法。前者更适合处理多条内子轨迹路径为网状结构 (即问题邻域内与之前用于检查的轨迹路径相似的子轨迹较少);后者处理多条内子轨迹路径单一的情况时 (即问题邻域内其他子轨迹与之前用于检查的轨迹路径相似),效果比较理想。
3.2 基于PAM聚类的路段信息提取基于聚类的道路信息提取是通过聚类方法将沿道路分布的轨迹采样点按一定的约束条件聚合成具有相似行为的簇,提取代表各个簇的聚类点作为反映道路几何特征的关键点拟合道路中心线。在研究了已有的众多聚类方法之后,笔者认为PAM (partitioning around medoids,k-medoids) 聚类方法比较适用于局部范围内的少量轨迹数据的道路提取计算。PAM聚类是对k-means算法的改进,它先对n个对象给出k个类簇划分,然后通过反复计算类簇内除中心点之外的各点到其他所有点的聚类最小值来找出更合适的中心点,对于较小的数据集非常有效。该方法不再使用k-means的几何中心点,转而在簇内的真实采样点中寻找中心点,最小化了簇内所有采样点之间的差值,从而能较好地排除异常值对于分簇结构的影响[24],即对于轨迹采样点的噪声和异常值不敏感。结合这些特点,本文选定欧式距离判定聚类参数,对问题路段邻域范围内的轨迹数据进行PAM聚类,提取问题路段信息。
基于轨迹点PAM聚类的局部道路信息提取具体分为以下3个步骤:
(1) 确定参与PAM聚类的轨迹点数n,计算聚类点的轮廓 (silhouette)[22]确定合适的聚类数k。
(2) 以任意k个轨迹点为中心开始,与其他n-k个轨迹点进行迭代计算,判定参加聚类行为的边界,以及替换中心点。
(3) 遍历所有聚类点,基于相邻间聚类点的转向角θ与距离D,设定阈值转角与距离阈值筛选结果,提取道路中心线。
3.3 基于缓冲区骨架的路段信息提取基于轨迹线缓冲区提取骨架的方法通过融合问题路段邻域内多条轨迹数据的轨迹线所生成缓冲区,从中提取融合后的缓冲区的骨架线作为道路中心线。缓冲区的骨架线与缓冲区多边形面本身保持一致的连通性和拓扑结构,可以在一定程度上反映道路的几何特征[25]。目前已有多种多边形的骨架线的提取方法较为成熟,考虑到轨迹数据的特点,以及算法本身的执行效率,本文选取简单易行的水平 (或垂直) 切割线中点来提取轨迹缓冲区的骨架线,依据轨迹缓冲区的形状可以大致确定切割线方向,在此基础上求取每条切割线与缓冲区边界的交点,最后计算每组交点的中心点,将其连接形成该缓冲区的骨架线。
局部道路骨架提取方法具体分为以下3个步骤:
(1) 将轨迹采样点数据分别依照各自的时间顺序连接形成多条轨迹线。
(2) 设置缓冲区半径,为每条轨迹线建立缓冲区,将生成的多个缓冲区融合成一个缓冲区。
(3) 判别缓冲区水平和垂直方向的投影,以较短的投影方向作为切割线方向,等间距切割缓冲区,提取中点连接线作为道路中心线。
3.4 局部路网数据更新前面已经从轨迹数据中提取了路网中缺失道路的几何信息,需要将新生成的路段数据添加到原路网中,并对原有路网中相应区域的道路信息的拓扑关系进行更新。两步操作处理路段信息错误和路段缺失的相关数据更新:① 处理不闭合路段信息;② 更新交叠信息。
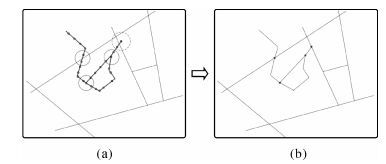
3.4.1 更新交叠信息检测新增路段与其周边领域内原有路段之间的连通关系,如果存在gap (如图 5(a)中虚线圆标出区域),则根据阈值 (本文以道路宽度或者两倍道路宽度作为阈值) 判定新增路段端点与原有路段的最短距离,将满足阈值条件的端点沿着最短距离路径拉伸至已有路段。
|
| 图 5 局部路网数据更新 Fig. 5 Renewal of local road network |
3.4.2 处理不闭合路段信息
新生成的路段数据会改变原路网数据中的拓扑关系,如图 5(b)所示,在新增路段与原有路段之间形成了新的交叠关系,需要对路网中的相关路段重新分割,生成新的路网节点与之相互连接。
4 试验示例 4.1 试验环境与真实数据本文选择64位Windows 8.1操作系统作为试验平台,以Visual Studio 2012(64位版) 为开发环境,基于ArcGIS 10.2提供的路网数据的处理基础工具,读取GPS轨迹,由地图匹配获取路段缺失位置,对缺失区域进行局部路网信息更新,并将最终结果显示在电子地图上。试验所用PC机的硬件环境为:Intel i7四核处理器、8G DDR3内存、NVIDIA Quadro 600显卡。
本文从已有的LBSN (location-based social network) 中选取OSM (open street map) 作为数据源,获取武汉市城区的路网数据,主要采用的轨迹数据包括武汉市100辆出租车轨迹辅以部分自行采集的轨迹。所用出租车轨迹数据的采样周期为30~60 s,行进过程中有效GPS卫星连接数在3~6之间。所有原始轨迹数据首先经过预处理阶段,以有效卫星、水平精度、距离、速度等阈值进行筛选。经过预处理之后,有17.3%的轨迹采样点被移除 (其中包括异常点和冗余点等)。
4.2 试验结果与分析试验选取8条轨迹数据对路网数据进行路段信息缺失检测,共发现了12处问题路段并建立对应邻域 (如图 6(b)所示),提取局部范围内的20条轨迹进行路段信息提取后生成了图 6(c)中所示的新增路段。

|
| 图 6 路网数据更新 Fig. 6 Renewal of road network |
分别依据邻域内轨迹数据的分布情况,选用基于PAM聚类方法 (聚类后轨迹提取率约为30%) 与缓冲区骨架线方法,提取反映该区域内路段几何信息的轨迹聚类点。每提取完一个问题路段邻域的道路几何信息,更新程序就增量处理一次路网数据更新,依据上文介绍的两种不同情况,在更新路网数据时,分别对生成路段端点以及交点处进行了处理。根据试验中用到的车载GPS的数据采集精度以及道路宽度,本文选定的距离阈值取武汉市除大道以外的主、次干道平均宽度2倍值,即30 m。
图 6(d)中将更新后的路网数据与遥感影像进行比对,可以发现自轨迹数据提取的新增道路结构与实际路网结构基本一致,仅在个别轨迹数据极其稀疏的路段出现较明显的偏差,仍存在有处于问题路段邻域内的路段没有被提取,这是因为试验中所收集到的轨迹数据没有覆盖这些路段。试验也从定量的角度分析计算了更新后路段与路网基线相应区域路段之间的几何完成度与拓扑完成度。
几何完成度=新生成路段中匹配路段长度/新生成路段总长度
拓扑完成度=新生成交点中匹配的个数/新生成交点总个数
本文设定新生路段的某一段与基线路段间的最大投影距离小于阈值 (本文选10 m),且方位角最大偏差在30°以内,则认定新路段中的该段与基线匹配;新生交点与路段基线交点间距离小于阈值 (本文选3 m),则认定新交点与基线匹配。12个问题路段邻域中更新后的路段相较于路网基线,平均几何完成度是78.4%,平均拓扑完成度是63.3%。平均拓扑完成度相对较低,是因为本文在处理不闭合情况时,将满足阈值条件的不闭合端点沿最短路径投影拉伸至已有路径,而实际情况下,可能该段并不是沿最短路径延伸的。后续可以通过改进不闭合的处理方法来提高拓扑完成度。其次,某些新路段内部的交点由于轨迹数据中在该邻域内运动的轨迹稀少,极个别路段上只存在1辆车的采样数据,且受周边高层建筑影响,轨迹数据质量不高,从而影响更新路段质量。
5 结论本文提出了一种基于轨迹地图匹配的路网数据更新方法。该方法以螺旋式过程推进,每次迭代通过轨迹地图匹配技术,快速探测到路网数据中存在的问题路段,进而有的放矢、有针性地建立问题路段邻域,提取轨迹数据中的路段几何信息,完成路网数据更新。更新过程以基于HMM轨迹地图匹配方法检测问题路网,以落入问题路段邻域内的轨迹数据为源,根据轨迹数据覆盖特点,分别采用PAM聚类和缓冲区骨架线两类方法,从轨迹数据中提取局部范围内的路段几何信息,进而依据路段的拓扑特征开始讨论,最终完成对原有路网数据的更新。文中提出的基于地图匹配的路网数据更新方法相对于其他已有路网数据更新应用,具有以下4个特点:
(1) 针对整个路网的更新是一个螺旋推进的迭代过程,每次的更新都建立在前一次的基础上,不断改进原有路网数据质量。
(2) 以轨迹的地图匹配过程作为探测手段,能迅速查找并锁定路网中存在的问题路段并记录其位置。
(3) 轨迹数据对于路网数据而言,所提取的路段几何信息仅在问题路段处有意义,在此基础上建立问题路段邻域,限定路段信息提取区域范围,以此最小化参与计算的轨迹数据,从而有效减少了路段提取的计算量。
(4) 在问题路段邻域的基础上,灵活选取PAM聚类和缓冲区骨架线两种不同的提取方法,增强了对于轨迹数据的实际覆盖情况的适应性。
本文研究重心在于设计并验证文中提出的螺旋式路网更新策略,并未对研究道路信息提取算法进行优化,计算结果在一定程度上受限于轨迹本身精度,但仍可作为路网研究者以及实测工作人员快速发现问题路段,进而提取道路信息的重要辅助。后续的研究工作将在此更新策略的基础上,进一步探究基于轨迹数据的道路信息提取算法,并考虑基于本文提出的方法研究个性化局部路网数据生成和更新方法。
| [1] | EKPENYONG F, PALMER-BROWN D, BRIMICOMBE A. Extracting Road Information from Recorded GPS Data Using Snap-drift Neural Network[J]. Neurocomputing, 2009, 73(1-3): 24–36. DOI:10.1016/j.neucom.2008.11.032 |
| [2] | CAO Lili, KRUMM J. From GPS Traces to a Routable Road Map[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Seattle, Washington: ACM, 2009: 3-12. |
| [3] | HU Jiuxiang, RAZDAN A, FEMIANI J C, et al. Road Network Extraction and Intersection Detection from Aerial Images by Tracking Road Footprints[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(12): 4144–4157. DOI:10.1109/TGRS.2007.906107 |
| [4] | DAL POZ A P, ZANIN R B, DO VALE G M. Automated Extraction of Road Network from Medium-and High-Resolution Images[J]. Pattern Recognition and Image Analysis, 2006, 16(2): 239–248. DOI:10.1134/S1054661806020118 |
| [5] | BRVNTRUP R, EDELKAMP S, JABBAR S, et al. Incremental Map Generation with GPS Traces[C]//Proceedings of 2005 IEEE Conference on Intelligent Transportation Systems. Vienna: IEEE, 2005: 574-579. |
| [6] | SCHROEDL S, WAGSTAFF K, ROGERS S, et al. Mining GPS Traces for Map Refinement[J]. Data Mining and Knowledge Discovery, 2004, 9(1): 59–87. DOI:10.1023/B:DAMI.0000026904.74892.89 |
| [7] | EDELKAMP S, SCHRÖDL S. Route Planning and Map Inference with Global Positioning Traces[M]//KLEIN R, SIX H W, WEGNER L. Computer Science in Perspective. Berlin Heidelberg: Springer, 2003: 128-151. |
| [8] | 唐炉亮, 刘章, 杨雪, 等. 符合认知规律的时空轨迹融合与路网生成方法[J]. 测绘学报, 2015, 44(11): 1271–1276. TANG Luliang, LIU Zhang, YANG Xue, et al. A Method of Spatio-temporal Trajectory Fusion and Road Network Generation Based on Cognitive Law[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1271–1276. DOI:10.11947/j.AGCS.2015.20140591 |
| [9] | ROGERS S, LANGLEY P, WILSON C. Mining GPS Data to Augment Road Models[C]//Proceedings of the fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego, California: ACM, 1999: 104-113. |
| [10] | GUO Tao, IWAMURA K, KOGA M. Towards High Accuracy Road Maps Generation from Massive GPS Traces Data[C]//Proceedings of 2007 IEEE International Geoscience and Remote Sensing Symposium. Barcelona: IEEE, 2007: 667-670. |
| [11] | KASEMSUPPAKORN P, KARIMI H A. A Pedestrian Network Construction Algorithm Based on Multiple GPS Traces[J]. Transportation Research Part C: Emerging Technologies, 2013, 26: 285–300. DOI:10.1016/j.trc.2012.09.007 |
| [12] | MURRAY C. Oracle Spatial and Graph Topology Data Model and Network Data Model Graph Developer's Guide, 12c Release 1 (12.1)[M]. 2013: 26-27. |
| [13] | Wikipedia. Map Matching[EB/OL]. [2015-04-21]. http://en.wikipedia.org/wiki/Map_matching. |
| [14] | JAWAD A, KERSTING K. Kernelized Map Matching for Noisy Trajectories[J]. Sig Spatial, 2010: 454–457. |
| [15] | BERNSTEIN D, KORNHAUSER A. An Introduction to Map-matching for Personal Navigation Assistants[EB/OL]. [2002-06-19]. http://www.njtude.org/reports/mapmatchintro.pdf. |
| [16] | KAPLAN E D, HEGARTY C J. Understanding GPS: Principles and Applications[M]. Boston: Artech House, 2006. |
| [17] | OCHIENG W Y, QUDDUS M A, NOLAND R B. Map-matching in Complex Urban Road Networks[J]. Brazilian Journal of Cartography, 2004, 55(2): 1–14. |
| [18] | YANG Dakai, CAI Baigen, YUAN Yifang. An Improved Map-matching Algorithm Used in Vehicle Navigation System[C]//Proceedings of 2003 IEEE Intelligent Transportation Systems. IEEE, 2003, 2: 1246-1250. |
| [19] | RAYMOND R, MORIMURA T, OSOGAMI T, et al. Map Matching with Hidden Markov Model on Sampled Road Network[C]//Proceedings of the 21st International Conference on Pattern Recognition. Tsukuba: IEEE, 2012: 2242-2245. |
| [20] | LOU Yin, ZHANG Chengyang, ZHENG Yu, et al. Map-matching for Low-sampling-rate GPS Trajectories[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Seattle, Washington: ACM, 2009: 352-361. |
| [21] | GOH C Y, DAUWELS J, MITROVIC N, et al. Online Map-matching Based on Hidden Markov Model for Real-time Traffic Sensing Applications[C]//Proceedings of the 15th International IEEE Conference on Intelligent Transportation Systems. Anchorage: IEEE, 2012: 776-781. |
| [22] | KAUFMAN L, ROUSSEEUW P J. Clustering by Means of Medoids[M]//DODGE Y. Statistical Data Analysis Based on the L1-Norm and Related Methods. Berlin Heidelberg: Springer, 1987: 405-416. |
| [23] | LI Yang, HUANG Qixing, KERBER M, et al. Large-scale Joint Map Matching of GPS Traces[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Orlando, Florida: ACM, 2013: 214-223. |
| [24] | KAUFMAN L, ROUSSEEUW P J. Finding Groups in Data: An Introduction to Cluster Analysis[M]. Hoboken: John Wiley & Sons, 1990: 68-123. |
| [25] | 杜世宏, 杜道生, 樊红, 等. 基于栅格数据提取主骨架线的新算法[J]. 武汉测绘科技大学学报, 2000, 25(5): 432–436. DU Shihong, DU Daosheng, FAN Hong, et al. A New Raster-based Algorithm for Extracting Main Skeleton Line of Polygon[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 432–436. |


