2. 中国测绘科学研究院, 北京 100830;
3. 东华理工大学测绘工程学院, 江西 南昌 330013
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. School of Geomatics, East China University of Tecnology, Nanchang 330013, China
线要素在地图要素中占比较大,用于道路、河流、等高线等重要线状地理要素的表达,因此,有关线要素的化简在制图综合领域中,一直是研究的热点,也取得了较好的结果。线要素化简算法的基本思想是在尽可能保持曲线形状特征的前提下,减其节点数量,如常用的Douglas-Peucker算法[1]、Li-Openshaw算法[2]以及改进的Li-Openshaw算法[3]和弧比弦算法[4]等。Douglas-Pecuker算法最为经典,能够对整条曲线进行压缩的同时,很好地保留曲线的特征弯曲点,但化简结果过于生硬且在特征点处容易产生尖角;Li-Openshaw算法则可以很好地光滑线要素特征弯曲点 (尖角),一定程度上克服了化简结果生硬的不足,但对所有特征弯曲点统一光滑却容易造成化简结果发生变形;改进后的Li-Openshaw算法很好地保留了曲线的局部极大值点,但由于未考虑该线要素与周边的整体空间关系,当遇到复杂密集线要素时,其处理结果会出现线相交或相接的缺陷[5]。
整体而言,现有线化简算法大多仅考虑单独线要素自身节点及其弧段特征,鲜有顾及线要素与周边邻近线要素的整体空间关系,当化简复杂线要素 (如密集等高线) 时,由于线间距离过小,难以避免化简结果出现线相交或相接的拓扑错误。有鉴于此,本文提出一种顾及空间关系约束的线化简算法,首先建立线要素全局化简方法 (LGSM),标识化简区域线要素的全局空间关系,然后,组合使用经典D-P、L-O算法对曲线进行自适应化简。
1 现有研究基础 1.1 Douglas-Peucker (D-P) 算法D-P算法出现较早,在线要素化简中影响较大。该算法的核心思想是对曲线上的点进行采样简化,即在曲线上取有限个点,将其变为折线,化简后的曲线可以在一定程度上保持原有的形状,化简效率高且不会产生多余的点。其原理如图 1(a)所示,thresholdv为设定的距离综合阈值,ABCDEFG为原折线,ACEG为化简后折线[5]。可以发现,该算法生成的化简结果保留了曲线上重要的点,对原线段进行了概括,然而该算法无法在特征点处做到光滑处理,这限制了该算法在线要素化简中的实际应用。
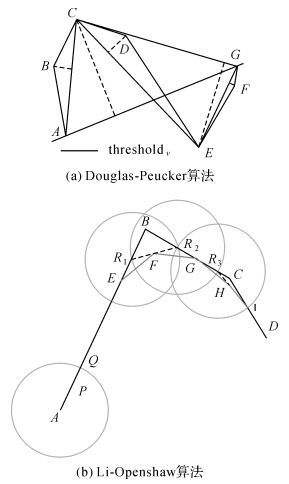
|
| 图 1 两中经典线化简算法示意图 Fig. 1 Two classic line simplification algorithms |
1.2 Li-Openshaw (L-O) 算法
Li-Openshaw算法是一种基于自然法则的自适应线状要素综合算法。该算法的核心思想是:首先,依据源比例尺和目标比例尺估算出圆形最小可视目标SVO (smallest visual object) 的尺寸R,见式 (1)
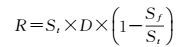 (1)
(1)
式中,St为需要化简后的目标比例尺分母;Sf为原比例尺分母;D为化简后地图上的SVO的一个参数。Muller[8]根据绘图笔的粗度和人眼分辨率推算在地图上D取0.4 mm为能保证视觉分辨的最小值。
然后,确定圆形SVO的起始位置,一般以待综合曲线的首节点作为首个圆心,如图 1(b)所示,以A点为圆心、圆形SVO的尺寸R为直径作圆,交曲线于点Q,选择AQ的中点P作为综合后的选取点,从Q点开始,重复迭代,直到曲线末端点D。
在图 1(b) 中,折线ABCD为原折线,AEFGHID为化简后折线[5],可以发现,经L-O算法化简的线要素比较光滑,局部特征处理美观,但因为算法会对局部特征点进行统一光滑概括,也导致了在对于整体形状具有支撑作用的局部特征点处会发生变形。
2 空间关系约束下的线化简算法原理与方法 2.1 空间关系约束下的线化简算法原理针对以上两种算法的不足,本文首先考虑化简区域线要素与周边邻近线要素的距离关系、整体拓扑关系,当线要素形状复杂、弯曲多而密集、数据量较大时,不仅要尽可能维持线要素形状,更要保证线要素空间关系不变,避免化简结果出现相交或相接。为此,本文设计空间关系约束条件下的线要素全局化简方法 (line global simplification method,LGSM),该方法细分为全局化简判断模型 (global simplification estimation model,GSEM) 和全局化简光滑模型 (global simplification smooth model,GSSM)。
GSEM用作标识化简区域线要素的全局空间关系
 (2)
(2)
式中,Fs指化简函数 (function simplification),SpacingL-Others指某一条线L与其他邻近线要素 (Others) 之间的间距值,SpatialRelationshipL-Others指某一条线L与其他邻近线要素之间的拓扑空间关系。
对于使用现有算法化简后,发生相交的部分多集中曲线曲度较大之处,如曲线“瓶颈”“凹槽”等部位,通常这些部分两条线间宽度间距较小。因此,为避免比例尺缩小时线化简出现拓扑变化,首先使用特征点计算这些部位的宽度间距SpacingL-Others[6-7],如果SpacingL-Others≤thresholdH(间距阈值),则标记这些部分,在化简处理时根据要素几何特征、语义优先级特征作出选取处理或跳过这些部分不作处理 (表 1);如果SpacingL-Others>thresholdH,且线要素之间符合空间拓扑约束 (图 2相接、相离),则可对这些部分进行线要素化简并记录化简前的空间关系。thresholdH是一种经验阈值,参考文献[8],考虑到屏幕分辨率或绘图笔的粗度,实际阈值的基础参考值可设为保证视觉分辨的最小值0.4 mm。
| 序号 | 情况描述 | 处理方法 | 图示 |
| 1 | 各个要素几何特征相似,优先级一致 | 选取处理:保留外侧曲线,删除中心曲线 |  |
| 2 | 各个要素几何特征相似,优先级不一致 | 选取处理:保留优先级较高曲线,删除优先级较低曲线 | |
| 3 | 各个要素几何特征不相似 | 标记这些部分,在化简时跳过这些部分不作处理,保证拓扑关系正确 |
对于符合化简条件的线要素,设计全局化简光滑模型进行光滑化简处理
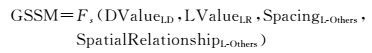 (3)
(3)
式中,Fs、SpacingL-Others、SpatialRelationshipL-Others要素指代含义与上述GSEM模型中各要素含义一致;DValueLD指应用D-P算法要事先设定的距离综合阈值 (line distance,LD),该值用来筛选过滤线要素的局部极值点,LValueLR指应用L-O算法估算出的圆形最小可视目标SVO的尺寸R。
由第2部分可知,单独应用D-P算法会使线要素化简结果不够光滑,单独应用L-O算法则会出现局部极值点缺失等情况,因此,本文尝试将Douglas-Peucker算法与Li-Openshaw算法结合应用,保留各自的算法优势并进行优化以实现曲线化简。GSSM用于对化简区域内的线要素进行光滑化简处理,每条曲线为一个处理单元,处理结束后计算线要素与其邻近要素之间的拓扑空间关系。如该线要素周围环境简单,则计算化简后的线要素与邻近线要素之间的间距是否符合后续制图表达时的间距要求,如小于间距要求,则对两线要素进行远离移位处理,如表 2所示;如线要素周围环境复杂,移位处理涉及多条线要素,则保留曲线化简前形状特征,对该部分不作处理 (如表 1序号3所示)。
| 序号 | 原始空间关系 | 化简后空间关系 | 处理方法 | 图示 |
| 1 | 相离 | 相接 | 遍历曲线上所有点,找到空间关系变化区域,对相接部分进行移位处理 | 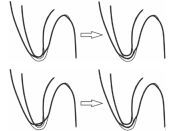 |
| 2 | 相离 | 相交 | 遍历曲线上所有点,找到空间关系变化区域,对相交部分进行移位处理 |
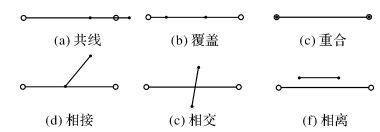
在线要素化简过程中,两条曲线之间的空间拓扑关系LL (代表任意的两条曲线) 可总结为6种[9-11],如图 2所示,具体的组合方式如下:① 共线,曲线L1与曲线L2部分重叠,图 2(a);② 覆盖,曲线L2被曲线L1覆盖,图 2(b);③ 重合,直线段L1全部位于直线段L2中,与L2完全重合图 2(c);④ 相接,L1一端点在曲线L2上,两曲线相交于此点,L1的另一端点在曲线L2的一侧,图 2(d);⑤ 相交,两曲线相交于非端点,L1的两个端点分别位于L2的两侧,图 2(e);⑥ 相离,端点都不重合,两曲线不共线,两曲线相离,图 2(f)。
|
| 图 2 两条曲线之间的空间拓扑关系 Fig. 2 Spatial topological relations between two curves |
以上定义的6种曲线之间的空间拓扑关系构成了整个线空间对象拓扑关系空间的一个覆盖,其他更加复杂的拓扑关系都可以用这6种拓扑关系的变形或复合来实现[12-14]。本文通过模型参数SpatialRelationshipL-Others来实现这些拓扑关系的运算、验证与表达。在线要素化简过程中,当两条曲线之间的空间拓扑关系为共线、覆盖、重合、相交时,不能进行化简,需进行拓扑纠正,以保证同一要素类中,线与线不能相互重叠、相交;同时,化简过程中,若相离关系因为线群密集或LValueLR值过大导致化简后线要素相接或相交,则需进行如表 2所示拓扑移位处理。
模型中,某一条线L与其他邻近线要素 (Others) 之间的间距值SpacingL-Others为L上的特征弯曲点到各个邻近线要素体之间的最短距离;D-P算法的距离综合阈值DValueLD为事先给定的经验值;L-O算法的圆形最小可视目标SVO的尺寸LValueLR值由公式 (1) 计算得到。
2.2 线要素全局化简方法 (LGSM) 计算流程线要素全局化简方法 (LGSM) 计算流程如下:
(1) 根据经验及综合前后的比例尺跨度,应用GSEM模型设立空间间距阈值并判断线要素之间的空间关系,若满足模型空间约束条件,执行步骤 (2);若不满足模型约束条件,则对不满足条件的曲线进行拓扑处理,拓扑处理属于本领域常用知识[15-16],这里不再赘述,对处理后满足条件的曲线执行步骤 (2)。
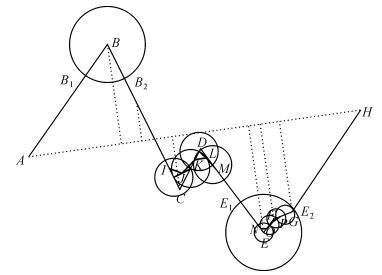
(2) 设定GSSM模型中的距离综合阈值DValueLD,采用D-P算法得到距离大于DValueLD的局部极值点集合,如图 3所示,B、E、F、G为满足条件的极值点。
|
| 图 3 线要素全局化简方法 (LGSM) Fig. 3 Line global simplification method |
(3) 应用公式 (1),按照目标比例尺和原比例尺来估算出GSSM模型中最小可视目标SVO的尺寸R。
(4) 以局部极值点为圆点,以2~3倍的R值为探测阈值,画SVO交原曲线于点B1、B2,记录B1、B2、E1、E2为处理分界点。
(5) 从首节点A开始至相邻分界点B1、分界点B2至分界点E1、分界点E2至末节点H应用L-O算法对该折线进行化简。
(6) 对于极值点稀疏处 (如图 3中极值点B处),分界点B1、B2之间不作处理,保留极值点B。
(7) 对于不包括极值点的曲线平滑部分 (如B2至C),为提高化简效率,减少节点数量,化简时不需逐点探测化简,采用如下优化算法找到该部分的“有效部分”:判断B2至C区间的距离 (L) 所包含的探测结构SVO (R为SVO的半径) 的个数n(n=1, 2, 3…),从点B2开始,对n×R距离内覆盖的平整曲线不作处理,而将 (L-n×R,L) 的部分记为该段曲线的“有效部分”,对“有效部分”使用L-O算法进行化简。
(8) 对于极值点聚集处 (如图 3中极值点E处,极值点F、G在其探测范围内),以E点为圆心,更改SVO半径 (如1/2R) 画圆对F、G极值点进行化简概括。
(9) 顺序处理,保存末节点H,单独曲线化简结束。图 3中,ABCDEFGH为原曲线,ABIJKLMNOPH为化简后曲线。
(10) 逐个线要素处理完成后,应用GSSM模型检验化简后的曲线周围的空间关系,对不满足化简间距要求的曲线进行远离移位,保证线要素之间空间关系不变,化简结束。
3 试验分析及评价 3.1 对比分析试验本文依托中国测绘科学研究院研制的NewMap软件平台WJ-III地图工作站,嵌入本文提出的线化简改进方法,以南方某城市0.007 km2范围等高线、7.43 km2范围道路与55.37 km2范围水系数据综合化简为例对本方法进行化简效果验证,同时,选取该算法与Douglas-Peucker、文献[3]中改进的Li-OpenShaw算法进行对比分析。其中,等高线数据由原始的1:5万比例尺地图综合至1:10万比例尺,对应的GSEM、GSSM模型分别为
GSEM=FS(0.4, R1d or f),
GSSM=FS(0.8, 20, 0.4, R2d or f)
式中,GSEM模型中0.4 mm为1:5万比例尺等高线数据图上间距阈值,R1d or f表示对符合图 2(d)、2(f)中的相接、相离空间拓扑关系的线要素进行化简;为突出3个算法的化简效果,GSSM模型中设定0.8 mm (0.2 mm×4) 为D-P算法图上距离综合阈值,由式 (1) 计算得到L-O算法的R值为20 m (实际距离),0.4 mm为1:10万比例尺等高线数据图上间距阈值,R2d or f为与R1d or f完全对应的空间关系,即保证化简前后线要素空间关系不发生变化。
道路和水系数据由原始1:1万地图综合取舍至1:10万比例尺,对应的GSEM、GSSM模型分别为
GSEM=FS(0.4, R1d or f),
GSSM=FS(0.8, 36, 0.4, R2d or f)
式中,GSEM模型中0.4 mm为1:1万比例尺道路和水系数据图上间距阈值,R1d or f表示对符合图 2(d)、2(f)中的相接、相离空间拓扑关系的线要素进行化简;同样为突出3种算法的化简效果,GSSM模型中设置0.8 mm (0.2 mm×4) 为D-P算法图上距离综合阈值,由式 (1) 计算得到L-O算法的R值为36 m (实际距离),0.4 mm为1:10万比例尺道路和水系数据图上间距阈值,R2d or f为与R1d or f完全对应的空间关系。
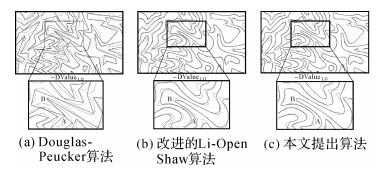
在相同的参数条件下用3种算法对等高线、道路和河流数据进行化简,图 4、图 5和图 6分别截取了部分化简结果,图中短线为D-P算法的距离综合阈值图解标识线。
|
| 图 4 等高线试验结果图 (粗线为化简后) Fig. 4 Contour simplification results (broad lines show the result after simplification) |
|
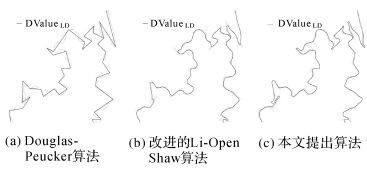
| 图 5 道路试验结果图 (粗线为化简后) Fig. 5 Road simplification results (broad lines show the result after simplification) |
|
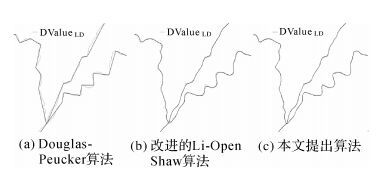
| 图 6 水系试验结果图 (粗线为化简后) Fig. 6 River simplification results (broad lines show the result after simplification) |
在处理等高线等线群密集的要素时,D-P算法化简效率最高,但是化简结果显得粗糙,线群密集时相交较多 (图 4(a)),且在处理小面积闭合等高线时,由于取长轴作为闭合等高线的首末节点连线,而短轴小于距离阈值,导致个别闭合等高线在化简时被删除,没有产生化简后的图形;改进的L-O算法在综合化简中对等高线线做到了光滑过滤,很好地保证了弯曲特征点,线线相交或相接次数减少,但局部特征点仍有缺失 (图 4(b)),化简后曲线密集处 (A-B) 仍有相交趋势,无法解决当综合前后的比例尺跨度较大时曲线的相交 (接) 问题;本文算法化简结果与原始数据贴合紧密,不仅在等高线要素化简中做到了光滑,而且精确地保留了局部极大值点,保证了曲线原有的形状特征不发生明显变化 (图 4(c)),且在曲线密集、两条线间宽度间距小于GSEM模型中的化简间距阈值时 (A-B部分),本文算法通过“标记”处理 (表 1序号3),保证了该部分曲线化简前后线线间间距、拓扑关系不变。
试验数据中,道路、水系线状要素结构平缓而稀疏,空间关系发生变化区域较少,数据化简特征与等高线效果相似,图 5(c)、图 6(c)中,改进的算法更多地保留了曲线特征拐点,与原始道路、水系形状贴合地更加一致,化简结果优于其他两种算法。
纵向对比3幅图的化简结果,当线要素平滑而稀疏时,改进的效果并不明显,而对于弯曲多且密集的线要素区域,本文提出的改进算法化简效果明显优于其他两种算法,化简后的线要素与原始数据贴合效果好,在保证了曲线压缩的基础上,最大程度地保留了曲线形状特征,且不会发生空间关系变化,因此本算法更加适用于制图综合及表达。
3.2 精度评价线要素制图综合中,算法化简对线要素几何精度的影响主要体现在曲线化简前后整体和局部的位移,因此,本文给出矢量位移、面积位移[17-19]、位移标准差和位置误差等评价指标[20-21],对本文提出的算法与Douglas-Peucker、改进的Li-OpenShaw两种算法进行位置精度比较评估。本文在矢量位移上采用线要素化简区域的平均偏移值,在面积位移上采用面积位移总和进行评价[5, 22]。
如表 3所示,本文提出的改进算法不仅在视觉感官上的效果优于其他两种算法,而且矢量平均偏移值和面积位移总和也远远小于优于其他两种算法,表明本文算法对于维持线状要素的形状特征更有优势。
| 等高线化简 | 道路化简 | 水系化简 | ||||||
| 算法 | 平均偏移值 /m |
面积位移总和 /m2 |
平均偏移值 /m |
面积位移总和 /m2 |
平均偏移值 /m |
面积位移总和 /m2 |
||
| Douglas-Peucker | 10.62 | 381.32 | 25.42 | 109 465.77 | 29.59 | 253 566.49 | ||
| 改进的Li-Openshaw | 7.56 | 235.36 | 18.61 | 12 1332.95 | 12.78 | 87 671.82 | ||
| 本文算法 | 6.34 | 139.78 | 15.92 | 79 078.67 | 12.69 | 72 709.61 | ||
位移标准差 (standardized measure of displac-ement,SMD)[20]计算方法如下
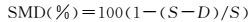 (4)
(4)
式中, S为算法化简后原始曲线上位移最大的点到曲线首末端点连线的距离;D为该点化简前后的位移值。SMD主要针对局部最大值进行评价,本文进一步采用位置误差来评价化简前后的整体位移,计算方法如下[20-21]
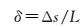 (5)
(5)
式中,Δs表示曲线化简前后相交围成的面积;L表示原始曲线的长度。
由表 4可以看出,本文算法展现出了良好的性能,在位移标准差与位置误差两方面都处于3种方法中的最优位置,尤其在位置误差指标上表现得最为优异,其值很小,表明该方法有效地维持了道路、水系数据的整体形状特征。
| 等高线化简 | 道路化简 | 水系化简 | ||||||
| 算法 | 位移标准差/(%) | 位置误差/m | 位移标准差/(%) | 位置误差/m | 位移标准差/(%) | 位置误差/m | ||
| Douglas-Peucker | 2.11 | 6.65 | 3.11 | 7.03 | 1.95 | 7.9 | ||
| 改进的Li-Openshaw | 1.47 | 1.96 | 1.93 | 3.85 | 0.91 | 2.53 | ||
| 本文算法 | 1.44 | 1.87 | 1.76 | 3.35 | 0.84 | 2.28 | ||
在线要素化简评估过程中,线要素的复杂度是评价的另一个重要指标,而节点数量是反映复杂度的一个主要指标,因此,本文统计线要素的节点数量并使用开方根模型规律[23-25]进行验证,见式 (6)
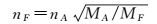 (6)
(6)
式中,nF为新编地物数量;nA为原始地物数量;MA为原始地图比例尺分母;MF为新编地图比例尺分母。
如表 5所示,在等高线、道路、水系3种地物要素中,对于节点数量化简程度最大的是D-P算法,因为其在化简过程中删除了数量最多的极值点;改进的L-O算法及本文算法因为保持线要素化简的形状特征,故化简后的节点数量相对较多,但仍符合方根模型规律,对于道路、水系等简单地物要素,化简后节点数量贴近方根模型约束节点数量,对于等高线等复杂地物,化简后节点数量远远小于模型约束数量,去复杂化程度明显。
| 算法 | 等高线化简 (节点数量) | 道路化简 (节点数量) | 水系化简 (节点数量) | ||||||||
| 原始地图 | 方根模型 约束 |
化简后地图 | 原始地图 | 方根模型 约束 |
化简后地图 | 原始地图 | 方根模型 约束 |
化简后地图 | |||
| Douglas-Peucker | 440 | 110 | 189 | ||||||||
| 改进的Li-Openshaw | 4540 | 3210 | 1560 | 2729 | 863 | 619 | 2948 | 932 | 982 | ||
| 本文算法 | 2023 | 723 | 954 | ||||||||
4 结束语
本文提出一种顾及空间关系约束及制图表达要求的线化简算法,在化简过程中以邻近空间关系符合制图要求为约束条件,以相邻线要素作为化简参考,构造线要素全局化简判断模型、线要素全局化简光滑模型实现曲线化简,并依托中国测绘科学研究院研制的WJ-III地图工作站,嵌入上述综合取舍算法。以南方某城市等高线、道路与水系数据为试验案例,进行了曲线化简,并将化简结果与D-P、改进的L-O算法进行了对比分析。试验结果表明:同已有两种经典算法相比,本文算法在线化简中顾及了线要素整体的空间关系,更好地保持了曲线的整体形状,保留了局部特征点的同时对曲线进行了光滑处理,化简结果具有更高的位置精度,更加适用于制图综合及表达。
本文目前所提线化简算法主要针对线要素空间特征、位置精度进行设计,并未考虑线要素的语义特征且并未顾及与其他点、面要素间的关系,这些都有待进一步探讨。
| [1] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. Cartographer, 1973, 10(2): 112–122. DOI:10.3138/FM57-6770-U75U-7727 |
| [2] | 李志林, OPENSHAWS. 基于客观综合自然规律的线状要素自动综合的算法[J]. 武测译文, 1994(1): 49–58. LI Zhilin, OPENSHAW S. Linear Feature's Self-adapted Generalization Algorithm Based on Impersonality Generalized Natural Law[J]. Translation of Wuhan Technical University of Surveying and Mapping, 1994(1): 49–58. |
| [3] | 朱鲲鹏, 武芳, 王辉连, 等. Li-Openshaw算法的改进与评价[J]. 测绘学报, 2007, 36(4): 450–456. ZHU Kunpeng, WU Fang, WANG Huilian, et al. Improvement and Assessment of Li-Openshaw Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 450–456. |
| [4] | 刘慧敏, 樊子德, 徐震, 等. 曲线化简的弧比弦算法改进及其评价[J]. 地理与地理信息科学, 2011, 27(1): 45–48. LIU Huimin, FAN Zide, XU Zhen, et al. An Improved Local Length Ratio Method for Curve Simplification and Its Evaluation[J]. Geography and Geo-Information Science, 2011, 27(1): 45–48. |
| [5] | 顾腾, 陈晓勇, 刘成强. 一种Douglas-Peucker与Li-Openshaw结合改进的曲线化简方法[J]. 东华理工大学学报 (自然科学版), 2016, 39(4): 396–400. GU Teng, CHEN Xiaoyong, LIU Chengqiang. A modified Line Simplification Method Combined Douglas-Peucker with Li-Openshaw[J]. Journal of East China University of Technology, 2016, 39(4): 396–400. |
| [6] | NAKOS B, MITROPOULOS V. Local Length Ratio as a Measure of Critical Points Detection for Line Simplification[C]//The Symposium of the 5th ICA Workshop on Progress in Automated Map Generalization. Paris, France: ICA, 2003: 28-30. |
| [7] | 艾廷华, 刘耀林. 保持空间分布特征的群点化简方法[J]. 测绘学报, 2002, 31(2): 175–181. AI Tinghua, LIU Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 175–181. |
| [8] | MULLER J C. Fractal and Automated Line Generalization[J]. The Cartographic Journal, 1987, 24(1): 27–34. DOI:10.1179/caj.1987.24.1.27 |
| [9] | 郭庆胜, 刘小利, 陈宇箭. 线与线之间的空间拓扑关系组合推理[J]. 武汉大学学报 (信息科学版), 2006, 31(1): 39–42. GUO Qingsheng, LIU Xiaoli, CHEN Yujian. Combinational Reasoning of Topological Spatial Relations between Two Lines[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 39–42. |
| [10] | 何建华, 刘耀林. GIS中拓扑和方向关系推理模型[J]. 测绘学报, 2004, 33(2): 156–162. HE Jianhua, LIU Yaolin. An Integrated Model for Topology & Direction Relation Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 156–162. DOI:10.3321/j.issn:1001-1595.2004.02.012 |
| [11] | 王家耀, 崔铁军, 王光霞. 图论在道路网自动选取中的应用[J]. 解放军测绘学院学报, 1985(1): 79–86. WANG Jiayao, CUI Tiejun, WANG Guangxia. Applications of Graph Theory in Automatic Selection of Road Network[J]. Journal of Geomatics Science and Technology, 1985(1): 79–86. |
| [12] | CHEN Jun, LI Chengming, LI Zhilin, et al. A Voronoi-based 9-intersection Model for Spatial Relations[J]. International Journal of Geographical Information Science, 2001, 15(3): 201–220. DOI:10.1080/13658810151072831 |
| [13] | WINTER S, FRANK A U. Topology in Raster and Vector Representation[J]. GeoInformatica, 2000, 4(1): 35–65. DOI:10.1023/A:1009828425380 |
| [14] | 邓敏, 李成名, 刘文宝. 利用拓扑和度量相结合的方法描述面目标间的空间关系[J]. 测绘学报, 2002, 31(2): 164–169. DENG Min, LI Chengming, LIU Wenbao. Describing Spatial Relations between Area Objects via Combining Topology with Metrization[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 164–169. |
| [15] | 陈述彭, 鲁学军, 周成虎. 地理信息系统导论[M]. 北京: 科学出版社, 1999. CHEN Shupeng, LU Xuejun, ZHOU Chenghu. Introduction to Geographic Information System[M]. Beijing: Science Press, 1999. |
| [16] | 王鹏波, 武芳, 翟仁健. 一种用于道路网综合的拓扑处理方法[J]. 测绘科学技术学报, 2009, 26(1): 64–68. WANG Pengbo, WU Fang, ZHAI Renjian. A Topologic Operation Method for Automated Generalization of Road Networks[J]. Journal of Geomatics Science and Technology, 2009, 26(1): 64–68. |
| [17] | WHITE E R. Assessment of Line-Generalization Algorithms Using Characteristic Points[J]. The American Cartographer, 1985, 12(1): 17–28. DOI:10.1559/152304085783914703 |
| [18] | MCMASTER R B. A Statistical Analysis of Mathematical Measures for Linear Simplification[J]. The American Cartographer, 1986, 13(2): 103–116. DOI:10.1559/152304086783900059 |
| [19] | MCMASTER R B. Automated Line Generalization[J]. Cartographica, 1987, 24(2): 74–111. DOI:10.3138/3535-7609-781G-4L20 |
| [20] | 武芳, 朱鲲鹏. 线要素化简算法几何精度评估[J]. 武汉大学学报 (信息科学版), 2008, 33(6): 600–603. WU Fang, ZHU Kunpeng. Geometric Accuracy Assessment of Linear Features' Simplification Algorithms[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6): 600–603. |
| [21] | 陈竞男, 钱海忠, 王骁, 等. 提高线要素匹配率的动态化简方法[J]. 测绘学报, 2016, 45(4): 486–493. CHEN Jingnan, QIAN Haizhong, WANG Xiao, et al. Improving the Matching Rate of Line Feature by Using Dynamic Simplification[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 486–493. DOI:10.11947/j.AGCS.2016.20150074 |
| [22] | 邓敏, 陈杰, 李志林, 等. 曲线简化中节点重要性度量方法比较及垂比弦法的改进[J]. 地理与地理信息科学, 2009, 25(1): 40–43. DENG Min, CHEN Jie, LI Zhilin, et al. An Improved Local Measure Method for the Importance of Vertices in Curve Simplification[J]. Geography and Geo-Information Science, 2009, 25(1): 40–43. |
| [23] | 何宗宜. 地图数据处理模型的原理与方法[M]. 武汉: 武汉大学出版社, 2004. HE Zongyi. Elements and Methods of Model for Cartographical Data Processing[M]. Wuhan: Wuhan University Press, 2004. |
| [24] | 张青年. 逐层分解选取指标的河系简化方法[J]. 地理研究, 2007, 26(2): 222–228. ZHANG Qingnian. Drainage Generalization by Layered Division of The Number of Retained Rivers in River Trees[J]. Geographical Research, 2007, 26(2): 222–228. |
| [25] | 邵黎霞, 何宗宜, 艾自兴, 等. 基于BP神经网络的河系自动综合研究[J]. 武汉大学学报 (信息科学版), 2004, 29(6): 555–557. SHAO Lixia, HE Zongyi, AI Zixing, et al. Automatic Generalization of River Network Based on BP Neural Network Techniques[J]. Geomatics and Information Science of Wuhan University, 2004, 29(6): 555–557. |



